CuPc/Au(1 1 0): Determination of the azimuthal alignment by a combination of angle-resolved photoemission and density functional theory

Highlights

• •Complete structural determination of a Copper-Phthalocyanice monolayer on Au(1 1 0).
• •Orbital tomography method identifies emission at 1.2 eV as the HOMO of CuPc.
• •Retain correct orbital order by using hybrid functional calculations.

Abstract

Here we report on a combined experimental and theoretical study on the structural and electronic properties of a monolayer of Copper-Phthalocyanine (CuPc) on the Au(1 1 0) surface. Low-energy electron diffraction reveals a commensurate overlayer unit cell containing one adsorbate species. The azimuthal alignment of the CuPc molecule is revealed by comparing experimental constant binding energy (k_xk_y)-maps using angle-resolved photoelectron spectroscopy with theoretical momentum maps of the free molecule's highest occupied molecular orbital (HOMO). This structural information is confirmed by total energy calculations within the framework of van-der-Waals corrected density functional theory. The electronic structure is further analyzed by computing the molecule-projected density of states, using both a semi-local and a hybrid exchange-correlation functional. In agreement with experiment, the HOMO is located about 1.2 eV below the Fermi-level, while there is no significant charge transfer into the molecule and the CuPc LUMO remains unoccupied on the Au(1 1 0) surface.

1. Introduction

The interface of organic thin films with noble metal surfaces has attracted considerable attention in the past years [1], [2], [3], [4]. On the one hand, this interest is driven by the application in organic electronic devices such as light emitting diodes, field effect transistors, or solar cells. On the other hand, the desire to understand the basic physical properties at metal–organic interfaces represents a more fundamental motivation. Here, a surface science approach combined with theoretical investigations is particularly useful when studying the adsorption of organic monolayers adsorbed on metallic surfaces. While various surface science techniques are capable of measuring the overlayer periodicities, adsorption sites, heights and orientations and are able to reveal the electronic structure of the interface, often only a combination of experiment and theory allows for creating a coherent picture of the system under study. One example are images from scanning tunneling microscopy (STM) where ab-initio electronic structure calculations are often necessary to overcome ambiguities in interpreting STM images. Another example is the interpretation of ultra-violet photoelectron spectroscopy experiments, in particular its angle-resolved variant. This will be theme of this contribution.

Angle-resolved photoelectron spectroscopy (ARPES) is the technique to study the occupied electronic band structure of solids by measuring the kinetic energy of the photoemitted electrons versus their angular distribution [5]. Particularly, many questions in nanophysics and interface engineering are often addressed by this experimental technique which, in combination with density-functional-theory calculations, leads to important physical insights. In recent years it has been shown that for highly-ordered layers of organic molecules, ARPES also provides a route to obtain information about the spatial structure of individual molecular orbitals [6], [7], [8], [9], [10]. By comparing measured ARPES data with simulations of the photoemission intensity based on density-functional theory (DFT) and approximating the final state of the photoemission process by a plane wave, molecular orbitals can be identified and molecular orientations can be determined [11], [12], [13], [14]. To date this approach, which has been termed orbital tomography [9], has allowed the orbital density reconstruction of the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) in highly-oriented monolayer films of sexiphenyl on Cu(1 1 0) [7] and pentacene and PTCDA on Ag(1 1 0) [15], respectively, and has enabled the analysis of the molecule-substrate hybridization in PTCDA and NTCDA layers on Ag(1 1 0) [9], [11], [16], [17]. It has also been used to unambiguously assign molecular emissions in coronene and hexa-benzo-coronene films on Ag(1 1 1) [13] and to analyze monolayers and bilayers of PTCDA on Ag(1 1 0) [12], [18], [19], [20]. In terms of determining molecular orientations, the orbital tomography method has led to the tilt angle of pentacene multilayer film [7] and azimuthal orientation of tetra-phenyl-porphyrine in a monolayer film on Cu(1 1 0) [14].

In this work, we focus on a monolayer film of copper-phthalocyanine (CuPc) on Au(1 1 0) surface. Phthalocyanines are among the most studied functional molecular materials due to their interesting optical and electronic properties and their potential in nonlinear optics, optical data storage, electronic sensors, xerography, solar energy conversion, nuclear chemistry, molecular magnetism, electrochromic displays and heterogeneous catalysis [21]. Their sub-monolayer to monolayer growth on various noble metal surfaces and the structural and electronic properties of the resulting interface has been studied intensively [22], [23], [24], [25], [26], [27], [28], [29], [30]. In terms of DFT calculations, both, various metal-Pc's [31] as well as the metal-free Pc [32] have been investigated on Au(1 1 1) and Au(1 1 0) surfaces, respectively, and the spin and orbital configuration of MePc chains assembled on the Au(1 1 0) have recently been investigated [33].

The goal of the present investigation is to fully characterize the CuPc/Au(1 1 0) interface of a fully developed monolayer in terms of its structural and electronic properties by means of a combined experimental and theoretical approach. In particular, the origin of the 1.2 eV binding energy peak in UPS data [25] needs to be clarified and the azimuthal alignment of the molecule to be determined. Moreover, it has been disputed whether the molecule adsorbs completely flat or exhibits a tilt angle with respect to the substrate surface [24], [28]. In terms of electronic structure, the level alignment and orbital ordering of the adsorbed CuPc is of prime interest. While the electronic structure of isolated CuPc molecule has been computed by means of high-level theoretical approaches [34], [35], it remains to be answered how issues arising from the self-interaction error of semi-local exchange-correlation functionals impact the electronic structure of such extended interfaces [36].

2. Method

2.1. Experimental details

The samples were prepared in an ultra-high vacuum chamber with a base pressure of 1 × 10⁻⁹ mbar attached to an analysis chamber for ARPES. A Au(1 1 0) single crystal was utilized applying a standard cleaning procedure of annealing and sputtering cycles. Surface cleanliness and order was checked by X-ray photoelectron spectroscopy (XPS) and low energy electron diffraction (LEED). The CuPc films were prepared by organic molecular beam epitaxy from a home made Knudsen cell with growth rates of about 0.03 monolayer per minute. The completion of the monolayer was identified by LEED by the well-known (5 × 3)-reconstruction [24], [25] and verified by XPS and ARPES. The quality of the lateral order was improved by an additional annealing step of 10 min at 280 °C. The ARPES measurement were carried out at room temperature with a monochromatized Helium discharge lamp (SPECS UVS300) using the He I_α-line at 21.22 eV. Photoelectrons were detected with a Scienta SES200 electron analyzer with an acceptance angle of ±7°. (k_x, k_y) momentum maps were derived by additional tilting the perpendicular polar angle in steps of 2° and azimuthal rotation by 10°. The intensity maps were corrected for the photoelectron emission characteristics by a cosine-function according to Lambert's law. In addition, the data was normalized to the channelplate function which was derived by measuring a polycrystalline Au-foil.

2.2. Computational details

All theoretical results presented here are obtained within the framework of density functional theory (DFT). Two types of calculations have been performed. First, orbital energies and corresponding wave functions of an isolated CuPc molecule are calculated by using either a generalized gradient approximation (GGA) in the Perdew–Burke–Ernzerhof flavor [37] for exchange and correlations effects or by employing a hybrid functional according to Heyd et al. (HSE) [38], [39]. These wave functions serve as input for the subsequent simulation of ARPES intensity maps within the one-step model of photoemission [40] and for which we approximate the final state by a plane wave [7]. Second, we have also performed calculations of an adsorbed monolayer on the Au(1 1 0) surface which we analyze in terms of molecule-projected density of states curves and charge density difference plots and for which we employ either a van-der-Waals-corrected GGA or HSE for exchange-correlation effects.

2.2.1. Simulation of ARPES maps

For the free CuPc molecule, we utilize the plane wave code ABINIT [41]. The all-electron potentials are replaced by extended norm-conserving, highly transferable Troullier-Martins pseudo potentials [42] using a plane wave cut-off of 50 Ryd. We employ a super cell approach with a box size of 50 × 50 × 22 Bohr³ and Γ point sampling of the Brillouin zone. The geometry of the free molecule is optimized by using a generalized gradient approximation (GGA) [37] for exchange-correlation effects. Due to the odd number of valence electrons in one CuPc molecule, all calculation are performed in a spin-polarized manner.

The orbitals ψ_i of the optimized molecule are utilized to evaluate the intensities of the ARPES within the so called one-step model [40].

$$I(\theta ,\varphi ;E_{\mathrm{kin}},\omega )\approx \sum _i|\langle {\psi }_f(\theta ,\varphi ;E_{\mathrm{kin}})|\text{A}·\text{p}|{\psi }_i\rangle {|}^2\times \delta (E_i+\mathrm{\Phi }+E_{\mathrm{kin}}-\hslash \omega ),$$ (1)

Here, θ and ϕ are the azimuthal and polar angle respectively, E_kin is the kinetic energy of the emitted electron and ω denotes the frequency of the incoming photon, Φ is the work function, and p and A are the momentum operator and the vector potential connected to the incoming radiation. We further approximate the final state ψ_f by a plane wave [43]. As outlined in more detail in a previous paper [7], and also noted earlier [44], [45], these approximations lead to the simple result that the PE intensity from a given initial state i is proportional to the square modulus of the Fourier transform of the initial state wave function $\tilde{\psi }(\text{k})$

$$I_i(\theta ,\varphi ;E_{\mathrm{kin}})\approx |\tilde{\psi }(\text{k}){|}^2|\text{A}·\text{k}{|}^2.$$ (2)

modulated by a weakly angle-dependent factor |A · k|² which depends on the angle between the polarization vector A of the incoming photon and the direction of the emitted electron. Note that in the simulated momentum maps shown below, we have chosen to neglect this factor, thus the simulated results only show the first factor of Eq. (2), i.e., the Fourier transform of the initial state.

2.2.2. Adsorbed monolayer calculations

Electronic structure calculations for the p(5 × 3) CuPc/Au(1 1 0) interface have been carried out within a repeated slab approach using the VASP code [46], [47]. The Au(1 1 0) substrate is modeled by 4 layers of Au with an additional vacuum layer of 10 Å. Either a GGA [37] or the hybrid functional HSE [38], [39] are used for exchange-correlation effects, and the projector augmented waves (PAW) [48] approach was used allowing for a relatively low kinetic energy cut-off of about 400 eV. We use a Monkhorst-Pack 4 × 3 × 1 grid of k-points [49], and a first-order Methfessel-Paxton smearing of 0.05 eV [50]. To avoid spurious electrical fields, a dipole layer is inserted in the vacuum region [51]. In order to circumvent issues concerning van-der-Waals interactions which are ill-described in standard GGA functionals [52], [53], we employ the empirical correction scheme according to Grimme [54] and take the Au van-der-Waals parameters from Amft et al. [55]. In the geometry optimizations, we allow for relaxations of the topmost Au-layer and all atoms in the molecule. As for the isolated molecule, also here all calculations are performed in the spin-polarized mode.

3. Results

3.1. Experimental results

Fig. 1a shows a PES spectrum of CuPc/Au(1 1 0) in a narrow energy window below the Fermi edge for three different coverages. The sub-monolayer regime is displayed as dashed line, while the completed monolayer is shown as black full line. In addition, a PES spectrum corresponding to a multilayer coverage is shown as grey line. In the sub-monolayer and monolayer regime, we observe a peak at a binding energy of 1.2 eV which is shifted to about 1.5 eV in the multilayer film in agreement with earlier observations [25]. In order to clarify the origin of this molecular emission at the monolayer coverage, we have measured the angular dependence of this emission in an energy window of 400 meV around 1.22 eV in order to obtain a full (k_x, k_y) momentum map at constant binding energy. This data is shown after symmetrization according to the two-fold symmetry of the substrate in Fig. 1b where red (purple) colors indicate high (low) photoemission intensity. In addition to features arising from molecular emissions, that can be identified as being relatively broad in k-space, there are also sharper features, for instance, around (k_x, k_y) = (1.3, 0.0) or around normal emission, which can be traced back to substrate emissions. In order to emphasize the molecular features, we have applied a fitting routine to the experimental data. The background arising from the Au(1 1 0) surface was respected by a linear function and the HOMO signal by a Gaussian peak (see Fig. 1a). This automated procedure might have a certain error in the intensity determination of a single spectrum, but this is averaged out in the images of the angular distribution of the Gaussian contribution as displayed in Fig. 1c. As will be demonstrated below, this momentum map can be utilized to unambiguously assign it to a given molecular orbital. Moreover, it also reveals the azimuthal alignment of the CuPc molecule on the surface.

Fig. 1.

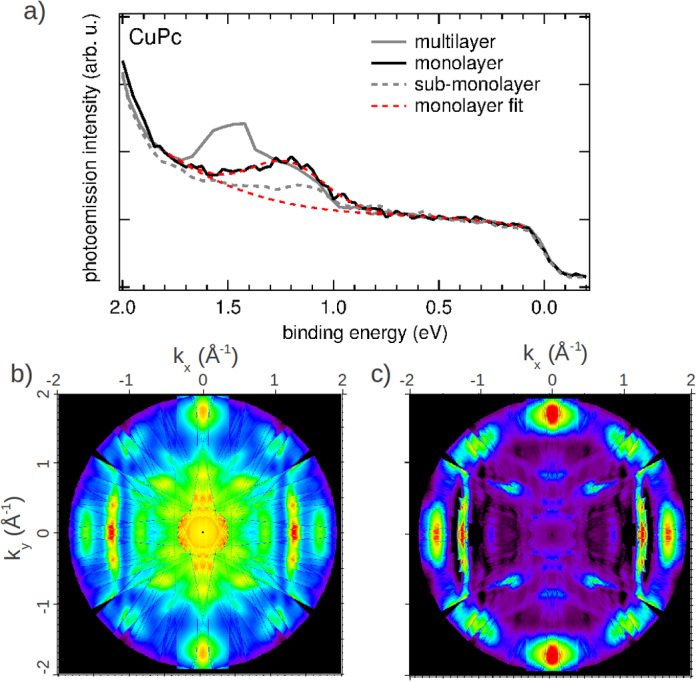
(a) Thickness-dependent PES spectra in a binding energy range between 2 eV and the Fermi edge. The dashed, black, and grey lines correspond to a sub-monolayer, monolayer, and multilayer coverage, respectively. The emission angle was 50°. The fitting procedure of the monolayer spectrum utilizing a linear background and a Gaussian peak is illustrated by the red dashed lines. (b) Experimental ARPES map of a monolayer of CuPc's recorded at the HOMO energy (400 meV integration window around 1.22 eV). (c) The experimental data of panel (b) with suppressed background. For the mathematical treatment a Gaussian was used for the CuPc HOMO and a linear function for the background from the substrate.

Before doing so, we further characterize the structure of the complete monolayer of CuPc/Au(1 1 0) by means of LEED which is shown in Fig. 2a at a beam energy of 14 eV. It reveals a commensurate structure with a rectangular 5 × 3 overlayer unit cell [24]. Using the substrate's unit cell vectors of $a_s=4.08/\sqrt{2}=2.88$ Å and b_s = 4.08 Å, experiment reveals a CuPc/Au(1 1 0) surface unit cell of a = 14.42 Å and b = 12.24 Å, thus having an area of  A= 176.5 Å².

Fig. 2.

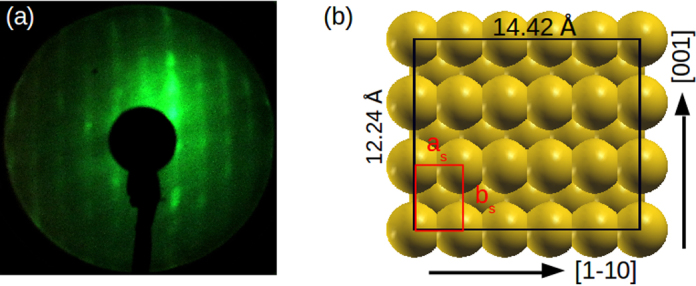
(a) Low energy electron diffraction pattern of CuPc/Au(1 1 0) as measured. (b) Surface supercell deduced from LEED. The red rectangle symbolizes the unit cell of the unreconstructed Au(1 1 0), whereas black rectangle shows the 5 × 3 unit cell of the overlayer. Here and in the following we choose the x axis along the substrate's [1 − 1 0] direction, and the y axis parallel to the [0 0 1] direction.

3.2. Isolated molecule calculations

In this section, we show how the comparison of simulated ARPES maps of various CuPc states leads to the identification of the molecular emission discussed above and at the same time also reveals the azimuthal alignment of the molecule. Fig. 3a and b shows gas phase spectra of CuPc computed within the GGA and HSE approximations for exchange-correlation effects, respectively. Note that the energy scale is with respect to the vacuum level, E_vac, and that we have introduced an artificial broadening of 0.1 eV. The gray areas display the total density of states while the blue and red lines, respectively, denote molecular states of π and σ symmetry. In the gas phase, CuPc belongs to the D_4h point group and thus its orbitals can be labeled according the irreducible representations of D_4h. In this work, we focus on the four frontier orbitals denoted as a_1u, e_g and the two spin-split states $b_{1g}^{\uparrow }$ and $b_{1g}^{\downarrow }$ whose energetic positions are indicated in Fig. 3a and b. The a_1u and e_g are anti-symmetric with respect to reflection at the molecular plane, thus are of π symmetry, while the b_1g orbitals are symmetric and thus are of σ symmetry. As can be seen from the corresponding orbital images in Fig. 3c computed within GGA, the two π orbitals are delocalized about the carbon macrocycle of the molecule, while the b_1g state is concentrated around the central Cu atom.

Fig. 3.

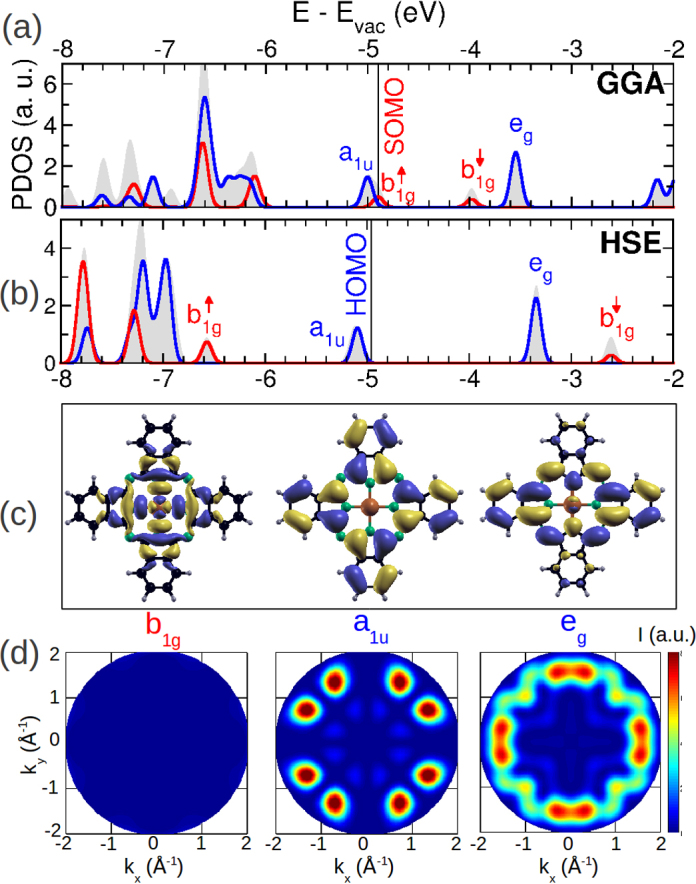
(a) and (b) Gas phase spectra of CuPc computed within GGA and HSE xc-approximations, respectively. Gray areas show the full DOS, while the red (blue) line displays the DOS projected onto σ and π states. Symmetry labels of selected states are shown, the vertical black lines indicates the Fermi level. (c) Orbital images of the b_1g, a_1u, and e_g states, while panel (d) shows the corresponding momentum maps as described in the text. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

As has been highlighted in earlier theoretical work [34], [35], [36], [56], this distinct degree of localizations gives rise to pronounced self-interaction errors which are present in approximate functionals such as the GGA. This can be clearly observed when comparing the spectra calculated within GGA and HSE in Fig. 3a and b. The most pronounced difference when incorporating a fraction of exact exchange according to the HSE prescription, is the downward (upward) shift of the $b_{1g}^{\uparrow }$ ($b_{1g}^{\downarrow }$) state. As a consequence, the two delocalized π-orbitals a_1u and e_g turn out to the HOMO and LUMO of the molecule in full accordance with a previous study [35]. As has been demonstrated [57], the improved description of the electronic structure within the hybrid functional HSE is not only due to a partial correction of the self-interaction error but also due to the changed interpretation of eigenvalues within a generalized Kohn-Sham framework [58].

Following Eq. (2), we simulate ARPES momentum maps of the three frontier molecular orbitals b_1g, a_1u, and e_g using a final kinetic energy of 15.8 eV. The results are depicted in panel (d) of Fig. 3 where the e_g map is in fact a superposition of two maps arising from the two degenerate e_g states. Note that our results closely resemble ARPES maps of the HOMO of NiPc and CoPc as obtained from the more sophisticated independent atomic center approximation including single scattering events [10] which also sheds new light on an early dispute about the validity of the plane-wave approximation for such large π-conjugated molecules [59], [60]. We also stress that our maps are computed from the GGA orbitals, but the corresponding maps of the HSE orbitals are almost indistinguishable from the former on the scale shown in the figure. While the two π-states give rise to a characteristic structure as a function of k_x and k_y, our plane-wave final state approach predicts a much smaller overall PE intensity for the b_1g state, which is hardly visible when using the same intensity range in the color map as for the other two maps. When comparing these maps with the experimental map from Fig. 1c, no resemblance can be recognized even when considering that the sharp experimental features around (k_x, k_y) = (1.3, 0.0) Å⁻¹ and (− 1.3, 0.0) Å⁻¹ originate from the sp-bands of Au. In particular, the strongest experimental features along the principal x and y directions are absent in the a_1u HOMO map, and appear split into two peaks in the e_g LUMO map. Most likely, also the $b_{1g}^{\uparrow }$ can not be the origin of the PES signature at 1.2 eV due to weak PE cross section of this σ state and its relatively large binding energy predicted from the gas phase HSE calculations.

In order to reconcile theory and experiment, we have to take into account the possibility that CuPc does not align along the high symmetry directions of the substrate but rather chooses to adsorb with a different azimuthal orientation. Taking into account the two-fold symmetry of the Au(1 1 0) substrate, this implies the existence of two mirror domains which are present in the experimental samples and the fact that the measured ARPES map of Fig. 1c is in fact a superposition of these two mirror domains [19]. When simulating various azimuthal orientations of CuPc, as characterized by the rotation angle ϕ_z of one CuPc molecule around the z-axis normal to the molecular xy-plane, and assuming equally weighted mirror domains, one obtains the images displayed in Fig. 4.

Fig. 4.

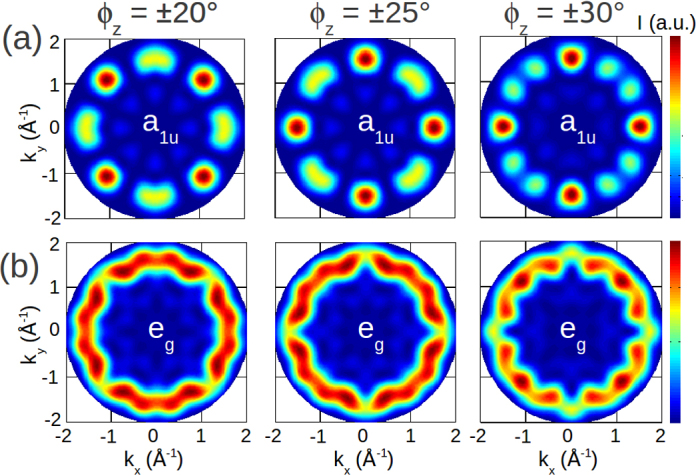
Simulated ARPES maps of the CuPc HOMO (a_1u) and LUMO (e_g) are shown in panels (a) and (b), respectively. Three azimuthal orientations of the CuPc molecule with respect to the high-symmetry substrate directions are presented, ϕ_z = ±20° (left), ϕ_z = ±25° (middle) and ϕ_z = ±30° (right).

Panel (a) of Fig. 4 shows simulated maps of the HOMO orbital (a_1u) while panel (b) shows the corresponding results for the LUMO orbital (e_g) computed for three different azimuthal orientations ϕ_z. A comparison with the experimental map in Fig. 1c shows that the best agreement is found for the HOMO map with an angle of ϕ_z = 25° (Fig. 4, top row, middle column). While it is perhaps not unexpected that the emission observed at 1.2 eV binding energy is due to the HOMO of CuPc, and not due to the LUMO which remains unoccupied owing to the comparably weak metal–molecule interactions on Au surfaces, the comparison with the simulated maps provides clear evidence for the origin of the molecular feature seen in the PES data of Fig. 1a. Moreover, the mutual agreement also allows us to determine the azimuthal orientation of the molecule. Given the rather strong dependence of the simulated maps on the angle ϕ_z, we estimate the error bars of this approach to be better than 5°.

3.3. Geometry relaxations

In order to confirm these findings, we determine the best adsorption site and orientation of a monolayer of CuPc/Au(1 1 0) in the experimental overlayer unit cell by means of total energy and force calculations within van-der-Waals corrected DFT [54], [55]. Taking into account the area of the surface unit cell, we can conclude that there is only one molecule per unit cell. We consider two adsorption sites characterized by the position of the Pc's central copper atom with respect to the substrate's gold atoms: in the first Cu is positioned directly on top of a gold atom of the topmost Au layer, while in the second, the Cu atom is placed in a hollow position between two Au-rows. As shown in Fig. 5, the orientation of the molecule is characterized by the three angles ϕ_x, ϕ_y, ϕ_z. Here, ϕ_z is the already familiar azimuthal orientation, and ϕ_x and ϕ_y describe tilts of the molecule away from a perfect planar adsorption geometry.

Fig. 5.

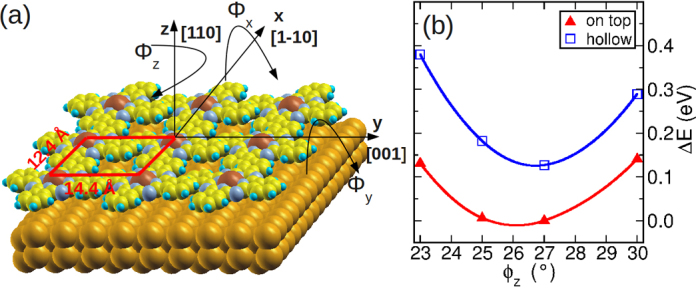
(a) Definition of the tilting angles (ϕ_x and ϕ_y) as well as the rotation angle (ϕ_z) describing the molecular orientation on the surface. (b) Total energy of the CuPc/Au(1 1 0) interface as a function of the azimuthal orientation ϕ_z for a fixed tilt of ϕ_x = 3° and ϕ_y = 9°. The red (blue) symbols are for the on-top (hollow) adsorption site of the central Cu atom. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

In a first attempt, we rigidly rotate the molecule stepwise by one of these angles and successively perform single-point total energy calculations. Here, the geometry of the molecule and the surface is kept constant and the vertical Cu-Au interatomic distance is fixed to 3 Å. As we are interested mainly in the orientations with respect to ϕ_z, Fig. 5b displays total energy differences as a function of ϕ_z, while the other two angles are kept as parameters. For geometric reasons, ϕ_x and ϕ_y must be restricted to rather small values of ≈3 −10°. Exceeding these numbers would cause parts of the molecule to approach the surface too close which would be energetically unfavorable. On the other hand, when these angles drop bellow ≈3°, i.e. perfectly flat lying molecule adjacent molecules would start to overlap with each other which would be again disadvantageous. Fig. 5b shows results for the optimal values of these angles which have been determined to ϕ_x = 3° and ϕ_y = 9°. We see that for both adsorption sites, the best azimuthal angle lies between 25° and 27°, where the on-top geometry is the energetically favored one yielding an azimuthal alignment of about ϕ_z = 26° which is in nice agreement with the value deduced from the ARPES momentum maps.

In order to refine this adsorption geometry, we fully relax the CuPc/Au(1 1 0) system only freezing in the three bottom-most Au layers. As a starting point for the relaxation, we use the azimuthal molecular alignments obtained from the mapping of the potential energy landscape described above, and we have stopped the geometry optimization when all forces fall below 0.02 eV/Å. The resulting adsorption geometry is depicted in Fig. 6. Note that the top site of the central Cu atom remains to be the energetically favorable and that the Cu atom has moved closer to the surface to a distance of 2.80 Å. In addition there appears a slight bending of the CuPc molecule, however, the azimuthal alignment as determined above from the rigid total energy calculations remains unaltered after this full geometry relaxation.

Fig. 6.

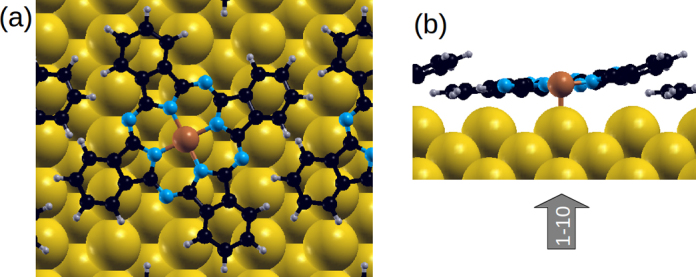
Top view (a) and side view along the (1 − 1 0) direction (b) of the relaxed CuPc/Au(1 1 0) structure.

3.4. Electronic structure

Knowing the correct adsorption site and geometry, we can analyze the electronic structure of the CuPc/Au(1 1 0) interface in more detail. Fig. 7 shows the projected density of states (PDOS) plots obtained from a GGA (panel a) and a HSE (panel b) calculation. For each type of exchange-correlation potential, the figure shows the PDOS for a free-standing layer (top) and the adsorbed monolayer (bottom). We use the same color code as in Fig. 3, thus the gray areas are the DOS projected onto the entire CuPc molecule, and the red (blue) lines indicate the PDOS of the molecular σ (π) states. The position of the Fermi level is shown as vertical black line.

Fig. 7.

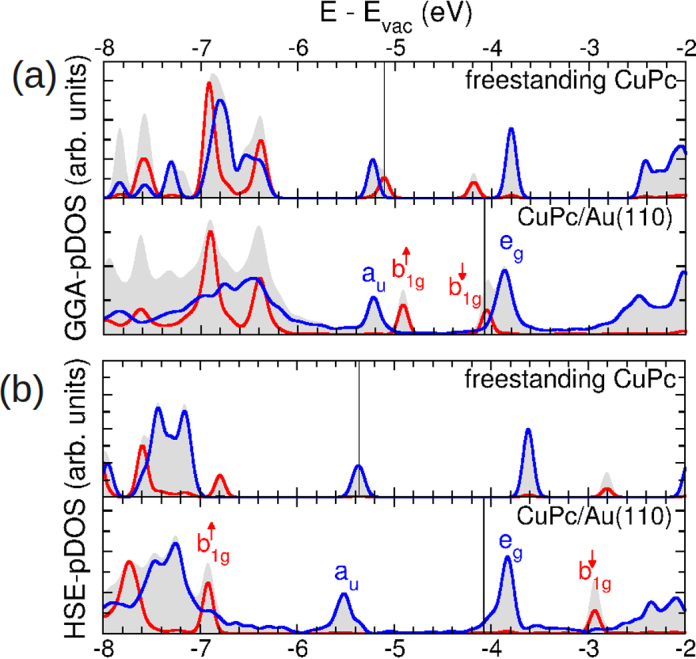
(a) and (b) Projected density of states curves for a free-standing layer of CuPc (top) and the adsorbed monolayer CuPc/Au(1 1 0) (bottom) computed within GGA (a) and HSE (b) xc-approximations, respectively. Gray areas show the DOS projected onto the CuPc molecule, while the red (blue) line displays the DOS projected onto σ and π states of CuPc. Symmetry labels of selected states are shown, the vertical black lines indicates the Fermi level. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

The electronic structure of the free-standing layer is quite similar to the one of the isolated molecule owing to the fact that intermolecular interactions are weak. We also observe that the GGA-PDOS results suffer from the same self-interaction problems which have already been discussed in the context of the isolated CuPc. Most importantly, HSE shifts the $b_{1g}^{\uparrow }$ level downward by the considerable amount of 1.7 eV leading to the fact that the HOMO (LUMO) level in the HSE calculation clearly is the a_1u (e_g) state. HSE predicts the ionization potential (electron affinity) of the free-standing layer to be 5.35 eV (3.60 eV), thus a gap of 1.75 eV.

When taking into account the interaction with the Au(1 1 0) in the full CuPc/Au(1 1 0) calculation, the molecular levels shift only moderately and appear weakly broadened with respect to the free-standing layer. While the GGA-PDOS has the already familiar problem that it underestimates (overestimates) the binding energy of the occupied (unoccupied) b_1g states, this deficiency is nicely corrected by applying the hybrid functional HSE calculations, which turn out to be quite costly for the full CuPc/Au(1 1 0) system. Similar observations have been made in a recent study of CuPc/Au(1 1 1) [61]. In the HSE result, the HOMO is at 5.5 eV below the vacuum level, thus slightly shifted downward with respect to the free-standing layer. The binding energy of the HOMO is 1.25 eV and 1.40 eV for GGA and HSE results. Thus, in contrast to the situation for b_1g, the GGA data agrees slightly better with the experimental value of 1.2 eV. As already inferred from the comparison of the experimental ARPES maps with the simulations, the CuPc LUMO remains unoccupied and is situated at an energy of 3.8 eV below the vacuum energy and thus slightly above the Fermi level.

Using Fig. 7, we can also analyze the work function of the system, for which our calculations yield a value of 4.13 eV for Au(1 1 1) surface covered by one complete monolayer of CuPc. Compared to the work function of 4.90 eV for 4 layer-thick Au(1 1 1) slab this indicates a reduction of 0.77 eV. Note that although the self-interaction errors disarrange the positions of the b_1g states in the GGA calculation, it yields the same work function as the hybrid functional calculation. These computed values can be compared to experimental data which show a work function reduction of 0.95 eV [25] with respect to a work function of 5.20 eV for the clean Au(1 1 0) surface [62]. We can understand the reduction of the work function from by analyzing the charge rearrangements leading to a bond dipole [63]. To this end, we define the charge density difference Δρ as the charge density of the full system (ρ_f) minus the sum of the charge densities of two the subsystems, i.e., the freestanding molecular layer ρ_m and the Au(1 1 0) slab (ρ_s)

$$\mathrm{\Delta }\rho (\text{r})={\rho }_f(\text{r})-({\rho }_m(\text{r})+{\rho }_s(\text{r})).$$ (3)

A real space plot of the plane-averaged charge density difference can be seen in Fig. 8. Here, red areas highlight regions of charge accumulation, while blue areas mark regions of charge depletion. We see that above the molecule charge is depleted while in the interfacial region between the molecule and the topmost Au-layer charge is accumulated followed by a series of weaker bond dipoles of decaying amplitude, but no overall significant charge transfer to the molecule takes place. When solving the one-dimensional Poisson equation for this charge density difference, i.e. integrating it twice along the z coordinate, we obtain the change in the electro-static potential induced by the adsorption of the molecule shown as black line in Fig. 8. From this analysis, we can deduce a potential jump of about 0.77 eV across the CuPc/Au(1 1 0) interface which is the reason for the reduction of the work function upon the adsorption of the CuPc monolayer. Here, 0.72 eV arise from the charge rearrangements (bond dipole) while a minor contribution (0.05 eV) comes from a molecular dipole induced by slight geometry distortions upon adsorption.

Fig. 8.

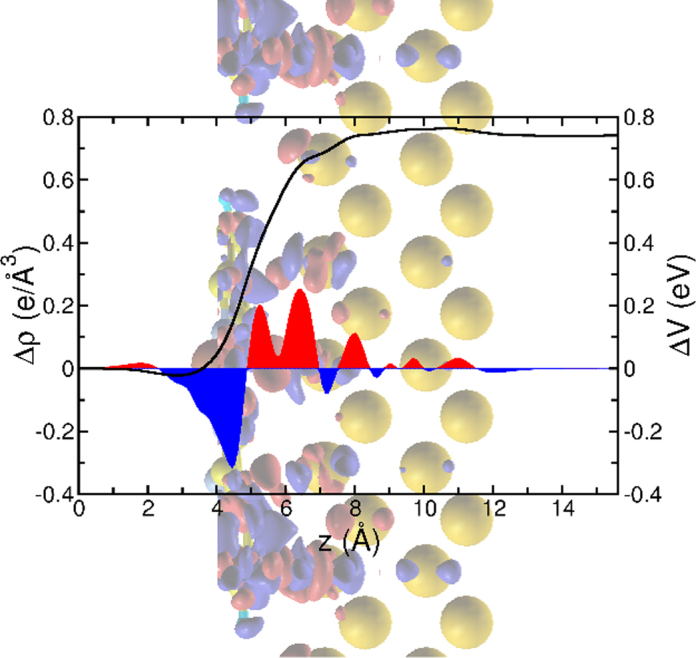
Plane-averaged charge density difference (red-blue curve, left axis) and electrostatic potential (black curve, right axis) as a function of the vertical direction z. The background graphics visualizes the adsorbed molecule on the surface projected onto the yz plane, including the 3D charge density difference plotted as iso-surface representation. Note that the scale of the graphs in z-direction are matching. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

4. Conclusions

In this combined experimental and theoretical investigation, the structural and electronic properties of the completed monolayer of Copper-Phthalocyanine on a Au(1 1 0) surface have been revealed. While our low-energy electron diffraction data confirms the (5 × 3) super structure containing one molecule per surface unit cell already reported earlier [24], [25], we apply the orbital tomography method using ARPES momentum maps to determine the azimuthal alignment of the molecule. Thereby, we unambiguously assign the molecular emission at 1.2 eV binding energy to the HOMO orbital of CuPc and the comparison with theoretical momentum maps further yields an azimuthal molecular rotation angle of 25°. This value is confirmed by total energy calculations within van-der-Waals corrected DFT which also leads to the adsorption site in which the central Cu atom is situated on top of a Au atom and to the adsorption height of 2.80 Å. We calculate the electronic structure of the CuPc/Au(1 1 0) interface, both using a generalized gradient approximation and utilizing a hybrid functional for exchange-correlation effects. The latter is shown to greatly improve the energetic positions of the Cu-localized b_1g states, while the computed work function modifications and the binding energies of the molecular π states turn out to be less sensitive to the choice of xc-functional. In summary, we disclose that the presented approach, combining momentum maps from angle-resolved photoemission spectroscopy with corresponding PE intensity simulations, demonstrated on the model interface CuPc/Au(1 1 0) has great potential for characterizing the structural and electronic properties of similar systems.