Electrostatic Interactions in the Binding Pathway of a Transient Protein Complex Studied by NMR and Isothermal Titration Calorimetry

Background: Electrostatic interactions are known accelerate binding in protein complexes with long lifetimes (minutes to hours).

Results: NMR and calorimetry were used to characterize binding kinetics in short lived (∼1 ms) protein-peptide complexes.

Conclusion: Electrostatic enhancement is much less and basal (electrostatic-free) association rates are greater than previously observed.

Significance: Electrostatics may play different roles in short lived and long lived protein complexes.

Abstract

Much of our knowledge of protein binding pathways is derived from extremely stable complexes that interact very tightly, with lifetimes of hours to days. Much less is known about weaker interactions and transient complexes because these are challenging to characterize experimentally. Nevertheless, these types of interactions are ubiquitous in living systems. The combination of NMR relaxation dispersion Carr–Purcell–Meiboom–Gill (CPMG) experiments and isothermal titration calorimetry allows the quantification of rapid binding kinetics for complexes with submillisecond lifetimes that are difficult to study using conventional techniques. We have used this approach to investigate the binding pathway of the Src homology 3 (SH3) domain from the Fyn tyrosine kinase, which forms complexes with peptide targets whose lifetimes are on the order of about a millisecond. Long range electrostatic interactions have been shown to play a critical role in the binding pathways of tightly binding complexes. The role of electrostatics in the binding pathways of transient complexes is less well understood. Similarly to previously studied tight complexes, we find that SH3 domain association rates are enhanced by long range electrostatics, whereas short range interactions are formed late in the docking process. However, the extent of electrostatic association rate enhancement is several orders of magnitudes less, whereas the electrostatic-free basal association rate is significantly greater. Thus, the SH3 domain is far less reliant on electrostatic enhancement to achieve rapid association kinetics than are previously studied systems. This suggests that there may be overall differences in the role played by electrostatics in the binding pathways of extremely stable versus transient complexes.

Introduction

Many biological processes rely on the rapid formation of protein-ligand complexes (1–5). Consequently, there has been great interest in elucidating the mechanisms through which binding partners are able to efficiently recognize each other in solution and adopt the correct conformations, relative positions, and orientations to form native stereo-specific complexes. This has been addressed theoretically (6, 7), by computer simulation (8, 9), and experimentally (1, 5, 10, 11). The association process is typically broken down into at least two steps. In the first step, the binding partners encounter each other through a random collision. For the small fraction of collisions in which the binding surfaces are correctly aligned (as few as 1 in 10⁵), the molecules proceed to the second step and dock to form the native stereo-specific complex (12). If the docking step occurs much more rapidly than the time scale of productive intermolecular collisions, the reaction is said to be “diffusion-controlled,” and the association rate is viscosity-dependent (6). When binding is diffusion-controlled, the protein and ligand pass through a free energy maximum en route to the bound state, in which translational-rotational entropy is reduced with little compensation from favorable interactions (12, 13). The ensemble of conformations at this free energy maximum has been referred to as an “encounter complex” (6), “transient complex” (14), or “transition state” (15). We shall use the term “transition state” throughout. For these systems, binding is essentially two-state, such that significant populations are observed only for the free and/or bound states, and a negligible fraction of molecules populate the high-energy transition state at any one time. Note that the two-state diffusion-controlled binding mechanism is compatible with conformational changes occurring after the transition state, provided that they proceed sufficiently rapidly (16). Additionally, transient conformational reorganization can occur prior to the intermolecular collision, leading to a “gated” diffusion-controlled binding mechanism (17). In either case, the structure of the transition state is key to understanding the binding pathway because it represents a kinetic bottleneck. Interactions that stabilize the transition state accelerate molecular association rates (6, 14, 15).

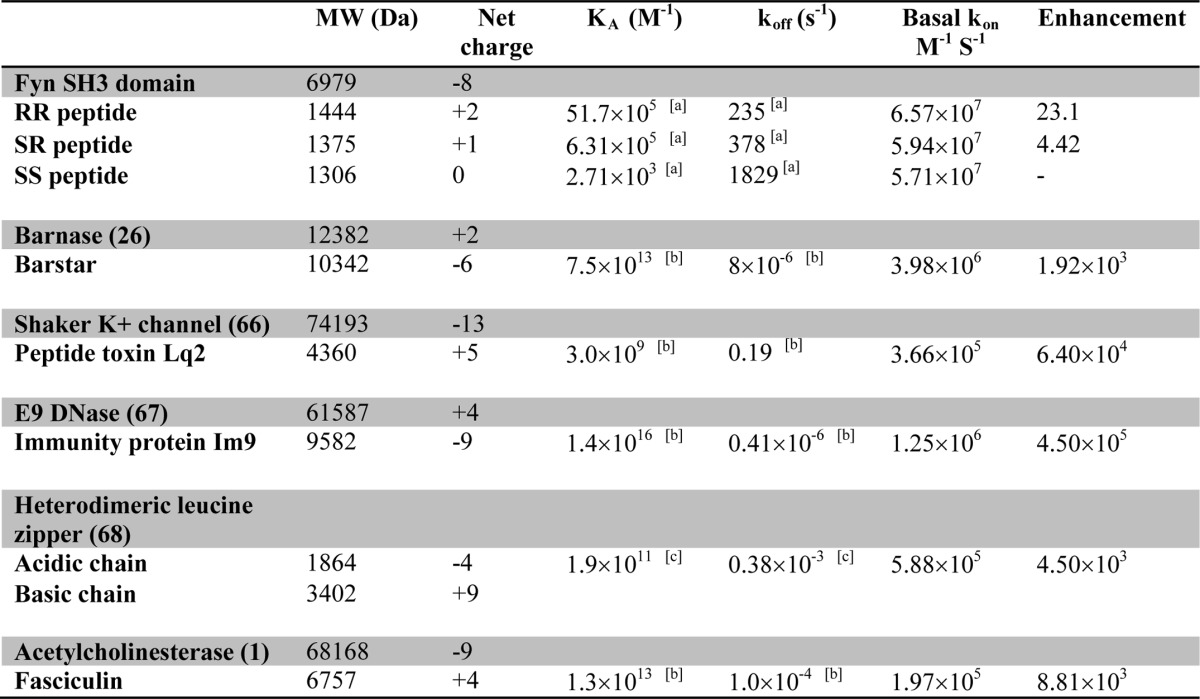
A variety of interactions have been proposed to contribute to the stability of transition states, including nonspecific hydrogen bonding, van der Waals interactions, non-polar desolvation, long range electrostatic interactions (6, 18–20), or subsets of native bound-like interactions (21). The role of electrostatics in binding pathways has been particularly well studied. For a number of systems, including barnase-barstar (5), E9-Im9 (10), IL4-IL4BP (11), and Fas-AchE (1), it has been found that electrostatic stabilization of weakly specific transition states can accelerate association by up to 4 or more orders of magnitude, compared with the basal rate (15). A combination of experimental and computational studies has led to a picture of the transition state in which the binding partners remain solvent-separated and interact almost exclusively by long range electrostatics (15, 22).

However, these investigations have focused on extremely tight protein-ligand interactions, as listed in Table 1. Equilibrium association constants have ranged from 10⁹ to 10¹³ m⁻¹ (K_D nanomolar to picomolar), with dissociation rates of 10⁻¹ to 10⁻⁶ s⁻¹ (lifetimes of seconds to days) Much less is known about the binding pathways of weaker complexes with lifetimes on the order of milliseconds. These types of short lived protein interactions are abundant in nature, raising the important question of to what extent long lived and short lived complexes follow similar binding pathways. In what follows, we will use “long lived” to refer to complexes that bind with <nm K_D and have lifetimes on the order of minutes or longer. We will use “short lived” to refer to complexes with at least micromolar K_D and lifetimes on the order of milliseconds. Several studies of short lived complexes have derived structural models of transient complexes that precede formation of the fully bound state (23–25). However, these investigations did not extract kinetic parameters or identify the interactions governing association rates, which is key to understanding binding pathways.

TABLE 1.

Electrostatic enhancement of protein association rates

^a Measurement obtained at I = 2 mm.

^b Measurement obtained at I = 25 mm.

^c Measurement obtained at I = 74 mm.

The binding kinetics of short lived complexes are challenging to measure experimentally. In typical stopped-flow binding measurements, the protein and ligand are rapidly mixed, and the extent of the reaction is monitored as a function of time using techniques including spectroscopic absorbance (21), fluorescence (10, 26, 27), enzymatic activity (1, 28, 29), and surface plasmon resonance (30, 31). These techniques are limited by the requirement that the lifetimes of the free and bound states must be severalfold longer than the time required to completely mix the protein and ligand solutions; otherwise, the reaction proceeds nearly to completion before the start of the measurement period.

The combination of nuclear magnetic resonance (NMR) spectroscopy and isothermal titration calorimetry (32) can characterize binding kinetics that are too rapid for standard stopped-flow techniques, on the order of 10⁴ s⁻¹ (33). In this approach, a substoichiometric amount of ligand is added to a protein sample whose signals are monitored by NMR spectroscopy. The resulting dynamical exchange between the free and bound states modulates the chemical shifts of nuclei in the protein on the millisecond to microsecond time scale, leading to signal broadening. The broadening is quantified by NMR relaxation dispersion experiments (34–36), which yield the dissociation rate constant, k_off. The equilibrium association constant of the interaction, K_a, is determined by ITC or NMR titration experiments. The second-order association rate constant is then given by the equation, k_on = K_a·k_off. These two parameters report on the binding pathway because K_a is related to the free energy difference between the free and bound states, whereas k_on is related to the free energy difference between the free state and the transition state.

Src homology 3 (SH3)² domains are typical of weakly binding proteins that form short lived complexes. These ∼60-amino acid modules are found in the context of larger multidomain proteins and mediate protein-protein interactions in signal transduction pathways (37, 38). The type I ligand recognized by many SH3 domains comprises a short peptide sequence, +XΦPXΦP, where P is proline, Φ is a hydrophobic amino acid, X is any amino acid, and + is a positively charged residue, typically arginine or lysine (38). The positions in the motif are numbered −3 to 3 such that the conserved + occupies site −3. Dissociation constants for SH3 domains are usually on the order of micromolar, and the lifetimes of their complexes are on the order of milliseconds (33, 39). We previously used NMR and ITC to study the binding kinetics of the SH3 domain from the Fyn tyrosine kinase. We showed that this protein binds a type I target peptide in a two-state manner with millisecond time scale kinetics and a temperature dependence of k_on that is consistent with diffusion-limited association (33). In the current study, we have focused on how positively charged residues within the SH3 binding motif and negatively charged residues in the binding site on the SH3 domain interact to influence association kinetics. Three different dodecapeptides were employed: one with a typical type I consensus motif with the conserved Arg⁻³ preceded by Ser⁻⁴ (SR, net charge +1), a second containing R⁻⁴R⁻³ (RR, net charge +2), and a third containing S⁻⁴S⁻³ (SS, net charge 0). We analyzed the contributions of the conserved Arg⁻³ and “extra” Arg⁻⁴ residues to the stabilities of the fully bound and transition states by comparing the binding affinities and association rates of the RR, SR, and SS peptides. Data were extrapolated to both zero ionic strength, where long range electrostatic interactions are maximal, and infinite ionic strength, where long range electrostatics are fully attenuated. We find that the conserved Arg⁻³ and the “extra” Arg⁻⁴ residues stabilize both the encounter and fully bound complexes via similar long range electrostatic interactions, which implies that the Fyn SH3 domain and peptide are fairly close in the transition state. Notably, Arg⁻³ additionally stabilizes the bound state via short range interactions that are not screened by adding salt. Likely candidates include a network of salt bridges and hydrogen bonds previously observed for this residue in the bound complex by NMR (40) and x-ray crystallography (Protein Data Bank entry 4EIK). These short range interactions involving Arg⁻³ are not present in the transition state and are only made after the molecules have crossed the free energy barrier, near the end of the binding pathway. Thus, the SH3-peptide transition state is fairly compact and stabilized primarily by long range electrostatic interactions, as seen for other protein-ligand systems (5, 14, 15, 22). However, there are surprising differences between the system studied here and the high-affinity long lived complexes investigated previously. We find that the electrostatic-free basal association rate for this system is significantly greater, whereas the electrostatic association rate enhancement is several orders of magnitude less. This result suggests that short lived complexes may rely less on electrostatic enhancement to achieve rapid binding than do high-affinity long lived complexes.

MATERIALS AND METHODS

Protein and Peptide Preparation

Wild-type chicken Fyn SH3 domain (residues 81–148) was expressed and purified as described previously (41). RR (Ac-WSLAR⁻⁴R⁻³P⁻²L⁻¹P⁰P¹L²P³-NH₂),SR (Ac-WSLAS⁻⁴R⁻³P⁻²L⁻¹P⁰P¹L²P³-NH₂), and SS (Ac-WSLAS⁻⁴S⁻³P⁻²L⁻¹P⁰P¹L²P³-NH₂) peptides were purchased from the Sheldon Biotechnology Centre (McGill University) and purified to homogeneity by reverse-phase HPLC. Protein and peptide samples were dialyzed against 5 mm MES, pH 6.0, at the desired NaCl concentration. For ionic strength calculations, it was assumed that the buffer contributed 2.57 mm charged ions. Most experiments were performed at 40 °C. This temperature was chosen to optimize the NMR CPMG relaxation dispersion profiles obtained with the RR and SR peptides and lies within the physiological temperature range of 40–42 °C (42).

ITC

Titrations were performed at 40 °C using a VP-ITC instrument (MicroCal LLC, Northampton, MA). Measurements were taken in triplicate for each NaCl concentration and consisted of 56 injections of 5 μl. RR peptide data were collected at 0.00, 0.01 0.03, 0.05, 0.10, 0.20, 0.30, 0.40, 0.50, 1.00, 1.50, and 2.00 m NaCl. For the SR and the SS peptide, measurements were taken at 0.00, 0.03, 0.20, and 0.30 m NaCl. Titrations were repeated for the SS peptide at 20 °C. Data were fitted using the one-set-of-independent-sites model in the Origin Software package (OriginLab, Northampton, MA) and in-house MATLAB scripts (MATLAB R2013a, The MathWorks, Natick, MA).

NMR

¹H-¹⁵N HSQC titration spectra, referenced to an internal 4,4-dimethyl-4-silapentane-1-sulfonic acid standard (43), were collected at 40 °C and 800 MHz for samples containing ∼0.3 mm protein and 16 different peptide concentrations. In the case of the SS peptide titration, chemical shift peak trajectories were fit globally according to Ref. 44,

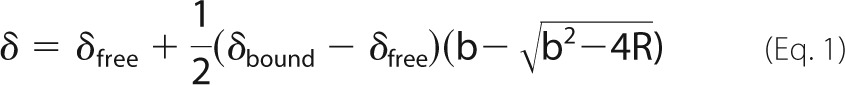where δ_free and δ_bound are the chemical shifts of the free and bound protein, R = [peptide]_total/[protein]_total, and b = 1 + R + (K_a × [protein]_total)⁻¹.

¹H-decoupled ¹⁵N CPMG experiments (36) with power compensation schemes (33) were performed at 40 °C and 500 and 800 MHz on 1 mm samples of the Fyn SH3 domain, free in solution (0 m NaCl), in the presence of 0.1 mm SS, SR, and RR peptides (0, 0.2, 0.3 m NaCl) and with saturating amounts of the RR peptide (0 m NaCl). Measurements were repeated at 20 °C for the SH3 domain alone (0 m NaCl) and in the presence of 0.1 mm SS peptide (0, 0.2, and 0.3 m NaCl). Experiments employed a constant relaxation delay, T_relax, of 40 ms and 23 values of ν_CPMG = 1/(2τ_CP) ranging from 25 to 1000 Hz, where τ_CP is the delay between consecutive pulses. Transverse relaxation rates, R₂, were calculated for each cross-peak signal at each ν_CPMG value according to the following,

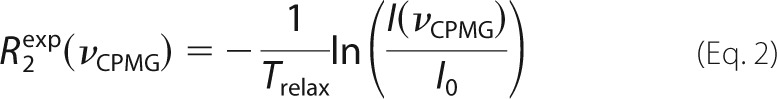where I(ν_CPMG) is the peak intensity at a given value of ν_CPMG, and I₀ is the signal intensity with T_relax = 0. The experimental uncertainties in peak intensities (σ_I) were considered to be the same for all values of ν_CPMG for a given residue at a given ionic strength and static magnetic field. CPMG experiments were repeated for a subset of ν_CPMG values (N_dup different values), with n_j replicates obtained at the jth repeated ν_CPMG value. The n_j replicates obtained at (ν_CPMG)_j for a given residue, ionic strength, and static magnetic field yield an S.D. value, s_j. The uncertainty in σ_I was calculated as follows,

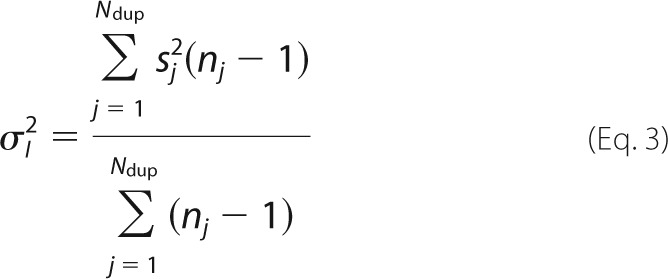and the associated errors in transverse relaxation rates, σ_R2, are given by the following.

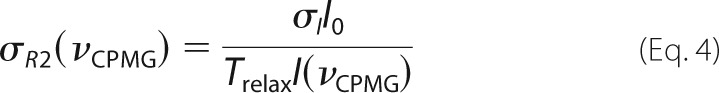CPMG data were fitted using a two-state model of conformational exchange,

where P is the protein, L is the ligand, PL is the complex, k_off is the dissociation rate constant, k_on is the association rate constant, [L] is the concentration of free peptide, and the difference between the precession frequencies of an ¹⁵N nucleus of the protein in the free and bound states is given by Δω. Dispersion profiles were fit to equations valid for the fast time scale regime (45) (Δω ≪ (k_off + k_on[L])) or all time scale regimes (46) based on the parameter α,

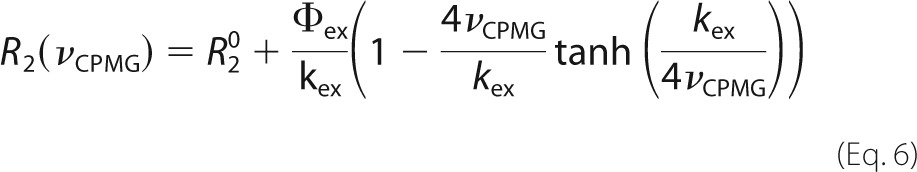where R_ex is the total exchange contribution to R₂, and B₀ is the static magnetic field (47). Profiles with α > 1.5 were considered to be in the fast exchange regime and were analyzed according to Ref. 45 as follows,

where p_free and p_bound are the relative populations of free and bound protein (p_free + p_bound = 1), k_ex = k_off + k_on[L], Φ_ex = p_freep_boundΔω², and R₂⁰ is the population-weighted average (broadening-free) transverse relaxation rate (R₂⁰ = p_freeR_2free⁰ + p_boundR_2bound⁰). All other dispersion profiles were analyzed according to Ref. 46 as follows.

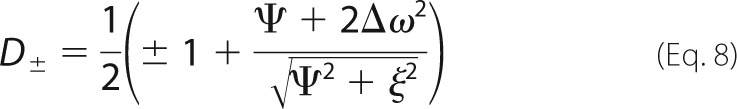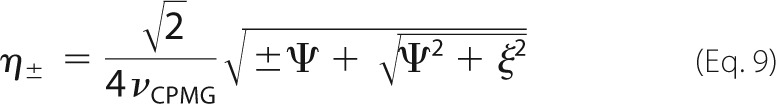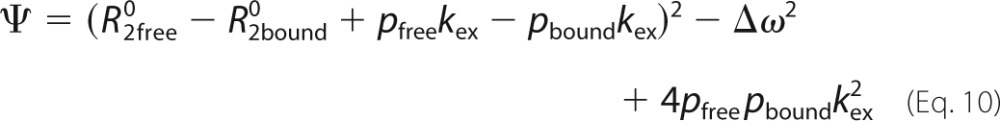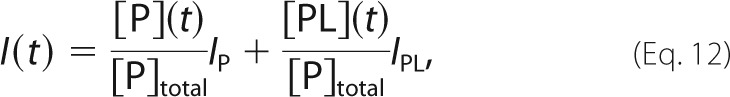We performed the analysis assuming that R_2free⁰ = R_2bound⁰. This is typically done in analyses of CPMG data because it is not possible to reliably extract separate values for R_2free⁰ and R_2bound⁰ (48). In this case, the approximation is probably valid because binding of the peptide is unlikely to substantially alter ¹⁵N transverse relaxation rates in the protein.

In the case of the RR and SR peptides at 40 °C with 0, 0.2, and 0.3 m NaCl, the data sets contained mixtures of dispersion profiles in the fast and intermediate time regimes, and data for all residues of a given sample were fitted simultaneously to extract global values of p_bound and k_ex, whereas Δω² or Φ_ex, R₂⁰(800 MHz), and R₂⁰(500 MHz) were obtained on a per-residue basis (49). For the SS peptide at 20 °C with 0 and 0.2 m NaCl, all but one of the dispersion profiles were in the fast time regime. In these cases, the value of p_bound was calculated based on the total concentrations of protein and peptide and the ITC-derived binding constants and was held fixed in the CPMG fits. Global values of k_ex were extracted, whereas Δω², R₂⁰(800 MHz), and R₂⁰(500 MHz) were obtained on a per-residue basis. Values of k_off were subsequently calculated as (1 - p_bound)k_ex. Errors in the extracted parameters were estimated using a Monte Carlo approach in which group fitting was performed on random subsets of the residues selected using a bootstrap procedure (50). Analyses were performed using scripts written in MATLAB (MALAB R2011b, The MathWorks, Natick, MA).

Electrostatic Enhancements

Log₁₀(K_a) values for the SS peptide were fitted as a linear function of ionic strength. Interpolated values were used to calculate the affinity enhancements of the SR and RR peptides. The corresponding linear interpolation was also used to calculate k_on enhancements. The ionic strength enhancements were plotted as a function of f_ion, Equation 22, setting R = 4 Å, which roughly corresponds to the size scale of a single Arg residue. The plot was not highly sensitive to the choice of R.

Stopped-flow Binding Kinetics

The kinetics of binding were characterized by rapidly mixing the SH3 domain and peptide and monitoring the progress of the reaction via intrinsic tryptophan fluorescence of the protein, which increases upon interacting with proline-rich peptides (51). We used a version of the RR peptide free of Trp and Tyr fluorophores (VSLARRPLPPLP); thus, the signal derives entirely from protein residues. We fit the binding data according to the following equation,

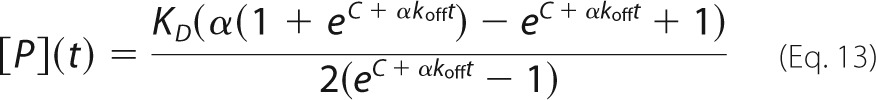where I(t) is the fluorescence signal at time t, [P](t) and [PL](t) are the concentrations of free protein and bound complex at time t, [P]_total = [P] + [PL] is the total concentration of protein, and I_P and I_PL are the fluorescence intensities of the free and bound states. The time dependence of [P](t) is given by Ref. 52 as follows,

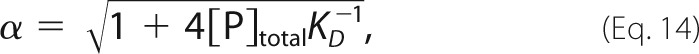where

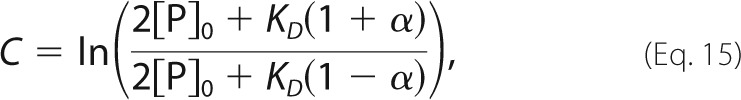and

k_off is the dissociation rate constant, K_D is the equilibrium dissociation constant, and [P]₀ is the initial concentration of free protein at t = 0, which is assumed to be equal to the initial concentration of free ligand, [L]₀ = [P]₀. Data were analyzed by non-linear least-squares fitting with the values of [P]_total and K_D held constant, while the values of I_P, I_PL, k_off, and [P]₀ were varied to minimize the function,

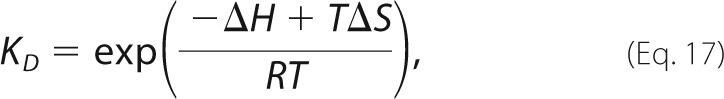where I(t)_calculated is given by Equation 1, and the sum runs over all data points. The value of [P]_total was obtained from the absorbance of the protein sample at 280 nm (53), the concentration of the peptide was determined by amino acid analysis (54), and the value of K_D was extrapolated from temperature-dependent ITC data for the Fyn SH3/RR peptide interaction (see below). Adjusting the value of [P]₀ accounts for binding that occurs during the dead time of the instrument (∼4 ms). The uncertainty in k_off was obtained by fitting random sets of the 100 individual stopped-flow traces selected according to the bootstrap method (50) and averaged. The error was taken as the S.D. value obtained after 100 iterations.

Experiments were performed using a Bio-Logic SFM 400 instrument coupled to a MOS-250 spectrometer using Biokine version 2.5 software for data acquisition. Intrinsic tryptophan fluorescence of the Fyn SH3 domain was measured with an excitation wavelength of 276 nm and a bandwidth of 20 nm. Emission at a wavelength of 320 nm and a bandwidth of 10 nm was recorded for 150 ms with measurements taken every 0.02 ms. The detector photomultiplier was operated at 860 V. For each trace, 201 μl of protein (1 μm) and 201 μl of RR peptide (1 μm) were mixed for a total injection volume of 402 μl at a flow rate of 13.5 ml s⁻¹ at 5 °C.

NMR-derived Binding Kinetics

We previously characterized the binding kinetics of the RR peptide using NMR and ITC over a temperature range of 10–50 °C (33). In this prior work, we employed both CPMG and ZZ magnetization exchange NMR experiments at 20 °C, obtaining very similar values for k_off: 11.2 and 12.8 s⁻¹, respectively. At 10 °C, only ZZ exchange experiments were used, yielding k_off = 4.5 s⁻¹. CPMG experiments were not performed because spectral broadening is minimal at this temperature. We extrapolated the expected kinetic and thermodynamic behavior to 5 °C according to the following,

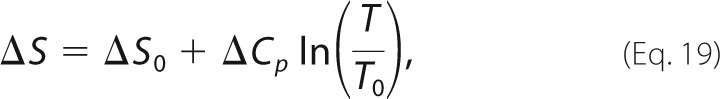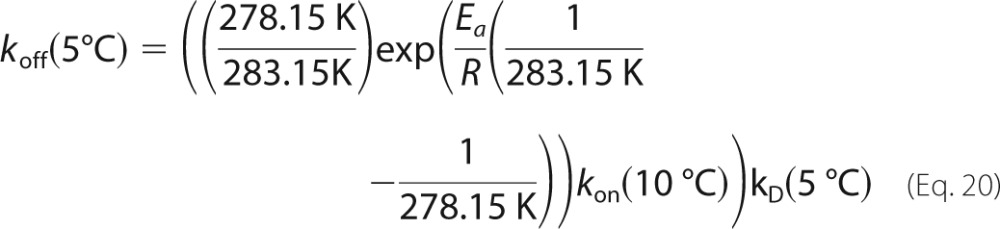where T₀ = 303.15 K, ΔH₀ = 15.4 kcal mol⁻¹, ΔS₀ = 20 cal mol⁻¹ K⁻¹, ΔC_p = 352 cal mol⁻¹ K⁻¹ (33), T = 278.15 K, R is the universal gas constant, and the equation,

where k_on(10 °C) = 1.03 ± 0.05 × 10⁸ m⁻¹ s⁻¹ (33), and E_a = 3.4 ± 0.5 kcal mol⁻¹. This yielded K_D(5 °C) = 36.7 nm and k_off^NMR(5 °C) = 3.3 ± 0.2 s⁻¹. For the sake of comparison, K_D(10 °C) = 46.1 nm.

RESULTS AND DISCUSSION

NMR Titration Experiments

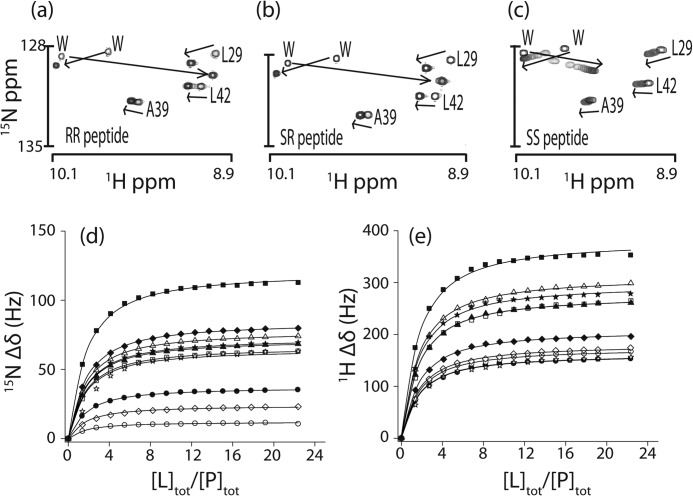
Series of protein ¹H-¹⁵N correlation HSQC NMR spectra were collected for the Fyn SH3 domain titrated with RR, SR, and SS peptides (Fig. 1) at 40 °C. Exchange between the free and bound states was intermediate on the NMR chemical time scale (47) for the RR and SR peptides and fast for the SS peptide. The signals for many of the same protein residues were displaced by the addition of each peptide (Fig. 1, a–c). This suggests that all three peptides occupy the same binding site, consistent with the idea that the ΦPXΦP motif is the minimal recognition sequence of the SH3 domain (37). The chemical shift displacements are color-coded on a structure of an SH3-peptide complex in Fig. 2. SS peptide titrations were repeated in the presence of 0, 0.2, and 0.3 m NaCl at 40 °C. Peak displacements (Fig. 1, d and e) were analyzed to extract the equilibrium association constants, K_a, yielding values in good agreement with the ITC-derived measurements (Table 2). A further SS peptide titration was performed at 20 °C in the presence of 0 m NaCl. Under these conditions, exchange was on the intermediate time scale; however, peak shifts were essentially identical to those obtained at 40 °C.

FIGURE 1.

a–c, regions of ¹⁵N/¹H HSQC spectra of the Fyn SH3 domain titrated with RR (a), SR (b), and SS (c) peptides. Shown are chemical shift displacements of SH3 domain signals in the ¹⁵N (d) and ¹H (e) dimensions upon titration with the SS peptide. Curves represent the global fit to a two-state binding equation.

FIGURE 2.

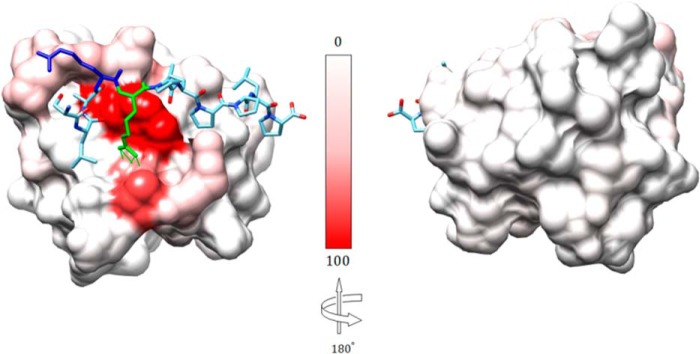
Structure of the Fyn SH3 domain in complex with a ligand identical to the RR peptide but containing Val rather than Trp at position −8 (Protein Data Bank entry 4EIK). Shown are relative ¹⁵N/¹H chemical shift perturbations (Δδ² = (10Δδ_1H)² + (Δδ_15N)²), normalized to the largest perturbation (Δδ = 12.98 ppm), color-coded on the protein surface, from 0% (white) to 100% (red). Peptide residues Arg⁻³ (green) and Arg⁻⁴ (blue) are illustrated in ball and stick format. Hydrogen bonds between Arg⁻³ in the peptide and Asp¹⁷ in the Fyn SH3 domain are indicated by green lines.

TABLE 2.

Thermodynamic and kinetic binding parameters for the Fyn SH3 domain

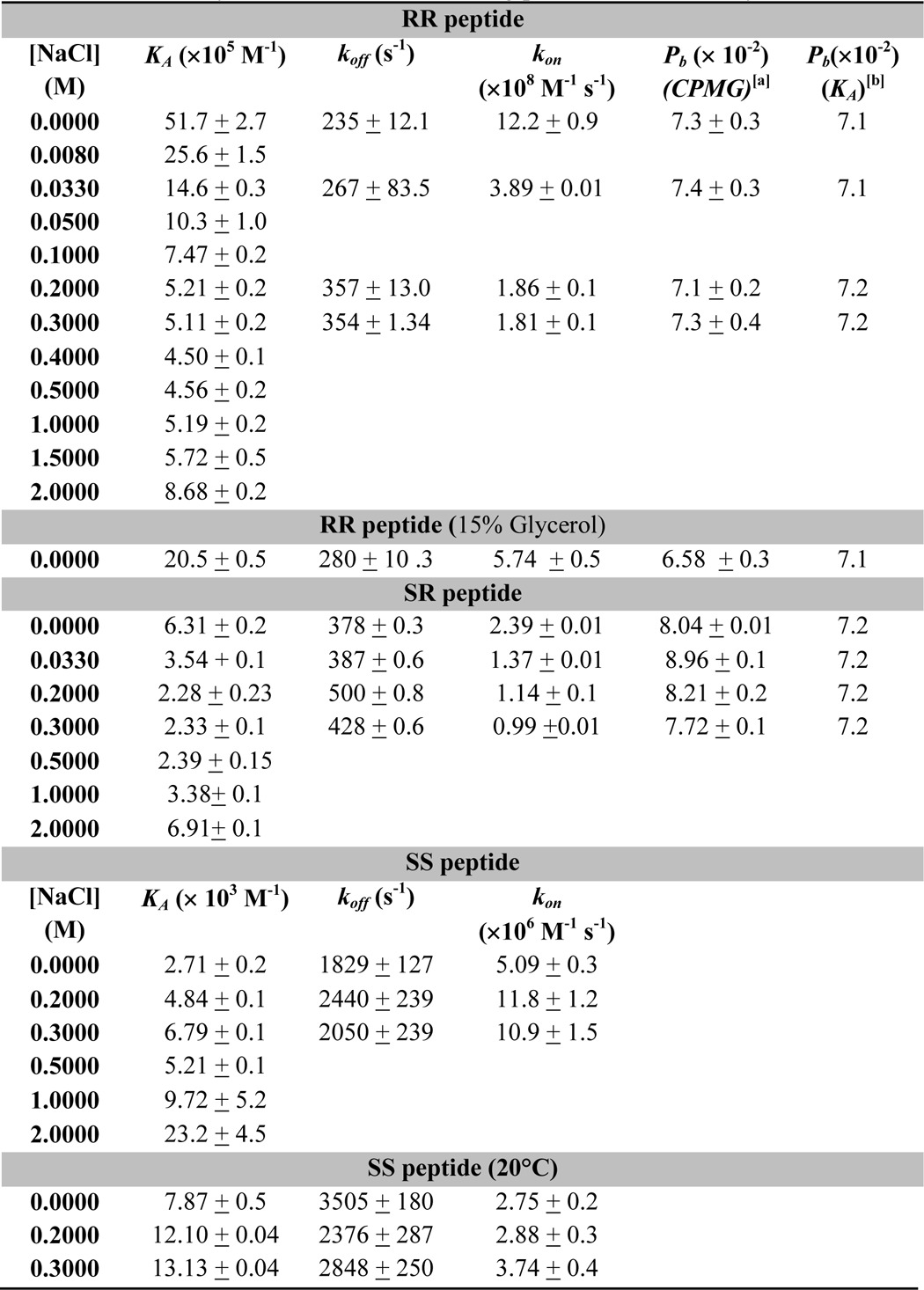
^a Population of the bound state extracted from CPMG data.

^b Population of the bound state calculated based on the ITC-derived affinity and concentrations of protein and peptide used.

Isothermal Titration Calorimetry

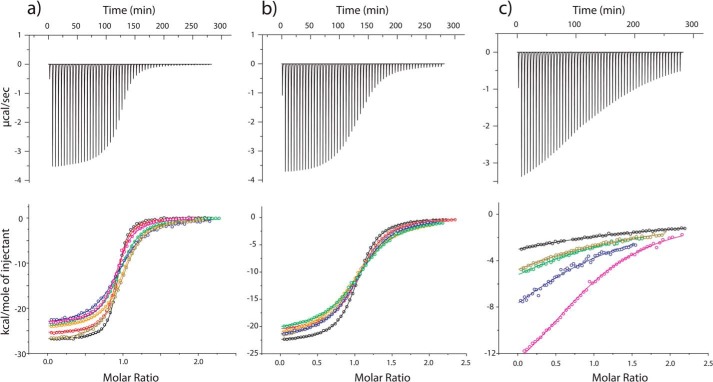
The affinities of the Fyn SH3 domain for the RR, SR, and SS peptides were characterized by ITC at 40 °C with NaCl concentrations ranging from 0 to 2 m (Fig. 3 and Table 2), yielding equilibrium association constants (K_a) plotted in Fig. 4. The affinity of the RR peptide shows a sharp decrease with increasing salt concentration up to about 0.25 m NaCl, followed by a gradual increase. The affinity of the SR peptide also decreases sharply up to 0.25 m NaCl. This is similar to the salt dependence of protein solubility, which typically shows an initial increase or “salting in” as electrostatic interactions are screened, followed by a decrease or “salting out” as hydrophobic interactions are enhanced by increasing salt concentration (55). The hydrophobic association of pairs of methane molecules in water and the chemical potential of methane dissolved in water both increase linearly with NaCl concentration (56, 57). The affinity of the SS peptide is roughly 3 orders of magnitude weaker than those of the SR and RR peptides (at 0 m NaCl) and increases linearly with increasing salt concentration. This molecule is uncharged, and its binding to the SH3 domain is driven by non-polar interactions involving the ΦPXΦP motif that are presumably enhanced by increasing salt concentrations. Thus, the initial downward slope of the RR affinity profile is due to the screening of electrostatics, whereas the slight upward slope at high NaCl concentrations is caused by the enhancement of hydrophobic interactions involving the ΦPXΦP binding motif. As discussed below, an additional set of ITC experiments was performed for the SS peptide at 20 °C with 0, 0.2, and 0.3 m NaCl.

FIGURE 3.

Isothermal titration calorimetry raw thermograms (top) and integrated heats (bottom) for RR (a), SR (b), and SS (c) peptides binding to the Fyn SH3 domain at 40 °C and different ionic strength. Black, 0 mm NaCl added; red, 33 mm; orange, 200 mm; dark yellow, 300 mm; green, 500 mm; blue, 1000 mm; magenta, 2000 mm. Raw thermograms were obtained with 0 m added salt.

FIGURE 4.

Base 10 logarithms of affinity constants, K_a, of the Fyn SH3 domain for RR (filled circles), SR (open squares), and SS peptides (open circles) plotted as a function of ionic strength. In some cases, the error bars are within the symbols used.

NMR Kinetics Experiments

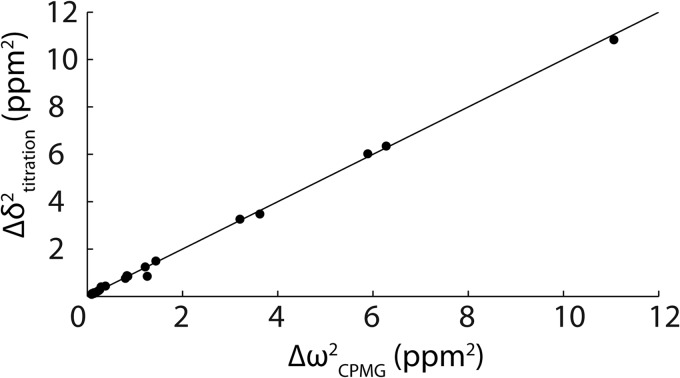
The kinetics of peptide binding were characterized using NMR CPMG relaxation dispersion experiments performed on ¹⁵N-enriched samples of the Fyn SH3 domain partially saturated with RR and SR peptides at 40 °C with NaCl concentrations of 0.00, 0.03, 0.20, and 0.30 m. Association/dissociation dynamics produce chemical shift fluctuations that contribute to ¹⁵N transverse relaxation rates, R₂. CPMG experiments quench these contributions with variable trains of 180° refocusing radiofrequency pulses applied during a constant relaxation delay (34, 35). Plots of R₂ versus ν_CPMG are shown in Fig. 5, where ν_CPMG = 1/(2τ), and τ is the delay between successive refocusing pulses. This spectral broadening reflects entirely exchange between the free and bound forms of the protein. Essentially flat dispersions are obtained for the protein in the absence of peptide, although the profiles of some residues in the free protein are very slightly sloped by 5 × 10⁻⁴ s⁻¹ Hz⁻¹. This indicates that the large dispersions that we observe are not due to internal dynamics of the protein itself because these would be evident when peptide is absent. Flat dispersions are also obtained with saturating amounts of the RR peptide. The populations of all protein and peptide species are at thermodynamic equilibrium throughout the CPMG experiment. Thus, any partly bound intermediate forms in the partially saturated sample would be present in the fully saturated sample as well. If the large dispersions were due to exchange between the bound state and an intermediate, they would also be observed for the fully saturated sample, which is not the case. Furthermore, chemical shift parameters extracted from the CPMG fits, Δω², provide a fingerprint of the exchanging species. In this case, we obtain quantitative agreement between Δω² and the peak displacements extracted from peptide titrations, Δδ², as observed previously (33) (Fig. 6). If the large dispersions were due exchange between the free protein and a binding intermediate, such good agreement would not be expected, unless the intermediate had chemical shifts identical to those of the bound state, which is unlikely. Thus, the relaxation dispersion analysis reports on the kinetics of exchange between the free and fully bound states. Dissociation rate constants (k_off) were extracted from the data, as described under “Materials and Methods,” and used to calculate k_on, according to the equation, k_on = K_a·k_off.

FIGURE 5.

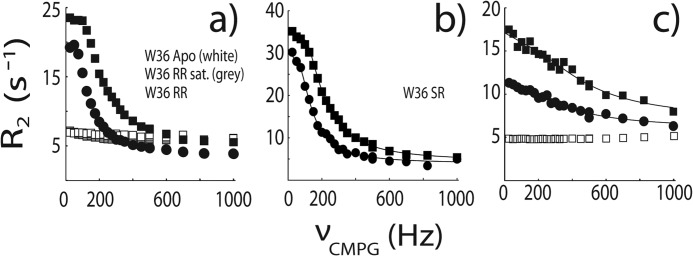
NMR ¹⁵N CPMG relaxation dispersion data for the backbone amide signal of W36 collected at 500 (circles) and 800 (squares) MHz and 0 m NaCl. In a, white, gray, and black symbols correspond to protein samples with an RR peptide/protein ratios of 0, 300, and ∼10% at 40 °C. In b, data were obtained with an SR peptide/protein ratio of ∼10% at 40 °C. In c, white and black symbols correspond to SS peptide/protein ratios of 0 and ∼10% at 20 °C. Lines indicate the global best fits as described under “Materials and Methods.”

FIGURE 6.

Comparison of Δω²¹⁵N chemical shift parameters extracted from CPMG relaxation dispersion NMR experiments performed on the Fyn SH3 domain partially saturated with the RR peptide (0 m NaCl) and Δδ² peak displacements from a comparison of the Fyn SH3 domain spectra free and saturated with the RR peptide (0 m NaCl). The line goes through the origin with a slope of 1.

Experiments with the RR peptide with 0.0 m NaCl were repeated in the presence of 15% glycerol, which translates into a 1.45-fold increase in solution viscosity, η (58). If binding rates are limited by diffusion in solution, then k_on should be inversely proportional to η (6), although in practice, the slope of a k_on/k_on⁰ versus η⁰/η plot can diverge somewhat from the theoretical value of 1 (59). We find that the peptide binds 2.13-fold more slowly in the presence of 15% glycerol, which lies well within the range of viscosity dependences reported for diffusion-limited protein association rates (59). We also find that the association rate constant is significantly (∼4-fold) more sensitive to ionic strength than the dissociation rate constant, which is a signature of diffusion-limited binding (13). In addition, we reported previously that the apparent activation enthalpy (E_a) for k_on is 3.4 kcal mol⁻¹ (33). This matches the expected E_a = 4.5 kcal mol⁻¹ for diffusion-limited reactions, reflecting the temperature dependence of water viscosity (16). Taken together, the NMR kinetics data strongly indicate that peptide binding to the SH3 domain is a diffusion-limited, two-state process.

In the case of the SS peptide at 40 °C, exchange kinetics are extremely rapid, leading to very small and essentially linear dispersion profiles. Due to their very small magnitudes, they are partially obscured by the slightly sloped profiles obtained for the free protein (which probably reflect some degree of internal motions unrelated to peptide binding). Therefore, in order to determine binding kinetics for the SS peptide, CPMG experiments were performed at 20 °C with 0, 0.2, and 0.3 m NaCl, conditions that produce large dispersions for the partially SS peptide-saturated protein sample, and completely horizontal dispersion profiles for the free protein, as shown in Fig. 5. Values of k_off determined at 20 °C were combined with affinities (K_a), measured by ITC at 20 °C to yield association rate constants (k_on). We used the previously determined value of E_a = 3.4 kcal mol⁻¹ to extrapolate k_on for the SS peptide from 20 to 40 °C according to the equation, k_on(T₂) ≈ (T₂/T₁) × k_on(T₁) × exp(E_a/R ×(1/T₁ − 1/T₂))c (60), where R is the gas constant. This leads to scaling of k_on by a factor of only 1.6, which is small compared with the up to 30-fold differences in k_on observed between the different peptides. Thus, the results are not sensitive to the exact choice of E_a.

Comparison of NMR and Stopped-flow Binding Kinetics

In order to cross-validate the NMR characterization of Fyn SH3 domain-peptide binding kinetics, we performed a stopped-flow spectroscopic analysis of the same system. However, the rates determined in the current study far exceed the limits of standard stopped-flow instruments (this is one of the advantages of the NMR-based approach). We therefore collected stopped-flow data at 5 °C, in order to slow the kinetics sufficiently for them to be amenable to this type of analysis. Fluorescence traces for the SH3 domain injected with buffer (green) and a peptide solution (blue) are shown in Fig. 7, with t = 0 aligned to the end of the injection. As expected, the fluorescence signal for the protein-peptide pair shows a time-dependent increase after the injection due to evolution of the binding reaction. This signal is above that of the free protein at t = 0 due to binding that occurs during the dead time of the instrument, which is about 4 ms. Analysis of the stopped-flow data yields k_off^SF(5 °C) = 8.9 ± 0.6 s⁻¹, whereas the NMR kinetics method yields k_off^NMR(5 °C) = 3.3 ± 0.2 s⁻¹, as described under “Materials and Methods.” These two values differ by about a factor of 3, which we believe is excellent agreement for such different experimental modalities. This gives us further confidence in the NMR-based kinetics method.

FIGURE 7.

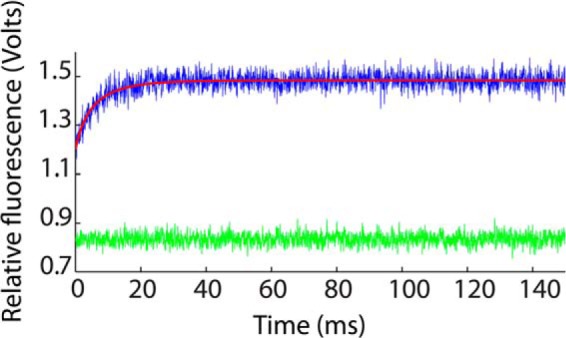
Stopped-flow fluorescence data for the Fyn SH3 domain rapidly mixed with buffer (green) and with a solution of the RR peptide (blue). Data shown are the averages of 100 individual stopped-flow traces. The best fit using Equation 12 is indicated with a red line.

Electrostatic Enhancement of Association Rates

We investigated the influence of electrostatics on SH3 domain ligand binding kinetics by varying the ionic strength of the samples, in order to attenuate long range coulombic interactions, and by comparing results for the RR, SR, and SS peptides, which carry formal charges of +2, +1, and 0. The screening of coulombic interactions by electrolyte solutions was analyzed in terms of the electrostatic attraction of two oppositely charged spheres with radii r, a center-center separation of 2r, and charges ±Z. Relative to infinite separation, the potential energy, V, is given by the expression (61, 62),

where e is the elemental charge, ϵ is the dielectric constant of the medium, κ is the inverse Debye length,

k_B is the Boltzmann constant, and I is the ionic strength. The parameter f_ion describes the ionic strength dependence of the potential energy, with limiting values of 1 (full interaction strength) in the absence of salt, and 0 (zero interaction strength) at infinite salt concentration.

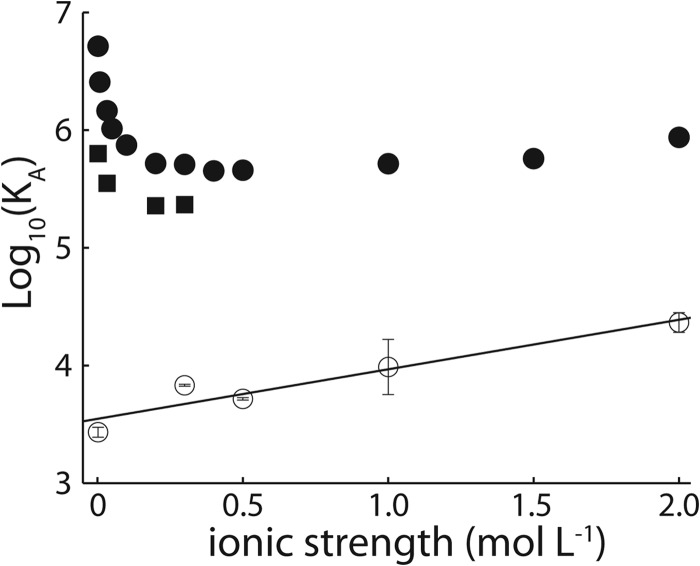
The logarithms of k_on are plotted as a function of f_ion for the RR, SR, and SS peptides in Fig. 8a, together with linear regression lines. Data for the RR and SR peptides have positive slopes, as expected, because larger values of f_ion correspond to lower salt concentrations, greater electrostatic stabilization of the transition state, and faster association. The data for the SS peptide are close to horizontal, as expected for an uncharged ligand. The slightly negative slope may be due to weak hydrophobic stabilization of the transition state that is enhanced at high salt concentrations. Notably, the lines for the three peptides nearly intersect at f_ion = 0 and a k_on value of about 6 × 10⁷ m⁻¹ s⁻¹. This corresponds to the basal, or electrostatic-free, association rate. The close agreement of basal association rates obtained for the three different peptides gives us confidence in the reliability of the extrapolation along f_ion. The slopes of the lines correspond to the logarithms of the maximum electrostatic enhancement of binding with zero ionic strength, log(k_on^enhanced/k_on^basal). We find that long range coulombic interactions accelerate binding of the RR and SR peptides by 23.1- and 4.42-fold, respectively, as listed in Table 1.

FIGURE 8.

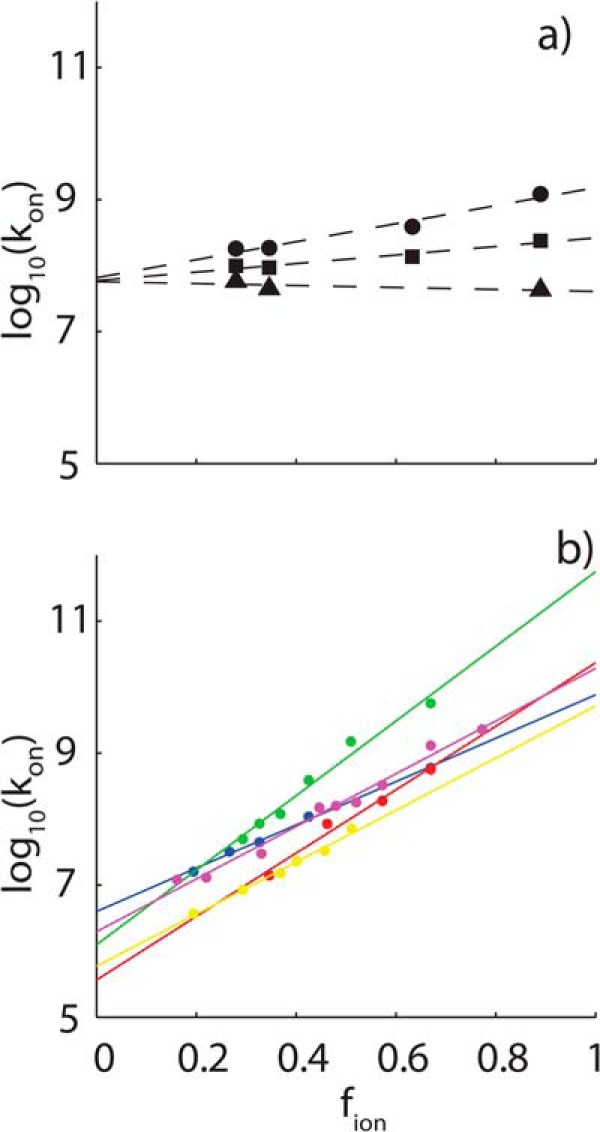
Ionic strength dependence of association rates. a, NMR and ITC-derived association rate constants (k_on) for the RR (circles) and SR (squares) and SS (triangles) peptides binding to the Fyn SH3 domain, plotted as a function of f_ion (Equation 22), which takes values between 1 at zero ionic strength and 0 at infinite ionic strength. Dashed lines, linear regression fits of the data. b, association constants for barnase-barstar (blue), shaker K⁺ channel-peptide toxin Lq2 (red), E9 DNase-immunity protein Im9 (green), heterodimeric leucine zipper (yellow), and acetylcholinesterase-fasciculin 2 (magenta) plotted as a function of f_ion.

The basal association rate for the SH3 domain is significantly greater, and the extent of electrostatic enhancement is much less, than observed previously for long lived complexes. Association rates for a data set of five different systems (13) are plotted as a function of f_ion in Fig. 6b, and the basal association rates and electrostatic enhancements extracted from the linear fits are listed in Table 1. These proteins bind roughly 10³ to 10¹⁰-fold more tightly and dissociate 10³ to 10⁹-fold more slowly than the SH3 domain studied here. Notably, all of these basal, electrostatic association rates are 10–100-fold slower than those obtained for the SH3 domain, whereas the electrostatic rate enhancements are 10² to 10⁴-fold greater.

It is likely that these differences are due to differences in the nature of the binding surfaces for the SH3 domain compared with the proteins in the long lived complex database. The barnase-barstar interface is fairly typical of those in the database in terms of size and complexity. It buries 1590 Ų of accessible surface area and involves the formation of 14 specific hydrogen bonds (63). In this case, only about 1 molecular collision in 1700 aligns the binding surfaces sufficiently accurately to proceed to the fully bound state in the absence of electrostatic enhancement, assuming no charged interactions and a molecular collision frequency of 6.6 × 10⁹ m⁻¹ s⁻¹ (12). In contrast, the complex formed by the SH3 domain and ΦPXΦP motif buries only 600 Ų and is stabilized entirely by hydrophobic interactions (40). In this case, about 1 in every 160 SH3-peptide collisions is sufficiently well aligned to progress to the bound state. Docking of the SS peptide onto the SH3 binding surface involves a significantly smaller contact area with fewer specific pairwise interactions. This probably results in less stringent geometric requirements for molecular collisions to lead to successful docking of the SS peptide and a more rapid basal association rate.

A less geometrically restricted transition state could explain our observation of lower electrostatic enhancement of SH3-peptide association rates compared with that of barnase-barstar and other long lived complexes. For barnase-barstar, it was found that the transition state is stabilized by specific charged residues that are in close proximity in the stereospecific complex. This implies that these residues are correctly oriented with respect to one another at the rate-limiting step of binding (5). The SH3 domain exhibits a greater basal association rate, suggesting that the transition state is less geometrically constrained. Thus, fewer specific interactions may be formed between charged residues in this state, leading to a smaller degree of electrostatic stabilization.

Thus, the SH3 domain and target peptide do not rely as heavily upon electrostatic enhancement to achieve rapid association kinetics as do many previously studied long lived complexes. It has been noted previously that the interfaces of high-affinity complexes tend to contain more charged residues than those of low-affinity ones, and that these coulombic interactions are sometimes, but not always, thermodynamically stabilizing (64). This is consistent with higher affinity complexes relying more heavily on electrostatic enhancement to achieve rapid binding kinetics than weaker complexes; however, the question is far from resolved.

Arginine Interactions in the Transition State and Bound State

In order to clarify the role played by the peptide arginine residues in the SH3 domain binding pathway, we compared K_a and k_on values for the RR and SR peptides with those of the SS peptide. The SS peptide carries no formal charges and binds in the same location as the SR and RR peptides, as evinced by similar patterns of peak movements in protein NMR titration experiments. The ratios of K_a and k_on obtained for the RR and SR peptides relative to those of the SS peptide describe the contributions of the conserved (Arg⁻³) and “extra” (Arg⁻⁴) Arg residues to the stabilities of the fully bound and transition states. The logarithms of the RR/SS and SR/SS ratios are plotted as a function of f_ion in Fig. 9 and exhibit excellent linear correlations over their full ranges of roughly 2 orders of magnitude. When extrapolated to infinite salt concentration at the y intercept, the affinity of the SR peptide is still enhanced by a factor of 26, relative to the SS peptide, which translates into a stabilization of the bound state by 2.0 kcal mol⁻¹. This enhancement is due to interactions formed by Arg⁻³ that are not screened by salt and therefore almost certainly involve short range forces. The slope for the RR peptide is greater than that of the SR peptide by about a factor of 2 in Fig. 9, consistent with the 2-fold difference in formal charge. However, when extrapolated to infinite salt concentration, the affinities of the two peptides are virtually identical, as evinced by the intersection of the two lines at the y axis (Fig. 7, solid lines). Thus, the “extra” Arg⁻⁴ forms long range electrostatic interactions in the bound state but no energetically significant short range (i.e. unscreened) interactions.

FIGURE 9.

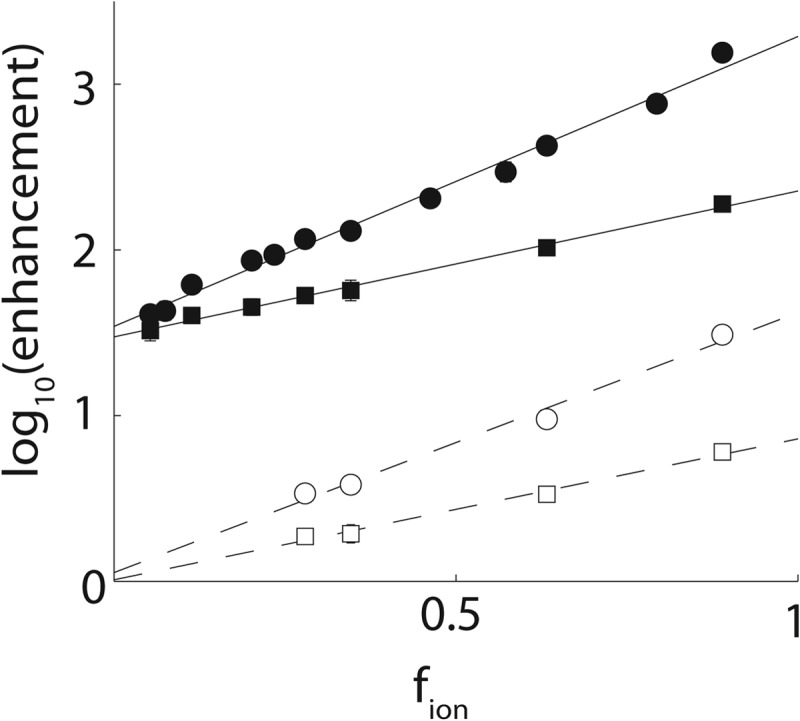
Enhancements in affinities (K_a^SR,RR/K_a^SS; solid lines, filled symbols) and association rates (k_on^SR,RR/k_on^SS; dashed lines, open symbols) for the RR (circles) and SR (squares) peptides relative to the SS peptide, plotted as a function of f_ion.

This is consistent with the x-ray crystal structure of the Fyn SH3 domain bound to a ligand very similar to the RR peptide used in this study (Trp⁻⁸ → Val⁻⁸), shown in Fig. 2 (40). The conserved Arg⁻³ forms a salt bridge (i.e. hydrogen-bonds) with Asp¹⁷, whereas the aliphatic portion of the residue packs against Trp³⁶. In contrast, the “extra” Arg, Arg⁻⁴, points away from Asp¹⁷ and makes no additional hydrogen bonds. However, negatively charged Glu³³ and Glu³⁴ are within about 6.5 Å, well positioned to interact with Arg⁻⁴ electrostatically. Guanidinium ions, equivalent to the guanidino moiety of the Arg side chain, interact with the Fyn SH3 domain specifically at the peptide binding site and compete with the RR peptide (65). Together, these data strongly suggest that the guanidino moiety of Arg⁻³ interacts with Fyn SH3 domain via a network of hydrogen bonds, whereas Arg⁻⁴ forms looser, long range electrostatic interactions in the fully bound complex.

The pattern of enhancements seen for k_on is similar but differs in an important respect. At 0 m NaCl, the RR peptide binds 5-fold more rapidly than the SR peptide, which binds 6-fold more rapidly than the SS peptide. This is consistent with both Arg⁻³ and Arg⁻⁴ forming long range electrostatic interactions in the transition state. However, in the extrapolation to infinite salt concentration, both RR and SR peptides bind with rates that are nearly identical to the value determined for the SS peptide. All of the interactions formed by the peptide Arg residues in the transition state are thus electrostatic and long range (i.e. are screened by salt). The short range interactions involving Arg⁻³ that are present in the fully bound complex are only formed after the protein-peptide pair have passed through the high-energy transition state (i.e. near the end of the binding process). The transition states of far more tightly binding partners are believed to be similarly dominated by long range electrostatic interactions and lacking in short range contacts (5, 14, 15, 22).

Ionic Strength Dependence of Dissociation Rates

For diffusion-limited binding reactions, values of k_on are typically far more sensitive to ionic strength than are values of k_off (1, 10, 26). In the case of the RR peptide, k_on is about 4 times more sensitive to ionic strength than k_off. This has been explained in terms of the structure of the transition state (13). Long range electrostatic interactions are fairly insensitive to small changes in charge separation. Thus, if the two binding partners remain close in the transition state, then long range electrostatics contribute similarly to the stabilities of the fully bound and transition states. Increasing the ionic strength screens the long range charge interactions present in both states to equal extents. Thus, the barrier to dissociation is not greatly affected, and k_off is essentially unchanged. In contrast, destabilization of the transition state by added salt increases the barrier to association and slows binding rates.

However, this explanation appears inconsistent with mutational analyses of charge interactions in the fully bound and transition states. In the case of barnase-barstar, mutagenesis-derived coupling energies between charged residues in the fully bound state range from 1 to 7 kcal mol⁻¹ (40), whereas coupling energies in the transition state are less than 0.5 kcal mol⁻¹ (5). Similarly, the SS peptide binds 250-fold more weakly than the SR peptide but only 6-fold more slowly. The SS peptide binds 1900-fold more weakly and only 29-fold more slowly than the RR peptide in the absence of salt. These results indicate that the interactions of charged residues are much weaker in the transition state than in the fully bound state. Adding salt should significantly destabilize the bound state without significantly affecting the transition state and thus should increase dissociation rates. Our results provide a simple explanation for this apparent contradiction. We directly measured electrostatic-free basal affinities and association rates for the SS peptide, which allowed us to separate the interaction energies of Arg⁻³ and Arg⁻⁴ into long range “screenable” electrostatic and short range “unscreenable” components. Notably, the long range components are comparable for the fully bound and transition states. For the SR compared with the SS peptide, long range interactions enhance the affinity and association rate by factors of 9 and 6, respectively, at 0 m NaCl, compared with 250- and 6-fold total enhancements. For the RR peptide, these long range enhancement factors are 73 and 29, compared with 1900- and 29-fold total enhancements. Thus, for the Fyn SH3 domain, long range electrostatic interactions are similar in the fully bound and transition states, leading to k_off values that are relatively insensitive to ionic strength. This has the implication that the peptide and SH3 domain are separated by a relatively short distance in the transition state, as seen previously for long lived protein complexes (13).

Conclusions

Most of our knowledge of protein binding kinetics derives from studies of extremely stable long lived complexes. The binding kinetics of short lived protein complexes are less well understood because these systems are challenging to characterize experimentally. We have applied a recently developed combination of NMR and ITC to study complexes of the Fyn SH3 domain and several peptides whose bound lifetimes are as short as 0.3 ms. This is beyond the range of standard stopped-flow techniques used to measure binding kinetics. We find that although the binding pathways of these transient SH3 complexes are similar to those of high-affinity long lived complexes, they differ in some important respects.

For the SH3 domain, as well as for high-affinity binding partners, the transition state is stabilized by long range electrostatic interactions, whereas short range stereo-specific contacts are formed late in the binding pathway. We find that the contributions of long range electrostatic interactions to both the fully bound and transition states are quite similar, implying that the separation between the SH3 domain and peptide is not large in the transition state. A similar situation is believed to hold true for the transition states of high-affinity systems. Thus, structural compactness and the dominance of long range electrostatic interactions appear to be universal features of diffusion-limited binding pathways involving affinities and lifetimes spanning up to 7 orders of magnitude.

However, the electrostatic acceleration of SH3 domain association rates is several orders of magnitude less than has been previously observed for stable long lived protein complexes. In contrast, the electrostatic-free basal association rate is much greater, possibly because of looser geometrical restrictions for molecular collisions to proceed to the bound state. This raises the interesting question of whether or not this is a general phenomenon. Do weakly bound, transient complexes intrinsically have more rapid basal association rates and less reliance on electrostatic enhancement than do tightly bound, long lived complexes? If so, how does this relate to the compositions and geometries of the binding interfaces? The combined NMR and calorimetric approach used here is uniquely suited for studying transient complexes to gain a better understanding of the relationships among binding affinities, basal association kinetics, and electrostatic rate enhancements and to shed light on the fundamental principles of molecular recognition.