Abstract
Algorithms for Markov boundary discovery from data constitute an important recent development in machine learning, primarily because they offer a principled solution to the variable/feature selection problem and give insight on local causal structure. Over the last decade many sound algorithms have been proposed to identify a single Markov boundary of the response variable. Even though faithful distributions and, more broadly, distributions that satisfy the intersection property always have a single Markov boundary, other distributions/data sets may have multiple Markov boundaries of the response variable. The latter distributions/data sets are common in practical data-analytic applications, and there are several reasons why it is important to induce multiple Markov boundaries from such data. However, there are currently no sound and efficient algorithms that can accomplish this task. This paper describes a family of algorithms TIE* that can discover all Markov boundaries in a distribution. The broad applicability as well as efficiency of the new algorithmic family is demonstrated in an extensive benchmarking study that involved comparison with 26 state-of-the-art algorithms/variants in 15 data sets from a diversity of application domains.
Keywords: Markov boundary discovery, variable/feature selection, information equivalence, violations of faithfulness
1. Introduction
The problem of variable/feature selection is of fundamental importance in machine learning, especially when it comes to analysis, modeling, and discovery from high-dimensional data sets (Guyon and Elisseeff, 2003; Kohavi and John, 1997). In addition to the promise of cost effectiveness (as a result of reducing the number of observed variables), two major goals of variable selection are to improve the predictive performance of classification/regression models and to provide a better understanding of the data-generative process (Guyon and Elisseeff, 2003). An emerging class of filter algorithms proposes solution of the variable selection problem by identification of a Markov boundary of the response variable of interest (Aliferis et al., 2010a, 2003a; Mani and Cooper, 2004; Peña et al., 2007; Tsamardinos and Aliferis, 2003; Tsamardinos et al., 2003a,b). The Markov boundary M is a minimal set of variables conditioned on which all the remaining variables in the data set, excluding the response variable T, are rendered statistically independent of the response variable T. Under certain assumptions about the learner and the loss function, Markov boundary is the solution of the variable selection problem (Tsamardinos and Aliferis, 2003), that is, it is the minimal set of variables with optimal predictive performance for the current distribution and response variable. Furthermore, in faithful distributions, Markov boundary corresponds to a local causal neighborhood of the response variable and consists of all its direct causes, effects, and causes of the direct effects (Neapolitan, 2004; Tsamardinos and Aliferis, 2003).
An important theoretical result states that if the distribution satisfies the intersection property (which is defined in Section 2.2), then it is guaranteed to have a unique Markov boundary of the response variable (Pearl, 1988). Faithful distributions, which constitute a subclass of distributions that satisfy the intersection property, also have a unique Markov boundary (Neapolitan, 2004; Tsamardinos and Aliferis, 2003). However, some real-life distributions contain multiple Markov boundaries and thus violate the intersection property and faithfulness condition. For example, a phenomenon ubiquitous in analysis of high-throughput molecular data, known as the “multiplicity” of molecular signatures (i.e., different gene/biomarker sets perform equally well in terms of predictive accuracy of phenotypes) suggests existence of multiple Markov boundaries in these distributions (Dougherty and Brun, 2006; Somorjai et al., 2003; Aliferis et al., 2010a). Likewise, many engineering systems such as digital circuits and engines typically contain deterministic components and thus can lead to multiple Markov boundaries (Gopnik and Schulz, 2007; Lemeire, 2007).
Related to the above, a distinguished statistician, the late Professor Leo Breiman, in his seminal work (Breiman, 2001) coined the term “Rashomon effect” that describes the phenomenon of multiple different predictive models that fit the data equally well. Breiman emphasized that “multiplicity problem and its effect on conclusions drawn from models needs serious attention” (Breiman, 2001).
There are at least three practical benefits of algorithms that could systematically discover from data multiple Markov boundaries of the response variable of interest:
First, such algorithms would improve discovery of the underlying mechanisms by not missing causative variables. For example, if a causal Bayesian network with the graph X ← Y → T → Z is parameterized such that variables X and Y contain equivalent information about T (see section 2.3 and the work by Lemeire, 2007), then there are two Markov boundaries of T: {X, Z} and {Y, Z}. If an algorithm discovers only a single Markov boundary {X, Z}, then it would miss the directly causative variable Y.
Second, such algorithms can be useful in exploring alternative cost-effective but equally predictive solutions in cases where different variables may have different costs associated with their acquisition. For example, some variables may correspond to cheaper and safer medical tests, while other equally predictive variables may correspond to more expensive and/or potentially unsafe tests. The American College of Radiology maintains Appropriateness Criteria for Diagnostic Imaging (http://www.acr.org/Quality-Safety/Appropriateness-Criteria/) that list diagnostic protocols (sets of radiographic procedures/variables) with the same sensitivity and specificity (i.e., these protocols can be thought of Markov boundaries of the diagnostic response variable) but different cost and radiation exposure level. Algorithms for induction of multiple Markov boundaries can be helpful for de-novo identification of such protocols from patient data.
Third, such algorithms would shed light on the predictor multiplicity phenomenon and how it affects the reproducibility of predictors. For example, in the domain of high-throughput molecular analytics, induction of multiple Markov boundaries with subsequent validation in independent data would allow testing whether multiple and equally predictive molecular signatures are due to intrinsic information redundancy in the biological networks, small sample statistical indistinguishability of signatures, correlated measurement noise, normalization/data preprocessing steps, or other factors (Aliferis et al., 2010a).
Even though there are several well-developed algorithms for learning a single Markov boundary (Aliferis et al., 2010a, 2003a; Mani and Cooper, 2004; Peña et al., 2007; Tsamardinos and Aliferis, 2003; Tsamardinos et al., 2003a,b), little research has been done in development of algorithms for identification of multiple Markov boundaries. The most notable advances in the field are stochastic Markov boundary algorithms that involve running multiple times either a standard or approximate Markov boundary induction algorithm initialized with a random seed, for example, KIAMB (Peña et al., 2007), EGS-NCMIGS and EGS-CMIM (Liu et al., 2010b). Another approach exemplified in the EGSG algorithm (Liu et al., 2010) involves first grouping variables into multiple clusters such that each cluster (i) has variables that are similar to each other and (ii) contributes “unique” information about the response variable, and then randomly sampling a representative from each cluster for the output Markov boundaries. In genomics data analysis, researchers try to induce multiple variable sets (that sometimes approximate Markov boundaries) via application of a standard variable selection algorithm to resampled data, for example, bootstrap samples (Ein-Dor et al., 2005; Michiels et al., 2005; Roepman et al., 2006). Finally, other bioinformatics researchers proposed a multiple variable set selection algorithm that iteratively applies a standard variable selection algorithm after removing from the data all variables that participate in the previously discovered variable sets with optimal classification performance (Natsoulis et al., 2005). As we will see in Sections 3 and 5 of this paper, the above early approaches are either highly heuristic and/or cannot be practically used to induce multiple Markov boundaries in high-dimensional data sets with relatively small sample size.
To address the limitations of prior methods, this work presents an algorithmic family TIE* (which is an acronym for “Target Information Equivalence”) for multiple Markov boundary induction. TIE* is presented in the form of a generative algorithm and can be instantiated differently for different distributions. TIE* is sound and can be practically applied in typical data-analytic tasks. We have previously introduced in the bioinformatics domain a specific instantiation of TIE* for development of multiple molecular signatures of the phenotype using microarray gene expression data (Statnikov and Aliferis, 2010a). The current paper significantly extends the earlier work for general machine learning use. This includes a detailed description of the generative algorithm, expanded theoretical and complexity analyses, various instantiations of the generative algorithm and its implementation details, and an extensive benchmarking study in 15 data sets from a diversity of application domains.
The remainder of this paper is organized as follows. Section 2 provides general theory and background. Section 3 lists prior algorithms for induction of multiple Markov boundaries and variable sets. Section 4 describes the TIE* generative algorithm, traces its execution, presents specific instantiations, proves algorithm correctness, and analyzes its computational complexity. This section also introduces a simpler and faster algorithm iTIE* for special distributions. Section 5 describes empirical experiments with the TIE* algorithm and comparison with prior methods in simulated and real data. The paper concludes with Section 6 that summarizes main findings, reiterates key principles of TIE* efficiency, demonstrates how the generative algorithm TIE* can be configured for optimal results, presents limitations of this study, and outlines directions for future research. The paper includes several appendices with additional details about our work: Appendix A proves theorems and lemmas; Appendix B presents parameterizations of example structures; Appendix C describes and performs theoretical analysis of prior algorithms for induction of multiple Markov boundaries and variable sets; Appendix D provides details about the TIE* algorithm and its implementations; Appendix E provides additional details about experiments with simulated and real data.
2. Background and Theory
This section provides general theory and background.
2.1 Notation and Key Definitions
In this paper upper-case letters in italics denote random variables (e.g., A, B, C) and lower-case letters in italics denote their values (e.g., a, b, c). Upper-case bold letters in italics denote random variable sets (e.g., X, Y, Z) and lower-case bold letters in italics denote their values (e.g., x, y, z). The terms “variables” and “vertices” are used interchangeably. If a graph contains an edge X → Y, then X is a parent of Y and Y is a child of X. A vertex X is a spouse of Y if they share a common child vertex. An undirected edge X – Y denotes an adjacency relation between X and Y (i.e., presence of an edge directly connecting X and Y). A path p is a set of consecutive edges (independent of the direction) without visiting a vertex more than once. A directed path p from X to Y is a set of consecutive edges with direction “→” connecting X with Y, that is, X → … → Y. X is an ancestor of Y (and Y is a descendant of X) if there exists a directed path p from X to Y. A directed cycle is a nonempty directed path that starts and ends on the same vertex X. Three classes of graphs are considered in this work: (i) directed graphs: graphs where vertices are connected only with edges “→”; (ii) directed acyclic graphs (DAGs): graphs without directed cycles and where vertices are connected only with edges “→”; and (iii) ancestral graphs: graphs without directed cycles and where vertices are connected with edges “→” or “↔” (an edge X ↔ Y implies that X is not an ancestor of Y and Y is not an ancestor of X).
When the two sets of variables X and Y are conditionally independent given a set of variables Z in the joint probability distribution , we denote this as X ⊥ Y | Z. For notational convenience, conditional dependence is defined as absence of conditional independence and denoted as X
 Y | Z . Two sets of variables X and Y are considered independent and denoted as X ⊥ Y , when X and Y are conditionally independent given an empty set of variables. Similarly, the dependence of X and Y is defined and denoted as X
Y | Z . Two sets of variables X and Y are considered independent and denoted as X ⊥ Y , when X and Y are conditionally independent given an empty set of variables. Similarly, the dependence of X and Y is defined and denoted as X
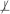 Y.
Y.
We further refer the readers to the work by Glymour and Copper (1991), Neapolitan (2004), Pearl (2009) and Spirtes et al. (2000) to review the standard definitions of collider, blocked path, d-separation, m-separation, Bayesian network, causation, direct/indirect causation, and causal Bayesian network that are used in this work. Below we state several essential definitions:
Definition 1 Local Markov condition: The joint probability distribution over variables V satisfies the local Markov condition for a directed acyclic graph (DAG) if and only if for each W in V, W is conditionally independent of all variables in V excluding descendants of W given parents of W (Richardson and Spirtes, 1999).
Definition 2 Global Markov condition: The joint probability distribution over variables V satisfies the global Markov condition for a directed graph (ancestral graph) if and only if for any three disjoint subsets of variables X, Y, Z from V, if X is d-separated (m-separated) from Y given Z in then X is independent of Y given Z in (Richardson and Spirtes, 1999, 2002).
It follows that if the underlying graph is a DAG, then the global Markov condition is equivalent to the local Markov condition (Richardson and Spirtes, 1999).
Finally, we provide several definitions of the faithfulness condition. This condition is fundamental for causal discovery and Markov boundary induction algorithms.
Definition 3 DAG-faithfulness: If all and only the conditional independence relations that are true in defined over variables V are entailed by the local Markov condition applied to a DAG , then and are DAG-faithful to one another (Spirtes et al., 2000).
The following definition extends DAG-faithfulness to any directed or ancestral graphs:
Definition 4 Graph-faithfulness: If all and only the conditional independence relations that are true in defined over variables V are entailed by the global Markov condition applied to a directed or ancestral graph , then and are graph-faithful to one another.
A relaxed version of the standard faithfulness assumption is given in the following definition:
Definition 5 Adjacency faithfulness: Given a directed or ancestral graph and a joint probability distribution defined over variables V, and are adjacency faithful to one another if every adjacency relation between X and Y in implies that X and Y are conditionally dependent given any subset of V \ {X, Y} in (Ramsey et al., 2006).
The adjacency faithfulness assumption can be relaxed to focus on the specific response variable of interest:
Definition 6 Local adjacency faithfulness: Given a directed or ancestral graph and a joint probability distribution defined over variables V, and are locally adjacency faithful with respect to T if every adjacency relation between T and X in implies that T and X are conditionally dependent given any subset of V \ {T, X} in
2.2 Basic Properties of Probability Distributions
The following theorem provides a set of useful tools for theoretical analysis of probability distributions and proofs of correctness of Markov boundary algorithms. It is stated similarly to the work by Peña et al. (2007) and its proof is given in the book by Pearl (1988).
Theorem 1 Let X, Y, Z, and W be any four subsets of variables from V.1 The following five properties hold in any joint probability distribution over variables V:
Symmetry: X ⊥ Y | Z ⇔ Y ⊥ X | Z,
Decomposition: X ⊥ (Y ∪ W) | Z ⇒ X ⊥ Y | Z and X ⊥ W | Z,
Weak union: X ⊥ (Y ∪ W) | Z ⇒ X ⊥ Y | (Z ∪ W),
Contraction: X ⊥ Y | Z and X ⊥ W | (Z ∪ Y) ⇒ X ⊥ (Y ∪ W) | Z,
Self-conditioning: X ⊥ Z | Z.
If is strictly positive, then in addition to the above five properties a sixth property holds:
Intersection: X ⊥ Y | (Z ∪ W) and X ⊥ W | (Z ∪ Y) ⇒ X ⊥ (Y ∪ W) | Z.
If is faithful to , then satisfies the above six properties and:
Composition: X ⊥ Y | Z and X ⊥ W | Z ⇒ X ⊥ (Y ∪ W) | Z.
The definition given below provides a relaxed version of the composition property that will be used later in the theoretical analysis of Markov boundary induction algorithms.
Definition 7 Local composition property: Let X, Y, Z be any three subsets of variables from V. The joint probability distribution over variables V satisfies the local composition property with respect to T if T ⊥ X|Z and T ⊥ Y |Z ⇒ T ⊥ (X ∪ Y)|Z.
2.3 Information Equivalence
In this subsection we review relevant information equivalence theory (Lemeire, 2007). We first formally define information equivalence that leads to violations of the intersection property and eliminates uniqueness of the Markov boundary (see next subsection). We then describe distributions that have information equivalence relations and point to a theoretical result that characterizes violations of the intersection property.
Definition 8 Equivalent information: Two subsets of variables X and Y from V contain equivalent information about a variable T iff the following conditions hold: T 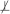 X, T
X, T 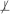 Y, T ⊥ X | Y and T ⊥ Y | X.
Y, T ⊥ X | Y and T ⊥ Y | X.
It follows from the definition of equivalent information and the definition of mutual information (Cover and Thomas, 1991) that both X and Y contain the same information about T, that is, mutual information I(X, T) = I(Y,T) (Lemeire, 2007).
Information equivalences can result from deterministic relations. For example, if we consider a Bayesian network with the graph 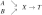 that is parameterized such that X = AND(A, B) and T
that is parameterized such that X = AND(A, B) and T
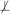 X, then {X} and {A, B} contain equivalent information with respect to T according to the above definition. However, information equivalences follow from a broader class of relations than just deterministic ones (see Example 2 and Figure 1 in the next subsection). We thus define the notion of equivalent partition that was originally introduced in the work by Lemeire (2007). To do so we first provide the definition of T-partition:
X, then {X} and {A, B} contain equivalent information with respect to T according to the above definition. However, information equivalences follow from a broader class of relations than just deterministic ones (see Example 2 and Figure 1 in the next subsection). We thus define the notion of equivalent partition that was originally introduced in the work by Lemeire (2007). To do so we first provide the definition of T-partition:
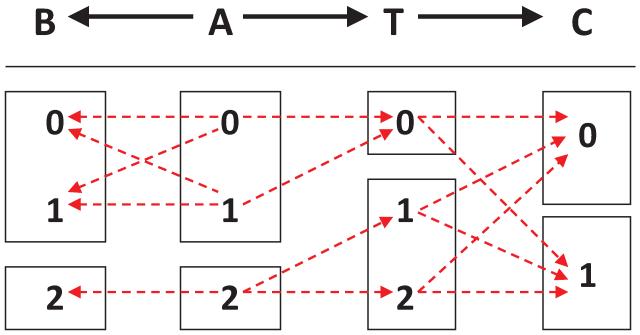
Figure 1.
Graph of a causal Bayesian network with four variables (top) and constraints on its parameterization (bottom). Variables A, B, T take three values {0,1,2}, and variable C takes two values {0,1}. Red dashed arrows denote non-zero conditional probabilities of each variable given its parents. For example, P(T = 0 | A = 1) ≠ 0, while P(T = 0 | A = 2) = 0.
Definition 9 T-partition: The domain of X, denoted by Xdom, can be partitioned into disjoint subsets for which P(T | x) is the same for all . We call this the T-partition of Xdom. We define κT(X) as the index of the subset of the partition.
Accordingly, the conditional distribution can be rewritten solely based on the index of T-partition, that is, P(T | X) = P(T | κT(X)).
Definition 10 Equivalent partition: A relation (where the “×” operator denotes the Cartesian product) defines an equivalent partition in Ydom to a partition of Xdom if:
for any x1 and x2 ∈ Xdom that do not belong to the same partition and for any y1 ∈ Ydom with , it must be that .
for all subsets of the partition, and ∃y1 ∈ Ydom such that .
In other words, for an equivalent partition, every partition corresponds to a partition . If an element of Ydom is related to an element of partition Xdom, then it is not related to an element of another partition, and each partition of Xdom has at least one element that is related to a partition of Ydom. An example of an equivalent partition is provided in Figure 1 in the next subsection.
In the following theorem the concept of equivalent partition is used to characterize violations of the intersection property; the proof of this theorem is given in the work by Lemeire (2007).
Theorem 2 If T
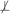 X and T ⊥ Y | X then T ⊥ X | Y if and only if the relation defined by P(x,y) > 0 with x∈ Xdom and y ∈ Ydom defines an equivalent partition in Ydom to the T-partition of Xdom.
X and T ⊥ Y | X then T ⊥ X | Y if and only if the relation defined by P(x,y) > 0 with x∈ Xdom and y ∈ Ydom defines an equivalent partition in Ydom to the T-partition of Xdom.
It is worthwhile to mention that the above definitions of T-partition, equivalent partition, and Theorem 2 can be trivially extended to sets of variables instead of individual variables X and Y.
Next we provide two more definitions of equivalent information that take into consideration values of other variables and also lead to violations of the intersection property.
Definition 11 Conditional equivalent information: Two subsets of variables X and Y from V contain equivalent information about a variable T conditioned on a non-empty subset of variables W iff the following conditions hold T
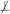 X | W, T
X | W, T
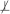 Y | W, T ⊥ X | (Y ∪ W), and T ⊥ Y | (X ∪ W).
Y | W, T ⊥ X | (Y ∪ W), and T ⊥ Y | (X ∪ W).
Definition 12 Context-independent equivalent information: Two subsets of variables X and Y from V contain context-independent equivalent information about a variable T iff X and Y contain equivalent information about T conditioned on any subset of variables V \(X ∪ Y ∪ {T}).
Finally, we point out that, in general, equivalent information does not always imply context-independent equivalent information. However, equivalent information due to deterministic relations always implies context-independent equivalent information.
2.4 Markov Boundary Theory
In this subsection we first define the concepts of Markov blanket and Markov boundary and theoretically characterize distributions with multiple Markov boundaries of the same response variable. Then we provide examples of such distributions and demonstrate that the number of Markov boundaries can even be exponential in the number of variables in the underlying network. We also state and prove theoretical results that connect the concepts of Markov blanket and Markov boundary with the data-generative graph. Finally, we define optimal predictor and prove a theorem that links the concept of Markov blanket with optimal predictor.
Definition 13 Markov blanket: A Markov blanket M of the response variable T ∈ V in the joint probability distribution over variables V is a set of variables conditioned on which all other variables are independent of T, that is, for every X ∈ (V \M\{T}), T ⊥ X | M.
Trivially, the set of all variables V excluding T is a Markov blanket of T. Also one can take a small Markov blanket and produce a larger one by adding arbitrary (predictively redundant or irrelevant) variables. Hence, only minimal Markov blankets are of interest.
Definition 14 Markov boundary: If no proper subset of M satisfies the definition of Markov blanket of T, then M is called a Markov boundary of T.
The following theorem states a sufficient assumption for the uniqueness of Markov boundaries and its proof is given in the book by Pearl (1988).
Theorem 3 If a joint probability distribution over variables V satisfies the intersection property, then for each X ∈ V, there exists a unique Markov boundary of X.
Since every joint probability distribution that is faithful to satisfies the intersection property (Theorem 1), then there is a unique Markov boundary in such distributions according to Theorem 3. However, Theorem 3 does not guarantee that Markov boundaries will be unique in distributions that do not satisfy the intersection property. In fact, as we will see below, Markov boundaries may not be unique in such distributions.
The following two lemmas allow us to explicitly construct and verify multiple Markov blankets and Markov boundaries when the distribution violates the intersection property (proofs are given in Appendix A).
Lemma 1 If M is a Markov blanket of T that contains a set Y, and there is a subset of variables Z such that Z and Y contain context-independent equivalent information about T, then Mnew = (M\Y)∪Z is also a Markov blanket of T.
Lemma 2 If M is a Markov blanket of T and there exists a subset of variables Mnew ⊆ V \{T} such that T ⊥ M | Mnew, then Mnew is also a Markov blanket of T.
The above lemmas also hold when M is a Markov boundary and immediately imply that Mnew is a Markov boundary assuming minimality of this subset.
The following three examples provide graphical structures and related probability distributions where multiple Markov boundaries exist. Notably, these examples also demonstrate that multiple Markov boundaries can exist even in large samples. Thus it is not an exclusively small-sample phenomenon, as it was postulated by earlier research (Ein-Dor et al., 2005, 2006).
Example 1 Consider a joint probability distribution described by a Bayesian network with graph A → B → T where A, B, and T are binary random variables that take values {0,1}. Given the local Markov condition, the joint probability distribution can be defined as follows: P(A = 0) = 0.3, P(B=0 |A=1)=1.0, P(B=1 |A=0)=1.0, P(T=0 | B=1)=0.2, P(T=0 | B=0)=0.4. Two Markov boundaries of T exist in this distribution: {A} and {B}.
Example 2 Figure 1 shows a graph of a causal Bayesian network and constraints on its parameterization.2 As can be seen, there is an equivalent partition in the domain of A to the T-partition of the domain of B. The following hold in any joint probability distribution of a causal Bayesian network that satisfies the constraints in the figure:
A and B are not deterministically related, yet they contain equivalent information about T;
There are two Markov boundaries of T ({A, C} and {B, C});
If an algorithm selects only one Markov boundary of T (e.g., {B, C}), then there is danger to miss causative variables (i.e., direct cause A) and focus instead on confounded ones (i.e., B);
The union of all Markov boundaries of T includes all variables that are adjacent with T ({A, C}).
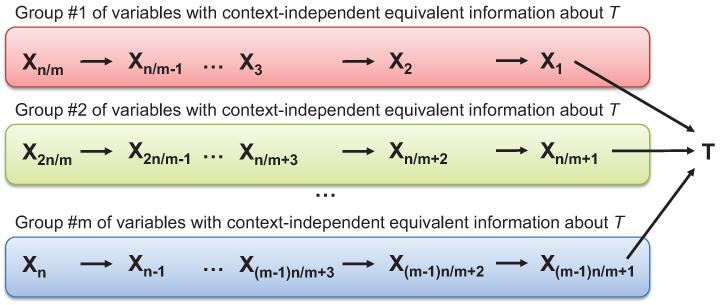
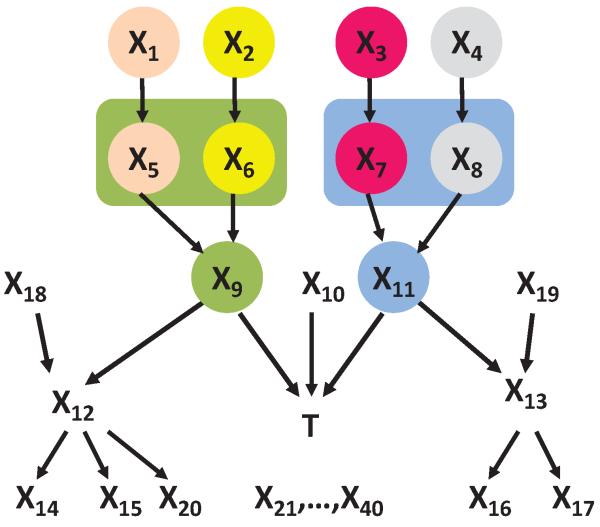
Example 3 Consider a Bayesian network shown in Figure 2. It involves n + 1 binary variables: X1,X2,…,Xn and a response variable T. Variables Xi can be divided into m groups such that any two variables in a group contain context-independent equivalent information about T. Assume that n is divisible by m. Since there are n/m variables in each group, the total number of Markov boundaries is (n/m)m. Now assume that k = n/m. Then the total number of Markov boundaries is km. Since k > 1 and m = O(n), it follows that the number of Markov boundaries grows exponentially in the number of variables in this example.
Figure 2.
Graph of a Bayesian network used to demonstrate that the number of Markov boundaries can be exponential in the number of variables in the network. The network parameterization is provided in Table 5 in Appendix B. The response variable is T. All variables take values {0,1}. All variables Xi in each group provide context-independent equivalent information about T.
Now we provide theoretical results that connect the concepts of Markov blanket and Markov boundary with the underlying causal graph. Theorem 4 was proved in the work by Neapolitan (2004) and Pearl (1988), Theorem 5 was proved in the work by Neapolitan (2004) and Tsamardinos and Aliferis (2003), and the proof of Theorem 6 is given in Appendix A.
Theorem 4 If a joint probability distribution satisfies the global Markov condition for directed graph , then the set of children, parents, and spouses of T is a Markov blanket of T.
Theorem 5 If a joint probability distribution is DAG-faithful to , then the set of children, parents, and spouses of T is a unique Markov boundary of T.
Theorem 6 If a joint probability distribution satisfies the global Markov condition for ancestral graph , then the set of children, parents, and spouses of T, and vertices connected with T or children of T by a bi-directed path (i.e., only with edges “↔”) and their respective parents is a Markov blanket of T.
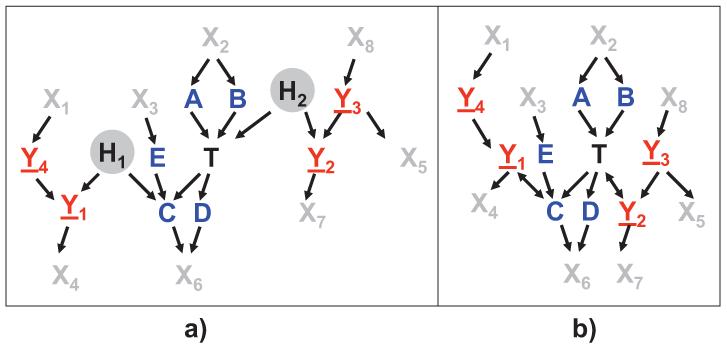
A graphical illustration of Theorem 6 is provided in Figure 3.
Figure 3.
Graphical illustration of a Markov blanket in an ancestral graph. a) Data-generative DAG, variables H1 and H2 are latent. b) Corresponding ancestral graph. The set of parents, children, and spouses of T are shown in blue. Vertices connected with T or children of T by a bi-directed path and their respective parents are shown in red and are underlined. If the global Markov condition holds for the graph and joint probability distribution, a Markov blanket of T consists of vertices shown in blue and red. All grey vertices will be then independent of T conditioned on the Markov blanket.
Definition 15 Optimal predictor: Given a data set (a sample from distribution ) for variables V, a learning algorithm , and a performance metric to assess learner's models, a variable set X ⊆ V \{T} is an optimal predictor of T if X maximizes the performance metric for predicting T using learner in the data set .
The following theorem links together the definitions of Markov blanket and optimal predictor, and its proof is given in Appendix A.
Theorem 7 If is a performance metric that is maximized only when P(T | V \{T}) is estimated accurately3 and is a learning algorithm that can approximate any conditional probability distribution,4 then M is a Markov blanket of T if and only if it is an optimal predictor of T.
2.5 Prior Algorithms for Learning a Single Markov Boundary
The Markov boundary algorithm IAMB is described in Figure 4 (Tsamardinos and Aliferis, 2003; Tsamardinos et al., 2003a). Originally, this algorithm was proved to be correct (i.e., that it identifies a Markov boundary) if the joint probability distribution is DAG-faithful to . Then it was proved to be correct when the composition property holds (Peña et al., 2007). The following theorem further relaxes conditions sufficient for correctness of IAMB, requiring that only the local composition property holds; the proof is given in Appendix A.
Figure 4.
IAMB algorithm.
Theorem 8 IAMB outputs a Markov boundary of T if the joint probability distribution satisfies the local composition property with respect to T.
Notice that IAMB identifies a Markov boundary of T by essentially implementing its definition and conditioning on the entire Markov boundary when testing variables for independence from the response T. Conditioning on the entire Markov boundary may become especially problematic in discrete data where the sample size required for high-confidence statistical tests of conditional independence grows exponentially in the size of the conditioning set. This in part motivated the development of the sample-efficient Markov boundary induction algorithmic family Generalized Local Learning, or GLL (Aliferis et al., 2010a). Figure 5 presents the Semi-Interleaved HITON-PC algorithm (Aliferis et al., 2010a), an instantiation of the GLL algorithmic family that we will use in the present paper. Originally, Semi-Interleaved HITON-PC was proved to correctly identify a set of parents and children of T in the Bayesian network if the joint probability distribution is DAG-faithful to and the so-called symmetry correction is not required (Aliferis et al., 2010a). The algorithm also retains its correctness for identification of a Markov boundary of T under more relaxed assumptions stated in Theorem 9 (proof is given in Appendix A).
Figure 5.
Semi-Interleaved HITON-PC algorithm (without “symmetry correction”), member of the Generalized Local Learning (GLL) algorithmic family. The algorithm is restated in a fashion similar to IAMB for ease of comparative understanding. Original pseudo-code is given in the work by Aliferis et al. (2010a).
Theorem 9 Semi-Interleaved HITON-PC outputs a Markov boundary of T if there is a Markov boundary of T in the joint probability distribution such that all its members are marginally dependent on T and are also conditionally dependent on T, except for violations of the intersection property that lead to context-independent information equivalence relations.
Theorem 9 can be also restated and proved using sufficient assumptions that are motivated by the common assumptions in the causal discovery literature: (i) the joint probability distribution and directed or ancestral graph are locally adjacency faithful with respect to T with the exception of violations of the intersection property that lead to context-independent information equivalence relations; (ii) satisfies the global Markov condition for ; (iii) the set of vertices adjacent with T in is a Markov blanket of T.
The proofs of correctness for the Markov boundary algorithms in Theorems 8 and 9 implicitly assume that the statistical decisions about dependence and independence are correct. This requirement is satisfied when the data set is a sufficiently large i.i.d. (independent and identically distributed) sample of the underlying probability distribution . When the sample size is small, the statistical tests of independence will incur type I and II errors. This may affect the correctness of the algorithms output Markov boundary.
In the empirical experiments of this work, we use Semi-Interleaved HITON-PC without “symmetry correction” as a primary method for Markov boundary induction because prior research has demonstrated empirical superiority of this algorithm compared to the version with the “symmetry correction”; the GLL-MB family of algorithms (including Semi-Interleaved HITON-MB) that can identify Markov boundary members that are non-adjacent spouses of T (and thus may be marginally independent with T); IAMB algorithms (Tsamardinos et al., 2003a); and other comparator Markov boundary induction methods (Aliferis et al., 2010a,b).
3. Prior Algorithms for Learning Multiple Markov Boundaries and Variable Sets
Table 1 summarizes the properties of prior algorithms for learning multiple Markov boundaries and variable sets, while a detailed description of the algorithms and their theoretical analysis is presented in Appendix C. As can be seen, there is no algorithm that is simultaneously theoretically correct, complete, computationally and sample efficient, and does not rely on extensive parameterization. This was our motivation for introducing the TIE* algorithmic family that is described in Section 4.
Table 1.
Prior algorithms for learning multiple Markov boundaries and variable sets. “+” means that the corresponding property is satisfied by a method, “−” means that the property is not satisfied, and “+/−” denotes cases where the property is satisfied under certain conditions.
| Markov boundary identification (assuming faithfulness except for violations of the intersection property) | Parameterization: does not require prior knowledge of | Computationally efficient | sample efficient | |||
|---|---|---|---|---|---|---|
| correct (identifies Markov boundaries) | complete (identifies all Markov boundaries) | the number of Markov boundaries/variable sets | the size of Markov boundaries/variable sets | |||
| KIAMB | + | + | − | + | − | − |
| EGS-CMIM | − | − | − | − | − | + |
| EGS-NCMIGS | − | − | − | +/− | − | + |
| EGSG | − | − | − | + | − | + |
| Resampling+RFE | − | − | − | + | − | + |
| Resampling+UAF | − | − | − | + | − | + |
| IR-HITON-PC | + | − | + | + | + | + |
| IR-SPLR | − | − | + | + | + | + |
We would like to note that not all algorithms listed in Table 1 are designed for identification of Markov boundaries; methods Resampling+RFE, Resampling+UAF, and IR-SPLR are designed for variable selection. However, sometimes variable sets output by these methods can approximate Markov boundaries, that is why we included these methods in our study (Aliferis et al., 2010a,b).
4. TIE*: A Family of Multiple Markov Boundary Induction Algorithms
In this section we present a generative anytime algorithm TIE* (which is an acronym for “Target Information Equivalence”) for learning from data all Markov boundaries of the response variable. This generative algorithm describes a family of related but not identical algorithms which can be seen as instantiations of the same broad algorithmic principles. We decided to state TIE* as a generative algorithm in order to facilitate a broader understanding of this methodology and devise formal conditions for correctness not only at the algorithm level but also at the level of algorithm family. The latter is achieved by specifying the general set of assumptions (admissibility rules) that apply to the generative algorithm and provide a set of flexible tools for constructing numerous algorithmic instantiations, each of which is guaranteed to be correct. This methodology thus significantly facilitates development of new correct algorithms for discovery of multiple Markov boundaries in various distributions.
4.1 Pseudo-Code and Trace
The pseudo-code of the TIE* generative algorithm is provided in Figure 6. On input TIE* receives (i) a data set (a sample from distribution ) for variables V, including a response variable T; (ii) a single Markov boundary induction algorithm ; (iii) a procedure to generate data sets from the so-called embedded distributions that are obtained by removing subsets of variables from the full set of variables V in the original distribution ; and (iv) a criterion to verify Markov boundaries of T. The inputs , , are selected to be suitable for the distribution at hand and should satisfy admissibility rules stated in Figure 7 for correctness of the algorithm (see next two subsections for details). The algorithm outputs all Markov boundaries of T that exist in the distribution .
Figure 6.
TIE* generative algorithm.
Figure 7.
Admissibility rules for inputs , , of the TIE* algorithm.
In step 1, TIE* uses a Markov boundary induction algorithm to learn a Markov boundary M of T from the data set for variables V (i.e., in the original distribution). Then M is output in step 2. In step 4, the algorithm uses a procedure to generate a data set that spans over a subset of variables that participate in . The motivation is that may lead to identification of a new Markov boundary of T that was previously “invisible” to a single Markov boundary induction algorithm because it was “masked” by another Markov boundary of T. Next, in step 5 the Markov boundary algorithm is applied to , resulting in a Markov boundary Mnew in the embedded distribution. If Mnew is also a Markov boundary of T in the original distribution according to criterion , then Mnew is output (step 6). The loop in steps 3–7 is repeated until all data sets generated by procedure have been considered.
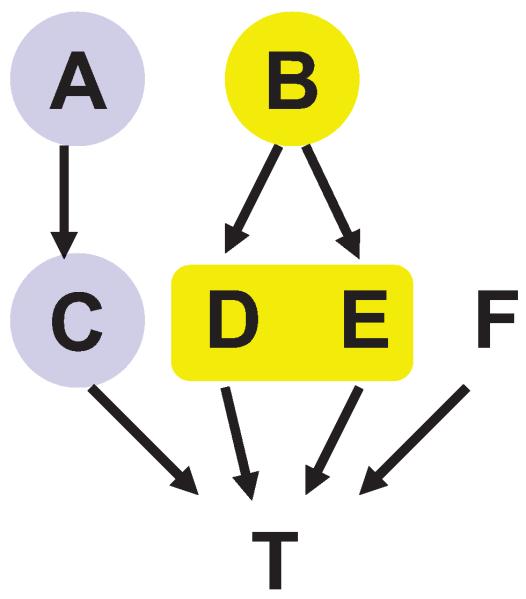
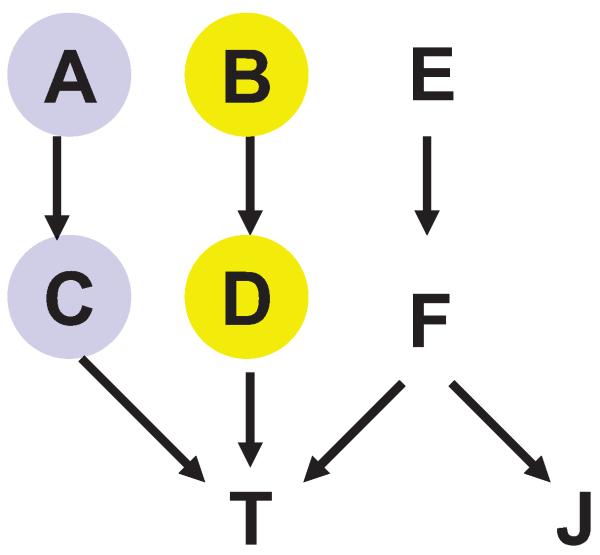
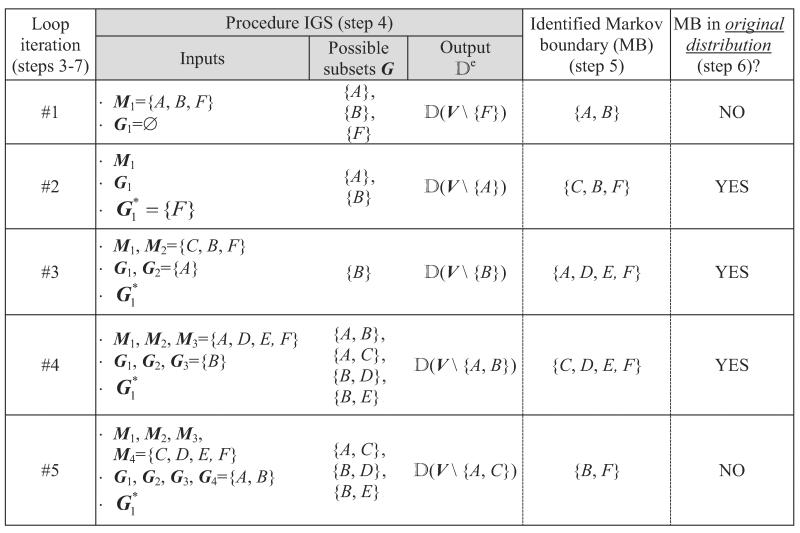
Next we provide a high-level trace of the algorithm. Consider running an instance of the TIE* algorithm with admissible inputs , , implemented by an oracle in the data set generated from the example causal Bayesian network shown in Figure 8.5 The response variable T is directly caused by C, D, E, and F. The underlying distribution is such that variables A and C contain equivalent information about T; likewise two variables {D,E} jointly and a single variable B contain equivalent information about T. In step 1 of TIE* (Figure 6), a Markov boundary induction algorithm is applied to learn a Markov boundary of T, resulting in M = {A,B,F}. Then M is output in step 2. In step 4, a procedure considers removing G = {F} and generates a data set for variables V \ G. Then in step 5 the Markov boundary induction algorithm is run on the data set . This yields a Markov boundary of T in the embedded distribution Mnew = {A,B}. The criterion in step 6 does not confirm that Mnew is also Markov boundary of T in the original distribution; thus Mnew is not output. The loop is run again. In step 4 the procedure considers removing G = {A} and generates a data set for variables V \ G. The Markov boundary induction algorithm in step 5 yields a Markov boundary of T in the embedded distribution Mnew = {C,B,F}. The criterion in step 6 confirms that Mnew is also a Markov boundary in the original distribution, thus it is returned. Similarly, when the Markov boundary induction algorithm is run on the data set where G = {B} or G = {A,B}, two additional Markov boundaries of T in the original distribution, {A,D,E,F} or {C,D,E,F}, respectively, are found and output. The algorithm terminates shortly. In total, four Markov boundaries of T are output by the algorithm: {A,B,F}, {C,B,F}, {A,D,E,F} and {C,D,E,F}. These are exactly all Markov boundaries of T that exist in the distribution.
Figure 8.
Graph of a causal Bayesian network used to trace the TIE* algorithm. The network parameterization is provided in Table 6 in Appendix B. The response variable is T. All variables take values {0,1} except for B that takes values {0,1,2,3}. Variables A and C contain equivalent information about T and are highlighted with the same color. Likewise, two variables {D,E} jointly and a single variable B contain equivalent information about T and thus are also highlighted with the same color.
4.2 Specific Instantiations
In this subsection we give several specific instantiations of the generative algorithm TIE* (Figure 6) and in the next subsection we prove their admissibility (i.e., that they satisfy rules stated in Figure 7). An instantiation of TIE* is specified by assigning its inputs , , to well-defined algorithms.
Input : This is a Markov boundary induction algorithm. For example, we can use IAMB (Figure 4) or Semi-Interleaved HITON-PC (Figure 5) algorithms that were described in Section 2.5. Other sound Markov boundary induction algorithms can be used as well (Aliferis et al., 2010a, 2003a; Mani and Cooper, 2004; Peña et al., 2007; Tsamardinos and Aliferis, 2003; Tsamardinos et al., 2003a,b).
Input : This is a procedure to generate data sets from the embedded distributions that would allow identification of new Markov boundaries of T. Before we give specific examples of this procedure, it is worthwhile to understand its use in TIE*. The main principle of TIE* is to first identify a Markov boundary of T in the original distribution and then iteratively run a Markov boundary induction algorithm in data sets from the embedded distributions (that are obtained by removing subsets of variables from M) in order to identify new Markov boundaries in the original distribution. Generating such data sets from the embedded distributions is the purpose of procedure . The reason why we need to remove subsets of variables from the original data and rerun Markov boundary induction algorithm in the data set is because some variables “mask” Markov boundaries during operation of conventional single Markov boundary induction algorithms by rendering some of the Markov boundary members conditionally independent of T. One possible approach is to generate data sets by removing subsets of the original Markov boundary, or, more broadly, subsets from all currently identified Markov boundaries. The procedure termed IGS (which is an acronym for “Incremental Generation of Subsets”) implements the above stated approach and is described in Figure 9.6
Figure 9.
Procedure IGS () to generate data sets from the embedded distributions Note that IGS is a procedure (not a function), and we assume that and G are accessible in the scope of TIE*.
Below and in Table 2 we revisit the trace of TIE* that was given in the previous subsection, now focusing on the operation of the procedure IGS () from Figure 9. Recall that application of the Markov boundary induction algorithm in step 1 of TIE* resulted in M = {A,B,F}. In step 4 of TIE*, the procedure IGS can generate data sets from the embedded distributions by removing any of the three possible subsets G = {A} or {B} or {F} from V (it will not consider larger subsets because of the requirement of the smallest subset size in step 1 of IGS, see Figure 9). Recall that next we considered a data set obtained by removing G = {F} and identified via algorithm a Markov boundary in the embedded distribution Mnew ={A,B} that did not turn out to be a Markov boundary in the original distribution. When the procedure IGS is executed in the following iterations of steps 3–7, it will never generate data set without {F} because and we require that G does not include for j = 1,…,m. In the next iteration, IGS can generate two possible data sets by removing G = {A} or {B} from V. In order to be consistent with our previous trace, assume that the procedure IGS output a data set obtained by removing G = {A} which led to identification of a new Markov boundary both in the original and embedded distribution Mnew={C,B,F}. When the procedure IGS is executed in the next iteration, it will generate a data set by removing a subset G = {B} from V (all other subsets will have two or more variables and thus will not be considered). This would lead to identification of a new Markov boundary both in the original and embedded distribution Mnew ={A,D,E,F}. When the procedure IGS is executed in the next iteration, it can generate data sets by removing G ={A,B} or{A,C} or {B,D} or {B,E} from V. Assume that the procedure generated a data set by removing G ={A,B}, which would lead to identification of a new Markov boundary both in the original and embedded distribution Mnew ={C,D,E,F}. Several more iterations will follow, but no new Markov boundaries in the original distribution will be identified (see Table 2 for one more iteration), and TIE* will terminate.
Table 2.
Part of the trace of TIE*, focusing on operation of the procedure .
|
As it follows from the above example, we may have several possibilities for the subset G (and thus for defining a data set ) in the procedure IGS and we need to define rules in order to select a single subset. We therefore provide three specific implementations of the procedure IGS:
IGS-Lex (“Lex” stands for “lexicographical”): Procedure IGS from Figure 9 where one chooses a subset G with the smallest lexicographical order of its variables;
IGS-MinAssoc (“MinAssoc” stands for “minimal association”): Procedure IGS from Figure 9 where one chooses a subset G with the smallest association with the response variable T;
IGS-MaxAssoc (“MaxAssoc” stands for “maximal association”): Procedure IGS from Figure 9 where one chooses a subset G with the largest association with the response variable T.
The above three instantiations of the procedure IGS may lead to different traces of the TIE* algorithm, however the final output of the algorithm will be the same (it will discover all Markov boundaries of T).
Input : This is a criterion that can verify whether Mnew, a Markov boundary in the embedded distribution (that was found by application of the Markov boundary induction algorithm in step 5 of TIE* to the data set ) is also a Markov boundary in the original distribution. In other words, it is a criterion to verify the Markov boundary property of Mnew in the original definition. For example, we can use the following two criteria given in Figures 10 and 11. Criterion Independence from Figure 10 is closely related to the definition of the Markov boundary, and essentially implies its verification. Criterion Predictivity from Figure 11 verifies Markov boundaries by assessing their predictive (classification or regression) performance using some learning algorithm and performance metric.
Figure 10.
Criterion Independence () to verify Markov boundaries.
Figure 11.
Criterion Predictivity () to verify Markov boundaries.
Appendix D provides two concrete admissible instantiations of the generative algorithm TIE*(admissibility follows from theoretical results presented in the next subsection). The instantiation in Figure 17 is obtained using = Semi-Interleaved HITON-PC, = IGS, = Predictivity. The instantiation in Figure 18 is obtained using = Semi-Interleaved HITON-PC, = IGS, = Independence. Appendix D also gives practical considerations for computer implementations of TIE*.
Figure 17.
An example of instantiated TIE* algorithm. This algorithm was used in experiments with real data in Section 5.2.
Figure 18.
An example of instantiated TIE* algorithm. This algorithm was used in experiments with simulated data in Section 5.1.
4.3 Analysis of the Algorithm Correctness
In this subsection we state theorems about correctness of TIE* and its specific instantiations that were described in the previous subsection and Appendix D. The proofs of all theorems are given in Appendix A.
First we show that the generative algorithm TIE* is sound and complete:
Theorem 10 The generative algorithm TIE* outputs all and only Markov boundaries of T that exist in the joint probability distribution if the inputs are admissible (i.e., satisfy admissibility rules in Figure 7).
Now we show that IAMB (Figure 4) and Semi-Interleaved HITON-PC (Figure 5) are admissible Markov boundary algorithms for TIE* under sufficient assumptions. In the case of the IAMB algorithm, the sufficient assumptions for TIE* admissibility are the same as sufficient assumptions for the general algorithm correctness (see Theorem 8). This leads to the following theorem.
Theorem 11 IAMB is an admissible Markov boundary induction algorithm for TIE* (input ) if the joint probability distribution satisfies the local composition property with respect to T.
However, the sufficient assumptions for the general correctness of Semi-Interleaved HITON-PC (Theorem 9) are not sufficient for TIE* admissibility and require further restriction. Specifically, we need to require that all members of all Markov boundaries retain marginal and conditional dependence on T, except for certain violations of the intersection property. This leads to the following theorem.
Theorem 12 Semi-Interleaved HITON-PC is an admissible Markov boundary induction algorithm for TIE* (input ) if all members of all Markov boundaries of T that exist in the joint probability distribution are marginally dependent on T and are also conditionally dependent on T, except for violations of the intersection property that lead to context-independent information equivalence relations.
The next theorem states that the procedure IGS (Figure 9) is admissible for TIE*:
Theorem 13 Procedure IGS to generate data sets from the embedded distributions (input ) is admissible for TIE*.
Finally we show that both criteria Independence (Figure 10) and Predictivity (Figure 11) for verification of Markov boundaries are admissible for TIE* and state sufficient assumptions for the latter criterion. The former criterion implicitly assumes correctness of statistical decisions, similarly to IAMB and Semi-Interleaved HITON-PC (see end of Section 2.5 for related discussion).
Theorem 14 Criterion Independence to verify Markov boundaries (input ) is admissible for TIE*
Theorem 15 Criterion Predictivity to verify Markov boundaries (input ) is admissible for TIE* if the following conditions hold: (i) the learning algorithm can accurately approximate any conditional probability distribution, and (ii) the performance metric is maximized only when P(T| V \ {T}) is estimated accurately.
As mentioned in the beginning of Section 4, the generative nature of TIE* facilitates design of new algorithms for discovery of multiple Markov boundaries by simply instantiating TIE* with input components , , . Furthermore, if , , { are admissible, then TIE* will be sound and complete according to Theorem 10, otherwise the algorithm will be heuristic. For example, one can take an established Markov boundary induction algorithm, prove its admissibility, and then plug it into TIE* with admissible components and (e.g., ones presented above). This will yield a new correct algorithm and significant economies in the proof of its correctness because one has only to prove admissibility of new input components.
4.4 Complexity Analysis
We first note that the computational complexity of TIE* depends on a specific instantiation of its input components (Markov boundary induction algorithm), (procedure for generating data sets from the embedded distributions) and (criterion for verifying Markov boundaries), and on the underlying joint probability distribution over a set variables V. In this subsection we will consider the complexity of the following two specific instantiations of TIE*: (= Semi-Interleaved HITON-PC, =IGS-Lex, =Independence) and (= IAMB, =IGS-Lex, =Independence).
Since in our experiments we found that Markov boundary induction (with input component ) was the most computationally expensive step in TIE* and accounted for > 99% of algorithm runtime, we will omit from consideration the complexity of components and , and will use the complexity of component to derive an estimate of the total computational complexity of TIE*. Following general practice in complexity analysis of Markov boundary and causal discovery algorithms, we measure computational complexity in terms of the number of statistical tests of conditional independence.7 For completeness we also note that there exist efficient implementations of the G2 test for discrete variables that can take only time nlog(n) in the number of training instances n. The time for computation of Fishers Z-test for continuous variables is also bounded by a low order polynomial in n because this test essentially involves solution of a linear system. See the work by Aliferis et al. (2010a) and Anderson (2003) for more details and discussion.
As with all sound and complete computational causal discovery algorithms, discovery of all Markov boundaries (and even one Markov boundary) is worst-case intractable. However we are interested in the average-case complexity of TIE* in real-life distributions that is more instructive to consider. Complexities of Markov boundary induction algorithms IAMB and Semi-Interleaved HITON-PC are O(|V||M|) and O(|V|2|M|), respectively, assuming that the size of the candidate Markov boundary M obtained in the Forward phase is close to the size of the true Markov boundary obtained after the Backward phase (see Figures 4 and 5), which is typically the case in practice (Aliferis et al., 2010a; Tsamardinos and Aliferis, 2003; Tsamardinos et al., 2003a). When TIE* is parameterized with the IGS procedure (as the component ) and there is only one Markov boundary M in the distribution, TIE* will invoke a Markov boundary induction algorithm , |M|+ 1 number of times. Thus, the total computational complexity of TIE* in this case becomes O(|V ||M|2) if and O(|V ||M| | 2|M|) if HITON-PC. When N Markov boundaries with the average size |M| are present in the distribution, TIE* with IGS procedure will invoke a Markov boundary induction algorithm no more than O(N2|M|) times. Therefore, the total complexity of TIE* with the IGS procedure is O(N2|M||V ||M|)) when and O(N|V |22|M|) when HITON-PC.
In practical applications of TIE* with Semi-Interleaved HITON-PC, we use an additional caching mechanism for conditional independence decisions, which alleviates the need to repeatedly conduct the same conditional independence tests during Markov boundary induction when we have only slightly altered the data set by removing a subset of variables G. In this case, induction of the first Markov boundary still takes O(|V |2|M|) independence tests, but all consecutive Markov boundaries typically require less than O(|V |) conditional independence tests. Thus, the overall complexity of TIE* with the IGS procedure and Semi-Interleaved HITON-PC becomes O(|V |2|M| + (N −1)|V |2|M|), or equivalently O(N|V |2|M|).
Finally, in practice we use parameters max-card for IGS procedure in TIE* and max-k for Semi-Interleaved HITON-PC to limit the number of conditional independence tests (see Appendix D). Thus, complexity of TIE* with the IGS procedure becomes O(N|V ||M|max-card+1) when and O(|V ||M|max-k + (N − 1)|V ||M|max-card) when HITON-PC.
4.5 A Simple and Fast Algorithm for Special Distributions
The TIE* algorithm allows to find all Markov boundaries when there are information equivalence relations between arbitrary sets of variables. A simpler and faster algorithm can be obtained by restricting consideration to distributions where all information equivalence relations follow from context-independent information equivalence relations between individual variables. The resulting algorithm is termed iTIE*(which is an acronym for “Individual Target Information Equivalence”) and is described in Figure 12. As can be seen, iTIE* can be described as a modification to Semi-Interleaved HITON-PC (or GLL-PC in general).
Figure 12.
iTIE* algorithm, presented as a modification of Semi-Interleaved HITON-PC. Similar algorithms may be obtained by modification of other members of the GLL-PC algorithmic family (Aliferis et al., 2010a).
Consider running the iTIE* algorithm on data generated from the example causal Bayesian network shown in Figure 13. The response variable T is directly caused by C, D, F. The underlying distribution is such that variables A and C contain equivalent information about T; likewise variables B and D contain equivalent information about T. iTIE* starts by executing Semi-Interleaved HITON-PC with the modified steps 6 and 7. Assume that we are running the loop in steps 3–8 of Semi-Interleaved HITON-PC and currently E = {C,D} and M = {A,B,F}; variables E and J were eliminated conditioned on F in previous iterations of the loop. In step 4 of Semi-Interleaved HITON-PC, the algorithm may select Y = C. Next the modified steps 6 and 7 of Semi-Interleaved HITON-PC proceed as described in Figure 12, namely: 1(a) we find that a subset Z={A} renders T independent of Y = C; 1(c) T is marginally dependent on Y = C,T is marginally dependent on Z = {A}, and Y = C renders T independent of Z = {A}, thus 1(d) we record in Θ that Y = C and Z = {A} contain equivalent information with respect to T. In the next iteration of the loop in steps 3– 8 of the modified Semi-Interleaved HITON-PC, we record in Θ that Y = D and Z = {B} contain equivalent information with respect to T. The Backward phase in steps 9–13 of Semi-Interleaved HITON-PC does not result in variable eliminations in this example, thus we have M = {A,B,F}. Finally, we build Cartesian product of information equivalence relations for subsets of M that are stored in Θ and obtain 4 Markov boundaries of T: {A,B,F},{A,D,F},{C,B,F}, and {C,D,F}.
Figure 13.
Graph of a causal Bayesian network used to trace the iTIE* algorithm. The network parameterization is provided in Table 7 in Appendix B. The response variable is T. All variables take values {0,1}. Variables A and C contain equivalent information about T and are highlighted with the same color. Likewise, variables B and D contain equivalent information about T and thus are also highlighted with the same color.
The iTIE* algorithm correctly identifies all Markov boundaries under the following sufficient assumptions: (a) all equivalence relations in the underlying distribution follow from context-independent equivalence relations of individual variables, and (b) the assumptions of Theorem 12 hold. The proof of correctness of iTIE* can be obtained from the proofs of Theorems 9 and 12 and Lemma 1.
It is also important to notice that in some cases iTIE* can identify all Markov boundaries even if the above stated sufficient assumption (a) is violated; that is why we do not exclude the possibility that Z can be a set of variables in steps 1(c,d) of iTIE*. Consider a Bayesian network with the graph 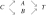 that is parameterized such that a variable C and the set of variables {A,B} jointly contain context-independent equivalent information about T, and T is marginally dependent on A,B,C. Thus, there are two Markov boundaries of T in the joint probability distribution: {C} and {A,B}. Now consider a situation when iTIE* first admits {A,B} to M during execution of the modified Semi-Interleaved HITON-PC or another instance of GLL-PC. Then the step 1(c) of iTIE* will reveal that while T ⊥ C | {A,B}, the following relations hold T
that is parameterized such that a variable C and the set of variables {A,B} jointly contain context-independent equivalent information about T, and T is marginally dependent on A,B,C. Thus, there are two Markov boundaries of T in the joint probability distribution: {C} and {A,B}. Now consider a situation when iTIE* first admits {A,B} to M during execution of the modified Semi-Interleaved HITON-PC or another instance of GLL-PC. Then the step 1(c) of iTIE* will reveal that while T ⊥ C | {A,B}, the following relations hold T
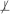 C, T
C, T
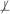 {A,B}, and T ⊥ {A,B} | C. Thus, the algorithm will identify that C and {A,B} contain equivalent information about T and will correctly find all Markov boundaries in the distribution. However, if iTIE* first admits C to M, then the algorithm will output only one Markov boundary of T that consists of a single variable C, because variables A and B, when considered separately, will be eliminated by conditioning on C and no equivalence relations will be found.
{A,B}, and T ⊥ {A,B} | C. Thus, the algorithm will identify that C and {A,B} contain equivalent information about T and will correctly find all Markov boundaries in the distribution. However, if iTIE* first admits C to M, then the algorithm will output only one Markov boundary of T that consists of a single variable C, because variables A and B, when considered separately, will be eliminated by conditioning on C and no equivalence relations will be found.
Notice that unlike TIE*, iTIE* does not rely on repeated invocation of a Markov boundary induction algorithm and instead extends Semi-Interleaved HITON-PC by potentially performing at most one additional independence test for each variable in V during the Forward phase, as shown in Figure 12.8 This allows iTIE* to maintain computational complexity of the same order as Semi-Interleaved HITON-PC, namely, O(|V |2|M|) conditional independence tests. As before, |M| denotes the average size of a Markov boundary and the above complexity bound assumes that the size of a candidate Markov boundary obtained in the Forward phase is close to the size of a true Markov boundary obtained at the end of the Backward phase (see Figure 5). In practical applications of iTIE*, we also use parameter max-k that limits the maximum size of a conditioning test, which brings complexity of iTIE* to O(|V ||M|max-k). Interestingly, iTIE* can efficiently identify all Markov boundaries in the distribution shown in Figure 2. This is due to the fact that the distribution in Figure 2 satisfies the assumption underlying iTIE* (i.e., that all information equivalences in a distribution follow from context-independent equivalences between individual variables) and thus allows it to capture all equivalence relationships between variables within groups in a single run of the Forward phase of the modified Semi-Interleaved HITON-PC. All Markov boundaries in the example in Figure 2 can then be reconstructed by taking the Cartesian product over sets of variables found to be equivalent with respect to T in step 2 of iTIE* (Figure 12).
For experiments reported in this work, we implemented and ran iTIE* based on the Causal Explorer code of Semi-Interleaved HITON-PC (Aliferis et al., 2003b; Statnikov et al., 2010) with values of parameters and statistical tests of independence that are described in Appendix D.
5. Empirical Experiments
In this section, we present experimental results obtained by applying methods for learning multiple Markov boundaries and variable sets on simulated and real data. The evaluated methods and their parameterizations are shown in Table 9 in Appendix E. These methods were chosen for our evaluation as they are the current state-of-the-art techniques for discovery of multiple Markov boundaries and variable sets. In order to study the behavior of these methods as a function of parameter settings, we considered several distinct parameterizations of each algorithm. In cases when parameter settings have been recommended by the authors of a method, we included these settings in our evaluation. A detailed description of parameters of prior methods for induction of multiple Markov boundaries and variable sets is provided in Appendix C.
Table 9.
Parameterizations of methods for discovery of multiple Markov boundaries and variable sets. Parameter settings that have been recommended by the authors of prior methods are underlined.

|
All experiments involving assessment of classification performance were executed by holdout validation or cross-validation (see below), whereby Markov boundaries and variable sets are discovered in a training subset of data samples (training set), classification models based on the above variables are also developed in the training set, and the reported performance of classification models is estimated in an independent testing set. Assessment of classification performance of the extracted Markov boundaries and variable sets was done using Support Vector Machines (SVMs) (Vapnik, 1998). We chose to use SVMs due to their excellent empirical performance across a wide range of application domains (especially with high-dimensional data and relatively small sample sizes), regularization capabilities, ability to learn both simple and complex classification functions, and tractable computational time (Cristianini and Shawe-Taylor, 2000; Schölkopf et al., 1999; Shawe-Taylor and Cristianini, 2004; Vapnik, 1998). When the response variable was multiclass, we applied SVMs in one-versus-rest fashion (Schölkopf et al., 1999). We used libSVM v.2.9.1 (http://www.csie.ntu.edu.tw/~cjlin/libsvm/) implementation of SVMs in all experiments (Fan et al., 2005). Polynomial kernels were used in SVMs as they have shown good classification performance across the data domains considered in this study. The degree d of the polynomial kernel and the penalty parameter C of SVM were optimized by cross-validation on the training data. Each variable in a data set was scaled to [0,1] range to facilitate SVM training. The scaling constants were computed on the training set of samples and then applied to the entire data set.
All experiments presented in this section were run on the Asclepius Compute Cluster at the Center for Health Informatics and Bioinformatics (CHIBI) at New York University Langone Medical Center (http://www.nyuinformatics.org) and the Advanced Computing Center for Research and Education (ACCRE) at Vanderbilt University (http://www.accre.vanderbilt.edu/). For comparative purposes all experiments used exclusively the latest generation of Intel Xeon Nehalem (x86) processors. Overall, it took >50 years of single CPU time to complete all reported experiments.
5.1 Experiments with Simulated Data
Below we present an evaluation of methods for extraction of multiple Markov boundaries and variable sets in simulated data. Simulated data allows us to evaluate methods in a controlled setting where the underlying causal process and all Markov boundaries of the response variable T are known exactly. Two data sets were used in this evaluation. One of these data sets, referred to as TIED, was previously used in an international causality challenge (Statnikov and Aliferis, 2010b). TIED contains 30 variables, including the response variable T. The underlying causal graph and its parameterization are given in the work by Statnikov and Aliferis (2010b). There are 72 distinct Markov boundaries of T. Each Markov boundary contains 5 variables: variable X10 and one variable from each of the four subsets {X1,X2,X3,X11}, {X5,X9}, {X12,X13,X14} and {X19,X20,X21}. Another simulated data set, referred to as TIED1000, contains 1,000 variables in total and was generated by the causal process of TIED augmented with an additional 970 variables that have no association with T. TIED1000 has the same set of Markov boundaries of T as TIED. TIED1000 allows us to study the behavior of different methods for learning multiple Markov boundaries and variable sets in an environment where the fraction of variables carrying relevant information about T is small.
For each of the two data sets, 750 observations were used for discovery of Markov boundaries/variable sets and training of the SVM classification models of the response variable T (with the goal to predict its values from the inferred Markov boundary variables), and an independent testing set of 3,000 observations was used for evaluation of the models' classification performance.
All methods for extracting multiple Markov boundaries and variable sets were assessed based on the following six performance criteria:
The number of distinct Markov boundaries/variable sets output by the method.
The average size of an output Markov boundary/variable set (number of variables).
The number of true Markov boundaries identified exactly, that is, without false positives and false negatives.9
The average Proportion of False Positives (PFP) in the output Markov boundaries/variable sets.10
The average False Negative Rate (FNR) in the output Markov boundaries/variable sets.11
The average classification performance (weighted accuracy) over all output Markov boundaries/variable sets.12 We also compared the average classification performance of the SVM models with the maximum a posteriori classifier in the true Bayesian network (denoted as MAP-BN) using the same data sample.
Technical details about computing performance criteria III–V are given in Appendix E.
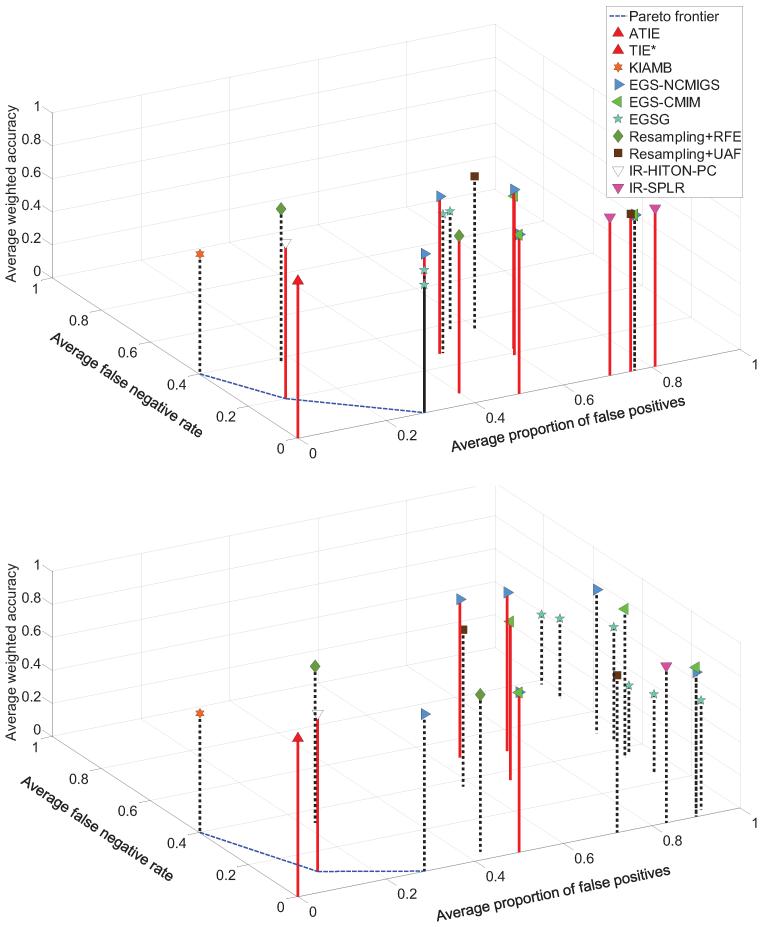
The results presented in Figure 14 in the manuscript, and Tables 10 and 11 and Figure 19 in Appendix E show that only TIE* and iTIE* identified exactly all and only true Markov boundaries of T in both simulated data sets, and their classification performance with the SVM classifier was statistically comparable to performance of the MAP-BN classifier. None of the comparator methods, regardless of the number of Markov boundaries/variable sets output, were able to identify exactly any of the 72 true Markov boundaries, except for Resampling+RFE (without statistical comparison) and IR-HITON-PC that identified exactly 1–2 out of 72 true Markov boundaries, depending on the data set. Overall prior methods had either large proportion of false positives or large false negative rate, and often their classification performance was significantly worse that the performance of the MAP-BN classifier. However, in some cases the classification performance of other methods was comparable to the MAP-BN classifier, regardless of the number of Markov boundaries identified exactly. This can be attributed to (i) the relative insensitivity of the SVM classifiers to false positives, (ii) connectivity in the underlying graph that compensates false negatives with other weakly relevant variables, and (iii) differences between the employed classification performance metric (weighted accuracy) and the metric which is maximized by the Markov boundary variables (that requires accurate estimation of P(T | V \{T}), which is a harder task than maximizing proportions of correct classification in the weighted accuracy metric). Thus, we remind the reader that a high classification performance is often a necessary but not sufficient condition for correct identification of Markov boundaries. Detailed discussion of the performance of comparator methods is given in Appendix E.
Figure 14.
Results for average classification performance (weighted accuracy), average false negative rate, and average proportion of false positives that were obtained in TIED (top figure) and TIED1000 (bottom figure) data sets. The style and color of a vertical line connecting each point with the plane shows whether the average SVM classification performance of a method is statistically comparable with the MAP-BN classifier in the same data sample (red solid line) or not (black dotted line). The Pareto frontier was constructed based on the average false negative rate and the average proportion of false positives over the comparator methods (i.e., non-TIE*). Results of TIE* and iTIE* were identical in both data sets.
Table 10.
Results obtained in simulated data set TIED. “MB” stands for “Markov boundary”, and “VS” stands for “variable set”. The 95% interval for weighted accuracy denotes the range in which weighted accuracies of 95% of the extracted Markov boundaries/variable sets fell. Classification performance of the MAP-BN classifier in the same data sample was 0.966 weighted accuracy. Highlighted in bold are results that are statistically comparable to the MAP-BN classification performance.
| Method | I. Number of distinct MBs or VSs | II. Average size of extracted distinct MBs or VSs | III. Number of true MBs identified exactly | IV. Average proportion of false positives | V. Average false negative rate | VI. Weighted accuracy over all extracted MBs or VSs | |||
|---|---|---|---|---|---|---|---|---|---|
| Average | 95% Interval | ||||||||
| TIE* | max-k = 3, α = 0.05 | 72 | 5.0 | 72 | 0.000 | 0.000 | 0.951 | 0.938 | 0.965 |
| iTIE* | max-k = 3, α = 0.05 | 72 | 5.0 | 72 | 0.000 | 0.000 | 0.951 | 0.938 | 0.965 |
| KIAMB | Number of runs = 5000, α = 0.05, K = 0.7 | 377 | 2.8 | 0 | 0.000 | 0.400 | 0.727 | 0.479 | 0.946 |
| Number of runs = 5000, α = 0.05, K = 0.8 | 377 | 2.8 | 0 | 0.000 | 0.400 | 0.727 | 0.479 | 0.946 | |
| Number of runs = 5000, α = 0.05, K = 0.9 | 377 | 2.8 | 0 | 0.000 | 0.400 | 0.727 | 0.479 | 0.946 | |
| EGS-NCMIGS | l = 7, δ = 0.015 | 6 | 7.0 | 0 | 0.286 | 0.000 | 0.964 | 0.963 | 0.965 |
| l = 7, K = 10 | 6 | 10.0 | 0 | 0.500 | 0.000 | 0.964 | 0.963 | 0.965 | |
| l = 7, K = 50 | 6 | 21.0 | 0 | 0.762 | 0.000 | 0.941 | 0.937 | 0.943 | |
| l = 5000, δ = 0.015 | 24 | 7.3 | 0 | 0.469 | 0.267 | 0.954 | 0.843 | 0.967 | |
| l = 5000, K = 10 | 20 | 10.0 | 0 | 0.610 | 0.220 | 0.964 | 0.954 | 0.970 | |
| l = 5000, K = 50 | 9 | 21.0 | 0 | 0.762 | 0.000 | 0.944 | 0.937 | 0.954 | |
| EGS-CMIM | l = 7, K = 10 | 6 | 10.0 | 0 | 0.500 | 0.000 | 0.963 | 0.963 | 0.965 |
| l = 7, K = 50 | 6 | 21.0 | 0 | 0.762 | 0.000 | 0.939 | 0.937 | 0.942 | |
| l = 5000, K = 10 | 20 | 10.0 | 0 | 0.595 | 0.190 | 0.963 | 0.951 | 0.969 | |
| l = 5000, K = 50 | 9 | 21.0 | 0 | 0.762 | 0.000 | 0.943 | 0.937 | 0.954 | |
| EGSG | Number of Markov boundaries = 30, t = 5 | 30 | 7.0 | 0 | 0.476 | 0.267 | 0.840 | 0.605 | 0.968 |
| Number of Markov boundaries = 30, t = 10 | 30 | 7.0 | 0 | 0.548 | 0.367 | 0.722 | 0.379 | 0.962 | |
| Number of Markov boundaries = 30, 1 = 15 | 30 | 7.0 | 0 | 0.548 | 0.367 | 0.722 | 0.379 | 0.962 | |
| Number of Markov boundaries = 5,000, t = 5 | 1,997 | 7.0 | 0 | 0.286 | 0.000 | 0.863 | 0.620 | 0.965 | |
| Number of Markov boundaries = 5,000, t = 10 | 3,027 | 7.0 | 0 | 0.286 | 0.000 | 0.774 | 0.500 | 0.965 | |
| Number of Markov boundaries = 5,000, t = 15 | 3,027 | 7.0 | 0 | 0.286 | 0.000 | 0.774 | 0.500 | 0.965 | |
| Resampling+RFE | without statistical comparison | 1,374 | 14.9 | 1 | 0.397 | 0.058 | 0.955 | 0.932 | 0.979 |
| with statistical comparison (α = 0.05) | 188 | 4.9 | 0 | 0.171 | 0.378 | 0.930 | 0.917 | 0.967 | |
| Resampling+UAF | without statistical comparison | 184 | 20.8 | 0 | 0.752 | 0.000 | 0.953 | 0.934 | 0.966 |
| with statistical comparison (α = 0.05) | 19 | 8.4 | 0 | 0.592 | 0.347 | 0.930 | 0.917 | 0.938 | |
| IR-HITON-PC | max-k = 3, α = 0.05 | 3 | 4.3 | 1 | 0.083 | 0.200 | 0.946 | 0.936 | 0.965 |
| IR-SPLR | without statistical comparison | 1 | 26.0 | 0 | 0.808 | 0.000 | 0.958 | 0.958 | 0.958 |
| with statistical comparison (α = 0.05) | 1 | 17.0 | 0 | 0.706 | 0.000 | 0.959 | 0.959 | 0.959 | |
Table 11.
Results obtained in simulated data set TIED1000. “MB” stands for “Markov boundary”, and “VS” stands for “variable set”. The 95% interval for weighted accuracy denotes the range in which weighted accuracies of 95% of the extracted Markov boundaries/variable sets fell. Classification performance of the MAP-BN classifier in the same data sample was 0.972 weighted accuracy. Highlighted in bold are results that are statistically comparable to the MAP-BN classification performance.
| Method | I. Number of distinct MBs or VSs | II. Average size of extracted distinct MBs or VSs | III. Number of true MBs identified exactly | IV. Average proportion of false positives | V. Average false negative rate | VI. Weighted accuracy over all extracted MBs or VSs | |||
|---|---|---|---|---|---|---|---|---|---|
| Average | 95% Interval | ||||||||
| TIE* | max-k = 3, α = 0.05 | 72 | 5.0 | 72 | 0.000 | 0.000 | 0.957 | 0.952 | 0.960 |
| iTIE* | max-k = 3, α = 0.05 | 72 | 5.0 | 72 | 0.000 | 0.000 | 0.957 | 0.952 | 0.960 |
| KIAMB | Number of runs = 5000, α = 0.05, K = 0.7 | 349 | 2.8 | 0 | 0.000 | 0.400 | 0.722 | 0.450 | 0.959 |
| Number of runs = 5000, α = 0.05, K = 0.8 | 349 | 2.8 | 0 | 0.000 | 0.400 | 0.722 | 0.450 | 0.959 | |
| Number of runs = 5000, α = 0.05, K = 0.9 | 349 | 2.8 | 0 | 0.000 | 0.400 | 0.722 | 0.450 | 0.959 | |
| EGS-NCMIGS | l = 7, δ = 0.015 | 6 | 7.0 | 0 | 0.286 | 0.000 | 0.953 | 0.952 | 0.956 |
| l = 7, K = 10 | 6 | 10.0 | 0 | 0.500 | 0.000 | 0.968 | 0.967 | 0.969 | |
| l = 7, K = 50 | 6 | 50.0 | 0 | 0.900 | 0.000 | 0.877 | 0.866 | 0.887 | |
| l = 5000, δ = 0.015 | 995 | 8.0 | 0 | 0.648 | 0.508 | 0.960 | 0.950 | 0.968 | |
| l = 5000, K = 10 | 990 | 10.0 | 0 | 0.747 | 0.494 | 0.961 | 0.952 | 0.968 | |
| l = 5000, K = 50 | 950 | 50.0 | 0 | 0.949 | 0.494 | 0.868 | 0.857 | 0.882 | |
| EGS-CMIM | l = 7, K = 10 | 6 | 10.0 | 0 | 0.500 | 0.000 | 0.967 | 0.965 | 0.968 |
| l = 7, K = 50 | 6 | 50.0 | 0 | 0.900 | 0.000 | 0.904 | 0.895 | 0.915 | |
| l = 5000, K = 10 | 990 | 10.0 | 0 | 0.676 | 0.353 | 0.961 | 0.953 | 0.967 | |
| l = 5000, K = 50 | 950 | 50.0 | 0 | 0.935 | 0.353 | 0.897 | 0.885 | 0.910 | |
| EGSG | Number of Markov boundaries = 30, t = 5 | 30 | 67.0 | 0 | 0.958 | 0.440 | 0.688 | 0.383 | 0.850 |
| Number of Markov boundaries = 30, t = 10 | 30 | 67.0 | 0 | 0.977 | 0.693 | 0.485 | 0.253 | 0.769 | |
| Number of Markov boundaries = 30, 1 = 15 | 30 | 67.0 | 0 | 0.984 | 0.780 | 0.422 | 0.246 | 0.739 | |
| Number of Markov boundaries = 5,000, t = 5 | 5,000 | 67.0 | 0 | 0.927 | 0.028 | 0.662 | 0.441 | 0.850 | |
| Number of Markov boundaries = 5,000, t = 10 | 5,000 | 67.0 | 0 | 0.944 | 0.250 | 0.476 | 0.248 | 0.780 | |
| Number of Markov boundaries = 5,000, t = 15 | 5,000 | 67.0 | 0 | 0.953 | 0.369 | 0.406 | 0.247 | 0.710 | |
| Resampling+RFE | without statistical comparison | 2,492 | 16.7 | 2 | 0.434 | 0.039 | 0.951 | 0.931 | 0.968 |
| with statistical comparison (α = 0.05) | 214 | 6.0 | 0 | 0.225 | 0.336 | 0.947 | 0.917 | 0.964 | |
| Resampling+UAF | without statistical comparison | 1,207 | 28.7 | 0 | 0.721 | 0.000 | 0.952 | 0.935 | 0.964 |
| with statistical comparison (α = 0.05) | 12 | 7.8 | 0 | 0.577 | 0.367 | 0.949 | 0.931 | 0.959 | |
| IR-HITON-PC | max-k = 3, α = 0.05 | 2 | 5.0 | 1 | 0.100 | 0.100 | 0.958 | 0.958 | 0.959 |
| IR-SPLR | without statistical comparison | 1 | 30.0 | 0 | 0.833 | 0.000 | 0.949 | 0.949 | 0.949 |
| with statistical comparison (α = 0.05) | 1 | 30.0 | 0 | 0.833 | 0.000 | 0.949 | 0.949 | 0.949 | |
Figure 19.
Results for average false negative rate and average proportion of false positives obtained in TIED (left) and TIED1000 (right) data sets. Results of TIE* and iTIE* were identical.
5.2 Experiments with Real Data
For evaluation of methods for learning multiple Markov boundaries and variable sets in real data, we used 13 data sets that cover a broad range of application domains (clinical outcome prediction, gene expression, proteomics, drug discovery, text categorization, digit recognition, ecology and finance), dimensionalities (from 86 to over 100,000), and sample sizes (from hundreds to thousands) that are representative of those appearing in practical applications. These data sets have recently been used in a broad benchmark (Aliferis et al., 2010a) of the current state-of-the-art single Markov boundary induction and feature selection methods, which is another reason why we chose to use the same data in this study. The data sets are described in detail in Table 12 in Appendix E. The data sets were preprocessed (imputed, discretized, etc.) as described in the work by Aliferis et al. (2010a).
Table 12.
Real data sets used in the experiments.
| Name | Domain | # of samples | # of variables | Response type | Data type | CV design | References |
|---|---|---|---|---|---|---|---|
| Infant_Mortality | clinical | 5,337 | 86 | Death within the first year | Discrete | Holdout | Mani and Cooper (1999) |
| Ohsumed | Text | 5,000 | 14,373 | Relevant to neonatal diseases | Continuous | Holdout | Joachims (2002) |
| ACPJ_Etiology | Text | 15,779 | 28,228 | Relevant to etiology | Continuous | Holdout | Aphinyanaphongs et al. (2006) |
| Lymphoma | Gene Expression | 227 | 7,399 | 3-year survival:dead vs. alive | Continuous | 10-fold | Rosenwald et al. (2002) |
| Gisette | Digit recognition | 7,000 | 5,000 | 4 vs. 9 | Continuous | Holdout | NIPS 2003 Feature Selection Challenge Guyon et al. (2006) |
| Dexter | Text | 600 | 19,999 | Relevant to corporate acquisitions | Continuous | 10-fold | NIPS 2003 Feature Selection Challenge Guyon et al. (2006) |
| Sylva | Ecology | 14,394 | 216 | Ponderosa vs. rest | Continuous | Holdout | WCCI 2006 Perf. Prediction Challenge |
| Ovarian_Cancer | Proteomics | 216 | 2,190 | Cancer vs. normal | Continuous | 10-fold | Conrads et al. (2004) |
| Thrombin | Drug discovery | 2,543 | 139,351 | Binding to thrombin | Discrete | Holdout | KDD Cup 2001 |
| Breast_Cancer | Gene Expression | 286 | 17,816 | ER+vs. ER− | Continuous | 10-fold | Wang et al. (2005) |
| Hiva | Drug discovery | 4,229 | 1,617 | Activity to HIV AIDS infection | Discrete | Holdout | WCCI 2006 Perf.Prediction Challenge |
| Nova | Text | 1,929 | 16,969 | Political topics vs. religious | Discrete | Holdout | WCCI 2006 Perf. Prediction Chanllenge |
| Bankruptcy | Financial | 7,063 | 147 | Personal bankruptcy | Continuous | Holdout | Foster and Stine (2004) |
In data sets with relatively large sample sizes (> 600), classification performance of the output Markov boundaries and variable sets was estimated by holdout validation with 75% of samples used for Markov boundary/variable set induction and SVM classifier training, and the remaining 25% of samples used for estimation of classification performance. In small-sample data sets, 10- fold cross-validation was used instead. Markov boundary/variable set induction and classifier training were both performed on the training sets from the 10-fold cross-validation design, with classification performance being subsequently estimated on the respective testing sets.
Evaluation of Markov boundary/variable selection methods in real data is challenging due to the lack of knowledge of the true Markov boundaries. In practical applications, however, the interest typically lies in the most compact subsets of variables that give the highest classification performance for reasonable and widely used classifiers (Guyon and Elisseeff, 2003). This consideration motivated the following two primary evaluation criteria (with the averages taken over all Markov boundaries/variable sets output by each method):
The average Proportion of Variables (PV) in the output Markov boundaries/variable sets.13
The average classification performance (AUC) of the output Markov boundaries/variable sets.14
In addition to the above two primary criteria, in some problems we are also interested in extracting as many of the maximally compact and predictive variable sets (i.e., optimal solutions to the variable selection problem) as possible. Therefore, we also considered a third criterion in our evaluation:
-
III
The number of distinct Markov boundaries/variable sets output by each method (N).
We note that criterion I (PV) on its own can be optimized independently of the actual classification problem by taking small subsets of variables (e.g., 1 or 2 variables in each subset) to be the presumed Markov boundaries of the response variable T. Criterion I may therefore be biased towards methods that output Markov boundaries/variable sets of a user-defined size (e.g., some parameterizations of EGS-NCMIGS). Similarly, criterion III (N) can be maximized independently of the response T by simply taking all 2|V|−1 − 1 non-empty subsets of the variable set V \{T} to be the presumed Markov boundaries of T. This criterion could be potentially biased towards Markov boundary/variable set extraction methods that output a number of Markov boundaries specified by a user-defined parameter (e.g., EGSG) rather than by a data driven process (e.g., TIE*). Criterion II (AUC) served as a modulator for criteria I and III, because high performance on the latter two criteria does not necessarily imply high classification performance.
We also ranked all methods on each of the three criteria averaged over all 13 real data sets, as described in Appendix E. The ranks incorporated permutation-based statistical comparison of difference in the performance of algorithms, in order to ensure that methods with statistically comparable performance receive the same rank.
Finally, given ranks on the individual criteria I (PV) and II (AUC), we defined a combined (PV, AUC) ranking criterion which reflects the ability of methods to find Markov boundaries in real data. This is because Markov boundaries are expected to maximize performance of the classifiers with universal approximation capabilities (maximize AUC of SVMs in our study) and be of minimal size (minimize PV in our study) (Tsamardinos and Aliferis, 2003). The combined (PV, AUC) criterion was defined as follows: First, the ranks on the individual criteria PV and AUC were normalized to the [0,1] interval to account for varying rank ranges that resulted from ties in performance. Second, the normalized ranks on the two criteria were averaged. Third, the resulting averages were used to establish a new ranking of methods, aided by a permutation-based testing approach to ensure that methods with statistically comparable performance receive the same rank (see Appendix E).
Other alternative combined (PV, AUC) ranking criteria, for example, one that performs ranking based on some combination of raw PV and AUC scores, can also be used for performance assessment in our study. We have confirmed that the best performing method remains the same when either combining normalized ranks of PV and AUC (our criterion) or raw scores of PV and AUC (alternative criterion) by an average function. This can be evidenced from Figure 15 and Tables 3 and 4 which are discussed below.
Figure 15.
Average performance of the evaluated methods across 13 real data sets. The Pareto frontier was constructed based on the average proportion of variables and the average AUC over the prior methods (i.e., non-TIE*). Detailed results are provided in Tables 3 and 4.
Table 3.
Number of distinct Markov boundaries or variable sets identified by the evaluated methods (N), proportion of variables in them (PV) and their classification performance (AUC) averaged across all 13 real data sets for each method. The color of highlighting signifies relative performance on each criterion with dark red corresponding to the best performance and light yellow to the worst. See Table 4 for ranks of methods that also incorporate formal statistical comparison of the observed differences between methods.
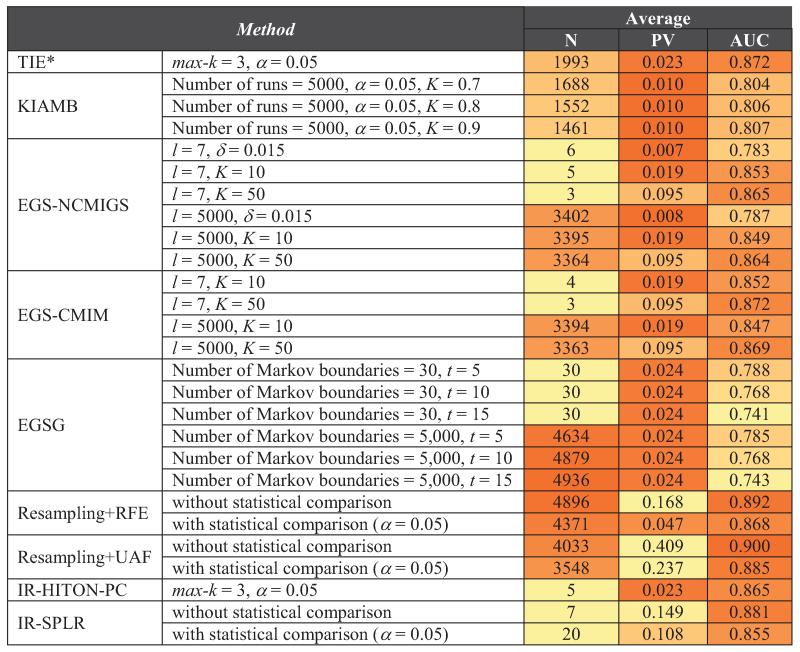
|
Table 4.
Ranks of methods based on individual and combined criteria. Smaller ranks correspond to better methods according to each criterion. As described in text, ranks were obtained using formal statistical comparison of the observed differences between methods; that is why they do not necessarily range between 1 and 27 (total number of tested methods).
| Method | Rank | ||||
|---|---|---|---|---|---|
| N | PV | AUC | (PV, AUC) | ||
| TIE* | max-k = 3, α = 0.05 | 4 | 5 | 2 | 1 |
| KIAMB | Number ofruns = 5000, α = 0.05, K = 0.7 | 4 | 2 | 4 | 5 |
| Number of runs = 5000, α = 0.05, K = 0.8 | 4 | 2 | 4 | 5 | |
| Number of runs = 5000, α = 0.05, K = 0.9 | 4 | 2 | 4 | 5 | |
| EGS-NCMIGS | l = 7, δ = 0.015 | 6 | 1 | 4 | 3 |
| l = 7, K = 10 | 6 | 5 | 3 | 6 | |
| l = 7, K = 50 | 6 | 9 | 3 | 11 | |
| l = 5000, δ = 0.015 | 3 | 2 | 4 | 5 | |
| l = 5000, K = 10 | 3 | 4 | 3 | 4 | |
| l = 5000, K = 50 | 3 | 9 | 3 | 11 | |
| EGS-CMIM | l = 1, K = 10 | 6 | 5 | 3 | 6 |
| l = 7, K = 50 | 6 | 9 | 2 | 8 | |
| l = 5000, K = 10 | 3 | 3 | 3 | 2 | |
| l = 5000, K = 50 | 3 | 9 | 2 | 8 | |
| EGSG | Number of Markov boundaries = 30, t = 5 | 5 | 6 | 4 | 10 |
| Number of Markov boundaries = 30, t = 10 | 5 | 6 | 4 | 10 | |
| Number of Markov boundaries = 30, t = 15 | 5 | 6 | 5 | 13 | |
| Number of Markov boundaries = 5,000, t = 5 | 2 | 9 | 4 | 14 | |
| Number of Markov boundaries = 5,000, t = 10 | 2 | 8 | 4 | 12 | |
| Number of Markov boundaries = 5,000, t = 15 | 1 | 7 | 5 | 15 | |
| Resampling+RFE | without statistical comparison | 2 | 10 | 2 | 9 |
| with statistical comparison (α = 0.05) | 2 | 9 | 3 | 11 | |
| Resampling+UAF | without statistical comparison | 3 | 11 | 1 | 7 |
| with statistical comparison (α = 0.05) | 3 | 10 | 2 | 9 | |
| IR-HITON-PC | max-k = 3, α = 0.05 | 6 | 5 | 3 | 6 |
| IR-SPLR | without statistical comparison | 6 | 10 | 2 | 9 |
| with statistical comparison (α = 0.05) | 5 | 9 | 3 | 11 | |
The results of experiments are presented in Figure 15 and Tables 3 and 4.15 Figure 15 shows a 2-dimensional plot of PV versus AUC and a 3-dimensional plot of PV versus AUC versus the number of extracted distinct Markov boundaries or variable sets (N). Each point in Figure 15 corresponds to the results of one of the methods considered in this evaluation, averaged over all 13 data sets. The Pareto frontier shown in Figure 15 was constructed based on the two primary evaluation criteria PV and AUC over the prior methods (i.e., non-TIE*). Methods on the Pareto frontier are such that no other non-TIE* method had both lower PV and higher AUC when averaged over all data sets. For ease of visualization, results on all variables (i.e., without variable selection) were omitted from Figure 15. When all variables were used for classification, the average PV and AUC were 100% and 0.902, respectively. These results did not alter the Pareto set of prior methods in Figure 15 and are reported in Table 13, 14 and 15 in Appendix E. The results averaged over all data sets are shown in Table 3. The results for all methods in each data set individually are presented in Table 13, 14 and 15 in Appendix E. Ranks of the methods were computed as described above and are shown in Table 4.
Table 13.
Results showing the number of distinct Markov boundaries or variable sets (N) extracted by each method, their average size in terms of the number of variables (S) and average classification performance (AUC) in each of 13 real data sets. The row labeled “All variables” shows performance of the entire set of variables available in each data set.
| Method | Infant_ Mortality | Ohsumed | ACPJ_ Etiology | Lymphoma | Gisette | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | S | AUC | N | S | AUC | N | S | AUC | N | S | AUC | N | S | AUC | ||
| All variables | 1 | 86 | 0.821 | 1 | 14,373 | 0.857 | 1 | 28,228 | 0.938 | 1 | 7,399 | 0.659 | 1 | 5,000 | 0.997 | |
| TIE* | max-k = 3, α =0.05 | 41 | 4 | 0.825 | 2,497 | 37 | 0.776 | 5,330 | 18 | 0.908 | 4,533 | 16 | 0.635 | 227 | 54 | 0.990 |
| KIAMB | Number of runs = 5000, α = 0.05, K = 0.7 | 67 | 4 | 0.753 | 250 | 7 | 0.651 | 1,354 | 9 | 0.884 | 88 | 3 | 0.562 | 5,000 | 8 | 0.871 |
| Number of runs = 5000, α = 0.05, K = 0.8 | 39 | 4 | 0.752 | 133 | 7 | 0.650 | 830 | 9 | 0.883 | 50 | 3 | 0.561 | 5,000 | 8 | 0.871 | |
| Number of runs = 5000, α = 0.05, K = 0.9 | 17 | 4 | 0.752 | 58 | 7 | 0.648 | 414 | 9 | 0.884 | 23 | 3 | 0.561 | 5,000 | 8 | 0.871 | |
| EGS-NCMIGS | l = 7, δ = 0.015 | 6 | 4 | 0.809 | 6 | 4 | 0.584 | 6 | 3 | 0.743 | 7 | 3 | 0.591 | 7 | 3 | 0.913 |
| l = 7, K = 10 | 3 | 10 | 0.874 | 1 | 10 | 0.691 | 3 | 10 | 0.780 | 5 | 10 | 0.615 | 7 | 10 | 0.952 | |
| l = 7, K = 50 | 1 | 50 | 0.821 | 1 | 50 | 0.828 | 3 | 35 | 0.842 | 3 | 50 | 0.662 | 5 | 50 | 0.986 | |
| l = 5000, δ = 0.015 | 84 | 4 | 0.806 | 4,999 | 4 | 0.564 | 4,999 | 4 | 0.770 | 4,992 | 3 | 0.574 | 4,999 | 5 | 0.920 | |
| l = 5000, K = 10 | 77 | 10 | 0.862 | 4,991 | 10 | 0.693 | 4,991 | 10 | 0.785 | 4,981 | 10 | 0.600 | 4,994 | 10 | 0.953 | |
| l = 5000, K = 50 | 39 | 50 | 0.822 | 4,951 | 50 | 0.830 | 4,981 | 31 | 0.843 | 4,947 | 50 | 0.653 | 4,957 | 50 | 0.987 | |
| EGS-CMIM | l = 7, K = 10 | 2 | 10 | 0.865 | 1 | 10 | 0.696 | 2 | 10 | 0.915 | 6 | 10 | 0.577 | 7 | 10 | 0.956 |
| l = 7, K = 50 | 1 | 50 | 0.829 | 1 | 50 | 0.843 | 1 | 32 | 0.917 | 4 | 50 | 0.608 | 5 | 50 | 0.987 | |
| l = 5000, K = 10 | 77 | 10 | 0.863 | 4,991 | 10 | 0.687 | 4,991 | 10 | 0.842 | 4,970 | 10 | 0.581 | 4,992 | 10 | 0.963 | |
| l = 5000, K = 50 | 38 | 50 | 0.827 | 4,951 | 50 | 0.841 | 4,982 | 31 | 0.857 | 4,942 | 50 | 0.613 | 4,957 | 50 | 0.987 | |
| EGSG | Number of Markov boundaries = 30, t = 5 | 30 | 12 | 0.634 | 30 | 70 | 0.653 | 30 | 84 | 0.840 | 30 | 58 | 0.600 | 30 | 35 | 0.959 |
| Number of Markov boundaries = 30, t = 10 | 30 | 12 | 0.568 | 30 | 70 | 0.634 | 30 | 84 | 0.835 | 30 | 58 | 0.616 | 30 | 35 | 0.946 | |
| Number of Markov boundaries = 30, t = 15 | 30 | 12 | 0.552 | 30 | 70 | 0.602 | 30 | 84 | 0.792 | 30 | 58 | 0.607 | 30 | 35 | 0.936 | |
| Number of Markov boundaries = 5,000, t = 5 | 991 | 12 | 0.631 | 5,000 | 70 | 0.649 | 5,000 | 84 | 0.837 | 5,000 | 58 | 0.604 | 5,000 | 35 | 0.961 | |
| Number of Markov boundaries = 5,000, t = 10 | 3,576 | 12 | 0.587 | 5,000 | 70 | 0.624 | 5,000 | 84 | 0.822 | 5,000 | 58 | 0.617 | 5,000 | 35 | 0.950 | |
| Number of Markov boundaries = 5,000, t = 15 | 4,272 | 12 | 0.556 | 5,000 | 70 | 0.606 | 5,000 | 84 | 0.780 | 5,000 | 58 | 0.609 | 5,000 | 35 | 0.941 | |
| Resampling+RFE | without statistical comparison | 4,230 | 17 | 0.825 | 4,942 | 3,889 | 0.846 | 5,000 | 2,441 | 0.924 | 4,919 | 1,293 | 0.634 | 4,948 | 697 | 0.997 |
| with statistical comparison (α = 0.05) | 3,222 | 9 | 0.814 | 5,000 | 914 | 0.836 | 5,000 | 308 | 0.864 | 4,962 | 45 | 0.587 | 5,000 | 134 | 0.995 | |
| Resampling+UAF | without statistical comparison | 4,868 | 26 | 0.859 | 2,533 | 10,722 | 0.855 | 4,963 | 3,883 | 0.929 | 4,215 | 2,546 | 0.647 | 5,000 | 1,673 | 0.999 |
| with statistical comparison (α = 0.05) | 3,141 | 15 | 0.777 | 4,925 | 7,690 | 0.864 | 5,000 | 1,600 | 0.918 | 4,895 | 195 | 0.600 | 5,000 | 1,088 | 0.998 | |
| IR-HITON-PC | max-k = 3, α = 0.05 | 1 | 5 | 0.857 | 2 | 40 | 0.778 | 4 | 22 | 0.875 | 12 | 10 | 0.593 | 3 | 64 | 0.990 |
| IR-SPLR | without statistical comparison | 1 | 8 | 0.835 | 1 | 176 | 0.829 | 4 | 123 | 0.885 | 16 | 456 | 0.577 | 1 | 466 | 0.996 |
| with statistical comparison (α = 0.05) | 1 | 2 | 0.828 | 3 | 122 | 0.728 | 5 | 26 | 0.844 | 139 | 47 | 0.572 | 1 | 261 | 0.996 | |
Table 14.
| Method | Dexter | Sylva | Ovarian_Cancer | Thrombin | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | S | AUC | N | S | AUC | N | S | AUC | N | S | AUC | ||
| All variables | 1 | 19,999 | 0.979 | 1 | 216 | 0.998 | 1 | 2,190 | 0.998 | 1 | 139,351 | 0.927 | |
| TIE* | max-k = 3, α = 0.05 | 4,791 | 17 | 0.959 | 1,483 | 27 | 0.996 | 223 | 7 | 0.973 | 298 | 11 | 0.813 |
| KIAMB | Number of runs = 5000, α = 0.05, K = 0.7 | 299 | 5 | 0.882 | 4,429 | 8 | 0.949 | 285 | 4 | 0.925 | 4,936 | 6 | 0.771 |
| Number of runs = 5000, α = 0.05, K = 0.8 | 193 | 5 | 0.884 | 4,384 | 8 | 0.948 | 180 | 4 | 0.927 | 4,900 | 6 | 0.774 | |
| Number of runs = 5000, α = 0.05, K = 0.9 | 120 | 5 | 0.887 | 4,385 | 8 | 0.947 | 106 | 4 | 0.928 | 4,854 | 6 | 0.774 | |
| EGS-NCMIGS | l = 7, δ = 0.015 | 6 | 4 | 0.839 | 4 | 5 | 0.960 | 6 | 5 | 0.951 | 7 | 3 | 0.781 |
| l = 7, K = 10 | 5 | 10 | 0.927 | 2 | 10 | 0.988 | 6 | 10 | 0.974 | 7 | 10 | 0.854 | |
| l = 7, K = 50 | 4 | 50 | 0.971 | 1 | 50 | 0.998 | 3 | 50 | 0.986 | 7 | 12 | 0.760 | |
| l = 5000, δ = 0.015 | 4,998 | 5 | 0.840 | 213 | 5 | 0.954 | 2,188 | 6 | 0.956 | 4,999 | 4 | 0.779 | |
| l = 5000, K = 10 | 4,991 | 10 | 0.927 | 207 | 10 | 0.987 | 2,183 | 10 | 0.971 | 4,996 | 10 | 0.858 | |
| l = 5000, K = 50 | 4,951 | 50 | 0.970 | 167 | 50 | 0.998 | 2,144 | 50 | 0.988 | 4,997 | 14 | 0.764 | |
| EGS-CMIM | l = 7, K = 10 | 5 | 10 | 0.942 | 2 | 10 | 0.991 | 5 | 10 | 0.976 | 7 | 10 | 0.799 |
| l = 7, K = 50 | 3 | 50 | 0.979 | 1 | 50 | 0.997 | 3 | 50 | 0.991 | 7 | 12 | 0.711 | |
| l = 5000, K = 10 | 4,991 | 10 | 0.943 | 207 | 10 | 0.992 | 2,182 | 10 | 0.973 | 4,999 | 10 | 0.856 | |
| l = 5000, K = 50 | 4,951 | 50 | 0.979 | 167 | 50 | 0.998 | 2,144 | 50 | 0.992 | 5,000 | 14 | 0.720 | |
| EGSG | Number of Markov boundaries = 30, t = 5 | 30 | 76 | 0.857 | 30 | 12 | 0.803 | 30 | 12 | 0.953 | 30 | 29 | 0.776 |
| Number of Markov boundaries = 30, t = 10 | 30 | 76 | 0.791 | 30 | 12 | 0.810 | 30 | 12 | 0.940 | 30 | 29 | 0.817 | |
| Number of Markov boundaries = 30, t = 15 | 30 | 76 | 0.749 | 30 | 12 | 0.744 | 30 | 12 | 0.930 | 30 | 29 | 0.757 | |
| Number of Markov boundaries = 5,000, t = 5 | 5,000 | 76 | 0.854 | 4,997 | 12 | 0.792 | 4,878 | 12 | 0.951 | 5,000 | 29 | 0.758 | |
| Number of Markov boundaries = 5,000, t = 10 | 5,000 | 76 | 0.787 | 5,000 | 12 | 0.803 | 4,990 | 12 | 0.936 | 5,000 | 29 | 0.815 | |
| Number of Markov boundaries = 5,000, t = 15 | 5,000 | 76 | 0.746 | 5,000 | 12 | 0.752 | 4,996 | 12 | 0.927 | 5,000 | 29 | 0.749 | |
| Resampling+RFE | without statistical comparison | 5,000 | 2,097 | 0.976 | 4,976 | 19 | 0.998 | 4,951 | 142 | 0.983 | 5,000 | 14,996 | 0.912 |
| with statistical comparison (α = 0.05) | 4,998 | 96 | 0.956 | 3,549 | 12 | 0.998 | 2,601 | 5 | 0.926 | 5,000 | 216 | 0.861 | |
| Resampling+UAF | without statistical comparison | 3,561 | 15,491 | 0.976 | 3,944 | 44 | 0.998 | 4,372 | 424 | 0.980 | 4,998 | 74,521 | 0.933 |
| with statistical comparison (α = 0.05) | 4,992 | 14,064 | 0.972 | 2,842 | 23 | 0.998 | 972 | 13 | 0.955 | 5,000 | 25,217 | 0.916 | |
| IR-HITON-PC | max-k = 3, α = 0.05 | 1 | 20 | 0.958 | 1 | 24 | 0.997 | 2 | 7 | 0.962 | 1 | 13 | 0.844 |
| IR-SPLR | without statistical comparison | 1 | 425 | 0.974 | 1 | 36 | 0.999 | 2 | 709 | 0.986 | 4 | 245 | 0.876 |
| with statistical comparison (α = 0.05) | 3 | 149 | 0.940 | 1 | 36 | 0.999 | 11 | 115 | 0.943 | 28 | 144 | 0.749 | |
Table 15.
| Method | Breast_Cancer | Hiva | Nova | Bankruptcy | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | S | AUC | N | S | AUC | N | S | AUC | N | S | AUC | ||
| All variables | 1 | 17,816 | 0.914 | 1 | 1,617 | 0.716 | 1 | 16,969 | 0.981 | 1 | 147 | 0.940 | |
| TIE* | max-k = 3, α = 0.05 | 1,011 | 10 | 0.906 | 246 | 8 | 0.712 | 3,751 | 41 | 0.922 | 1,478 | 14 | 0.923 |
| KIAMB | Number of runs = 5000, α = 0.05, K = 0.7 | 418 | 4 | 0.873 | 876 | 7 | 0.735 | 130 | 6 | 0.759 | 3,810 | 6 | 0.839 |
| Number of runs = 5000, α = 0.05, K = 0.8 | 255 | 4 | 0.874 | 439 | 7 | 0.754 | 57 | 6 | 0.764 | 3,713 | 5 | 0.836 | |
| Number of runs = 5000, α = 0.05, K = 0.9 | 136 | 4 | 0.879 | 172 | 7 | 0.755 | 23 | 6 | 0.771 | 3,681 | 5 | 0.838 | |
| EGS-NCMIGS | l = 7, δ = 0.015 | 6 | 4 | 0.922 | 7 | 3 | 0.661 | 5 | 4 | 0.730 | 7 | 4 | 0.698 |
| l = 7, K = 10 | 6 | 10 | 0.926 | 7 | 10 | 0.750 | 2 | 10 | 0.815 | 6 | 10 | 0.936 | |
| l = 7, K = 50 | 6 | 50 | 0.928 | 7 | 50 | 0.668 | 1 | 50 | 0.849 | 3 | 50 | 0.953 | |
| l = 5000, δ = 0.015 | 4,994 | 4 | 0.911 | 1,616 | 4 | 0.696 | 4,998 | 5 | 0.735 | 145 | 4 | 0.721 | |
| l = 5000, K = 10 | 4,985 | 10 | 0.926 | 1,610 | 10 | 0.760 | 4,991 | 10 | 0.780 | 139 | 10 | 0.936 | |
| l = 5000, K = 50 | 4,973 | 50 | 0.927 | 1,570 | 50 | 0.658 | 4,951 | 50 | 0.846 | 101 | 50 | 0.953 | |
| EGS-CMIM | l = 7, K = 10 | 7 | 10 | 0.914 | 5 | 10 | 0.713 | 3 | 10 | 0.818 | 3 | 10 | 0.913 |
| l = 7, K = 50 | 6 | 50 | 0.902 | 5 | 50 | 0.727 | 1 | 50 | 0.886 | 1 | 50 | 0.954 | |
| l = 5000, K = 10 | 4,978 | 10 | 0.906 | 1,608 | 10 | 0.724 | 4,992 | 10 | 0.780 | 139 | 10 | 0.901 | |
| l = 5000, K = 50 | 4,966 | 50 | 0.907 | 1,577 | 50 | 0.729 | 4,951 | 50 | 0.897 | 99 | 50 | 0.954 | |
| EGSG | Number of Markov boundaries = 30, t = 5 | 30 | 205 | 0.893 | 30 | 17 | 0.705 | 30 | 89 | 0.751 | 30 | 9 | 0.815 |
| Number of Markov boundaries = 30, t = 10 | 30 | 205 | 0.886 | 30 | 17 | 0.660 | 30 | 89 | 0.722 | 30 | 9 | 0.754 | |
| Number of Markov boundaries = 30, t = 15 | 30 | 205 | 0.890 | 30 | 17 | 0.633 | 30 | 89 | 0.687 | 30 | 9 | 0.752 | |
| Number of Markov boundaries = 5,000, t = 5 | 5,000 | 205 | 0.892 | 5,000 | 17 | 0.701 | 5,000 | 89 | 0.751 | 4,373 | 9 | 0.819 | |
| Number of Markov boundaries = 5,000, t = 10 | 5,000 | 205 | 0.888 | 5,000 | 17 | 0.652 | 5,000 | 89 | 0.720 | 4,856 | 9 | 0.786 | |
| Number of Markov boundaries = 5,000, t = 15 | 5,000 | 205 | 0.889 | 5,000 | 17 | 0.638 | 5,000 | 89 | 0.682 | 4,905 | 9 | 0.787 | |
| Resampling+RFE | without statistical comparison | 4,848 | 1,067 | 0.901 | 4,938 | 220 | 0.679 | 4,948 | 5,305 | 0.982 | 4,949 | 66 | 0.940 |
| with statistical comparison (α = 0.05) | 2,922 | 10 | 0.894 | 4,598 | 13 | 0.646 | 5,000 | 1,261 | 0.966 | 4,972 | 38 | 0.946 | |
| Resampling+UAF | without statistical comparison | 4,365 | 3,359 | 0.905 | 4,587 | 309 | 0.685 | 645 | 13,950 | 0.981 | 4,379 | 79 | 0.952 |
| with statistical comparison (α = 0.05) | 1,295 | 42 | 0.917 | 4,250 | 36 | 0.663 | 3,185 | 12,503 | 0.978 | 628 | 47 | 0.946 | |
| IR-HITON-PC | max-k = 3, α = 0.05 | 12 | 9 | 0.890 | 23 | 6 | 0.673 | 2 | 49 | 0.920 | 3 | 15 | 0.910 |
| IR-SPLR | without statistical comparison | 47 | 159 | 0.892 | 10 | 129 | 0.661 | 1 | 10,289 | 0.981 | 1 | 69 | 0.956 |
| with statistical comparison (α = 0.05) | 54 | 27 | 0.880 | 7 | 22 | 0.694 | 1 | 10,289 | 0.981 | 1 | 69 | 0.956 | |
As can be seen in Figure 15 and Tables 3 and 4, none of the prior methods had both more compact Markov boundaries or variable sets (lower PV) and better classification performance (higher AUC) than TIE*. This is evidenced by TIE*s performance laying beyond the Pareto frontier constructed over the prior methods in Figure 15. While a few methods had comparable or slightly higher AUC (Table 3), their Markov boundaries or variable sets were substantially larger with the average PV reaching as high as 41% (see Resampling+UAF in Table 3). In contrast, Markov boundaries output by TIE* were much more compact with an average PV of 2.3%. On the other hand, methods that had PV lower than TIE* also had lower AUC. KIAMB, for example, had a PV of 1% and an AUC of about 0.8, which was 7–8% lower than the AUC of TIE*. Overall, TIE* ranked first out of 15 on the combined (PV, AUC) criterion. Please see Appendix E for a detailed discussion of the results of prior methods.
It is worth noting that use of the AUC metric for verification of Markov boundaries in the Predictivity criterion of TIE* can result in some spurious multiplicity of the output Markov boundaries. This can happen due to a possible mismatch between subsets of variables that lead to maximization of the AUC metric for a given classifier and those that render the response variable T conditionally independent of all other variables (thus effectively optimizing a metric that requires accurate estimation of P(T | V \{T})). Consider an example where only a subset of variables from some Markov boundary is sufficient to obtain the same AUC as the entire Markov boundary. Suppose there are in total five variables {A,B,C,D,T} in the data set and M1 = {A,B,C,D} is the only Markov boundary of the response variable T. Suppose also that the subset M2 = {A,B,C} yields the same classification performance as the Markov boundary M1 according to the AUC metric. Once TIE* discovers the Markov boundary M1 = {A,B,C,D}, it will consider removing {D}, as well as other subsets of M1, to discover other possible Markov boundaries. After removing subset {D} from the data, TIE* would identify M2 = {A,B,C} as a candidate Markov boundary to be verified by the Predictivity criterion. Because M1 and M2 have the same classification performance (AUC), M2 will be admitted as a Markov boundary by the Predictivity criterion. In order to control for possible presence of such spurious Markov boundaries in the output of TIE*, we performed an additional analysis of its output whereby for each data set, we considered only those Markov boundaries that were not proper subsets of any other Markov boundary extracted by TIE* in the same data set. We refer to such Markov boundaries as minimal. The average number of minimal Markov boundaries identified by TIE* was 1,484 (versus the average number of all Markov boundaries identified by TIE* equal to 1,993). The average size (2.3% PV) and classification performance (0.872 AUC) of the minimal Markov boundaries were statistically indistinguishable from the results obtained on all Markov boundaries identified by TIE* and so were the ranks on the PV, AUC and (PV, AUC) criteria.
In summary, TIE* extracted multiple compact Markov boundaries with high classification performance and surpassed all other methods on the combined (PV, AUC) criterion. Since the data-generative process in experiments with real data sets is unknown, a question that arises is: do multiple Markov boundaries exist in real data? Prior work using the same data has established that performance patterns of single Markov boundaries identified by Semi-Interleaved HITON-PC (an instantiation of the GLL framework) are highly consistent with the Markov boundary induction theory and that GLL algorithms dominated an extensive panel of prior state-of-the-art Markov boundary and variable selection methods in terms of compactness and classification performance (Aliferis et al., 2010a). In this paper, we showed that TIE* parameterized with Semi-Interleaved HITON-PC as the base Markov boundary induction algorithm was able to identify multiple compact Markov boundaries with consistently high classification performance in real data. For example, in the ACPJ Etiology data set, TIE* identified 5,330 distinct Markov boundaries (and 4,263 minimal ones) that on average contained 18 variables out of 28,228 and had an AUC of 0.91. Out of all prior methods for learning multiple Markov boundaries and variable sets applied to the same data set, Resampling+UAF had the highest classification performance with an AUC of 0.93, which was statistically non-distinguishable from TIE*, while variable sets extracted by Resampling+UAF, on average, were more than two orders of magnitude larger and contained 3,883 variables. A similar pattern can be observed in the Dexter data set where TIE* identified 4,791 distinct Markov boundaries (and 3,498 minimal ones) with an average size of 17 variables out of 19,999 and an AUC of 0.96. The best performer among prior methods in the same data was EGS-CMIM with Markov boundaries containing 50 variables each and an average AUC of 0.98, the latter being statistically non-distinguishable from TIE*. The compactness of Markov boundaries extracted by TIE* coupled with their high classification performance provides strong evidence that there are indeed multiple Markov boundaries in many real-life problem domains.
6. Discussion
This section summarizes main findings, reiterates key principles of TIE* efficiency, demonstrates how the generative algorithm TIE* can be configured for optimal results, presents limitations of this study, and outlines directions for future research.
6.1 Main Findings
There are two major contribution of this study. First, we presented TIE*, a generative anytime algorithm for discovery of multiple Markov boundaries. TIE* is sound under well-defined sufficient conditions and can be practically applied to high-dimensional data sets with relatively small sample. We performed a theoretical analysis of the algorithm correctness and derived estimates of its computational complexity. To make our paper valuable for practitioners, we provided several specific instantiations of the generative algorithm TIE* and described their implementation details.
Second, we conducted an empirical comparison of TIE* with 26 state-of-the-art methods for discovery of multiple Markov boundaries and variable sets. The empirical study was performed on 2 simulated data sets with exactly known Markov boundaries and 13 real data sets from a diversity of application domains. We found that unlike prior methods, TIE* identifies exactly all true Markov boundaries in simulated data, and in real data it yields Markov boundaries with simultaneously better classification performance and smaller number of variables compared to prior methods.
Other notable contributions of this work include: (i) developing a deeper theoretical understanding of distributions with multiple Markov boundaries of the same variable (Sections 2.2–2.4), (ii) theoretical analysis of prior state-of-the-art algorithms for discovery of multiple Markov boundaries and variable sets (Appendix C), (iii) a novel simple and fast algorithm iTIE* for learning multiple Markov boundaries in special distributions (Section 4.5), and (iv) evidence that multiple Markov boundaries exist in real data (Section 5.2).
6.2 Key Principles of TIE* Efficiency
We will illustrate key principles of TIE* efficiency using a simple example. Consider a distribution that spans over variables M = {T,X1,X2,X3,X4,X5,Y1,Y2,Z1,…,Z1000} and contains two Markov boundaries of T: M1 = {X1,X2,X3,X4,X5} and M2 = {X1,X2,X3, X4,Y1,Y2}, because X5 and {Y1,Y2} contain context-independent equivalent information about T. Assuming that we can apply a standard single Markov boundary induction algorithm to identify M1, one naive approach to discover multiple Markov boundaries in this distribution is to exhaustively consider whether a variable subset in M1 can be substituted with a variable subset in V \ M1 \ {T} to obtain a new Markov boundary. In this example we will have to substitute 31 non-empty subsets in M1 with approximately 21002 − 1 non-empty subsets of V \ M1 \ {T} (the latter number being orders of magnitude larger than the number of atoms in the universe). This approach is clearly computationally prohibitive in high-dimensional data sets. The first core efficiency principle in TIE* is to avoid explicit search of all possible subsets of V \ M1 \ {T} and repeatedly run a fast Markov boundary induction algorithm on the data for variables in V \ G, where G is a subset of the previously found Markov boundaries. In the example stated above, this would lead to running a Markov boundary induction algorithm 27 = 128 times (because there are 7 members in the union of all Markov boundaries) to find all Markov boundaries that exist in the distribution. The second core efficiency principle in TIE* dictates to consider removing from V only certain subsets G of the previously found Markov boundaries. Specifically, we consider only subsets G that do not include a subset of variables G* (i.e., G* ⊄ G) that did not result in discovery of a Markov boundary when the Markov boundary induction algorithm has been previously run on the data for variables in V \ G*. Coupled with the heuristic to first generate subsets G of the smallest size, this principle can significantly decrease the number of runs of the Markov boundary induction algorithm. In the example stated above, this principle as exemplified in IGS procedure would lead to running a single Markov boundary induction algorithm only 8 times in order to find all Markov boundaries that exist in the distribution. Specifically, we will have to consider G = ⊘,{X1},{X2},{X3},{X4},{X5},{X5,Y1}, and {X5,Y2}. We would not need to consider G = {X1,X2} because its subset (G* = {X1} or {X2}) did not lead to discovery of any Markov boundary when the algorithm was run on the data for variables in V \ G*. Finally, since very fast single Markov boundary induction algorithms have been recently introduced (Aliferis et al., 2010a, 2003a; Peña et al., 2007; Tsamardinos et al., 2003a,b), the overall TIE* operation is very fast.
6.3 The Generative Nature of TIE* Allows to Configure the Algorithm for Optimal Results
TIE* is a generative algorithm that can be instantiated differently for different distributions. For example, distributions that violate the local composition property with respect to T for members of Markov boundaries (e.g., when T is defined as a parity function of its Markov boundary members that are unrelated and have balanced priors) are incompatible with the assumptions of Markov boundary induction algorithms IAMB and Semi-Interleaved HITON-PC that were considered in this work. The generative nature of TIE* suggests to use an admissible Markov boundary induction algorithm that is suitable for the distribution at hand.
Consider running TIE* algorithm on data generated from the example causal Bayesian network shown in Figure 16. There are 25 distinct Markov boundaries of T in this distribution. Each of these Markov boundaries contains 3 or 5 variables: (i) X9 or {X5,X6} or {X1,X2} or {X1,X6} or {X5,X2}, (ii) X10, and (iii) X11 or {X7,X8} or {X3,X4} or {X3,X8} or {X7,X4}. The local composition property with respect to T is violated here because T = XOR(X9,X10,X11). To illustrate applicability to such distributions, we ran TIE* with a Markov boundary induction algorithm SVM-FSMB (Brown et al., 2012; Tsamardinos and Brown, 2008) as input component and , . In brief, SVM-FSMB works by first extracting features from the polynomial SVM feature space that have largest SVM weights and then running a Markov boundary induction algorithm Semi-Interleaved HITON-MB in the SVM feature space on the constructed features. This allows SVM-FSMB to circumvent the requirement for the local composition property. We found that in a sufficiently large sample size (≥ 2,000), TIE* can discover all 25 true Markov boundaries with only 1 false positive in each extracted Markov boundary. This showcases how the generative nature of TIE* allows to optimally configure the algorithm for the distribution at hand.
Figure 16.
Graph of a causal Bayesian network used to trace the TIE* algorithm. The network parameterization is provided in Table 8 in Appendix B. The response variable is T. All variables take values {0,1}. Variables that contain equivalent information about T are highlighted with the same color, for example, variables X1 and X5 provide equivalent information about T; variable X9 and each of the four variable sets {X5,X6}, {X1,X2}, {X1,X6}, {X5,X2} provide equivalent information about T.
6.4 Limitations and Open Problems
The empirical evaluation of TIE* performed in this study used 13 real data sets from a diversity of application domains and provided evidence about existence of multiple Markov boundaries in real-life data, primarily based on compactness of output variable sets and high classification performance. The absence of knowledge about the true Markov boundaries in real data sets is a limitation of the study, which is in our opinion mitigated by strong empirical evidence for existence of multiple Markov boundaries.
Related to the above, the present work does not address the source of multiplicity of Markov boundaries induced in real data. In other words, we do not separate intrinsic multiplicity of Markov boundaries (that exists in the underlying probability distribution) from apparent multiplicity due to various factors including (but not limited to) small sample size, hidden variables, correlated measurement noise, and artifacts of normalization and/or data pre-processing (Statnikov and Aliferis, 2010a).
Also, as we have pointed out, the use of the AUC metric for verification of Markov boundaries in the Predictivity criterion of TIE* can result in a small percentage of spurious Markov boundaries in the output of the algorithm. This can happen due to a possible mismatch between subsets of variables that lead to maximization of the AUC metric for a given classifier and those that render the response variable T conditionally independent of all other variables (thus effectively optimizing a metric that requires accurate estimation of P(T | V \{T})). In this paper we experimented with one approach to reduce spurious multiplicity of TIE* by filtering extracted Markov boundaries to the minimal ones. A more conventional approach to this problem is to augment the Markov boundary induction method with an additional backward wrapping step (Aliferis et al., 2010a; Kohavi and John, 1997). However, backward wrappers are prone to overfitting because they evaluate a large number of classifier models with various variable subsets (Aliferis et al., 2010a), thus negatively affecting generalizability of TIE*. We have conducted preliminary experiments with a backward wrapping method applied on 13 real data sets, and indeed the results revealed a significant reduction in classification performance, as theoretically expected. We believe that it is still worthwhile to explore more sophisticated wrapping strategies (especially ones that guard against overfitting) in order to optimize the output of a Markov boundary inducer for a specific performance metric and classifier.
Finally, another limitation of this study is that we included in empirical experiments both algorithms for discovery of multiple Markov boundaries and algorithms for discovery of multiple variable sets. Even though the latter family of algorithms are not theoretically designed for Markov boundary induction, many researchers use them (Pellet and Elisseeff, 2008). This motivated us to include in our study methods for selection of multiple variable sets.
6.5 Directions for Future Research
In addition to addressing open problems outlined in the previous subsection, there are several promising directions for future research.
First, it is interesting to routinely apply TIE* to discover multiple Markov boundaries in various application domains. This would allow one to learn whether some problem domains are more prone to multiplicity of Markov boundaries than others. These results would instruct data-analysts about potential existence of many more solutions and can form guidelines for performing analysis in such data.
Second, it is important to extend existing causal graph discovery methods to take into account violations of the intersection property that lead to multiple Markov boundaries. For example, recent work was able to modify the PC algorithm to account for information equivalence relations between variables (Lemeire et al., 2010). However, many more algorithms remain to be improved upon.
Third, a useful direction for future research is to improve computational efficiency and run time of TIE* by using high-performance computers with parallel and/or distributed architectures. We have previously designed parallel versions of Markov boundary induction algorithms (Aliferis et al., 2010b, 2002) and in some cases were able to achieve more than linear increase of computational efficiency. At face value, this suggests that modifications of TIE* that run on parallel/distributed architectures can discover multiple Markov boundaries in domains where TIE*'s run time was prohibitive.
Acknowledgments
The empirical evaluation was supported in part by grants R01 LM011179-01A1 and R56 LM007948-04A1 from the NLM/NIH and 1UL1RR029893 from the NCRR/NIH. The authors are also grateful to Efstratios Efstathiadis, Frank E. Harrell Jr., Carie Lee Kennedy, and Eric Peskin for help with providing access and running experiments on high performance computing facilities. Finally, the authors would like to thank Alexander V. Alekseyenko, Mikael Henaff, and Yindalon Aphinyanaphongs for their useful comments on the manuscript.
Appendix A. Proofs of Theorems and Lemmas
Proof Lemma 1 : Assume that M ∩ Mnew = N. Then it follows that M=N ∪ Y and Mnew = N∪Z. Since M is a Markov blanket, T ⊥ (V \{T}\(N ∪ Y)) | (N ∪ Y). By the self-conditioning property, it follows that T ⊥ (V \{T}) | (N ∪ Y). The previous independence relation is equivalent to T ⊥ ((V \{T}\Z) ∪ Z) | (N ∪ Y). By the weak union property, T ⊥ (V \{T}\Z) | (N ∪ Y ∪ Z). By the self-conditioning property, T ⊥ (V \{T}) | (N ∪ Y ∪ Z). Equivalently, we can rewrite the previous relation as T ⊥ (V \{T}) | ((N ∪ Y) ∪ (N ∪ Z)). Since Z and Y provide context independent equivalent information about T and by the self-conditioning property T ⊥ (N ∪ Y) | (N ∪ Z). By the contraction property, T ⊥ (V \{T}) | ((N ∪ Y) ∪ (N ∪ Z)) and T ⊥ (N ∪ Y) | (N ∪ Z) imply that T ⊥ ((V \{T}) ∪ (N ∪ Y)) | (N ∪ Z). This is equivalent to T ⊥ (V \{T}) | (N ∪ Z). By the decomposition property this implies that Mnew = N ∪ Z is also a Markov blanket of T. (Q.E.D.)
Proof Lemma 2 : By definition of the Markov blanket, T ⊥ (V \M\{T}) | M. By the self-conditioning property, it follows that T ⊥ (V \{T}) | M. Since (V \{T}) = (V \{T}) ∪ Mnew and according to the weak union property, T ⊥ (V \{T}\Mnew) | (M ∪ Mnew). By the self-conditioning property, it follows that T ⊥ (V \{T}) | (M ∪ Mnew). Since T ⊥ M | Mnew and T ⊥ (V \{T}) | (M ∪ Mnew), the contraction property implies that T ⊥ ((V \{T}) ∪ M) | Mnew. Next, since (V \{T}) = (V \{T}) ∪ M, it follows that T ⊥ (V \{T}) | Mnew. By the decomposition property this implies that Mnew is a Markov blanket of T. (Q.E.D.)
Proof Theorem 6 : Given an ancestral graph , let M denote the set containing all parents and children of T and every variable X connected to T by a path from T to X in such that: (i) the first edge on the path is either bi-directed or away from T, (ii) all other edges except the last are bi-directed, and (iii) the last edge is either bi-directed or is away from X. Note that spouses of T satisfy the above conditions and are therefore included in M.
We first show that set M m-separates T and every other variable Y ∈ V \M\{T}. To see this, suppose that M does not m-separate T from some variable Y ∈ V \M\{T}. Then, there must exist a path p connecting Y and T that is not blocked by M. By definition of M, Y cannot be directly connected to T and not be in M. Additionally, path p cannot be through parents of T, its spouses, or parents of variables connected to T or its children by bi-directed paths, because any such variable would act as a non-collider that is in M and would therefore block the path p. The only remaining possibility is for path p to contain a variable X ∈ V \M\{T} that is a child of a variable Z ∈ M that is either (i) a child of T, or (ii) connected to T by a bi-directed path, or (iii) connected to a child of T by a bi-directed path. However, in this case, variable Z would be a non-collider on path p and would therefore block it. It follows that set M m-separates T and every other variable Y ∈ V \M\{T}.
From the definition of the global Markov condition it follows that every m-separation relation in implies conditional independence in every joint probability distribution that satisfies the global Markov condition for . Thus, we have T ⊥ Y | M in for every variable Y ∈ V \M\{T}, from which it follows that M is a Markov blanket of T. (Q.E.D.)
Proof Theorem 7 : First we prove that any Markov blanket of T is an optimal predictor of T. If M is a Markov blanket of T, then by definition it is the optimal predictor of T because P(T | M) = P(T | V \{T}) and this distribution can be accurately approximated by , which implies that will be maximized.
Now we prove that any optimal predictor of T is a Markov blanket of T. Assume that X ⊆ V \{T} is an optimal predictor of T but it is not a Markov blanket of T. This implies that, P(T | X) ≠ P(T | V \{T}). By definition, V \{T} is always a Markov blanket of T. By first part of the theorem, V \{T} is an optimal predictor of T similarly to X. Therefore, the following should hold: P(T | X) = P(T | V \{T}). This contradicts the assumption that X is not a Markov blanket of T. Therefore, X is a Markov blanket of T. (Q.E.D.)
Proof Theorem 8 : First we prove that M is a Markov blanket of T at the end of Phase I. Suppose it is not, that is, T
 (V \M\{T}) | M. By the local composition property with respect to T, there exists Y ∈ (V \M\{T}) such that T
(V \M\{T}) | M. By the local composition property with respect to T, there exists Y ∈ (V \M\{T}) such that T
 Y | M. This contradicts the exit condition from the loop in step 9 that states that E should be empty, which can be the case if and only if for every Y ∈ (V \M\{T}), T ⊥ Y | M. Therefore, M is a Markov blanket of T at the end of Phase I.
Y | M. This contradicts the exit condition from the loop in step 9 that states that E should be empty, which can be the case if and only if for every Y ∈ (V \M\{T}), T ⊥ Y | M. Therefore, M is a Markov blanket of T at the end of Phase I.
Next we prove that M remains a Markov blanket of T at the end of Phase II. Assume that a variable Y ∈ M can be rendered independent from T by conditioning on the remaining variables in M, that is, T ⊥ Y | (M\{Y}). From Phase I it follows that T ⊥ (V \M\{T}) | M. The above two independence relations by the contraction property imply that T ⊥ (V \(M\{Y})\{T}) | (M\{Y}). Thus, M is a Markov blanket of T at the end of Phase II of the algorithm.
Finally we prove that M is a Markov boundary of T at the end of Phase II. Suppose it is not and thus there exists N ⊂ M that is a Markov blanket of T. Let Y ∈ M\N and Z ⊆ (V \N\{T}\{Y}). By definition of the Markov blanket, T ⊥ (V \N\{T}) | N. By the decomposition property, T ⊥ (Z ∪ {Y}) | N. The latter independence relation implies T ⊥ Y | (N ∪ Z) by the weak union property. Therefore, any variable Y ∈ M\N would be removed by the algorithm in step 12 which contradicts the assumption that the algorithm output M and N ⊂ M is another Markov blanket of T. Therefore, M is a Markov boundary of T at the end of Phase II. (Q.E.D.)
Proof Theorem 9 : First we prove that the set M is a Markov blanket of T at the end of Phase I. Because of the assumptions of the theorem, there are only two reasons for existence of a subset Z that renders Y independent of T: either Y is a non-Markov boundary member or there is a violation of the intersection property that leads to context-independent information equivalence relations. The former case does not compromise the Markov blanket property of M, thus we consider only the latter case. For example, we can consider the following situation T ⊥ Y | Z, T ⊥ Z | Y and T
 ({Y} ∪ Z) that led to removal of Y. From Lemma 1 we know that if Y is a member of some Markov blanket M1 = N ∪ {Y}, then M2 = N ∪ Z is also a Markov blanket of T because Y and Z contain context-independent equivalent information about T. Therefore the set M is a Markov blanket of T at the end of Phase I.
({Y} ∪ Z) that led to removal of Y. From Lemma 1 we know that if Y is a member of some Markov blanket M1 = N ∪ {Y}, then M2 = N ∪ Z is also a Markov blanket of T because Y and Z contain context-independent equivalent information about T. Therefore the set M is a Markov blanket of T at the end of Phase I.
The proofs that M remains a Markov blanket of T at the end of Phase II and that M is a Markov boundary of T at the end of Phase II are similar to the ones in IAMB algorithm (Theorem 8) and will not be repeated here. (Q.E.D.)
Proof Theorem 10 : TIE* will output only Markov boundaries of T when the inputs and are admissible (see Figure 7). Assume that there exists a Markov boundary W that is not output by TIE*. Because of admissibility of inputs and (Figure 7), Mnew = W was not identified in step 5 of the algorithm. However, because of admissibility of input (Figure 7), in some iteration of the algorithm in step 4 a data set will be generated where a Markov boundary W can be discovered by in step 5. The admissibility of input implies that W will be successfully verified and output in step 6. Therefore, a contradiction is reached, and TIE* would never miss Markov boundaries. (Q.E.D.)
Proof Theorem 11 : Since (i) all variables from each embedded distribution belong to the original distribution, and (ii) the joint probability distribution of variables in each embedded distribution is the same as marginal in the original one, the local composition property with respect to T also holds in each embedded distribution. Therefore according to Theorem 8, IAMB will correctly identify a Markov boundary in every embedded distribution. Thus, IAMB is an admissible Markov boundary induction algorithm for TIE*. (Q.E.D.)
Proof Theorem 12 : The proof follows from fact that assumptions of Theorem 9 are satisfied in each embedded distribution that contains a Markov boundary of T. Thus, Semi-Interleaved HITON-PC is an admissible Markov boundary induction algorithm for TIE*. (Q.E.D.)
Proof Theorem 13 : The procedure IGS is executed iteratively in TIE* and generates data sets from the embedded distributions by removing subsets G from the full set of variables V. Such procedure is admissible if it uses as G all possible subsets of V. This is because eventually the procedure will generate a data set for every Markov boundary of T such that each data set contains all members of only one Markov boundary and thus a single Markov boundary induction algorithm can discover it. By similar argument, the procedure to generate embedded distributions is admissible if it uses as G all possible subsets of all Markov boundaries. Notice that in IGS, G is constructed iteratively from all possible subsets of the previously found Markov boundaries with the following modification in order to increase efficiency of TIE* (see Section 6.2). If we find that for some subset G* a data set leads to a Markov boundary Mnew in the embedded distribution (as determined in step 5 of TIE*) that is not a Markov boundary in the original distribution (as determined in step 6 of TIE*), then IGS does not consider generating data sets where G includes G*. Below we prove by contradiction that this modification does not compromise admissibility of IGS.
Assume that there is W that is a Markov boundary of T in the original distribution and it was not output by TIE* because for some G+ : G+ ⊃ G* has not been generated by IGS.
• Since W is a Markov blanket of T in the original distribution and Mnew is not, Theorem 7 implies that performance of a learning algorithm (that can approximate any conditional probability distribution) for prediction of T measured by the metric (that is maximized only when P(T | V \{T}) is estimated accurately) is larger for W than for Mnew.
• Since W satisfies T ⊥ (V \W \{T}) | W by the definition of Markov blanket, decomposition property implies that T ⊥ (V \W \G*\{T}) | W, that is, W similarly to Mnew is a Markov blanket of T in the embedded distribution after removal of G*. Therefore by Theorem 7, performance of a learning algorithm (that can approximate any conditional probability distribution) for prediction of T measured by metric (that is maximized only when P(T | V \{T}) is estimated accurately) should be the same for W and Mnew.
The above two points are contradictory, thus W does not exist. (Q.E.D.)
Proof Theorem 14 : Consider that there exists a set of variables Mnew ⊆ V \ {T} such that T ⊥ M | Mnew. Since M is a Markov boundary of T in the original distribution, it is also a Markov blanket of T in the original distribution. From Lemma 2 we know that Mnew is a Markov blanket of T in the original distribution. Since Mnew is a Markov boundary of T in the embedded distribution and it is a Markov blanket of T in the original distribution, it is also a Markov boundary of T in the original distribution. (Q.E.D.)
Proof Theorem 15 : The proof that this criterion can identify whether Mnew is a Markov blanket of T in the original distribution or not follows from Theorem 7. If Mnew is a Markov blanket of T in the original distribution, it is also a Markov boundary of T in the original distribution because Mnew is a Markov boundary of T in the embedded distribution. (Q.E.D.)
Appendix B. Parameterizations of Example Structures
This appendix provides parameterizations of example structures from the manuscript that are shown in Tables 5, 6, 7, and 8.
Table 5.
Parameterization of the Bayesian network shown in Figure 2

|
Table 6.
Parameterization of the causal Bayesian netwoxrk shown in Figure 8.
|
Table 7.
Parameterization of the causal Bayesian network shown in Figure 13.

|
Table 8.
Parameterization of the causal Bayesian network shown in Figure 16. All variables are binary and take values {0,1}.

|
Appendix C. Description and Theoretical Analysis of Prior Algorithms for Learning Multiple Markov Boundaries and Variable Sets
This appendix provides description and theoretical analysis of prior algorithms for learning multiple Markov boundaries and variable sets.
C.1 Stochastic Markov Boundary Algorithms: KIAMB
Reference
The work by Peña et al. (2007).
Description
Recall that the IAMB algorithm (Figure 4) requires only the local composition property for its correctness (per Theorem 8) which is compatible with the existence of multiple Markov boundaries of the response variable T. However, due to IAMB's reliance on a greedy deterministic strategy for adding variables into the (candidate) Markov boundary in Phase I (Forward), the algorithm can identify only a single Markov boundary of T. KIAMB addresses this limitation of IAMB by employing a stochastic search heuristic that repeatedly disrupts the order in which variables are selected for inclusion into the Markov boundary, thereby introducing a chance of discovering alternative Markov boundaries of T. KIAMB allows the user to control the tradeoff between stochasticity and greediness of the search by setting the value of a single parameter K ∈ [0,1]. Specifically, instead of picking the conditionally maximally associated variable Y from the set E in step 4 of IAMB, in KIAMB a maximally associated variable is selected from a randomly chosen subset of all the associated variables outside the current Markov boundary M. The size of this subset relative to the size of the complete set of associated variables is determined by parameter K. Setting K equal to 0 results in a purely stochastic search where a single randomly chosen associated variable is added into M on each iteration in Phase I. Setting K equal to 1 results exactly in IAMB algorithm with its greedy deterministic search.
Analysis
KIAMB correctly identifies Markov boundaries assuming the local composition property. Theoretically, KIAMB can identify all Markov boundaries if given the chance to explore a large enough number of different sequences of additions of associated variables into the current Markov boundary in Phase I. However, KIAMB is computationally inefficient, because a large fraction of its runs may yield previously identified Markov boundaries. For example, suppose the causal graph consists of 11 variables: a response variable T and variables X1,…,X10 such that T ← X10 ← X9 ← … ← X1 and each Xi(i = 1, …,10) contains equivalent information about T and is significantly associated with it. Thus, there are 10 Markov boundaries {X1}, …,{X10} of T in this distribution. Suppose also that parameter K was set equal to 0.7, which would mean that in Phase I, KIAMB will first randomly select 7 variables out of 10 and will then select out of these 7 variables, one with the highest association with T. Because all variables in this example contain equivalent information about T, all variables will have equal association with T (Lemeire, 2007). Selection of a single variable for inclusion in the Markov boundary could then be done based on lexicographic ordering. There are 120 ways to select 7 variables out of 10, but 84 (or 70%) of such subsets of size 7 will contain variable X1 that precedes all other variables in lexicographic ordering. Therefore, on average, we can expect 70% of the runs of KIAMB to return Markov boundary {X1} in this example. In order for KIAMB to identify Markov boundary {X1}, variables X1,X2,X3 must not be among the 7 randomly selected variables. On average, this would happen in only roughly 0.8% of the runs of KIAMB. Note also that in the above scenario, KIAMB will not be able to discover Markov boundaries {X5}, …,{X10}, because there is no way to select 7 variables out of 10 and avoid including at least one variable from the subset {X1, …,X4}. KIAMB could eventually discover all 10 Markov boundaries if instead of lexicographic ordering, ties were broken by random selection, or alternatively if parameter K was set equal to a smaller value. In both of these cases, however, the probability that KIAMB will discover all 10 Markov boundaries after 10 runs is only about 0.04%, indicating that a large number of runs may be necessary to recover all 10 Markov boundaries. Thus, in order to produce the complete set of Markov boundaries, the value of parameter K and the number of runs of KIAMB must be determined based on the topology of the causal graph and the number of Markov boundaries of T, neither of which are known in real-world causal discovery applications. Finally, KIAMB suffers from the same sample inefficiency as IAMB, which arises from conditioning on the entire Markov boundary when testing variables for independence from the response variable T.
C.2 Stochastic Markov Boundary Algorithms: EGS-CMIM and EGS-NCMIGS
Reference
The work by Liu et al. (2010b).
Description
These algorithms attempt to extract multiple Markov boundaries by repeatedly invoking single Markov boundary extraction methods CMIM (Fleuret, 2004) and NCMIGS (Liu et al., 2010b), respectively. Conceptually, CMIM and NCMIGS are very similar and differ primarily in the types of measures of association between variables. Both methods employ only a greedy forward selection strategy similar to Phase I of IAMB and rely on mutual information-based functions for measuring (conditional) association between variables and the response T. The algorithmic framework of CMIM and NCMIGS is as follows. First, all variables are ordered by decreasing association with the response T. A Markov boundary M is initialized to be the empty set. The t-th highest associated variable (where t is a user-defined parameter) is then added into M and an iterative addition of other variables begins. On each iteration, a new variable that maximizes the value of a selection criterion J(X) (discussed below) is added to the Markov boundary M. The algorithm stops once a termination condition is reached. CMIM terminates when the Markov boundary reaches a user-defined size k. NCMIGS offers two different stopping criteria that the user could choose from. The first stopping criterion is the same as in CMIM controlled by the parameter k. The other termination criterion alleviates the requirement of explicitly specifying the size of the Markov boundary and forces iterative selection to stop if the value of the selection criterion J(X) changes from one iteration to the next by no more than δ (a user-defined parameter), that is, if | J(Xi) − J(Xi−1) |≤ δ, where Xi denotes the variable selected for addition into M on the i-th iteration of NCMIGS.
CMIM employs an approximation to the conditional mutual information I(X,T | M) as the selection criterion JCMIM(X) for adding variables into the Markov boundary. The approximation is achieved by conditioning on a single variable instead of the entire Markov boundary M (as in KIAMB), that is, JCMIM(X) = argminY∈M I(X,T |Y). NCMIGS uses a very similar selection criterion that is based on a normalized conditional mutual information JNCMIGS(X) = argminY∈M I(X,T | Y)/H(X,T), where H(X,T) denotes the joint entropy of variable X and response T. Conditioning on a single variable instead of the entire Markov boundary makes CMIM and NCMIGS sample efficient by circumventing the problem of exponential growth in the number of parameters and sample size required for estimating the conditional mutual information I(X,Y | M) in discrete data as the size of the Markov boundary M increases.
Analysis
Recall that EGS-CMIM (EGS-NCMIGS) extracts multiple Markov boundaries by calling CMIM (NCMIGS) with different values of the input parameter t = 1, …,l, where l is a user-defined parameter that bounds from above the total number of Markov boundaries that will be output. Therefore, EGS-CMIM and EGS-NCMIGS require prior knowledge/estimate of the number of Markov boundaries. Note that while admissible values of t (and therefore of l) are by design bounded from above by the number of variables in the data, the actual number of true Markov boundaries may be much higher. There is also no guarantee that different values of t will yield different Markov boundaries, which makes these methods computationally inefficient (similarly to KIAMB). In addition, because CMIM and NCMIGS implement only forward selection and employ conditioning on a single variable, these methods are prone to inclusion of false positives in their output. False positives may enter a Markov boundary for two reasons: (i) when more than one variable from the current Markov boundary is required to establish independence of the response T from some other variable being considered for addition into the Markov boundary, and (ii) when some of the variables added into the Markov boundary are independent of the response T conditional on variables that were added in later iterations. Furthermore, the stopping criteria in CMIM and NCMIGS are heuristic, which may lead to an arbitrary number of false negatives in the output. This may happen, for instance, if the value of parameter k (size of a Markov boundary) is set smaller than the true size of the Markov boundary. The alternative stopping criterion of NCMIGS does not fully solve the problem of false negatives, because the absolute difference | J(Xi) − J(Xi−1) | may be small, while the individual values J(Xi) and J(Xi−1) of the selection criterion may still be large indicating that the considered variable Xi is highly associated with the response T and that it may be too early to stop. In summary, EGS-CMIM and EGS-NCMIGS offer no formal guarantees of neither correctness nor completeness of their output, require prior knowledge/estimate of the number of Markov boundaries and their size, are computationally inefficient, but are sample efficient.
C.3 Variable Grouping Followed by Random Sampling of Variables from Each Group: EGSG
Reference
The work by Liu et al. (2010).
Description
EGSG uses normalized version of mutual information JEGSG(X,Y) = I(X,Y)/H(X,Y) for measuring pair-wise association between variables and partitions them into disjoint groups. Each group has a “centroid”, which is the first variable that formed the group. A variable X is added into a group if (i) X has a higher association with the groups centroid C than with the response T (i.e., if JEGSG(X,C) ≥ JEGSG(X,T)), and (ii) X has lower association with T than does C (i.e., if JEGSG(C,T) ≥ JEGSG(X,T)). If no such group is found, then a new group is created with X as the groups centroid. Variables within a group are implicitly assumed to carry similar information about T. Under this assumption, it is sufficient to select one variable from each group to form a Markov boundary of T. In EGSG, one of the top t variables most associated with the response T is sampled at random from each group to form a single Markov boundary. Here, the value of parameter t is given by the user. In order to extract multiple Markov boundaries, the above sampling is repeated a number of times determined by the user.
Analysis
From the point of view of soundness and completeness, EGSG suffers from two major drawbacks. First, the number of Markov boundaries output by EGSG is an arbitrary parameter and is independent of the data-generating causal graph. Second, Markov boundaries output by EGSG may contain an arbitrary number of false positives as well as false negatives. False positives may appear, for instance, if a variable from one group is independent of the response T conditional on a variable from another group. EGSG does not test for conditional independence and could include both variables in a Markov boundary. Moreover, since only one variable is sampled from each group, false negatives may appear in the output of EGSG if several variables within a group in reality belong to the same Markov boundary. Therefore, no guarantees can be made regarding the correctness and completeness of the output of EGSG. The method is not computationally efficient for discovery of distinct Markov boundaries, because EGSG may produce the same Markov boundary multiple times due to random sampling of variables from each group. However, its computationally efficiency can be improved by constructing Markov boundaries from the Cartesian product of top-t members of each group. EGSG is sample efficient, because it does not conduct any conditional independence tests, but only computes pair-wise associations between variables.
C.4 Resampling-based Methods: Resampling+RFE and Resampling+UAF
Reference
The work by Ein-Dor et al. (2005), Michiels et al. (2005), Roepman et al. (2006) and Statnikov and Aliferis (2010a).
Description
In resampling-based methods, multiple variable sets are extracted by repeatedly applying a variable selection method to different bootstrap samples of the data (Ein-Dor et al., 2005; Michiels et al., 2005; Roepman et al., 2006; Statnikov and Aliferis, 2010a). The two variable selection methods employed in the resampling framework in this paper are Univariate Association Filtering (UAF) (Hollander and Wolfe, 1999; Statnikov et al., 2005) and Recursive Feature Elimination (RFE) (Guyon et al., 2002). These methods implement only the backward selection akin to Phase II of IAMB. Namely, given a bootstrap sample, all variables are first ordered by decreasing association with the response T. UAF orders variables using p-values and test statistics from Kruskal-Wallis non-parametric ANOVA (Hollander and Wolfe, 1999). RFE orders variables by decreasing absolute values of the SVM weights (Guyon et al., 2002). Once all variables have been ordered, a portion of the least significant variables is removed, performance of the remaining variables for predicting the response T is evaluated, and this variable elimination process is recursively applied to the remaining variables. The smallest nested subset of variables with the maximum predictive performance is then output. The proportion of variables to be removed on each iteration is controlled by a user-defined parameter called “reduction coefficient”.16 Assessment of predictive performance can be performed by training and evaluating a classifier model (e.g., SVM). One can also use variants of UAF and RFE, where the smallest nested subset of variables with predictive performance statistically indistinguishable from the nominally maximum predictive performance is output. This often produces smaller variable sets than the former approach.
Analysis
Neither UAF nor RFE, which are at the core of resampling-based methods, offer formal guarantees of the correctness of their output, because both methods are based on a heuristic approach to finding the most predictive subset of variables and not the Markov boundary (Aliferis et al., 2010b). Therefore, neither Resampling+UAF nor Resampling+RFE are sound and complete for extraction of multiple Markov boundaries. Resampling+UAF and Resampling+RFE are also computationally inefficient, because runs of UAF and RFE on different bootstrap samples may produce identical variable sets, especially when the sample size is large. In addition, the number of runs is a user-defined parameter that requires prior knowledge of the number of Markov boundaries in the data. Both resampling techniques are sample efficient, because UAF does not rely on conditional independence tests and because RFE leverages SVMs regularized loss function that allows for parameter estimation in high-dimensional data with small sample sizes.
C.5 Iterative Removal Methods: IR-HITON-PC and IR-SPLR
Reference
The work by Natsoulis et al. (2005) and Statnikov and Aliferis (2010a).
Description
Iterative removal methods identify multiple Markov boundaries (IR-HITON-PC) or multiple variable sets (IR-SPLR) by repeatedly executing the following two steps. Step 1: Extract a Markov boundary/variable set M from the current set W of variables (initially W = V \{T}). Step 2: If M is the first Markov boundary/variable set extracted or if its predictive performance is statistically indistinguishable from performance of the first Markov boundary/variable set, then output M, remove all of its variables from further consideration (W ← W \M) and go to Step 1. Otherwise, terminate. IR-HITON-PC uses Semi-Interleaved HITON-PC as the base Markov boundary extraction method. IR-SPLR extracts variable sets using regularized Logistic regression with a L1 norm penalty term, which induces sparsity in the regression coefficients. All variables with non-zero coefficients are taken to belong to an output variable set.
Analysis
IR-HITON-PC is correct because it uses Semi-Interleaved HITON-PC to identify Markov boundaries (per Theorem 9). On the other hand, IR-SPLR relies on a heuristic regression-based approach to finding the most predictive subset of variables and not the Markov boundary; thus this method has no theoretical guarantees for correct identification of Markov boundaries. Furthermore, neither iterative removal method is guaranteed to be complete, because these methods output disjoint Markov boundaries or variable sets, while in general multiple Markov boundaries may share a number of variables. IR-HITON-PC and IR-SPLR neither require prior knowledge of the number of Markov boundaries nor their size, and these methods are computationally and sample efficient.
Appendix D. Details about the TIE* Algorithm
This appendix provides details about the generative TIE* algorithm.
D.1 Example Instantiations of the Generative Algorithm
Example instantiations of the generative algorithm TIE* are given in Figures 17 and 18.
D.2 Specific Implementation Details
We proceed below with details about TIE* implementations. We discuss Markov boundary induction algorithm (), procedure to generate data sets from the embedded distributions (), and criterion to verify Markov boundaries of T ().
Markov boundary induction algorithm IAMB (Figure 4)
We used the Matlab implementation of the algorithm from the Causal Explorer toolkit (Aliferis et al., 2003b; Statnikov et al., 2010). When the algorithm was run on discrete data, we assessed independence of variables with G2 test at significance level α = 0.05. In our implementation of G2 test, we required at least 5 samples per cell in the contingency tables. For continuous data, one can use Fishers Z test to assess independence of variables. To measure association Association(T,X | M) in step 4 of the algorithm we used negative p-values returned by the corresponding test of independence T ⊥ X | M.17 Since the IAMB algorithm can be run multiple times in TIE*, we programmed on top of the Causal Explorer code a caching method to store and retrieve results of conditional independence tests.
Markov boundary induction algorithm Semi-Interleaved HITON-PC (Figure 5)
We used the Matlab implementation of the algorithm from the Causal Explorer toolkit (Aliferis et al., 2003b; Statnikov et al., 2010). Semi-Interleaved HITON-PC was implemented without so-called “symmetry correction” (Aliferis et al., 2010a). Similarly to IAMB, to assess independence of variables in discrete data we used G2 test at α = 0.05, and one can use Fisher's Z test for continuous data. To measure Association(T,X) in step 4 of the algorithm, we used negative p-values returned by the corresponding test of independence T ⊥ X. The parameter max-k which denotes the upper bound on the size of the conditioning set in Semi-Interleaved HITON-PC (i.e., the maximum size of the subset Z in steps 6 and 10 of the algorithm) was set equal to 3. The choice of this value for max-k parameter is justified by empirical performance in a variety of data distributions, as well as by sample size limitations in our data (Aliferis et al., 2010a,b). Since the Semi-Interleaved HITON-PC algorithm can be run multiple times in TIE*, we programmed on top of the Causal Explorer codes a caching method to store and retrieve results of conditional independence tests.
Procedures IGS-Lex, IGS-MinAssoc, and IGS-MaxAssoc to generate data sets from the embedded distributions (Figure 9)
These procedures were implemented by (i) constructing all subsets G such that {Gi} ⊂ G ⊆ {Mi ∪ Gi} and |G| ≤ parameter max-card, (ii) excluding subsets that either include or coincide with Gk, (iii) considering first subsets with the smallest number of variables, and (iv) using a subset G with the either smallest lexicographical order of variables, or minimum association with T, or maximum association with T (depending on the employed procedure). The association with T was assessed with the appropriate statistical test, as described above for the Markov boundary induction algorithms. The parameter max-card was set equal to 4 in all experiments except for experiments with simulated data where it was set equal to 8. The purpose of this parameter is to trade off completeness of the TIE* output for execution speed. We also experimented with larger values of max-card until no more new Markov boundaries can be obtained.
Criterion Independence to verify Markov boundaries (Figure 10)
This criterion was implemented using statistical tests that were described above for the Markov boundary induction algorithms. Since the Markov boundary in the original distribution (M) and the examined Markov boundary in the embedded distribution (Mnew) are often significantly overlapping, we used a sample efficient implementation where we do not need to condition on the entire Markov boundary in the embedded distribution Mnew. Consider that M ∩ Mnew = W, M\Mnew = S1, and Mnew\M = S2. Then context-independent information equivalence of S1 and S2 implies information equivalence of M= S1 ∪ W and Mnew = S2 ∪ W. Therefore, it suffices to verify that T ⊥ S1 | S2 and T ⊥ S2 | S1 instead of T ⊥ M | Mnew. This was the essence of our implementation of the Independence criterion for Markov boundary verification.
Criterion Predictivity to verify Markov boundaries (Figure 11)
As a learning algorithm , we used linear support vector machines (SVMs) with default value of the penalty parameter C = 1 (Fan et al., 2005; Vapnik, 1998). As a performance metric , we used area under ROC curve (AUC) (Fawcett, 2003) and weighted accuracy (Guyon et al., 2006) for binary and multiclass responses, respectively. We estimated classification performance (using either AUC or weighted accuracy) by holdout validation (Weiss and Kulikowski, 1991), whereby 2/3 of data samples were used for Markov boundary induction and classifier training and remaining 1/3 for classifier testing. Statistical comparison of AUC estimates was performed using DeLong's test at α = 0.05 (DeLong et al., 1988) and comparison of weighted accuracy estimates was performed by permutation-based testing with 10,000 permutations of the vectors of classifier predictions (Good, 2000). We also experimented with other SVM kernels and parameters in the criterion Predictivity, but the final results were similar because SVMs are used here only for relative assessment of the classifier performance (i.e., to compare performance of the Markov boundary M from the original distribution with performance of the new Markov boundary Mnew from the embedded distribution). Final assessment of the classifier performance for induced Markov boundary variables was carried out using SVMs with polynomial kernel and parameters C and degree d optimized by holdout validation or cross-validation, as described in Section 5.
Appendix E. Additional Information about Empirical Experiments
This appendix provides additional information about empirical experiments.
E.1 Parameterizations of Methods in Empirical Experiments
Parameterizations of methods in empirical experiments are given in Table 9.
E.2 On Computation of Performance Criteria in Experiments with Simulated Data
Since the number of distinct Markov boundaries/variable sets extracted by a given method in our evaluation may differ from the number of true Markov boundaries in the causal graph, it is necessary to establish a matching between the true Markov boundaries and the extracted Markov boundaries/variable sets before computing values of criteria III–V. This matching was performed by finding a minimum-weight matching in a complete bipartite graph , where vertices in V1 corresponded to the true Markov boundaries and vertices in V2 corresponded to the extracted Markov boundaries/variable sets. The weight of an edge (u,v) ∈ E,u ∈ V1,v ∈ V2, was set equal to the sum of PFP and FNR that would have resulted from matching the true Markov boundary u with the extracted Markov boundary/variable set v. The extracted Markov boundaries/variable sets that were not matched to any true Markov boundary did not participate in the computation of criteria III–V. A limitation of this approach to evaluation of different methods is that methods that are parameterized to produce a number of Markov boundaries/variable sets that is much larger than the number of true Markov boundaries could potentially show better performance on criteria III–V than methods/parameterizations that output only a few Markov boundaries/variable sets. In order to control for this effect, whenever a method allowed it, some of its parameterizations were targeted towards producing the same “large” number of Markov boundaries/variable sets (5,000 in our case). In addition, since the true Markov boundaries are unknown in practical applications, the average classification performance (criterion VI) was computed over all distinct Markov boundaries/variable sets extracted by a method. This way of computing the average classification performance, in a sense, counteracts the potential bias in criteria III–V towards methods that produce large numbers of Markov boundaries/variable sets, since if many of the extracted Markov boundaries/variable sets do not contain the variables truly relevant to prediction of T (i.e., members of its true Markov boundaries), the classification performance may suffer.
E.3 Additional Discussion of the Results of Experiments with Simulated Data
KIAMB did not identify any true Markov boundaries exactly due to this method's sample inefficiency arising from conditioning on the entire (candidate) Markov boundary. The average classification performance of Markov boundaries extracted by KIAMB was about 20% lower than of the MAP-BN classifier in both data sets.
Performance of EGS-NCMIGS and EGS-CMIM was very similar and varied widely depending on parameterization, with the average PFP ranging from 29% to 76% and average FNR ranging from 0% to 27% in TIED. The high ends (i.e., worse results) of these measures increased to 95% PFP and 51% FNR in TIED1000 demonstrating the sensitivity of these methods to the presence of irrelevant variables in the data. The alternative stopping criterion of EGS-NCMIGS helped reduce the PFP relative to other parameterizations, but failed to reduce the FNR. The other stopping criterion that requires the size K of Markov boundaries to be specified, was able to achieve 0% FNR in TIED (for large enough K; see Table 10). This suggests that, even though the alternative stopping criterion has the advantage of not requiring prior knowledge of the size of Markov boundaries, it makes EGS-NCMIGS susceptible to premature termination as discussed in Appendix C. The average classification performance of Markov boundaries extracted by EGS-NCMIGS and EGS-CMIM was statistically comparable to the MAP-BN classification performance for all parameterizations except those with K = 50 in both data sets and also for (l = 7, δ = 0.015) in TIED1000. The reduction in classification performance relative to MAP-BN reached as high as 10% and was due to presence of false positives and false negatives in the extracted Markov boundaries.
EGSG proved to be extremely sensitive to the presence of irrelevant variables with PFP and FNR increasing across all parameterizations from highs of 55% PFP and 37% FNR in TIED to uniformly above 93% PFP and high of 78% FNR in TIED1000. In addition, the average size of Markov boundaries extracted by EGSG increased almost 10-fold, from 7 in TIED to 67 in TIED1000, while the number of variables conditionally dependent on T in the underlying network remained unchanged. Consistent with the theoretical analysis in Appendix C, these results demonstrate the lack of control for false positives as well as false negatives in the output of EGSG. Classification performance was sensitive to the values of parameter t, with increasing values resulting in degradation of classification performance in both data sets, which is due to the fact that as t increases, Markov boundaries extracted by EGSG increasingly resemble subsets of randomly selected variables from the complete set of variables. Classification performance of Markov boundaries extracted by EGSG was lower than performance of the MAP-BN classifier by 9–23% (depending on parameter settings) in TIED and by 27–55% in TIED1000. In addition, classification performance in TIED1000 was lower than in TIED uniformly across all parameterizations of EGSG.
Variable sets extracted by Resampling+UAF were 24–50% larger than those found by Resampling+RFE, which helped Resampling+UAF reach slightly lower FNR (by 3–6% in TIED and by 2–4% in TIED1000), but also resulted in significantly higher PFP (by about 42–46% in TIED and by 30–35% in TIED1000). The larger size of the extracted variable sets and higher PFP are likely due to UAF's ranking of variables based solely on univariate association with the response T, whereas RFE's ranking is “multivariate” in a sense that it takes into account not only each variable's individual classification performance, but also the information that other variables in the current nested subset carry about T (Guyon et al., 2002). In fact, Resampling+RFE produced more compact variable sets than Resampling+UAF in every simulated and real data set considered in this study. In simulated data, parameterizations of Resampling+RFE and Resampling+UAF with statistical comparison of classification performance estimates produced variable sets that were on average 60–70% smaller than those found by parameterizations without statistical comparison, resulting in about 20% decreases in PFP, but causing roughly 30–36% increases in FNR. The average classification performance of variable sets extracted by Resampling+RFE in simulated data was statistically indistinguishable from Resampling+UAF with similar parameterizations. The average classification performance of both methods parameterized without statistical comparison was comparable with performance of the MAP-BN classifier in TIED and was slightly lower (by about 1–2%) in TIED1000. Parameterizations with statistical comparison underperformed the MAP-BN classifier by about 2–3% in both data sets. The results in both simulated data sets also show that the number of distinct variable sets out of the 5,000 extracted by each parameterization of Resampling+RFE and Resampling+UAF ranged from 0.24% to 50%, and hence roughly 99% to 50% of computational resources were spent retrieving the same variable sets multiple times.
IR-HITON-PC was able to identify exactly only a single true Markov boundary in both data sets. This was a direct consequence of a violation of the iterative removal's underlying assumption that the true Markov boundaries are disjoint sets of variables. All true Markov boundaries in TIED and TIED1000 share variable X10. However, once that variable was found to be in a Markov boundary by an iterative removal method, it was then removed from further consideration thus preventing all other extracted Markov boundaries from containing this variable. Markov boundaries extracted by IR-HITON-PC had 8–10% PFP (depending on the data set) and 10–20% FNR. The low PFP was due to Semi-Interleaved HITON-PC's built-in control for the false discovery rate (Aliferis et al., 2010b), while the high FNR was a consequence of the iterative removal scheme. As a result of high FNR in TIED, the average classification performance of Markov boundaries extracted by IR-HITON-PC was about 2% lower than of the MAP-BN classifier in the same data set. The FNR was lower in TIED1000 than in TIED, which resulted in classification performance becoming statistically comparable with the MAP-BN performance.
IR-SPLR was not able to identify any true Markov boundaries exactly in neither TIED or TIED1000. Each parameterization of IR-SPLR extracted only one variable set in both simulated data sets. Variable sets extracted by IR-SPLR in simulated data were 4–6 times larger than those found by IR-HITON-PC, which resulted in about 60–70% increase in PFP (depending on the data set), but zero FNR. The PFP of IR-SPLR did not increase significantly in TIED1000 relative to TIED, which demonstrates the often-cited benefit of the L1-norm regularization, that is, its ability to exclude irrelevant variables from the model. Classification performance of the extracted variable sets was statistically comparable to the MAP-BN performance in TIED and was about 2% lower in TIED1000 due to an increase in PFP.
E.4 Real Data sets Used in the Experiments
The list of real data sets used in the experiments is given in Table 12.
E.5 On Computation of Performance Criteria in Experiments with Real Data
In order to rank all methods based on a given performance criterion, the average value of this criterion was first computed over all evaluation data sets for each method. The methods were then ordered from best to worst performing according to these averages. The best performer was assigned rank 1 and designated as the current “reference method”. Performance of the next unranked method in the ordered list was compared to performance of the reference method using permutation-based testing at significance level 5% and with 10,000 permutations of the vectors of criterion values computed on each data set. If performance of the two methods was found to be statistically comparable, the unranked method received the same rank as the reference method. Otherwise, the next lowest rank was assigned to the unranked method and this method was designated as the new reference method. This process was repeated until each method was assigned a rank.
E.6 Additional Discussion of the Results of Experiments with Real Data
KIAMB produced some of the more compact Markov boundaries with the average PV of 1% and ranked second out of 11 by that criterion. Small sizes of the extracted Markov boundaries were, to a large extent, due to KIAMB's sample inefficiency resulting in inability to perform some of the required tests of independence as discussed in Appendix C. As a result, classification performance of Markov boundaries extracted by KIAMB was lower than of most other methods with KIAMB ranking 4 out of 5 by AUC. Consequently, KIAMB ranked 5 out of 15 on the (PV, AUC) criterion. Although, KIAMB was parameterized to produce 5,000 Markov boundaries, only about 30% of them were distinct, which means that 70% of computational time was spent on repeated retrieval of the same Markov boundaries.
EGS-NCMIGS with the alternative stopping criterion produced the smallest Markov boundaries at the expense of a significant reduction in AUC (~ 9% below TIE*). Parameterizations of EGS-NCMIGS with the alternative stopping criterion ranked first and second out of 11 by PV and fourth out of 5 by AUC. Overall, performance of EGS-NCMIGS and EGS-CMIM varied widely depending on parameterization. Ranks of these methods ranged from 2 to 11 out of 15 on the (PV, AUC) criterion.
EGSG showed an overall poor performance, ranking between 10 and 15 out of 15 on (PV, AUC). Markov boundaries extracted by EGSG were larger than Markov boundaries identified by many other methods and had the lowest average classification performance.
Resampling+RFE and Resampling+UAF extracted variable sets that were the largest in comparison with other methods, but that also had highest classification performance. Resampling+RFE and Resampling+UAF ranked between 9 and 11 out of 11 by PV and between 1 and 3 by AUC. Notably, variable sets extracted by Resampling+UAF had an average PV between 24% and 41%, depending on parameterization. Resampling+RFE extracted more compact variable sets than Resampling+UAF in every data set, with the average PV between 5% and 17%. Due to poor performance on the PV criterion, Resampling+RFE and Resampling+UAF ranked in the mid to poor range on the combined (PV, AUC) criterion, scoring between 7 and 11 out of 15.
Iterative removal methods IR-HITON-PC and IR-SPLR extracted small numbers of Markov boundaries/variable sets and ranked between 5 and 6 out of 6 by that criterion. IR-HITON-PC produced more compact Markov boundaries than the variable sets of IR-SPLR. Markov boundaries extracted by IR-HITON-PC had an average PV of 2.3%, which was significantly smaller than the 11%–15% average PV of IR-SPLR. IR-HITON-PC method ranked 5 out of 11 by PV while IR-SPLR methods ranked 9 and 10 by the same criterion. Despite the smaller average size of the extracted Markov boundaries, IR-HITON-PC ranked on par with IR-SPLR (parameterized with statistical comparison) by AUC, scoring third out of 5. Among all parameterizations of iterative removal methods, IR-SPLR without statistical comparison produced the largest variable sets, which helped this method reach a higher average classification performance and rank second out of 5 by AUC. Higher average PV of variable sets extracted by IR-SPLR caused these methods to rank 9 and 11 out of 15 on the combined (PV, AUC) criterion. IR-HITON-PC ranked sixth on the same criterion as a result of moderate ranks on PV and AUC.
Footnotes
Pearl originally provided this theorem for disjoint sets of variables (Pearl, 1988). However, he stated that the disjoint requirement is made for the sake of clarity, and that the theorem can be extended to include overlapping subsets as well.
This example has been previously published in the work by Statnikov and Aliferis (2010a) and is presented here with the intent to illustrate the definition of equivalent partition.
For example, can be negative mean squared error between estimated and true values of P(T | V \{T}) (Tsamardinos and Aliferis, 2003).
For example, can be feed-forward neural networks or support vector machines that are known to have universal approximation capabilities (Hammer and Gersmann, 2003; Pinkus, 1999; Scarselli and Chung Tsoi, 1998).
Specific examples of inputs , , are given in the next subsection and are omitted here in order to emphasize core algorithmic principles of TIE*.
To retain simplicity of the TIE* pseudo-code (Figure 6), we implicitly assume that are stored during operation of the generative algorithm TIE*. This can be implemented by setting a counter of all identified Markov boundaries in the original distribution (i) and a counter of all identified Markov boundaries in the embedded distribution that are not Markov boundaries the original distribution (j). Then the following assignments should be made: M1←M and after step 1 of TIE*;M←Mnew and in step 6 of TIE* if Mnew is a Markov boundary in the original distribution; and in step 6 of TIE* if Mnew is not a Markov boundary in the original distribution.
Since we use negative p-values from a conditional independence test as the measure of association in IAMB and Semi-Interleaved HITON-PC (see Appendix D), we assume that complexity of computing an association is equal to the complexity of conditional independence testing.
This is a test T ⊥ Z | Y. Other necessary tests T
 Y and T
Y and T
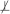 Z have been previously computed in step 4 of Semi-Interleaved HITON-PC algorithm, and their results can be retrieved from the cache.
Z have been previously computed in step 4 of Semi-Interleaved HITON-PC algorithm, and their results can be retrieved from the cache.
False positives are variables that do not belong to any true Markov boundary of T in the causal graph, but are included in a Markov boundary/variable set extracted by some method. False negatives are variables that belong to a true Markov boundary of T, but are absent in the extracted Markov boundary/variable set.
PFP is the number of false positives in an output Markov boundary/variable set divided by its size.
FNR is the number of false negatives in an output Markov boundary/variable set divided by the size of the true Markov boundary.
Given that the response variable T had four possible values, classification performance was measured by the weighted accuracy metric that allows to measure classification performance independent of class priors and can be applied to multiclass responses (Guyon et al., 2006). In brief, weighted accuracy is obtained by computing proportion of correct classifications in each class and combining these proportions by weighting using prior probabilities in each class.
The PV of an output Markov boundary/variable set measures its compactness and is defined as the number of variables in the output Markov boundary/variable set divided by the total number of variables in the data set.
Classification performance was measured using area under ROC curve (AUC) (Fawcett, 2003), because all response variables were binary.
We did not include iTIE* in this comparison, because we anticipated that it will be outperformed by TIE* due to its broader distributional assumptions than the ones of iTIE*.
Reduction coefficient = 1.2 means that every iteration retains 1/1.2 = 83% of variables from the previous iteration.
For the Fishers Z test and G2 test, p-value is inversely related to the test statistic, given a fixed degree of freedom. Thus, larger test statistics correspond to smaller p-values, and vice-versa.
References
- Aliferis CF, Tsamardinos I, Statnikov A. Large-scale feature selection using markov blanket induction for the prediction of protein-drug binding. Technical Report DSL 02–06. 2002 [Google Scholar]
- Aliferis CF, Tsamardinos I, Statnikov A. Hiton: a novel markov blanket algorithm for optimal variable selection. AMIA 2003 Annual Symposium Proceedings; 2003a. pp. 21–25. [PMC free article] [PubMed] [Google Scholar]
- Aliferis CF, Tsamardinos I, Statnikov A, Brown LE. Causal explorer: a causal probabilistic network learning toolkit for biomedical discovery. Proceedings of the 2003 International Conference on Mathematics and Engineering Techniques in Medicine and Biological Sciences (METMBS).2003b. [Google Scholar]
- Aliferis CF, Statnikov A, Tsamardinos I, Mani S, Koutsoukos XD. Local causal and markov blanket induction for causal discovery and feature selection for classification. part i: Algorithms and empirical evaluation. Journal of Machine Learning Research. 2010a;11:171–234. [Google Scholar]
- Aliferis CF, Statnikov A, Tsamardinos I, Mani S, Koutsoukos XD. Local causal and markov blanket induction for causal discovery and feature selection for classification. part ii: Analysis and extensions. Journal of Machine Learning Research. 2010b;11:235–284. [Google Scholar]
- Anderson TW. An Introduction to Multivariate Statistical Analysis, volume 3rd of Wiley Series in Probability and Statistics. Wiley-Interscience; Hoboken, N.J: 2003. [Google Scholar]
- Aphinyanaphongs Y, Statnikov A, Aliferis CF. A comparison of citation metrics to machine learning filters for the identification of high quality medline documents. J.Am.Med.Inform.Assoc. 2006;13(4):446–455. doi: 10.1197/jamia.M2031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breiman L. Statistical modeling: the two cultures. Statistical Science. 2001;16(3):199–215. [Google Scholar]
- Brown LE, Tsamardinos I, Hardin D. To feature space and back: Identifying top-weighted features in polynomial support vector machine models. Intelligent Data Analysis. 2012;16(4) [Google Scholar]
- Conrads TP, Fusaro VA, Ross S, Johann D, Rajapakse V, Hitt BA, Steinberg SM, Kohn EC, Fishman DA, Whitely G, Barrett JC, Liotta LA, III, Petricoin EF, Veenstra TD. High-resolution serum proteomic features for ovarian cancer detection. Endocr.Relat Cancer. 2004;11(2):163–178. doi: 10.1677/erc.0.0110163. [DOI] [PubMed] [Google Scholar]
- Cover TM, Thomas JA. Elements of Information Theory. Wiley; New York: 1991. [Google Scholar]
- Cristianini N, Shawe-Taylor J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods. Cambridge University Press; Cambridge: 2000. [Google Scholar]
- DeLong ER, DeLong DM, Clarke-Pearson DL. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics. 1988;44(3):837–845. [PubMed] [Google Scholar]
- Dougherty E, Brun M. On the number of close-to-optimal feature sets. Cancer Informatics. 2006;2:189–196. [PMC free article] [PubMed] [Google Scholar]
- Ein-Dor L, Kela I, Getz G, Givol D, Domany E. Outcome signature genes in breast cancer: is there a unique set? Bioinformatics. 2005;21(2):171–178. doi: 10.1093/bioinformatics/bth469. [DOI] [PubMed] [Google Scholar]
- Ein-Dor L, Zuk O, Domany E. Thousands of samples are needed to generate a robust gene list for predicting outcome in cancer. Proc.Natl.Acad.Sci.U.S.A. 2006;103(15):5923–5928. doi: 10.1073/pnas.0601231103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan RE, Chen PH, Lin CJ. Working set selection using second order information for training support vector machines. Journal of Machine Learning Research. 2005;6(1889):1918. [Google Scholar]
- Fawcett T. Roc graphs: Notes and practical considerations for researchers. Technical Report, HPL-2003-4, HP Laboratories. 2003 [Google Scholar]
- Fleuret F. Fast binary feature selection with conditional mutual information. Journal of Machine Learning Research. 2004;5:1531–1555. [Google Scholar]
- Foster DP, Stine RA. Variable selecion in data mining: Building a predictive model for bankruptcy. Journal of the American Statistical Association. 2004;99(466):303–314. [Google Scholar]
- Glymour CN, Copper GF. Computation, Causation and Discovery. AAAI Press; Menlo Park, Calif: 1991. [Google Scholar]
- Good PI. Permutation Tests: A Practical Guide to Resampling Methods for Testing Hypotheses, volume 2nd of Springer series in statistics. Springer; New York: 2000. [Google Scholar]
- Gopnik A, Schulz L. Causal Learning: Psychology, Philosophy, and Computation. Oxford University Press; Oxford: 2007. [Google Scholar]
- Guyon I, Elisseeff A. An introduction to variable and feature selection. Journal of Machine Learning Research. 2003;3(1):1157–1182. [Google Scholar]
- Guyon I, Weston J, Barnhill S, Vapnik V. Gene selection for cancer classification using support vector machines. Machine Learning. 2002;46(1):389–422. [Google Scholar]
- Guyon I, Gunn S, Nikravesh M, Zadeh LA. Feature Extraction: Foundations and Applications. Springer-Verlag; Berlin: 2006. Studies in fuzziness and soft computing. [Google Scholar]
- Hammer B, Gersmann K. A note on the universal approximation capability of support vector machines. Neural Processing Letters. 2003;17(1):43–53. [Google Scholar]
- Hollander M, Wolfe D. Nonparametric statistical methods, volume 2nd of Wiley Series in Probability and Statistics. Wiley; New York, NY, USA: 1999. [Google Scholar]
- Joachims T. Learning to Classify Text Using Support Vector Machines. Kluwer Academic Publishers; Boston: 2002. (Kluwer international series in engineering and computer science). [Google Scholar]
- Kohavi R, John GH. Wrappers for feature subset selection. Artificial Intelligence. 1997;97(1–2):273–324. [Google Scholar]
- Lemeire J. PhD thesis. 2007. Learning Causal Models of Multivariate Systems and the Value of It for the Performance Modeling of Computer Programs. [Google Scholar]
- Lemeire J, Meganck S, Cartella F. Robust independence-based causal structure learning in absence of adjacency faithfulness. Proccedings of the Fifth European Workshop on Probabilistic Graphical Models (PGM 2010).2010. [Google Scholar]
- Liu H, Liu L, Zhang H. Ensemble gene selection by grouping for microarray data classification. J.Biomed.Inform. 2010;43(1):81–87. doi: 10.1016/j.jbi.2009.08.010. [DOI] [PubMed] [Google Scholar]
- Liu H, Liu L, Zhang H. Ensemble gene selection for cancer classification. Pattern Recognition. 2010b;43(8):2763–2772. [Google Scholar]
- Mani S, Cooper GF. A study in causal discovery from population-based infant birth and death records. Proceedings of the AMIA Annual Fall Symposium; p. 1999. [PMC free article] [PubMed] [Google Scholar]
- Mani S, Cooper GF. Causal discovery using a bayesian local causal discovery algorithm. Medinfo 2004. 2004;11(Pt 1):731–735. [PubMed] [Google Scholar]
- Michiels S, Koscielny S, Hill C. Prediction of cancer outcome with microarrays: a multiple random validation strategy. Lancet. 2005;365(9458):488–492. doi: 10.1016/S0140-6736(05)17866-0. [DOI] [PubMed] [Google Scholar]
- Natsoulis G, El Ghaoui L, Lanckriet GR, Tolley AM, Leroy F, Dunlea S, Eynon BP, Pearson CI, Tugendreich S, Jarnagin K. Classification of a large microarray data set: algorithm comparison and analysis of drug signatures. Genome Res. 2005;15(5):724–736. doi: 10.1101/gr.2807605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neapolitan RE. Learning Bayesian Networks. Pearson Prentice Hall; Upper Saddle River, NJ: 2004. (Prentice Hall series in artificial intelligence). [Google Scholar]
- Peña J, Nilsson R, Björkegren J, Tegnér J. Towards scalable and data efficient learning of markov boundaries. International Journal of Approximate Reasoning. 2007;45(2):211–232. [Google Scholar]
- Pearl J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. Morgan Kaufmann Publishers; San Mateo, California: 1988. (The Morgan Kaufmann series in representation and reasoning). [Google Scholar]
- Pearl J. Causality: Models, Reasoning, and Inference. ume 2nd. Cambridge University Press; Cambridge, U.K: 2009. [Google Scholar]
- Pellet JP, Elisseeff A. Using markov blankets for causal structure learning. The Journal of Machine Learning Research. 2008;9:1295–1342. [Google Scholar]
- Pinkus A. Approximation theory of the mlp model in neural networks. Acta Numerica. 1999;8:143–195. [Google Scholar]
- Ramsey J, Zhang J, Spirtes P. Adjacency-faithfulness and conservative causal inference. Proceedings of the 22nd Annual Conference on Uncertainty in Artificial Intelligence (UAI-2006).2006. pp. 401–408. [Google Scholar]
- Richardson T, Spirtes P. Automated Discovery of Linear Feedback Models. MIT Press; Menlo Park, CA: 1999. [Google Scholar]
- Richardson TS, Spirtes P. Ancestral graph markov models. Annals of Statistics. 2002;30(4):962–1030. [Google Scholar]
- Roepman P, Kemmeren P, Wessels LF, Slootweg PJ, Holstege FC. Multiple robust signatures for detecting lymph node metastasis in head and neck cancer. Cancer Res. 2006;66(4):2361–2366. doi: 10.1158/0008-5472.CAN-05-3960. [DOI] [PubMed] [Google Scholar]
- Rosenwald A, Wright G, Chan WC, Connors JM, Campo E, Fisher RI, Gascoyne RD, Muller-Hermelink HK, Smeland EB, Giltnane JM, Hurt EM, Zhao H, Averett L, Yang L, Wilson WH, Jaffe ES, Simon R, Klausner RD, Powell J, Duffey PL, Longo DL, Greiner TC, Weisenburger DD, Sanger WG, Dave BJ, Lynch JC, Vose J, Armitage JO, Montserrat E, Lopez-Guillermo A, Grogan TM, Miller TP, LeBlanc M, Ott G, Kvaloy S, Delabie J, Holte H, Krajci P, Stokke T, Staudt LM. The use of molecular profiling to predict survival after chemotherapy for diffuse large-b-cell lymphoma. N.Engl.J Med. 2002;346(25):1937–1947. doi: 10.1056/NEJMoa012914. [DOI] [PubMed] [Google Scholar]
- Scarselli F, Chung Tsoi A. Universal approximation using feedforward neural networks: A survey of some existing methods, and some new results. Neural Networks. 1998;11(1):15–37. doi: 10.1016/s0893-6080(97)00097-x. [DOI] [PubMed] [Google Scholar]
- Schölkopf B, Burges CJC, Smola AJ. Advances in Kernel Methods: Support Vector Learning. MIT Press; Cambridge, Mass: 1999. [Google Scholar]
- Shawe-Taylor J, Cristianini N. Kernel Methods for Pattern Analysis. Cambridge University Press; Cambridge, UK: 2004. [Google Scholar]
- Somorjai RL, Dolenko B, Baumgartner R. Class prediction and discovery using gene microarray and proteomics mass spectroscopy data: curses, caveats, cautions. Bioinformatics. 2003;19(12):1484–1491. doi: 10.1093/bioinformatics/btg182. [DOI] [PubMed] [Google Scholar]
- Spirtes P, Glymour CN, Scheines R. Causation, Prediction, and Search, volume 2nd of Adaptive computation and machine learning. MIT Press; Cambridge, Mass: 2000. [Google Scholar]
- Statnikov A, Aliferis CF. Analysis and computational dissection of molecular signature multiplicity. PLoS Computational Biology. 2010a;6(5):e1000790. doi: 10.1371/journal.pcbi.1000790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Statnikov A, Aliferis CF. TIED: An Artificially Simulated Dataset with Multiple Markov Boundaries. Journal of Machine Learning Research Workshop and Conference Proceedings, Volume 6: Causality: Objectives and Assessment (NIPS 2008) 2010b;6:249–256. [Google Scholar]
- Statnikov A, Aliferis CF, Tsamardinos I, Hardin D, Levy S. A comprehensive evaluation of multicategory classification methods for microarray gene expression cancer diagnosis. Bioinformatics. 2005;21(5):631–643. doi: 10.1093/bioinformatics/bti033. [DOI] [PubMed] [Google Scholar]
- Statnikov A, Tsamardinos I, Brown LE, Aliferis CF. Causal Explorer: A Matlab Library of Algorithms for Causal Discovery and Variable Selection for Classification. In: Guyon I, Aliferis CF, Cooper GF, Elisseeff A, Pellet JP, Spirtes P, Statnikov A, editors. Challenges in Machine Learning. Volume 2: Causation and Prediction Challenge. Microtome Publishing, Bookline; Massachusetts: 2010. [Google Scholar]
- Tsamardinos I, Aliferis CF. Towards principled feature selection: relevancy, filters and wrappers. Proceedings of the Ninth International Workshop on Artificial Intelligence and Statistics(AI and Stats).2003. [Google Scholar]
- Tsamardinos I, Brown LE. Markov blanket-based variable selection in feature space. Technical Report DSL-08-01. 2008 [Google Scholar]
- Tsamardinos I, Aliferis CF, Statnikov A. Algorithms for large scale markov blanket discovery. Proceedings of the Sixteenth International Florida Artificial Intelligence Research Society Conference (FLAIRS).2003a. pp. 376–381. [Google Scholar]
- Tsamardinos I, Aliferis CF, Statnikov A. Time and sample efficient discovery of markov blankets and direct causal relations. Proceedings of the Ninth International Conference on Knowledge Discovery and Data Mining (KDD).2003b. pp. 673–678. [Google Scholar]
- Vapnik VN. Adaptive and learning systems for signal processing, communications, and control. Wiley; New York: 1998. Statistical Learning Theory. [Google Scholar]
- Wang Y, Klijn JG, Zhang Y, Sieuwerts AM, Look MP, Yang F, Talantov D, Timmermans M, Meijer-van Gelder ME, Yu J, Jatkoe T, Berns EM, Atkins D, Foekens JA. Gene-expression profiles to predict distant metastasis of lymph-node-negative primary breast cancer. Lancet. 2005;365(9460):671–679. doi: 10.1016/S0140-6736(05)17947-1. [DOI] [PubMed] [Google Scholar]
- Weiss SM, Kulikowski CA. Computer Systems that Learn: Classification and Prediction Methods from Statistics, Neural Nets, Machine Learning, and Expert Systems. M. Kaufmann Publishers; San Mateo, Calif: 1991. [Google Scholar]