Drug repositioning by integrating target information through a heterogeneous network model

Abstract

Motivation: The emergence of network medicine not only offers more opportunities for better and more complete understanding of the molecular complexities of diseases, but also serves as a promising tool for identifying new drug targets and establishing new relationships among diseases that enable drug repositioning. Computational approaches for drug repositioning by integrating information from multiple sources and multiple levels have the potential to provide great insights to the complex relationships among drugs, targets, disease genes and diseases at a system level.

Results: In this article, we have proposed a computational framework based on a heterogeneous network model and applied the approach on drug repositioning by using existing omics data about diseases, drugs and drug targets. The novelty of the framework lies in the fact that the strength between a disease–drug pair is calculated through an iterative algorithm on the heterogeneous graph that also incorporates drug-target information. Comprehensive experimental results show that the proposed approach significantly outperforms several recent approaches. Case studies further illustrate its practical usefulness.

Availability and implementation: http://cbc.case.edu

Contact: jingli@cwru.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Traditionally, drug discovery and drug development mainly rely on cell-based or target-based screening of chemical compounds to identify a small subset of ‘hits’, properties of which are then studied to further increase their affinity, efficacy and selectivity, before moving forward to animal tests and clinical trials (Paul et al., 2010). Even with advance in technology and knowledge about the molecular bases of diseases, the whole process of drug development is still lengthy, expensive and with high-failure rates. It is estimated that the cost for developing a new drug is ∼$1.8 billion dollars, and the average time is ∼13.5 years (Paul et al., 2010). Drug repositioning, which aims to identify new indications of existing drugs, offers a promising alternative to reduce the total time and cost because of existing safety, toleration and efficacy data on known drugs (Ashburn and Thor, 2004). Several successfully repositioned drugs (e.g. sildenafil) have generated significant revenues for their patent holders/companies.

The generation of large-scale genomic, transcriptomic, proteomic data and their integration with signaling and metabolimic data in a network framework have provided new insights of molecular basis of complex diseases and have enabled a network-based view of drug discovery and development (Hopkins, 2008). The emergence of network medicine not only offers more opportunities for better and more complete understanding of molecular complexities of diseases (Goh and Choi, 2012; Goh et al., 2007), but also serves as a promising tool for identifying new drug targets (Campillos et al., 2008; Yildirim et al., 2007) and establishing new relationships among diseases that enable drug repositioning (Barabasi et al., 2011). Since these earlier works, many computational approaches have been proposed either for target prediction (Bleakley and Yamanishi, 2009; Campillos et al., 2008; Cheng et al., 2012; Emig, 2013; Keiser et al., 2009; Perlman et al., 2011; Wang et al., 2013; Yamanishi et al., 2008) or drug repositioning (Chiang and Butte, 2009; Gottlieb et al., 2011; Lamb et al., 2006; Li et al., 2009; Sirota et al., 2011), many of which have used network-based algorithms.

In many of these studies, drug target prediction and drug repositioning were treated as two separate tasks. We argue that by incorporating target information directly into drug repositioning, we can potentially make more meaningful predictions. The underlying assumption is based on the principle of rational drug design: therapeutic effect of chemical compounds on diseases is through their binding to biological targets that are relevant to diseases themselves. Although it is not feasible to fully adopt the rational drug-design strategy in large-scale systematic assessment of relationships among all drugs and all diseases, it is a promising direction to include target information in drug repositioning. This principle has been recognized by many researchers (e.g. Gottlieb et al., 2011; Li et al., 2009). What is lacking is a systematic approach to automatically integrate drug-target information into drug repositioning.

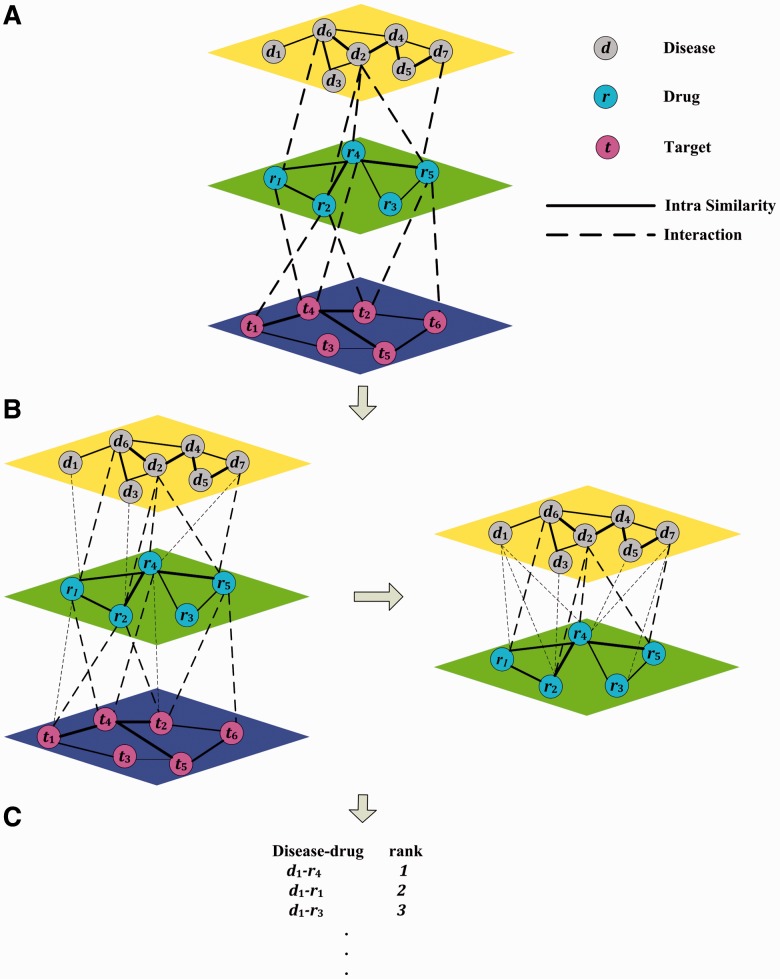
In this article, we propose a novel heterogeneous network model that seamlessly integrates drug repositioning and target prediction into one unified framework. The full heterogeneous graph model consists of three different types of nodes: diseases, drugs and drug targets (Fig. 1). Disease–drug relationships and drug–target relationships are constructed based on prior knowledge from existing databases such as DrugBank (Knox et al., 2011). Disease–disease, drug–drug and target–target relationships are constructed based on their similarities. The drug repositioning is thus formulated as a missing edge prediction problem on this heterogeneous graph. An iterative updating algorithm that propagates information across the network is then developed to solve the missing edge prediction problem. Our approach is based on the guilt-by-association principle (Altshuler et al., 2000) that has been validated repeatedly in many studies, including studies on drug repositioning (Chiang and Butte, 2009). A unique characteristic of our framework is that it automatically incorporates drug-target information into drug–disease association prediction.

Fig. 1.

Procedure of predicting disease–drug associations with TL_HGBI. (A) Constructing a triple-layer network with intra similarities and interactions among diseases, drugs and targets. (B) Calculating prediction scores in two steps. (C) Ranking candidate drugs based on their prediction scores

Although the primary goal of this article is to investigate the drug repositioning problem, it is also worth noting that by using the newly proposed heterogeneous model and the iterative updating algorithm, new drug–target relationships will also be automatically constructed simultaneously. When only diseases and drugs are considered or only drugs and targets are considered, the triple layer model is reduced to a two-layer model. The two-layer model using drugs and targets for target prediction was investigated by our group in a recent paper, and its iterative updating algorithm was termed Heterogeneous Graph Based Inference (HGBI) (Wang et al., 2013). The same algorithm can also be used for the two-layer model consisting of diseases and drugs for drug repositioning. However, it cannot be directly extended to the tree-layer model, which will be the focus of this study.

To evaluate the newly proposed three-layer model (termed TL_HGBI, for Triple Layer Heterogeneous Graph Based Inference) for drug repositioning, we will compare its performance with the performance of the two-layer model consisting of only diseases and drugs by using the HGBI algorithm originally developed for drug target prediction (Wang et al., 2013). The evaluation is mainly based on leave-one-out cross-validation (LOOCV) experiments on large-scale omics data from existing databases [e.g. DrugBank, OMIM (Hamosh et al., 2005)]. Three additional state-of-the-art approaches, namely, GBA (Chiang and Butte, 2009), BLM (Bleakley and Yamanishi, 2009) and NBI (Cheng et al., 2012) are also included in the comparison. Although BLM and NBI (HGBI as well) were originally developed for drug–target association prediction, the algorithms have been used on drug–disease association prediction (Gottlieb et al., 2011; Perlman et al., 2011) and can naturally be applied on drug repositioning. Experimental results show that TL_HGBI performs the best with highest AUC (area under the receiver operating characteristic, i.e. ROC curve). In particular, when focusing on the top 1% predicted drug–disease associations, TL_HGBI successfully retrieves 304 interactions of 1382 true disease–drug interactions, whereas HGBI, BLM and NBI retrieve 290, 15 and 2 such interactions. Furthermore, in a case study of five different diseases, many of the top-ranked drugs are strongly supported by recent literature, knowledge of which was not included in the experiment.

2 METHODS

2.1 A two-layer heterogeneous network model for drug repositioning

We first introduce the two-layer heterogeneous network model for drug repositioning. The network consists of two types of nodes, i.e. disease nodes and drug nodes, and three types of edges, i.e. disease–disease edges, drug–drug edges and disease–drug edges. Let $D=\{d_1,d_2,\mathrm{...},d_n\}$ denote the n diseases; $R=\{r_1,r_2,\mathrm{...},r_m\}$ denote the m drugs. Let $E_{dd}$ and $E_{rr}$ denote edges between diseases and drugs, respectively. Let $W_{dd}$ and $W_{rr}$ denote edge weights, which reflect disease–disease and drug–drug similarities. Let $E_{dr}$ denote the known disease–drug relationships. The weights on all these disease–drug edges are initially assigned 1 and denoted by W_dr. The drug repositioning problem can therefore be formulated as missing edge prediction problem on the heterogeneous graph $G_{DR}=\left\{\right\{D,R\},\{E_{dd},E_{rr},E_{dr}\},\{W_{dd},W_{rr},W_{dr}\left\}\right\}$. The objective is to capture hidden relationships between drugs and diseases based on drug–drug similarities, disease–disease similarities and known drug–target interactions. Structure-wise, this model is the same as the two-layer model we developed for drug target prediction (Wang et al., 2013). Therefore, we will use the same iterative algorithm HGBI to solve the problem.

2.2 A three-layer heterogeneous network model for drug repositioning

The three-layer heterogeneous network model consists of three types of nodes: disease nodes, drug nodes and target nodes. Let $D=\{d_1,d_2,\mathrm{...},d_n\}$ denote the n disease nodes, $R=\{r_1,r_2,\mathrm{...},r_m\}$ denote the m drug nodes and $T=\{t_1,t_2,\mathrm{...},t_l\}$ denote the l target nodes. The edges among these nodes are defined based on their relationships. For example, the intraconnections between the same types of nodes can be defined based on their similarities or their relationships from other data sources. For our initial investigations, we will use similarity measures to define intraconnections. Disease similarities can be calculated based on their phenotypic descriptions (Van Driel et al., 2006). Drug similarities can be calculated based on their chemical structures (Steinbeck et al., 2006). Target similarities can be calculated based on their protein sequence similarities (Bleakley and Yamanishi, 2009). Distributions of these similarity measures will be investigated, and proper thresholds will be selected to construct the network. Two nodes of the same type will be connected if and only if their similarity measure is greater than the selected threshold, and the similarity is treated as edge weight. The interconnections between different types of nodes can be established based on existing knowledge. Initial disease–drug interactions can be obtained from previous studies (Gottlieb et al., 2011). Initial drug–target interactions can be collected from the DrugBank database. The weights of all disease–drug and drug–target edges are originally assigned as one. Direct links between diseases and targets are generally unknown.

Let E_dd, E_rr, E_tt, E_dr and E_rt represent the sets of edges between disease–disease, drug–drug, target–target, disease–drug and drug–target, respectively, and W_dd, W_rr, W_tt, W_dr and W_rt represent the weight matrices on these edges. The heterogeneous disease–drug–target graph can be represented as $G_{DRT}=\left\{\right\{D,R,T\},\{E_{dd},E_{tt},E_{rr},E_{dr},E_{rt}\},\{W_{dd},W_{rr},W_{tt},$ $W_{dr},W_{rt}\left\}\right\}$. Our goal of drug repositioning based on this graph is to establish new edges between drugs and diseases and to assess their reliability. Essentially, the original heterogeneous graph G_DRT is considered as an incomplete graph with missing edges between disease nodes and drug nodes. The objective is to capture those interactions based on disease–disease, drug–drug and target–target similarities, as well as known disease–drug, drug–target interactions.

2.3 An iterative updating algorithm

Based on the guilt-by-association principle (e.g. Barabasi et al., 2011; Chiang and Butte, 2009), new disease–drug relationships can be inferred through existing relationships between similar diseases and similar drugs. Likewise, novel drug–target relationship can be inferred through existing relationships between similar drugs and similar targets (Wang et al., 2013). Therefore, we infer new disease–drug relationships in the newly proposed three-layer model by using an information flow-based method. Intuitively, to establish the relationship between a drug r and a disease d that have no connections originally, one can calculate a new weight

$$w(d,r)={\displaystyle \sum _{d_i\in D}{\displaystyle \sum _{r_j\in R}w(d,d_i)\times w(d_i,r_j)\times w(r,r_j)}}$$ (1)

where there is a direct link between disease d_i and drug r_j, and w(d, d_i) and w(r, r_j) represent disease–disease and drug–drug similarities. This serves as a baseline method for a two-layer mode. We further improve this simple model in four aspects. First, based on the principle of rational drug design, we incorporate target information into our model. Second, new links between diseases and targets will be established and updated. Third, once a new weight is estimated, it can also be used to update other weights. Therefore, an iterative updating algorithm is proposed. Fourth, during the process, the initial links need to be treated differently from newly established links because the initial links represent existing knowledge, whereas the newly established links represent predictions.To incorporate target information, we first propose an association coefficient/weight between a disease d and a target t as follows:

$$w(d,t)={\displaystyle \sum _{r_i\in R}{\displaystyle \sum _{r_j\in R}w(d,r_i)\times w(r_i,r_j)\times w(r_j,t)}}$$ (2)

which incorporates all drugs connected to d and t, as well as their similarities. Once the relationships between diseases and targets are established, new weights between diseases and drugs can be defined by considering these relationships:

$$w(d,r)={\displaystyle \sum _{t_i\in T}{\displaystyle \sum _{t_j\in T}w(d,t_i)\times w(t_i,t_j)\times w(t_j,r)}}$$ (3)

The definition in Equation 3 is potentially more powerful in capturing drug–disease relationship than the one in Equation 1 because of the consideration of targets. As a by-product from the model, we can also obtain a new weight between each drug and target pair by incorporating disease information, which can be used to predict novel target for existing drugs:

$$w(r,t)={\displaystyle \sum _{d_i\in D}{\displaystyle \sum _{d_j\in D}w(r,d_i)\times w(d_i,d_j)\times w(d_j,t)}}$$ (4)

Equations 2–4 can be rewritten in a matrix format,

(5)

The superscript T represents the transpose of the corresponding matrix. We treat W_dt as a temporary value and replace it in the right sides of the last two equations using the right hand side of the first equation in 5, which results in Equations 6 and 7, respectively.

$$W_{dr}^{new}=W_{dr}\times W_{rr}\times W_{rt}\times W_{tt}\times W_{rt}^T=W_{dr}\times (W_{rr}\times W_{rt}\times W_{tt}\times W_{rt}^T)$$ (6)

(7)

Once the new weights (W_dr and W_rt) are obtained, they can be fed into the right hand side of Equations 6 and 7, so we will have an iterative updating procedure. Finally, to treat the initial links between diseases and drugs and initial links between drugs and targets differently from those predicted ones, our final model can be written as:

$$W_{dr}^{k+1}=\alpha W_{dr}^k\times (W_{rr}\times W_{rt}^k\times W_{tt}\times W_{rt}^k{}_{}^T)+(1-\alpha )W_{dr}^0$$ (8)

$$W_{rt}^{k+1}=\alpha (W_{dr}^k{}_{}^T\times W_{dd}\times W_{dr}^k\times W_{rr})\times W_{rt}^k+(1-\alpha )W_{rt}^0$$ (9)

Here $1-\alpha$ is a decay factor in the range of (0–1). $W_{dr}^0$ and $W_{rt}^0$ represent the initial disease–drug and drug–target interactions, respectively. These two equations can be solved in an iterative propagation-based manner, after proper normalization, which is summarized as a theorem.

Theorem —

$W_{dr}^k$ and $W_{rt}^k$ defined in Equations 8 and 9 will converge after proper normalization (the proof can be found in the Appendix).

Although conceptual, the three-layer model is a straightforward extension of our previous two-layer model (Wang et al., 2013); to ensure convergence, the iterative algorithm proposed here is different from the one for two-layer model. For example, the iterative algorithm above can only predict new interactions between diseases and drugs with known interactions, whereas the original iterative algorithm for the two-layer model can also predict new interactions for disease–drug pairs without known interactions (Wang et al., 2013). To predict interactions between disease–drug pairs with no known interactions, we take a two-step approach: first, apply the algorithm proposed here, and then apply the algorithm in (Wang et al., 2013) on the newly obtained graph but only consisting of diseases and drugs, and their interactions with new weights (Fig. 1B, right panel).

2.4 Datasets

To construct the network, we first downloaded drug, target and disease information from different data sources. All pairwise disease–disease, drug–drug and target–target similarities were then calculated. Nodes of the same types were connected if their similarities are greater than a threshold, which was determined using cross-validation. Known disease–drug and the drug–target interactions were obtained from existing databases. The methods in calculating these similarities and connections are outlined here.

2.4.1 Drug–drug similarities

We first obtained all the approved drugs from the DrugBank database (Knox et al., 2011). Drug–drug similarities were calculated based on their chemical structures. First, chemical structures of all drug compounds in the Canonical Simplified Molecular-Input Line-Entry System (SMILES) format (Weininger, 1988) were downloaded from DrugBank. Then, the Chemical Development Kit (Steinbeck et al., 2006) was used to calculate a binary fingerprint for each drug. Finally, Tanimoto score (Tanimoto, 1957) of two drugs was calculated based on their fingerprints, which is in the range of [0, 1].

2.4.2 Target–target similarities

Our target database not only includes known drug targets, but also includes potential targets, i.e. proteins encoded by druggable genes. A druggable gene is defined as a human protein coding gene that contributes to a disease phenotype and can be modified by a small molecule drug. The term ‘druggable genome’ has been used to denote a list of computationally predicted genes that their proteins can serve as suitable targets for developing therapeutic drugs. The list of druggable genes/targets was downloaded from the Sophic Integrated Druggable Genome Database (http://www.sophicalliance.com/). The target–target similarities were calculated using the Smith–Waterman algorithm (Smith and Waterman, 1981) based on the amino acid sequences of their corresponding proteins. The similarities were normalized using the same method proposed in (Bleakley and Yamanishi, 2009).

2.4.3 Disease–disease similarities

A phenotype based disease–disease similarity dataset was downloaded from MimMiner (Van Driel et al., 2006), which was constructed by calculating similarities based on the numbers of occurrences of MeSH (medical subject headings vocabulary) terms in the medical descriptions of each pair of diseases from the OMIM database (Hamosh et al., 2005). According to the MimMiner database description, the similarities have already been normalized to the range [0, 1].

2.4.4 Drug target interactions

Initial drug–target interactions were collected from the DrugBank database, but limited to drugs that have associated diseases in OMIM database (Hamosh et al., 2005), which are the same as the one used in Gottlieb et al. (2011). The corresponding value in the matrix $W_{rt}^0$ was set to 1 if an interaction exists and 0 otherwise.

2.4.5 Disease–drug interactions

Initial disease–drug interactions were obtained from Gottlieb et al. (2011), where disease and drug interactions were assembled for diseases listed in the OMIM database (Hamosh et al., 2005) and their associated drugs [but limit to the ones registered in the DrugBank database (Knox et al., 2011)]. The corresponding value in the matrix $W_{dr}^0$ was set to 1 if an interaction exists and 0 otherwise.

2.5 Experimental design

To systematically evaluate the proposed approach on the collected datasets, we adopt a LOOCV strategy for the experiments. Basically, for each disease, at each iteration, one of its disease–drug connections is treated as the test data and all the remaining observations as the training data. After we perform the algorithm on the training data, the tested drug is ranked together with all other drugs in descending order according to their final connection weights to the disease. For each specific ranking threshold, if the rank of the testing connection is above the threshold, it is regarded as a true positive. The number of times that a true positive is discovered over all possible disease–drug relationships is regarded as the true-positive rate corresponding to the specified threshold. On the other hand, if the rank of an unknown connection is above the threshold, it is regarded as a false positive. True-positive rate and false-positive rate are calculated with varying ranking thresholds to construct the ROC curve. AUC represents the overall performance of the algorithm. In addition, we also examine the performance of the algorithm on the top-ranked results, i.e. the numbers of correctly retrieved testing connections based on various top percentiles (the most left side of the ROC curve), because the top-ranked results are more important in practice. Finally, to test the capacity of the algorithm in detecting novel interactions for diseases with no known drugs, we collect all diseases that only have a single known drug and perform the experiment by removing the only interaction.

3 RESULTS

3.1 Preliminary analysis of datasets

The dataset consists of 5080 diseases, 1409 drugs and 3989 targets. Majority of similarity values among the same type of nodes are small (Supplementary Appendix Fig. A1 in Appendix). Based on previous studies (Chen et al., 2011a; Van Driel et al., 2006; Vanunu et al., 2010), low-level similarity values provide little information or even adversely affect prediction performance for interaction inference. We chose the same similarity threshold (0.3) as the one in Vanunu et al. (2010), which used the same disease set in their study. We chose the value of the decay factor α to be 0.4, so the initial connections have slightly more weights. After we obtained the main results, we performed a sensitivity study using a 10-fold cross-validation on different combinations of similarity thresholds and the decay factor. The results (Supplementary Appendix Table A1 in Appendix) show that for a fixed decay factor, a similarity score of 0.4 gives the best results for TL_HGBI. For a fixed similarity score of 0.3, the model is very robust, and the performance does not change much for the decay factor from 0.1–0.7, though smaller values (more weight on original data) have slightly better performance.

The interconnections between different types of nodes are sparse. There are only 1461 connections between 233 diseases and 549 drugs, and 2098 connections between 554 drugs and 602 targets. Furthermore, among the nodes with connections, many of them have more than one connection (Supplementary Appendix Fig. A2 in Appendix), which indicates that known information about diseases, drugs and targets is highly concentrated on a small subset of all diseases/drugs/targets.

3.2 Validation of guilt-by-association assumption

To validate the basic assumption that similar drugs tend to be associated with similar diseases on the collected datasets, similarities of drugs from the same diseases and similarities of drugs from different diseases were compared. The overall average similarity score of drug pairs from the same diseases, calculated by averaging the similarities of all drug pairs that belong to the same diseases for all diseases, is 0.177. In contrast, the average similarity score of drug pairs from different diseases is 0.143. Further test using Wilcoxon rank-sum indicates that the difference is statistically significant (P < 1E-159). Likewise, the average similarity score of disease pairs from the same drugs is 0.157, whereas the average similarity score of disease pairs from different drugs is only 0.103, which is significantly different (Wilcoxon rank-sum test, P < 1E-53). In addition, similar results exist in drug–target relationships. The average similarity score of drug pairs from the same targets and the average similarity score of target pairs from the same drugs are 0.251 and 0.106, respectively. In contrast, the average similarity of drug pairs from different targets and the average similarity of target pairs from different drugs are 0.143 and 0.022, respectively. The differences are also significant based on Wilcoxon rank-sum test (both P-values are smaller than 1E-250). Based on these results (more details can be found in Supplementary Appendix Fig. A3 in Appendix), the dataset shows that drugs for the same diseases and drugs targeting the same proteins are more likely to be similar. The guilt-by-association principle can be used in this study.

3.3 Comparison with existing methods on disease with known drugs

To evaluate the performance of the proposed approach, we compared it with three popular approaches: GBA (Chiang and Butte, 2009), BLM (Bleakley and Yamanishi, 2009) and NBI (Cheng et al., 2012), as well as HGBI (Wang et al., 2013). GBA (Chiang and Butte, 2009) is a simple application of the guilt-by-association principle where drugs for one disease is used for another disease if the two diseases sharing some common drugs. BLM (Bleakley and Yamanishi, 2009) uses a supervised learning approach [i.e. support vector machine (SVM)] on a bipartite graph model. We used the scores generated by SVM as the ranking criterion. The number of negative samples for SVM training was chosen based on cross-validation results (Supplementary Appendix Fig. A4). The final result of BLM was obtained by averaging results from five runs, with the same configuration but different negative training samples. NBI (Cheng et al., 2012) is a network-based inference approach based on a two-step diffusion model on a bipartite graph.

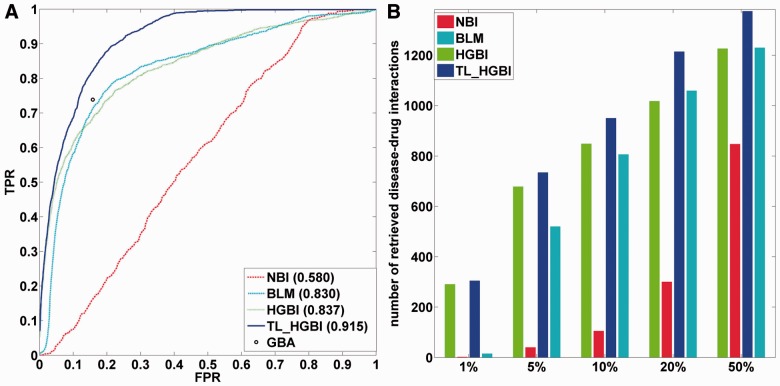
The LOOCV experiment for disease–drug association prediction was conducted on all diseases, which has at least two known drugs. In total, there are 154 such diseases and 1382 initial disease–drug interactions. The ROC curves and AUC values are given in Figure 2A. It shows that TL_HGBI (AUC: 0.915) outperforms all other methods significantly. HGBI (AUC: 0.837) and BLM (AUC: 0.830) perform similarly, while NBI has the worst performance (AUC: 0.580), indicating that a two-step diffusion is not sufficient to accurately predict disease–drug associations. Because GBA does not rank its prediction, a full ROC curve could not be constructed. Instead, the true-positive rate of GBA is 0.739, with a false positive rate of 0.158 (the point in the figure, which is below the ROC curve of TL_HGBI). The numbers of correctly retrieved disease–drug interactions according to different percentiles are given in Figure 2B. For a specified percentile, a true disease–drug interaction is considered as correctly retrieved if the predicted ranking of this interaction is higher than the specified percentile. Clearly, TL_HGBI performs the best among all approaches. More importantly, when focusing on the top-ranked results, TL_HGBI (as well as HGBI) significantly outperformed NBI and BLM. For example, among the 1382 true disease–drug interactions, 304/290 of them are among the top 1% ranked predictions based on TL_HGBI/HGBI. However, only 15 and 2 are among the top 1% predictions for BLM and NBI, respectively. The top-ranked predictions are particularly important because they contain smaller number of false positives. Therefore, TL_HGBI can be more useful in practice than other approaches.

Fig. 2.

(A) ROC curves of disease–drug association predictions by different approaches. The single gray point is the result of GBA. (B) The number of correctly retrieved drug–disease interactions out of total 1382 true interactions for different percentiles by different approaches

The differences between TL_HGBI and HGBI illustrate that including target information can indeed improve disease–drug association predictions. To systematically evaluate the advantage of using target information in drug repositioning, we further performed more experiments by randomly removing 15%, 30% and 60% of known drug–target links in the graph. Results show that AUC values gradually decrease when more links are removed (Supplementary Appendix Fig. A5), which demonstrates the contribution of target information in drug repositioning.

3.4 Evaluation on diseases with no known drugs

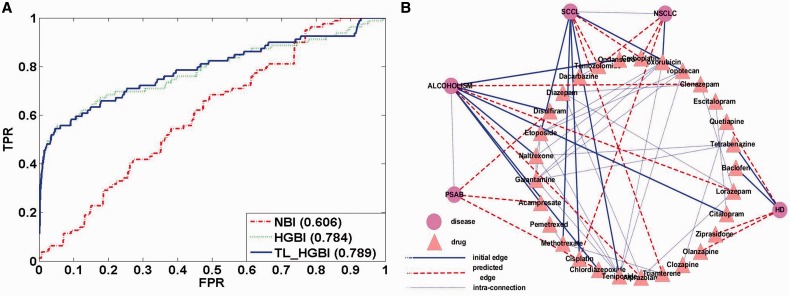
To illustrate the effectiveness of the proposed approach in predicting drugs for diseases with no known drugs, all diseases that have exactly one associated drug in the dataset were collected. There are 79 such diseases in total. The single interaction was removed in this experiment to test capacity of each algorithm to recover it. Because GBA and BLM cannot predict novel drugs for diseases with no known drugs, we only compared NBI, HGBI and TL_HGBI. The ROC curves and AUC values are given in Figure 3A. Once again, TL_HGBI (AUC: 0.789) and HGBI (AUC: 0.784) performed significantly better than NBI (AUC: 0.606). In this case, TL_HGBI and HGBI performed similarly, and both of them were not as good as their own results using diseases with known drugs. Nevertheless, the steep curves on the left side of Figure 3A still show their good performance for top-ranked predictions.

Fig. 3.

(A)ROC curves for diseases with no known drugs. (B) Case study results on disease–drug association predictions

3.5 Case studies

In addition to the leave-one-out cross-validation experiments, we also applied TL_HGBI on all the collected data to make novel drug usage predictions. Results for all diseases will be made available on our Web site once the article gets published. We present results of five selected diseases here, which include Huntington disease (HD, OMIM 143100), Non–small-cell lung cancer (NSCLC, OMIM 211980), Alcohol dependence (AD, OMIM 103780), Small-cell lung cancer (SCLC, OMIM 182280) and Polysubstance abuse, Susceptibility to (PSAB, OMIM 606581). For each disease, all the drugs that are known for the disease and the top 10 ranked predictions can be found in Table 1. The diseases, drugs and their connections are also shown in Figure 3B (only showing the top three predicted drugs of each disease for clarity). Even this small set of examples shows some interesting observations. First, similar diseases such as NSCLC and SCLC do share some common predictions, although these drugs were not known for any of the diseases. Second, TL_HGBI predicted some novel usage of drugs for diseases with no known drugs (e.g. PSAB). In this case, as the disease is only connected to disease alcohol dependence (node ALCOHOLISM in Fig. 3B), it is not surprising that its top-ranked predictions are from drugs for alcohol dependence.

Table 1.

Case study results: the top 10 predictions for five selected diseases

Disease	Known drugs (DrugBank IDs)	Top 10 ranked predictions
HD (OMIM ID: 143100)	Baclofen (DB00181)	Olanzapine (DB00334), Quetiapine (DB01224), Ziprasidone (DB00246), Clozapine (DB00363), Risperidone (DB00734), Amitriptyline (DB00321), Doxepin (DB01142), Methotrimeprazine (DB01403), Aripiprazole (DB01238), Tramadol (DB00193)
	Tetrabenazine (DB04844)
NSCLC (OMIM ID: 211980)	Doxorubicin (DB00997)	Cisplatin (DB00515), Carboplatin (DB00958), Temozolomide (DB00853), Methotrexate (DB00563), Dacarbazine (DB00851), Triamterene (DB00384), Anastrozole (DB01217), Daunorubicin (DB00694), Epirubicin (DB00445), Letrozole (DB01006)
AD (OMIM ID: 103780)	Citalopram (DB00215), Chlordiazepoxide (DB00475), Acamprosate (DB00659), Naltrexone (DB00704), Disulfiram (DB00822), Ondansetron (DB00904)	Lorazepam (DB00186), Alprazolam (DB00404), Clonazepam (DB01068), Diazepam (DB00829), Escitalopram (DB01175), Ziprasidone (DB00246), Risperidone (DB00734), Pergolide (DB01186), Olanzapine (DB00334), Bromocriptine (DB01200)
SCLC (OMIM ID: 182280)	Cisplatin (DB00515)	Triamterene (DB00384), Carboplatin (DB00958), Temozolomide (DB00853), Galantamine (DB00674), Pemetrexed (DB00642), Bromocriptine (DB01200), Daunorubicin (DB00694), Morphine (DB00295), Codeine (DB00318), Olanzapine (DB00334)
	Methotrexate (DB00563)
	Teniposide (DB00444)
	Etoposide (DB00773)
	Topotecan (DB01030)
PSAB, (OMIM ID: 606581)	None	Chlordiazepoxide (DB00475), Disulfiram (DB00822), Acamprosate (DB00659), Citalopram (DB00215), Escitalopram (DB01175), Niacin (DB00627), Ondansetron (DB00904), Ethosuximide (DB00593), Clofibrate (DB00636), Pyridoxal (DB00147)

We further searched the literature and found that some top-ranked drugs are supported by recently published papers, knowledge of which was not found in the databases used in this study. For HD, all top fiveranked drugs have already been studied for this disease (Alpay and Koroshetz, 2006; Bonelli et al., 2003; Duff et al., 2008; Paleacu et al., 2002; Van Vugt et al., 1997). The top three predicted drugs for NSCLC have also been studied for the disease (Ardizzoni et al., 2007; Dziadziuszko et al., 2003). For AD, the drug Lorazepam (DB00186) has already been tested in clinical trial (Clinicaltrials.Gov, 2012a). For SCLC, it was also found that Carboplatin (DB00958) and Temozolomide (DB00853) had already been tested in clinical trials for curing this disease (Clinicaltrials.Gov, 2012b, 2012c). All these results have shown that the proposed approach can potentially be very effective in predicting novel drugs for diseases.

To assess the effectiveness of incorporating target information in these case studies, for the above top candidates with reference support, we compared their ranks by TL_HGBI and by HGBI (Supplementary Appendix Table A2). Results show that for NSCLC and SCLC, the ranks of these candidates by TL_HGBI and HGBI have little differences. This is not surprising because most of these cancer drugs are non-target-specific and the results were mostly based on disease similarities for both TL_HGBI and HGBI. In contrast, for AD, Lorazepam is ranked number 1 by TL_HGBI, but only ranked 1051 by HGBI. Investigation shows that Lorazepam has 20 targets, majority of which are gamma-aminobutyric acid (GABA) A receptor subunits. GABA A receptors occur in central nervous system and play a role in many brain functions. TL_HGBI was able to identify Lorazepam as the top candidate by using target information. For HD, we have also observed improvements in ranking when including target information.

3.6 Drug–target association predictions

As we mentioned earlier, as a by-product, TL_HGBI also reports novel drug–target associations. Comparing with HGBI, TL_HGBI uses disease information in predicting novel drug targets. We therefore compared the performance of TL_HGBI with HGBI for drug target predictions for drugs with and without known targets (Supplementary Appendix Figs A6 and A7 in Appendix). Results show that TL_HGBI performs a little better than HGBI, but the difference is really subtle [AUC: 0.936 (TL_HGBI) versus 0.932 (HGBI) for diseases with known drugs; 0.953 (TL_HGBI) vs. 0.931 (HGBI) for diseases without known drugs]. This result indicates disease similarities contribute little to drug–target association predictions.

4 DISCUSSION

In this article, we have proposed a three-layer heterogeneous graph model that captures inter- and intrarelationships among diseases, drugs and targets, with the purpose of novel drug usage prediction. Based on this framework, we have developed an iterative algorithm to obtain final proximity scores between diseases and drugs, which can be used to rank candidate drugs for each disease. Experimental results on diseases with and without known drugs have shown that TL_HGBI outperforms other three popular methods, as well as the two-layer model proposed earlier by our group. In particular, TL_HGBI is more useful in practice than other approaches tested here because of its top-ranked drugs consisting of many true drug–disease relationships. A case study on five diseases using all existing data indicates that results obtained by TL_HGBI can be of high importance, supported by existing literature.

One should notice that there exist many other types of data (e.g. side effect information of drugs, gene expression data) that can also be used to predict drug–disease/drug–target associations (e.g. Yang and Agarwal, 2011). Some existing methods (e.g. PREDICT by Gottlieb et al., 2011) have used different datasets in predicting disease–drug associations, which makes it impractical to directly compare their performance with the performance of the proposed approach. In addition to datasets, there are different ways in defining relationships among nodes of the same type. For example, connections between targets can be defined based on protein–protein interaction data or based on protein structural information (e.g. focusing on binding domains). Disease relationships can be defined based on ontology. The relative merits using different metrics are worth further investigations. Nevertheless, valuable information has been lost for approaches not considering relationships among nodes of the same type (Li and Lu, 2013).

We plan to address both issues in our future work by extending the proposed framework in several possible directions. To include more diverse datasets of different types (other than the three discussed here), one direct extension is to add more layers (and more links) to the system. The key is then how to generalize the iterative updating algorithm to the new multi-layer model. In the case where additional datasets can actually be treated as properties of one of the three entities, another possible extension is to represent drugs/diseases/proteins using feature vectors, the elements of which will be defined based on those additional datasets. For example, to incorporate drug side effect information, each drug will be presented by a feature vector, which may include drug compound structure, drug side effect information and some other properties. For each drug pair, one score is calculated for each feature. Scores of all features will be converted into percentile-based scores in a similar way as we did in an earlier study for gene prioritization based on multiple data sources (Chen et al., 2011b). Drug–drug relationships can then be defined based on the most significant score. Similarly, gene expression information and protein interaction information can be incorporated into the protein/target layer. Essentially, the relationships between the same types of nodes are redefined based on more data sources. Another possible direction is to incorporate semantics (Chen et al., 2012).

Finally, both diseases and targets can be separated into different subclasses based on their mechanisms. It will be interesting to see how the performance will change when we only include subsets of data with the same mechanism. Eventually, wet lab experimental testing is a necessary step to validate the proposed approach, which cannot be done without collaborations with investigators with expertise in biochemistry and drug development.