Improving peak detection in high-resolution LC/MS metabolomics data using preexisting knowledge and machine learning approach

Abstract

Motivation: Peak detection is a key step in the preprocessing of untargeted metabolomics data generated from high-resolution liquid chromatography-mass spectrometry (LC/MS). The common practice is to use filters with predetermined parameters to select peaks in the LC/MS profile. This rigid approach can cause suboptimal performance when the choice of peak model and parameters do not suit the data characteristics.

Results: Here we present a method that learns directly from various data features of the extracted ion chromatograms (EICs) to differentiate between true peak regions from noise regions in the LC/MS profile. It utilizes the knowledge of known metabolites, as well as robust machine learning approaches. Unlike currently available methods, this new approach does not assume a parametric peak shape model and allows maximum flexibility. We demonstrate the superiority of the new approach using real data. Because matching to known metabolites entails uncertainties and cannot be considered a gold standard, we also developed a probabilistic receiver-operating characteristic (pROC) approach that can incorporate uncertainties.

Availability and implementation: The new peak detection approach is implemented as part of the apLCMS package available at http://web1.sph.emory.edu/apLCMS/

Contact: tyu8@emory.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Metabolomics is becoming a major area of interest in high-throughput biology (Issaq et al., 2009). Measuring thousands of metabolites at a time, untargeted metabolomics using liquid chromatography coupled with mass spectrometry (LC/MS) helps to unravel systematic response to drugs, detect pollutants in humans, find gene functions and discover disease markers and mechanisms (Nicholson et al., 2008; Yu and Bai, 2013; Zhou et al., 2012). High-resolution LC/MS platforms generate highly accurate mass-to-charge ratio (m/z) measurements, facilitating metabolite identification (Patti et al., 2012). At the same time, the raw data are large and noisy. Complex preprocessing routines are necessary to ensure high-quality peak detection, quantification and alignment across profiles (Katajamaa and Oresic, 2007; Want and Masson, 2011; Zhou et al., 2012). Critical to the success of data analysis is the detection of peaks from the raw data. A number of methods have been developed, each assuming certain characteristics can differentiate peaks from noise (Aberg et al., 2008; Katajamaa et al., 2006; Smith et al., 2006; Stolt et al., 2006; Takahashi et al., 2011; Tautenhahn et al., 2008; Wei et al., 2012; Yu et al., 2009). As examples, the XCMS package uses a matched filter based on the second derivative of the Gaussian function (Smith et al., 2006), and the apLCMS package uses a run filter based on point distribution patterns (Yu et al., 2009). Currently, peak detection in high-resolution LC/MS data is still less than satisfactory, especially for peaks of lower intensity.

A wealth of knowledge exists about common metabolites. Some of them are documented in openly available databases such as the Human Metabolome Database (HMDB) (Wishart et al., 2009), Madison Metabolomics Consortium Database (MMCD) (Cui et al., 2008) and Metlin (Smith et al., 2005). We have previously developed a hybrid approach utilizing existing knowledge to improve peak detection (Yu et al., 2013). While greatly improving the detection rate of known metabolites, as well as peaks consistently detected in historical data, it does not help peaks derived from metabolites that are not yet documented in the database. In this study, we ask the question: can we learn patterns from the part of data that match to known metabolites, such that the knowledge can improve the detection of unknown metabolites? Moreover, each dataset may have different characteristics because of changes in experimental conditions, such as peak width and signal-to-noise ratio. Can the method find the best criterion driven by the data characteristics?

To this end, we consider machine learning techniques that are effective in high-dimensional data, as well as resistant to high collinearity in the data. We first separate the data into extracted ion chromatograms (EICs) using adaptive binning (Yu et al., 2009; Yu and Peng, 2010). We use ‘EIC’ to refer to the data slices after binning. Each EIC contains some raw data points, which may or may not be a real peak. We then take a large number of data feature measurements from every EIC. In this article, we shall use ‘data feature’ to refer to the characteristics of the EIC data, instead of metabolic features detected in the data.

Given the data, our ultimate goal is to find a scoring system that best separates EICs that contain real peaks from those that do not contain real peaks. Certainly, such a scoring system cannot be obtained because we do not have the knowledge as to which EICs contain real peaks. However, some of the EICs have m/z values closely matched to known metabolites. Those matched are likely to contain real peaks, whereas those unmatched have much lower chances to contain real peaks. We hypothesize that by finding a scoring system that best separates the matched/unmatched EICs, we have a good proxy to the ultimate goal of differentiating peak regions from noise. We use machine learning techniques to find the optimal rule to discriminate matched EICs from unmatched EICs, using classification models such as logistic regression, boosting, support vector machine (SVM) and random forest (RF) (Hastie et al., 2009). After the best model is selected by cross-validation, all the unmatched EICs are given scores based on this model. Higher scores will signify the EIC is more likely to contain a real peak.

2 METHODS

The general workflow

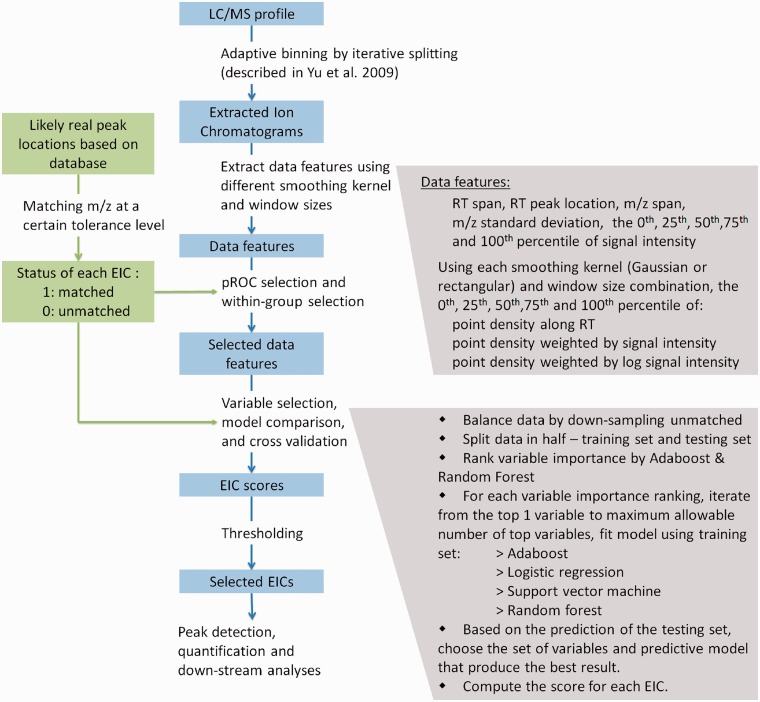
Figure 1 shows the general workflow of the new machine learning-based approach. The key idea is to first slice the data into EICs and take a large number of data features from each EIC. Then use machine learning approach to give the EIC scores to predict which EICs are more likely to be real signals.

Fig. 1.

The workflow of the machine learning-based peak detection approach

To generate the EICs, the adaptive binning method that slices the data based on local point density patterns has proven to work effectively (Yu et al., 2009, 2013). After obtaining the EICs using this method, we take a number of data characteristic measurements from each EIC, including m/z span, m/z standard deviation, retention time (RT) span, RT peak location and summary statistics on the raw intensity values of the EIC. We also centroid the data in each EIC such that they become two-dimensional data (intensity versus RT). We then apply different smoothers (shape/window size) in combination of different weighting schemes (unweighted, weighted with intensity, weighted with log intensity) to each EIC. At each smoothing setting, we record summary statistics of smoothed data. In total, we generate over 100 different data features for each EIC.

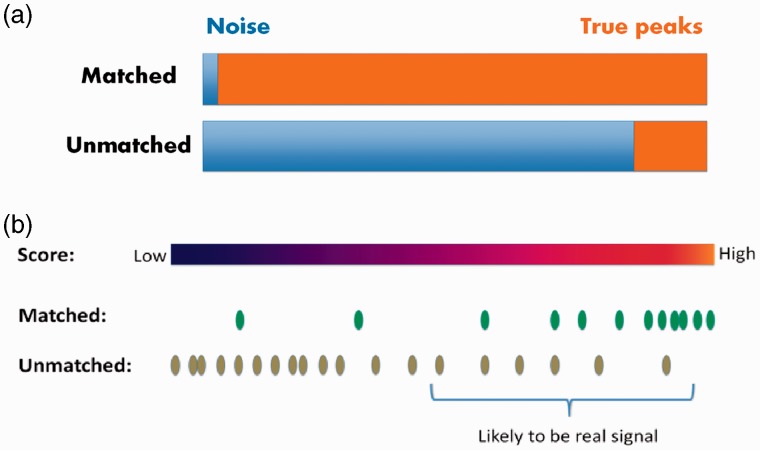
The next step is to generate a quality score for each EIC. Not willing to assume artificial models that could introduce bias, we resort to database matching for this purpose. The logic is straightforward—EICs with m/z values matched to common ion forms of known metabolites are more likely to be real signal than those unmatched. At the same time, those unmatched still contain a lot of true peaks. We treat the problem as a classification problem, i.e. seeking a scoring system that best separates the matched and unmatched classes, knowing that the matched/unmatched status of the data does not equate to peak/noise status. Although the training data are imperfect, given the matched/unmatched EICs have different likelihoods of being true peaks, the resulting score is still highly correlated to the ideal score that we seek—a score that separates the peaks from noise. After the scores are obtained, peaks are selected based on their scores (Fig. 2). The purpose of this study is to find whether the scoring system is meaningful enough to allow the method to outperform existing filters.

Fig. 2.

Illustration of the general idea of using matched/unmatched status as a proxy of true peaks/noise status to construct predictive models. (a) Proportion of true peaks is drastically different for matched/unmatched EICs. (b) The goal of the scoring system is to allow real peaks to be called from unmatched EICs

Building and selecting classifiers

After calculating the data features from every EIC, we have a matrix X with several thousand rows (EICs) and a few hundred columns (data feature measurements).

Step 1 —

Database matching. By matching m/z values of the EICs to dominant ion forms of common metabolites, we have a y vector that takes zero/one values: y_i = 1 if the EIC has a median m/z value that matches to a dominant ion derivative of a common metabolite, and y_i = 0 if unmatched. Throughout this study, we used 5 ppm as the matching threshold.

Step 2 —

Training and testing data. As the number of unmatched EICs is much larger than matched, we randomly sample a subset of the rows for which y_i = 0 to make the data balanced. The purpose of this step is to avoid adverse impact of data imbalance on the performance of the predictive models. Down-sampling is an effective method to address the issue of imbalance when sufficient data are available (Kubat and Matwin, 1997; Liu et al., 2006). We use random down-sampling, as there is no data stratification in this case. Because the number of rows is in the order of tens of thousands, and the number of matched rows is in the order of several hundreds, the subsample is a representative subset of the full data. We further discuss this point in the Supplementary Materials (Section S1; Supplementary Fig. S1). We then split the rows of the data in half randomly. One half of the data serves as the training data of the methods, and the other half serves as the testing data.

Step 3 —

(Optional) Ranking and reducing the data features. We use the probabilistic receiver-operating characteristic (pROC; described in the next section) to calculate the predictive power of every data feature. Second, as an optional step, we trim the data features by conducting a within-group comparison. Because five data features were collected at each smoothing setting—the 0th, 25th, 50th, 75th and 100th percentiles of the smoothed data, which can be redundant—we choose one data feature from the five by selecting the one with the highest pAUC value.

Step 4 —

Predictor (data feature) ordering. Using the training data, we rank the data features (columns of X) by their importance in predicting y. Two ranking methods are used: the Adaboost and the RF. Each yields an order of the data features from the most important to the least important. The two methods tend to rank data features differently. The Adaboost ranking is not impacted by collinearity. If two features are highly correlated with each other, they can still both receive high ranking if they both predict the outcome very well. On the other hand, the RF method takes into account collinearity. Having a highly correlated feature tends to reduce the importance of a feature.

Step 5 —

Fitting a series of models. Using each of the two orders, iterate the following: take the first m most important columns of X, fit a predictive model of y using the training data with each of the four methods—logistic regression (R library stats), Adaboost (R library gbm), SVM (R library e1071) and RF (R library randomForest). Default parameters of the methods are used because the input data matrix is of normal dimensions for these methods.

With each model, find the prediction accuracy on the testing data. Increase m from 1 to a maximum allowable number (10 in this study). There are several reasons for selecting a subset of features to fit the model. The first is to avoid overfitting for logistic regression. The second is that it has been empirically observed that when the majority of the variables are irrelevant to the outcome, a model using a subset often outperforms the model using all the features. Third, it reflects our belief that only a limited number of data features are relevant in predicting the quality of an EIC.

Step 6 —

The final model. From all the combinations (ranking method × fitting method × m), select the one that produces the best testing data prediction accuracy. Combine the training and testing data and re-fit the model using the combined data. This is the final model for EIC scoring.

Step 7 —

EIC selection. Calculate the scores for all rows of X using the final model. Because the likelihoods between matched/unmatched is not truly the likelihoods between peak/noise, a heuristic cutoff needs to be used as the decision boundary. In this study, we use cutoffs on the percentage of unmatched EICs selected.

ROC analysis with class label uncertainty

We use the ROC curve approach to gauge the performance of individual variables and predictive models to differentiate the true peaks from noise (Fawcett, 2006; Yu, 2012). Peaks with m/z matched to known metabolites are considered likely to be true metabolites, whereas unmatched peaks are considered likely to be noise. However, the databases are incomplete, and there is high noise in the data. Peaks unmatched to the database could still be real signal, whereas peaks matched to the database still have a small chance to be noise. Thus, we developed the probabilistic ROC (pROC) to incorporate the uncertainty.

We consider the situation where there are two classes, true peaks and true noise. Each data point is a pair (z_i, s_i), where z_i is the score of the i-th EIC, and s_i is the confidence level that the EIC contains a true peak. It takes value between zero and one. Ideally, s_i should be Prob (the i-th EIC contains a true peak). In application, as probabilistic measures are often difficult to obtain, s_i could be a score assigned heuristically. In this study, as there is no rigorous basis to assign likelihood values to the s_is, we used values based on expert opinion: 0.95 for matched EICs, and 0.1 for unmatched EICs.

In the construction of traditional ROC curves, no uncertainty of class membership is considered. The building of an ROC curve/surface involves calculating a few quantities at all cutoff points—the true-positive rate (TPR; the number of true positives selected at the cutoff point divided by the total number of points actually belonging to the positive class), false-positive rate (FPR; the number of negatives falsely selected at the cutoff point divided by the total number of points actually belonging to the negative class) and the true discovery rate (TDR; the number of true positives selected at the cutoff point divided by the total number of points selected at the cutoff point) (Yu, 2012).

The pROC approach differs from traditional ROC by replacing counts with expected values given the uncertainty in the class membership. Although the TDR values are not used in this study, we include its estimation for completeness. At any cutoff value α, we have

$$\begin{array}{ll}pTP{R}_{\alpha }\hfill & =\frac{E(truepositivescalledatthreshold\alpha )}{E(truepositives)}=\frac{{{\displaystyle \sum }}_{i=1}^N{s}_{i}I\left(z_i>\alpha \right)}{{{\displaystyle \sum }}_{i=1}^N{s}_i},\hfill \\ \hfill pFP{R}_{\alpha }& =\frac{E(\text{\#}truenegativescalledatthreshold\alpha )}{E(\text{\#}truenegatives)}=\frac{{{\displaystyle \sum }}_{i=1}^N(1-s_i)I\left(z_i>\alpha \right)}{{{\displaystyle \sum }}_{i=1}^N(1-s_i)},\hfill \\ \hfill pTD{R}_{\alpha }& =\frac{E(\text{\#}truepositivescalledatthreshold\alpha )}{\text{\#}featurescalledatthreshold\alpha }=\frac{{{\displaystyle \sum }}_{i=1}^N{s}_{i}I\left(z_i>\alpha \right)}{{{\displaystyle \sum }}_{i=1}^{N}I\left(z_i>\alpha \right)},\hfill \end{array}$$

Where I() is an indicator function, which takes the value of 1 when the statement in the parenthesis is true, and 0 otherwise. By varying the α values, a series of pTPR_α, pFPR_α, pTDR_α values are obtained. Using them in the place of TPR_α, FPR_α and TDR_α, the ROC curve or ROC surface can be generated, and the corresponding area under the curve or volume under the surface can be computed in the traditional manner (Fawcett, 2006; Yu, 2012).

The databases used in this study

For known metabolites, we used the HMDB (Wishart et al., 2009). We randomly selected half of the unique molecular compositions of known metabolites as the training data. Because the data in this study were generated from anion exchange chromatography and electrospray ionization, we used the [M + H]⁺ derivatives of the training data. To benchmark the performance of different methods, the detected peaks were then matched to the [M + H]⁺ derivatives of the other half of the unique molecular compositions of HMDB (a more stringent set), as well as the [M + H]⁺, [M + K]⁺, [M + Na]⁺ or [M + NH₄]⁺ ion forms in the MMCD (a more relaxed set) (Cui et al., 2008).

The high-resolution LC/MS data used in this study

Two datasets were used in this proof-of-concept study. The first dataset was generated from the Standard Reference Material (SRM) 1950—Metabolites in Human Plasma, made available by the National Institute of Standards and Technology (NIST). We analyzed the SRM 1950 sample using anion exchange chromatography combined with the Thermo Orbitrap-Velos (Thermo Fisher, San Diego, CA) mass spectrometer using an m/z range of 85–850. The experiment was repeated eight times, each in triplicate, at discrete time points spanning a month. In total, 24 LC/MS profiles were analyzed. The second dataset was generated using four healthy human plasma samples, each analyzed eight times with anion exchanged combined with a Thermo LTQ-FT mass spectrometer using an m/z range of 85–850. Excluding two outliers, 30 LC/MS profiles were analyzed. For experimental details, please refer to Johnson et al. (2010).

3 RESULTS

In this proof-of-concept study, we compared the performance of the new machine learning-based approach with existing methods XCMS (Smith et al., 2006) and apLCMS (Yu et al., 2009). Although apLCMS does have a hybrid approach that involves targeted search of known metabolites (Yu et al., 2013), we did not use this option because our purpose was to find whether the new method brought improvement on the detection of previously unknown peaks, on which the hybrid apLCMS does not help.

Among the three methods, only the new method requires a list of known metabolites. We first found the unique m/z values of HMDB metabolites and split them in half randomly. The [M + H]⁺ ions of half of the HMDB data were used as the known m/z values for the new method. To avoid the impact of parameter choices, we tried our best to tune the methods and allowed each method a number of parameter settings. The parameters were specific to the datasets. They are described in detail below.

To assess the performance of peak detection, we based our judgment on the matching of detected peaks to known metabolites. First, from the results of all three methods, we removed peaks matched to the [M + H]⁺ ions of the half HMDB metabolites that were used as training data. We then matched the m/z values found by each method at each parameter setting to (1) the [M + H]⁺ ions of the other half of HMDB metabolites, and (2) the [M + H]⁺, [M + K]⁺, [M + Na]⁺ or [M + NH₄]⁺ ion forms in the MMCD (Cui et al., 2008). The former was a more stringent set, and the latter was a more relaxed set. The number of peaks detected, together with the percentage of detected peaks matched to the known metabolites, gave us measurements of the quality of the peak detection.

SRM 1950 data measured by Orbitrap-Velos mass spectrometer

Twenty-four LC/MS profiles generated from the SRM 1950 standard sample were analyzed. For the new machine learning method, we allowed 5, 10, 20, 30, 40, 50 and 60% of the originally unmatched peaks to be reported. For XCMS, we tuned six parameters: step (step size to use for profile generation; values = 0.005, 0.02, 0.05), fwhm (full width at half maximum of matched filtration Gaussian model peak; values = 15, 30), mzdiff (minimum difference in m/z for peaks with overlapping RTs; values = 0.01, 0.05, 0.2), bw (bandwidth of Gaussian smoothing kernel in peak density chromatogram; values = 20,40), mzwid (width of overlapping m/z slices for creating peak density chromatograms; values = 0.005,0.05), snthresh (signal-to-noise ratio threshold; values = 5, 10). All combinations of possible values of the six parameters were tested. For apLCMS, we tuned two parameters: min.run (minimum length of a peak in RT; values = 15, 20, 30, 40), and min.pres (minimum proportion of non-missing signal in the ion trace; values = 0.5, 0.6, 0.7, 0.8). All combinations of possible values of the two parameters were tested.

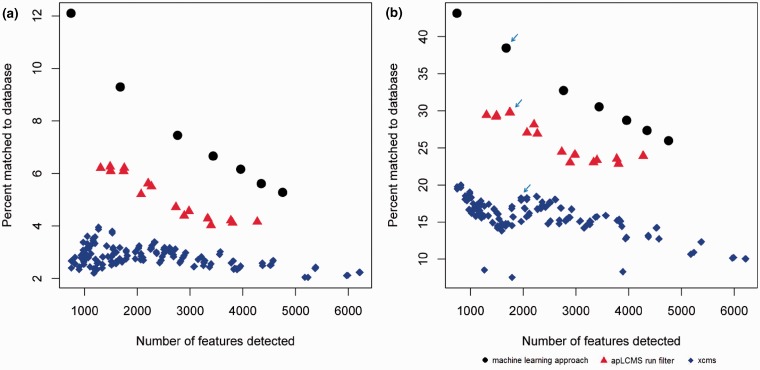
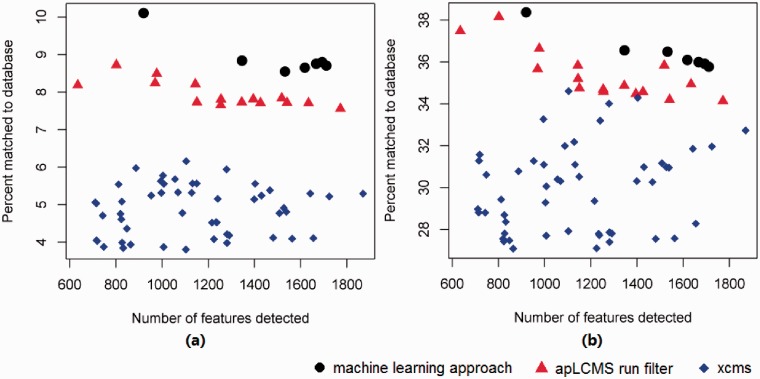
At every parameter setting, each method conducted peak detection and alignment. For the new method, post-peak detection processing was performed by subroutines of apLCMS. Peaks found in at least 6 of the 24 profiles were retained. To make a fair comparison, we removed peaks matching to the [M + H]⁺ ions of the half HMDB unique m/z values used for training the machine learning approach from all the results. We then matched the remaining peaks to (1) the [M + H]⁺ ions of the half HMDB unique m/z values not used for training, and (2) the [M + H]⁺, [M + K]⁺, [M + Na]⁺ or [M + NH₄]⁺ ion forms in MMCD. We plotted the percentage matched against the number of peaks detected (Fig. 3). Every point in the plot corresponds to a parameter setting.

Fig. 3.

Comparing the percentage of peaks matched to known metabolite derivatives between the new machine learning approach against the existing run filter of apLCMS, and the matched filter of XCMS. All m/z values used in the training of the machine learning approach were removed. Orbitrap data generated from the NIST SRM 1950 samples was used. All three methods were allowed a number of parameter combinations. Each point represents a parameter combination. Matching was based on m/z value at the 5 ppm tolerance level. (a) Percent of newly detected features matched to the [M + H]⁺ ion forms of the half metabolites from HMDB held back from the methods. (b) Percent of newly detected peaks matched to [M + H]⁺, [M + K]⁺, [M + Na]⁺ or [M + NH₄]⁺ ion forms in the MMCD. Arrows: data used in further analysis shown in Figure 4

We first examined the matching of found peaks to the [M + H]⁺ ions of the half HMDB unique m/z values not used for training (Fig. 3a). With the increase in the number of peaks detected, which corresponds to less stringent peak detection criterion, all three methods showed a lower percentage of peaks matched to the [M + H]⁺ ions of known metabolites. The new machine learning approach clearly had an advantage over the other two methods at all stringency levels (Fig. 3a). Overall, the new method had ∼3% higher matching rate than apLCMS run filter. Given that the run filter matching rate is 4–6%, in relative terms, the improvement is ∼40%.

When matched to a more relaxed set, the [M + H]⁺, [M + K]⁺, [M + Na]⁺ or [M + NH₄]⁺ ion forms in MMCD, the exact same trend was observed, except the overall level of matching percentages was much higher (Fig. 3b). Overall, the new methods had ∼30% matching, whereas the apLCMS fell behind by ∼5%. Given that the run filter matching rate is 22–30%, this is a ∼20% improvement in relative terms. The XCMS matching rates were generally <20% (Fig. 3b).

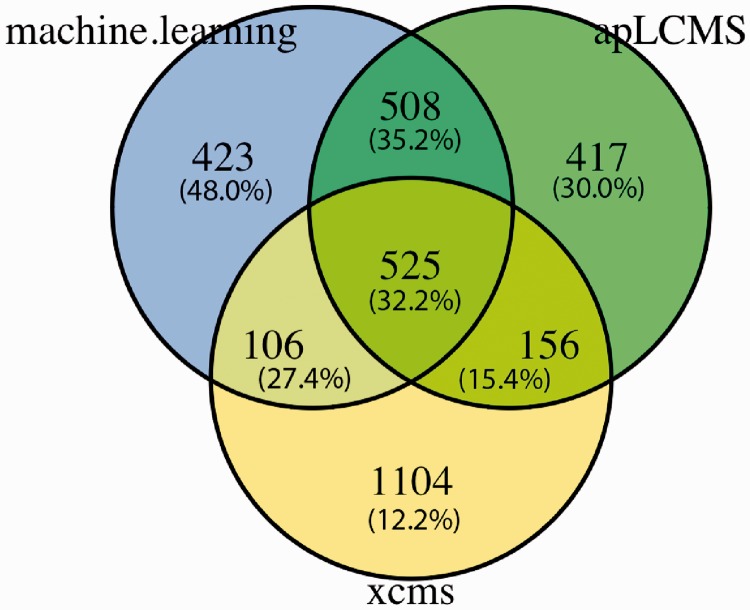
We further selected one peak list from each of the three methods that contain similar numbers of peaks (arrows in Fig. 3b). We took the unique m/z values from each list and matched the values at 5 ppm tolerance level across the three lists. The counts of overlaps were summarized in a Venn diagram (Fig. 4). The peaks detected by the machine learning method overlapped with those detected by apLCMS by over 60%. The overlap between the machine learning method and XCMS was <40%, and the overlap between apLCMS and XCMS was ∼40% (Fig. 4). We further matched the m/z values falling into each of the areas of the Venn diagram to the [M + H]⁺, [M + K]⁺, [M + Na]⁺ or [M + NH₄]⁺ ion forms in MMCD. We found that m/z values uniquely detected by the new machine learning approach had the highest rate of matching (48.0%), and m/z values uniquely detected by XCMS had the lowest rate of matching (12.2%) (Fig. 4; values in the parentheses).

Fig. 4.

Overlapping between unique m/z values found by the new machine learning approach, apLCMS and XCMS. All m/z values used in the training of the machine learning approach were removed. Numbers in parentheses are the percentage of the peaks matched to [M + H]⁺, [M + K]⁺, [M + Na]⁺ or [M + NH₄]⁺ ion forms in MMCD. Matching between the methods and to the database was based on m/z value at the 5 ppm tolerance level

Next we examined a small group of high-confidence metabolites in the SRM 1950 sample. We received a list of 94 characterized metabolites with ion forms detectable in LC/MS from Dr. Paul Rudnick’s group at NIST. Fifty-six of the 94 metabolites were not matched to the training data generated from HMDB. We examined how many of these 56 metabolites were recovered using each of the three methods. Using the parameter settings that are indicated by the arrows in Figure 3(b), the machine learning method detected 10 of the 56 metabolites, whereas apLCMS detected 5 and XCMS detected 2. Given differences in the experimental conditions between our laboratory and NIST, and the fact that a large proportion of the 56 metabolites are unresolved by the anion exchange column (Yu et al., 2013), the number of detected metabolites are reasonable. We plotted the EICs of the five NIST-confirmed metabolites identified by the new machine learning method alone (Supplementary Fig. S2). Visually examining the plots, we found clear patterns of peaks. At other parameter settings, the same trend was observed—the new machine learning method consistently detected more of the confirmed metabolites than the other two methods (Supplementary Fig. S3).

Human blood plasma samples measured by Thermo LTQ-Fourier Transform (FT) mass spectrometer

Generated on a different LC/MS platform, the dataset is of different property than the SRM1950 dataset. Again, we tuned all three methods to best fit the data. For the new machine learning method, we allowed 5, 10, 20, 30, 40, 50 and 60% of the originally unmatched peaks to be reported. For XCMS, we tuned six parameters: step (values = 0.001, 0.01), fwhm (values = 5, 10, 15), mzdiff (values = 0.001, 0.01), bw (values = 15, 30, 60), mzwid (values = 0.05, 0.25, 0.5), snthresh (values = 2, 4). All combinations of possible values of the six parameters were tested. For apLCMS, we tuned two parameters: min.run (values = 10, 15, 20, 30) and min.pres (values = 0.5, 0.6, 0.7, 0.8). All combinations of possible values of the two parameters were tested.

Figure 5 shows the results of matching the found peaks to common ion forms of known metabolites. For XCMS, we omitted the results generated by XCMS using snthresh = 4 because too few peaks were detected. Again, from all the results, we removed peaks matching to the [M + H]⁺ ions of the half HMDB unique m/z values used for training the machine learning approach.

Fig. 5.

Comparing the percentage of peaks matched to known metabolite derivatives between the new machine learning approach against the existing run filter of apLCMS, and the matched filter of XCMS. All m/z values used in the training of the machine learning approach were removed. The data was generated from human plasma samples using LC-Fourier Transform MS, as described in Johnson et al. (2010). All three methods were allowed a number of parameter combinations. Each point represents a parameter combination. Matching was based on m/z value at the 5 ppm tolerance level. (a) Percent of newly detected features matched to the [M + H]⁺ ion forms of the half metabolites from HMDB held back from the methods. (b) Percent of newly detected peaks matched to [M + H]⁺, [M + K]⁺, [M + Na]⁺ or [M + NH₄]⁺ ion forms in the MMCD

When we matched the detected m/z values to databases, the same trend as seen for the SRM1950 data was observed (Fig. 5). However, the difference in performance between the new method and apLCMS was not as pronounced as on the SRM1950 data. The new method showed a ∼1% advantage over apLCMS when matching to the half [M + H]⁺ ions of known metabolites, whereas apLCMS was consistently better than XCMS (Fig. 5a). When matching to the four common ion derivatives of the metabolites in the MMCD database, the gap between the new method and apLCMS became smaller, especially when larger number of peaks were detected using looser criteria (Fig. 5b). At the same time, a few parameter settings of XCMS generated results close to apLCMS. Still, the overall trend was clear—the new method outperformed apLCMS, which in turn outperformed XCMS.

Through the analyses of the two datasets, we clearly saw that the new machine learning approach outperformed the apLCMS and XCMS in terms of detecting peaks that are matched to common ion forms of known metabolites, which indicates a higher reliability in detecting true signals. At the same time, the new method required the least amount of tuning, as indicated by the number of points representing each method in Figures 3 and 5.

4 DISCUSSIONS

In this study, we presented a new machine learning approach for peak detection from high-resolution LC/MS data. It substantially outperforms existing methods in real data analysis in terms of detecting more reliable peaks. In our workflow, the peak detection step precedes peak quantification by statistical model fitting (Yu and Peng, 2010). Other methods may achieve the two goals simultaneously (Smith et al., 2006). Noise filtering can be conducted in the peak quantification step. Later steps include RT correction and peak alignment (Katajamaa and Oresic, 2007). Because only selected EICs will be sent to peak quantification and later steps, peak detection is most critical in ensuring the quality of the data processing. Our method is applicable to high-resolution data only because reliable matching to databases is necessary. Compared with the hybrid feature detection approach (Yu et al., 2013), this new method helps to better detect peaks that are not yet documented in the databases.

Our method is based on classification between EICs that are matched/unmatched to dominant ion forms of documented metabolites. It can also be extended to using historically consistently detected m/z values. To date, databases of metabolites are far from complete. Large portions of peaks from LC/MS data are not matched to databases. On the other hand, even with high-resolution LC/MS, those EICs matched to database may still be noise, albeit with a very low chance. However, given the two groups of EICs have very different chances to be real peaks, a discrimination rule separating them is still able to catch much of the information of how the real peak EICs differ from noise.

The machine learning methods are resistant to nuisance variables and collinearity, which allows us to use a large number of data features from each EIC. Although a lot of the data features may not have predicting power, their presence does not hamper the performance, especially given a variable selection component is included. Currently, we allow different data features to be selected for each profile. Given the high collinearity between features, the method may select different features for each profile because of minor differences between the profiles. We analyzed the models and data features in detail in the Supplementary Materials (Supplementary Section S3). Clearly the two datasets showed distinct preferences in model and data feature utilization. However, some important data features were consistently utilized in both datasets, including the m/z value spread within each EIC, the RT location of the highest intensity of the EIC, and log-intensity-weighted smoothed point distribution with a narrow bandwidth. These results shed light on dataset characteristics and what data features are important in signifying real peaks. Our method outputs the model and data features involved for each LC/MS profile, allowing users to examine the data characteristics and make interpretations.

It is possible that combining data features from all LC/MS profiles in a study can yield a more robust overall model. In this study, the reasons for allowing different models for different LC/MS profiles are as follows. (i) Each LC/MS profile contains sufficient training data to fit a reliable model. This is evidenced by the results in the manuscript. Because we held back half the HMDB data for testing, we expect that in real data applications, the training data will double the size of those shown in the manuscript. Given each LC/MS profile may be slightly different, and LC/MS profiles from different experimental batches may show substantially different properties, allowing flexible models may be beneficial. (ii) There are RT shifts between LC/MS profiles. To build a single model for all LC/MS profiles in a study, we need to first conduct RT adjustment to utilize any data feature that involves RT. Both apLCMS and XCMS conduct RT adjustment after peak quantification. It is difficult to conduct reliable RT adjustment before noise filtering and peak detection. Nonetheless, it is possible that a joint model may be more reliable than a collection of individual models. This requires substantial changes to the workflow beyond peak detection itself. It will be subjected to our future studies. We plan to develop parallel feature selection scheme in the future to ensure a single set of features is used for a dataset to achieve better data interpretation.

The data features used in this study include various percentiles of smoothed data. The smoothing was conducted using three different weighting schemes, two different kernels and several window size values. The data features contain most of the information that the run filter of apLCMS captures. In apLCMS, the run filter can only be used at a single parameter setting. By allowing many smoothing settings, the new method effectively captures the information that correspond to many run filter settings simultaneously. In a sense, the best filter is selected based on database matching, which makes the new method easier to tune, and allows it to be more adaptive to data with different characteristics without much user intervention.

In LC/MS data, each metabolite may generate multiple peaks because of different isotopes and ion forms. If utilized, they will allow the borrowing of information between EICs to help make better decision (Kuhl et al., 2012). However, because the detection of different ion forms of a low abundance peak is difficult, we did not use such information in this study. This is a subject of future research.