Probabilistic Graphical Model Representation in Phylogenetics

Abstract

Recent years have seen a rapid expansion of the model space explored in statistical phylogenetics, emphasizing the need for new approaches to statistical model representation and software development. Clear communication and representation of the chosen model is crucial for: (i) reproducibility of an analysis, (ii) model development, and (iii) software design. Moreover, a unified, clear and understandable framework for model representation lowers the barrier for beginners and nonspecialists to grasp complex phylogenetic models, including their assumptions and parameter/variable dependencies. Graphical modeling is a unifying framework that has gained in popularity in the statistical literature in recent years. The core idea is to break complex models into conditionally independent distributions. The strength lies in the comprehensibility, flexibility, and adaptability of this formalism, and the large body of computational work based on it. Graphical models are well-suited to teach statistical models, to facilitate communication among phylogeneticists and in the development of generic software for simulation and statistical inference. Here, we provide an introduction to graphical models for phylogeneticists and extend the standard graphical model representation to the realm of phylogenetics. We introduce a new graphical model component, tree plates, to capture the changing structure of the subgraph corresponding to a phylogenetic tree. We describe a range of phylogenetic models using the graphical model framework and introduce modules to simplify the representation of standard components in large and complex models. Phylogenetic model graphs can be readily used in simulation, maximum likelihood inference, and Bayesian inference using, for example, Metropolis–Hastings or Gibbs sampling of the posterior distribution. [Computation; graphical models; inference; modularization; statistical phylogenetics; tree plate.]

… early attempts at reconstructing evolutionary trees using computers are leading to a clarification of our basic ideas as to how it should be done. It has become particularly clear that any attempt at producing an evolutionary tree must be based on a specific model, for only then can proper statistical procedures be adopted, and only then are the assumptions implicit in the method clear for all to see.

          — A. W. F. Edwards (1966:440)

A basic phylogenetic model consists of a tree with branch lengths and a continuous-time Markov model describing how the characters—morphological or molecular—change along the branches of the tree. Almost every described phylogenetic model fits this theme, which makes it tempting to think that biologists face simple modeling considerations. Yet, this is decidedly not the case. The variations on the theme of a continuous-time Markov model running along the branches of a tree are seemingly endless. From all described models, consider this incomplete list: JC69, K2P, K3P, TN92, TN93, F81, HKY85, GTR, TKF91, TKF92, WAG, BLOSUM, PAM, JTT92, LG08, REV, MTREV, GY94, MG95, NY98, M₀,M₁,…M₁₃, CAT (and CAT again), MKv, Dayhoff, ECM, DEC, BM, OU, EB, CATBP, GG98, TS98, G01, UCLN, UCG, RLC, ACLN, CIR, and WN. (The field has inconsistently adopted the practice of naming models with the initials of the authors followed by the year of publication. Hence, JC69 refers to the model first described by Jukes and Cantor in 1969.) The number of models can be combinatorically increased by the addition of suffixes, such as “ + I”, “ + Γ”, “ + I + Γ”, and “ + SS”, which are different models for accounting for rate variation across characters. The number of models that are implemented in software and available to the biologist is clearly large. Moreover, the scheme adopted by phylogeneticists to name models suggests the field has a considerable degree of opaqueness. Clearly, the field could benefit from a generic method—a method that can both represent all of the variables contained in a model and their dependencies—for representing phylogenetic models.

The number and complexity of phylogenetic models presents significant challenges to the biologist. In some ways, the barriers to understanding a phylogenetic analysis have never been higher. Software that is intended to simplify phylogenetic analyses can sometimes be counterproductive. For example, some software automates the choice of the phylogenetic model for an analysis. However, this does not lead to any greater understanding of the assumptions of the analysis by the user (though such software may ensure a greater overall quality of phylogenetic analysis). Failure to understand the details of alternative phylogenetic models can lead to innocent mistakes caused by different models having the same name (such as the CAT model, which is used as a model for rate variation across sites and also as a model for allowing stationary frequencies to vary across a sequence).

To address these challenges, we believe it is time to adopt a standardized way to describe phylogenetic models. Specifically, we suggest following the lead of the statistics literature, where similar problems are encountered, and where graphical models are routinely used to characterize complex models (Gilks et al. 1994; Lunn et al. 2000; Jordan 2004; Koller and Friedman 2009; Lunn et al. 2009). Graphical models provide a general methodology that works for simple models as well as for large models with thousands, or even millions, of parameters (Jordan 2004). Such models are visualized in a simple but comprehensible and exact manner. They are independent of the criterion and algorithm used for inference: as long as the model is the same, it does not matter whether inference is performed under the maximum likelihood or Bayesian criterion, or whether Newton's method, Markov chain Monte Carlo sampling or Expectation Maximization is used.

The article is divided into three parts, each with a different focus of required expertise in statistical phylogenetics. We start with a general introduction to graphical models for users of phylogenetic methods. To this end we model the distribution of the presence/absence of “the most diverse of bones,” the baculum, in mammals (Long and Frank 1968). We draw the corresponding graphical model representation, which we use to introduce the graphical model formalism. We progressively transition into phylogenetic models for discrete, continuous and sequence characters but keep the mathematical and technical details to a minimum.

In the second part, we discuss graphical model representations of more typical models used in statistical phylogenetics today. We introduce the concept of a tree plate, which captures the structure learning (tree topology estimation) part of a phylogenetic model and greatly simplifies the resulting graph. We also discuss how large and complex phylogenetic model graphs can be modularized to produce more effective views on the overall structure of the model while simultaneously allowing detailed analysis of the model components of particular interest. In the third part, we present a more formal description of phylogenetic graphical models. We also provide some well-known algorithms on model graphs and relate them to standard algorithms in phylogenetics to demonstrate the benefits of drawing from the vast computational literature on probabilistic graphical models. We conclude with a discussion on the use and importance of graphical models to the phylogenetics community.

An Introduction to Probabilistic Graphical Models

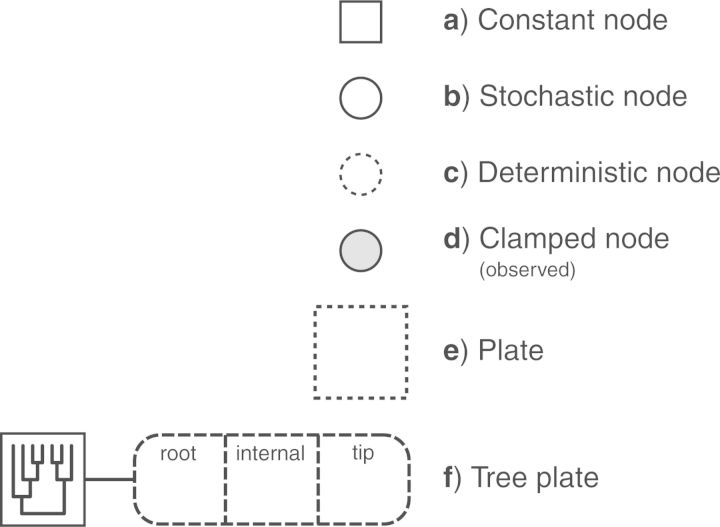
The graphical model framework provides a valuable set of tools for visually representing models. The various components of a graphical model representation are defined in Figure 1. The following examples will introduce each of the elements needed for constructing model graphs.

Figure 1.

The symbols for a visual representation of a graphical model. a) Solid squares represent constant nodes, which specify fixed-valued variables. b) Stochastic nodes are represented by solid circles. These variables correspond to random variables and may depend on other variables. c) Deterministic nodes (dotted circles) indicate variables that are determined by a specific function applied to another variable. They can be thought of as variable transformations. d) Observed states are placed in clamped stochastic nodes, represented by gray-shaded circles. e) Replication over a set of variables is indicated by enclosing the replicated nodes in a plate (dashed rectangle). f) We introduce replication over a structured tree topology using a tree plate. This is represented by the divided, dashed rectangle with rounded corners. The subsections of the tree plate demark the different classes of nodes of the tree. The tree topology orders the nodes in the tree plate and may be a constant node (as in this example) or a stochastic node (if the topology node is a solid circle).

A Non-phylogenetic presence/absence Model

The os penis (penis bone) of mammals, or baculum, has an uneven taxonomic distribution. It occurs in five orders of mammals (Patterson and Thaeler Carnivora, Chiroptera, Insectivora, Primates, and Rodentia; 1982) but is absent in all other mammalian orders, including marsupials and monotremes. The evolution of this character has been studied to determine potential use of the presence of the baculum. Potential hypotheses for the evolution of the baculum include (i) a purpose as a stiffener for species with extended intromission, (ii) to assist in sperm transport, or (iii) to provide rigidity to stimulate female ovulation (Lariviére and Ferguson 2002). Here we consider some of the modeling considerations for a phylogenetic analysis of this character. We choose to use Bayesian methods to conduct these inferences, which means that we will need to specify prior probability distributions for the variables of our models. To simplify our analyses, we will sample five species: a dog, a bat, a rat, a human, and a koala. The Supplementary Material (http://dx.doi.org/10.5061/dryad.nt898) presents similar analyses with a much better taxonomic sampling of 274 species.

Our first attempt at modeling the distribution of the baculum assumes that all species are independent of one another but share the same probability of having a baculum. The probability of obtaining a baculum follows a Bernoulli distribution: with some probability p, a species receives a baculum, and with probability 1 − p, it does not. We specify a Beta prior probability distribution on the value of p, which is adequate for values between 0 and 1. This Beta distribution itself has two parameters α and β, both of which we set to 1. This choice conveys our lack of knowledge regarding the value of p as it generates a uniform distribution over [0,1]. The corresponding model is represented in Figure 2. The graph is composed of nodes and arrows joining them. The nodes correspond to variables of our model, such as the Bernoulli parameter p, and the arrows correspond to dependencies between the variables. For instance, the top arrows show that the value of p depends upon the parameters α and β. In fact, the dependency structure in a graphical model is easily read by following the arrows backwards from a dependent variable, to which an arrow points, to the variable it depends upon. In contrast, if we were to simulate data according to a graphical model, the flow of the simulation would be forwards along the direction of the arrows.

Figure 2.

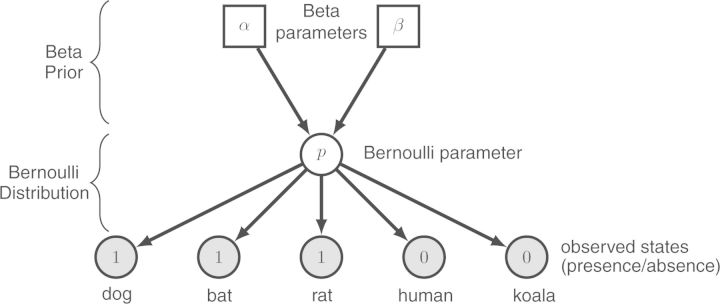
An explicit graphical model of the distribution of a binary trait. Descriptions of the objects have been added for pedagogical purpose. The presence or absence of the binary trait is assumed to follow a Bernoulli distribution with parameter p. This parameter is equal to the probability of the presence of the baculum in an independently sampled species. We place a Beta prior density on the Bernoulli distribution parameter, such that p∼Beta(α,β), where α = 1 and β = 1 are the shape parameters of the Beta distribution. This probability density is defined on the interval [0,1], thus 0 ≤ p ≤ 1.

In Figure 2, we have chosen a somewhat verbose description, with labels next to the nodes and arrows. In more complex models, it is customary to dispense with these names and only rely on the symbols inside the nodes to avoid cluttering. In the same manner that algebraic symbols are indispensable for solving complex equations, the use of short symbols is indispensable for representing complex probabilistic models. However, the representation of nodes in the graph carries additional information: square nodes are constant nodes (e.g., α and β) that depend on no other node (thus sometimes called source nodes), and circular nodes are not constant (see Fig. 1). In the present model, all circular nodes are stochastic, that is, each circular node corresponds to a random variable, whose value comes from a probability distribution. Some of our stochastic nodes have been shaded (Fig. 2), which means that they have been “clamped.” A clamped node is a stochastic node whose value has been observed and thus data are attached to the node. In our case, the bottom nodes have been clamped because they correspond to anatomical observations in the species of interest. We inferred the value of p in this model using a Markov chain Monte Carlo (MCMC) algorithm, and found that its value was 0.57 with 95% highest posterior density (HPD) interval of [0.23,0.88] ($\hat{p}=0.48$, HPD = [0.42,0.54] on the larger dataset, see Supplementary Material).

A Simple Phylogenetic Model

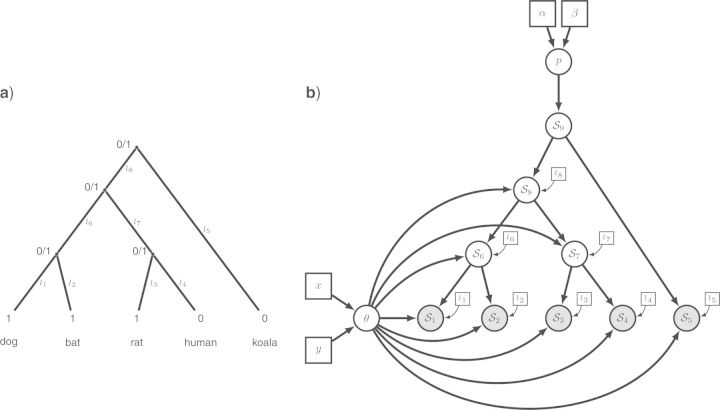
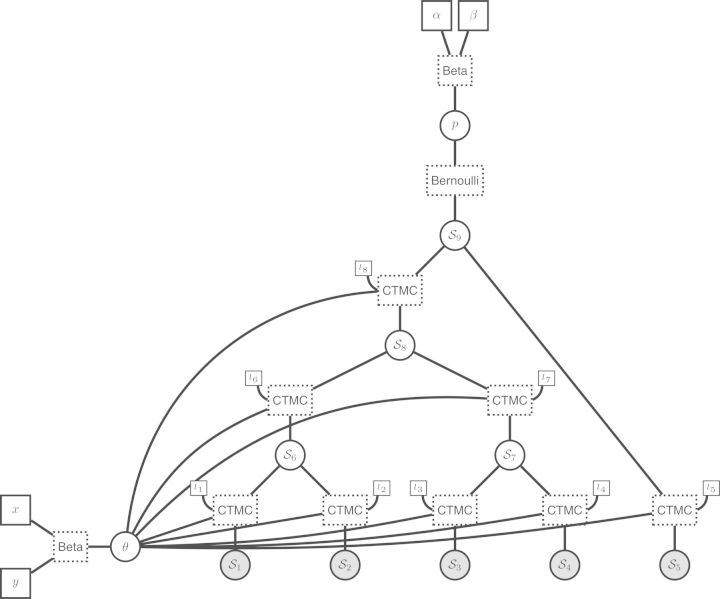
Obviously, this model fails to take into account the known phylogenetic structure underlying the distribution of the baculum among mammalian species. We therefore propose a second model, in which the presence/absence of a baculum is represented as a binary character evolving along the mammalian phylogeny. The evolution of this binary character is modeled by a continuous time Markov process, which only needs two parameters, the equilibrium frequency θ of character “1” and the set of branch lengths, assuming that the Markov process is parametrized in units of time (no transformation of the branch lengths is necessary). At the root of the tree, we need to specify a prior probability distribution over the parameter p representing the probability of the presence/absence of a baculum. As for the first model, we use a Beta prior distribution with parameters α and β both set to 1 (p∼Beta(α,β)). We also need another parameter θ for the equilibrium frequency of the state 1, parameterized the same way as p. We use the dated phylogeny of dos Reis et al. (2012), pruned to contain only the five species of interest or the 274 species in our dataset (Supplementary Material; http://dx.doi.org/10.5061/dryad.nt898). We assume this phylogeny is known without error (Fig. 3a). Comparing Figure 3a and Figure 3b demonstrates how the structure of the phylogenetic tree (partially) forms the structure of the graphical model. The structure of the phylogenetic tree can be recovered as a central subset of the graphical model, because each node of the phylogenetic tree is a stochastic variable in our model, taking values 0/1, and depending only on its parent node, the branch length and on the parameter θ of the continuous time Markov process. In the Supplementary Material (http://dx.doi.org/10.5061/dryad.nt898), we provide scripts for performing Bayesian inference with this model and the complete dataset; it turns out there is a 50/50 chance that the ancestor of mammals had a baculum.

Figure 3.

The evolution of a single binary character represented as a phylogenetic graphical model. a) The phylogenetic relationships of the five mammalian species. The observed state of the character (1: presence or 0: absence of the baculum) is given for each species. Other states at the internal nodes represent the unknown ancestral state. The branches of the tree (1,…,8) are labeled and assigned a fixed length (l₁,…,l₈). b) The corresponding graphical model, in which the species tree topology is still evident. We represent the state for each node with generic notation: S₁ is the presence/absence state for node 1. The clamped nodes, in grey, indicate observed states, whereas unobserved states for ancestral species are in white. Constant nodes indicate fixed/known branch lengths. Under this model, the state for the root of the tree (S₉) is drawn from a Bernoulli distribution with probability p. A Beta prior is assigned to the parameter of the Bernoulli distribution so that p∼Beta(α,β), where the parameters of the Beta distribution are constant nodes and assigned fixed values. The states of the nodes descended from the root of the tree (S₁,…,S₈) are dependent on the equilibrium frequency parameter (θ) and their respective branch lengths (constant nodes l₁,…,l₈). A second Beta distribution is applied as a prior on the parameter θ, where θ∼Beta(x,y).

We believe such a graphical model representation is a very powerful pedagogical construct, as it displays the entire structure of our probabilistic model. It makes it easy for a student or a reviewer to identify key assumptions made by this model. For example, although the evolutionary process is the same along all branches of the phylogenetic tree, the model is not stationary, because the root has an extra parameter for the probability of presence/absence of the baculum (p ≠ θ). However, even though our model is simple and contains few species, our graph is already quite busy. Clearly, an explicit representation is impractical for large numbers of characters, or for much more complex models, and some factorization needs to be performed.

Using Plates to Represent Repetition in the Graph

Data are inherently repetitive and this feature must be efficiently captured by a graphical model. What if, in addition to the baculum, we also wanted to analyze the distribution of the os baubellum (clitoris bone), found in females, and of a few other binary characters? Our model graph would quickly become cluttered. To circumvent this problem, the graphical model literature uses plates to represent iteration (Jordan 2004; Koller and Friedman 2009). Plates are represented as a dotted rectangles on top of which repetitive nodes are placed (Fig. 4). In a corner of the plate, the number of repetitions—in our case binary characters—is given. Assuming we analyze N binary characters using the same underlying Markov process running along the branches of the phylogenetic tree, we need to put the entire phylogenetic tree on the plate. In fact, the variables of both the leaves and the internal nodes of the phylogenetic tree differ for each character in our data matrix, because they correspond to different characters and their ancestral states, though the ancestor/descendant relationships remain unchanged. We chose to leave the parameters of the probability of presence/absence at the root off the plate, which means that we assume the probability of presence at the root is the same for all N characters. Similarly, we have left θ off the plate, assuming that all N characters evolve under the same transition probabilities. These very strong and debatable assumptions are highlighted by the graphical model representation.

Figure 4.

A phylogenetic graphical model of N independently evolving binary characters. When sampling N different binary characters for each extant species, we assume that these characters are independent and identically distributed. Thus the model for each character is the same as in Figure 3b. Yet, the state for each character 1,…,N can be different. We use the plate notation to represent repetition over a vector of elements. In this figure, the dashed box and the iterator i indicate the replicated variables. Thus, the plate represents separate variables of binary character evolution for i in characters 1,2,3,…,N.

Graphical models are high-level representations that do not depend on details of the model, such as which distribution is applied to a variable. As a result, similar models will have similar structural representations. We provide in the Supplementary Material (http://dx.doi.org/10.5061/dryad.nt898) the example of a Brownian motion model of the evolution of continuous characters to convey this point (Felsenstein 1985), and show here in more detail the example of a model of sequence evolution. Note that graphical model representations are not unique. In particular, the level of detail in the representation may vary greatly. Here, we use a relatively fine-grained representation but later we will encounter more summary-like representations of the same or similar models.

A General-Time-Reversible Model for Sequence Evolution

One of the most popular models of sequence evolution is the general time reversible (GTR) substitution model (Tavaré 1986). Here we give a simple example of a GTR model for a fixed, nonclock tree with fixed branch lengths. In this case, branch lengths are not defined in units of time as in the previous examples, but instead in expected numbers of substitutions and for simplicity we consider that we have some trustworthy exterior information about them. The resulting graphical model is depicted in Figure 5a, and is very similar to the previous figures for the binary and continuous characters (Fig. 4 and Supplementary Fig. S.1; http://dx.doi.org/10.5061/dryad.nt898). The tree sits on a plate because it is replicated for N sites. In this example, every character evolves under a continuous time Markov model with transition rate matrix Q and branch length l_j where j denotes the index of the branch. The transition rate matrix Q is defined as a deterministic function computing the transition rates by multiplying the exchangeability rates with the base frequencies. This deterministic computation is represented differently from other dependencies among nodes, with a dashed arrow pointing into a dashed node. The visually distinctive representation of deterministic nodes is used to show that the value of a variable is deterministically computed from the values of parameters it depends upon, that is, by a transformation of the parameters. This completes our compendium of nodes used in graphical models.

Figure 5.

Explicit graphical model representation of a GTR model with a fixed tree topology. For pure convenience, we show here rooted trees that demonstrate the similarity to previous figures. The model of character evolution is a continuous time Markov model parameterized by an instantaneous rate matrix. The rate matrix Q is a deterministic variable computed by multiplying the base frequencies π with the exchangeability rates ε. A Dirichlet distribution is applied as the prior distribution on both the base frequencies π and the exchangeability rates ε. a) A GTR model with fixed branch lengths. b) A GTR model with estimated branch lengths. Each branch length is independent and identically distributed under an exponential distribution.

Of course, branch lengths are often estimated instead of being considered constant. In a Bayesian context one would then have to provide priors for the branch lengths. In Figure 5b, we show the graphical model corresponding to a GTR model for a fixed tree, but in which branch lengths are estimated. As is customary in computer programs such as MrBayes (Ronquist et al. 2012), we use an exponential prior on branch lengths, with parameter λ. This choice of prior distribution can naturally be replaced by other distributions, such as a gamma distribution. Although this model is more complex and its representation busier, the structure of the tree can still be recovered from the graph. In fact, all phylogenetic examples provided thus far share a common structure, namely the underlying tree structure. We believe these strong similarities contribute to making graphical model representation powerful for teaching and understanding phylogenetic models. With some use, it becomes easy to identify the unique parts of a particular model, and the parts that relate it to alternative models.

To summarize this introduction to the graphical model framework (see Fig. 1), we have constant variables represented with square nodes, and variables whose value can change—during simulation or inference—represented with circular nodes. Circular nodes can be stochastic, with solid lines, or deterministic, with dashed lines. Arrows pointing into variable nodes represent conditional dependencies, visualized in solid or dashed lines depending on the nodes they point into. In addition, we have plates, which convey the concept of repetition. In more formal terms, nodes placed on a plate correspond to independent, identically distributed variables. This list of graphical representations is commonly used in the statistics literature (Lauritzen 1996; Jordan 2004; Koller and Friedman 2009). For phylogenetics, where we often handle phylogenetic trees that can contain large numbers of nodes, and whose topology is often unknown and needs to be estimated, other constructs are needed. Those constructs, for example tree plates, are introduced in the next section.

Phylogenetic Model Graphs

Ordinary graphical models are impractical for describing realistic phylogenetic models for two reasons: first, visual representations of these models become crowded as the number of tips grow, and essential information may become buried in a litany of details. Second, ordinary graphical models fail to represent topological (structural) uncertainty because the dependency structure of the nodes in the graph, corresponding to the phylogenetic tree topology, is fixed. We solve both problems by adding a new element to the list of graphical model conventions: a tree plate.

Tree Plates

A tree plate is very similar to a plate. However, where a plate symbolizes repetition of a particular element in the model, a tree plate symbolizes recursion: a given variable depends upon a conceptually similar variable. Recursion is a concept that fits naturally within a tree, given that many nodes in a tree are both parents and children of other nodes at the same time. Naturally, recursive constructs need initiating and terminating: the recursive description of a tree starts at the root node, and terminates at the tips. This suggests that a tree plate needs to account for three classes of nodes at least: the root node, internal nodes, and tip nodes. Contrary to internal nodes and tips, the root node does not depend on a parent node in the tree. Contrary to internal nodes, tips are often clamped to observed values. Figure 6 represents a tree plate as a big, rounded rectangle divided into three parts, one for each class of nodes, with a tree variable attached to it providing the structural information. Parent–child relationships are handled by special functions for the indexing of the parent node: $\tilde{p}(j)$ represents the parent in the tree of node j and $\tilde{c}(i,j)$ represents the i-th child of node j in the tree. A comparison between Figure 5 and Figure 6 shows how a tree plate can simplify the representation of a phylogenetic model, and how it interacts nicely with a plate. The example is extended in the Supplementary Material (http://dx.doi.org/10.5061/dryad.nt898) by the commonly used mixture model for rate variation across sites, the GTR + Γ model (Yang 1994, 1996) (see Supplementary Fig. S.2; http://dx.doi.org/10.5061/dryad.nt898).

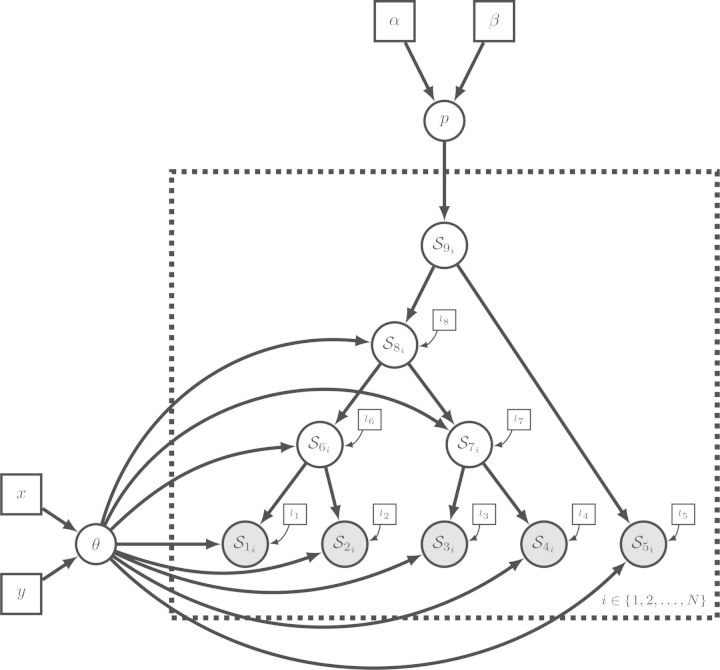
Figure 6.

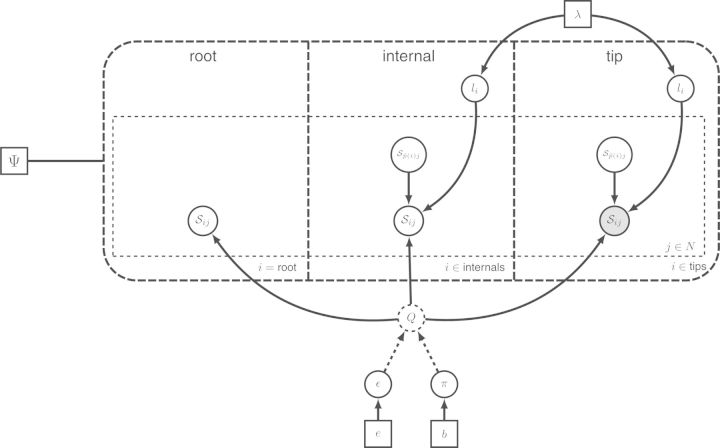
Simplified representation of the GTR model of Figure 5b using a tree plate. The tree plate, a big dashed box, divides the nodes into three classes: the root node, internal nodes and tip nodes. The character state variables are named S_ij where i denotes the i-th node and j the j-th site. The root node does not have a parent node in the tree while the other nodes do. The internal nodes and the tip nodes depend on the ancestral states. The ancestral variable of node i is obtained using the parent indicator function $\tilde{p}(i)$. Tip nodes are clamped and thus shaded. A tree topology is attached to the tree plate via the tree variable Ψ shown on the left. The tree variable informs the plate of the structure and if the tree variable changes, the structure of the resulting graph changes too.

Importantly, the recursive representation of a tree plate protects it against cluttering as the size of the tree grows: no matter how many tips are included in the tree, these three classes of nodes are enough to describe most phylogenetic models. More classes are only needed when the model further distinguishes between nodes, for example when different models of sequence evolution are associated with different subtrees or when particular nodes are associated with time calibration information. The tree plate also adequately addresses the representation of topological uncertainty. Because the tree plate uses a high-level, recursive representation of a tree, it transcends a specific tree topology and instead allows any tree topology. Only the specific value of the tree variable ordering the tree plate reveals the actual graphical structure of the model.

Modularization

Although tree plates simplify the representation of a phylogenetic model, visualization remains a challenge for the most complex models. As an example consider the common case of a multilocus analysis using a multispecies coalescent model, an uncorrelated relaxed clock and a GTR + Γ substitution model, which would contain, among others, Supplementary Figure S2 and Figure S3 (http://dx.doi.org/10.5061/dryad.nt898) merged together. Clearly, such a figure would be overwhelming. Ideally, one would like a method that allows one to quickly convey the bigger picture while allowing parts of special interest to be exposed in all the necessary detail. For instance, it is common practice to create new phylogenetic models by combining existing model components, possibly in new patterns, with new components. In such situations, it is practical for a computational phylogeneticist to use a simplified, high-level representation of the complete model graph, and focus on the model subgraph(s) of interest in the discussion of the novelties. Similarly, an evolutionary biologist might be interested in effectively communicating the crucial differences in the overall structure of some models without going into all the model details. To address these challenges, we propose a factorization of phylogenetic model graphs into modules, each of which corresponds to a subgraph of potential interest. The modules can be collapsed into simple graphical objects to allow compact high-level representation of a large model. One or more modules can also be expanded to expose all the details of the corresponding model subgraph. This allows one to communicate both the overall structure of a large model and the details of the model components of particular interest.

Module decomposition of a phylogenetic model

To factorize a complex phylogenetic model graph into modules, we introduce a new concept: pivot nodes. A pivot node is simply a node sitting on the boundary between different modules. A pivot node may be unique (e.g., a tree variable or a rate matrix variable) or replicated (e.g., a set of branch rates). Suitable pivot nodes are variables that differ in alternative models (see Fig. 7). After a pivot has been identified, the model graph is partitioned into two modules, one module representing the upstream structure of the model graph and the other module representing the downstream structure, with the pivot node being represented in both modules (see Fig. 8).

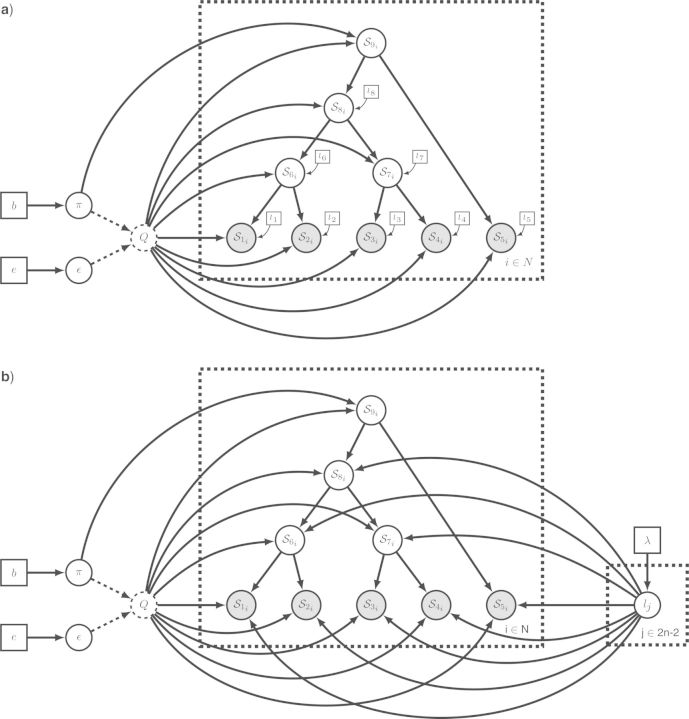
Figure 7.

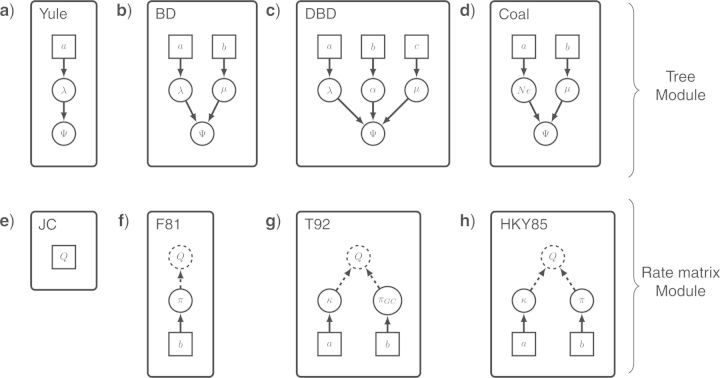
Top panel: module representation of different tree priors with Ψ as a pivot node (note that Ψ denotes a time tree with edge lengths here, not simply a topology): a) Yule process (Yule 1925), b) constant rate birth–death process (Nee et al. 1994), c) decreasing speciation rate birth–death process [speciation rate: λ*exp(− αt), e.g., in Höhna (2014)] and d) Coalescent process (Kingman 1982). Bottom panel: different rate matrix modules with Q as a pivot node: e) Jukes–Cantor rate matrix where all exchangeability rates and all base frequencies are equal (Jukes and Cantor 1969), f) F81 rate matrix where all exchangeability rates are equal but the base frequencies are drawn from a Dirichlet distribution (Felsenstein 1981), g) T92 rate matrix with a parameter for the frequency of the GC content π_GC and a transition-transversion rate (Tamura 1992) and h) HKY85 rate matrix with the base frequencies drawn from a Dirichlet distribution and an estimated transition-transversion rate (Hasegawa et al. 1985).

Figure 8.

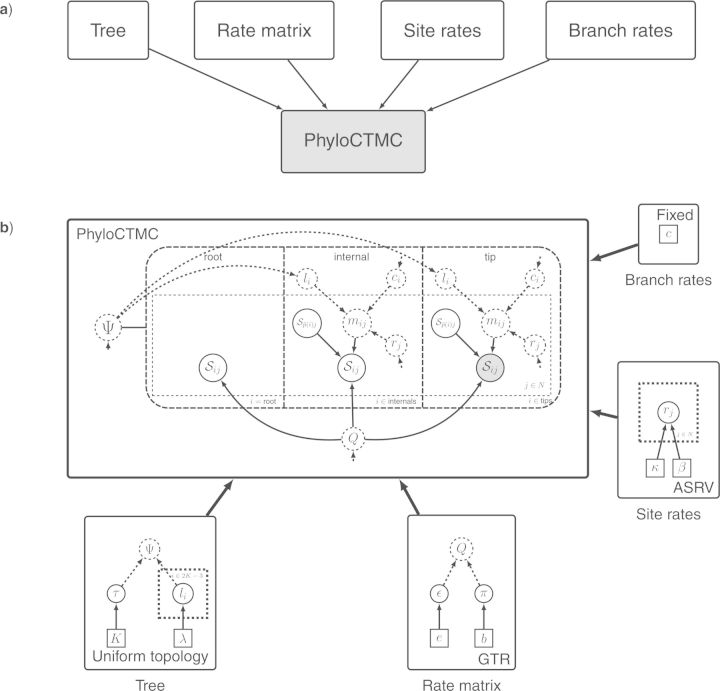
The graphical model of Figure 6, a GTR + Γ model, represented in modular form. a) The model is broken into five different modules: Tree, Rate matrix, Site rates, Branch rates and PhyloCTMC (Phylogenetic Continuous Time Markov Chain). By representing all modules in collapsed form, we obtain a compact high-level visualization of the model. Arrows point from upstream to downstream components in the complete model graph. b) By expanding the modules to expose the model subgraphs they contain, we obtain a detailed description of the model. Note that the four upstream modules (Tree, Rate matrix, Site rates, and Branch rates) are all named after the corresponding pivot variable. Also note that the symbols used for pivot variables are matched across connected modules, both by name and by plate or tree plate indices. Small arrows aid the search for pivot variables. The only new variable added here, m_ij, is the deterministically computed rate multiplier for branch i and site j, obtained by multiplying the branch length l_i with the branch rate c_i and the site rate r_j. Details of the modules are provided in the text.

As a high-level representation of a module, we use a solid rectangle containing appropriate text describing the module. An upstream module is connected to a downstream module by an arrow pointing to the latter and thus depicts the dependency structure. When a module is expanded to expose the details of the model subgraph it contains, we use the standard phylogenetic graphical model conventions. The connections between the modules are made explicit by using the same variable names and plate indices in all modules. Across alternative complex models, a pivot node may be stochastic, deterministic, or constant (see Fig. 7e–h). To preserve the subgraph representation of the downstream module in such cases, we suggest using a deterministic node representation of the pivots in the downstream module. This is compatible with the graphical model conventions, in that the value of the pivot variable in the downstream module can always be obtained as an identity transformation of the corresponding variable in the upstream module, regardless of whether the pivot variable is constant, deterministic, or stochastic in the latter. Moreover, a downstream pivot may be replicated (e.g., the branch rates), while the upstream version is not (e.g., a single rate applying to all branches). In such cases, it is assumed that the downstream instances are obtained by replication of the upstream variable.

The most practical choice of pivot variables and the corresponding modularization of phylogenetic model graphs is not obvious in all cases. These problems will undoubtedly be discussed in the phylogenetics community, and we expect that the use of modules will evolve to some extent over time. However, we propose some obvious pivot variables and associated modules here, as a starting point for further discussion. Figure 8 presents one potential module factorization of the GTR model (Fig. 6).

PhyloCTMC module

The PhyloCTMC module is commonly the core of a phylogenetic analysis. Typically, the nodes representing the leaves of a phylogenetic tree would be clamped to the observations contained in a character matrix, such as a set of aligned DNA sequences. A standard phylogenetic model contains a single PhyloCTMC module, but more complex models might have replicated PhyloCTMC modules, for example, one PhyloCTMC module for each gene using different rate matrices. It may be used in a simple model where all characters evolve homogeneously or it may be extended by, for example, using site-specific rate-multipliers (Yang 1994, 1996), branch-specific rate-multipliers (Thorne et al. 1998), branch-specific substitution rate matrices (Yang and Roberts 1995; Galtier and Gouy 1998), and site-specific tree topologies (Boussau et al. 2009). Some of these extension are described in the next modules.

Tree module

The tree module represents the subgraph describing the tree model, that is, the model of tree topology and associated branch lengths or node ages. A tree module could be used to represent a fixed topology with or without fixed branch lengths. More commonly, the tree module would be used to specify a prior distribution on trees or topologies. In the main example shown here (Fig. 8), the tree module is a uniform distribution on unrooted topologies for K tips. In this case, it is necessary to assemble the tree from the topology and the branch lengths which can for example be fixed or drawn from some distribution (e.g., an exponential distribution with rate λ). Alternative tree modules (Fig. 7a–d) include the Yule or pure-birth process (Yule 1925), the birth–death process with a constant speciation and extinction rate (Thompson 1975; Nee et al. 1994), the decreasing speciation rate birth–death model [SPVAR in Rabosky and Lovette (2008) and Models 5 and 6 in Höhna (2014)], and the coalescent process (Kingman 1982).

Branch rates module

Other suitable pivot variables are the branch rate variables, producing an upstream branch rates module. A branch rates module specifies the model on a rate multiplier applied to the branch lengths. The multiplier could either apply to all branches in the tree (if it were represented by a single variable as in Fig. 8) or applied per branch (if it were replicated across the tree plate). The branch rates module would be a central component of relaxed clock models. It could also be used to describe a rate multiplier for different gene partitions, in which case the pivot variable would be replicated across the gene partition plate in the downstream core of the phylogenetic model, rather than across the tree plate as in a relaxed clock model. An example of the branch rates module for the autocorrelated lognormal distributed rates (Thorne et al. 1998; Heath 2012) is given in the Supplementary Material (see Fig. S.3; http://dx.doi.org/10.5061/dryad.nt898).

Rate matrix module

The instantaneous rate matrix of the substitution model is the pivot variable of the rate matrix module. The pivot variable may be unique and apply to all sites and branches in the PhyloCTMC module in a branch-homogeneous substitution process. It may also be replicated in the tree plate, for example, across branches, in which case each branch would potentially be characterized by a unique substitution process (Yang and Roberts 1995; Galtier and Gouy 1998; Groussin et al. 2013), across sites (Lartillot and Philippe 2004), or according to models with explicit dependencies between neighboring branches (Blanquart and Lartillot 2006). In all such cases, the rate matrix module would describe the dependency structure of the rate matrix variable. For instance, a GTR rate matrix would be computed deterministically from a vector of stationary state frequencies and a vector of exchangeability rates (Fig. 8b). A large portion of the phylogenetic model space considered currently can be characterized by variations on the subgraph structure corresponding to the rate matrix module. Some examples are shown in Figure 7e–h.

Site rates module

The final pivot variable we consider here is the variable used to model heterogeneity of rates across sites (Yang 1994, 1996) embedded in the site rates module. Commonly, the rates for each site are considered drawn from a gamma distribution. The distribution is typically discretized for computational reasons. Interestingly, a discrete gamma model could be explicitly described by assuming that the site rates are drawn from a discrete mixture of rates, each rate being deterministically derived by computing the appropriate discrete representation of a gamma distribution (see Supplementary Material Fig. S.2; http://dx.doi.org/10.5061/dryad.nt898). Alternatively, each site rate may be drawn directly from the gamma distribution, as in our example (Fig. 8b). Other distributions than the gamma can be used for the rate variation across sites, sometimes leading to better results (Mayrose et al. 2005). In addition to models based on simple continuous distributions, any mixture model of rates (Pagel and Meade 2004, 2005) would be eligible for the site rates module. For instance, a standard model considered in the literature is a mixture of invariable sites (rate zero) and gamma-distributed rates.

High-level modular graphs

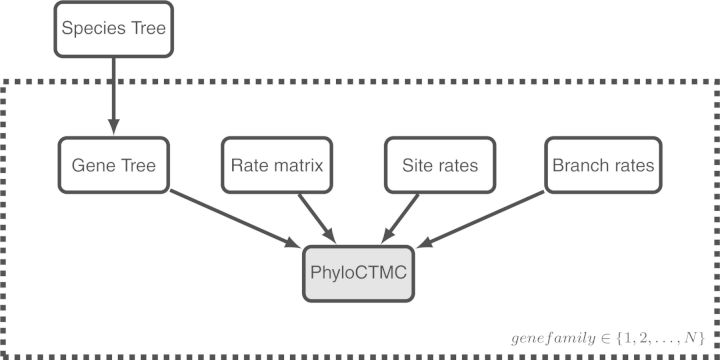
We end this section by a simple example illustrating the power of high-level modular graphs in summarizing the essential structure of a large and complex model. For this example, let us consider a model where we want to simultaneously estimate a set of gene trees and the species tree into which they fold. The high-level representation is obtained by extending the previous module graph with a species tree–gene tree model (Fig. 9). The gene-tree part of the model sits on a plate representing the replication over genes. The PhyloCTMC module is shaded to reflect the fact that it is clamped to the observations, that is, the sequences at the leaves. All gene trees depend on a single species tree through an appropriate model, for instance the multispecies coalescent. The species tree itself is a tree module, just as the gene-tree module, but it is simpler in structure. For instance, the species tree model might be a birth–death process (see Fig. 7).

Figure 9.

Module representation for a species tree-gene tree model. We simply extend the previous phylogenetic model by substituting the simple tree module by a modular representation of a species tree prior and a gene-tree distribution given the species tree. The gene tree with the entire substitution process sits on a plate representing that the model is repeated across genes. The PhyloCTMC module is shaded to reflect the fact that it is clamped to observations.

This concludes our introduction to tree plates and modular graphs, essential concepts in providing compact representations of phylogenetic graphical models. Tree plates capture the variable, stochastic nature of the dependency structure of the model subgraph corresponding to the phylogeny. They also exploit the repetitive, recursive structure of phylogenetic trees to provide stringent summaries of the essential details. Modular graphs are essential in providing high-level, compact representations of large and complex phylogenetic models. They provide a lot of flexibility through the possibility of collapsing and expanding various model components according to the specific needs in a particular situation. Large sets of complex models with minor variations in some model components are summarized very efficiently.

Computations on Model Graphs

Probabilistic graphical models, often denoted as Bayesian networks, have long been a major focus in statistics and computer science, and the resulting body of knowledge applies directly to phylogenetic graphical models (PhyloGMs). In fact, unbeknownst to many in our field, the algorithms used in phylogenetics usually have well-studied equivalents in the computer science literature. Below, we first provide a mathematical definition of directed acyclic graphs (DAGs), and discuss the rationale for using them in PhyloGMs. We continue by showing how the generative nature of probabilistic graphical models can be used directly in simulation We then describe some of the standard algorithms on probability graphs and their applications to phylogenetic problems. For a more thorough introduction to the field of graphical model algorithms, we direct the reader elsewhere (e.g., Koller and Friedman 2009).

DAGs

We begin with some mathematical notation that we need to explain the computation on model graphs. A directed graph G consists of a set of nodes (vertices) V and a set of directed edges ε connecting those nodes, that is, G = (V,ε). A directed edge from node a to node b is denoted by the pair (a,b). Direction implies that if (a,b) ∈ ε then (b,a) ∉ ε. A path through the graph is a sequence of nodes, where each node (except the last one) is connected by a directed edge from itself to its successor. If a path visits the same node twice, the path contains a cycle. By definition, a directed graph is acyclic if there does not exist any path in the graph that contains a cycle.

DAGs predominate phylogenetic models for two reasons. First, the relationships among study taxa, on which we build the core of a phylogenetic model, are inherently directed (tipwards) and acyclic because the transmission of genetic material is exclusively from ancestor to descendant. Second, there are good reasons also from a statistical perspective to focus on DAGs. A random variable depends on the parameters of its distribution, which form its parents in the model graph. This is naturally related to causation, and justifies the use of directionality in model graphs. Undirected or cyclic graphs can be used as well to represent a model, but these representations are complex and typically avoided by statisticians, and currently we see no need for them in phylogenetics.

Simulation

Simulating data from a model is essential in many applications, for instance in exploring model properties (Huelsenbeck 1995) or in model adequacy testing (Bollback 2002; Brown and ElDabaje 2009; Höhna 2013). Simulations are also used to validate inference methods and to initialize MCMC runs. Since probabilistic graphical models are generative, that is, they specify how to generate data from the model, simulation is straightforward. We simply traverse the model graph from the source nodes toward the sink nodes, drawing values of each random variable conditioned on the already generated values of its parent nodes.

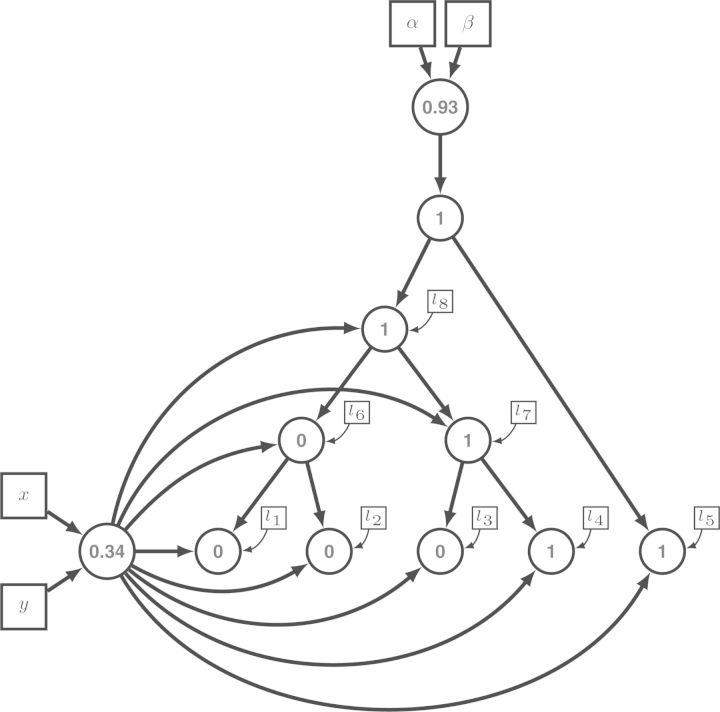
As an example, consider the evolution of a binary character under the model presented in Figure 3. The key to the simulation is the simulation sequence of the random variables, obtained from the structure of the model graph. That is, the parameter of the process, the root frequency and the stationary frequency, are simulated first. Afterwards, a realization of the two-state continuous time Markov process is simulated (see Fig. 10).

Figure 10.

Simulation of data using the graphical model of Figure 3. All simulated values are colored in blue. First, the root probability is drawn from a Beta(α = 1,β = 1) distribution, yielding 0.93, and the stationary probability is drawn from a Beta(x = 1,y = 1) distribution resulting 0.34. Then, the characters of the root node followed by the characters of the internal nodes and tip nodes are simulated under the two-state continuous time Markov process.

Simulations can be used directly for inference. For instance, the posterior probability of the parameters of interest can be computed by generating many random draws from the unclamped model, only keeping those that yield the observed data. This approach is very inefficient in most cases, and it is better to estimate the probability using other methods, as described below.

Factorization

A fundamental justification for a graphical model is that it helps us answer questions about the random variables in the model. Perhaps the most important question concerns the joint probability of a set of variables. The model graph allows us to compute this efficiently using factorization. Let us define the set U as the collection of random variable nodes in the model (with U being a subset of V). U is the complete set of stochastic variables in V and all remaining variables are either constant or deterministic. For each u ∈ U, there is a corresponding random variable in the model, X_u. The set of parent nodes of a node u is denoted by π_u. Note, π_u denotes all parents in the model graph and not only the single parent specified by tree structure mapping function p(u). If a variable is indexed by a set of indices such as π_u we mean the set of random variables with {X_p: p ∈ π_u} and use the short form $\left\{X_{{\pi }_u}\right\}$. Let x_u represent a realization of X_u. For notational convenience, we will assume in this section that all random variables are discrete, although generalization to continuous variables is trivial in most cases (excluding only marginalization and variable elimination). The conditional independence structure of the model graph allows us to break the problem into pieces (factors), each restricted to one node and its immediate parents, resulting in convenient and efficient computation. Specifically, given the set of conditional probabilities (or probability density functions) $\{\mathbb{P}(x_u|x_{{\pi }_u})\}$, the joint probability (density) is obtained as

$$\mathbb{P}(\{x_u:u\in \mathcal{U}\})={\displaystyle \prod _{u\in \mathcal{U}}\mathbb{P}}(x_u|x_{{\pi }_u})\text{.}$$ (1)

We return to example provided in Figure 3. The model contains the variables with their probability distributions:

$$\begin{array}{l}p\sim \text{Beta}(\alpha =1,\beta =1)\\ \theta \sim \text{Beta}(\alpha =1,\beta =1)\\ S_9\sim \text{Bernoulli}(p)\\ S_i\sim \text{CTMC}(S_{\tilde{p}(i)},l_i,p)\text{ for }i\text{ in }\{1,\dots ,8\}.\end{array}$$

Then, the joint probability density of the all variables is

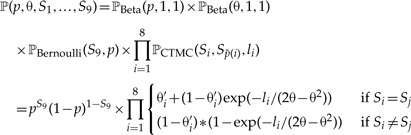(2)

where ${\theta }_i^{\text{'}}=\theta$ if S_i = 1 and ${\theta }_i^{\text{'}}=1-\theta$ if S_i = 0. This joint probability density can be used to estimate the maximum likelihood parameter estimates, or, as we did in our analysis, to compute the posterior probability density of individual parameters. Equation (2) is often denoted as the posterior probability density in Bayesian analyses and the posterior density of single parameters is obtained by marginalizing over all other parameters.

Conditional and Marginal Distribution

A common set of questions concerns the conditional probability or marginal distribution of one or more random variables (the query nodes), given fixed values of some other variables (the evidence nodes), summarizing over all possible values of (marginalizing out or eliminating) the remaining variables. For instance, we might have observed the character states of the tip nodes in a phylogenetic tree (evidence nodes), and want to infer the probabilities of the different states of a named interior node (query node), summarizing over all possible state assignments to other interior nodes (remaining nodes). Formally, let E be the set of (indices of) evidence nodes, F the query node, and R the remaining stochastic nodes. To obtain the conditional probability of a state x_F of the query node (conditioned only on x_E), we need to sum the probabilities over all possible assignments of states to the R nodes. To obtain the marginal distribution of the query node and the evidence nodes, we need to compute

$$\mathbb{P}(x_E,x_F)={\displaystyle \sum _{x_R}\mathbb{P}}(x_E,x_F,x_R)\text{,}$$ (3)

which can be further marginalized over the query node states to give the marginal probability of the evidence nodes

$$\mathbb{P}(x_E)={\displaystyle \sum _{x_F}\mathbb{P}}(x_E,x_F)\text{,}$$ (4)

from which we obtain the conditional probability of the query node

$$\mathbb{P}(x_F|x_E)=\frac{\mathbb{P}(x_E,x_F)}{\mathbb{P}(x_E)}\text{.}$$ (5)

The problem here is that ${\displaystyle {\sum }_{xR}}$ expands into a series of summations with a large number of terms. If there are |R| random variables, each of which can take on k values (e.g., four nucleotide states or 20 amino acid states), we have k^|R| terms in total. The large number of terms makes naive summation impossible except in the most trivial cases of very few variables with few states. The solution is to eliminate the R nodes one by one using the variable elimination algorithm (Koller and Friedman 2009). The computational complexity of variable elimination depends on the elimination order and the dependency structure of the graph (it is exponential with the tree width of the graph). In general, finding the optimal order is NP-hard, but good heuristic algorithms are available for the general case, and optimal orderings are known for many common types of graphs such as chain graphs and tree graphs. Variable elimination algorithms are routinely used for marginal ancestral state reconstruction on phylogenetic trees (Yang et al., 1995).

Sum-Product Algorithm and Belief Propagation

Trees are important types of graphs, and variable elimination in such graphs is accomplished by the so called sum-product algorithm (Gallager 1962; Pearl 1982; Jordan 2004; Ahmadi et al. 2012). In phylogenetics, the algorithm is known as Felsenstein's pruning algorithm (Felsenstein 1981). The sum-product algorithm is more limited than variable elimination, in that it is restricted to tree graphs. However, it is more general in that it can compute the marginals of all nodes in the tree using just two passes over the tree, each with the same time complexity as simple variable elimination. The sum-product algorithm is often described as message passing or belief propagation, both important concepts in graphical model algorithms. Here we provide a short description of belief propagation and refer the reader to Kschischang et al. (2001) and Ahmadi et al. (2012) for more detailed elaborations.

Belief propagation gets its name from the exchange of requests for messages and messages between nodes of the model. In the first pass, requests are propagated, and then in the second pass messages are propagated. More precisely, the algorithm works as follows:

1. Send message requests to all neighboring nodes, starting by the (arbitrarily chosen) root node.

2. Only process a request for a message from a neighbor if all messages from other neighbors have been received, and send out request if necessary.

3. When all messages have been received, compute the marginal probabilities.

A message consists of a vector of (typically unnormalized) marginal probabilities, one for each possible state. For instance, in a nucleotide model there would be four probabilities in the message, one for each state (A, C, G, or T). More formally, a node j would send a message m_ji to a neighbor i consisting of elements of the kind

$$m_{ji}(x_i)={\displaystyle \sum _{x_j}\left(\mathbb{P}(x_i,x_j){\displaystyle \prod _{k\in N(j)\setminus i}{m}_{kj}}(x_j)\right)}\text{,}$$ (6)

where N(j) are the immediate neighbors of node j in the tree graph, and ℙ(x_i, x_j) represents the probability of a substitution from state x_i to state x_j (or in the other direction, depending on the direction of the edge connecting i and j). The sum and product signs appearing in the message equation give the algorithm its name.

The nodes are visited first in a depth-first (postorder) traversal of the tree to guarantee effective sequential processing, from the tips toward the root, and then in the reverse order (preorder), proceeding from the root toward the tips (Fig. 11). Undirected (unrooted) trees are rooted first on an arbitrarily chosen node in order to apply the standard traversal algorithms. When the root has been reached in the first pass, we have all the necessary information to compute the probability (or likelihood) of the whole tree. We simply multiply all messages received by the root node to obtain the marginal probability for each state. Averaging over states then gives p_E, the probability of the entire tree given the tip states (the evidence). Then, the second pass over the tree starts from the chosen root node again and consists only of sent messages of the marginal probabilities for each state toward the tips (see Fig. 11b). The second pre-order traversal of the tree is only needed if the marginal probabilities are to be computed for other nodes in the tree, for instance, if one wants to draw ancestral states of nonroot nodes from the corresponding marginal distributions.

Figure 11.

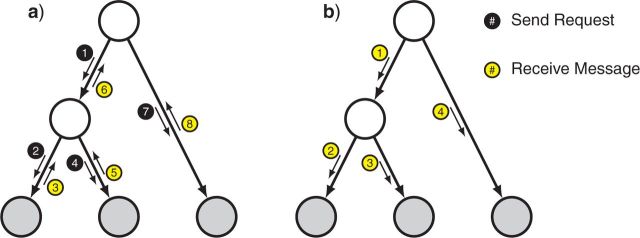
Message passing (belief propagation) on a tree graph. a) First phase, passing messages from the tips toward the root. b) Second phase, passing messages from the root towards the tips. After the second phase, all nodes have received messages from all of their neighbors, and their marginals can be computed. If only the probability of the entire tree or the marginals of the root node are of interest, the second phase is not needed.

Factor Graphs

Many algorithms on graphical models, such as belief propagation, are designed and/or optimized for factor graphs (Kschischang et al. 2001; Loeliger 2004; Ahmadi et al. 2012). Moreover, algorithms studied for various types of graphical models are unified by factor graphs and many general results and insights can thus be transfered from one application to another. Factor graphs are favored to describe belief propagation because the messages are passed to and from the factor (computation) nodes along the edges containing the variables.

Factor graphs are more fine-grained versions of graphical models, in which the probability distribution (the factors) of each random variable are made explicit by including the distribution as separate nodes in the graph (Fig. 12). Furthermore, the direction is dropped in the model graph to show that the computed value of the factor (the probability) depends on the parameters as well as the random value. Every model graph that is represented by a DAG can be converted into a factor (see Ahmadi et al. (2012) for some examples and elaborations). We show an example of the conversion in Figure 12.

Figure 12.

A factor graph representing the binary character evolution model introduced in Figure 3. The factor graph additionally displays the probability distributions (the factors) as part of the model graph, for example, a Beta distribution, Bernoulli distribution and continuous time Markov chain (CTMC). A factor graph is always an undirected graph showing only the relationship between the variables and the corresponding distributions.

The factors, or local functions, are simply the conditional probability density function (Ahmadi et al. 2012). In the example given in Figure 12 the factorization yields

$$\begin{array}{l}f(p,\theta ,S_1,\dots ,S_9)=f_{\text{Beta}}(p,\alpha ,\beta )\times f_{\text{Beta}}(\theta ,x,y)\\ \times f_{\text{Bernoulli}}(S_9,p)\times {\displaystyle \prod _{i=1}^8{f}_{\text{CTMC}}}(S_i,S_{\tilde{p}(i)},l_i)\end{array}$$ (7)

which corresponds exactly to Equation (2). However, the reverse transformation is not that simple and not every factor graph can be represented as a DAG without major modifications.

Belief propagation on factor graphs goes far beyond tree-like (cycle free) graphs and therefore also far beyond Felsenstein's pruning algorithm, which corresponds to the first pass of the algorithm. It can be extended to accommodate other types of graphs than trees (Loeliger 2004). A phylogenetic example is the variable elimination in a GTR + Γ model, which involves elimination of both character states and rate categories in a graph that is not a tree. Thus, any additional mixture model component of the substitution process may be integrated/summed over numerically by applying the belief propagation algorithm. Hence, belief propagation can be used in various other examples such as a mixture over the rates of positive selection (Yang and Nielsen 2002; Huelsenbeck and Dyer 2004), mixture over tree topologies (Boussau et al. 2009), and mixture over branch rates (Heath 2012).

Modifications of the computation of the message in the belief propagation algorithm can be used to find the maximum a posteriori probability (the so-called Viterbi algorithm (Forney Jr, 1973)) or the maximum a posteriori configuration over a set of stochastic nodes (max-product or min-sum algorithm (Tanner, 1981)). An example of the latter would be the computation of the set of character states at ancestral nodes most likely to have produced an observed set of tip states. Belief propagation is a type of dynamic programming, which is one of the most important techniques in computational optimization.

MCMC Sampling

MCMC sampling is a core technique used in Bayesian inference. It is relatively straightforward to set up a Markov chain that has the distribution of interest, the posterior probability, as its stationary distribution but convergence to the target distribution is often relatively slow. Therefore, the algorithm needs to be run for many generations, and computational efficiency is paramount. Model graphs provide an elegant way of structuring the conditional dependencies in such a way that the computational efficiency of MCMC algorithms can be maximized. It is no coincidence that BUGS (Spiegelhalter and Lauritzen 1990; Lunn et al. 2000, 2009, 2012), one of the most successful software packages for Bayesian inference, is built entirely around graphical models. In fact, the BUGS team were among the early adopters of graphical models and contributed importantly to their development, for example, by introducing deterministic nodes to capture variable transformations.

We illustrate the use of graphical models in Bayesian MCMC sampling in the context of the standard Metropolis–Hastings algorithm (Metropolis et al. 1953; Hastings 1970). In iteration t of the algorithm, the stochastic nodes U start out having the values $x^{(t)}=\left\{x_u^{(t)}\right\}$. The iteration then consists of the following steps:

1. Propose new values x′ according to a proposal density q(x′|x^(t)).

2. Compute the acceptance probability $\alpha =\min \left(1,\frac{\mathbb{P}(x^{\prime })}{\mathbb{P}(x^{(t)})}\times \frac{q(x^{(t)}|x^{\prime })}{q(x^{\prime }|x^{(t)})}\right)$.

3. With probability α accept the proposal and set x^(t + 1) = x′; otherwise reject the proposal and set x^(t + 1) = x^(t).

The computationally expensive step is to obtain the ratio of the joint probability of the model before and after the proposal, p(x′)/p(x^(t)). In theory, a proposal could involve changing values of all nonclamped stochastic nodes in the model, making it difficult to achieve computational efficiency. In practice, however, a mixture of many different proposal mechanisms is used, with each proposal changing the value of only one or a few stochastic nodes. Taking advantage of the conditional-independence factorization provided by the graphical model formalism, we can quickly identify the minimal set of conditional probabilities that need to be updated.

Consider a proposal changing just one stochastic node i and let c(i) denote the children of that node. In principle, we need to calculate

$$\frac{\mathbb{P}(x^{\prime })}{\mathbb{P}(x^{(t)})}={\displaystyle \prod _{u\in \mathcal{U}}\frac{\mathbb{P}(x_u^{\text{'}}|x_{{\pi }_u}^{\text{'}})}{\mathbb{P}(x_u^{(t)}|x_{{\pi }_u}^{(t)})}}\text{,}$$

a product over all nodes in the graph. However, for all nodes in U except i and c(i), the conditional probabilities are going to be the same before and after the move. Therefore, we can simplify the calculation to

$$\frac{\mathbb{P}(x^{\prime })}{\mathbb{P}(x^{(t)})}=\frac{\mathbb{P}(x_i^{\text{'}}|x_{{\pi }_i}^{(t)})}{\mathbb{P}(x_i|x_{{\pi }_i}^{(t)})}\times {\displaystyle \prod _{u\in c(i)}\frac{\mathbb{P}(x_u^{(t)}|x_i^{\text{'}})}{\mathbb{P}(x_u^{(t)}|x_i^{(t)})}}\text{.}$$

Thus, only the changed node and its children need to be considered in calculating the model probability ratio (Spiegelhalter and Lauritzen 1990). Similarly, if the proposal changes the values of a set of nodes rather than a single node, it is sufficient to consider the changed nodes and their children in calculating the probability ratio. As an illustrative example consider the case when a new value for the probability p of a baculum of the common ancestor of all taxa is proposed (see Fig. 3). The joint probability density was given in Equation (2) and the computation for the full dataset contains many factors. However, the probability ratio simplifies to

$$\frac{\mathbb{P}(p^{\prime })}{\mathbb{P}(p^{(t)})}={\left(\frac{p^{\prime }}{p^{(t)}}\right)}^{S_9}{\left(\frac{1-p^{\prime }}{1-p^{(t)}}\right)}^{1-S_9}$$ (8)

regardless of how many taxa are included in the study. The probability ratio is clearly simpler than the joint posterior probability density and the ratio thereof and the computation is much faster.

Finally, consider Gibbs sampling (Geman and Geman 1984; Gelfand and Smith 1990), a special case of the Metropolis–Hastings algorithm, in which the proposal distribution is the posterior probability distribution of the changed variable(s), conditional on the values of the other random variables in the model. Simultaneous Gibbs sampling of all unclamped random variables in a model would be equivalent to random draws from the target distribution, which is difficult to beat in terms of sampling performance. In practice, one is happy if it is possible to do Gibbs sampling of individual random variables in the model. Specifically, Gibbs sampling of a random variable is possible when the distribution from which it is drawn (the prior) is conjugate with respect to its conditional posterior. In this context, conjugate means that the two distributions come from the same family of distributions. The graphical model structure is helpful both in checking for conjugate distributions and in implementing Gibbs sampling where it is feasible. This property of graphical model has been exploited extensively by BUGS (Spiegelhalter and Lauritzen 1990; Lunn et al. 2000, 2009, 2012).

More Computation on Model Graphs

In this section, we have only skimmed the surface of the literature on graphical-model computation. We have not covered methods that allow efficient maximum likelihood inference by using the structure of graphical models, such as the expectation maximization (EM) algorithm or variational methods that minimize Kullback–Leibler divergence (Koller and Friedman 2009). We have not discussed the analysis of conditional independence, and many other methods of interest. However, our examples have hopefully demonstrated the relevance of the rich graphical-model literature to statistical phylogenetics. Our point is not that phylogeneticists have necessarily been hampered significantly thus far by ignoring graphical models. However, the benefits of adopting the graphical models framework will increase rapidly over the coming years, as phylogenetic models become increasingly complex.

Discussion

Statistical phylogenetics has developed to the point where the number and complexity of phylogenetic models are posing serious challenges to theoreticians, empiricists, and software developers alike. It would represent a big step forward if the field adopted a standardized and efficient way of describing phylogenetic models and exposing their underlying structure. We argue that the graphical models framework, used by statisticians to address similar challenges, provides an appropriate tool to this end. Graphical models have not been used in phylogenetics previously (except in the code of Coevol (Lartillot and Poujol 2011)) but they have been applied to many other research areas and several workers have suggested their use in phylogenetics (Lunn et al. 2000; Friedman et al. 2002; Friedman 2004; Jordan 2004; Lunn et al. 2009; Koller and Friedman 2009).

Graphical models are based on the idea of breaking large probabilistic models into components representing conditionally independent probability distributions. Additional representational power is obtained by using plates for replication and deterministic nodes for variable transformations. Although many aspects of phylogenetic models can be readily described using these standard graphical model concepts, the phylogenetic models also present some special difficulties.

The core part of a PhyloGM, the one corresponding to the evolutionary tree, is unusual in a graphical models perspective both because it can be so large and because the graph structure (the topology) is considered a random variable subject to estimation. To address these challenges, we introduced tree plates. They allow efficient representation of large trees with many tips and they also capture the structure learning nature of tree topology inference. We further simplified the representation of large and complex phylogenetic models by introducing a modular representation that breaks them into connected subgraphs at carefully chosen variable nodes, called pivot nodes. The modular representation is highly flexible, allowing both compact high-level representation of models and efficient detailed exposition of the model subgraphs of particular interest. By combining different modules in various patterns, a large set of models can be represented very efficiently.

With the addition of tree plates and modularization, we believe that graphical models are ready for wide use in the statistical phylogenetics community. They provide a rich framework for teaching and communicating probabilistic models. With their explicit representation of assumptions and variable dependencies, they facilitate the understanding of complex models and they reduce the risk of similar models being confused. Graphical models should be useful both for empiricists who want to learn the essential features of models and for theoreticians who want to communicate new models and put them in the context of previously published models.

Of course, graphical models also have limitations. Some distributions cannot be broken into smaller components, for example, the birth–death process or joint processes affecting multiple variables. A more serious challenge is to represent uncertainty concerning the structure of the graph. For instance, an evolutionary model for unaligned sequences has an element of structural uncertainty because we wish to learn how individual sequence positions are related (aligned) to each other. It is always possible to construct a large joint distribution in such cases, but this limits the power of the graphical model representation. A better approach might be to find notational extensions, similar to the tree plate.

Clearly, adopting the graphical model approach would help connect statistical phylogenetics to other science areas, promoting interdisciplinary cross-fertilization that may well turn out to be productive. For example, graphical models have been well studied from a computational perspective. Many algorithms are known for efficiently computing joint or marginal probabilities, and for performing MCMC sampling or simulation on probabilistic model graphs. In fact, as we have shown, many of the standard algorithms used in computational phylogenetics have older and well-studied equivalents in the literature on model graphs. As phylogenetic models grow in complexity in the future, the existing work on model graph algorithms may well prove to be a treasure trove for phylogeneticists, greatly facilitating the development and implementation of new models. For example, we only provided some algorithms to sample from the posterior probability distribution (Metropolis–Hastings and Gibbs sampling) although other strategies, such as data augmentation, have been shown to be more efficient (Rodrigue et al. 2008; Landis et al. 2013) and have been used in conjunction with graphical models (Lartillot and Poujol 2011).

Graphical models may also help forge links between statistical phylogenetics and other fields of applied statistics. Applied statisticians often summarize models using formulae of the type y∼f(α,β), specifying that a random variable y is drawn from some distribution f with parameters α and β (for a range of examples, see Lunn et al. 2012). Such model formulae are rarely used in phylogenetics today. However, they are closely related to graphical model concepts, so phylogeneticists adopting this framework are likely to find such model formulae helpful and informative summaries of their models. This, in turn, will make it easier for applied statisticians to contribute to phylogenetics.

Last but not least, the adoption of graphical models would facilitate the design and development of computational phylogenetics software. There are decidedly some challenges involved in doing this, particularly in finding efficient software representation of the huge PhyloGMs. However, regular plates and tree plates help identify some of the replicated structure that can be used in efficient implementation of PhyloGMs. Modularization also encourages good software engineering principles, in that it supports a natural, high-level design with exchangeable and reusable components corresponding to standard modules in PhyloGMs.

Supplementary Material

Data available from the Dryad Digital Repository at http://dx.doi.org/10.5061/dryad.nt898.

Funding

NIH [GM-069801 and GM-086887 to J.P.H.]; NSF [DEB-1256993 to T.A.H]; Swedish Research Council [2011-5622 to F.R.].