Diels–Alder Reactions of Allene with Benzene and Butadiene: Concerted, Stepwise, and Ambimodal Transition States

Abstract

Multiconfigurational complete active space methods (CASSCF and CASPT2) have been used to investigate the (4 + 2) cycloadditions of allene with butadiene and with benzene. Both concerted and stepwise radical pathways were examined to determine the mechanism of the Diels–Alder reactions with an allene dienophile. Reaction with butadiene occurs via a single ambimodal transition state that can lead to either the concerted or stepwise trajectories along the potential energy surface, while reaction with benzene involves two separate transition states and favors the concerted mechanism relative to the stepwise mechanism via a diradical intermediate.

Introduction

Allenes readily undergo thermal pericyclic reactions, including Diels–Alder, 1,3-dipolar, and (2 + 2) cycloadditions.¹ There is some evidence that these reactions are stepwise, although few systematic investigations are available. We report multiconfigurational complete active space (CAS) computational studies of the reactions of allene with butadiene and with benzene, aliphatic and aromatic dienes in Diels–Alder reactions (Figure 1).^2,3 For the butadiene–allene reaction, we have discovered that a single ambimodal transition state leads to a path bifurcation to either the (4 + 2) cycloadduct, via a concerted reaction, or to a diradical intermediate that can subsequently give either Diels–Alder or (2 + 2) adduct. In contrast, benzene and allene react through a transition state that leads only to a concerted pathway, forming both C–C bonds simultaneously and avoiding the loss of aromaticity in an intermediate. A higher energy transition state leads to a diradical intermediate.

Figure 1.

Diels–Alder and (2 + 2) cycloaddition reactions of allene with butadiene and benzene.

Background

Pericyclic reactions involving allenes are known and have been used extensively in the syntheses of natural products.⁴ These reactions include [1,n]-, [2,3]-, and [3,3]-sigmatropic shifts⁵ and electrocyclizations.⁶ The relative reactivity of allenes, alkynes, and alkenes in these processes have been the subject of some interest. For instance, the Cope rearrangement was found to proceed through similar transition structures, independent of the identity and degree of unsaturation of the π-components.⁷ Allenes also participate in (4 + 2) cycloadditions, 1,3-dipolar cycloadditions, and (2 + 2) cycloadditions; examples of each of these studied experimentally are shown in Figure 2. Maier utilized both cyclopentadiene and Boc-protected pyrrole with monosubstituted allenes to generate bridged bicyclic compounds through the Diels–Alder reaction.⁸ The 1,3-dipolar cycloaddition of C-phenyl-N-methylnitrone with electron-deficient allenes produces methyleneisoxazolidines at 40 °C.⁹ Allene dimerization has been known for decades,¹⁰ and Dolbier investigated the preference for formation of 1,2-dimethylenecyclobutane over the 1,3-regioisomer.¹¹

Figure 2.

(4 + 2), 1,3-dipolar, and (2 + 2) cycloadditions of allenes.

Computational mechanistic studies of allenes as reaction partners in 1,3-dipolar¹² and (2 + 2) cycloadditions¹³ have been reported. There are, however, limited theoretical investigations of allenes as dienophiles in (4 + 2) reactions. Venuvanalingam studied the concerted Diels–Alder cycloadditions of dienes with allenes and fluoroallenes as dienophiles with semiempirical AM1 and PM3 methods.¹⁴ Gandolfi studied concerted Diels–Alder cycloadditions of allene and fluoroallene with cyclopentadiene and furan with the ab initio Hartree–Fock method and MP3 single-point calculations.¹⁵ Houk and co-workers conducted a DFT study of the concerted and stepwise pathways of the parent butadiene–allene cycloaddition as well as some furan cycloadditions with allene but were unable to locate a number of important stationary points.¹⁶ In light of the numerous studies contrasting the Diels–Alder reactions of alkene and alkyne dienophiles,¹⁷ we have undertaken a thorough investigation of the butadiene–allene system.

A variety of substituted dienes undergo Diels–Alder reactions with allenes. As shown in Figure 3, Danishefsky dienes 1 react with unsymmetrically 1,3-disubstituted allenes 2 to give aromatic products 4 and 5.¹⁸ These reactions were thought to involve Diels–Alder cycloadditions via intermediate 3. However, Jung and co-workers have shown for similar cases that (2 + 2) adducts may precede Diels–Alder adduct formation.¹⁹ Reactions of dienes 6 with allenoic ester 7 give exo-methylenevinylcyclobutane intermediates 8, formal (2 + 2) adducts, when the reaction time is 5 h (Figure 4). These adducts undergo formal Cope rearrangements to give the Diels–Alder products 9 and 10 after extended reaction times. The Cope rearrangement of the unsubstituted exo-methylenevinylcyclobutane was found in previous computational studies by Houk and co-workers to rearrange to the Diels–Alder adduct in a stepwise fashion through a bis-allylic diradical.²⁰ Based on previous studies and experimental results in the literature, it is proposed that (4 + 2) reactions of this nature are stepwise and proceed first through a formal (2 + 2) cycloaddition, followed by a formal 1,3- or 3,3-shift to afford the Diels–Alder adduct.

Figure 3.

Diels–Alder reactions of dimethyl 1,3-allenedicarboxylate 2 with Danishefsky dienes 1.

Figure 4.

Formation of exo-methylenevinylcyclobutane intermediate prior to rearrangement to Diels–Alder adducts.

Himbert and Henn have shown that intramolecular (4 + 2) cycloadditions between allenyl amides and tethered aryl groups occur efficiently at elevated temperatures, despite the required disruption of aromaticity (Figure 5a).²¹ The polar stepwise mechanism was ruled out by the insensitivity of the kinetics of the reaction to varying electron-donating and electron-withdrawing groups on the benzene and allene moieties. However, although a concerted mechanism was initially proposed, a stepwise diradical mechanism could not be ruled out. Vanderwal has recently explored this dearomatizing intramolecular Diels–Alder reaction and has incorporated a subsequent ring-rearranging metathesis to form complex polycyclic scaffolds (Figure 5b).²² Together, our groups uncovered important mechanistic insights into these intramolecular cycloadditions of allene to benzene derivatives.²³ In order to understand the energetics of concerted and stepwise pathways in benzene–allene cycloadditions and to make direct comparisons with nonaromatic diene reactions, we have undertaken a systematic investigation of the benzene-allene and butadiene-allene reactions with multiconfigurational CASSCF and CASPT2 methods.

Figure 5.

Intramolecular Diels–Alder reaction of arenes and allenes.

Computational Methodology

We have studied these reactions with complete active space (CAS) multiconfigurational methods. Stationary point structures were optimized using the CASSCF(8,8)/6-31G(d)²⁴ and CASSCF(10,10)/6-31G(d) methods in Gaussian 09²⁵ for the butadiene/allene and benzene/allene systems, respectively. Single-point calculations with second-order perturbation theory CASPT2/6-31G(d)²⁶ were carried out on the optimized structures, using the program MOLCAS²⁷ version 7.4, to account for dynamic electron correlation. CASSCF thermal corrections and zero-point energies are included in the CASPT2 electronic energies. Vibrational frequencies were computed for all optimized structures in order to verify that they are minima or transition states. Intrinsic reaction coordinate (IRC) calculations were also performed on several transition structures to verify that these transition structures originated from the correct reactants and led to the expected intermediates or products. CASSCF and CASPT2 has been found by Houk and co-workers to provide reasonable energetics for various diradical and pericyclic reactions.²⁸ DFT methods were also employed for optimizations, but we had difficulty locating relevant stationary points.¹⁶ Furthermore, several unrestricted DFT methods gave unrealistically high energy diradicals for the benzene–allene reaction. Consequently, we have used more robust multiconfigurational methods for the entirety of the investigation. A summary of our DFT results can be found in the Supporting Information.

Results/Discussion

Mechanism of the Reaction of Butadiene and Allene

The reaction of butadiene 16 with allene 17 can occur by either a concerted or stepwise radical mechanism (Figure 6). The concerted pathway has previously been studied using semiempirical¹⁴ as well as UB3LYP methods.¹⁶ Alternatively, the reaction can give diradical 18 that can subsequently cyclize to Diels–Alder adduct 19 or to the (2 + 2) adduct 3-methylenevinylcyclobutane 20. The (2 + 2) adduct can reopen to 18 and then cyclize to yield 19. This Cope rearrangement to the Diels–Alder adduct of the unsubstituted 3-methylenevinylcyclobutane was found in previous computational studies by Houk and co-workers to occur in stepwise fashion through a bis-allylic diradical intermediate.²⁹ The stereoselectivity was postulated to be governed by dynamic effects. Reaction of the diene in the s-cis conformation is necessary to permit cyclization to the Diels–Alder adduct; the transoid diradical 18(trans) could be formed and undergo bond rotation around the partial double bond to furnish the cisoid diradical 18(cis), which can then cyclize to 19, but this would require rotation around the partial double bond of the allyl radical.

Figure 6.

Possible mechanisms of butadiene 16 and allene 17.

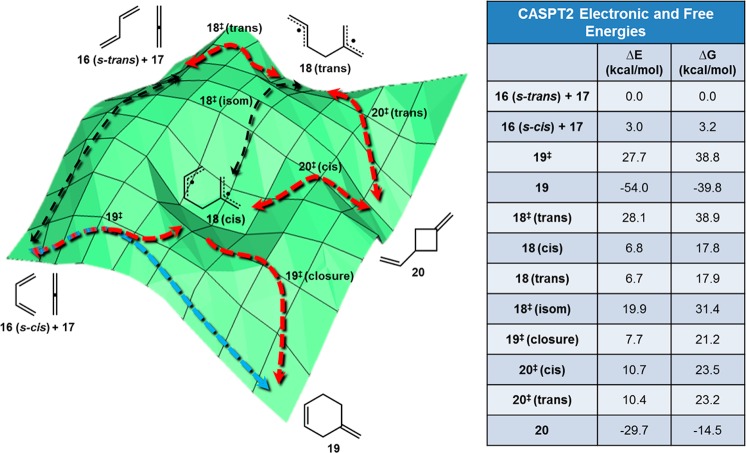
Four possible reaction pathways were examined using CASPT2//CASSCF(8,8) calculations. The active space was chosen to include the electrons involved in the formation of new bonds, namely the eight π-electrons of butadiene and allene. A schematic of the energy surface was generated from the quantum-chemically calculated values and is shown in Figure 7. Reported energies are relative to the lowest energy conformations of separated allene and s-trans butadiene. At the left of the diagram, the s-cis and s-trans butadiene reactants are shown. The s-cis butadiene is 3.0 kcal/mol higher in energy, consistent with the 2.6–4.0 kcal/mol values for the gauche conformation of s-cis butadiene found in prior calculations and experiments.³⁰ The barrier to interconversion is approximately 6 kcal/mol to switch from s-trans butadiene to s-cis butadiene. To the right of the diagram in Figure 7 are shown the electronic energies of the stationary points. Free energies calculated at room temperature (25 °C) have also been included, since reaction rates are determined from free energies through transition state theory. Because of the entropic penalty (−TΔS term in free energy) of bringing two molecules together, ΔG values are uniformly 11–14 kcal/mol higher than the corresponding ΔE values for all stationary points other than the separated reactants. Consequently, the reaction surfaces generated from both electronic and free energies have similar topologies, and we will proceed by referring to electronic energies for consistency.

Figure 7.

Schematic of the potential energy surface for the reaction between butadiene and allene. CASPT2//CASSCF(8,8)/6-31G* gas-phase energies are shown in kcal/mol. Red arrows refer to the stepwise pathways, the blue arrow is the concerted pathway, and black arrows are for cis/trans and s-cis/s-trans interconversions.

Along the lower border, the concerted Diels–Alder reaction pathway is shown. 19^‡ is the concerted transition state at 27.7 kcal/mol but is described in detail in the next section; this is also the transition state leading to the cis-diradical 18(cis). Several Diels–Alder reactions of two dienes involving bifurcations are known.³¹ Singleton has also studied a bifurcation that occurs in the Diels–Alder reactions of ketenes with cyclopentadiene which leads to an intermediate or a cycloadduct, as found here.³² At 28.1 kcal/mol, the transition state leading to the trans-diradical, 18^‡(trans) will compete with 19^‡. Both the trans and cis diradicals can give the 3-vinylmethylenecyclobutane 20 through transition states of only 10–11 kcal/mol. The transition state for formation of Diels–Alder product, 19^‡(closure), is 7.7 kcal/mol with respect to the reactant and only 0.9 kcal/mol higher in energy than the diradical intermediate 18(cis). Our calculations predict that Diels–Alder adduct 19 and 3-vinylmethylenecyclobutane 20 should both be formed thermally, with the former being the thermodynamically and kinetically favored major product.

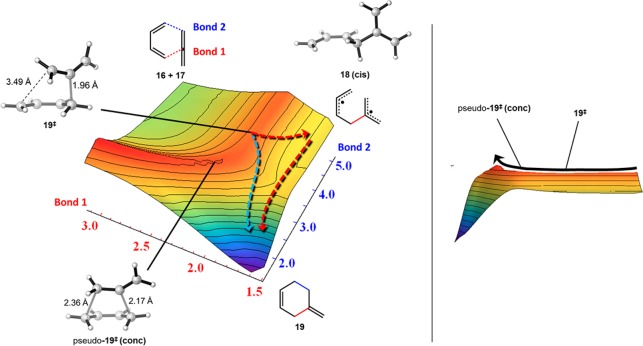
In order to understand the region around 19^‡, a detailed potential energy surface was generated (Figure 8). The energies were calculated by fixing the distance between the internal carbon of the allene and a terminal carbon of butadiene (bond 1) and varying the distance corresponding to the second forming σ-bond (bond 2). CASSCF(8,8) single-point calculations were conducted on each structure, and the same protocol was applied to increasing lengths of bond 1. Examination of the surface shows that only one saddle point exists, corresponding to ambimodal transition state 19^‡. An IRC calculation shows that the steepest downhill trajectory leads to formation of diradical 18(cis). From this diradical, there is only a small barrier 19^‡(closure) to radical recombination to form 4-methylenecyclohexene 19 (red arrows). However, an alternative trajectory can lead directly to 19 which, although not the steepest trajectory, bypasses 18 and 19^‡(closure) (blue arrow). In a study of the allenic Cope rearrangement of 1,2,6-heptatriene, Borden observed a similar phenomenon where both a concerted and a stepwise pathway can emerge after traversing a common transition state.³³ Despite the large preference for reaction at the central carbon of allenes, the allylic stabilization found in the diradical intermediates is not substantial in the transition structures, suggesting the possibility for direct formation of product without passage through an intermediate. This result is in line with the discovery that Cope rearrangements involving alkenes, allenes, and alkynes are all mechanistically and kinetically similar.⁷

Figure 8.

Left: Potential energy surface (PES) region of the possible transition states of initial bond formation, generated with CASSCF(8,8)/6-31G*. Energy levels are designated by the following color spectrum: red = high energy, violet = low energy. The red arrows outline the stepwise pathway from ambimodal transition state 19^‡, while the blue arrow outlines the concerted pathway. Right: Side view of the PES, demonstrating the saddle point for 19^‡.

The lengths of the forming σ-bonds in 19^‡ differ by 1.5 Å, suggesting significant diradical character. The occupations of the HOMO and LUMO natural orbitals are 1.65 and 0.36, respectively; occupations of 2 and 0 are expected for ideal closed-shell species, while 1 and 1 would represent a pure diradical. To further probe the existence of a distinct concerted transition state, pseudo-19^‡(conc) was optimized with bond distance restraints of 2.17 and 2.36 Å, established from successful location of the concerted stationary point using the 3-21G basis set; the greater synchronicity of the transition state may be an artifact of the smaller basis set. The potential energy surface connecting 19^‡ and pseudo-19^‡(conc) is very flat, requiring only a minor geometric change to interconvert the two structures. Hence, when butadiene is in the cis conformation, only a single transition state 19^‡ leads to diradical 18(cis) and to Diels–Alder cycloadduct 19. All optimized structures are shown in Figure 9.

Figure 9.

Optimized structures of the stationary points for the cycloaddition of butadiene 16 and allene 17.

Although both the blue and red downhill trajectories in Figure 8 are barrierless on the potential energy surface, Singleton has shown that inclusion of entropic factors can reveal hidden dynamical bottlenecks.^32a From 19^‡, formation of a single C–C bond resulting in diradical 18(cis) will have a lower entropic penalty than simultaneously establishing the two new σ bonds of 19. Also, examination of the transition-state region shows that the location of the highly asynchronous transition structure 19^‡ is skewed toward 18(cis). This may cause an entropic bottleneck between 19^‡ and 19, establishing a barrier for the blue concerted pathway in Figure 8 and leading to exclusive formation of intermediate 18(cis) prior to forming the Diels–Alder adduct 19. Thus, despite the fact that the potential energy surface contains only one initial bond-forming transition state that can seemingly form either a cycloadduct or a diradical, accounting for entropy would likely lead to preferential diradical formation. Molecular dynamics simulations may be a valuable tool in validating this notion and further probing the surface around the transition state. A similar situation where an IRC predicts a concerted pathway while dynamics suggests a stepwise route has been uncovered in the intramolecular heterolysis of pinacolyl alcohol.³⁴

Formation of the bis-allyl diradical can result in either the cisoid (18(cis)) or the transoid (18(trans)) intermediate, depending on the orientation of the butadiene prior to bond formation. The intermediates are essentially isoenergetic, but transition state 19^‡ lies 0.4 kcal/mol lower than 18^‡(trans). The cisoid and transoid intermediates can interconvert only by traversing a 13 kcal/mol barrier due to rotation around the partial double bond of the allyl radical.

From the cisoid diradical intermediate 18(cis), both 3-methylenevinylcyclobutane 20 and 4-methylenecyclohexene 19 can be formed by radical combination through 20^‡(cis) and 19^‡(closure), respectively, while 18(trans) can only form cyclobutane product 20. The transition states 20^‡(cis) and 20^‡(trans) have the same energy; the structures are identical except for the conformation of the distal double bond. The formation of 20 is exoergic by 29.7 kcal/mol; longer reaction times or higher temperatures result in radical ring-opening back to either stereoisomer of bis-allyl diradical 18. Although the barrier for the ring-opening of 20 is high (∼40 kcal/mol) for the unsubstituted system, substituents stabilizing the diradical intermediate will result in a lower barrier for the ring-opening of 20. The cisoid intermediate can then irreversibly produce the Diels–Alder product 19 through transition state 19^‡(closure), which is lower in energy than 20^‡(cis) and 20^‡(trans) by 3 kcal/mol.

These results parallel the experimental results reported by Jung on substituted substrates (Figure 4).¹⁹ After a few hours of heating mixtures containing substituted butadienes and allenyl ester 7, the formal (2 + 2) products were isolated. Heating the cyclobutanes over a period of days resulted in rearrangement to the formal Diels–Alder products. This vinylcyclobutane–cyclohexene rearrangement has previously been studied by our group.²⁰

Allene dimerizes readily,^10,11,35 and the mechanism has been studied theoretically at a coupled-cluster level of theory.¹³ Johnson calculated the dimerization to occur with an energetic barrier ΔE^⧧ = 32.9 kcal/mol for initial diradical formation, approximately 5 kcal/mol higher than our calculated barrier for reaction with butadiene. Previous successes in (4 + 2) cycloadditions with substituted butadienes illustrate this preference of Diels–Alder reaction over dimerization.^18,19

Mechanism of the Cycloaddition Reaction of Benzene with Allene

The (4 + 2) reaction of benzene 21 and allene 17 was also explored (Figure 10). This cycloaddition does not occur in the parent cases because allenes dimerize and oligomerize more rapidly than they react with benzene.^10,11,35 As mentioned previously, Himbert,²¹ Orahovats,³⁶ and more recently Vanderwal^22,23 have demonstrated that substituted benzenes and allenes can form intramolecular cycloadducts. The intramolecular cycloadditions of N-arylallenylamides are known (Figure 5) and prompted our study of the benzene–allene reaction.

Figure 10.

Possible mechanisms of cycloadditions of benzene 21 and allene 17.

The cycloaddition can occur through a concerted (23^‡(conc)) mechanism or through the stabilized pentadienyl radical 22. Either route can lead to (4 + 2) cycloadduct 23, with the latter proceeding through 23^‡(closure). The (2 + 2) product 24 can also be formed.

Optimizations were carried out with CASSCF(10,10) involving an active space of the six π-electrons of benzene and the four π-electrons of allene. A schematic of the reaction profile and energy values are shown in Figure 11. The concerted transition state 23^‡(conc) lies 5.0 kcal/mol lower than the stepwise 22^‡(step), in contrast to the union of these into a single transition state found with s-cis butadiene and ethylene. Formation of the first C–C bond gives intermediate 22, containing allyl and pentadienyl radicals. Although these radicals are stabilized, loss of aromaticity offsets the favorable conjugation so that 22 is 32.2 kcal/mol higher than the reactants. The allyl radical resulting from the allene does not initially benefit from delocalization; rotations about the C–C bonds are necessary before proper orbital alignment allows for conjugation. Conversely, the concerted 23^‡(conc) better offsets the loss of aromaticity and maintains most of the benzene stabilization by providing an aromatic transition state.

Figure 11.

Schematic of the potential energy surface for the reaction between benzene 21 and allene 17. CASPT2//CASSCF(10,10)/6-31G* gas-phase energies are shown in kcal/mol. Red arrows refer to the stepwise pathways, blue arrow for the concerted pathway.

Ring closure of the diradical to form the (4 + 2) adduct 23 is favored over formation of the (2 + 2) adduct 24 by 5.9 kcal/mol. The formation of 24 is endoergic by 5.0 kcal/mol and is reversible. The methylenecyclobutane 24 can ring-open to 22 and ultimately form the thermodynamically favorable product 23. Optimized structures are shown in Figure 12.

Figure 12.

Optimized structures of the stationary points for the cycloaddition of benzene 21 and allene 17.

Allene oligomerizes readily in benzene at temperatures of >130 °C. The 37.1 kcal/mol required for the (4 + 2) cycloaddition of benzene and allene is greater than the 32.9 kcal/mol barrier for dimerization, as calculated by Johnson (Figure 13).¹⁰ Furthermore, 1,2-dimethylenecyclobutane formation is exoergic by 45.0 kcal/mol, compared to only 8.9 kcal/mol for 23. The dimerization of allene is thermodynamically and kinetically favored relative to Diels–Alder reaction with benzene, consistent with the lack of formation of 23.

Figure 13.

Energetics of the Diels–Alder reaction of benzene and allene (left) and the dimerization of allene (right). Calculations of the dimerization of allene were conducted by Johnson et al.¹⁰

DFT optimizations using both UB3LYP/6-31G(d) and UM06-2X/6-31G(d) methods were also utilized for the butadiene–allene and benzene–allene systems; energetics and optimized structures can be found in Supporting Information. For the butadiene–allene system, UM06-2X predicts energies for all stationary points to within 5 kcal/mol of CASPT2. However, DFT calculations on the benzene–allene system resulted in largely overestimated energies for the open-shell diradical species. The spin-contamination observed with DFT methods,³⁷ which changes over the course of the reaction pathways, may be a large contribution. This outcome has been observed in prior DFT studies of arene–allene cycloadditions.²³ Aside from the unexpectedly high energies for the intermediate in benzene–allene system, unrestricted M06-2X computations predict values that are comparable to the CASSCF and CASPT2 methods.

Having established the energetics and mechanism of reactions of allene with butadiene and benzene, we conclude by comparing these results to previously reported studies of the dienes with ethylene and acetylene^17,38,39 (Figure 14). The Diels–Alder reactions of allenes, with both butadiene and benzene, have higher activation barriers than their diatomic counterparts. The reactions of ethylene and acetylene with butadiene have a barrier of 22.4 kcal/mol for the concerted cycloaddition, 5.3 kcal/mol lower than that for allene. With benzene, reactions with ethylene and acetylene have reported barriers of 31.9 and 35 kcal/mol, respectively. An allene dienophile raises the activation barrier to 37.1 kcal/mol. Despite the destabilizing cumulated double bonds of allene, computations suggest diminished reactivity toward dienes relative to the [4 + 2] reaction of ethylene and acetylene.

Figure 14.

Table of activation energies (kcal/mol) for the concerted Diels–Alder reaction of butadiene and benzene with unsaturated dienophiles. (a) Calculated using B3LYP/6-31G(d).³⁸ (b) Experimentally derived³⁹ (c) Calculated using MP2/6-31G(d).^17a

Conclusions

The cycloaddition reactions of allene with butadiene and with benzene have been elucidated using multiconfigurational CASPT2 calculations. Although the reactions investigated here are not explicitly observed experimentally due to the presence of more favorable processes (allene oligomerization) or decomposition under the required reaction conditions (high temperatures), many substituted analogues have resulted in successful Diels–Alder cycloadditions. Reaction with butadiene occurs through a single ambimodal transition state that can proceed to product along both concerted and stepwise pathways, although inclusion of entropy may ultimately favor the latter. If a diradical intermediate is formed, either the (2 + 2) or (4 + 2) cycloadduct can result; the (2 + 2) adduct can reversibly ring-open to yield the diradical and proceed to the more thermodynamically stable (4 + 2) product.

Conversely, the loss of aromaticity largely affects the reaction profile of benzene and allene cycloaddition; the propensity of benzene to retain aromaticity prompts the cycloaddition of allene and benzene to occur through a concerted yet asynchronous mechanism, forming both σ-bonds simultaneously through a pericyclic transition state. The resulting cycloadduct also suffers from the disruption of aromaticity, causing a large decrease in reaction exothermicity relative to the butadiene–allene system. In lieu of computationally intensive CASSCF optimizations, unrestricted DFT methods can be also used to model such systems, but care must be taken when applying them to cycloadditions of aromatic compounds with allenes. Additionally, molecular dynamics simulations on the butadiene-allene Diels–Alder reaction may increase our understanding of possible ambimodal transition states and subsequent bifurcations in allene chemistry.

Supporting Information Available

All computational data, including CASPT2, CASSCF, and DFT energies and optimized structures. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States