ADAPTIVE CONTROL OF CENTER OF MASS (GLOBAL) MOTION AND ITS JOINT (LOCAL) ORIGIN IN GAIT

Abstract

Dynamic gait stability can be quantified by the relationship of the motion state (i.e. the position and velocity) between the body center of mass (COM) and its base of support (BOS). Humans learn how to adaptively control stability by regulating the absolute COM motion state (i.e., its position and velocity) or by controlling the BOS (through stepping) in a predictable manner, or by doing both simultaneously following an external perturbation that disrupts their regular relationship. Post repeated-slip perturbation training, for instance, older adults learned to forward shift their COM position while walking with a reduced step length, hence reduced their likelihood of falls. How and to what extent each individual joint influences such adaptive alterations is mostly unknown. A three-dimensional individualized human kinematic model was established. Based on the human model, sensitivity analysis was used to systematically quantify the influence of each lower limb joint on the COM position relative to the BOS and the step length during gait. It was found that the leading foot had the greatest effect on regulating the COM position relative to the BOS; and both hips bear the most influence on the step length. These findings could guide cost-effective but efficient fall-reduction training paradigm among older population.

Introduction

A vital functional plasticity of human locomotion lies in its ability to make motor adaptations in the adaptations to guarantee stability. Dynamic gait stability can be characterized and quantified by the relationship of the motion state (i.e. the position and velocity) between the body center of mass (COM) and its base of support (BOS) (Armpatzis et al., 2011; Hof et al., 2005; Yang et al., 2009). After encountering perturbation that commonly occurs in everyday living, a person must maintain his/her body at a stable condition by adjusting his or her (absolute) COM motion state or altering the BOS (through modified stepping), or doing both at the same time. The BOS is the area under the stance foot while it becomes the outline area under and between both feet during double-stance phase in gait (more on this definition can be found in Online Supplement). Post repeated-slip exposure in laboratory observations (Bhatt et al., 2006; Cham and Redfern, 2002a), for instance, older adults would adaptively shift their COM anteriorly relative to the BOS at step touchdown (TD) in walking while simultaneously shorten their step length. Such alterations make their gait pattern more robust and stable, because they can well sustain the next slip should it occur unknowingly again without falling backward – the direction of vulnerability, from anatomical and functional perspectives.

How will such (global) objectives pertaining to the COM and BOS be achieved at joint (local) level? Given the large number of mechanical degrees-of-freedom (DOF) of the human body segments, these adaptive alterations in gait pattern could theoretically be achieved by an infinite number of options (i.e. the combinations of changes in joint angles) as eloquently addressed by Bernstein (Bernstein, 1967). Too many options are not necessarily desirable, because it may require great complexity in the control of these movements (Bernstein, 1967). Hence, it is also suggested that for movements that involve multiple body segments, vast options may be reduced to a small set of variables (Sadeghi, 2003; Soechting and Lacquaniti, 1981). The question arises should the central nervous system (CNS) organize or simplify the adaptive control of the body degrees of freedom in accordance with physical rules?

Before such question can be addressed satisfactorily, the physical rules themselves must be clearly formulated. It was found that subjects, after perturbation training, would land foot more flat (Cham and Redfern, 2002a; Marigold and Patla, 2002) with more knee flexion (Cham and Redfern, 2002a) at TD than the pre-training gait. As mentioned above, body COM is directly related to joint angles. It is possible that these changes in lower limb joint kinematics took place because they are more suitable than others to affect COM position and step length in that joint configuration (posture). The impact to global changes in the COM motion state or changes in step length may vary from one joint to another. A physical rule can be such that those joints bearing greater kinematical advantage should be more active (with greater change in motion) than the others. Before such hypothesis can be tested, however, a clear picture on how each individual joint influences on and contributes to the body COM position relative to the BOS and step length will provide us useful insights to understand each joint’s (or lack of) kinematical advantage.

The purposes of this study was to develop an approach to investigate the influence of each individual lower limb joint on COM position relative to BOS and step length during gait. It has been identified that gait stability (Bhatt et al., 2011) and foot kinematics (Cham and Redfern, 2002b) at TD may differentiate ones with high risk of falls from others. Therefore, our study would focus on the instant of TD. The findings from the present study could provide insights into the underlying mechanisms of adaptive changes in gait pattern after the perturbation training.

Methods

2.1 Human model and sensitivity analysis

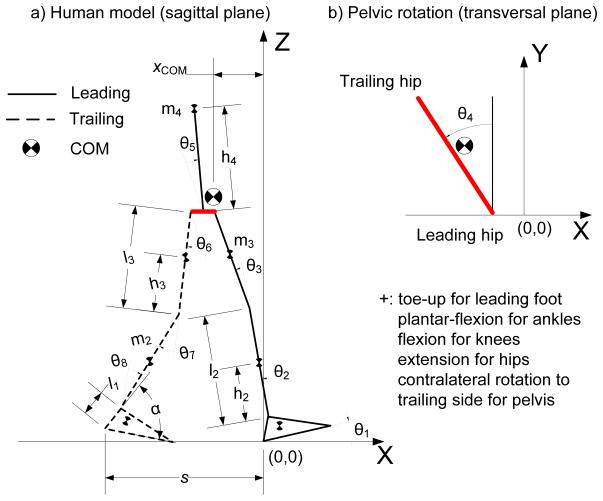
A three-dimensional human biomechanical model comprised of eight rigid body segments was developed (Fig. 1). The segments included a lumped head, arms, and trunk (HAT) segment as well as both feet, legs, thighs, and a segment connecting both hip joints. This mass-less link segment between hips was for considering the effect of pelvic rotation on the COM position and step length (Fig. 1b). For each subject, the anthropometric parameters for every segment were computed using the gender-dependent segmental inertial parameters based on the experimental data (see below) (de Leva, 1996). The body COM position (x_COM) relative to the BOS (i.e. the leading heel) and the step length (s) during walking were analytically represented as the functions of the segment anthropometric parameters and joint angles (see Online Supplement for derivation). Both feet were excluded when calculating the COM position due to their negligible mass ratio (1.4%) (Winter, 2005). The functions for the COM position relative to BOS and step length were,

Fig. 1.

a) the sagittal plane and b) transverse plane of the schematic of the eight-link, three-dimensional, model of the human body with leading heel at the point of (0, 0, 0). Solid thick and dashed line respectively represents the leading and trailing sides of the body. The model includes a lumped head, arms, and trunk (HAT) segment as well as both feet, legs, thighs, and a segment connecting both hip joints. This link segment between hips, which was mass-less, was for considering the effect of pelvic rotation on the step length. α is the angle formed by the line connecting ankle and heel and the sole. Its value is fixed for each individual subject, but may vary among subjects. The segmental length and mass and the position of each segment’s center of mass (COM) were calculated for each individual subject. The COM position (x_COM) is represented relative to the base of support (BOS, i.e. the leading heel). The step length (s) is calculated as the distance between two heels in the anteroposterior direction at the instant of touchdown. Joint angles θ_i (i = 1, 2, 3, …, 8) specify the angles of the leading foot, leading ankle, leading knee, pelvic rotation, leading hip, trailing hip, trailing knee, and trailing ankle, respectively. On the leading side, the positive direction of the rotation axes is along the negative Y-axis (laterally to the leading side), but for the trailing side of the body the joint axes were in the direction of the positive Y-axis (laterally to the trailing side). The positive direction of the pelvic rotation is along the positive Z-axis. The positive X-axis is the direction of forward progression, the positive Y-axis is leftward, and the positive Z-axis is upward.

$$\begin{array}{l}{x}_{\text{COM}}=x_{\text{COM}}\left({\theta }_{1,2,3,\cdots ,7}\right)\\ =l_{1}cos({\theta }_1+\alpha )+\frac{\begin{array}{l}{m}_2\left[\begin{array}{l}-(h_2+l_2)sin({\theta }_1+{\theta }_2)-l_{3}sin({\theta }_1+{\theta }_2+{\theta }_3)\hfill \\ -l_{4}sin{\theta }_4-l_{3}sin({\theta }_6-{\theta }_1-{\theta }_2-{\theta }_3-{\theta }_5)\hfill \\ -(l_2-h_2)sin({\theta }_6+{\theta }_7-{\theta }_1-{\theta }_2-{\theta }_3-{\theta }_5)\hfill \end{array}\right]\\ +m_3\left[\begin{array}{l}-2l_{2}sin({\theta }_1+{\theta }_2)-(h_3+l_3)sin({\theta }_1+{\theta }_2+{\theta }_3)\hfill \\ -l_{4}sin{\theta }_4-(l_3-h_3)sin({\theta }_6-{\theta }_1-{\theta }_2-{\theta }_3-{\theta }_5)\hfill \end{array}\right]\\ +m_4\left[\begin{array}{l}-l_{2}sin({\theta }_1+{\theta }_2)-l_{3}sin({\theta }_1+{\theta }_2+{\theta }_3)-\frac{1}{2}{l}_{4}sin{\theta }_4\hfill \\ -h_{4}sin({\theta }_1+{\theta }_2+{\theta }_3+{\theta }_5)\hfill \end{array}\right]\end{array}}{2m_2+2m_3+m_4}\end{array}$$ (1)

$$\begin{array}{l}s=s\left({\theta }_{1,2,3,\cdots ,8}\right)\\ =-l_{1}cos({\theta }_1+\alpha )+l_{2}sin({\theta }_1+{\theta }_2)+l_{3}sin({\theta }_1+{\theta }_2+{\theta }_3)+l_{4}sin{\theta }_4\\ +l_{3}sin({\theta }_6-{\theta }_1-{\theta }_2-{\theta }_3-{\theta }_5)+l_{2}sin({\theta }_6+{\theta }_7-{\theta }_1-{\theta }_2-{\theta }_3-{\theta }_5)\\ +l_{1}cos(\alpha -{\theta }_6-{\theta }_7-{\theta }_8+{\theta }_1+{\theta }_2+{\theta }_3+{\theta }_5)\end{array}$$ (2)

where θ_i (i = 1, 2, 3,…, 8) respectively specified the joint angle of the leading foot, leading ankle, leading knee, pelvic rotation, leading hip, trailing hip, trailing knee, and trailing ankle. l₁ represented the distance between ankle and heel. l₂ and l₃ were the segmental length of the leg and thigh, respectively.l₄ depicted the width of the pelvis. h_i (i = 2, 3, 4) respectively indicated the distance from the distal end to the segmental COM of the leg, thigh, and HAT. m_i (i = 2, 3, 4) respectively was the segmental mass of the leg, thigh, and HAT. α was the angle formed by the line connecting ankle and heel and the sole (Fig. 1).

By taking the COM position’s and step length’s partial derivatives with respect to each joint angle, the sensitivity of COM position and step length to each joint angle could be obtained as Eqs. (3–4). The sensitivity quantifies the extent to which the COM position or step length changes in response to the increment in the joint angle by one unit (i.e. one degree).

$$c_i=\frac{\partial x_{\text{COM}}}{\partial {\theta }_i}i=1,2,3,\cdots ,7$$ (3)

$$e_i=\frac{\partial s}{\partial {\theta }_i}i=1,2,3,\cdots ,8$$ (4)

2.2 Subjects and experimental protocol

A pool of 73 community-living healthy older adults (72.6±5.4 years) giving written informed consent participated in this study (Yang and Pai, 2013). All subjects underwent approximately 10 normal walking trials on a 7-m walkway. Beneath the walkway, there were four force plates (AMTI, Watertown, MA) recording the ground reaction force (GRF) (Yang and Pai, 2007). The last trial was selected to represent the regular spontaneous gait. Full body kinematics data from 26 retro-reflective markers placed on the subjects’ body were gathered using an 8-camera motion capture system (MAC, Santa Rosa, CA) synchronized with the force plates.

2.3 Data reduction

Marker displacement data were low-pass filtered at marker-specific cut-off frequencies (range 4.5–9 Hz determined through a residual analysis) (Winter, 2005) using fourth-order Butterworth filters. Three dimensional locations of joint centers, heels, and toes were computed from the filtered marker positions. The angles for all eight joints (Fig. 1a) at TD were computed from the joint centers and then input to Eqs. (3–4) to calculate all sensitivities. TD was identified from GRF: a vertical force greater than 10N corresponds to TD of that foot (Ghoussayni et al., 2004).

Results

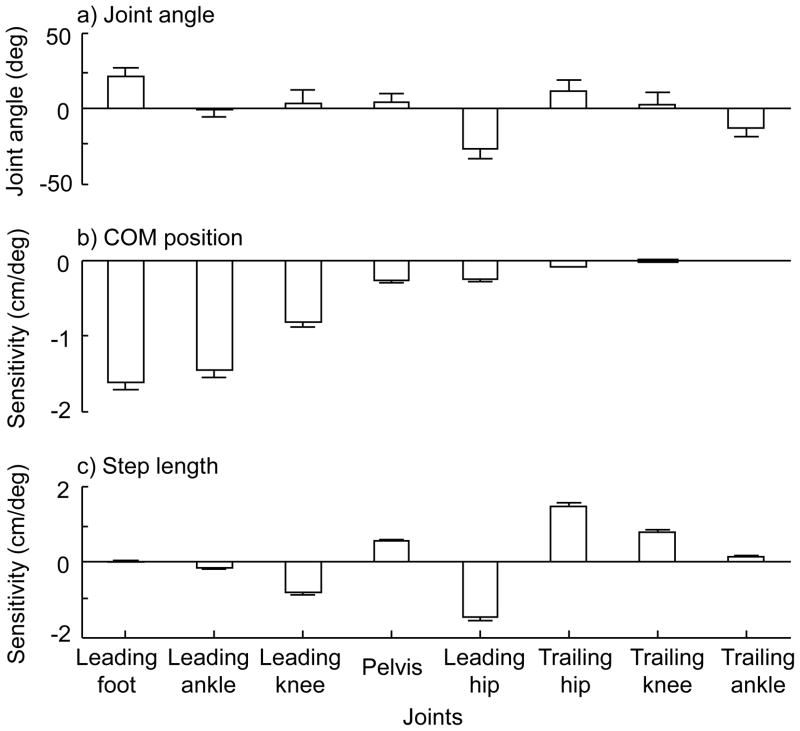
Our sensitivity analysis revealed that the leading foot angle had the greatest influence on the COM position at TD. A unit decrease in the leading foot angle (i.e. more flatfoot landing by one degree) would result in approximately 1.62±0.10cm forward movement of the COM position relative to the BOS (Fig. 2b). Following the leading foot, the leading ankle and leading knee both had significant influence on COM position at TD. A unit more plantar-flexion in the leading ankle angle would move the COM posteriorly by 1.46±0.09cm (Fig. 2b). A unit more flexion in the leading knee resulted in 0.82±0.06cm backward movement of the COM position relative to the BOS (Fig. 2b). Other joint angles had relatively small influence on COM position (ranging from −0.01 to −0.28cm/deg, Fig. 2b).

Fig. 2.

Group means (column height) and standard deviations (bar) of a) angles of all joints at the instant of leading foot touchdown (TD), b) the sensitivity of the body center of mass (COM) position relative to the base of support to the changes in angle of the leading foot, leading ankle, leading knee, the pelvis, the leading hip, trailing hip, trailing knee, and trailing ankle at TD, and c) the sensitivity of the step length to changes in angle of the leading foot, leading ankle, leading knee, the pelvis, the leading hip, trailing hip, trialing knee, and trailing ankle at TD.

Both hip joints had the greatest impact on the step length at TD (Fig. 2c). A unit more flexion in the leading hip angle could cause 1.45±0.10cm increase in the step length (Fig. 2c). However, a unit reduction in the extension of the trailing hip joint would result in the same amount in step length reduction (Fig. 2c). A unit increase of flexion at the leading knee caused reduction in step length with the magnitude of 0.81±0.07cm (Fig. 2c). Conversely, a unit increase of flexion at the trailing knee led to increase in step length with the level of 0.78±0.06cm. The influence of the pelvis rotation on step length was 0.55±0.05cm/deg. That means a unit less pelvic rotation would result in 0.55cm decrease in the step length. Other joints’ effects on the step length varied from −0.16 to 0.0001cm/deg (Fig. 2c).

Discussion

Human lower extremity joints are not born with equal functionality in locomotion. The nature of multiple DOF affords a person many movement options. The present study has demonstrated how each individual lower limb joint influences on the COM position relative to the BOS and the step length at TD during gait based on a kinematic human model with the aid of sensitivity analysis. The findings indicated that the leading foot influenced the COM position relative to the BOS the most; and both hip joints had the greatest effect on regulating the step length.

It has been reported that repeated-slip exposure enabled young and older adults to proactively improve their stability before slip occurrence (Pai and Bhatt, 2007). It was postulated that the reduced foot angle decreases one’s reliance on floor friction for braking forward momentum when the slip occurs, thereby reducing the peak slip velocity the subject experiences during the slip (Chambers and Cham, 2007). The results in the present study provided us a kinematic perspective to view these adaptive changes in foot landing. Because the leading foot is the joint bearing the most significant influence on the COM position relative to the BOS (Fig. 2b), the body adopted the most effective way to adjust the COM position at touchdown after perturbation training. Such adjustment shifted the COM anteriorly and consequently to increase the COM dynamic stability in order to avoid backward balance loss and falls (Yang and Pai, 2013). Our findings provided analytical insights that the leading foot angle is indeed the joint possessing the greatest influence on COM position relative to BOS at TD. The agreement between the empirical (the experimental observations) and the analytical findings (from the present study) indicates that the CNS was able to select the most effective way from all options to alter the post-training COM position relative to the BOS in order to keep body stable.

There is also empirical and analytical agreement that the more flexed the leading knee joint upon the post-training gait reduces the slip severity by reducing the demand on friction from GRF (Cham and Redfern, 2002a; Yang and Pai, 2010). The results in the present study demonstrated that the more flexed leading knee has a significant effect in reduce the step length (Fig. 2c). A short step could reduce its severity in case of a slip, because it would require a less forceful push off from the trailing limb during double stance phase that in turn would exacerbate the initiation of slip. Therefore, a short step length would reduce the severity of a slip (Lockhart et al., 2003; Moyer et al., 2006). However, the more flexed leading knee has the negative effect of moving COM backward relative to the BOS which would make one less stable (Fig. 2b). Given the contradictory effects of the leading knee on influencing the COM position and step length, the human motor control system must take an optimal strategy to adjust the knee flexion to maximize its overall effect in improving the fall-resisting capability. Such optimal control mechanisms merit further research effort.

The pelvic rotation during walking has been identified as a determinant of gait (Inman, 1966). The pelvic rotation produces a longer step length for the same amount of hip flexion of the leading leg and hip extension of the trailing leg. Our results support this argument. In this study, the sensitivity of the step length to the pelvic rotation is around 0.55cm/deg (Fig. 2c). The pelvic rotation has also detectable effect on the COM position at the level of −0.28cm/deg. Given such a significant influence of the pelvic rotation on step length and COM position, the human model developed in the present study is a better predictor of step length and COM position than a simple limb-based sagittal model (Jamshidi et al., 2009).

In summary, our results revealed that the developed approach was able to examine the influence of each individual lower limb joint on COM position relative to the BOS and the step length. The findings will assist us in developing simple but efficient fall-prevention training paradigm aiming at the older population.