Abstract
One of the main perceived advantages of using a case-cohort design compared to a nested case-control design in an epidemiologic study is the ability to evaluate with the same subcohort outcomes other than the primary outcome of interest. In this paper, we show that valid inferences about secondary outcomes can also be achieved in nested case-control studies by using the inclusion probability weighting method originally proposed by Samuelsen (1997) in combination with an approximate jackknife standard error that can be computed using existing software. Simulation studies demonstrate that when the sample size is sufficient, this approach yields valid type 1 error and coverage rates for the analysis of secondary outcomes in nested case-control designs. Interestingly, the statistical power of the nested case-control design was comparable to that of the case-cohort design when the primary and secondary outcomes were positively correlated. The proposed method is illustrated with data from a cohort in Cardiovascular Health Study to study the association of C-reactive protein levels and the incidence of congestive heart failure.
Keywords: Incidence density sampling, Nested case-control design, Secondary outcomes
INTRODUCTION
The case-cohort and the nested case-control designs are two of the most widely used approaches for reducing the costs of exposure assessment in a prospective epidemiologic study since exposure and other covariate data are obtained on only a subset of the full cohort yet without much loss of efficiency. Case-cohort designs include all cases and a randomly selected sub-cohort from the risk set at baseline [1]. Nested case-control designs (or equivalently, incidence density sampling designs) include all cases and a pre-specified number of controls randomly chosen from the risk set of each failure time [2]. Both approaches require a clear specification of a primary outcome that is used to define case status.
After an initial study of the primary outcome is complete, however, it is common for new hypotheses to be generated about the association of the main exposure of interest with another outcome. For example, in a study of breast cancer patients in which the primary outcome is mortality, distant metastasis may also be of interest as a secondary outcome. The use of the same study to evaluate the secondary outcome is clearly cost-effective, and even when the power for this outcome is not optimal, relative risk estimates can still be used as preliminary data to design a future larger scale study. One of the commonly known advantages of the case-cohort study is that the same sub-cohort can be used to analyze multiple outcomes [3]. However, methods for analyzing secondary outcomes in nested case-control studies are lacking in the literature. As a result, there has not been any report in the epidemiological literature of secondary outcome analysis in nested case-control studies using Cox proportional hazards model.
Nested case-control studies are almost exclusively analyzed by means of the conditional logistic regression approach of Thomas [2] but this approach cannot be applied to evaluate secondary outcomes. Among 16 nested case-control studies published in the American Journal of Epidemiology between 2009 and 2011, fourteen were analyzed with the conditional logistic regression approach of Thomas and the other two with unconditional logistic regression (Supplementary Table 1).
Samuelsen [4] proposed an alternative method for analyzing nested case-control studies in which the individual log-likelihood contributions are weighted by the inverse of the inclusion probabilities of ever being included in the nested case-control study. This method was shown to be more efficient than the conditional logistic regression approach. Chen [5, 6] considered the same form of the likelihood, but refined the weights by averaging the observed covariates from subjects with similar failure times to estimate the contribution from unselected controls.
Recently, Salim et al [7] showed that efficiency can be gained in a nested case-control study by applying inverse probability weighting method to reuse controls from another nested case-control study. However, their samples always include all secondary cases in the full cohort. In addition, they considered Weibull failure time model and not the commonly used Cox proportional hazards model.
In this paper, we demonstrate that the inverse probability weighting method can also be applied to obtain valid inferences about secondary outcomes in nested case-control studies using Cox proportional hazards model. This is possible with or without augmenting secondary cases. We propose an approximate jackknife standard error of log hazard ratios that is readily computable with existing software. Moreover, we show empirically that the statistical power of nested case-control designs is even higher than that of case-cohort studies when the primary and secondary outcomes are positively correlated. The methods are illustrated using data from a blood biomarker study examining the association of circulating C-reactive protein levels with risk of incident cardiovascular disease events in a longitudinal cohort study of older adults [8].
METHODS
Consider a cohort of N subjects who are followed for the occurrence of a primary outcome, denoted as failure event “A”. Assume that the ith subject (i=1…N) enters the study at time ai. Let denote the time to failure for event A of the ith subject, Ci denote the censoring time that is independent of , and denote the observed time. Assume the hazard function (t) of the failure time for the ith subject follows the proportional hazards model
| (1) |
where (t) is the baseline hazard function, βA is the parameter vector of interest, and Xi(Yi) is a time-dependent covariate vector for the ith subject. Then, inferences are typically made by maximizing the Cox partial likelihood:
| (2) |
Where if subject i failed during the study and 0 otherwise; is the set of subjects at risk in the underlying cohort at time .
In nested case-control studies, m controls are sampled from without replacement at each where = 1, i.e., for each case, m controls are randomly selected from the subjects still at risk at the time of the failure of the case. Notice that the controls may include both failures and non-failures. Let Si denote this set of m controls and denote all subjects who were included in the nested case-control study. Then is the set of subjects included in the nested case-control study who are at risk at time . For estimation of βA, Samuelsen [4] proposed maximizing the following partial-likelihood:
| (3) |
where , and is the probability that subject i is included in the nested case-control study.
Samuelsen calculated the inclusion probabilities in a nested case-control study assuming no additional matching factors. To provide a more general form of the inclusion probability that accounts for ties and matching (or stratification) on additional factors, let Hi denote the set of subjects in the underlying cohort with the same matching variables as subject i. The probability that subject i is included in the nested case-control study can be expressed as the following:
| (4) |
where kji is the size of , the number of subjects at risk at with the same values of the matching variables as subject i, and bji is the number of tied subjects in Hi that failed exactly at . In the absence of additional matching variables or ties in failure times, the inclusion probability simplifies to that of Samuelsen [4]. The calculation of minimum in (4) is for the late failure times when all subjects in are sampled because kji−bji < m bji.
Now consider a secondary outcome of interest denoted as event “B” with failure time and observed time . We note that competing risks are not considered and thus both and are always observable. Let be the set of subjects at risk at and denote the subjects in the original nested case-control study who are at risk at . As in the primary outcome analysis, assume follows a proportional hazards model where βB is the parameter vector of interest. For the secondary outcome analysis, we propose maximizing the following partial likelihood:
| (5) |
where if subject i had failure event “B” during the study and 0 otherwise . Notice that while each weight (or inverse of the inclusion probability) in the denominator is determined by the design of the nested case-control study based on the primary outcome, i.e., , the risk set is defined by the secondary outcome.
For the primary outcome, Samuelsen [4] proved consistency of the estimator and demonstrated asymptotic normality by simulation studies. Since the proof does not depend on whether the inclusion probabilities were determined by the primary or secondary outcomes, the inclusion probability weighting method is also valid for secondary outcomes. In addition, we note that since the matching used in creating the original case-control sets is ignored in the secondary analysis, any matching factors that could affect the secondary outcome should be controlled for by including them as additional covariates or stratification factors in the regression model.
STANDARD ERROR ESTIMATION
Samuelsen [4] and Chen [6] both derived asymptotic variances for βA, but the formulas are complex and cannot be computed using commonly available statistical software. We propose an approximate jackknife variance estimator that can be computed using existing software. We note that although we show the standard error estimator for the secondary outcome analysis, the proposed standard error can also be used in primary outcome analysis by defining risk sets based on the primary outcome. Following Therneau’s approximate jackknife argument in a full cohort [9], we avoid iterative refitting of the model by first estimating the βB by a Newton-Raphson algorithm, and performing just one more iteration after deleting subject i to get . The estimating equation resulting from is the following:
where is the weighted average of the covariates. We define as the score residuals of ith subject and jth covariate. Notice that would be the typical score residual for Cox’s partial likelihood if were the frequency weight. We simplify the notation by defining the score residual matrix so that the score vector is where Λw is the diagonal matrix of weights and z is the vector of 1’s. Following Therneau [9], we will call dfbeta where Iw = −∂Uw/∂β B is the negative Jacobian. The amount of change of the estimate in each iteration is . Removing subject i and recalculating score residuals while fixing Iw is equivalent to removing Di, the ith row from D. Therefore −Di is the approximate value for and the approximate jackknife variance estimator is
| (6) |
The approximate jackknife estimation approach in the full cohort Cox model was first discussed by Reid and Crepeau [10]. Lin and Wei [11] also derived it as a sandwich estimator to account for model misspecification without using the jackknife argument; consistency was shown in cohort data. In more recent work, Samuelsen [12] proposed a similar standard error for nested case-control studies that is computationally easy to estimate.
The proposed standard error (5) is readily computable using existing software provided it can accommodate frequency weights in the Cox procedure for a full cohort study and can calculate the covariance matrix of linear coefficients and the score residuals. Examples of the computation using R and SAS software are in the Appendix.
COMPARISON WITH THE CASE-COHORT DESIGN
Case-cohort studies include all cases and a randomly selected sub-cohort from the risk set at baseline [1]. Since the proportion of the underlying cohort that comprises the sub-cohort is fixed at, say π, the probability that subject i is included in the study is the following:
For estimation of βA in case-cohort studies, we have shown [13] that the inclusion probability method to maximize the same form of the partial-likelihood (3) where is more powerful than the methods by Prentice [1], Barlow [14], or Self & Prentice [15]. In the current simulation studies and the examples below, βB for the secondary outcome in the case-cohort design was estimated the same way as in the nested case-control studies by maximizing the partial likelihood for the secondary outcome (5).
SIMULATION STUDIES
Bivariate exponential failure times (TA, TB) with correlation coefficient ρ and marginal failure rates exp(βA,1X1+βA,2X2) and exp(βB,1X1+βB,3X3) were generated for full cohorts of size N = 1,000 or 2,000 using the strategy detailed in the Appendix. In addition, X1, the main exposure variable of interest, was assumed to be distributed as a standard normal variable, and X2 and X3 were specified as independent Bernoulli variables with success probability of (1+exp(−X1))−1. The distribution of covariates was set up so that a mild multicollinearity existed and the marginal failure rates depended on a different set of covariates for the primary and secondary outcomes. The true log hazard ratios were set as βA,1=βB,1=0.5 and βA,2=βB,3=(1−ρ)0.5. The correlation coefficient, ρ, between failure times of the primary and secondary outcomes assumed values of 0, 0.2, 0.4… 1.0. Censoring times were uniformly distributed between 0 and c. The upper limit of censoring and intercepts were varied so that the proportion of failures was 10% for the primary outcome and 5%, 10%, or 20% for the secondary outcomes in the full cohort. For each subject, either the failure or censoring time was observed, whichever occurred earlier. The log hazard ratios of the secondary outcome and their standard errors in the full cohort were estimated under the Cox proportional hazards model.
Nested case-control samples were than selected with varying numbers of controls, m = 1, 2, or 5, at each failure time TA of the primary outcome. When each nested case-control sample was selected, a case-cohort sample was also selected, again based on the primary outcome. To force the average sample size of the two designs to be the same, the case-cohort sample consisted of all failures for the primary outcome as well as a subcohort selected with a sampling proportion equal to the number of non-failures in the nested case-control sample divided by the number of non-failures in the full cohort. For simplicity, additional matching factors were not used in the simulation studies. Supplementary Figure 1 shows the number of secondary cases included in the nested case-control study averaged over 5,000 nested case-control samples. The number of primary cases in the full cohort, and thereby in the nested case-control studies, is fixed by design at 10% of the size of the full cohort (the bold solid line). The number of secondary cases in the nested case-control study increased as ρ, the correlation between the primary and secondary outcomes, or the prevalence of the secondary outcome increased. Notice that when the prevalence is high, there may be more secondary cases than the primary cases.
For each simulated nested case-control data set, the log hazard ratios for the secondary outcome were estimated according to the partial likelihood for the secondary outcome (5) along with the proposed approximate jackknife standard errors (6). Each case-cohort data set was analyzed as described above. We also created ‘augmented’ nested case-control data sets by adding in all remaining failures for the secondary outcome in the underlying cohort that were not part of the original nested case-control sample. ‘Augmented’ case-cohort samples were constructed by adding the same number of failures. The augmented samples were analyzed similarly with the weights for the augmented secondary cases set as one.
This overall process including the generation of the full cohort, nested case-control sample, case-cohort sample, and the corresponding augmented samples was repeated 5,000 times. For the estimation of empirical type 1 error, the overall process was repeated 20,000 times.
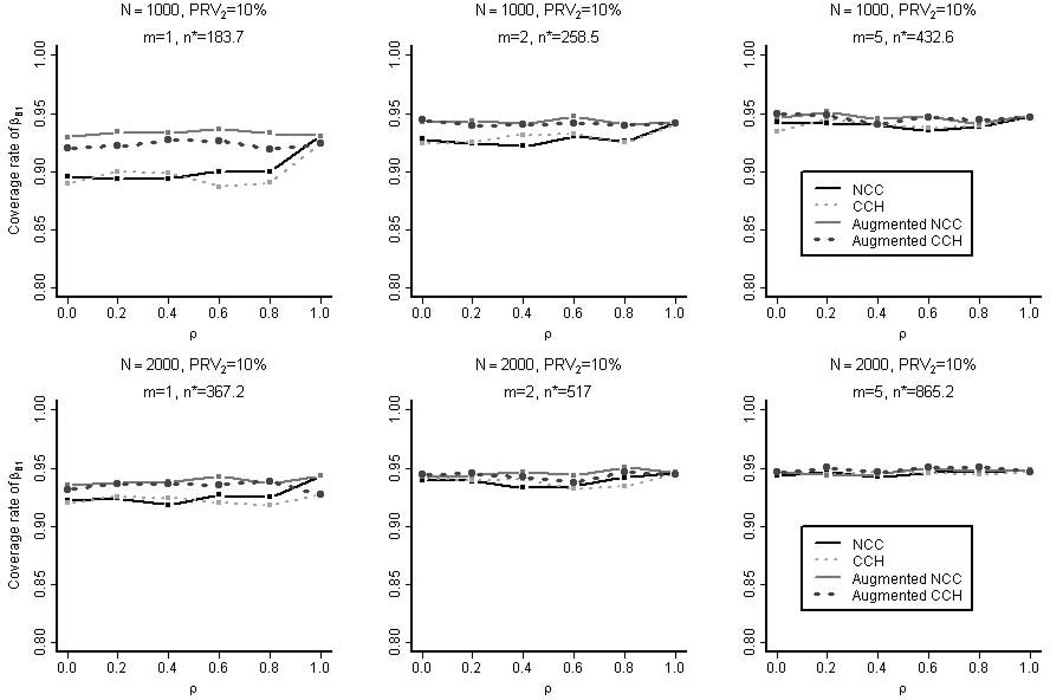
When the prevalence of the secondary outcome was 10%, Figure 1 shows the coverage rate of the 95% confidence intervals for βB,1 (log hazard ratio for the secondary outcome) for the four types of designs considered: nested case-control, case-cohort, augmented nested case-control, and augmented case-cohort. The coverage rates were all close to 95% except for the smallest sample sizes considered (m=1 without augmentation and ρ ≤ 0.8). In this case, there were less than fifty secondary failure events in both the nested case-control and case-cohort designs. The inadequate coverage rates in these instances were in part due to the absence of terms in the approximate jackknife standard errors for reducing the small sample bias. Supplementary Figure 2 shows the empirical coverage rate based on the nested case-control studies selected from the full cohorts with varying degrees of prevalence of the secondary outcome (PRV2=5%, 10%, or 20%). The prevalence of the primary outcome was fixed at 10%. The samples typically showed better coverage rates when they were selected from the cohorts with higher secondary prevalence or higher correlation between the two outcomes. This is due to the large number of secondary cases in the selected samples. However, when there were too many secondary cases in the samples, even more than the controls, the coverage rates were negatively affected (e.g. when ρ > 0.8 and secondary prevalence at 20%).
Figure 1. The Empirical Coverage Rate in the Simulation Studies.
The empirical coverage rate of the 95% confidence intervals for βB,1 (log hazard ratios for secondary outcomes) for the four types of samples is shown: nested case-control (NCC), case-cohort (CCH), augmented nested case-control, and augmented case-cohort. These samples were selected from the full cohorts with 10% prevalence of the secondary outcome (PRV2). n* is the average overall size of the un-augmented nested case-control samples.
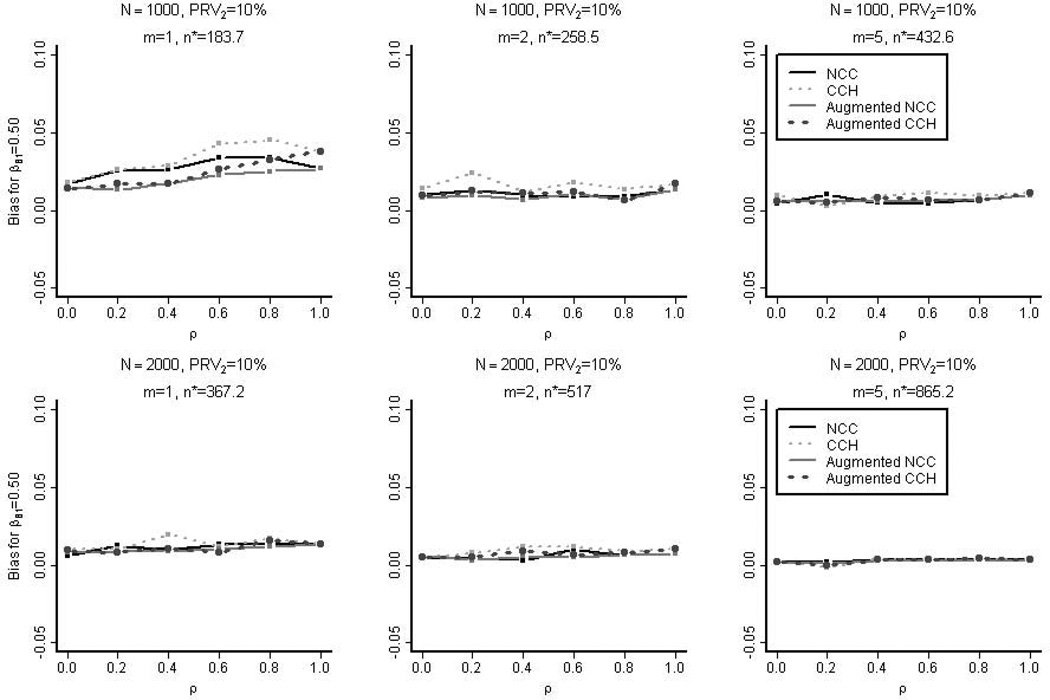
Figure 2 shows the bias in estimating βB,1=0.5. The nested case-control estimates were less biased than the case-cohort estimates. The bias was at most approximately 6% when the number of secondary cases was small (< 50) and became negligible as the sample size increased.
Figure 2. The Empirical Bias in the Simulation Studies.
The empirical bias in estimating βB,1=0.5 for the four designs is shown: nested case-control (NCC), case-cohort (CCH), augmented nested case-control, and augmented case-cohort. These samples were selected from the full cohorts with 10% prevalence of the secondary outcome (PRV2). n* is the average overall size of the un-augmented nested case-control samples.
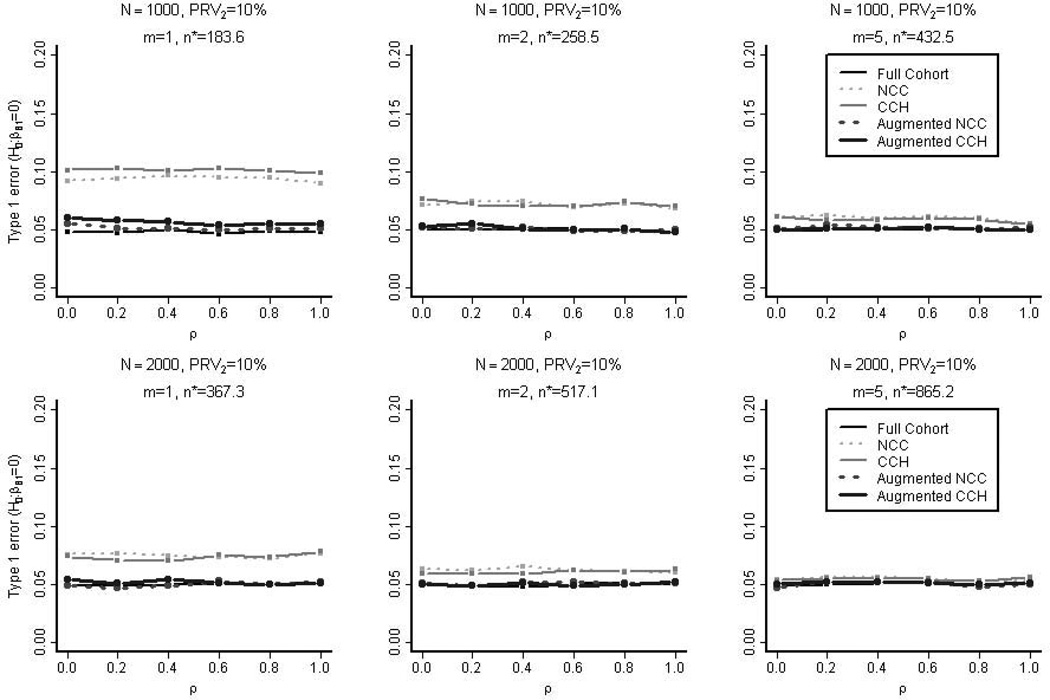
Controlling the nominal type 1 error rate at 0.05, we measured the empirical power and type 1 error rate in testing the null hypothesis H0: βB,1=0 for the four types of study designs as well as for the full cohort. As was the case with the empirical coverage rates, Figure 3 demonstrates that type 1 error rates were close to the nominal rate except when the sample sizes were small (N=1000, PRV2=10%, m=1 without augmentation).
Figure 3. The Empirical Type 1 Error Rate in the Simulation Studies.
Simulation data were regenerated but this time with the true linear coefficient set as βB,1=0. Controlling the nominal type 1 error rate at 0.05, the empirical type 1 error in testing the null hypothesis H0: βB,1=0 were measured for the five types of designs (full cohort, nested case-control (NCC), case-cohort (CCH), augmented nested case-control, and augmented case-cohort). These samples were selected from the full cohorts with 10% prevalence of the secondary outcome (PRV2). n* is the average overall size of the un-augmented nested case-control samples.
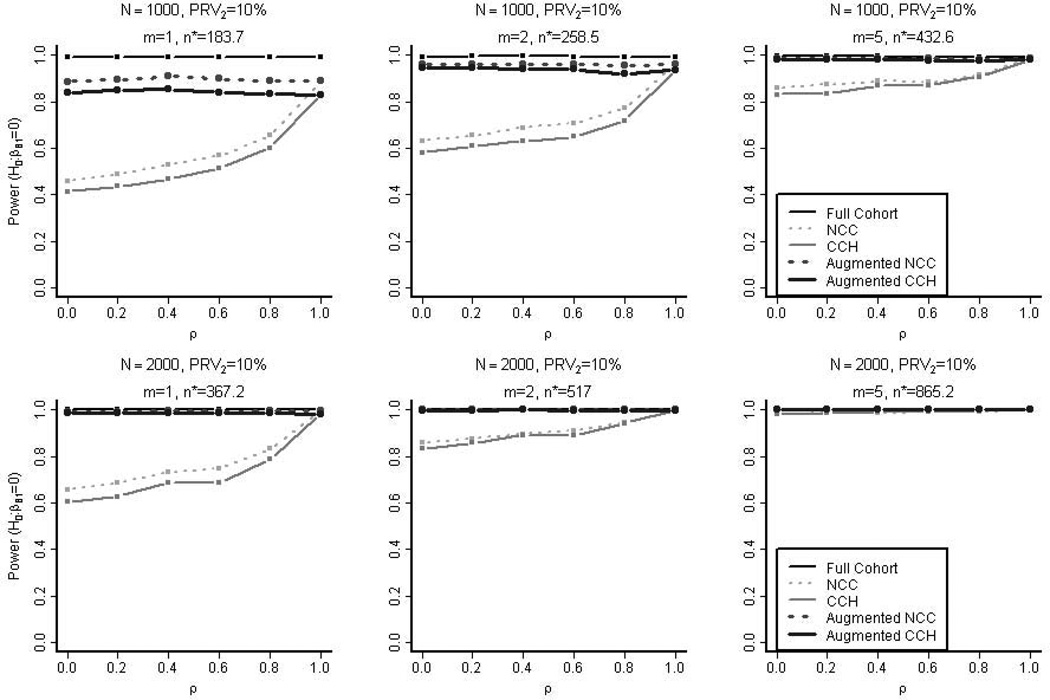
It should be noted that the empirical power of the nested case-control design was higher than that of the case-cohort design in both the augmented and un-augmented samples and across varying magnitudes of the correlation between the primary and secondary outcomes (Figure 4). Both the un-augmented nested case-control and case-cohort designs gained statistical power as the correlation increased since this in turn increased the number of available cases for the secondary outcome. In Figure 4, the empirical power when the sample sizes were small (N=1000, PRV2=10%, m=1 without augmentation) were over estimated because the empirical type 1 error rates were higher than 0.05. Nevertheless, the trends are consistent with our finding that the nested case-control design tends to be more powerful than the case-cohort design in both augmented and un-augmented sample and across varying degrees of correlation between the primary and secondary outcomes. Supplementary Figure 3 shows the empirical power based on nested case-control studies selected from the full cohorts with varying degrees of prevalence of the secondary outcome (5%, 10%, or 20%). Again, the studies sampled from the cohorts with higher secondary prevalence and higher correlation between the two outcomes typically showed higher power due to higher number of secondary cases. However, too many secondary cases, sometimes more than the controls, negatively affected the power (e.g. when ρ > 0.8 and secondary prevalence at 20%).
Figure 4. The Empirical Power in the Simulation Studies.
Controlling the nominal type 1 error rate at 0.05, the empirical power in testing the null hypothesis H0: βB,1=0 is measured for the five types of designs (full cohort, nested case-control, case-cohort, augmented nested case-control, and augmented case-cohort). These samples were selected from the full cohorts with 10% prevalence of the secondary outcome (PRV2). n* is the average overall size of the nested case-control samples without augmentation.
CARDIOVASCULAR DISEASE EXAMPLE
The methods are illustrated using a full cohort data of 5,888 subjects aged 65 years and older who were enrolled in the Cardiovascular Health Study [8]. Follow-up information on clinical outcomes was obtained from semi-annual contacts with participants [16]. For the purpose of this paper, the primary outcome of interest is incident diagnosis of claudication and the secondary outcome is incident diagnosis of congestive heart failure among participants free of these conditions at study enrollment. There were 5,490 subjects who did not experience claudication or congestive heart failure prior to entering the study. The main exposure of interest was circulating concentration of C-reactive protein (x1; in mg/L). The level of C-reactive protein was measured at study enrollment visits by enzyme-linked immunosorbent assay [17]. We excluded subjects who had C-reactive protein level of 10 mg/L or higher, as is conventional in similar studies, to eliminate from analyses individuals with an acute illness that may have produced transient elevations in C-reactive protein levels [18]. We controlled for two additional important variables: the gender (x2; binary) and whether the subject ever smoked (x3; binary). Among the 4,858 subjects who were included in analyses, 279 experienced claudication, 1,585 experienced congestive heart failure, and 163 experienced both during the follow-up phase of the study. Both outcomes were not fatal in this cohort. A small number (36) of subjects experienced congestive heart failure along with other fatal events such as fatal myocardial infarction before experiencing claudication: these subjects were considered censored immediately after congestive heart failures. The full cohort estimate of the log hazard ratio for each 1 unit higher level of C-reactive protein was 0.156 (SE = 0.024) for claudication (βA,1) and 0.093 (SE = 0.011) for congestive heart failure (βB,1), after adjusting for gender and smoking history as additional covariates in the Cox model.
A nested case-control study sample was then created from the full cohort using all cases of claudication, the primary outcome, and randomly choosing two controls (m = 2) per case who were at risk at the time the case developed claudication and further matched the case on the gender (x2) and smoking history (x3). Supplementary Table 2 shows the number of subjects across different strata. This resulted in a total sample size of 756 (279 with claudication). Of these 1,035 subjects, 306 experienced the secondary outcome, congestive heart failure. The log hazard ratio for congestive heart failure was estimated to be 0.088 (SE=0.031) using the proposed partial likelihood for the secondary outcome (5) and the approximate jackknife standard error (6). In comparison, a naïve estimate based on the Cox proportional hazards model without using the inverse probability weighting approach was further away from the full cohort estimate (log HR = 0.129; SE = 0.024).
Again, five thousand nested case-control samples were repeatedly selected from the full cohort with varying numbers of controls (m=1, 2, 5) matched on gender and smoking history to each case of claudication, and analyzed using the aforementioned methods. Case-cohort samples with the same average sample size and stratified on gender and smoking history were also generated and analyzed using the method described above.
The empirical bias for the log hazard ratio for the secondary outcome, congestive heart failure, was calculated as the average difference between the full cohort estimate and either the nested case-control or case-cohort estimates. Both the nested case-control and case-cohort designs yielded estimates with low empirical bias (<2.2% of the full cohort estimate of the log hazard ratio; Table 1), which is consistent with the results from the earlier simulations studies. In comparison, the average bias of the naïve unweighted Cox estimates was ten to fourty times greater than that of the inverse probability weighting methods.
Table 1.
The Empirical Bias for Estimating βB,1 in Cardiovascular Health Study
| m=1 | m=2 | m=5 | |
|---|---|---|---|
| NCC | 0.00092 n*=536.3 |
0.00205 n*=773.9 |
0.00142 n*=1384.9 |
| CCH | 0.00119 n*=535.8 |
0.00114 n*=773.4 |
0.00055 n*=1384.3 |
| Naïve NCC | 0.03348 n*=536.3 |
0.03015 n*=773.9 |
0.01849 n*=1384.9 |
The empirical bias in estimates of log hazard ratio and the sample size (n*) averaged over 5,000 iterations are shown in each cell. The empirical bias was defined as the difference between the estimates and the full cohort estimate. The full cohort estimate of βB,1, the log hazard ratio for the secondary outcome (i.e. congestive heart failure) associated with a one-unit difference in C-reactive protein level, was 0.0925 (SE=0.0111). The last row shows the biases of the naïve Cox estimates.
Table 2 shows the empirical and average estimated standard errors for each sampling design. The empirical variance due to both infinite and finite sampling was estimated by adding the estimated variance for the full cohort estimates to the empirical variance resulting from the simulation. The results again show that the proposed standard error estimator is valid for the nested case-control samples, especially when both the sample size and the number of failures were sufficiently large.
Table 2.
The Empirical and Estimated Standard errors for Estimating βB,1 in Cardiovascular Health Study
| m=1 | m=2 | m=5 | |
|---|---|---|---|
| NCC | 0.05501 (0.04974) n*=536.3 |
0.03948 (0.03722) n*=773.9 |
0.0261 (0.02534) n*=1,384.9 |
| CCH | 0.04767 (0.04524) n*=535.8 |
0.03335 (0.03273) n*=773.4 |
0.0221 (0.02207) n*=1,384.3 |
The empirical standard error of log hazard ratios, the estimated standard error (in parentheses), and the sample size (n*) averaged over 5,000 iterations are shown in each cell. The empirical variance due to both infinite and finite sampling was estimated by adding the estimated variance for the full cohort estimates to the empirical variance resulting from the simulation. The standard error from the full cohort (N=4,388) was 0.0111.
DISCUSSION
This paper demonstrates that valid analyses of secondary outcomes under Cox proportional hazards model can be accomplished in nested case-control studies using inverse probability weighting methods. In addition, the proposed approximate jackknife standard error is useful since it is readily computable with existing software. Although the proposed approach was based primarily on Samuelsen’s method, other inverse probability weighting methods such as those of Chen [5, 6] can also be used for the analysis of secondary outcomes. Nested case-control designs have become a common approach for initial large-scale investigation of biomarkers for prospectively identified health events to reduce the cost and to preserve limited archived samples in cohort studies. The proposed methods provide the ability to investigate the association with the secondary outcomes without additional cost.
In our simulation studies, the statistical power for the secondary outcome in nested case-control design was found to be higher than that of case-cohort when the secondary outcome is positively correlated with the primary outcome. This is not surprising since for primary outcomes, the nested case-control design is generally more efficient than the case-cohort design when inverse probability methods are used (See Figure 4 when ρ = 1). The same advantage carries over to the analysis of the secondary outcome when the two outcomes are correlated. The reason is that given the way the controls are sampled in the main study, a higher proportion of subjects in the nested case-control design will have longer follow-up times of the two outcomes and therefore contribute to multiple risk sets in the analysis of the secondary outcome compared to the case-cohort design.
Still the answer to which design is more efficient between the two designs may be a rather nuanced one. The factors that may affect the relative performance include prevalence, the type of censoring, and the degree of overlap between risk sets. This is part of the reason that there are conflicting reports to which design is more efficient [1, 15, 19]. In the case of primary outcome analysis, we are writing a manuscript sorting out the settings in which each design works more efficiently. However, the main contribution of this paper is showing the validity of the secondary outcome analysis in the nested case-control studies. It is practically meaningful that the efficiency of the nested case-control design is comparable to that of the case-cohort design, but there are different factors that may benefit each design.
In a nested case-control sample, the case subjects for secondary outcomes may outnumber case subjects for the primary outcome. This is likely to be true 1) when the secondary outcome has high incidence in the underlying population, or 2) when the analysis of secondary outcome is performed years after the initial study of the primary outcome is conducted. In such settings or when the hazard of the secondary outcome is greater than that of the primary outcome, secondary outcome analysis can have higher statistical power than the primary outcome analysis. Otherwise, un-augmented analyses of the secondary outcome can be underpowered especially when the correlation between the secondary and primary outcomes is low or the hazard of the secondary outcome is less than that of the primary outcome. In such cases, results of these analyses should be viewed as exploratory and the proposed method can be used in practice for generating new hypotheses or obtaining preliminary estimates to design a larger scale study of the secondary outcome.
One may need to perform power analysis to plan for augmentation of secondary cases. Unfortunately, sample size methods for nested case-control analyses using the inverse probability weighting method have not been developed even for the primary outcome and existing methods for nested case-control studies [20] and conditional logistic regression [21] will give conservative estimates.
We did not model primary and secondary outcomes as joint failure times e.g. with frailty models, nor as competing risks. Future research on such models is likely to further improve the efficiency of secondary outcomes analysis in nested case-control studies. We did not consider how statistical power changes by the inclusion of additional controls, but the result is expected to be similar to what was observed under the Weibull model [7] where efficiency was gradually gained as the number of new controls per case increases.
Finally, we note that the proposed method requires the retrospective access to the primary outcome and the matching variables of the full cohort in order to compute inclusion probabilities. We also note that the conditional logistic approach to analyze nested case-control studies may work as analytically matching known or unknown time-dependent confounders. When such confounders exist, our approach requires the model specification of adjustment or stratification to be accurate in order to produce consistent estimators.
Supplementary Material
ACKNOWLEDGEMENTS
The authors are very grateful to Drs Mimi Kim and Xiaonan Xue for their review and guidance of this paper. This work was supported by the National Institutes of Health Grants 1UL1RR025750-01, P30 CA01330-35 (to RSK); 1R01AG031890 from the National Institute of Aging (to RCK); and the National Research Foundation of Korea Grant NRF-2012-S1A3A2033416 (to RSK).
APPENDIX
Generation of bivariate exponential failure times
A bivariate exponential variable with a positive correlation coefficient ρ and both marginal rates equal to 1 can be generated by setting (E1, E2) = (G1+Y, G2+Y) where G1 and G2 are both gamma random variables with the rate equal to 1 and the shape parameters 1-ρ, and Y is a gamma random variable with the rate equal to 1 and the shape parameter ρ. G1, G2, and Y have to be specified to be mutually independent. Then, a bivariate exponential failure time with a correlation coefficient ρ and the marginal rates λ1 and λ2 can be generated by setting (T1, T2) = (E1/λ1, E2/λ2).
Syntax codes in R and SAS software
Once the inverse inclusion probabilities (wt) are computed, the following command will compute the proposed linear estimators and jackknife approximate standard errors in R.
coxph(formula= Surv(Y,delta)~ x1+x2+x3,robust=T,weights=wt,data=nccdt)
The same can be accomplished in SAS with the following commands:
proc phreg data=nccdt covs;
class x1 x2 x3;
model Y*delta(0) = x1 x2 x3;
weight wt;
Note that when a user specifies the weight option, both programs treat the weights as frequencies. To our advantage, however, the programs compute (6) when the option is coupled with robust standard error computation and does not the compute standard error assuming weights are frequencies. We also provide in Supplementary material an R program to compute inclusion probabilities (4).
REFERENCES
- 1.Prentice RL. A case-cohort design for epidemiologic cohort studies and disease prevention trials. Biometrika. 1986;73:1–11. [Google Scholar]
- 2.Thomas D. Addendum to 'Methods of cohort analysis: Appraisal by application to asbestos mining'. In: Liddell FDK, McDonald JC, Thomas DC, editors. Journal of the Royal Statistical Society. A 140. 1977. pp. 469–491. [Google Scholar]
- 3.Wacholder J. Practical Considerations in Choosing between the Case-Cohort and NCC Designs. Epidemiology. 1991;2:155–158. doi: 10.1097/00001648-199103000-00013. [DOI] [PubMed] [Google Scholar]
- 4.Samuelsen S. A pseudo-likelihood approach to analysis of nested case-control studies. Biometrika. 1997;84:379–394. [Google Scholar]
- 5.Chen KN. Statistical estimation in the proportional hazards model with risk set sampling. Annals of Statistics. 2004;32:1513–1532. [Google Scholar]
- 6.Chen KN. Generalized case-cohort sampling. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2001;63 [Google Scholar]
- 7.Salim A, Yanga QRM. The value of reusing prior nested case-control data in new studies with different outcome. Statistics in Medicine. 2012;31:1291–1302. doi: 10.1002/sim.4494. [DOI] [PubMed] [Google Scholar]
- 8.Fried LP, Borhani NO, Enright P, Furberg CD, Gardin JM, Kronmal RA, Kuller LH, Manolio TA, Mittelmark MB, Newman A. The Cardiovascular Health Study: design and rationale. Annals of Epidemiology. 1991;1:263–276. doi: 10.1016/1047-2797(91)90005-w. [DOI] [PubMed] [Google Scholar]
- 9.Therneau TM, Grambsch P, Grambsch PM. Modeling Survival Data: Extending the Cox Model. New York: Springer-Verlag; 2000. [Google Scholar]
- 10.Reid N, Crepeau H. Influence function for proportional hazards regression. Biometrika. 1985;72:1–9. [Google Scholar]
- 11.Lin DY, Wei LJ. The robust inference for the Cox proportional hazards model. Journal of the American Statistical Association. 1989;84 [Google Scholar]
- 12.Samuelsen SO, H Å, A S. Stratified case-cohort analysis of general cohort sampling designs. Scandinavian Journal of Statistics. 2007;34:103–119. [Google Scholar]
- 13.Kim RS. Division of Biostaistics. City: Albert Einstein College of Medicine; 2014. A Comparison of Nested Case-Control and Case-Cohort Designs and Methods. In A Comparison of Nested Case-Control and Case-Cohort Designs and Methods. Editor (ed)^(eds) [Google Scholar]
- 14.Barlow WE. Robust variance estimation for the case-cohort design. Biometrics. 1994;50:1064–1072. [PubMed] [Google Scholar]
- 15.Self SG, Prentice RL. Asymptotic distribution theory and efficiency results for case-cohort studies. The Annals of Statistics. 1988;16:64–81. [Google Scholar]
- 16.Ives DG, Fitzpatrick AL, Bild DE, Psaty BM, Kuller LH, Crowley PM, Cruise RG, Theroux S. Surveillance and ascertainment of cardiovascular events. The Cardiovascular Health Study. Annals of Epidemiology. 1995;5:278–285. doi: 10.1016/1047-2797(94)00093-9. [DOI] [PubMed] [Google Scholar]
- 17.Tracy RP, Lemaitre RN, Psaty BM, Ives DG, Evans RW, Cushman M, Meilahn EN, Kuller LH. Relationship of C-Reactive Protein to Risk of Cardiovascular Disease in the Elderly Results From the Cardiovascular Health Study and the Rural Health Promotion Project. Arteriosclerosis, Thrombosis, and Vascular Biology. 1997;17:1121–1127. doi: 10.1161/01.atv.17.6.1121. [DOI] [PubMed] [Google Scholar]
- 18.Smith SCJ, Anderson JL, Cannon ROr, Fadl YY, Koenig W, Libby P, Lipshultz SE, Mensah GA, Ridker PM, Rosenson R, CDC AHA. CDC/AHA Workshop on Markers of Inflammation and Cardiovascular Disease: Application to Clinical and Public Health Practice: report from the clinical practice discussion group. Circulation. 2004;110:e550–e553. doi: 10.1161/01.CIR.0000148981.71644.C7. [DOI] [PubMed] [Google Scholar]
- 19.Langholz B, Thomas D. Nested case-control and case-cohort methods of sampling from a cohort: a critical comparison. American Journal of Epidemiology. 1990;131:169–176. doi: 10.1093/oxfordjournals.aje.a115471. [DOI] [PubMed] [Google Scholar]
- 20.Pang D. A relative power table for nested matched case-control studies. Occupational Environmental Medicine. 1999;56:67–69. doi: 10.1136/oem.56.1.67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Dupont W. Power Calculations for Matched Case-Control Studies. Biometrics. 1988;44:1157–1168. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.