A multiple imputation strategy for sequential multiple assignment randomized trials

Abstract

Sequential multiple assignment randomized trials (SMARTs) are increasingly being used to inform clinical and intervention science. In a SMART, each patient is repeatedly randomized over time. Each randomization occurs at a critical decision point in the treatment course. These critical decision points often correspond to milestones in the disease process or other changes in a patient’s health status. Thus, the timing and number of randomizations may vary across patients and depend on evolving patient-specific information. This presents unique challenges when analyzing data from a SMART in the presence of missing data. This paper presents the first comprehensive discussion of missing data issues typical of SMART studies: we describe five specific challenges, and propose a flexible imputation strategy to facilitate valid statistical estimation and inference using incomplete data from a SMART. To illustrate these contributions, we consider data from the Clinical Antipsychotic Trial of Intervention and Effectiveness (CATIE), one of the most well-known SMARTs to date.

1. Introduction

Sequential multiple assignment randomized trials (SMARTs) [1, 2, 3] are increasingly being advocated and used as a way to generate high-quality data concerning the effects of sequences of treatments. In a SMART, patients move through stages of treatment; they are randomized to an initial treatment at study entry, and then possibly re-randomized to additional treatments at subsequent treatment stages. An important practical difficulty with analyzing clinical trial data, such as data collected in a SMART, is missing data. The structure of missing data in a SMART can be complex because transition times and randomization probabilities are outcome dependent. Contributions of this paper include identifying five key challenges that are associated with missing data in SMARTs and developing a flexible imputation strategy to facilitate valid estimation and inference.

Data collected in a SMART study can be used to estimate sequential individualized treatment strategies known as dynamic treatment regimes [4], treatment polices [5], adaptive interventions [6], or adaptive treatment strategies [7]. Precursors to SMARTs include the CALGB study 8923 for treating elderly patients with primary acute myelogenous leukemia [8], and the STAR*D study for treatment of depression [9, 10, 11]. Recent examples of SMARTs include trials for treating cancer at the University of Texas MD Anderson Cancer Center [12]; the ExTENd trial concerning alcohol dependence at the University of Pennsylvania [13]; and the Adaptive Interventions for Children with ADHD at SUNY Buffalo [14]. See [15] for descriptions of more SMART studies. One of the most well-known sequential randomized trials is the Clinical Antipsychotic Trials of Intervention and Effectiveness (CATIE) study for patients with schizophrenia [16]. The work presented in this paper is motivated by our involvement with the CATIE study which we use as a running illustrative example.

Dynamic treatment regimes formalize clinical decision making as a sequence of decision rules, one for each critical decision point, that map up-to-date patient information to a recommended treatment [17, 18, 19, 20, 21]. The sequential and longitudinal nature of SMART studies which facilitates estimation of dynamic treatment regimes also presents unique challenges for estimation and inference when data are missing. There is a large body of work on accommodating missing data in non-sequential trials [22, 23, and references therein]. Multiple imputation [22, 24, 25] has emerged as a popular method for dealing with missing data due to its flexibility, and general applicability. Multiple imputation has been successfully applied in a wide range of domains including longitudinal data [26, 27, 28, 29]. It is particularly appealing in this context as it accommodates both item missingness and missingness due to study attrition and is capable of preserving smoothness across longitudinal outcomes in the imputed data.

We propose a time-ordered nested conditional imputation strategy for use with SMART data. This imputation strategy allows for longitudinal variables that are used in the clinical trial design, either in dictating treatment randomization probabilities or determining the collection schedule of other variables. In SMARTs, as in many longitudinal studies, study attrition accounts for much of the missing data which produces a nearly monotone pattern of missing data. We exploit this missing data pattern to ensure a coherent multivariate predictive distribution exists, while retaining flexibility, scalability, and smoothness across longitudinal outcomes.

The remainder of this paper is organized as follows. In Section 2 we identify five key challenges to applying imputation methods to data collected from SMARTs and illustrate these challenges using the CATIE study. In Section 3 we introduce a time-ordered nested conditional imputation strategy for SMARTs. In Section 4 we apply this imputation methodology to the CATIE study. An analysis of the CATIE data based on the imputations is presented in Section 5. We close with a discussion in Section 6.

2. Background

2.1. Missing Data Challenges Arising in SMART studies

There are at least five issues that present difficulties for building an effective imputation model for missing data in SMARTs. Issue 1: the transition from one treatment stage to the next does not necessarily occur at pre-specified times, but instead is determined by a patient’s outcomes. Issue 2: Some outcome variables are collected at the end of irregularly spaced stages, in replacement of, or in addition to, variables collected during regularly scheduled study visits, resulting in irregular collection times for these variables. Issue 3: The observation of some variables may depend on patient covariate and outcome history, resulting in structural missingness for a data-dependent portion of information on some of the participants. Issue 4: Some individuals will be lost to follow-up prior to leaving a treatment stage, and thus theirend-of-stage variables, along with regularly scheduled outcome variables, that would have been used to determine the randomization probabilities for treatment assignment in remaining stages are missing. Issue 5: Some individuals will be lost to follow-up prior to entering some treatment stages, and thus, treatments that they would have been assigned in remaining stages are unknown.

2.2. The CATIE Study

The CATIE study was an 18 month SMART that enrolled 1460 patients with schizophrenia. Schizophrenia is a chronic disease characterized by abnormalities in a person’s perception of reality, such as hallucinations, delusions, and confused speech and thought processes. Effective management of schizophrenia requires sequential, individualized, adaption of treatment due the chronic nature of the disease, heterogenous treatment response, poor adherence, and/or intolerable side effects. As CATIE is described in detail elsewhere [16, 30, 31, 32, 33], we only give a simplified overview of the study, placing emphasis on missing data.

There were two main randomized treatment stages in CATIE, which we term stage 1 and stage 2. In CATIE, as in most SMARTs, two types of time-varying variables were collected, scheduled variables and end-of-stage variables. Scheduled variables are collected at pre-specified collection times on all individuals; e.g., treatment adherence was measured monthly on all CATIE participants. End-of-stage variables are specific to SMARTs and are collected only at the end of a treatment stage. An example of an end-of-stage variable is the reason for discontinuing current treatment.

A large number of variables were collected at CATIE enrollment, e.g., demographics and disease history. Longitudinal scheduled variables, e.g., symptom measurements, adherence, and side effects, were planned to be collected either monthly, quarterly, or semi-annually (depending on the variable). At an end-of-stage visit, the reason for discontinuing current treatment, as well as all time-varying outcome variables, were collected regardless of the regular collection schedule. See Table 1 for a partial list of variables and their collection schedules in CATIE.

Table 1.

Variables collected during CATIE utilized in the imputation strategy and the months they were scheduled to be collected. The type of the variable is indicated in parentheses; continuous variables are denoted with (cont), dichotomous variables with (dich), and categorical with (cat).

Variables with no missing information:

Time independent variables.

Age (cont), Sex (dich), Race (cat), Tardive dyskinesia status at baseline (dich), Marital status at baseline  (dich), Patient education (cat), Hospitalization history in 3 months prior to CATIE (dich), Clinical setting  in which patient received CATIE treatment (cat), Treatment prior to CATIE enrollment (cat), stage 1  randomized treatment assignment (cat)

Variables with missing information:

Time independent variables:

Employment status at baseline (cat), Years since first prescribed anti-psychotic medication at baseline  (cont), Neurocognitive composite score at baseline (cont)

Variables recorded at all months 1-18 and at end-of-stage visits:

Adherence measured by the proportion of capsules taken since last visit (cont)

Variables recorded at months 0,1,3,6,9,12,15,18 and at end-of-stage visits:

Body mass index (cont), Clinical drug use scale (cat), Clinical alcohol use scale (cat), Clinical global  impressions of Severity of illness score (cat), Positive and negative syndrome scale (cont), Calgary  Depression Score (cont), Simpson-Angus EP mean scale (cont), Barnes akathisia scale (cont), Total  movement severity score (cont)

Variables recorded at months 0, 6, 12, 18 and at end-of-stage visits:

Quality of life total score (cont), SF-12 Mental health summary (cont), SF-12 Physical health summary  (cont), Illicit drug use (dich)

Variables recorded only at end-of-stage visits:

Reason for discontinuing treatment (cat), Stage 2 randomization arm (dich, when applicable), Stage 2  treatment (cat, when applicable)

At study entry, CATIE patients were randomized to one of five stage 1 treatments: olanzapine, risperidone, quetiapine, ziprasidone, or perphenazine. At any monthly visit, a patient, in consultation with his/her care provider, could decide to discontinue their current assigned treatment and enter the next treatment stage (Issues 1 and 2 above). At any monthly visit in which a patient’s current treatment was deemed adequate, only scheduled variables were collected (see Table 1). Thus, no end-of-stage variables were collected from CATIE participants who had adequate response to their stage 1 treatment for the entire CATIE trial (i.e., never transitioned into a later CATIE treatment stage; Issue 3 above).

Patients who transitioned into the second treatment stage were offered a choice of two randomization arms, the tolerability arm or the efficacy arm. The tolerability arm was intended for individuals experiencing intolerable side effects; in this arm participants were randomized to olanzapine, risperidone, quetiapine, or ziprasidone, excluding previous treatment. The efficacy arm was intended for participants experiencing a lack of symptom control; in this arm participants were randomized to either clozapine, olanzapine, risperidone, or quetiapine, excluding previous treatment.^†

Study attrition was high in CATIE with only 705 of 1460 patients staying for the full 18 months. The distribution of most baseline covariates appeared similar for participants that completed the CATIE ztudy and those that dropped out. However, individuals who completed the CATIE study were more likely to be white, less likely to be treatment naive at baseline, and more likely to be abstinent from drugs and alcohol (see Supplementary Material for full comparison.). Of the 705 participants who left the CATIE study, 509 dropped out of the study before entering stage 2 (Issue 4 and 5 above). Dropout is generally high in studies of antipsychotics for schizophrenia [34]. Additionally, in the CATIE study, the primary outcome was time until all-cause treatment discontinuation, providing little incentive for clinicians to keep non-adherent patients enrolled. Consequently, the majority of missing data (78.1%) was due to study attrition which produced a nearly monotone missing data pattern.

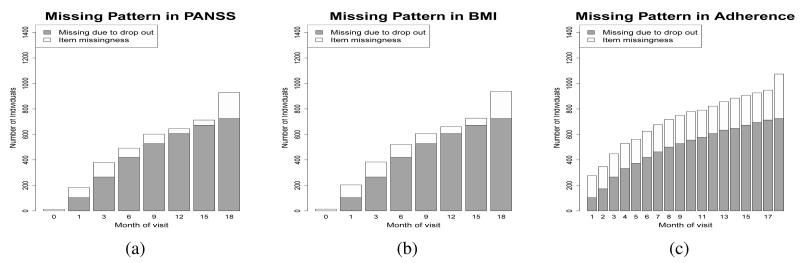
The trend in the amount of missing data over time, and the proportion of missing data due to dropout, are similar for all scheduled time-varying variables collected during the CATIE study. We use three variables to illustrate this pattern: Positive and negative syndrome scale (PANSS), Body mass index (BMI), and treatment adherence. The PANSS score is the standard medical scale for measuring symptom severity in patients with schizophrenia with higher values corresponding to more symptoms [35]. Weight gain, captured by BMI, is an important side effect associated with many antipsychotics that impacts a patient’s overall health and their likelihood to adhere to treatment [36, 37]. Monitoring a patient’s treatment adherence is important for optimal therapeutic benefit; adherence is measured using the proportion of prescribed pills taken since the last visit. Figure 1 shows the proportion of missing data in PANSS, BMI, and treatment adherence at scheduled visits. As illustrated here, most missing data is due to participant dropout [22, 38].

Figure 1.

Bar plots showing the amount of missing data in the CATIE study. The total height of the bar displays the absolute number of people who have missing (a) PANSS, (b) BMI, and (c) adherence, as measured by pill count, at each of the monthly visits at which the scheduled variable was collected. The dark grey area represents individuals with missing values because they have dropped out of the study prior to that month. The unshaded area is the amount of item missingness in each variable.

3. Imputation Methods

There are three types of missing data generating mechanisms: missing completely at random (MCAR) in which the missing data pattern is independent of any variables, measured or unmeasured; missing at random (MAR) in which the missing data pattern is dependent on observed variables; and not missing not at random (NMAR) in which the missing data pattern depends on unobserved variables [39, 22]. Imputation methods, such as those described here, assume an MAR generating mechanism.

Generally, imputation models fall into one of two categories: fully conditional models wherein a separate model is fit for each variable [40, 41, 42], or joint multivariate models wherein a single joint model is fit to all variables [22, 25]. The data-dependent structural missingness inherent to SMART designs makes specifying a single joint distribution difficult. For this reason we opt for conditional imputation models. However, we exploit the near-monotonicity and SMART-specific, sequential, structure of the data to ensure a coherent multivariate joint distribution.

Let t = 0, 1, …, T denote the scheduled clinic visit times where t = 0, denotes baseline and t = T denotes the end-of-study visit (see below for details). At each time t let v_t,1, …, v_t,Jt denote the set of all covariates on all n trial participants that could potentially be collected on any participant at time t. In general, the covariates potentially collected at time t need not be identical to those potentially collected as some other time s ≠ t as collection schedules vary across variables. In our implementation, the order v_t,1, …, v_t,Jt includes first the covariates which, according to the protocol, dictate when and if additional covariates should be collected and second include variables which are potentially missing by design. For example, in CATIE, an indicator of treatment discontinuation, would precede a variable coding reason for treatment discontinuation. The imputation models used at each time point t are nested so that the model for v_t,k depends only on v_t,k−1, …, v_t,1; this sequential conditioning framework provides a straightforward approach for specifying a coherent multivariate distribution. An example dataset based on the CATIE study with the foregoing time-ordered structure is provided in the Supplemental Materials. Below we describe this time-order conditional nested imputation modeling framework in general terms, before illustrating this approach with the CATIE data.

3.1. Overview of Time-ordered Nested Conditional Imputation Models

Fully Conditional Specification (FCS) imputation methods have been used to accommodate missing data in a wide range of applications [43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53]. In general, FCS methods only require the specification of conditional distributions for each variable, and not a full joint distribution. When no restrictions are placed on which variables are used as predictors in these conditional models, a number of theoretical and practical issues can arise. For example, the existence of a joint multivariate distribution that is consistent with all conditional distribution models is not guaranteed [54, 55, 38, 41] and convergence properties are not yet known [41, 46]. Nonetheless this approach appears to work well in practice, where missing data is imputed with a pseudo-Gibbs sampler, applying repeated iterations through the conditional distribution models [55, 41].

Conditionally specified imputation models extend naturally to time-ordered data collected from longitudinal clinical trials. For example, assuming all baseline variables are observed, these variables can be used as predictors in an imputation model for missing data from the first follow-up visit. The imputed and observed values from this first visit, in addition to the observed values from the baseline visit, can then be used as predictors in an imputation model for missing information at the second follow-up visit, and so on. The predictors at earlier visits are a subset of predictors at later visits, creating a time-ordered nested structure in the set of predictors used in the conditional imputation models. Thus, the set of potential predictors used in imputation models increases with t.

Conditional models have been used to specify complex joint distributions in many areas [56, 38, 54]. Provided that at least some of the baseline variables are fully observed, a time-ordered nested conditional imputation model avoids some of the problems associated with general FCS, e.g., lack of convergence, or lack of joint multivariate distribution that is consistent with the conditional models. The tradeoff, in terms of model quality, is that one does not use future information, say at time t + h, to impute data occurring at time t. But as long as the pattern of missing data is monotone or nearly monotone, i.e. if a participant is missing information at time t then all information at any time t + h is also missing, then little is lost in terms of efficiency or bias.

We employ a Bayesian framework for generating values to impute missing information [57]. As before denote the vector of the j^th variable collected at time t for all n trial participants by v_t,j with v_t,j,obs denoting the observed values and v_t,j,miss denoting the missing information. Define ${\mathcal{D}}_{t-1}\equiv {\mathbf{v}}_0,{\mathbf{v}}_{1,1},\dots {\mathbf{v}}_{1,J_1},\dots ,{\mathbf{v}}_{t-1,1},\dots ,{\mathbf{v}}_{t-1},J_{t-1}$.

Denote the conditional distribution of v_t,j by $f({\mathbf{v}}_{t,j}\mid {\mathcal{D}}_{t-1};{\theta }_{t,j})$, the prior distribution of θ_t,j by π(θ_t,j), and the posterior distribution of θ_t,j by $\pi ({\theta }_{t,j}\mid {\mathcal{D}}_{t-1},{\mathbf{v}}_{t,j,\mathrm{obs}},{\theta }_{1,1},\dots {\theta }_{t-1,J_t}\dots {\theta }_{t,j-1})$. Then, assuming fully observed v₀ for ease of notation, the resulting joint posterior predictive distribution of the missing observations given the observed is:

$$\int \cdots \int \prod _{t=1}^T\prod _{j=1}^{J_t}f({\mathbf{v}}_{t,j}\mid {\mathcal{D}}_{t-1},{\theta }_{t,j})\pi ({\theta }_{t,j}\mid {\mathcal{D}}_{t-1},{\mathbf{v}}_{t,j,\mathrm{obs}},{\theta }_{1,1},\dots ,{\theta }_{t-1,J_t},\dots ,{\theta }_{t,j-1})d{\theta }_{t,j}.$$

We sample from this distribution by first evaluating the posterior distribution π(θ_1,1|v₀, v_1,1,obs), then sampling a value of ${\theta }_{1,1}^{\ast }$ to impute the missing values of v_1,1 using $f({\mathbf{v}}_{1,1}\mid {\mathcal{D}}_0,{\theta }_{1,1}^{\ast })$. We use these imputations to estimate $\pi ({\theta }_{1,2}\mid {\mathcal{D}}_{1,2},{\mathbf{v}}_{1,2,\mathrm{obs}},{\theta }_{1,1}^{\ast })$, again sampling a value ${\theta }_{1,2}^{\ast }$ to impute missing values of v_1,2 using $f({\mathbf{v}}_{1,2}\mid {\mathcal{D}}_0,{\theta }_{1,2}^{\ast })$. We continue until all posterior distributions have been estimated and all missing values have been imputed. The foregoing process yields a single imputed dataset, which we repeat to produce multiple complete datasets. Multiple imputation is recommended over a single imputation because the uncertainty in the imputed values can be better accounted for in an analysis [22].

This imputation strategy accommodates the missing data issues cataloged in Section 2.1. By first imputing missing patient outcomes from early study visits, this information can be use to impute missing patient-specific transition times, end-of-stage variables, and treatment assignments at later stages. Additionally, this time-ordered nested approach can be used to accommodate data-dependent structural missingness by first imputing patient information needed to determine the collection timing, and then imputing non-structurally missing values.

3.2. Specifying the Conditional Models

Because it considers separate models for each covariate, the general FCS framework has two important strengths: scalability and flexibility. However, one potential drawback of specifying each univariate conditional model separately at each time point is that smoothness in the mean (or variance) of longitudinal outcomes is not imposed. In many situations, one can expect the time-varying mean of a longitudinal process to be smooth. For example, in the CATIE study one would expect that symptom severity and BMI would exhibit such smoothness. We use a longitudinal Baysian Mixed Effects Model (BMEM) [58] to impose smoothness on conditional imputation models for longitudinal variables when warranted.

To the best of our knowledge, a description of how to incorporate longitudinal imputation methods that use time-varying predictors with missing information in the conditional specification framework is lacking. Below we detail how to incorporate the BMEM into the proposed nested conditionally specified framework. For clarity, we focus on a continuous outcome variable at time t denoted by R_t (appropriate generalized linear BMEMs can be implemented for binary or categorical variables).

We construct a model for the distribution of R_t conditional on {R₀, R₁, …, R_t−1} and all other variables at all times s ≤ t. This conditional model is derived from a BMEM for {R₀, R₁, …, R_t} using random effects to model correlation between observations on the same individual and a spline (or similar smooth function) to enforce smoothness over time on the conditional mean of {R₀, R₁, …, R_t}. Equation (1) provides an example BMEM with the subscript i denoting individual i:

$$R_{s,i}=({\gamma }_0+g_i)+{\gamma }_b^{⊺}{\mathbf{v}}_{0,i}+{\gamma }_b^{⊺}{\mathbf{v}}_{s,i}+\sum _{j=1}^s{v}_j{(s-j)}_{+}+{∊}_{s,i}\text{for}s\le t.$$ (1)

The random intercept terms, g_i, i = 1, …, n are assumed to be independent and normally distributed, allowing individual outcomes to vary independently across trial participants. The error terms ε_s,i, i = 1, …, n, s = 1, … t, are also assumed to be normally distributed and independent across both trial participants and study visits. In this example, a linear spline is used to model the smoothness in the expected value of the longitudinal outcome, R over time, with the coefficients, ν_j j = 1, …, t, constrained so that Eq. (1) is continuous in s ≤ t. Note that the normally distributed error term and random effects terms will define the covariance matrix for {R₀, R₁, …, R_t}. The conditional distribution implied by this multivariate normal distribution defines our model for the distribution of R_t conditional on {R₀, R₁, …, R_t−1} and all other variables at all times s ≤ t. The Bayesian imputation model is estimated by defining priors on the fixed-effects coefficients in Eq (1) and the variances of the Gaussian models the random intercept and error terms are drawn from. Using this model, we sample from the posterior predictive distribution to impute the missing values of R_t.

We construct a new BMEM at each time t, specify priors on the fixed-effects coefficients in Eq (1), the variances of the random intercepts and variances of the error terms. Then if needed, we use this model to impute missing values in R_t. This strategy borrows more information over time at later time points for estimating imputation models than at earlier ones; due to study attrition, this is precisely when more information is needed. Evaluating a BMEM at an early time point using this strategy will utilize information on many independent individuals (as little attrition has occurred), but fewer time-varying observations on R for any one individual. Later time points will utilize information from measurements on R over more time points because more longitudinal observations on the same individuals are used to evaluate the imputation models, but fewer independent observations (due to attrition) are present at later time points.

Our use of the BMEM builds on the strengths of conditionally specified imputation models (scalability and flexibility), while incorporating the advantage of using longitudinal imputation models to borrow information over time. This imputation strategy is not restricted to imputing missing data collected from a SMART, and can be generalized to any longitudinal missing data problem. Due to the conditional nature of the trial design, the time-ordered conditional structure is especially powerful for imputing missing information from a SMART.

4. CATIE Schizophrenia Trial

In Section 2.1, we described five characteristics of SMART studies that present challenges for imputation. In Section 3 we proposed a time-ordered nested imputation strategy to meet these challenges. Here we illustrate the proposed strategy with data from the CATIE study. The primary motivation for using imputation to accommodate missing data in CATIE is to perform a range of secondary analyses, including estimation of an optimal dynamic treatment regime [17, 19], which we demonstrate in Section 5. The primary outcome for the CATIE study was time until treatment discontinuation, but a large amount of longitudinal information was collected on all participants, and several secondary outcomes are of clinical interest. For clarity, PANSS will be the only variable imputed with a BMEM.

The multiple imputation methods we employ are essentially the same across time points; thus, we describe the imputation procedure for a generic time point t. The imputation process is repeated to generate twenty-five complete CATIE datasets. In some special cases, substantive and logical arguments can be used to justify a single imputation for a missing variable, in these cases, the imputed value will be the same across all completed datasets.

We first describe our imputation procedure for baseline variables. We then determine if, and when, a participant who dropped out of CATIE should be imputed to transition into a subsequent treatment stage. We then describe imputation models for end-of-stage variables and treatment assignment for these later stages. Finally, we detail how to interweavethe imputation of these transition times, treatment assignments, end-of-stage variables, and scheduled variables within the time-ordered nested format. In Section 4.6 we provide algorithm implementation details.

4.1. Imputing baseline variables

There are 11 baseline variables in CATIE with no missing data, and 16 that contain some missing values; a total of 3% of these baseline observations are missing. We use independent conditionally specified models to impute the small amount of missing data at baseline, conditioning on the variables that were fully observed (see Table 1). As this is standard, we omit a description.

4.2. Imputing stage transition times

We assume that had an individual who dropped out of CATIE instead remained in the study, s/he would have elected to discontinue their current treatment at the month they were observed to dropout. Hence, individuals who dropped out of CATIE at stage 1 are, at the month of dropout, singly imputed to transition into the next treatment stage and thus receive a different treatment. The rationale for this decision is that schizophrenia is a chronic disease requiring continuous treatment. Furthermore since treatment in CATIE is blinded, it is unlikely that an individual who drops out of CATIE will continue to be treated with their assigned CATIE medication.

The single-imputation for transition times in CATIE relies on an assumption informed by clinical practice. In other settings such an assumption may not be plausible and an imputation model for the transition time could be used. For example, one could impute a binary indicator of transition at each clinic visit subsequent to patient dropout.

4.3. Imputing end-of-stage variables

Some end-of-stage information will also be singly imputed. When an individual chose to stop participating in CATIE while at a study visit, the CATIE protocol required clinicians to record the reason for this early termination and collect all time-varying participant information, that is, the same information that is recorded at an end-of-stage visit. Thus, we singly impute all end-of-stage information, including reason for discontinuing treatment, with information collected at the participant’s exit visit when available. Not all individuals had information collected before leaving the CATIE study; we multiply impute all remaining missing end-of-stage information for these subjects.

With the exception of PANSS (see Section 4.5 below), we utilize a univariate regression model for each end-of-stage variable. The predictors in the univariate end-of-stage imputation models are baseline variables, most recent treatment and scheduled time-varying variables, and the reason for discontinuing previous treatment. Because the distribution of end-of-stage variables for individuals who discontinue treatment due to lack of therapeutic results will likely be different from that of individuals who discontinued treatment due to intolerable side effects, we nest the most recent scheduled variables within reason for discontinuing treatment in the imputation models. This allows the distribution of end-of-stage variables to depend on reason for discontinuing treatment, while preserving computational tractability.

In CATIE, a small number of observed stage transitions occurred in any given month. Consequently, we pool the data within time-windows: months {1}, {2, 3}, {4, 5, 6}, {7, 8, 9}, {10, 11, 12}, {13, 14, 15}, {16, 17, 18}, to increase stability in estimating the parameters in the end-of-stage imputation models. That is, data from individuals who transition into the next treatment stage within one time-window are used to estimate imputation models for end-of-stage variables within that time-window. These time-windows were chosen because most scheduled variables were collected at months 0, 1, 3, 6, 9, 12, 15 and 18.

4.4. Imputing new randomly assigned treatment

If an individual dropped out during stage 1, the choice of stage 2 randomization arm must be imputed. Reason for discontinuing previous treatment was highly predictive of treatment arm choice; of the 99 individuals who were observedto enter the stage 2 efficacy arm, 75 (85.9%) gave “lack of therapeutic effect” as their primary reason for discontinuing treatment. Thus, our imputation model for the choice of stage 2 randomization arm includes all baseline variables, previous treatment, reason for discontinuing previous treatment, and all end-of-stage variables. After the randomization arm is multiply imputed, assigned treatment is imputed using stage 2 treatment randomization probabilities defined in the CATIE protocol.

4.5. Imputing additional missing time-varying information

As detailed in Table 1, collection schedules differed for variables collected in CATIE. For each scheduled variable collected at month t (except PANSS) we estimate a separate imputation model. For example, treatment adherence was measured monthly; thus, separate imputation models were utilized for each month. The imputation models for all scheduled variables (except PANSS) include as predictors: baseline covariates, previous scheduled time-varying variables, current stage and randomized treatment. Appropriate conditional models were selected to suit the variable type (binary, continuous, etc.).

Recall from the discussion in the beginning of Section 3 that at each month t the variables are ordered; we put PANSS last in this ordering. Thus the model for PANSS at month t can utilize all other variables collected at month t. The nested structure described in Section 3.2 uses a series of longitudinal mixed effect imputation models, one for each time point. For example, suppose we are imputing missing values in PANSS at month t; the model uses the PANSS score at months 0, 1, …, t as the longitudinal outcome and predictors: baseline covariates, currently assigned treatment, treatment stage, all time-varying variables measured at the month of PANSS observation, and a spline on month of observation. The spline included knots at monthly intervals, with spline coefficients constrained so the mean of PANSS was continuous in time. In our implementation we include a random (participant specific) intercept to model the correlation of PANSS scores measured on the same individual over time. We nest all time-varying predictors within a binary indicator variable for if the PANSS measurement is a scheduled or end-of-stage variable; if it is an end-of-stage variable, then the time-varying predictors are further nested within reason for discontinuing previous treatment. It is worth emphasizing that we estimate a separate PANSS BMEM imputation model at each time-point PANSS was scheduled to be collected; each BMEM includes observations for all time points up to the current one.

4.6. Algorithmic details for CATIE imputations

Here we outline some algorithmic details for creating multiple complete datasets using data from the CATIE study. There are many implementations for standard imputation methods [59, 60, 61, 62, 63]. We implemented the methods described in Sections 4.2-4.5 using the R software packages mice [63] and pan [62]. The former was used to estimate the univariate conditionally specified models, while the latter to estimate a longitudinal BMEM for PANSS. In both mice and pan, imputed values are drawn from the posterior predictive conditional distribution of the missing data given the selected predictors and the observed values of the variable being imputed [57].

The mice “norm” argument was used for continuous variables (sometimes transformations were applied prior to imputing); this assumes a Gaussian conditional distribution. To form conditional models for binary and categorical variables we used the “logreg” and “polyreg” arguments in mice which correspond to logistic and multinomial logistic regression models respectively [63]. We used the packages’s default flat, improper priors; the priors are independent both across models and across parameters in these models. We modified the mice package to permit interaction terms and to enforce upper and lower bounds on imputed values. Finally, we added internal checks to increase stability when near singularities occur due to small sample sizes and collinearity. Imputing PANSS with the R package pan implies a multivariate Gaussian distribution for the imputation model. The default priors for this model are a flat improper prior for the fixed effects with Inverse-Wishart priors placed on the variance components of the random effect and error terms. Sensitivity analyses can be used to assess the influence of the prior distribution of the imputed data [64].

We first used mice to impute missing values in baseline variables, conditioning on the fully observed baseline variables. Next, we used mice to impute the missing month 1 variables. Note that the missing values of baseline variables in theconditioning set were filled in on the prior step with mice. To impute missing values of the month 1 longitudinal outcome, R₁, we used pan to evaluate a BMEM for the longitudinal outcome {R₀, R₁}. Draws from the posterior predictive distribution were used to impute missing values of R₁. The imputation with pan was performed as if there were no missing values in the baseline and month 1 variables (except PANSS), as any missing values have been filled in. This interweaving of mice and pan continued though all 18 months of CATIE until all missing values were imputed. The Supplementary Material contains an artificial CATIE data set with missing data and corresponding R code implementing the imputation strategy described here.

5. Evaluating CATIE treatment regimes

The goal of a SMART study is not just to compare one treatment with another, but to compare entire treatment regimes. As an illustration we compare nine treatment regimes in terms of expected PANSS score averaged over the quarterly PANSS scores collected during the CATIE study. Here, a treatment regime is composed of two decision rules with the first decision rule dictating the first treatment, and the second decision rule dictating a second treatment if the first treatment is discontinued. The regimes under evaluation are given in Table 2. Ziprasidone was approved by the US Food and Drug Administration after CATIE enrollment had begun, consequently Ziprasidone was not included as a first stage treatment option for 571 CATIE participants; thus, Ziprasidone is not included as a first stage treatment option in Table 2. We also excluded Perphanazine since it cannot be taken by subjects with a prior diagnosis of tardive dyskensia, a movement disorder and side-effect of first generation anti-psychotics. The remaining 1014 CATIE participants were eligible to be included in our comparison of treatment regimes and were randomized to one of olanzapine, risperidone, or quetiapine in the first CATIE treatment stage.

Table 2.

Estimated mean PANSS score over the 18 months of the CATIE study for each of the 9 treatment regimes and 95% confidence intervals. The columns entitled Complete Case report the number of people (N) contributing information to estimating the mean response for each regime, the estimated mean response and corresponding 95% CI. The columns entitled Multiple Imputation report the number of people (N) averaged over 25 imputations contributing information to estimating the mean response for each regime as well as the estimated mean response and 95% CI.

	Complete Case		Multiple Imputation
Treatment Regimes	N	Mean [95% CI]	N	Mean [95% CI]
Olanzapine, if nonresponder, then Quetiapine	101	62.41 [60.05, 64.76]	186.3	65.99 [63.97, 68.00]
Olanzapine, if nonresponder, then Risperidone Olanzapine, if nonresponder	103	62.93 [60.46, 65.40]	186.8	66.08 [64.09, 68.07]
due to efficacy, then clozapine,    due to tolerance, then ziprasidone	109	63.21 [60.77, 65.65]	208.9	66.96 [65.04, 68.87]
Quetiapine, if nonresponder, then Olanzapine	56	64.09 [60.66,67.51]	145.4	68.86 [66.57,71.15]
Quetiapine, if nonresponder, then Risperidone Quetiapine, if nonresponder	61	65.12 [62.01,68.23]	146.1	69.32 [67.06,71.57]
due to efficacy, then clozapine,    due to tolerance, then ziprasidone	64	65.75 [62.62, 68.89]	169.5	70.25 [67.92, 72.57]
Risperidone, if nonresponder, then Olanzapine	83	66.67 [63.80, 69.54]	167.5	69.14 [66.92,71.35]
Risperidone, if nonresponder, then Quetiapine Risperidone, if nonresponder	79	65.49 [62.55, 68.44]	168.8	69.51 [67.31,71.71]
due to efficacy, then clozapine,    due to tolerance, then ziprasidone	83	66.32 [63.50,69.14]	186.7	70.29 [68.08, 72.49]

Recall that a CATIE participant, in consultation with their clinician, could decide at any visit that their stage 1 treatment was no longer adequate and choose to enter the next treatment stage. We define this choice to switch treatment a non-response to the first line of treatment. For non-responders, we consider three possible second line treatments: always assign olanzapine, quetiapine, or risperadone. According to the CATIE protocol, a participant could not be re-randomized to the same treatment they received in the first treatment stage; thus, each participant is only eligible for two of these three treatments. We also consider a second stage decision rule that depends on the reason given for non-response: if non-response is due to insufficient therapeutic effects treat with clozapine, if non-response is due to intolerable side-effects treat with ziprasidone. Note that in this example we use treatment arm choice as a proxy for reason for discontinuing treatment. In CATIE, reason for treatment discontinuation and treatment arm were highly (but not perfectly) correlated.

Our analysis employs methods described in [65, 66]. In particular, we used weighted regression to estimate the mean response and corresponding confidence intervals (CIs) for each regime under consideration (the weights are used to adjust for unequal randomization probabilities). Individuals who remain on their stage 1 treatment for the full 18 months are replicated to contribute information to all treatment regimes beginning with that treatment. The sandwich estimator for standard errors accounts for the weights and replicated observations [65, 66, 67].

Table 2 reports estimated mean responses and 95% CIs based on 25 imputed datasets constructed using the algorithm described in Section 4.1. The mean response is averaged over 25 imputations. Standard corrections are applied to adjust CIs to accommodate uncertainty in the imputations [22, p. 86-87]. We also report the average number of individuals over the 25 completed datasets that contribute information to the estimated mean response of each regime. For comparison, we report the corresponding estimates based on a complete case analysis limited to CATIE individuals for whom all baseline covariate information was collected, who remained in the CATIE study through the full 18 month and for whom PANSS was recorded at all quarterly scheduled visits. (N=321)

Note that the complete case estimates appear to be systematically lower and more variable than estimates using imputation. The lower mean is partially explained by the fact that patients with favorable responses had a higher propensityto remain in the study. This is the type of bias we aim to correct using imputation. Using the 25 imputations, the estimated treatment regimes that first treat with olanzapine all have the lowest expected PANSS scores. The previously published primary analysis, also found that olanzapine was the most effective first-line medication in the CATIE study [31].

6. Discussion

As more SMARTs are implemented, it becomes increasingly important to provide practical and reliable methods for dealing with missing data. In this paper, we identified five key challenges to applying imputation methods to SMARTs, and proposed an imputation procedure to meet these challenges. We specified a joint distribution over all variables by using time-ordered nested conditional models, and used a BMEM to induce smoothness in longitudinal variables. While we used the CATIE study as an illustration, the issues we raised and addressed apply to SMARTs in general.

Dropout is a major source of missing data in all longitudinal studies, as it was in CATIE [23]. While strategies to minimize study dropout should be applied in the SMART setting, these strategies cannot completely eliminate participant dropout. For this reason, developing new, and evaluating existing, methods for accommodating missing data in SMARTs is an important area of research. Multiple imputation is one of several approaches for addressing the problem of missing data in these settings. Multiple imputation is a natural choice for CATIE because of the need to conduct a variety of secondary analyses. In particular, we not only want to facilitate a variety of longitudinal analyses, we also want to investigate the quality of several dynamic treatment regimes using different variables for individualizing treatment and possibly different outcomes, as illustrated in Section 5. Two alternate approaches to multiple imputation are inverse probability weighting and likelihood methods [22, 68, 69]; a comparison of multiple imputation to these methods is needed in the SMART setting.

There are a number of interesting directions in which this work might be extended. While it is common for data from a SMART to exhibit a (nearly) monotone missingness pattern, this need not always be the case. When the missingness pattern is not monotone, imputation models for variables measured at time t should utilize variables measured at subsequent times s > t. A principled approach to imputing data for non-monotone missing data in SMARTs is needed. Afurther issue is extending imputation models for longitudinal covariates with non-normal distributions, and constructing data-driven diagnostics to indicate when such extensions are needed. Additionally, multiple imputation relies on the untestable assumption that the data are missing at random (MAR). It is unclear how violations of the MAR assumption will impact the estimation of dynamic treatment regimes using data collected from a SMART. Specifically, it is unclear if violations of this assumption will differentially impact the results of different methods for managing missing data. In addition to the diagnostics, which can be found in the web appendix (web address), sensitivity analyses [70] could be performed to evaluate the impact of any violations to the MAR assumption on a particular analysis.