Abstract
Multiple Indicators, Multiple Causes Models (MIMIC) are often employed by researchers studying the effects of an unobservable latent variable on a set of outcomes, when causes of the latent variable are observed. There are times however when the causes of the latent variable are not observed because measurements of the causal variable are contaminated by measurement error. The objectives of this paper are: (1) to develop a novel model by extending the classical linear MIMIC model to allow both Berkson and classical measurement errors, defining the MIMIC measurement error (MIMIC ME) model, (2) to develop likelihood based estimation methods for the MIMIC ME model, (3) to apply the newly defined MIMIC ME model to atomic bomb survivor data to study the impact of dyslipidemia and radiation dose on the physical manifestations of dyslipidemia. As a by-product of our work, we also obtain a data-driven estimate of the variance of the classical measurement error associated with an estimate of the amount of radiation dose received by atomic bomb survivors at the time of their exposure.
Keywords: Atomic bomb survivor data, Berkson error, Dyslipidemia, Instrumental Variables, Latent variables, Measurement error, MIMIC models
1 Motivating Example
The presence of measurement error in assessing the impact of ionizing radiation on various health outcomes within an exposed cohort such as the survivor of the atomic bombs in Hiroshima and Nagasaki, Japan, is unavoidable [1]. Following the exposures in 1945, survivors in both Hiroshima and Nagasaki were identified based on the 1950 Japanese census survey and were interviewed to identify their location and shielding at the time of exposure. A radiation dosimetry system was subsequently developed for estimating the dosage of ionizing radiation received from the exposure. Individual dosage of radiation was estimated for each survivor of the bombings based on a physical dosimetry system that included inputs such as air moisture, bomb output, distance and environmental, global and local shielding. The initial dosimetry system used in estimating individual radiation dose was implemented in 1965, modified in 1986 (DS86) and updated in 2002, resulting in the current Dosimetry System 2002 (DS02). The dose estimates are based on survivor recall of their location (translated into distance) and shielding at the time of detonation, on outputs of the respective bombs, and humidity in the air, etc. Since these measures are based on survivor-reported measures of distance and observations on shielding, DS02 estimates are contaminated by measurement errors, which affect disease outcome model parameter estimates as well as parametric inferences [2–4]. The type of error introduced to the DS02 system due to its reliance on self-reported distance and shielding is a classical measurement error, u. The classical measurement error varies around the true value of radiation dose [1].
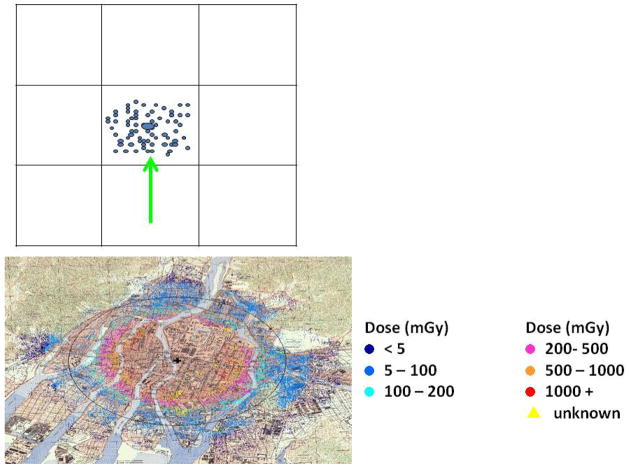
Once the self-reported measures of distance and shielding information have been obtained from the survivors, the survivors’ locations are placed on grids corresponding to coordinates on a US army map that was placed over the map of the city, see Figure 1. Individuals who reported having been at a particular location are classified into a square region of the grid and the estimated radiation dose associated with the center of each square is assigned to all individuals whose reported location puts them in the assigned square grid. The Berkson error or shared uncertainty in the DS02 system arises from assigning the estimated group mean radiation dose to individuals who reported having being at a location in close proximity to other group members [1, 3, 5–7]. It has recently been noted in the literature that both Berkson and classical measurement error need to be accounted for when performing analysis of the effects of radiation dose on various health outcomes among atomic bomb survivors [3].
Figure 1.
Illustration of Berkson error in DS02 estimates. The bottom map indicates a sample map which was placed over the city and the grids within which the survivor-reported distances from the hypocenter were classified. DS02 estimates were calculated by assigning the calculated dose for the center of the grid for all reported distances within each grid, introducing a shared error or Berkson error into the radiation dose estimation.
Dyslipidemia is a disorder which affects the lipoprotein metabolism and is usually physically manifested by an elevation of the individual’s total cholesterol or low density lipoprotein (LDL) cholesterol and triglyceride concentrations while decreasing the level of high density lipoprotein (HDL) cholesterol in the individual’s blood [8]. In studying the effects of radiation on the longitudinal trends of total serum cholesterol of the survivors of the atomic bombs in Hiroshima and Nagasaki, Japan, Wong et al. [9] use a growth curve model to study the cholesterol trends of the survivors over a 28 year period (1958–1986). In their longitudinal analysis, log(DS86) was used as an estimate of true radiation dose while adjusting for the classical measurement error associated with DS86 under the assumption that the coefficient of variation associated with the classical measurement error is 0.35. In studying the effects of radiation on risk factors for coronary heart disease (fatty liver, obesity, hypertension, hypercholesterolemia, low HDL cholesterol, hypertriglyeridemia and diabetes mellitus), Akahoshi and colleagues [10] studied Nagasaki survivors who had measured levels of risk factors of the cardio-metabolic risk syndrome between November 1990 and October 1992. The DS86 system was used to estimate radiation dose under the assumption of classical measurement error only and a coefficient of variation of 0.35.
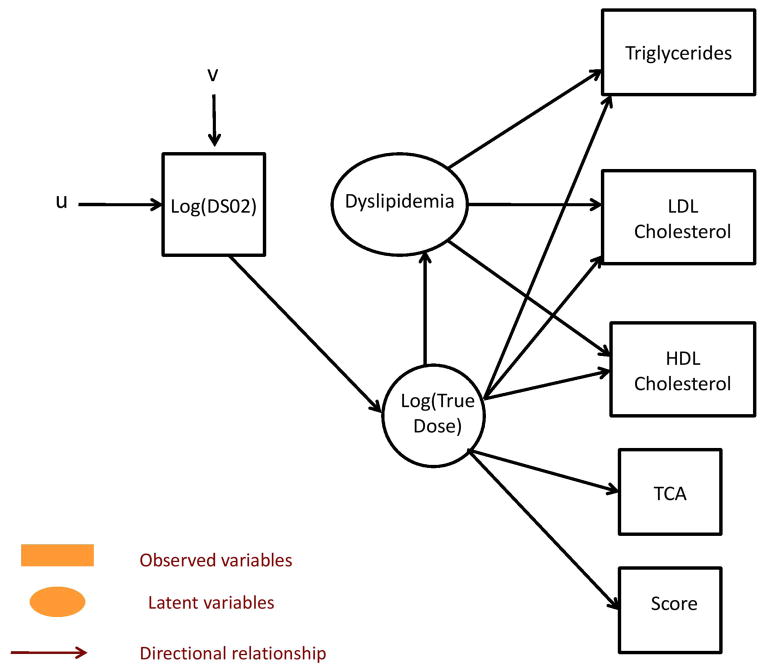
In this paper, we study dyslipidemia among atomic bomb survivors while recognizing that there are two sources of measurement error in the DS02 dosimetry system. We also recognize that dyslipidemia is a latent construct with three physical manifestations, see Figure 2. This example involves the studying of the effect of a latent construct, dyslipidemia, and latent true radiation dose on the physical outcomes of dyslipidemia (triglycerides, LDL and HDL cholesterol) among atomic bomb survivors, where true radiation dose is treated as an underlying cause of the latent dyslipidemia and is also allowed to have a direct effect on the outcomes of dyslipidemia, as indicated by the arrows from true dose to triglycerides, LDL, and HDL cholesterol. The arrow from true dose to dyslipidemia also indicates that true dose has an effect on the latent construct (see Figure 2). Dyslipidemia is a major risk factor for cardiovascular disease in diabetes mellitus [8], therefore it is important that both potential measurement errors be accounted for in understanding this disorder among atomic bomb survivors. In addition, since dyslipidemia is on the causal pathway to other cardio-metabolic diseases such as diabetes, which are becoming growing public health concerns, we would like to know if exposure to the ionizing radiation from the atomic bombs also has an impact on the physical manifestations of dyslipidemia. Since dyslipidemia is a latent construct which cannot be measured directly, using a multivariate model, one can assess the impact of true radiation dose on the multiple outcomes of dyslipidemia allowing us to better understand how true radiation dose impacts the development of dyslipidemia among individuals exposed to ionizing radiation. This paper is the first to assess the associations of dyslipidemia with its multiple indicators and the impact of radiation dose on the physical outcomes of dyslipidemia (triglycerides, LDL cholesterol and HDL cholesterol) in the presence of both classical and Berkson measurement error.
Figure 2.
Illustration of the dyslipidemia example. Dyslipidemia is a latent construct which is physically measured by triglycerides, HDL and LDL cholesterol levels. True radiation dose received at the time of exposure also has an impact on the physical measures of dyslipidemia (triglycerides, HDL and LDL cholesterol). True radiation dose is not directly observable, it is therefore estimated by log(DS02) which is affected by both classical (u) and Berkson (v) measurement errors. While transformed chromosome aberrations (TCA) and scores of acute symptoms of radiation exposure (score) are instrumental variables for true radiation dose.
In the next section, we provide a background on MIMIC models. The MIMIC ME model is defined in Section 3. The application, results and discussions from the application of the MIMIC ME model to our motivating example are presented in Sections 4 to 6, respectively.
2 Background
Multiple Indicators, Multiple Causes Models (MIMIC) [11, 12] are employed by researchers studying the effects of an unobservable latent variable, T, on a set of outcomes or indicators. The model has had a wide range of applications such as in evaluating effects of early experiences of tobacco use on current smoking [13], studying the behavioral and psychological symptoms of dementia [14], applied econometrics [15] and in studying physical and cognitive function among geriatric patients [16].
For individual i = 1, …, n, let Ti denote dyslipidemia or the unobservable latent variable of interest, and let Xi be a K × 1 vector of observable exogenous multiple causes of Ti. In our motivating example, true radiation dose, Xi is scalar. In the classical MIMIC model, one observes multiple indicators and multiple causes of a single latent variable [11, 12]. An indicator or observed outcome variable is one whose value is determined by the underlying latent variable. The multiple causes in the MIMIC model setting refer to the multiple predictors in the regression equation for the unobservable latent variable. These predictors are assumed to be causing the underlying latent construct. In a MIMIC model setting, the unobservable latent variable induces certain relationships among the observable variables. Here and throughout, we center all observed random variables so that they have mean zero. The model specification for the classical linear MIMIC model is that for j = 1, …, J indicators,
| (1) |
| (2) |
where Yij is the jth indicator (observed outcome) for the ith individual, εi1, …, εiJ are random errors, and ηi is the model error in the causal equation for Ti. Joreskog and Goldberger assume that all the random errors are mutually independent and normally distributed with mean zero. Because the model is the same if we multiply Ti by a constant and divide both α and ηi in equation (2) by that same constant, identifiability requires that var(ηi) must be known, and we set this variance = 1. The MIMIC model can be seen as an extension of a confirmatory factor analysis model which allows covariates.
In previous applications of the model, it has been assumed that the multiple causes, Xi, of the latent variable are all observed. There are times however when the causes of the latent variable are not observed because measurements of the causal variables are contaminated by measurement error, as in Section 1. The objectives of this paper are: (1) to develop a novel model by extending the classical linear MIMIC model to allow both Berkson and classical measurement errors, thus defining the MIMIC ME measurement error (MIMIC ME) model, (2) to develop likelihood based estimation methods to fit the model, (3) to apply the MIMIC ME model to atomic bomb survivor data to study the impact of dyslipidemia and radiation dose on the physical manifestations of dyslipidemia, and (4) to obtain a data-driven estimate of the variance of the classical measurement error associated with log(DS02), an estimate of the log amount of radiation dose received by atomic bomb survivors at the time of their exposure.
3 MIMIC Measurement Error Models
3.1 The General Model
The MIMIC model described in (1) and (2) assumes that the multiple causes, Xi, are measured without error. In our example, however, some of the multiple causes of the latent variable are not measured exactly, e.g., when the multiple causes are based on self-reported variables, such as self-reported distance in the atomic bomb survival data. It has been well documented that self-reported measures are often affected by recall bias and day-to-day variability, therefore, any statistical method used to analyze the data arising from self-reported measures need to account for the bias introduced by the self-reported measures [4, 17]. On the other hand, Berkson measurement error is introduced when a single predictor of the true value is assigned to all individuals within a group with a common underlying characteristic [5, 18]. An example of Berkson error is found with uranium workers where the observed radiation dose assigned to a uranium worker is based on the average radiation dose calculated for all miners within the same work location and period at the time of exposure [5]. In our example, these imperfect measures of the multiple causes introduce both classical and Berkson measurement error into the MIMIC model setting.
Let Wi denote the measured version of Xi, and let Zij be additional covariates measured without error found in the jth indicator equation. To incorporate the mixture of classical and Berkson measurement errors, we employ latent intermediate variables Li [5, 6, 19], so that the MIMIC measurement error model for the ith individual is
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
where Xi, Li, Wi and Ui are all K × 1 vectors, and ζ is K × K. The intermediate latent variables, Li, are intermediate between Xi and Wi and allow for the modeling of the mixture of measurement errors [4, 6, 19].
Equation (3) is an extension of Equation (1) by allowing the multiple causes of Ti and Xi, to be measured imperfectly prone to measurement error. Not only is the MIMIC measurement error model novel, but in MIMIC models in general a combination of Berkson and classical measurement errors has not been considered. We make the following assumptions.
The εij are conditionally independent with variance given the unobservable variables Ti, Xi and the error free covariates, Zij. This is a standard assumption in MIMIC models [11].
The components of Yi are multiple indicators of the underlying latent construct, Ti, and are assumed to be conditionally independent given the unobservable variables Ti, Xi and the error free covariates, Zij.
The random variables Vi, Ui and ηi have mean zero, are mutually independent and are independent of the εij’s. As in model (2), for identifiability var(ηi) = 1. We also define cov(
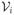 ) = Σvv with
and cov(Ui) = Σuu with
. The Vi and Ui are the vectors corresponding to the Berkson and classical measurement errors, respectively.
) = Σvv with
and cov(Ui) = Σuu with
. The Vi and Ui are the vectors corresponding to the Berkson and classical measurement errors, respectively.The causal variable, Ti, is independent of Vi, Ui, εi, and Zi.
The random variable ξi has mean zero, covariance matrix ΣL and is independent of all other random variables except Xi.
The Xi are independent of the error terms ηi and Ui.
3.2 Reduced Form Equations
The MIMIC measurement error model can be rewritten in its reduced form by substituting the causal equation (4) for Ti into the structural equation models (3) for the outcome variables. The reduced form equations for the ith subject thus combine (3)–(4) into
| (8) |
where κj = β1j + β2jα. The κj allows the assessment of the total effect of Xi on Yij. The estimation of the parameters in the models is based on the reduced form model. Therefore, the impacts of the latent causal variables on the outcome variables are assessed indirectly with their total effects, κj. Similarly, the impact of the underlying latent construct is assessed directly through β2j.
Model (5)–(8) thus forms the model for the observed data. As in any measurement error model, identifiability requires additional information on the measurement error process, and must be done on a case-by-case basis. In our example, this additional information comes from a combination of previous experiments and instrumental variables, see Section 4.
4 Application of the MIMIC Measurement Error Model With Instrumental Variables
4.1 Background on the Data Set
The development of the MIMIC measurement error model was motivated by studies of the effects of radiation exposure from the detonation of the atomics bombs over Hiroshima and Nagasaki, Japan. The atomic bomb survivor data maintained by the Radiation Effects Research Foundation [RERF, see http://rerf.jp] provides us with a rich resource for studying the effects of radiation on various health outcomes.
In assessing the relationship between dyslipidemia and radiation dose, we apply the MIMIC measurement error model to a subset of the Adult Health Study (AHS) cohort of the atomic bomb survivor data. The AHS cohort consists of 22,397 survivors with 15,054 Hiroshima and 7,343 Nagasaki survivors. The current study consists of 209 survivors in Nagasaki who were within 500 to 2500 meters of the hypocenter at the time of the exposure. Subjects who were seen between January, 1988 and January, 1996 are included in the analysis. Nagasaki survivors had blood measures taken between 1988 and 1996, therefore, these survivors had data on the outcomes. No validation data were available. In this application, dyslipidemia is the latent variable T while true radiation dose at the time of exposure is the scalar latent causal variable X.
4.2 The Data
Dyslipidemia is a metabolic syndrome with three outcomes: elevated levels of LDL cholesterol and triglycerides concentrations and decreased levels of HDL cholesterol. The J = 3 multiple indicators included in the current application are transformed to achieve normality (Y1, Y2, Y3), with Y1 being log{log(triglycerides)}, Y2 being log(low-density lipoprotein) and Y3 being the log(high-density cholesterol). These outcomes are assumed to be physical manifestations of dyslipidemia. The error-free covariates included in the indicator models are age at the time of measurement, sex, number of cigarettes smoked per day, and body mass index (BMI). There are two instrumental variables included in the analysis, namely M1 = log(TCA) and M2 = score. The instrumental variable, log(TCA), is a log transformation of the arc sine of the proportion of stable chromosome aberrations per cell in order to achieve normality. The score variable is a combination of epilation, bleeding of the gums and oral lesions, which are all indicators of acute exposure to radiation.
4.3 Model and Instruments
In our data, K = 1, so that X, W, L, U, V, Σuu and Σvv are all scalar, and we denote the latter two as and . Two instrumental variables are used to identify the variance of the classical measurement error, , while we assume is known based on a calculation from summary data from previous experiments. A side goal of our analysis is to obtain a data driven estimate of . Currently, a coefficient of variation 0.35, corresponding to a of 0.1155, is assumed by researchers largely based on weak evidence and/or heuristic terms. Again, remembering that all observed random variables are centered to have mean zero, the MIMIC measurement error model for our current application can then be expressed as (3)–(7) with the addition that for r = 1, 2,
| (9) |
where (ωi1, ωi2) are independent of all other random variables and has mean zero and covariance matrix . The instrument is dependent of course on the causal variable T, and we are assuming that the errors in (9) are independent given Xi, although this restriction can be relaxed. Obviously, the reduced form equations remain (8).
It is easy to develop conditions under which the model is identified as long as is known and additional information such as instrumental variables are available in the data, see the Appendix for a proof when instrumental variables are used as the identifying information. As it happens, in our example, was previously estimated based on previously collected data in Chapter 13 of [20] while an initial value of 0.181 is used for based on a previous estimate.
For modeling the multiple outcomes (Y1, Y2, Y3), we include the covariates Z1, consisting of age at measurement, sex, smoking status and body mass index. For the two instruments, we also include covariates Z21 consisting of age at which the TCA measure was obtained, sex, smoking status and body mass index, while Z22 consists of the age at time of exposure to the atomic bomb, sex, smoking status and body mass index.
4.4 Model Fitting
The models (3)–(9) can be fit in any number of ways. Because all components of these models are linear, the model can be fit consistently without distributional assumptions by assuming normality and computing the maximum likelihood estimator using the reduced form (5)–(9), which gives the mean and covariance matrix of (Yi1, …, YiJ, Wi, Mi1, …, Mir) given (Zi, Zi21, …, Zi2R). Indeed, since E(Xi|Zi) = ζZi, , E(Wi|Zi) = ζZi and E(Mir|Zi2r) = ζZiδ1r + Zi2rδ2r. In addition, since Xi = ζZi + ξi + Vi, . In addition, since Wi = ζZi + ξi + Ui, . In addition, . Of course, var(Wi|Zi) = ΣL + Σuu. Further, cov(Wi, Mir) = cov{ξi + Ui, (ξi + Vi)Tδ1r}ΣLδ1r, , and , where the (r, s) element of Σω is Σω(r, s). Hence the likelihood is easily computed analytically. Using matrix derivatives, it is then possible to implement Fisher-scoring, with analytical score and the expectation of the Hessian.
An alternative is to use an EM algorithm [21], and indeed it is even easier to implement a Monte-Carlo EM algorithm [22], based on the models (3)–(7) and (9), where we treat (Xi, Li, ηi) as missing data. Here the conditional distributions of the missing data given the observed data (Yi1, …, YiJ, Wi, Mi1, …, MiR) and the current values of the parameters are all normally distributed and analytically computable, and having generated values of the missing data, the structure of the models make the M-step trivial. We generated 2, 000 values of the missing data at each E-step for this purpose. The starting values for the coefficient on the error free covariates were obtained by fitting regression models to the observed outcomes under the assumption of no measurement error, while the coefficients on ηi and the unique variances for the manifest variables were obtained by fitting a principal components factor analysis model to the partial residuals from the manifest equations. The methods were implemented using R and WinBUGS. Details are available from the first author.
5 Results of the Example
5.1 Summary Statistics
In this section, we present the results from the application of the MIMIC measurement error model with instrumental variables to RERF data to study the effects of dyslipidemia and true radiation dose on the physical manifestations of dyslipidemia among atomic bomb survivors in Nagasaki, Japan. Table 1 provides the descriptive summary of the data used in the analysis. Our total sample size included in the analysis was 209. The number of individuals also used in the instrumental variable analysis was 209. About 41% of the sampled survivors in our analysis are males (n = 86) while about 59% (n = 123) of the sample are females. The range of the number of cigarettes smoked per day ranged from 0–40. The average estimated radiation dose was 1286.91 μGy or equivalently an average log(DS02) of 7.16 (SD = 0.60), while the average age of the survivors included in the analysis was 60.88 years.
Table 1.
Descriptive statistics of the outcomes and covariates included in the analytic sample.
| Variable | N | Mean | SD | Min | Max |
|---|---|---|---|---|---|
| log{log(trig)} | 209 | 1.55 | 0.10 | 1.30 | 1.864 |
| log(HDL) | 209 | 3.95 | 0.26 | 3.25 | 4.59 |
| log(LDL) | 209 | 5.00 | 0.25 | 4.41 | 5.59 |
| log(DS02) | 209 | 7.16 | 0.60 | 5.53 | 8.75 |
| log(TCA) | 209 | −1.55 | 0.45 | −2.30 | −0.47 |
| Score | 209 | 1.072 | 1.11 | 0.0 | 3.00 |
| Age | 209 | 60.88 | 9.25 | 43.24 | 83.92 |
| BMI | 209 | 22.38 | 3.16 | 13.90 | 29.90 |
| AGECA | 209 | 52.95 | 10.17 | 24.42 | 75.49 |
| AgeATB | 209 | 17.27 | 9.18 | 0.15 | 39.82 |
| Smoking | 209 | 4.65 | 9.81 | 0 | 40 |
Trig: triglycerides, HDL: high density lipoprotein cholesterol, LDL: low density lipoprotein cholesterol, DS02: radiation dosimetry 2002 (current dosimetry system used at the Radiation Effects Research Foundation), TCA: arc since of the proportion of stable chromosome aberrations per cell, Score: aggregate score of epilation, bleeding of gums, and oral lesions which are all indicators of acute exposure to radiation, age: at the time of measurement, BMI: body mass index, AGECA: age at the time of TCA collection, smoking: number of cigarettes smoked per day.
5.2 Analysis of Radiation Effects on the Instrumental Variables
We now discuss the results of the analysis of the instrumental variables. Table 2 provides a summary of the results from the assessment of the effect of true radiation dose on the log of transformed chromosome aberrations after adjusting for age at the time of CA measurement, sex, smoking and BMI. We found that the survivor’s gender, smoking status and BMI level have no statistical significant impact on the log of transformed chromosome aberrations with p-values of 0.28, 0.43 and 0.073 respectively, after controlling for other variables in the model. Survivor’s age at the time of measurement had a statistically significant effect on this outcome (p-value < 0.0001). Our analysis also confirmed a statistically significant association between chromosome aberrations and radiation dose (p-value < 0.0001) after adjusting for ageCA, sex, smoking, and BMI. The variance of the error term in the model was estimated to be 0.1169. Approximately, 41% of the variation is explained by the effect of radiation dose.
Table 2.
Results from the analysis of log(TCA), where TCA is the arc sine transformation of the proportion of chromosome aberrations per cell. The covariates included in the model are age at measurement, gender, number of cigarettes smoking per day, BMI, and true radiation.
| Variable | β̂ | SE | P-value |
|---|---|---|---|
| Age | 0.006 | 0.0017 | < 0.0001 |
| Sex | −0.044 | 0.04 | 0.28 |
| Smoking | −0.002 | 0.002 | 0.43 |
| BMI | −0.009 | 0.005 | 0.073 |
| True Dose | 0.49 | 0.0103 | < 0.0001 |
| R2 {Radj(z)2} | 0.12 | 0.43 | 0.41 |
In Table 3, we report the results of the modeling of the aggregate score of acute symptoms of exposure to radiation as an instrumental variable for true radiation dose. We found that the survivor’s gender, smoking status and BMI had no statistically significant effects on the survivor’s acute symptoms as measured by the aggregate score (p-value = 0.15, 0.47, 0.26, respectively) after adjusting for the other error free covariates and true radiation dose. Age at the time of bombing or exposure had a statistically significant effect (p-value = 0.004) after adjusting for the other error free covariates and true radiation dose. That is, the older the survivor at the time of exposure, the higher the score of acute symptoms. We also found a statistically significant relationship between true radiation dose and the acute symptoms score (p-value < 0.0001). The estimated for this model was 0.83, while the R2 was 0.31. The percent of the score of acute symptoms of radiation explained by the presence of radiation dose in the model was 33%.
Table 3.
Results from the analysis of Score, where score is an aggregate score of the acute symptoms of radiation dose exposure. The covariates included in the model are age at the time of exposure, gender, number of cigarettes smoking per day, BMI, and true radiation.
| Variable | β̂ | SE | P-value |
|---|---|---|---|
| Age | 0.015 | 0.0051 | 0.004 |
| Sex | −0.154 | 0.11 | 0.15 |
| Smoking | 0.004 | 0.006 | 0.47 |
| BMI | 0.016 | 0.144 | 0.26 |
| True Dose | 1.02 | 0.022 | < 0.0001 |
| R2 {Radj(z)2} | 0.83 | 0.31 | 0.33 |
5.3 Analysis of Triglycerides
Table 4 provides the results from fitting the outcome model for transformed triglycerides. Based on our fit, we find that there is a highly statistically significant relationship between triglycerides and dyslipidemia (p-value < 0.0001) after adjusting for the effects of age, sex, smoking status, BMI and radiation dose. As the dyslipidemia becomes more severe, triglycerides levels increase. True radiation dose was also found to have a highly statistically significant effect on the survivor’s triglyceride level (p-value < 0.0001) after adjusting for age at the time of triglyceride measurement, sex, number of cigarettes smoked per day, BMI and dyslipidemia. The effects of true radiation dose are assessed indirectly through its total effects, κ̂1. Age, sex, smoking and BMI were also found to have statistically significant effects on the triglyceride level (p-value < 0.0001, < 0.0001, < 0.0001, < 0.0001, respectively) after adjusting for the other covariates in the model. Male survivors generally had higher levels of triglycerides when compared to the females in the study. Also, on average, as the survivor’s age increases by a year, we predict a decrease of 0.0019 in the individual’s transformed triglyceride level when holding the other covariates included in the analysis constant. Increasing BMI, by one unit, results in an increase of 0.01 in the survivor’s log{log(trig)} level after adjusting for all the other covariates included in the model. After adjusting for both the Berkson and classical measurement errors as well as the error free covariates and dyslipidemia, we find that on average log{log(trig)} is increased by 0.014 when the survivor’s true radiation dose is increased by one unit while an increase of 0.094 is expected in log{log(trig)} when dyslipidemia is increased by one unit after adjusting for all the covariates included in the analysis.
Table 4.
Results from the analysis of log{log(triglycerides)}. The covariates included in the model are age at measurement, gender, number of cigarettes smoking per day, BMI, true radiation dose and dyslipidemia. The table also includes the estimated variance and adjusted correlations coefficients.
| Variable | β̂ | SE | P-value |
|---|---|---|---|
| Age | −0.0019 | 0.0004 | < 0.0001 |
| Sex | −0.02 | 0.0008 | < 0.0001 |
| Smoking | 0.0002 | 0.00004 | < 0.0001 |
| BMI | 0.009 | 0.00011 | < 0.0001 |
| True Dose | 0.014 | 0.0006 | < 0.0001 |
| Dyslipidemia | 0.094 | 0.0003 | < 0.0001 |
| (R2) | 0.00(0.99) | ||
| Radj(η)2 {Radj(z)2} | 0.85(0.01) |
The partial R2 value for dyslipidemia in this model was calculated and found to be 0.85 {0.0942/(0.1022)}. Therefore, we find that after adjusting for true radiation dose and all the error free covariates, approximately 85% of the total variation in the transformed triglyceride data can be explained by variation in the severity of dyslipidemia. The variance of the error term in the model was estimated to be 0.00005 and the full model R2 was 0.995 {= (0.1022 − 0.0005)/(0.1022)}. The model error variance for this model was estimated to be close to zero because the estimate was converging to zero as we increase the number of MCEM iterations. Thus, we have a boundary value problem in this analysis. Inferences concerning the parameters included in the model are affected by the boundary value problem. An explanation for this result is that log{log(trig)} is highly correlated with the latent construct, dyslipidemia. Approximately, 2% of the variation is explained by the total effect of radiation dose.
5.4 Analysis of LDL Cholesterol
Table 5 provides the results for fitting the outcome model for the log of LDL cholesterol. Based on our fit, we find that there is a statistically significant relationship between LDL cholesterol and the latent construct, dyslipidemia (p-value < 0.0001) after adjusting for the potential effects of age, sex, smoking status, BMI and true radiation dose. In fact, as the survivor’s level of dyslipidemia increases, so does the LDL cholesterol level. True radiation dose was not found to have a statistically significant effect on the survivor’s bad cholesterol level (p-value = 0.14) after adjusting for the other covariates in the model. The survivor’s gender and BMI level were both found to have statistically significant relationships with LDL cholesterol level (p-value < 0.0001 and < 0.0001, respectively) after adjusting for the other covariates included in the model. There was no statistical significant relationship between the survivor’s LDL cholesterol level and the survivor’s age or the number of cigarettes smoked per day (smoking) after adjusting for the other covariates included in the model (p-value = 0.42 and 0.49, respectively). We find that the females included in the study had higher LDL cholesterol levels than did the males included in the study, while a one unit increase in the survivor’s BMI level on average resulted in an increase of 0.022 in log(LDL) after adjusting for the other covariates included in the model. After adjusting for radiation dose and the error free covariates, we find that the survivor’s log(LDL) increases by 0.093 for each unit increase in the latent construct, dyslipidemia.
Table 5.
Results from the analysis of log(LDL cholesterol). The covariates included in the model are age at measurement, gender, number of cigarettes smoking per day, BMI, true radiation dose and dyslipidemia. The table also includes the estimated variance and adjusted correlations coefficients.
| Variable | β̂ | SE | P-value |
|---|---|---|---|
| Age | −0.0009 | 0.0011 | 0.42 |
| Sex | 0.132 | 0.024 | < 0.0001 |
| Smoking | −0.00085 | 0.0012 | 0.49 |
| BMI | 0.022 | 0.0032 | < 0.0001 |
| True Dose | 0.025 | 0.017 | 0.14 |
| Dyslipidemia | 0.093 | 0.01 | < 0.0001 |
| (R2) | 0.04 (0.33) | ||
| Radj(η)2 {Radj(z)2} | 0.14(0.00) |
The partial R2 for dyslipidemia indicates that approximately 14% of the total variation in the LDL cholesterol data can be explained by the variation in dyslipidemia. The variance for the error term in the model is estimated to be 0.042, and the overall R2 for the model was 0.327. Approximately, 0.35% of the variation is explained by the total effect of radiation dose.
5.5 Analysis of HDL Cholesterol
Table 6 provides the results for fitting the model for log(HDL) cholesterol. There was a statistically significant relationship between log(HDL) and dyslipidemia (p-value < 0.0001) after adjusting for the potential effects of age, sex, smoking status, BMI and true radiation dose. As the dyslipidemia level increases, the log(HDL) cholesterol decreases, indicating an inverse relationship between dyslipidemia and the HDL cholesterol. True radiation dose is also found to have a highly statistically significant effect on the survivor’s log(HDL) level (p-value = 0.001) after adjusting for the error free covariates and dyslipidemia. The survivor’s gender and BMI were statistically significant (p-value = 0.009 and < 0.0001, respectively) after adjusting for the other covariates included in the analysis. No statistically significant effect was found for the age of the survivor at the time of measurement (p-value = 0.61) after adjusting for the other error free covariates, dyslipidemia and true radiation dose. Women generally had higher log(HDL) levels than the men in the study. A one unit increase in BMI results in a reduction of 0.024 in log(HDL) when holding the other error free covariates, true radiation dose and dyslipidemia constant. We also found that an increase of one unit in true radiation dose results in a decrease of 0.06 in log(HDL), on average, when holding dyslipidemia and the error free covariates constant. A reduction of 0.10 in log(HDL) was seen with a one unit increase in dyslipidemia.
Table 6.
Results from the analysis of log(HDL cholesterol). The covariates included in the model are age at measurement, gender, number of cigarettes smoking per day, BMI, true radiation dose and dyslipidemia. The table also includes the estimated variance and adjusted correlations coefficients.
| Variable | β̂ | SE | P-value |
|---|---|---|---|
| Age | 0.0006 | 0.0012 | 0.61 |
| Sex | 0.068 | 0.026 | 0.009 |
| Smoking | −0.0021 | 0.001 | 0.014 |
| BMI | −0.024 | 0.0035 | < 0.0001 |
| True Dose | −0.06 | 0.0184 | 0.001 |
| Dyslipidemia | −0.10 | 0.01 | < 0.0001 |
| (R2) | 0.05 (0.28) | ||
| Radj(η)2 {Radj(z)2} | 0.15(0.018) |
The partial R2 for dyslipidemia was 0.15 indicating that approximately 15% of the variation in the HDL cholesterol data is due to variation in dyslipidemia while the overall R2 for the model was 0.281. The variance for the error term in the model was estimated to be 0.0492. Approximately, 18% of the variation is explained by the total effect of radiation dose.
5.6 Estimating
Two instrumental variables were used to identify the model due to the presence of the classical measurement error, u, in the amount of radiation received by the survivors. Based on our analysis, was estimated to be 0.092. Our estimated value for is based on an adjustment for both classical and Berkson measurement errors.
The corresponding coefficient of variation based on our estimated value for is 0.31. The current coefficient of variation being used at RERF is 0.35, which corresponds to a of 0.1156. The estimated mean for L was μ̂L = 7.16 while . In summary, we assume is known and while two instrumental variables are used to identify allowing us to have sufficient moments to identify the model parameters.
5.7 Impact of Measurement Error on Parameter Estimates
In this section, we briefly discuss the impact of not adjusting for the mixture of measurement errors on the estimated coefficients from the MIMIC ME model. The impact of classical measurement error in a simple linear regression model with an additive classical measurement error is to attenuate the parameter estimates toward zero [4]. While the naive parameter estimates obtained in the presence of Berkson measurement error alone in the simple linear regression model are unbiased [4]. However, the impact of the mixture of these two measurement errors on the parameter estimates in a multiple regression setting is more complex. In our current application, most of the estimated coefficients from the indicator models remain unchanged when comparing the measurement error adjusted coefficients to the unadjusted coefficients. However, the coefficient on true dose was estimated to be 0.025 in measurement error adjusted model for log(LDL) while the unadjusted estimated coefficient was 0.004. We also observed a downward bias on the coefficients for true radiation dose in the instrumental variable models when we failed to adjust for the measurement errors. The coefficient for true radiation dose after the adjustment in the log(TCA) model was 0.049 while the unadjusted estimated coefficient was 0.36. Similarly, in the instrumental variable model for the aggregate score of the acute symptoms of radiation dose exposure, we found the estimated coefficient on true radiation dose to be 1.02 while it was estimated to be 0.745 in the unadjusted model. The error free covariates in the unadjusted models were equivalent to the estimated coefficients under the mixed measurement error adjusted models. In summary, we conclude that the impact of adjusting for the mixture of measurement errors in the MIMIC ME model is massive but its direction depends on the model.
5.8 Simulation Study on the Impact of the Magnitude of the Measurement Error Values on the Parameter Estimates
Pierce et al. [3] find that after adjusting for both types of measurement error in assessing cancer risk, the risk estimates were not very sensitive to the assumed magnitudes of the radiation dose errors. In this section, we assess the impact of the assumed magnitude of the radiation dose error for both types of measurement errors on the estimated coefficients. We also assess the impact of these assumed values in obtaining a data driven estimate for the variance of the classical measurement error, . In our simulation study, the estimated model parameters from the adjusted MIMIC ME models were treated as the true parameter values and we allowed the value of the variance of the Berkson error, , to range from 0.02 to 0.08 while the values of ranged between 0.05 to 0.25.
Based on our simulation study, we find that the estimated parameters were not very sensitive to the assumed values of both and . We also find the same patterns on the coefficients on true radiation dose and dyslipidemia over all the range of the values considered for the dose errors. However, as increased to 0.08, we find that the estimated coefficients on radiation dose, log(TCA), and score slightly reduced from their true parameter value when compared to the estimated values obtained under and .
The objective of this application was to assess the impact of radiation dose on the indicators of dyslipidemia among survivors of the atomic bomb. However, by applying our proposed model, we are also able to obtain a data driven estimate for as a by-product of the model. In our simulation study, we also assessed the impact of the magnitudes of the assumed values for the dose errors in obtaining a data driven estimate for . We find that the estimated value for is highly dependent on the assumed value for , as the value of increases, the data driven estimate for decreases. We also find that the estimated value for is highly sensitive to the data as well as the true value of the parameters.
6 Discussion
In this paper, we developed and applied the MIMIC measurement error model with instrumental variables to assess the impact of true radiation dose and dyslipidemia on the physical manifestations of dyslipidemia. In addition to studying the relationship between true radiation dose and dyslipidemia on the physical manifestations of dyslipidemia, a by-product of these analyses was to obtain a data driven estimate for the variance of the classical measurement error, .
In addition to estimating , we applied our defined model to assess the impact of true adjusted radiation dose on the physical outcomes of dyslipidemia. Based on our analysis, we found that exposure to radiation has an impact on all three physical manifestations of dyslipidemia, namely, triglycerides, LDL and HDL cholesterol.
Our current analysis confirms the previous finding reported on the relationship between dyslipidemia and radiation dose, as well as the relationship between radiation dose and cholesterol levels. The advantage of the current analysis is that it accounts for the effects of both Berkson and classical measurement error by using an instrumental variable approach and has, therefore, resulted in a data driven estimate for . The data driven estimate for provides an alternative estimate for which can be used to reduce the bias introduced by the presence of classical measurement error in obtaining radiation dose risk estimates among individuals exposed to ionizing radiation.
Acknowledgments
This work represents part of the Ph.D. dissertation at the University at Buffalo of the first author. The Radiation Effects Research Foundation (RERF), Hiroshima and Nagasaki, Japan is a private, non-profit foundation funded by the Japanese Ministry of Health, Labour and Welfare (MHLW) and the U.S. Department of Energy (DOE), the latter in part through the DOE Award DE-HS0000031 to the National Academy of Sciences. This publication was supported by RERF Research Protocol RP 18-59. Tekwe was also supported by a research assistantship from University at Buffalo’s Department of Biostatistics and a postdoctoral training grant from the National Cancer Institute (R25T - CA090301). Carroll’s research was supported by a grant from the National Cancer Institute (R27-CA057030). This publication is based in part on work supported by Award Number KUS-CI-016-04, made by King Abdullah University of Science and Technology (KAUST). The views of the authors do not necessarily reflect those of the two governments.
Appendix: Sketch of Technical Arguments
A.1 Identifiability and Method of Moments Estimates in the Example
In our data, we know . The unknown parameters that appear in the covariance matrix are , Σω, (β21, …, β2J), (κ1, …, βJ), (δ11, …, δ1R). In our example, R = 2, J = 3 and there are thus 16 unknown parameters in the covariance matrix of (Yi1, …, YiJ, Wi, Mi1, …, Mir). However, as seen in Section 4.4, there are 21 sufficient statistics for the covariance matrix, and so at least in principle the parameters are over-identified from the sufficient statistics.
Taking J = 3 and R = 2, the parameters other than (β21, …, β2J) and (
) are readily identified from moments calculations. For example,
, and hence
is identified. Then for example,
and hence δ1r is identified. Similarly,
, so that κj is identified, and of course
, and thus
is identified. By appropriate subtraction of these identified terms, we are left with a covariance matrix arising from the factor model
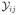 = β2jηi + εij, and thus (
) are identified as are the absolute values of (β21, …, β2J). Since the parameters in the covariance matrix are identified, it is readily seen that the remaining unknown parameters in the mean functions are also identified. These calculations also lead to good starting values for the parameters.
= β2jηi + εij, and thus (
) are identified as are the absolute values of (β21, …, β2J). Since the parameters in the covariance matrix are identified, it is readily seen that the remaining unknown parameters in the mean functions are also identified. These calculations also lead to good starting values for the parameters.
Contributor Information
Carmen D. Tekwe, Email: cdtekwe@srph.tamhsc.edu, Department of Epidemiology and Biostatistics, Texas A&M University, 1266 TAMU, College Station, TX 77843-1266
Randy L. Carter, Department of Biostatistics, University at Buffalo, 706 Kimball Tower, Buffalo, NY, 14214-3000
Harry M. Cullings, Department of Statistics, Radiation Effects Research Foundation, Hiroshima, Japan
Raymond J. Carroll, Department of Statistics, Texas A&M University, 3143 TAMU, College Station, TX 77843-3143
References
- 1.Heid IM, Kuchenhoff H, Miles J, Kreienbrock L, Wichmann HE. Two Dimensions of Measurement Error: Classical and Berkson Error in Residential Radon Exposure Assessment. Journal of Exposure Analysis and Environmental Epidemiology. 2004;14:365–377. doi: 10.1038/sj.jea.7500332. [DOI] [PubMed] [Google Scholar]
- 2.Jablon S. Technical Report TR 23–71. 1971. Atomic Bomb Radiation Dose Estimation at ABCC. [Google Scholar]
- 3.Pierce DA, Vaeth M, Cologne JB. Allowance for Random Dose-Estimation Errors in Atomic Bomb Survivors Studies: A Revision. Radiation Research. 2008;170:118–126. doi: 10.1667/RR1059.1. [DOI] [PubMed] [Google Scholar]
- 4.Carroll RJ, Ruppert D, Stefanski LA, Crainiceanu CM. Measurement Error in Nonlinear Models: A Modern Perspective. 2. Chapman and Hall; New York: 2006. [Google Scholar]
- 5.Schafer DW, Gilbert ES. Some Statistical Implications of Dose Uncertainty in Radiation Dose Response Analyses. Radiation Research. 2006;166(1):303–312. doi: 10.1667/RR3358.1. [DOI] [PubMed] [Google Scholar]
- 6.Mallick B, Hoffman FO, Carroll RJ. Semiparametric Regression Modeling with Mixtures of Berkson and Classical Error with Application to Fallout from the Nevada Test Site. Biometrics. 2002;58(1):13–20. doi: 10.1111/j.0006-341x.2002.00013.x. [DOI] [PubMed] [Google Scholar]
- 7.Li Y, Guolo A, Hoffman FO, Carroll RJ. Shared Uncertainty in Measurement Error Problems, with Application to Nevada Test Site Fallout. Biometrics. 2007;63:1226–1236. doi: 10.1111/j.1541-0420.2007.00810.x. [DOI] [PubMed] [Google Scholar]
- 8.Mooradian AD. Dyslipidemia in Type 2 Diabetes Mellitus. Nature Clinical Practice. 2009;5:150–159. doi: 10.1038/ncpendmet1066. [DOI] [PubMed] [Google Scholar]
- 9.Wong FL, Yamada M, Sasaki H, Kodama K, Hosoda Y. Effects of Radiation Research on the Longitudinal Trends of Total Serum Cholesterol Levels in the Atomic Bomb Survivors. Radiation Research. 1999;151:736–746. [PubMed] [Google Scholar]
- 10.Akahoshi M, Seto S. Ionizing Radiation is Related to Fatty Liver and Dsylipidemia among Atomic Bomb Survivors in Nagasaki. Circulation Journal. 2002;66(Suppl 1) [Google Scholar]
- 11.Joreskog KG, Goldberger AS. Estimation of a Model with Multiple Indicators and Multiple Causes of a Single Latent Variation. Journal of American Statistical Association. 1975;70:631–639. [Google Scholar]
- 12.Chen C. The EM Approach to the Multiple Indicators and Multiple Causes Model via the Estimation of the Latent Variable. Journal of American Statistical Association. 1981;76:704–708. [Google Scholar]
- 13.Rios-Bedoya CF, Pomerleau CS, Neuman RJ, Pomerleau OF. Using MIMIC Models to Examine the Relationship between Current Smoking and Early Smoking Experiences. Nicotine and Tobacco Research. 2009;11:1035–1041. doi: 10.1093/ntr/ntp093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Proitsi P, Hamilton G, Tsolaki M, Lupton M, Daniilidou M, Hollingworth P, Archer N, Foy C, Stylios F, McGuinness B, Todd S, Lawlor B, Gill M, Brayne C, Rubinstzein DC, Owen M, Williams J, Craig D, Passmore P, Lovestone S, Powell JF. A Multiple Indicators Multiple Causes (MIMIC) Model of Behavioural and Psychological Symptoms in Dementia (BPSD) Neurobiology of Aging. 2011;32:434–442. doi: 10.1016/j.neurobiolaging.2009.03.005. [DOI] [PubMed] [Google Scholar]
- 15.McCluskey JJ, Quagrainie KK. Measurement of Industry Conduct with a Latent Structure. Journal of Applied Econometrics. 2004;19:887–897. [Google Scholar]
- 16.Mast BT, Lichtenberg PA. Assessment of Functional Abilities among Geriatric Patients: A MIMIC model of the Functional Independence Measure. Rehabilitation Psychology. 2000;45(1):49–64. [Google Scholar]
- 17.Fuller W. Measurement Error Models. Wiley; New York: 1987. [Google Scholar]
- 18.Berkson J. Are there two regressions? Journal of American Statistical Association. 1950;45:164–180. [Google Scholar]
- 19.Reeves GK, Cox DR, Darby SC, Whitley E. Some Aspects of Measurement Error in Explanatory Variables for Continuous and Binary Regression Models. Statistics in Medicine. 1998;17:2157–2177. doi: 10.1002/(sici)1097-0258(19981015)17:19<2157::aid-sim916>3.0.co;2-f. [DOI] [PubMed] [Google Scholar]
- 20.Young RW, Kerr GD, editors. Reassessment of the Atomic Bomb Radiation Dosimetry for Hiroshima and Nagasaki: Dosimetry 2002. The Radiation Effects Research Foundation; Hiroshima, Japan: 2005. [Google Scholar]
- 21.Dempster AP, Laird NM, Rubin DB. Maximum Likelihood From Incomplete Data via the EM Algorithm. JRSS B. 1977;39:1–38. [Google Scholar]
- 22.Wei GCG, Tanner MA. A Monte Carlo Implementation of the EM Algorithms and the Poor Man’s Data Augmentation Algorithms. Journal of the American Statistical Association. 1990;85:669–704. [Google Scholar]