Efficient Blockwise Permutation Tests Preserving Exchangeability

Abstract

In this paper, we present a new blockwise permutation test approach based on the moments of the test statistic. The method is of importance to neuroimaging studies. In order to preserve the exchangeability condition required in permutation tests, we divide the entire set of data into certain exchangeability blocks. In addition, computationally efficient moments-based permutation tests are performed by approximating the permutation distribution of the test statistic with the Pearson distribution series. This involves the calculation of the first four moments of the permutation distribution within each block and then over the entire set of data. The accuracy and efficiency of the proposed method are demonstrated through simulated experiment on the magnetic resonance imaging (MRI) brain data, specifically the multi-site voxel-based morphometry analysis from structural MRI (sMRI).

1. INTRODUCTION

Hypothesis testing has been widely used in neuroimaging data analysis, such as morphometry analysis [1–5], brain activation detection and inference [6–10], and functional integration and connectivity [11]. Traditionally, brain imaging researchers perform statistical analysis by using parametric hypothesis testing, including commonly used F test, t test, Z test and Hotelling’s T² test [6, 10–12]. In general, a parametric method models the distribution of a test statistic with a parametric form which is mathematically tractable. Parametric methods work well when data can be modelled as independent and normally distributed. However, in neuroimaging studies, the data distribution is usually unknown. If the sample size is too small, this can lead to biased or incorrect results, as there is no guarantee that the Central Limit Theorem underlying many standard parametric tests will hold. Furthermore, sometimes, certain test statistics are desirable but mathematically intractable. Nonparametric hypothesis testing methods are preferable in these cases [4, 7, 8, 13]. Bootstrapping and permutation tests are both popular and computationally intensive nonparametric methods but primarily for different uses. The bootstrapping is best for estimating confidence intervals and the permutation test is best for testing hypotheses. Some detailed comparison between bootstrapping and permutation can be found in Good’s book [14, chapter 3]. In this paper, we focus on permutation tests.

In order to deal with small sample size neuroimaging data with unknown distribution, nonparametric permutation tests are employed [4, 7]. Permutation tests construct the distribution of a test statistic by resampling data without replacement. They are flexible and distribution-free. The key assumption for permutation tests is data exchangeability; that is, permutation tests are exact only if the rearranged data points are exchangeable under the null hypothesis. In the two-sample hypothesis testing case, data exchangeability means the distributions of two group data are identical under the null hypothesis [14, 15]. We can then randomly permute n_a data to one group and the remainder n_b data to the other group. Here, n_a and n_b are the sample sizes of the two groups. As a result, the empirical distribution of a test statistic is constructed using test statistic values for all possible permutations. The original observation can be considered as one of all possible permutation setups. To measure how strongly the observed data support the null hypothesis, we calculate the p-value by dividing the frequency of permutations having more extreme test statistic values by the number of all permutations. The statistical decision is made based on whether the p-value is less than a pre-chosen significance level. We reject the null hypothesis if the p-value is smaller than the pre-chosen significance level since it is unlikely to occur under the null hypothesis.

In real applications, the data exchangeability condition is not always valid. Although permutation tests still work when the exchangeability assumption is slightly violated, it is important to preserve data exchangeability to a reasonable level [14, 15]. In neuroimaging data analysis, the main effect (i.e. the effect of interest or the effect to be tested) is often confounded with the undesirable artifacts. For example, multi-site studies of neuroanatomical structures are increasingly becoming a standard element of clinical neurodegenerative research for diagnosing and evaluating neurological impairments [1, 16]. Multi-site collaboration is needed due to the quantitative and demographic nature of the study. One of the challenges of analyzing data from different sites is the image variability caused by technological factors (e.g., hardware differences, hardware imperfections), as such variability may be confounded with specific disease-related changes in the images thus limiting the power to detect structural differences over different populations. The exchangeability of the data from different sites is often violated because different MRI scanners typically have different inhomogeneity fields [17–19]. The spatial artifacts listed above in sMRI can be reduced in the data preprocessing but are unlikely to be taken away completely [17–19]. Therefore, the global data exchangeability does not usually hold. Nichols and Holmes [8] proposed a restrictive permutation scheme by segmenting the entire dataset into certain blocks such that the data exchangeability approximately holds within a block. The similar strategy can also be applied to the multi-site case by grouping data based on sites. The blockwise permutation tests only allow permutations within each block to preserve data exchangeability and prohibit any permutation across blocks.

Another critical issue involved in permutation tests is the computational complexity. There are three common approaches to construct the permutation distribution [14, 20, 21]: (1) exact permutation enumerating all possible arrangements; (2) approximate permutation based on random sampling from all possible permutations; (3) approximate permutation using the analytical moments of the exact permutation distribution under the null hypothesis. The main disadvantage of the exact permutation is the computational cost, due to the factorial increase in the number of permutations with the increasing number of subjects. The second technique often gives inflated type I errors caused by random sampling. When a large number of repeated tests are needed, the random permutation strategy is also computationally expensive to achieve satisfactory accuracy. Regarding the third approach, the exact permutation distribution may not have moments or moments with tractability. In most applications, it is not the existence but the derivation of moments that limits the third approach. In [13], we proposed a solution by converting the permutation of data to that of the statistic coefficients symmetric to the permutation. Since the test statistic coefficients usually have simple presentations, it is often easier to track the permutation of the test statistic coefficients than that of data. However, this method requires the derivation of the permutation for each specific test statistic, which is not easily accessible in real world scenarios. Recently, we have been developing a new, computationally efficient and more general recursive algorithm to calculate the moments of the permutation distribution by a simple sumproduct of data partition sums and index partition sums [5]. The data partition sums and index partition sums are computed recursively, from the simplest to the most complex sum. For the first four moments, the computation can be done in the first order or third order polynomial time for univariate and multivariate test statistics, respectively. Given the first four moments, the permutation distribution can be well fitted by the Pearson distribution series [22]. Extensive validation of accuracy or error rate when the Pearson distribution is used to approximate the permutation distribution has been performed in our previous work [5, 13].

In this paper, we propose and develop a novel moments-based blockwise permutation test method. We first divide the entire set of data into certain blocks. For each block, we apply our new recursive algorithm to obtain the first four moments. The first four moments of the entire set of data are computed by combining the first four moments from all blocks through an efficient representation. With this computationally efficient moments-based blockwise permutation tests scheme, we maintain the flexibility of permutation tests, preserve the exchangeability condition, and reduce the computational cost dramatically. We apply the proposed method to neuroimaging data for voxel-based morphometry from simulated multi-site sMRI, compensating for the undesirable spatial effects/artifacts with more sensitive and robust imaging data analyses.

2. METHODOLOGY

In this section, we first briefly describe and summarize our efficient algorithm for moments calculation. Then we demonstrate the idea of blockwise permutation tests in Section 2.2, using sMRI as an illustrating example. In Section 2.3, we propose our efficient moments-based blockwise permutation tests algorithm.

2.1. Computationally Efficient Moments Calculation

Here, we assume that the test statistic T can be expressed as a weighted v-statistic [5, 23] of degree d as following:

$$T(x)=\sum _{i_1=1}^n\cdots \sum _{i_d=1}^{n}w(i,\cdots ,i_d)h(x_{i_1},\cdots x_{i_d}),$$

where x = (x₁,x₂,…,x_n )^T is a dataset with n observations, w is an index function, and h is a symmetric data function that is invariant under permutation of (i₁,…, i_d ). If the data function h is not symmetric, the symmetric function $1/d!{\displaystyle \sum _p}h(x_{i_1},\cdots ,x_{i_d})$ may be used as a replacement, with ${\displaystyle \sum _p}$ denoting summation over all permutations of (i₁,…, i_d ). Note that each observation x_k can be either univariate or multivariate. In this way, the r-th moment of the test statistic from the permutated data is represented as:

$$\begin{array}{l}{E}_{\pi }(T^r(x))=E_{\pi }{(\sum _{i_1,i_2,\cdots ,i_d}w(i_1,\cdots ,i_d)h(x_{\pi (i_1)},\cdots ,x_{\pi (i_d)}))}^r\\ =E_{\pi }[\sum _{\begin{array}{l}{i_1}^{(1)},\cdots ,{i_1}^{(r)},\\ \cdots \\ {i_d}^{(1)},\cdots ,{i_d}^{(r)}\end{array}}\{(\prod _{k=1}^{r}w({i_1}^{(k)},\cdots ,{i_d}^{(k)})(\prod _{k=1}^{r}h(x_{\pi ({i_1}^{(k)})},\cdots ,x_{\pi ({i_d}^{(k)})})\}],\end{array}$$ (1)

where Π is the permutation operator. Any moment of permutation distribution can therefore be considered as a summation of the product of data function term and index function term over a high dimensional index set and all possible permutations.

To address the high computational cost in calculating the summation directly, we can exchange the summation order of the permutations and the indices. Eq. (1) thus takes the form below:

$$E_{\pi }(T^r(x))=\sum _{\begin{array}{l}{i_1}^{(1)},\cdots ,{i_1}^{(r)}\\ \cdots \\ {i_d}^{(1)},\cdots ,{i_d}^{(r)}\end{array}}\{(\prod _{k=1}^{r}w({i_1}^{(k)},\cdots ,{i_d}^{(k)})E_{\pi }(\prod _{k=1}^{r}h(x_{\pi ({i_i}^{(k)})},\cdots ,x_{\pi ({i_d}^{(k)})})\}.$$

We divide the whole index set U ={i₁,…,i_d }^r = {(i₁⁽¹⁾,…, i_d⁽¹⁾),…, (i₁^(r), …, i_d^(r))}into the union of disjoint index subsets, in which $E_{\pi }({\displaystyle \prod _{k=1}^r}h(x_{\pi ({i_1}^{(k)})},\cdots ,x_{\pi ({i_d}^{(k)})})$ is invariant. The r-th moment of permutation distribution can be calculated by a sumproduct of data partition sums and index partition sums. A data partition sum is $E_{\pi }({\displaystyle \prod _{k=1}^r}h(x_{\pi ({i_1}^{(k)})},\cdots ,x_{\pi ({i_d}^{(k)})})$ within an index subset. An index partition sum is the sum of ${\displaystyle \prod _{k=1}^r}w({i_1}^{(k)},\cdots ,{i_d}^{(k)})$ over an index subset. With this strategy, all partition sums can be calculated without any real permutation. In addition, we calculate the partition sums recursively, from the simplest one to the most complex one, so that the computational cost can be further reduced. Our recent work [5] provides the details of index partition and recursive calculation.

The above approach can be applied to not only any weighted v-statistic, but also its equivalent test statistics. For permutation tests, two test statistics are equivalent if they have the same p-value for all observations.

2.2. Blockwise Permutation Tests

Let us consider a multi-scanner sMRI comparative study which is used to determine a treatment effect between the treatment group and the control group. The sMRI images are obtained with multiple different scanners which may carry different artifacts through scanning. Let x = [x(1), x(2), …, x(n)] denote sMRI values at the same interested location of size n (i.e. n subjects). Each subject is associated with a membership, for example, “treatment” or “control”. To test the main effect (i.e. the effect of interest or the effect to be tested), we may choose a test statistic to measure the difference between treatment group and control group. One choice could be the mean difference test statistic, which calculates the difference between the mean of “treatment” subjects and that of “control” subjects. In this case, we formulate the test statistic as:

$$T(x)=\sum _{i}c(i)x(i),$$

where c(i) = 1/n_t if the membership of the i-th subject is “treatment”, c(i) = −1/n_c elsewhere. Here, n_t and n_c are respectively the numbers of “treatment” and “control” subjects.

Since the main effect is usually confounded with the undesirable artifacts of different scanners, the exchangeability condition may not hold for the entire set of scans. To tackle this, we divide the scans into certain blocks. Each block includes all sMRI data collected from the same scanner. Since subjects are typically independent, we assume that the exchangeability is preserved within each block, which can be defined as an exchangeability block (EB) [8], i.e.,

$$x=[x(1),\dots ,x(n_1);\mathrm{x}(n_1+1),\dots ,x(n_1+n_2);\dots ;x(n-n_g+1),\dots ,x(n)]=[x_1;x_2;\dots ;x_g],$$

where x₁ = [x(1), …, x(n₁)], …, x_g = [x(n-n_g+1), …, x(n)] are g EBs. Next, we perform all possible permutations within each block and conduct blockwise permutation tests. To preserve exchangeability, no cross-block permutation is allowed. Note that the number of total possible blockwise permutations is equal to the product of the numbers of permutations within each block, i.e., #(π) = #(π₁) #(π₂ )…#(π_g ), where Π is the blockwise permutation, and Π_i is the permutation within the i-th block. Although this number is smaller than the number of general non-blockwise permutations, it is still large enough to lead to high computational cost for a typical multi-scanner dataset.

2.3. Moments-Based Blockwise Permutation Tests

To estimate the p-value, the permutation distribution needs to be constructed using test statistic values corresponding to all possible permutations. However, it is computationally expensive to enumerate all possible blockwise permutations. To reduce the computational cost, we fit the permutation distribution with the Pearson distribution series [22] without performing any permutation. The Pearson distribution series is a widely used four-parameter system. The four parameters required are the mean, variance, skewness, and kurtosis, which can all be calculated from the first four moments. We describe next how to calculate the moments of our blockwise permutation distribution.

Based on the efficient recursive algorithm introduced in Section 2.1, we calculate the moments of a regular (non-blockwise) permutation distribution. To obtain the moments of blockwise permutation distribution for the entire set of data, the key idea is to formulate it as a combination of the moments of a regular permutation distribution from all EBs (see Eq. (2)). Here, we assume the test statistic is summable. That is,

$$T(x,\pi )=T(x_1,{\pi }_1)+T(x_2,{\pi }_2)+\cdots +T(x_g,{\pi }_g).$$

This is a reasonable assumption and works for most popular test statistics or their equivalent test statistics [14, 15, 21].

The r-th moment of the blockwise permutation tests is:

$$\begin{array}{l}E(T{(x,\pi )}^r)=\sum _{\pi }{(T(x_1,{\pi }_1)+\cdots +T(x_g,{\pi }_g))}^r/\#(\pi )\\ =\sum _{{\pi }_1}\cdots \sum _{{\pi }_g}{(T(x_1,{\pi }_1)+\cdots +T(x_g,{\pi }_g))}^r/\#(\pi )\\ =\sum _{{\pi }_1}\cdots \sum _{{\pi }_g}\sum _{k_1,\cdots ,k_g}\left(k_1\stackrel{r}{,\cdots ,}{k}_g\right)(T{(x_1,{\pi }_1)}^{k_1}\cdots T{(x_g,{\pi }_g)}^{k_g}/\#(\pi )\\ =\sum _{k_1,\cdots ,k_g}\left(k_1\stackrel{r}{,\cdots ,}{k}_g\right)\sum _{{\pi }_1}(T{(x_1,{\pi }_1)}^{k_1}\cdots \sum _{{\pi }_g}T{(x_g,{\pi }_g)}^{k_g}/\#(\pi )\\ =\sum _{k_1,\cdots ,k_g}\left(k_1\stackrel{r}{,\cdots ,}{k}_g\right)E(\sum _{{\pi }_1}(T{(x_1,{\pi }_1)}^{k_1}\cdots E(\sum _{{\pi }_g}T{(x_g,{\pi }_g)}^{k_g}/\#(\pi )\end{array}$$ (2)

In order to further reduce the computational cost, we represent the first four moments by several symmetric functions:

$$m_j(i)=\sum _{{\pi }_i}(T{(x_i,{\pi }_i)}^j)/\#({\pi }_i)=E(T{(x_i,{\pi }_i)}^j),$$

$$m_j=\sum _i{m}_j(i),$$

$$E(T(x,\pi ))=m_1,$$

$$E(T{(x,\pi )}^2)=m_2+{m_1}^2-\sum _i{m}_1{(i)}^2,$$

$$\begin{array}{l}E(T{(x,\pi )}^3)=\sum _{i}E\left(\sum _{{\pi }_i}T{(x_i,{\pi }_i)}^3\right)+3\sum _{i\ne j}E\left(\sum _{{\pi }_i}T{(x_i,{\pi }_i)}^2\right)E\left(\sum _{{\pi }_j}T(x_j,{\pi }_j)\right)+\sum _{i\ne j,j\ne k,i\ne k}E\left(\sum _{{\pi }_i}T(x_i,{\pi }_i)\right)E\left(\sum _{{\pi }_j}T(x_j,{\pi }_j)\right)E\left(\sum _{{\pi }_k}T(x_k,{\pi }_k)\right)\\ =m_3+\left(3m_1{m}_2-3\sum _i{m}_1(i)m_2(i)\right)+\left({m_1}^3-3m_1\sum _i{m}_1{(i)}^2+2\sum _i{m}_1{(i)}^3\right)\end{array}$$

$$\begin{array}{l}E(T{(x,\pi )}^4)=\sum _{i}E\left(\sum _{{\pi }_i}T{(x_i,{\pi }_i)}^4\right)+4\sum _{i\ne j}E\left(\sum _{{\pi }_i}T{(x_i,{\pi }_i)}^3\right)E\left(\sum _{{\pi }_j}T(x_j,{\pi }_j)\right)\\ +3\sum _{i\ne j}E\left(\sum _{{\pi }_i}T{(x_i,{\pi }_i)}^2\right)E\left(\sum _{{\pi }_j}T{(x_j,{\pi }_j)}^2\right)\\ +6\sum _{i\ne j,j\ne k,i\ne k}E\left(\sum _{{\pi }_i}T{(x_i,{\pi }_i)}^2\right)\\ E\left(\sum _{{\pi }_j}T(x_j,{\pi }_j)\right)E\left(\sum _{{\pi }_k}T(x_k,{\pi }_k)\right)\\ +\sum _{\begin{array}{l}i\ne j,j\ne k,i\ne k\\ i\ne l,j\ne l,k\ne l\end{array}}E\left(\sum _{{\pi }_i}T(x_i,{\pi }_i)\right)E\left(\sum _{{\pi }_j}T(x_j,{\pi }_j)\right)\\ E\left(\sum _{{\pi }_k}T(x_k,{\pi }_k)\right)E\left(\sum _{{\pi }_l}T(x_l,{\pi }_l)\right)\\ =m_4+\left(4m_1{m}_3-4\sum _i{m}_1(i)m_3(i)\right)+\left(3{m_2}^2-3\sum _i{m}_2{(i)}^2\right)\\ +6[{m_1}^2{m}_2-6m_2\sum _i{m}_1{(i)}^2-12m_1\sum _i{m}_1(i)m_2(i)+12\sum _i{m}_1{(i)}^2{m}_2(i)]\\ +[{m_1}^4-\sum _i{m}_1{(i)}^4-4m_1\sum _i{m}_1{(i)}^3+4\sum _i{m}_1{(i)}^4\\ -3{\left(\sum _i{m}_1{(i)}^2\right)}^2+3\sum _i{m}_1{(i)}^4\\ -6{m_1}^2\sum _i{m}_1{(i)}^2+6{\left(\sum _i{m}_1{(i)}^2\right)}^2\\ +12m_1\sum _i{m}_1{(i)}^3-12\sum _i{m}_1{(i)}^4]\\ =m_4+4m_1{m}_3+3{m_2}^2+6{m_1}^2{m}_2+{m_1}^4\\ +8m_1\sum _i{m}_1{(i)}^3-6{m_1}^2\sum _i{m}_1{(i)}^2-6m_2\sum _i{m}_1{(i)}^2\\ -4\sum _i{m}_1(i)m_3(i)+3{\left(\sum _i{m}_1{(i)}^2\right)}^2-3\sum _i{m}_2{(i)}^2\\ -6\sum _i{m}_1{(i)}^4-12m_1\sum _i{m}_1(i)m_2(i)+12\sum _i{m}_1{(i)}^2{m}_2(i)\end{array}$$

where m_j(i) is the j-th moment for the i-th block. All within-block moments m_j(i) can be obtained through our newly developed recursive algorithm as described in Section 2.1. Here, the within-block moments are the moments for an EB data using the same test statistic function as that for the complete data. For example, when n = 8, and the membership is [treatment, control, treatment, control, treatment, control, treatment, control], we choose the mean difference test statistic for the complete scans, i.e.,

$$T=(x(1)+x(3)+x(5)+x(7))/4-(x(2)+x(4)+x(6)+x(8))/4$$

If we divide the scans by scanner into two blocks,

$$x_1=[x(1),x(2),x(3),x(4)]\text{and}{x}_2=[x(5),x(6),x(7),x(8)]$$

For each block, for example x₁, T(x₁) should be:

$$(x(1)+x(3))/4-(x(2)+x(4))/4$$

rather than the mean difference for the block:

$$(x(1)+x(3))/2-(x(2)+x(4))/2$$

The above efficient blockwise permutation test method not only works for the linear test statistic $T(x)={\displaystyle \sum _i}c(i)x(i)$, but also for any weighted v-statistic of degree d, that is,

$$T(x)=\sum _{i_1=1}^n\cdots \sum _{i_d=1}^{n}w(i_1,\cdots ,i_d)h(x_{i_1},\cdots ,x_{i_d}).$$

This is because the weighted v-statistic is always summable.

In summary, we convert the moments calculation for blockwise permutation tests to a simple combination of a moments calculation for regular permutation tests without restriction. The computational cost due to this simple combination can be ignored, compared with the cost of a moments calculation for regular permutation tests. If we assume the entire set of data is divided into g blocks with equal size, the computational costs are O(n/g)g = O(n) and O(n³/g³)g = O(n³/g²) for weighted v-statistics with d = 1 and d = 2, respectively, since the computational cost for each group is O(n/g) and O((n/g)³) [5]. For random permutations, the computational costs of calculating the test statistics are respectively O(n/g)g = O(n) and O((n/g)²)g = O(n²/g) per permutation for weighted v-statistics with d = 1 and d = 2. If we use 10,000 random permutations, the total costs are correspondingly O(10,000n) and O(10,000n²/g). Therefore, our method is much more computationally efficient than the popular random permutation method as long as the sample size is not too large (n ≪ 10,000). When lots of samples are available, the standard parametric tests can be used due to the large sample theorem and permutation tests are not necessary.

3. EXPERIMENTS SIMULATION AND RESULTS

Here, we apply our blockwise permutation method to a simulated multi-site sMRI data set for voxel-based morphometry (VBM). VBM involves a voxel-wise comparison of the local anatomical differences between two groups of subjects [12]. First, we generate 32 copies of real brain MRI data. Then we add Gaussian noise to each copy. The entire data set is evenly divided into two groups, group A and group B. Each group has 16 3D brain MRI images.

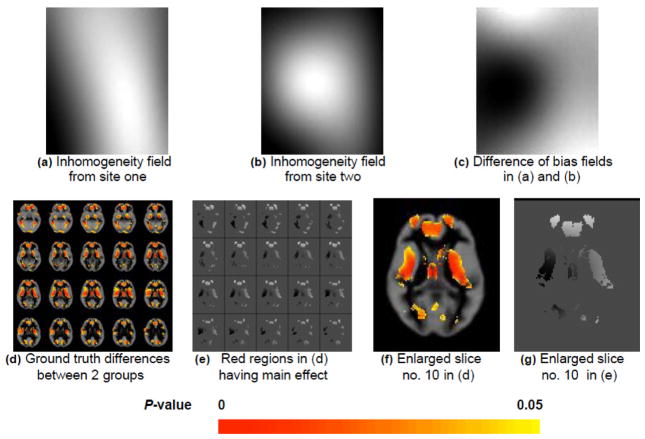
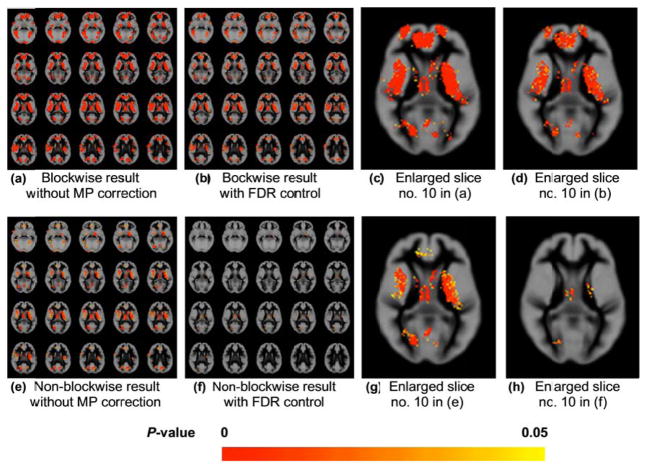
We add the generated anatomical group difference (Figure 1d) to group A to simulate the main effect of interest. We also simulate the multi-site effect by adding two different inhomogeneity fields (Figure 1a and 1b) to both groups. For each group, we add inhomogeneity field one to 8 of the 16 3D brain images, and add inhomogeneity field two to the rest 8 images. Without blocking, we permute data at each voxel location by randomly assigning 16 observations into group A and the other 16 to group B. The group comparison result (Figure 2f or 2h) is severely affected by the confounded multi-site effect. Thus, we can only detect regions having small or negligible multi-site effect (i.e. the regions in Figure 1e or 1g with gray level intensity similar to background, denoting the difference between the two inhomogeneity fields is close to zero). The regular permutation tests failed in identifying regions severely confounded by the site effect (i.e. the very bright or dark regions in Figure 1e or 1g, denoting the strong positive or negative difference between the two inhomogeneity fields). On the other hand, we can successfully detect the anatomical differences between the two subject groups using our blockwise permutation test (Figure 2b or 2d). In this case, we randomly assign 8 observations of site one and 8 observations of site two to group A and the remaining 16 to group B during the permutation, to handle the multi-site effect. Note that a false discovery rate (FDR) control [24, 25] is used in this experiment to correct the multiple testing/comparison problem [9, 12]. Without the FDR control, the detection leads to false positive differences, as shown in Figure 2a and 2c compared with the ground truth in Figure 1d and 1f.

Figure 1.

Multi-site sMRI experiment: data generation process with ground truth. (a) and (b): inhomogeneity fields from site one and site two, respectively. (c): difference of bias fields in (a) and (b), with positive differences shown as light regions and negative differences as dark regions. (d): generated ground truth anatomical differences between two subject groups. (e): difference of bias fields in the regions having main effect (i.e. the red regions in (d)). (f) and (g): enlarged version of slice no. 10 in (d) and (e), respectively (i.e. the last slice of the second row in (d) and (e)).

Figure 2.

Multi-site sMRI experiment: data analysis results comparing the effects of blockwise and multiple comparison (MP) correction. (a) and (b): results from our moments-based blockwise permutation tests without multiple comparison (MP) correction (a) and with false discovery rate (FDR) control at significance level α = 0.05 (b). (c) and (d): enlarged version of slide no. 10 in (a) and (b), respectively (i.e. the last slice of the second row in (a) and (b)). (e) and (f): results from our moments-based regular permutation tests without MP correction (e) and with FDR control at α = 0.05 (f). (g) and (h): enlarged version of slide no. 10 in (e) and (f), respectively (i.e. the last slice of the second row in (e) and (f)). Note that the regular permutation tests (see (f) and (h)) can only detect the regions with small or negligible bias field difference (gray level close to background in Figure 1e or Figure 1g.

4. CONCLUSION AND DISCUSSION

We have developed a new moments-based blockwise permutation test approach based on the moments of the test statistic, and applied it to structural neuroimaging data analysis. To preserve the exchangeability condition, the entire data set is first divided into several exchangeability blocks. Next, computationally efficient moments-based permutation tests are performed by approximating the permutation distribution of the test statistic with the Pearson distribution series. This involves the computation of the first four moments of the permutation distribution within each block and then over the entire set of the data. Our method works for both balanced and unbalanced designs. Experimental results demonstrated the advantages of the proposed method.

As our next goal, we would like to apply the developed blockwise permutation method to imaging-based real neuroscience research and clinical diagnosis. Although we focus on sMRI data analysis in this paper, the method is general and applicable to many other situations and biomedical image modalities involving hypothesis tests and group comparisons.

One issue that needs investigating in the future is the dependence of the size and the number of blocks on the performance of the method. There is little literature addressing how to choose the optimal block size for blockwise permutation tests. Based on the specific applications, different strategies can be utilized. For multi-site studies, it is obvious that the optimal blocking is to group the data by site, as in our sMRI experiment in Section 3. Alternatively or in some other applications, the choice of block size could depend on the property of undesired artifacts. One strategy we could take is to test the exchangeability for a set of choices of block size. That is, given a block size, we test whether the artifact is exchangeable under the same main effect condition. Since the permutation tests are more powerful with less restriction on permutations, we prefer the largest block size that can pass the exchangeability test.