Abstract
Purpose
To present a novel registration approach called LATIS (Local Affine Transformation assisted by Internal Structures) for co-registering post prostatectomy pseudo-whole mount (PWM) pathological sections with in vivo MRI (Magnetic Resonance Imaging) images.
Materials and Methods
Thirty-five patients with biopsy-proven prostate cancer were imaged at 3T with an endorectal coil. Excised prostate specimens underwent quarter mount step-section pathologic processing, digitization, annotation and assembly into a PWM. Manually annotated macro-structures on both pathology and MRI were used to assist registration using a relaxed local affine transformation approximation. Registration accuracy was assessed by calculation of the dice similarity coefficient (DSC) between transformed and target capsule masks and least square distance between transformed and target landmark positions.
Results
LATIS registration resulted in a DSC value of 0.991±0.004 and registration accuracy of 1.54±0.64 mm based on identified landmarks common to both datasets. Image registration performed without the use of internal structures led to an 87% increase in landmark based registration error. Derived transformation matrices were used to map regions of pathologically defined disease to MRI.
Conclusion
LATIS was used to successfully co-register digital pathology with in vivo MRI to facilitate improved correlative studies between pathologically identified features of prostate cancer and multi-parametric MRI.
Keywords: Deformable registration, histology, whole mount section, prostate cancer, dice similarity coefficient, correlative pathology
INTRODUCTION
Prostate cancer is the second leading cause of cancer-related deaths among men in the United States (1) and is the sixth leading cause of cancer-related deaths among men globally (2). Multi-parametric maps of anatomic, vascular and metabolic data of the prostate acquired using multi-parametric MRI can yield improved discrimination of the extent and aggressiveness of prostate disease (3–5). An important step in developing and validating multi-parametric MRI biomarkers to detect the extent and aggressiveness of prostate cancer is the registration of in vivo MR images with histopathological sections obtained from prostatectomy. This multi-modal registration would enable correlation of MRI with postoperative histopathological determination of extent and tumor grade, and ultimately the molecular assessment of aggressiveness.
There has been much interest in the multi-modal co-registration of prostate MRI with other imaging modalities such as CT for treatment planning (6–9), ultrasound for guiding biopsies(10), and pathology for validation of cancer detection (11). With each combination of source and target data come unique challenges for the registration procedure. In this work, the goal was to register in vivo MRI data obtained with a balloon-type endorectal coil (ERC-inMR) with images of pseudo-whole mounts (PWM) constructed from quarter mount histologic sections. The prostate images from in vivo MRI and pathology possess different amounts of deformation/distortion with respect to each other. For example, after digitally assembling quarter mount histological sections into a PWM, the resulting PWM is different from a true whole mount image in multiple ways, including: (a) the boundary shape of the prostate, (b) the unfilled space or gaps between the quarter mount histological sections, and (c) deformation/distortion of each individual quarter. Additionally, the difference between the ERC-inMR and the tissue observed on pathology is a result of multiple factors, including: (a) physical distortion of the prostate due to the presence of the inflated endorectal coil, (b) deformation of the tissue after excision and (c) shrinking of the tissue due to fixation. Without completely characterizing all the intermediate deformations, the registration procedure described in this work focuses on directly registering ERC-inMR with PWM images due to the fact that both data sets are readily available, and characterization of the intermediate deformations are not easily obtainable.
We have developed a technique using a relaxed Local Affine Transformation approximation assisted by the identification of large Internal Structures (LATIS). In LATIS, the prostate capsule and large internal anatomic structures are used as constraints for registration. This technique does not require the accurate definition of a set of multiple paired landmarks between the source and target data which are difficult to obtain in general and the basis for leading registration methods tackling similar problems. The large structures are, arguably, easier to manually identify on both pathology and MRI and provide a larger continuum of spatial information to guide the registration procedure. In this manuscript, the ability of LATIS to co-register PWM and ERC-inMR images is evaluated, and the use of this registration to map regions of pathologically identified cancer onto the in vivo MRI is demonstrated.
MATERIALS AND METHODS
Data used in this manuscript was obtained from patients with biopsy-proven prostate cancer (35 men, age range 50–73 years, mean age 62 years) after obtaining written signed consent for a study reviewed and approved by the local Institutional Review Board.
In vivo MR Acquisition
Patients were imaged on a 3T scanner (Siemens Healthcare, Erlangen Germany). A surface array combined with an ERC was used for all imaging. The ERC was inflated with 60 ml of perfluorocarbon to reduce air induced susceptibility artifacts. T2-weighted (T2w) axial MR images were generated using a multi-slice Turbo Spin Echo acquisition with 4m 42s scan duration, TR/TE 6860/107 ms; ETL 23, NEX 2, BW 190 Hz/Px, 3 mm slice thickness, 140° flip angle, 2562 matrix, 19 slices and 140 mm2 FOV. The axial images were positioned such that the slice plane passed perpendicular to the posterior surface of the prostate.
Pathology Processing
Excised prostates were formalin fixed and then gross sectioned to match, as close as possible, the MR imaging planes. For this purpose, a special sectioning box (Figure 1) was constructed and a sectioning protocol established (Figures 2a and 2b). After amputation of the seminal vesicles and vasa deferentia at the base and shaving off 1mm of the proximal urethral margin, the prostate was placed in the sectioning box so that the posterior surface of the prostate was approximately parallel to the bottom and the long axis of the box. Vertical slits in the box, 3 mm apart, allowed the consistent parallel sections to be cut perpendicular to the posterior surface of the prostate with a thickness of 3 mm to match the orientation and thickness of the axial ERC-inMR slices. Gross sectioned prostates were subjected to quarter mount histological section (QMHS) pathologic processing. Sections were paraffin embedded, Hematoxylin and Eosin (H&E) stained, and cut at 4 μm thickness. H&E stained slides were digitized using a whole slide scanner (ScanScope CS, Aperio, Vista, CA). The prostate pseudo-capsule and tumor regions within the digitized sections were annotated by a board certified pathologist with 15 years’ experience (SCS), at 20X magnification (resolution 0.58μm per pixel) using a pen tablet screen (Cintiq 21UX, Wacom, Kazo-shi, Saitama, Japan). Digitally annotated QMHS slides were then manually assembled into PWM by aligning the capsule annotations of the quartered pathology sections to form a continuous capsule while minimizing overlap of tissues between the combined sections. Anatomic features in the pathology sections being assembled also aided in aligning the QMHS images (Figures 2c and 2d). From the assembled PWM, binary masks of both annotated tumor regions and the prostate capsule were generated (Figure 3). For each patient, a single PWM at the center of the index lesion was chosen for registration.
Figure 1.
Prostate sectioning box made of Acrylic and Teflon. The box is shown with a spherical prostate model and the movable walls on the left (WL) right (WR) and base (WB) are pushed in to hold the model securely. Each moveable wall is held in place with a locking screws SL, SR and SB, respectively. A standard pathology blade is inserted through the milled slits in the acrylic pieces that make up the left and right walls. Each successive axial cut through the prostate requires passing through the next slit in the side walls. The tolerance is such that the blade can only traverse through the corresponding slit on the opposite side.
Figure 2.
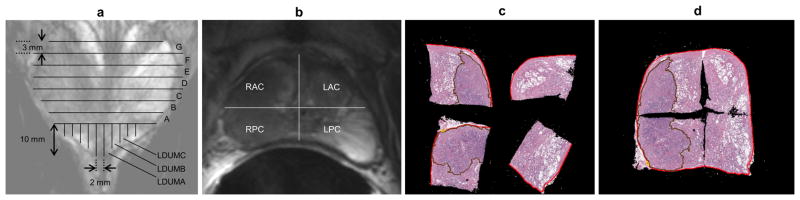
Diagrams of pathologic sectioning protocol overlaid on a coronal (a) and axial (b) T2w image. After placing the prostate in the sectioning box, the first cut made is approximately 0.6 mm from the apex of the gland to create the apical section, with successive axial cuts 3mm apart moving towards the base. The axial cross-sections are designated by letters “A”, “B”, “C”, etc., depending on the size of the prostate, with “A” being the most apical slice. Slices are divided into four quarters (b). Each quarter is labeled based on the letter of the slice from which it comes and its position in the slice (e.g. anterior/posterior = A/P and right/left = R/L). After removal from the box, the apical portion is sectioned in 2mm intervals with parallel cuts emanating from the urethra. The sections near the urethra are labeled “RDUMA” (right distal urethral margin A) and “LDUMA” (left distal urethral margin A). The next two sections from the center are then labeled “RDUMB” and “LDUMB”, etc. This process continues out to the lateral margins of the apical section. Each slice section is then embedded in a paraffin block and one 4-micrometer H&E-stained slide is prepared from each section and digitized. A pathologist then digitally annotates the prostate capsule (red contour) and cancer regions (brown contour) on each slide (c). Slides from a complete axial slice are then manually assembled into a PWM by aligning the capsule annotations of the quartered pathology sections to form a continuous capsule while minimizing the overlap of tissues between the combined sections (d).
Figure 3.
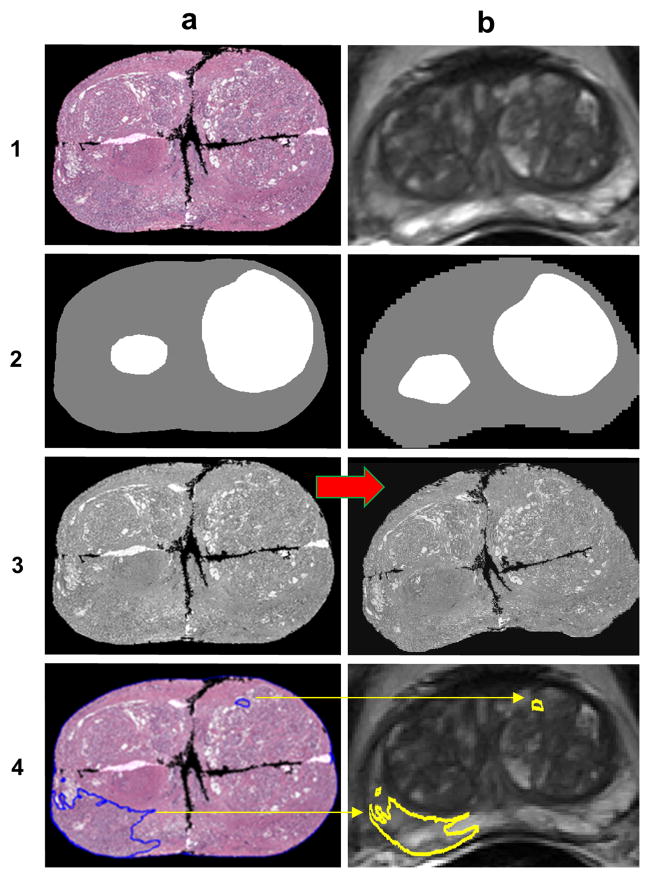
A schematic demonstrating the procedure to co-register pathology to T2w MRI using LATIS. First, the source (1a) and target (1b) images are segmented, scaled and translated. Second, the prostate capsule and internal structure masks are identified to constrain the pathology transformation. The source and target masks (2a and 2b) are registered and a transformation matrix is obtained. Third, the transformation matrix is applied (red arrow) to the pathology (3a) which places it in spatial correspondence to the T2w MRI resulting in (3b). Lastly, applying the transformation matrix to each one of the annotated cancer regions (4a) places them in the spatial framework of the anatomic T2w images (4b).
Image Registration
In order to register the PWM (source image) to the ERC-inMR (target image) (Figure 3), a transformation that can map the source image to the target image must be found. Since the source and target image belong to two completely different imaging modalities, a direct mapping relationship between these two images cannot be readily established without additional inputs or modifications. The first step in the process involved manually converting the source and target into tri-intensity grayscale images (Figure 3) such that the internal structures had a grayscale value of 128 and the rest of the prostate has a value of 255. This created the potential for developing a direct mapping between the two datasets. To register the two tri-intensity grayscale images, some assumptions are introduced:
The 2-dimensional source and target images correspond to the same cross-section of the prostate in terms of the position and the outward normal direction.
There exists a path-independent, unique mapping between the source and the target image.
The image intensity between the source and target image is conserved.
These three assumptions are reasonable and can be easily satisfied in most cases. The first assumption is met by the standard data collection and sectioning protocols employed in this study. This condition is of the upmost importance because, as the source and target images diverge in terms of their spatial correspondence, there is decreasing benefit to perform the registration since the cancer region annotated in the source image cannot be guaranteed to exist in the target image.
The second assumption establishes that the problem is well-posed. Supposing assumption No.1 holds, there exists a mapping relation between the source and target images as they both represent different realizations of the same cross-section of the prostate. Employing a linear approximation for the mapping will guarantee a unique and path-independent solution. The existence of a solution and its uniqueness establish that the problem is well-posed (12), hence the solution is guaranteed.
The third assumption forms the basis for the image registration procedure. With assumption No. 1, both the source and the target images are referring to the same cross-section of the prostate but differ due to in-plane deformation. After converting the source and target images to the tri-grayscale-images, the intensity conservation principle (13) is readily applicable and a relationship can be established between the source and target images. With this established relationship, the mapping relation between the source and target image can subsequently be derived with the help of assumption No. 2. The derivation is shown in next section. In summary, although three assumptions were introduced, assumption No. 1 is the most fundamental. If assumption No. 1 is achievable, assumptions No. 2 and 3 are imposed, both of which serve as a foundation for the following registration derivation.
Theory
Let I(x, y, t) be the intensity of an image, which is a function of space and time. When the source and the target tri-grayscale-images are treated as the images of a deforming prostate at two different time points, time is involved. Therefore, one can assign the source image at t1 and assign the target image at t2. Following assumption No.1, assumption No. 3 imposes the intensity conservation principle which implies that the total derivative of the intensity is invariant, i.e.
| [1] |
Expanding the left hand side (LHS) of the equation, it becomes
| [2] |
According to assumption No. 2, there exists a transformation such that the above equation (Eq. 2) is satisfied. Since this exact transformation is unknown, the assumption of a local affine transformation is made between the source and target image, which is,
| [3] |
where (x, y) represents the source image at t1, (x̃, ỹ) represents the target image at t2, (Lx, Ly) is the translation, and θ is the rotational angle. And since the local affine transformation is a proposed approximation, a more relaxed linear approximation can be adopted, namely,
| [4] |
which relaxes the θ constraint between the transformation parameters {α1, α2, α4, α5, α6}. This linear approximation satisfies assumption No. 2. With respect to the approximation, there is no qualitative difference between Eq. 3 and Eq. 4 since they are both linear functions but, as shown in a later part of this section, it is desirable to select Eq. 4 over Eq. 3 to reduce the correlation between the transformation parameters resulting in a simpler solution procedure. Substituting Eq. 4 into Eq. 2 leads to the LHS not being equal to zero because Eq. 4 is an approximation and an approximations result in errors. Therefore, locally, we have an error function in terms of (x̃, ỹ) where Ĩx, Ĩy, and Ĩt are functions of (x̃, ỹ), which states that
| [5] |
Now the objective of the registration process is to find a set of transformation parameters α⃗ = (α1, α2, α3, α4, α5, α6)T such that error function e is equal to or is minimal with respect to zero. In order to seek the solution for the transformation parameters, a quadric error functional is constructed as
| [6] |
Further taking the variation of the quadratic functional, yields,
| [7] |
Since the transformation parameters are constants, the higher order terms vanish after taking the first variation of the quadratic functional, i.e. α⃗i = 0, for all i > 1. And according to the Ekeland’s variational principle (14), there exist a solution for α⃗ such that δΠ = 0 which corresponding to the minimization of the error function e. Since δα⃗ is arbitrary and is not always equal to zero, the only possibility to yield δΠ = 0 is that the following equation is always satisfied,
| [8] |
where
| [9] |
| [10] |
Therefore, the transformation parameters can be solved from the following equation
| [11] |
where the resulting transformation parameters are the optimal solution satisfying Eq. 2 and subsequently, provides the transformation satisfying Eq. 4.
A pixel by pixel solution of the transformation parameters is computationally expensive and may be ill-posed in the sense of Hadamard (12). For reducing the computational cost, the transformation parameters can be solved weakly, i.e., for a neighborhood of n by n pixels,
| [12] |
where Ω represents the domain of the image and i and j are referring to the index of the pixels in the x and y directions, respectively. The image is broken up into a grid of these neighborhoods such that the larger the neighborhood, the coarser the grid. However, due to the properties of the tri-intensity grayscale images, Eq. 12 is ill-posed (non-invertible). This is because for the entire neighborhood of n by n pixels located within the same intensity grayscale region, we have
| [13] |
and,
| [14] |
In order to achieve a solution for Eq. 12, the matrix of the left hand side needs to be diagonally dominant. Thus, the following modifications can be made in Eq. 11 to add a diagonal matrix on both the left hand side and right hand side:
| [15] |
where η is a diagonal constant matrix with a reasonably large positive number for the diagonal elements and zeroes for the off-diagonals. Based on our experience, a ηkk=1010 is chosen. Since the same quantities are added equally on both side of the equation, it does not change or affect the solution of the original equation but makes it always solvable. Thus Eq. 11 becomes
| [16] |
The fixed-point iteration method can now be readily employed for solving Eq. 16. Employing the fixed-point iteration method (49), α⃗ can be solved iteratively from
| [17] |
with an initial guess of α⃗(0) = 0 when m=0 for the initial step.
Multi-Resolution Optimization
Two principle causes of potentially large deformations in local regions of the prostate between the PWM and ERC-inMR images result from the sectioning and reassembly of the pathology specimens and the use of an ERC. The optimal neighborhood size, n x n, over which α⃗ needs to be solved is unknown. For neighborhoods too large, the accuracy of the registration would be insufficient, and for neighborhoods to small, the registration method would be ill-posed in the sense of Hadamard (12). Therefore, instead of choosing a fixed neighborhood size, a multi-resolution optimization strategy is employed.
The idea behind the method of multi-resolution optimization for registration is that the starting grid of neighborhoods covering the image is small (low resolution) while as the optimization progresses the resolution of the grid increases (i.e. decreasing neighborhood size). The solution in each step in the progression of the grid refinement provides an improved initial guess for the subsequent higher resolution grid. In the course of registering PWM to the ERC-inMR image, a sequence of 2n grids are used, where n is equal to 0, 1, 2 … etc. The final transformation is the accumulated transformation of the multiple steps with the criteria to stop the refinement of the grid mesh being when the L2-norm of the displacement between step n and step n+1 is less than 0.1 pixels.
Registration Procedure
The image registration workflow for a sample case is shown in the Figure 3. After choosing the assembled pathology PWM slice, the corresponding target T2w ERC-inMR slice was identified by choosing a slice at the same approximate position from the apex and verifying the existence of similar anatomic features. The source (PWM) is shown in Figure 3.1a. The target (ERC-inMR, T2w) is shown in Figure 3.1b. The prostate region in the ERC-inMR image was extracted masking with capsule contours drawn in a semi-automated segmentation program (Segasist, Ontario, Canada) by an experienced prostate MRI researcher (GJM). The PWM images were also masked by the combined capsule annotations defined by the study pathologist (SCS). The masked ERC-inMR image was upsampled to 512×512, to match the matrix size of the PWM, and translated to achieve a greater than 50% overlap with the masked PWM. New annotation regions defining the easily identifiable large internal structures for the PWM data were generated while simultaneously annotating similar structures on the ERC-inMR. These internal structures were defined by a number of identifiable features including the central gland-peripheral zone boundary, transition zone, apex-semicircular sphincter and bilateral nodules of benign prostatic hypertrophy. These images were converted into tri-intensity (White = 255, Black = 0, Gray = 128) grayscale source and target images (Figures 3.2a and 3.2b) where the white regions delineate the internal structures. Using the pre-defined controls (large internal structures and prostate boundary) found in the source and target, LATIS was used to register the two images. The local affine transformation component of the registration procedure was adapted from methods originally published by Periaswamy and Farid (15–17). The application of the final transformation matrix to the masked grayscale PWM image (Figure 3.3a) and the resulting warped source image (Figure 3.3b) is shown. The application of the final transformation matrix warping the tumor region masks from the PWM to the ERC-inMR can be seen in Figures 3.4a and 3.4b. Other than where specifically stated, the registration steps and the visualization of results were performed in Matlab (MathWorks, MA, USA) running on a Windows 2.80 GHz Intel i5 CPU machine with 12 GB RAM.
Analysis
Two metrics were used to evaluate the accuracy of the registration methods. The first method was the Dice similarity coefficient (DSC) which measures the overlap between the target and registered source. The DSC for two images A and B is defined as the intersection of the two images divided by the mean sum of the images
| [18] |
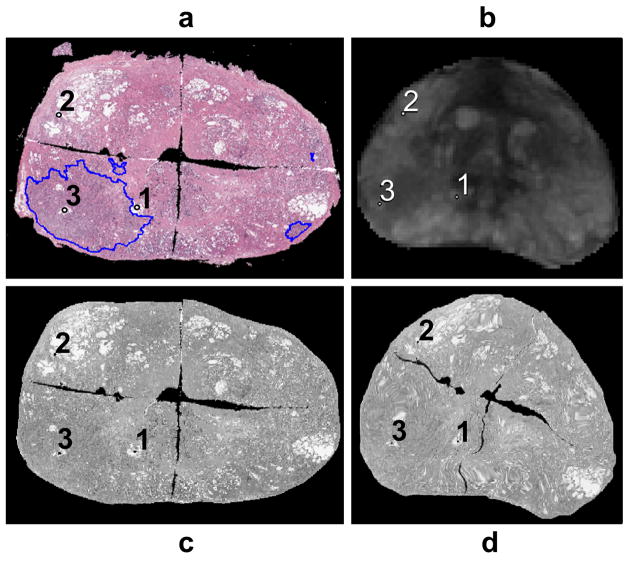
The second validation method involved identifying identical landmarks by visual inspection on both the native PWM and ERC-inMR images. The process of identifying landmarks was independently performed by two experienced prostate researchers with four (CK) and eleven years (GJM) experience. The landmarks selected were also done so independently from the large internal structures used for registration. Landmark positions on the PWM were masked using circular ROIs (radius, 8 pixels, pixel size = 0.54 mm) to give a feature marked PWM (fmPWM) image. A circular area of this magnitude was chosen to easily identify the feature in the downscaled registered source. The transformation matrix, obtained earlier for this case, was applied to the fmPWM image and transformed pixel positions were obtained from the registered fmPWM image. Target registration error (TRE) in mm was calculated using the root mean squared distance between the transformed pixel positions from the fmPWM and the target pixel position on the ERC-inMR. For the thirty five cases, landmarks for the registration accuracy calculation were drawn and a total of 103 such landmarks were identified by the two observers for error analysis. To ascertain the impact of the internal structures as a guide for image registration, these thirty five cases were again registered without using internal structures and the registration accuracy assessed. The source and target images in this case were the masked PWM and ERC-inMR capsule masks.
Statistical Analysis
The average TRE and DSC are reported as the mean ± standard deviation and were calculated using Matlab (MathWorks, MA, USA). A p-value <0.005 was considered statistically significant when evaluating the difference in registration accuracy with and without the use of internal structures. The p-value analysis was performed in OriginLab 9.0 (Origin Lab Corporation, USA).
RESULTS
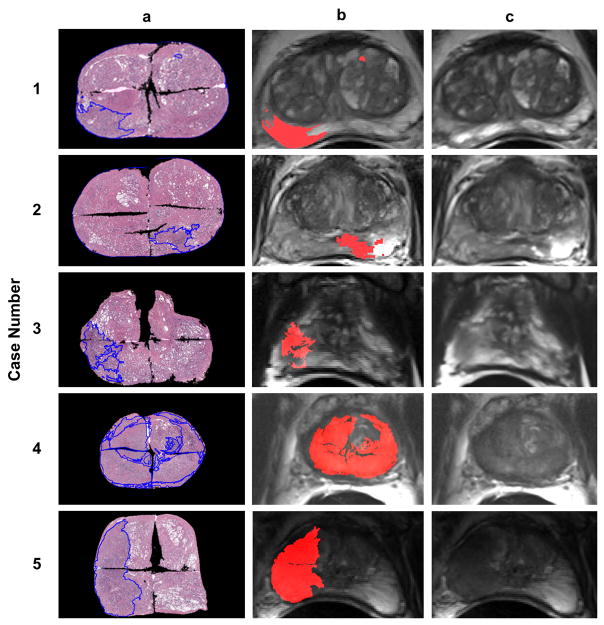
Five representative cases are provided in Figure 4. The assembled PWM images are shown with the annotated tumor regions and cropped to the capsule borders by using the combined capsule annotations created by the study pathologist. LATIS was used to register the PWM data to the ERC-inMR. The transformation was then used to warp all annotated cancer regions from the assembled pathology to MRI (Figure 4 Column b). The registration calculation per case took on the order of 11 minutes.
Figure 4.
Registration results. Column ‘a’ shows the masked PWM with annotated tumor regions. Column ‘b’ shows the registered tumor regions overlaid on the ERC-inMR. Column ‘c’ shows the original ERC-inMR.
The mean DSC after registration was 0.991±0.004 which represents nearly total correspondence by this metric after registration. The mean, minimum, maximum and standard deviation of the registration error based on the landmark method are given in Table 1. The average overall registration error was 1.54±0.64 mm when using internal structures and 2.92±1.76 mm without internal structures, a statistically significant increase in registration error of 87% in the absence of additional information to guide registration (p < 0.0001). An example of the landmark registration accuracy assessment is shown in Figure 5.
Table 1.
Multi–user registration accuracy metric statistics.
| Mean/Min/Max (mm) | Std. Dev. (mm) | # Points | |
|---|---|---|---|
| Total | 1.54/0.19/3.26 | 0.64 | 103 |
| Observer1 | 1.57/0.43/2.92 | 0.65 | 36 |
| Observer 2 | 1.51/0.19/3.26 | 0.64 | 67 |
Figure 5.
Registration accuracy metric calculation workflow - (a) Feature marked masked PWM. (b) Corresponding features on ERC-inMR. (c) Warped feature embedded masked PWM. (d) Feature embedded masked ERC-inMR.
DISCUSSION
A registration approach using a relaxed local affine transformation approximation, assisted by large internal structures as constraints to improve registration accuracy, has been presented for co-registering post prostatectomy pseudo-whole mount pathological sections with T2-weighted in vivo MRI images obtained with an ERC. In this study, slides made from quarter mount histologic sections were used to generate the PWM images as the ability to section, store and digitize whole mount data does not exist at our institution. Many institutions find themselves with similar limitations in terms of processing the excised prostate, therefore the methods presented here are very relevant for MRI studies wanting to use correlative pathology for identifying and validating MRI biomarkers for prostate cancer detection and grading.
Registration Methods
The registration between prostate histopathology and MRI images belongs to the category of multi-modal registration. Previous work in this area has investigated registering whole mount pathology (WM) to in vivo MRI (inMR) acquired without an ERC (11), in vivo MRI acquired with an ERC (ERC-inMR) (18–23) and ex vivo MRI (exMR, paraformaldehyde fixed prostatectomy specimen) (23–25). While less prevalent in the literature, registration with PWM pathology has also been performed with exMR (18,26–28), inMR acquired without an ERC and inMR (22) acquired with an ERC (29).
Two dominant approaches exist in published literature addressing the registration of pathology to MRI; the thin plate spline (TPS)-based (11,18,20–23,26,27,30) and B-spline (BSp)-based (24,31,32) methods. The TPS approach utilizes pre-defined control point pairs identified from different images to warp the source image to the target image using a multidimensional interpolation method (30). The result of the TPS-based methods is highly dependent on the manual selection of the control point pairs, which requires knowledge of the control point locations and distributions in both images. Such information may not be readily available in all the cases within the ERC-inMR and PWM images. Also, since each pair of control points in the TPS method influences the entire image, this method assumes continuous source and target images, smooth deformation and distribution of control points over the entire image. Such assumptions are not valid for the PWM images used in this study.
In contrast to the TPS-based approach, the influence of the control points for the BSp-based approach is localized especially when it is combined with free form deformation (FFD) (31). With the FFD BSp approach, each control point is predominately influenced by the neighboring grid tiles. This feature makes it suitable for registering the WM to both exMR and inMR images as well as the WM to the ERC-inMR images. The BSp approach however, provides a smooth and continuous deformation field and thus is far from ideal for directly registering PWM to ERC-inMR.
Some studies have used mutual information (MI) as an alignment measure (19,28,29,33–37). MI has been specifically designed to address registration of multi-modal data (37) and is based on information theory (36). The robustness of the MI approach for dissimilar modalities can be enhanced via the combined feature ensemble mutual information (COFEMI) technique which incorporates additional information for one of the modalities in the form of image features (28). The robustness and the results of this technique are highly dependent on the selection of the image features. The MI-based approach incorporated by the COFEMI technique has been used for registering WM to both exMR and inMR images (28) while the Spatial Weighting Mutual Information (SWMI) technique has been used for registering PWM to ERC-inMR images (29), addressing the same problem focused on in the current manuscript. While the SWMI work addressed the same challenging problem of registering in vivo MRI with PWM data presented in this work, only a limited number of cases were demonstrated. While the SWMI method doesn’t require the identification of the capsule border it also demonstrated lower registration accuracy compared to LATIS with a DSC of 0.83 on average.
Given the scope of registration problems best handled by the previously described methods, we desired a new approach which was more appropriate to register PWM and ERC-inMR and required a minimum amount of a priori information. First of all, the existing methods available in the literature required an investigator, or sometimes feature recognition software, to identify sufficient numbers and distributions of control points to guide the registration between the histopathological and MRI images. Recognizing the fact that registration between two images requires some pre-defined controls, we observed that there were clearly some features that could be defined with reasonable precision. One feature was the prostate boundary and the others were larger internal structures like the central gland-peripheral zone boundary, transition zone, apex-semicircular sphincter and bilateral nodules of benign prostatic hypertrophy. This addressed the challenge of identifying numerous control points with exact spatial correspondence between the source and target images as required by the BSp and TPS methods. Identification of landmarks was often difficult and the number of points would have been insufficient for guiding registration. The difficulty of selecting spatially corresponding control points is evidenced by the large discrepancy between the number of points the two researchers selected for determination of registration accuracy. However, the identification of larger anatomic structures was always possible in our test cases.
The second issue with the aforementioned methods was the underlying assumption of a continuous deformation field which is less appropriate when registration involves PWM data. Therefore, we developed a method based on the invariance of the image intensity function, which does not require the assumption of continuous deformation fields. This feature makes the resulting method suitable to handle the local distortions that lie within the PWM images such as the unfilled space or gaps between the QMHS.
To address the discontinuous nature of the reassembled PWM images and to overcome the overall challenge of multi-modal registration, tri-intensity masks of both datasets taking into account the prostate border and large internal structures were used as the source and target images for registration. While not the focus of this work, it could easily be envisioned that BSp and TPS could be used for registering the tri-intensity images in place of the local affine transformation chosen here however, the identification and selection of control points would still be necessary and a limiting factor to their successful implementation.
Registration and Pathology Limitations
Both LATIS, and the other referenced registration studies, have addressed a two-dimensional registration problem. Therefore, an important requirement (i.e. the first assumption in LATIS) is that the source and target images originate from the same plane through the prostate. Even with careful attention to the sectioning protocol multiple factors can lead to axial planes which do not match between the MRI and pathology, including non-linear shrinking of the tissue during fixation. This lack of correspondence would further complicate, if not eliminate, the possibility to find features for guiding registration. The selection of control points used by TPS and BSp based on small structural features would arguably be the most affected. However, LATIS may be less sensitive to the same offsets due to the persistence of larger structural features through plane. The influence of both through-plane offsets and in-plane registration errors must be considered when evaluating the registration accuracy of annotated cancer regions from pathology to imaging. The relative impact of any error would be greater for smaller areas of disease.
Additional limitations exist in the most apical and basal regions. As described in the sectioning protocol, the most apical section of the prostate is removed and cut in the sagittal orientation. Using LATIS in this orientation has not been explored to date. One obvious limitation is the absence of a complete capsule contour. In the base, several aspects of the sectioning protocol and the anatomy make identification of the prostatic capsule and assembly of the PWM difficult including, the ambiguous prostate-bladder border, amputation of the seminal vesicles and vasa deferentia at the base and shaving of the proximal urethral margin to a thickness prior to placement in the sectioning box. The end result is the absence of a well-defined capsule in the most basal slices which makes them difficult to handle with the proposed methods.
Despite the previously described limitations, the sectioning protocol and registration methods have proven to be relatively robust in the cases studied to date. In general, less than 15% of cases handled in our lab needed to be excluded from registration due to mismatches in slice orientation (i.e. an obvious violation of assumption No. 1) and less than 3% of cases had to be excluded due to index lesions too for inferior or superior in the prostate.
Assessment of Registration Error
The assessment of image registration accuracy in literature has been has been accomplished using a variety of error metrics. In the present study registration accuracy was calculated using 1) the dice similarity as a “global” metric for characterizing the registration of the tri-intensity images (i.e. capsule and large internal structures) and 2) corresponding landmarks identified manually in both source and target images to characterize registration accuracy of internal features of the prostate. Similar methods have been used in the literature to assess registration accuracy (38–46).
The need to perform accurate registration between PWM and ERC-inMR stems from the desire to use pathological results as the ground truth for interpreting the MRI results for determining the extent and aggressiveness of disease. A “perfect” registration would permit a reliable pixel–wise analysis of MRI with respect to histopathology however, the ability to approach this ideal correspondence is difficult due to the complexity of the distortions and the limited information available to correct for them. To improve our registration method, future implementations could incorporate other MRI visible structures like the urethra. The LATIS approach could also serve as a baseline method in a cascaded registration procedure, where additional registration steps incorporating other previously proposed strategies and information may be used to further improve the correspondence of salient features between the datasets. Using LATIS would be a valuable first step for the reasons stated above, including that 1) it relies on the selection of large structures rather than specific points which makes it more robust in cases where the prostate slicing and MRI imaging plane are not exactly the same, 2) it does not rely on image intensity from the multi-modal data and 3) it does not assume a smooth continuous deformation field, an assumption, which is violated in the case of the PWM data.
In the future improved error metrics for assessing registration accuracy would also be desired in order to compare LATIS with other registration methods and potentially cascaded approaches. Potentially this is possible by acquiring additional information in the process of generating the PWM and acquiring the ERC-inMR data such as images of the gross pathology sections cut into quarters prior to paraffin embedding and imaging of the prostate after excision and before sectioning. This information may help elucidate the deformations present between the source PWM data and the target ERC-inMR and provide a more complete characterization of the deformations to better evaluate other strategies which do not require the labor and time to acquire the additional data.
In conclusion, the main geometric issues in histopathology-MR image registration are the distortions resulting from the use of an endorectal coil when acquiring the inMR data, the deformation due to removal, and fixation and distortion of individual QMHS which result in discontinuities in the final assembled PWM. In this work, this registration problem is addressed by using LATIS which involves identifying large internal structures along with the prostate boundary to guide registration. While the method to assess the registration accuracy was subjective, it is an important first step in the validation of the technique. Future studies will focus on providing a better metric for assessing registration accuracy and will investigate cascading LATIS with other deformable strategies to further improve registration of local features between histopathology and in vivo MRI results.
Acknowledgments
Grant Support
This project was supported by NCI R01 CA155268, NCI R01 CA131013, NCI R01 CA131013-S1, NIBIB P41 EB015894, S10 RR26783 and the WM KECK Foundation.
The authors would like to acknowledge Drs. Badrinath Konety and Christopher Warlick from the University of Minnesota, Department of Urology for their continued clinical support in securing patients and coordinating sectioning of tissues after prostatectomy; Drs. Andrew Johnson and Laura Moench from the Department of Laboratory Medicine and Pathology who has been instrumental in annotating cases; and Sarah Bowell and Jonathan Henriksen from the University of Minnesota BioNet core facility for case tracking and digital imaging support.
References
- 1.Siegel R, Naishadham D, Jemal A. Cancer statistics, 2012. CA Cancer J Clin. 2012;62(1):10–29. doi: 10.3322/caac.20138. [DOI] [PubMed] [Google Scholar]
- 2.Baade PD, Youlden DR, Krnjacki LJ. International epidemiology of prostate cancer: geographical distribution and secular trends. Mol Nutr Food Res. 2009;53(2):171–184. doi: 10.1002/mnfr.200700511. [DOI] [PubMed] [Google Scholar]
- 3.Langer DL, van der Kwast TH, Evans AJ, Trachtenberg J, Wilson BC, Haider MA. Prostate cancer detection with multi-parametric MRI: logistic regression analysis of quantitative T2, diffusion-weighted imaging, and dynamic contrast-enhanced MRI. J Magn Reson Imaging. 2009;30(2):327–334. doi: 10.1002/jmri.21824. [DOI] [PubMed] [Google Scholar]
- 4.Turkbey B, Pinto PA, Mani H, et al. Prostate Cancer: Value of Multiparametric MR Imaging at 3 T for Detection—Histopathologic Correlation 1. Radiology. 2010;255(1):89–99. doi: 10.1148/radiol.09090475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Vilanova JC, Barceló-Vidal C, Comet J, et al. Usefulness of prebiopsy multifunctional and morphologic MRI combined with free-to-total prostate-specific antigen ratio in the detection of prostate cancer. AJR Am J Roentgenol. 2011;196(6):W715–722. doi: 10.2214/AJR.10.5700. [DOI] [PubMed] [Google Scholar]
- 6.McLaughlin PW, Narayana V, Kessler M, et al. The use of mutual information in registration of CT and MRI datasets post permanent implant. Brachytherapy. 2004;3(2):61–70. doi: 10.1016/j.brachy.2004.06.001. [DOI] [PubMed] [Google Scholar]
- 7.Lian J, Xing L, Hunjan S, et al. Mapping of the prostate in endorectal coil-based MRI/MRSI and CT: a deformable registration and validation study. Medical physics. 2004;31(11):3087–3094. doi: 10.1118/1.1806292. [DOI] [PubMed] [Google Scholar]
- 8.Mizowaki T, Cohen GaN, Fung AYC, Zaider M. Towards integrating functional imaging in the treatment of prostate cancer with radiation: the registration of the MR spectroscopy imaging to ultrasound/CT images and its implementation in treatment planning. International Journal of Radiation Oncology*Biology*Physics. 2002;54(5):1558–1564. doi: 10.1016/s0360-3016(02)03805-1. [DOI] [PubMed] [Google Scholar]
- 9.Parker CC, Damyanovich A, Haycocks T, Haider M, Bayley A, Catton CN. Magnetic resonance imaging in the radiation treatment planning of localized prostate cancer using intra-prostatic fiducial markers for computed tomography co-registration. Radiother Oncol. 2003;66(2):217–224. doi: 10.1016/s0167-8140(02)00407-3. [DOI] [PubMed] [Google Scholar]
- 10.Hu Y, Ahmed HU, Allen C, et al. MR to Ultrasound Image Registration for Guiding Prostate Biopsy and Interventions. In: Yang G-Z, Hawkes D, Rueckert D, Noble A, Taylor C, editors. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2009. Vol. 5761. Berlin, Heidelberg: Springer Berlin Heidelberg; 2009. pp. 787–794. [DOI] [PubMed] [Google Scholar]
- 11.Groenendaal G, Moman MR, Korporaal JG, et al. Validation of functional imaging with pathology for tumor delineation in the prostate. Radiother Oncol. 2010;94(2):145–150. doi: 10.1016/j.radonc.2009.12.034. [DOI] [PubMed] [Google Scholar]
- 12.Hadamard J. Sur les problèmes aux dérivées partielles et leur signification physique. Princeton university bulletin. 1902;13(49–52):28. [Google Scholar]
- 13.König D, Rolski T, Schmidt V, Stoyan D. Stochastic processes with imbedded marked point processes (pmp) and thcir application in queneing. Mathematische Operationsforschung und Statistik Series Optimization. 1978;9(1):125–141. [Google Scholar]
- 14.Ekeland I. On the variational principle. Journal of Mathematical Analysis and Applications. 1974;47(2):324–353. [Google Scholar]
- 15.Periaswamy S, Weaver JB, Healy JDM, Rockmore DN, Kostelec PJ, Farid H. Differential affine motion estimation for medical image registration. In: Akram A, AFL, Unser MA, editors. Proceedings of the Medical Imaging 2000: Wavelet Applications in Signal and Image Processing. Vol. 4119. San Diego, California, United States: SPIE; 2000. pp. 1066–1075. [Google Scholar]
- 16.Periaswamy S, Farid H. Elastic registration in the presence of intensity variations. IEEE Transactions on Medical Imaging. 2003;22(7):865–874. doi: 10.1109/TMI.2003.815069. [DOI] [PubMed] [Google Scholar]
- 17.Periaswamy S. Computer Science. Ann Arbor: Dartmouth College; 2003. General purpose medical image registration; pp. 158–158. [Google Scholar]
- 18.Viswanath S, Bloch BN, Genega E, et al. A comprehensive segmentation, registration, and cancer detection scheme on 3 Tesla in vivo prostate DCE-MRI. Med Image Comput Comput Assist Interv Int Conf Med Image Comput Comput Assist Interv. 2008;11(Pt 1):662–669. doi: 10.1007/978-3-540-85988-8_79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chappelow J, Madabhushi A. In: Niessen WJ, Meijering E, editors. Multi-attribute combined mutual information (MACMI): An image registration framework for leveraging multiple data channels; Proceedings of the 2010 7th IEEE International Symposium on Biomedical Imaging: From Nano to Macro; Rotterdam, Netherlands. 2010. pp. 376–379. [Google Scholar]
- 20.Ward AD, Crukley C, McKenzie C, et al. Registration of in vivo prostate magnetic resonance images to digital histopathology images. Proceedings of International Workshop on Prostate cancer imaging: computer-aided diagnosis, prognosis, and intervention, Held in Conjunction with MICCAI 2010, MICCAI’10; Beijing, China: Springer-Verlag; 2010. pp. 66–76. [Google Scholar]
- 21.Ward AD, Crukley C, McKenzie CA, et al. Prostate: registration of digital histopathologic images to in vivo MR images acquired by using endorectal receive coil. Radiology. 2012;263(3):856–864. doi: 10.1148/radiol.12102294. [DOI] [PubMed] [Google Scholar]
- 22.Jo HH, Jung J, Jang Y, Hong H, Lee HJ. Histopathology and MR image fusion of the prostate. In: Reinhardt JM, Pluim JPW, editors. Proceedings of the Medical Imaging 2008: Image Processing. Vol. 6914. San Diego, CA, USA: SPIE; 2008. pp. 691430–691430. [Google Scholar]
- 23.Park H, Kwee S, Thibault GP, et al. Registration methods for histological slides and ex vivo MRI of prostate. Proceedings of the 2007 IEEE Nuclear Science Symposium Conference; Honolulu, Hawaii, United States. 2007. pp. 3102–3104. [Google Scholar]
- 24.Alic L, Haeck JC, Klein S, et al. Multi-modal image registration: matching MRI with histology. In: CMR, Weaver JB, editors. Proceedings of the Medical Imaging 2010: Biomedical Applications in Molecular, Structural, and Functional Imaging. Vol. 7626. San Diego, California, United States: SPIE; 2010. pp. 762603–762609. [Google Scholar]
- 25.Chappelow J, Madabhushi A, Rosen M, Tomaszeweski J, Feldman M. Multimodal image registration of ex vivo 4 Tesla MRI with whole mount histology for prostate cancer detection. In: Pluim JPW, MRJ, editors. Proceedings of the Medical Imaging 2007: Image Processing. Vol. 6512. San Deigo, California, United States: SPIE; 2007. pp. 65121S–65112. [Google Scholar]
- 26.Zhan Y, Ou Y, Feldman M, Tomaszeweski J, Davatzikos C, Shen D. Registering Histological and MR Images of Prostate for Image-based Cancer Detection. Acad Radiol. 2007;14(11):1367–1381. doi: 10.1016/j.acra.2007.07.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ou Y, Shen D, Feldman M, Tomaszewski J, Davatzikos C. Non-rigid registration between histological and MR images of the prostate: A joint segmentation and registration framework. Proceedings of the 2009 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops; Miami, Florida, USA: IEEE Computer Society; 2009. pp. 125–132. [Google Scholar]
- 28.Chappelow J, Madabhushi A, Rosen M, Tomaszeweski J, Feldman M. A combined feature ensemble based mutual information scheme for robust inter-modal, inter-protocol image registration. Proceedings of the 2007 4th IEEE International Symposium on Biomedical Imaging: From Nano to Macro; Arlington, Virginia, United States: IEEE; 2007. pp. 644–647. [Google Scholar]
- 29.Patel P, Chappelow J, Tomaszewski J, et al. Spatially weighted mutual information (SWMI) for registration of digitally reconstructed ex vivo whole mount histology and in vivo prostate MRI. Engineering in Medicine and Biology Society, EMBC, 2011 Annual International Conference of the IEEE; 2011. pp. 6269–6272. [DOI] [PubMed] [Google Scholar]
- 30.Bookstein FL. Principal warps: thin-plate splines and the decomposition of deformations. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1989;11(6):567–585. [Google Scholar]
- 31.Kybic J, Unser M. Fast parametric elastic image registration. IEEE Transactions on Image Processing. 2003;12(11):1427–1442. doi: 10.1109/TIP.2003.813139. [DOI] [PubMed] [Google Scholar]
- 32.Xie Z, Farin GE. Image registration using hierarchical B-splines. IEEE Transactions on Visualization and Computer Graphics. 2004;10(1):85–94. doi: 10.1109/TVCG.2004.1260760. [DOI] [PubMed] [Google Scholar]
- 33.Meyer CR, Moffat BA, Kuszpit KK, et al. A methodology for registration of a histological slide and in vivo MRI volume based on optimizing mutual information. Mol Imaging. 2006;5(1):16–23. [PMC free article] [PubMed] [Google Scholar]
- 34.Pluim JPW, Maintz JBA, Viergever MA. Image registration by maximization of combined mutual information and gradient information. IEEE Transactions on Medical Imaging. 2000;19(8):809–814. doi: 10.1109/42.876307. [DOI] [PubMed] [Google Scholar]
- 35.Pluim JPW, Maintz JBA, Viergever MA. Mutual-information-based registration of medical images: a survey. IEEE Transactions on Medical Imaging. 2003;22(8):986–1004. doi: 10.1109/TMI.2003.815867. [DOI] [PubMed] [Google Scholar]
- 36.Viola P, Wells WM., III Alignment by maximization of mutual information. Proceeding of the 1995 IEEE 5th International Conference on Computer Vision; Cambridge, Massachusetts, United States. 1995. pp. 16–23. [Google Scholar]
- 37.Wells WM, 3rd, Viola P, Atsumi H, Nakajima S, Kikinis R. Multi-modal volume registration by maximization of mutual information. Medical image analysis. 1996;1(1):35–51. doi: 10.1016/s1361-8415(01)80004-9. [DOI] [PubMed] [Google Scholar]
- 38.Boldea V, Sharp GC, Jiang SB, Sarrut D. 4D-CT lung motion estimation with deformable registration: quantification of motion nonlinearity and hysteresis. Medical Physics. 2008;35(3):1008–1018. doi: 10.1118/1.2839103. [DOI] [PubMed] [Google Scholar]
- 39.Brock KK, Nichol AM, Ménard C, et al. Accuracy and sensitivity of finite element model-based deformable registration of the prostate. Medical Physics. 2008:35. doi: 10.1118/1.2965263. [DOI] [PubMed] [Google Scholar]
- 40.Brock KK, Sharpe MB, Dawson LA, Kim SM, Jaffray DA. Accuracy of finite element model-based multi-organ deformable image registration. Medical Physics. 2005;32(6) doi: 10.1118/1.1915012. [DOI] [PubMed] [Google Scholar]
- 41.Dice LR. Measures of the amount of ecologic association between species. Ecology. 1945;26(3):297–302. [Google Scholar]
- 42.Fitzpatrick JM, Hill DLG, Shyr Y, West J, Studholme C, Maurer CR. Visual assessment of the accuracy of retrospective registration of MR and CT images of the brain. IEEE Transactions on Medical Imaging. 1998;17(4):571–585. doi: 10.1109/42.730402. [DOI] [PubMed] [Google Scholar]
- 43.Kaus MR, Brock KK, Pekar V, Dawson LA, Nichol AM, Jaffray DA. Assessment of a model-based deformable image registration approach for radiation therapy planning. Int J Radiat Oncol Biol Phys. 2007;68(2):572–580. doi: 10.1016/j.ijrobp.2007.01.056. [DOI] [PubMed] [Google Scholar]
- 44.Rietzel E, Chen GTY. Deformable registration of 4D computed tomography data. Medical Physics. 2006;33(11):4423–4430. doi: 10.1118/1.2361077. [DOI] [PubMed] [Google Scholar]
- 45.Wong JCH, Studholme C, Hawkes DJ, Maisey MN. Evaluation of the limits of visual detection of image misregistration in a brain fluorine-18 fluorodeoxyglucose PET MRI study. European Journal of Nuclear Medicine. 1997;24:642–650. doi: 10.1007/BF00841402. [DOI] [PubMed] [Google Scholar]
- 46.Woods RP. Handbook of Medical Image Processing and Analysis. 2. Burlington: Academic Press; 2009. Validation of Registration Accuracy; pp. 569–575. [Google Scholar]