Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Oct 6;4:6529. doi: 10.1038/srep06529

How fragility makes phase-change data storage robust: insights from ab initio simulations

Wei Zhang 1,2, Ider Ronneberger 1, Peter Zalden 2,3, Ming Xu 2, Martin Salinga 2, Matthias Wuttig 2,4, Riccardo Mazzarello 1,4,a
PMCID: PMC4185410  PMID: 25284316

Abstract

Phase-change materials are technologically important due to their manifold applications in data storage. Here we report on ab initio molecular dynamics simulations of crystallization of the phase change material Ag4In3Sb67Te26 (AIST). We show that, at high temperature, the observed crystal growth mechanisms and crystallization speed are in good agreement with experimental data. We provide an in-depth understanding of the crystallization mechanisms at the atomic level. At temperatures below 550 K, the computed growth velocities are much higher than those obtained from time-resolved reflectivity measurements, due to large deviations in the diffusion coefficients. As a consequence of the high fragility of AIST, experimental diffusivities display a dramatic increase in activation energies and prefactors at temperatures below 550 K. This property is essential to ensure fast crystallization at high temperature and a stable amorphous state at low temperature. On the other hand, no such change in the temperature dependence of the diffusivity is observed in our simulations, down to 450 K. We also attribute this different behavior to the fragility of the system, in combination with the very fast quenching times employed in the simulations.

Phase-change materials (PCMs) possess a peculiar combination of properties1,2. They are capable of switching extremely rapidly and reversibly between the amorphous and crystalline phase at high temperature. Yet the two phases are very stable at room temperature and exhibit a pronounced optical and electrical contrast. The property contrast stems from the difference in the atomic arrangement and chemical bonding between the two phases3,4. Exploitation of these properties has led to applications in rewritable optical devices (CD, DVD, Blu-Ray Disc) and electronic non-volatile random access memories (PC-RAM), where heating is induced by laser irradiation and the Joule effect, respectively. Two families of PCMs are widely employed in data storage, namely GeTe-Sb2Te3 pseudobinary alloys5,6,7,8,9,10,11,12, such as GeTe and Ge2Sb2Te5, and Sb-Te compounds13,14,15, such as doped Sb2Te16,17.

The fast crystallization of these materials identifies them as poor glass formers, with a glass transition temperature (Tg) of around half of the melting temperature18. Recent experimental19,20 and theoretical21,22 studies linked the rapid crystallization to the high fragility of PCMs, i.e. to the fact that the viscosity η of the liquid behaves in a non-Arrhenius fashion. This property makes PCMs of fundamental interest in the field of glasses and disordered solids as well.

More specifically, ultrafast differential scanning calorimetric (DSC) experiments19 explained the tremendous increase in the crystal growth rate of as-deposited amorphous Ge2Sb2Te5 at temperatures above Tg in terms of its high fragility and of the breakdown in the Stokes-Einstein relation between the viscosity and the diffusivity D, η ∝ D−1, near Tg. Molecular dynamics simulations of melt-quenched GeTe employing classical neural-network potentials also yielded a decoupling of viscosities and diffusivities21,22.

On the other hand, time-resolved reflectivity measurements of melt-quenched Ag4In3Sb67Te26 (AIST)20 showed that, for very fast quenching rates of the order of 1010 K/s (comparable to the rates occurring in memory cells), Tg increases by at least 100 K with respect to the value determined for as-deposited samples using DSC measurements, with heating rates of less than 1 K/s18. This finding agrees with the fact that Tg generally depends on the cooling/heating rates23. The growth velocity of the fast-quenched glassy state was shown to obey the Arrhenius law below 550 K20, corresponding to diffusivities with high activation energy Ea = 2.78 eV and large prefactor D0 = 2 × 1015 m2/s. In contrast, at higher temperatures an activation barrier of about 0.24 eV and a prefactor of 4 × 10−8 cm2/s is observed for similar compounds24. The change in Ea and D0 ensures the combination of fast recrystallization at elevated T and high stability of the amorphous phase at low T. Understanding the crystallization mechanisms at high T and the origin of said change is hence crucial to unravel the two most important features of PCMs.

With these goals in mind, we have performed density functional theory (DFT) calculations to investigate the temperature dependence of the crystal growth velocity and to identify the underlying microscopic mechanisms. It is known that crystallization of small amorphous marks of AIST surrounded by a crystalline region is dominated by the growth at the interface20. More generally, with decreasing cell size in nonvolatile PC-RAM memories25, this recrystallization mechanism is expected to prevail over nucleation, regardless of the PCM employed. Hence, we considered amorphous and supercooled liquid models of AIST inside a crystalline matrix and investigated the growth of the interface at different temperatures. This strategy requires the largest feasible models, in this case containing 810 atoms, to produce realistic amorphous structures. These models are considerably larger than those investigated in previous ab initio studies of crystallization of PCMs26,27,28.

Results

Structural properties

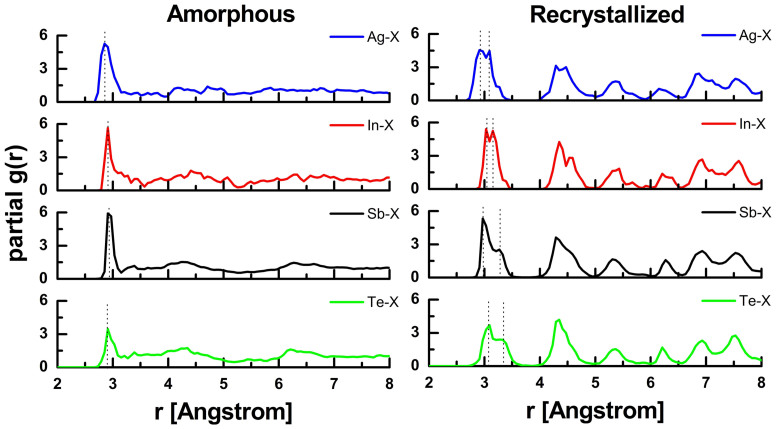
We first compare the structural properties of the simulated melt-quenched amorphous models and recrystallized models of AIST with our experimental data for as-deposited and oven-crystallized AIST. The partial pair correlation functions (PPCFs) based on the ab initio molecular dynamics (AIMD) trajectory of the amorphous and recrystallized models at 10 K are shown in Fig. 1. The PPCFs of the amorphous model are in good agreement with those presented in Ref. 14. The recrystallized models form an A7 lattice, in line with our X-ray diffraction measurements (see section A of the Supplementary Information), and Ag, In, Sb and Te atoms occupy the crystalline sites in a random fashion. The PPCFs for Sb and Te display a double peak at 2.97–3.28 Å and 3.07–3.30 Å, respectively, corresponding to a 3 + 3 coordination due to Peierls distortion. The nearest neighbor bond lengths and coordination numbers (CNs) derived from our extended X-ray absorption fine structure experiments agree fairly well with those obtained from AIMD simulations for both phases, as shown in Table I. For some PCMs, such as Ge15Te85, inclusion of van der Waals corrections to the generalized gradient approximation (GGA) used here has been shown to improve the agreement between the structural properties of AIMD models and experimental data29. Our results indicate that, for amorphous AIST, simulations based on plain GGA functionals agree satisfactorily with experiments. Some Ag and In atoms are found to occupy interstitial sites in both AIMD recrystallized models and oven-crystallized experimental samples, leading to significantly shorter bonds and higher CNs. A thorough analysis of the structural properties of both phases, including measured and simulated EXAFS curves, is provided in the Supplementary Information (section A).

Figure 1. Partial pair-correlation functions of amorphous and recrystallized AIST calculated at T = 10 K.

Figure 1

Open in a new tab

Vertical dashed lines indicate the primary peak positions. The experimental amorphous density13 (instead of the crystalline one) is used in these simulations of the amorphous models.

Table 1. The nearest neighbour bond lengths and coordination numbers for amorphous and recrystallized AIST, obtained from AIMD simulations and EXAFS experiments. Experiments are performed on as-deposited amorphous samples, without crystalline surroundings. Hence, for a fair comparison, the experimental amorphous density13 is used in the corresponding set of AIMD simulations, instead of the crystalline one. To calculate the CNs from the AIMD simulations, cutoff distances of 3.1 Å (amorphous AIST) and 3.4 Å (recrystallized AIST) are employed.

Atom rEXAFS(Å) rAIMD(Å) NEXAFS NAIMD
Amorphous        
Ag 2.81(1) 2.85 4.0 ± 0.7 4.5
In 2.82(1) 2.90 2.7 ± 0.5 3.0
Sb 2.87(1) 2.92 3.4 ± 0.6 3.2
Te 2.83(1) 2.90 1.6 ± 0.4 2.3
Recrystallized        
Ag 2.84(3),3.02(3) 2.92,3.07 7.2 ± 0.7 6.2
In 2.80(1),2.99(1) 3.00,3.14 6.6 ± 0.7 6.0
Sb 2.89(1),3.32(1) 2.97,3.28 6.2 ± 0.6 5.9
Te 2.94(1),3.39(3) 3.07,3.30 3.8 ± 0.5 5.4
Open in a new tab

High-temperature growth process

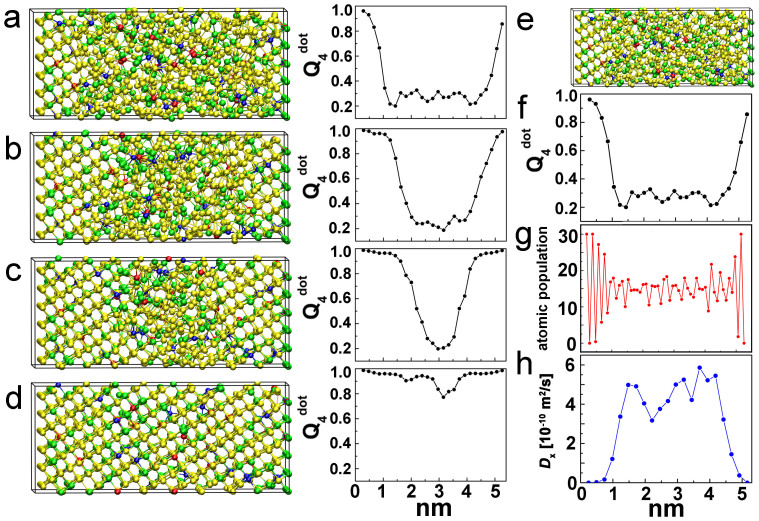
Next, we focus on the crystallization process at high temperature (585 K). We consider crystal growth along the [0001] direction of the hexagonal lattice. Crystallization is observed to occur at the amorphous-crystalline interface (see some snapshots in Figs. 2(a)–(d) and the Supplementary Video). To verify that the interface growth process is smooth and the amorphous region is devoid of nuclei during crystallization, we employ the bond order parameter “dot-product”, qdot430, which can appropriately distinguish the two phases. We divide the supercell into slabs along the growth direction (parallel to x) and average qdot4 over all the atoms within each slab. We denote the averaged qdot4 values as Qdot4. The amorphous-crystalline interface corresponds to the region where Qdot4 increases from the “amorphous” (~0.3) to the “crystalline” (~0.9) value (see section B of the Supplementary Information). The evolution of the Qdot4 profiles reveals that, indeed, no nucleation processes occur inside the amorphous region (see Figs. 2(a)–(d)), in line with the experimental observations of Ref. 20.

Figure 2.

Figure 2

Open in a new tab

(a)–(d) Snapshots of the crystallization process (at T = 585 K) at 0, 60, 120 and 170 ps and corresponding Qdot4 profiles. Ag, In, Sb and Te atoms are rendered with blue, red, yellow and green spheres respectively. Qdot4 is averaged both over the atoms within each slab and over time (0.6 ps). (e) Snapshot at the initial stage of crystallization and corresponding Qdot4 profile (f), atomic population profile (g) and diffusivity Dx profile (h). The atomic population is obtained by computing the total number of atoms in each slab, averaged over 0.6 ps. The profile of Dx is derived from the mean-square displacements in x-direction, which are calculated by averaging over the atoms in each slab and over time (30 ps).

Based on the crystallization trajectory, we also derive the growth velocity vg. Specifically, we calculate the evolution of the number of crystalline-like particles, Nc (see Fig. S6). By multiplying the ratio Nc/N (where N is the total number of particles) by the cell parameter along the growth direction and dividing by the corresponding time Δt, vg is obtained. We observe that, in the last part of the trajectories, there is a spurious interaction between the interfaces which accelerates crystallization, albeit not dramatically. To overcome this problem, we do not include this part in the calculation of the growth velocity. Averaging over four trajectories, we obtain vg = 7.8 m/s. This value is consistent with the time-resolved reflectivity measurements20.

To better understand the crystallization mechanisms, it is useful to inspect more closely the properties of the amorphous-crystalline interface. We calculate the profiles of the atomic population and of the diffusion coefficient D along the growth direction (denoted Dx) at the initial stage of crystallization. The coefficients Dx are computed by evaluating the atomic mean square displacements within each slab. The profiles of Qdot4 and of the atomic population (see Figs. 2(e)–(g)) indicate that the interface is thin: it extends over ~8 Å only. In the amorphous region, the diffusion coefficients fluctuate around the bulk value of 5.0 × 10−10 m2/s (Fig. 2(h)), which we obtained from independent simulations of purely amorphous models. Furthermore, the diffusion profile shows that the decrease in mobility at the interface is as sharp as the interface itself. Recently, it was suggested that different thicknesses of the crystal/liquid interface can result in different crystal growth rate and glass forming ability of structurally similar compounds31. In the case of AIST, the sharp interface ensures a very high mobility of the atoms near the crystalline surface, resulting in fast crystal growth.

During the crystallization process, a fraction of the atoms impinging on the crystalline [0001] surface form three strong chemical bonds with the underlying atoms. In-plane interactions with neighboring atoms on the surface are weak, since the in-plane nearest-neighbor atomic distance is about 4.25 Å. Even after occupying a crystalline site on the surface, the atom has a finite probability to escape from it (see Fig. S8). We can better quantify the growth process by calculating the deposition rate k+, i.e. the rate at which atoms impinge on the surface and occupy empty crystalline sites, and the sticking coefficient S, i.e. the probability for an atom occupying such a site to stick permanently to the surface and become part of the crystal (see section C of the Supplementary Information for details). In fact, vg is proportional to the product of k+ and S with a proportionality factor λ having the unit of length. λ is typically of the order of the diffusional jump distance. In the Wilson-Frenkel (WF) limit32,33, k+ and S are proportional to the diffusion coefficient D and the driving force respectively, and the growth velocity reads

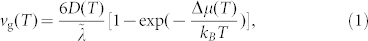graphic file with name srep06529-m1.jpg

where Δμ(T) is the chemical potential difference between the supercooled liquid and the solid phase and 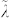Inline graphic is also of the order of the interatomic distance. The values of S and k+ calculated from the MD trajectories (without resorting to the WF approximation) are 0.38 and 0.12 ps−1, respectively. k+ is very large, reflecting the high atomic mobility near the interface. Comparing these values with the growth velocity calculated directly from the trajectories (vg = 7.8 m/s), one obtains a very reasonable estimate for λ, 1.7 Å.

Temperature dependence of the growth velocity

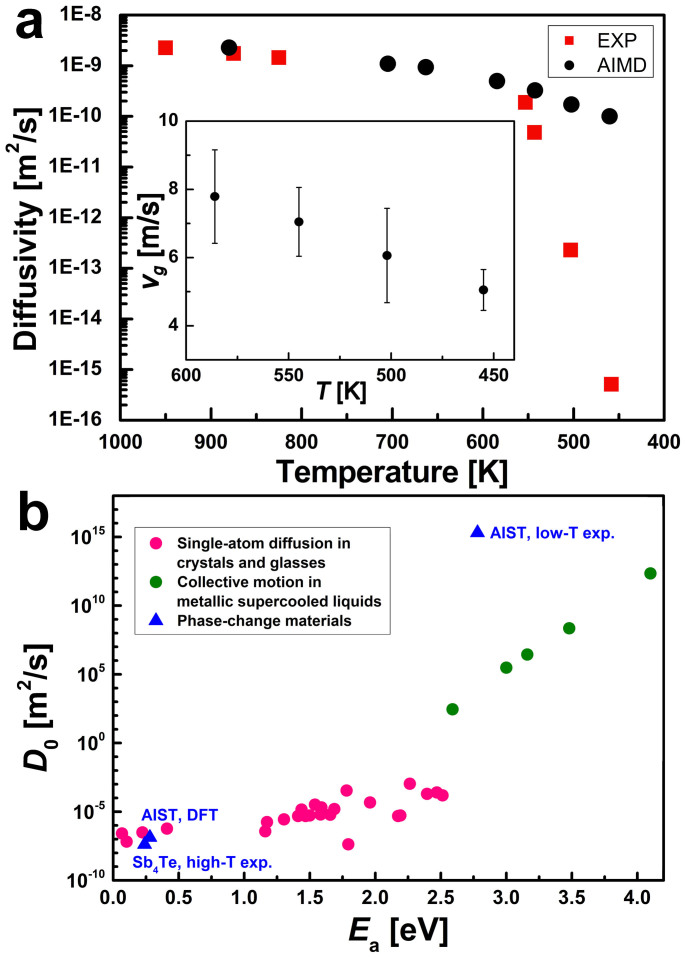
We now consider the growth velocity of AIST at lower temperatures. We calculate vg at 3 additional temperatures (550 K, 500 K and 455 K) following 3 approaches. The first one is based on the temporal evolution of the number of crystalline-like particles (a). The corresponding results are shown in the inset of Fig. 3(a). Table II also contains these data, as well as the values of vg obtained by using (b) the expression vg = λk+S and (c) Formula (1), with the bulk values of D and Thompson-Spaepen expression34 for μ(T) (see also section C of the Supplementary Information). The agreement between the first 2 methods is quite good. The 3rd approach (WF formula) also agrees fairly well with the first two. A small source of discrepancy is the fact that D(T) is not exactly proportional to k+(T): the ratio k+/D changes by a factor of two from 585 K to 455 K. This is probably due to finite size effects. Overall, the 3 methods provide a similar temperature dependence of vg.

Figure 3.

Figure 3

Open in a new tab

(a) Calculated and experimental diffusion coefficients of AIST. The theoretical coefficients are obtained by evaluating the atomic mean square displacements in the amorphous models without crystalline boundaries, on an 80 ps time scale. Experimental values of D at T below 600 K are obtained from the measured growth velocities vg20 by assuming that vg can be described by the WF equation (1) and by using Thompson-Spaepen formula34 to estimate Δμ(T). The high-T diffusivity values refer to liquid Sb4Te and are taken from Ref. 24. The inset shows the theoretical values of vg for AIST, which we compute from the evolution of the number of crystalline-like particles. (c) Experimental values of Ea and D0 for diffusion processes in selected crystals, glasses and supercooled liquid metals (taken from Refs. 35 and 36), compared with the experimental20 and DFT values for AIST.

Table 2. Comparison of the growth velocities vg obtained from (a) the evolution of the number of crystalline-like particles (see also Fig. 3; in this Table the average values of vg are shown), (b) the product λk+·S and (c) Wilson-Frenkel (WF) formula. The value of λ = 1.7 Å is obtained by comparing the first and second approach at T = 585 K. We also assume that the quantity 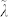Inline graphic entering the WF formula is equal to λ.

Temperature [K] 585 543 503 455
simulations        
vg [m/s] 7.80 7.28 6.68 5.33
vg = λk+·S        
τ [ps] 8.30 11.27 14.37 20.15
k+ 0.1204 0.0884 0.0696 0.0496
S 0.38 0.44 0.46 0.50
vg [m/s] 7.80 6.62 5.44 4.22
WF formula        
D [×10−10 m2/s] 4.97 3.27 1.72 1.00
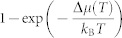Inline graphic 0.54 0.62 0.68 0.75
vg [m/s] 9.51 7.11 4.12 2.63
Open in a new tab

We compare the computed growth velocities with the time-resolved reflectivity measurements of Ref. 20. It turns out that our values of vg at T = 455 K and 500 K are in very poor agreement with these experiments, which yielded growth velocities between 10−2–10−5 m/s in this temperature range. This discrepancy mainly stems from the kinetic term, namely the large difference between the calculated and experimental diffusion coefficients at these temperatures, as shown in Fig. 3(a).

By fitting the theoretical data for D(T) in the temperature range between 450 K and 585 K with Formula

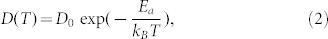graphic file with name srep06529-m2.jpg

we obtain Ea = 0.30 eV and D0 = 2.15 × 10−7 m2/s. The computed values of Ea and D0 are in fair agreement with the high-temperature experimental values for Sb4Te24 (see also Fig. 3(a)), namely Ea = 0.24 eV and D0 = 4.10 × 10−8 m2/s. They are also comparable to the typical values for diffusion processes in crystals and glasses, where atomic rearrangements are governed by the motion of single atoms, such as tracer and impurity diffusion35 (see Fig. 3(b)).

On the other hand, according to the experiments of Ref. 20, a pronounced change in the temperature dependence of D occurs at some T around 550 K. Below this temperature, reflectivity measurements yielded Ea = 2.78 eV, D0 = 2.03 × 1015 m2/s20. Large values of Ea and D0 are also observed in supercooled liquid metals (Fig. 3(b)), where they are attributed to the cooperative nature of the rearrangement process36. The low-T prefactor for AIST is even larger. Remarkably, such large activation energies and prefactors are essential for PCMs to ensure a stable amorphous state at low T. Fast crystallization at higher T is instead brought about by the small Ea and D0 in the supercooled liquid regime. The two properties are crucial for the utilization of PCMs in data storage applications. Large prefactors and activation energies for crystal growth in Ge2Sb2Te5 have also been inferred from low-temperature measurements37. In a recent work38, the existence of two crystallization regimes with different activation energies was shown to be a necessary ingredient for the modeling of crystallization kinetics in PCM devices.

Discussion

The change in Ea and D0 near Tg is an important property of fragile systems. It reflects the slowing down of the kinetics, which stems from an increasingly cooperative character of the atomic motion39. Hence, models of crystallization based on movements of individual atoms cannot grasp the crystallization processes in PCMs below and near Tg, but only in the supercooled liquid regime at high T.

The extrapolation of the theoretical curve for D(T) to low temperatures (below 450 K) yields too large growth velocities, in contrast with the high stability of amorphous AIST in this temperature range. To rule out the possibility that, in our simulations, Tg occurs at temperatures around 450 K, we also perform simulations at 400 K. A small but significant growth of the crystal is observed during our 280 ps run. A rough estimate of vg yields a value of order 1 m/s. More details are provided in section D of the Supplementary Information.

Finite size effects in our simulations certainly lead to non-negligible errors in the evaluation of both vg and D. As already mentioned, the interaction between the two amorphous-crystalline interfaces becomes significant in the last part of the trajectories (in that the thickness of the amorphous part is small) and Nc as a function of t deviates from the linear behavior observed at smaller t. We do not include these data in the linear regression analysis. To further assess finite size effects, we also consider a smaller model of AIST containing 540 atoms (corresponding to 18 layers of the crystalline phase). The resulting growth velocity is within the error bar estimated from the simulations of the large models (see also section D of the Supplementary Information). Hence, we can conclude that the spurious effects due to the small size of our models cannot account for the large mismatch between simulations and experiments.

It is also important to stress that our models are reheated to the target temperature after quenching to 300 K, in contrast to experiments, where crystallization occurred directly after quenching the liquid to the target temperature20. The dynamical properties of the states obtained by these two procedures are different, however the experimental procedure would be expected to yield states with larger diffusivities than those generated by quenching and reheating21 (for fixed quenching rates), which makes the discrepancy between theory and experiments even more pronounced. Furthermore, the equilibration times (at 300 K) and heating times in our simulations are also extremely short and we thus expect that no significant relaxation of the amorphous state occurs during this procedure. It is worth mentioning that, in principle, the procedure adopted in our simulations is more relevant to practical data storage applications.

The AIMD method we use is intrinsically (slightly) dissipative and is typically employed in combination with stochastic Langevin thermostats, so that it properly samples the canonical distribution40,41. It is well known that thermostats (in particular, stochastic thermostats) can affect the dynamical properties of a system significantly. For this reason, it is generally recommended to perform NVE simulations after equilibration to compute diffusion coefficients42. Since a stochastic thermostat has to be used for the simulations of crystallization, we employ the same thermostat for the independent evaluation of D as well, for the sake of consistency. To estimate the error due to the thermostat, we also perform some NVE simulations and find that the resulting D for AIST are up to 50% larger than those obtained using Langevin thermostats. Hence, although these deviations are significant, they clearly do not affect the main conclusions of our work. In particular, the temperature dependence of the diffusion coefficients is the same.

We think that the most plausible explanation for the discrepancy is the difference in quenching rates, namely, 1013 K/s (simulations) versus 1010 K/s (experiments). If the cooling rate applied to a fragile system is too fast with respect to some “optimum” rate (which depends on the system under study), the resulting glass is less stable and more prone to crystallization43. Fast quenching generally results in poor sampling of the potential energy landscape. In a fragile system, due to the complex topography of the energy landscape, which typically consists of well-separated large basins23, poor sampling should lead to markedly different dynamical properties. Strong glasses should not exhibit this behaviour. In our simulations, the activation energy for diffusion at low T is almost the same as the one of the supercooled liquid at high temperature (see Fig. 2(a)). This suggests that sampling of the energy landscape is extremely poor and the system basically explores the same basins (consisting of low potential barriers) as the ones sampled by the supercooled liquid at high temperature. The high values of vg observed in our simulations should be related to this property and, thus, provide indirect evidence for the fragility of AIST. Therefore, we believe that the utilization of more realistic quenching times close to the experimental values (which are still beyond the capabilities of present-day supercomputers) would lead to a crystallization behavior in much better agreement with experiments.

In conclusion, our ab initio simulations of AIST show that, at high temperatures (e.g. 585 K), fast crystallization is due to the large diffusion constants and sticking coefficients, as well as to the thin amorphous-crystalline interface, which ensures that the atomic mobility is high even at the very surface of the crystal. At temperatures below 550 K, the dynamical properties of the amorphous models, obtained by extremely fast simulated quenching from the melt (with rates of 1013 K/s), differ dramatically from the experimentally determined properties of samples quenched at slower rates (1010 K/s). This discrepancy is attributed to the high fragility of AIST. The more pronounced decrease in growth velocity observed in experiments is due to the increasingly cooperative motion of the particles at low T, which also stems from fragility. These findings call for further experimental and theoretical research to address the dependence of the dynamical properties of amorphous PCMs on quenching rates.

Methods

X-ray diffraction

Experiments were performed at room temperature using Cu K-α radiation in grazing incidence to measure the diffracted intensities of a polycrystalline thin film of AIST on a Si substrate.

X-ray absorption spectroscopy

EXAFS measurements were performed at beamline CEMO of the accelerator ring DORIS III, as part of Hasylab, DESY. All four K-edges of AIST were measured in transmission geometry on powderous samples pressed to pellets. The samples were cooled to 10 K and measured at least twice to check for statistical deviations between subsequent scans. The resulting data were normalized to pre- and post-edge ranges and Fourier transformed. In this way, experimental EXAFS spectra on the as-deposited amorphous and oven-crystallized phases were obtained.

Ab initio simulations

We employed the “second-generation” Car-Parrinello scheme40 implemented in the CP2K suite of programs44. GGA exchange-correlation functionals45 and scalar-relativistic Goedecker pseudopotentials46 were used. The amorphous models were generated by quenching from the melt, with a quenching rate of 1013 K/s. Two atomic layers were fixed at the crystalline positions during melting and quenching of these models, and 2–3 additional crystalline layers were formed during the very rapid quenching process: since we employed periodic boundary conditions in all three directions, these layers acted as a crystalline matrix from which the crystal grew in the subsequent simulations. The density was fixed at the experimental value of the crystalline phase13. Simulations at fixed density are relevant to the experimental setup of Ref. 20 and to phase-change memory cells, wherein the crystalline matrix surrounding the amorphous marks constrains the volume available during the recrystallization process. Amorphous models of AIST containing 540 atoms, with and without crystallization seeds, were also generated. Further details about the simulation setup and the models are provided in section E of the Supplementary Information.

Author Contributions

W.Z. performed most of the simulations. Analysis of the data was carried out by W.Z., I.R. and R.M. Experiments were performed and analyzed by P.Z. The paper was written by R.M. and M.W., with help from all co-authors, in particular W.Z. and M.X. The project was initiated by W.Z., M.S., M.W. and R.M.

Supplementary Material

Supplementary Information

How fragility makes phase-change data storage robust: insights from ab initio simulations

srep06529-s1.pdf (4MB, pdf)
Supplementary Information

Crystallization Video

Download video file (7.4MB, wmv)

Acknowledgments

We thank M. Apel, E. Brener, J. Benke, G. C. Sosso, M. Bernasconi and C. Massobrio for useful discussions. We also acknowledge the computational resources granted by JARA-HPC from RWTH Aachen University under project JARA0046, as well as funding by the DFG (German Science Foundation) within the collaborative research centre SFB 917 “Nanoswitches”. W. Z. acknowledges DAAD and CSC for financial support. M. X. acknowledges the Alexander von Humboldt foundation.

References

  1. Wuttig M. & Yamada N. Phase-change materials for rewriteable data storage. Nature Mater 6, 824–832 (2007). [DOI] [PubMed] [Google Scholar]
  2. Raoux S., Welnic W. & Ielmini D. Phase Change Materials and Their Application to Nonvolatile Memories. Chem Rev 110, 240–267 (2010). [DOI] [PubMed] [Google Scholar]
  3. Shportko K. et al. Resonant bonding in crystalline phase-change materials. Nature Mater 7, 653–658 (2008). [DOI] [PubMed] [Google Scholar]
  4. Lencer D. et al. A map for phase-change materials. Nature Mater 7, 972–977 (2008). [DOI] [PubMed] [Google Scholar]
  5. Kolobov A. V. et al. Understanding the phase-change mechanism of rewritable optical media. Nature Mater 3, 703–708 (2004). [DOI] [PubMed] [Google Scholar]
  6. Baker D., Paesler M., Lucovsky G., Agarwal S. & Taylor P. Application of Bond Constraint Theory to the Switchable Optical Memory Material Ge2Sb2Te5. Phys Rev Lett 96, 255501 (2006). [DOI] [PubMed] [Google Scholar]
  7. Caravati S., Bernasconi M., Kühne T. D., Krack M. & Parrinello M. Coexistence of tetrahedral- and octahedral-like sites in amorphous phase change materials. Appl Phys Lett 91, 171906 (2007). [Google Scholar]
  8. Akola J. & Jones R. Structural phase transitions on the nanoscale: The crucial pattern in the phase-change materials Ge2Sb2Te5 and GeTe. Phys Rev B 76, 235201 (2007). [Google Scholar]
  9. Mazzarello R., Caravati S., Angioletti-Uberti S., Bernasconi M. & Parrinello M. Signature of Tetrahedral Ge in the Raman Spectrum of Amorphous Phase-Change Materials. Phys Rev Lett 104, 085503 (2010). [DOI] [PubMed] [Google Scholar]
  10. Kalb J., Spaepen F. & Wuttig M. Atomic force microscopy measurements of crystal nucleation and growth rates in thin films of amorphous Te alloys. Appl Phys Lett 84, 5240 (2004). [Google Scholar]
  11. Zhang W. et al. Role of vacancies in metal-insulator transitions of crystalline phase-change materials. Nature Mater 11, 952–956 (2012). [DOI] [PubMed] [Google Scholar]
  12. Deringer V. et al. Bonding nature of local structural motifs in amorphous GeTe. Angew Chem Int Ed 53, 10817–20 (2014). [DOI] [PubMed] [Google Scholar]
  13. Njoroge W. K. & Wuttig M. Crystallization kinetics of sputter-deposited amorphous AgInSbTe films. J Appl Phys 90, 3816 (2001). [Google Scholar]
  14. Matsunaga T. et al. From local structure to nanosecond recrystallization dynamics in AgInSbTe phase-change materials. Nature Mater 10, 129–134 (2011). [DOI] [PubMed] [Google Scholar]
  15. Zhang W., Ronneberger I., Li Y. & Mazzarello R. Ab initio investigation of amorphous Sb2Te. Monatsh Chem 145, 97 (2014). [Google Scholar]
  16. van Pieterson L., Lankhorst M. H. R., van Schijndel M., Kuiper A. E. T. & Roosen J. H. J. Phase-change recording materials with a growth-dominated crystallization mechanism: A materials overview. J Appl Phys 97, 083520 (2005). [Google Scholar]
  17. Hong S.-H., Bae B.-J. & Lee H. Fast switching behavior of nanoscale Ag6In5Sb59Te30 based nanopillar type phase change memory. Nanotech 21, 025703 (2010). [DOI] [PubMed] [Google Scholar]
  18. Kalb J., Wuttig M. & Spaepen F. Calorimetric measurements of structural relaxation and glass transition temperatures in sputtered films of amorphous Te alloys used for phase change recording. J Mater Res 22, 748–754 (2007). [Google Scholar]
  19. Orava J., Greer A. L., Gholipour B., Hewak D. W. & Smith C. E. Characterization of supercooled liquid Ge2Sb2Te5 and its crystallization by ultrafast-heating calorimetry. Nature Mater 11, 279–283 (2012). [DOI] [PubMed] [Google Scholar]
  20. Salinga M. et al. Measurement of crystal growth velocity in a melt-quenched phase-change material. Nature Comm 4, 2371 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Sosso G. C., Behler J. & Bernasconi M. Breakdown of Stokes-Einstein relation in the supercooled liquid state of phase change materials. Physica Status Solidi (b) 249, 1880–1885 (2012). [Google Scholar]
  22. Sosso G. C. et al. Fast Crystallization of the Phase Change Compound GeTe by Large-Scale Molecular Dynamics Simulations. J Phys Chem Lett 4, 4241–4246 (2013). [DOI] [PubMed] [Google Scholar]
  23. Debenedetti P. G. & Stillinger F. H. Supercooled liquids and the glass transitiontransition. Nature 410, 259–267 (2001). [DOI] [PubMed] [Google Scholar]
  24. Herwig F. W. Measurements of viscosity in the systems antimony tellurium and tin tellurium. Z Metallkd 83, 35–39 (1992). [Google Scholar]
  25. Im D. H. et al. A Unified 7.5 nm Dash-Type Confined Cell for High Performance PRAM Device. Proc IEEE Int Electron Devices Meeting, 10.1109/IEDM.2008.4796654 (2008). [Google Scholar]
  26. Hegedüs J. & Elliott S. R. Microscopic origin of the fast crystallization ability of Ge-Sb-Te phase-change memory materials. Nature Mater 7, 399–405 (2008). [DOI] [PubMed] [Google Scholar]
  27. Lee T. H. & Elliott S. R. Ab Initio Computer Simulation of the Early Stages of Crystallization: Application to Ge2Sb2Te5 Phase-Change Materials. Phys Rev Lett 107, 145702 (2011). [DOI] [PubMed] [Google Scholar]
  28. Kalikka J., Akola J., Larrucea J. & Jones R. O. Nucleus-driven crystallization of amorphous Ge2Sb2Te5: A density functional study. Phys Rev B 86, 144113 (2012). [Google Scholar]
  29. Micoulaut M. Communication: Van der Waals corrections for an improved structural description of telluride based materials. J. Chem Phys 138, 061103 (2013). [DOI] [PubMed] [Google Scholar]
  30. ten Wolde P., Ruiz-Montero M. J. & Frenkel D. Simulation of homogeneous crystal nucleation close to coexistence. Faraday Discuss 104, 93–110 (1996). [Google Scholar]
  31. Tang C. & Harrowell P. Anomalously slow crystal growth of the glass-forming alloy CuZr. Nature Mater 12, 507–511 (2013). [DOI] [PubMed] [Google Scholar]
  32. Wilson H. A. On the velocity of solidification and viscosity of super-cooled liquids. Phil Mag 50, 238–250 (1900). [Google Scholar]
  33. Frenkel Y. The Kinetic Theory of Liquids. Oxford University Press (1946). [Google Scholar]
  34. Thompson C. V. & Spaepen F. On the approximation of the free energy change on crystallization. Acta Metall Mater 27, 1855–1859 (1979). [Google Scholar]
  35. Naundorf V., Macht M.-P., Bakai A. S. & Lazarev N. The pre-factor D0 of the diffusion coefficient in amorphous alloys and grain boundaries. J Non-Cryst Solids 250, 679–683 (1999). [Google Scholar]
  36. Fielitz P., Macht M.-P., Naundorf V. & Frohberg G. Diffusion in ZrTiCuNiBe bulk glasses at temperatures around the glass transition. J Non-Cryst Solids 250, 674–678 (1999). [Google Scholar]
  37. Ielmini D. & Bonardi M. Common signature of many-body thermal excitation in structural relaxation and crystallization of chalcogenide glasses. Appl Phys Lett 94, 091906 (2009). [Google Scholar]
  38. Cassinerio M., Ciocchini N. & Ielmini D. Evidence for electrically induced drift of threshold voltage in Ge2Sb2Te5. Appl Phys Lett 103, 023502 (2013). [Google Scholar]
  39. Bauer T., Lunkenheimer P. & Loidl A. Cooperativity and the Freezing of Molecular Motion at the Glass Transition. Phys Rev Lett 111, 225702 (2013). [DOI] [PubMed] [Google Scholar]
  40. Kühne T., Krack M., Mohamed F. & Parrinello M. Efficient and Accurate Car-Parrinello-like Approach to Born-Oppenheimer Molecular Dynamics. Phys Rev Lett 98, 066401 (2007). [DOI] [PubMed] [Google Scholar]
  41. Kühne T., Krack M. & Parrinello M. Static and Dynamical Properties of Liquid Water from First Principles by a Novel Car-Parrinello like Approach. J Chem Theory Comp 5, 235–241 (2009). [DOI] [PubMed] [Google Scholar]
  42. Frenkel D. & Smit B. Understanding Molecular Simulation. Academic Press, San Diego (2002). [Google Scholar]
  43. Jund P., Caprion D. & Jullien R. Is There an Ideal Quenching Rate for an Ideal Glass. Phys Rev Lett 79, 91–94 (1997). [Google Scholar]
  44. Hutter J., Iannuzzi M., Schiffmann F. & VandeVondele J. cp2k:atomistic simulations of condensed matter systems. Wiley Interdisciplinary Reviews: Computational Molecular Science 4, 15–25 (2014). [Google Scholar]
  45. Perdew J. P., Burke K. & Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys Rev Lett 77, 3865–3868 (1996). [DOI] [PubMed] [Google Scholar]
  46. Goedecker S., Teter M. & Hutter J. Separable dual-space Gaussian pseudopotentials. Phys Rev B 54, 1703–1710 (1996). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

How fragility makes phase-change data storage robust: insights from ab initio simulations

srep06529-s1.pdf (4MB, pdf)
Supplementary Information

Crystallization Video

Download video file (7.4MB, wmv)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES