Evaluation of Conoscopic Holography for Estimating Tumor Resection Cavities in Model-Based Image-Guided Neurosurgery

Abstract

Surgical navigation relies on accurately mapping the intraoperative state of the patient to models derived from preoperative images. In image-guided neurosurgery, soft tissue deformations are common and have been shown to compromise the accuracy of guidance systems. In lieu of whole-brain intraoperative imaging, some advocate the use of intraoperatively acquired sparse data from laser-range scans, ultrasound imaging, or stereo reconstruction coupled with a computational model to drive subsurface deformations. Some authors have reported on compensating for brain sag, swelling, retraction, and the application of pharmaceuticals such as mannitol with these models. To date, strategies for modeling tissue resection have been limited. In this paper, we report our experiences with a novel digitization approach, called a conoprobe, to document tissue resection cavities and assess the impact of resection on model-based guidance systems. Specifically, the conoprobe was used to digitize the interior of the resection cavity during eight brain tumor resection surgeries and then compared against model prediction results of tumor locations. We should note that no effort was made to incorporate resection into the model but rather the objective was to determine if measurement was possible to study the impact on modeling tissue resection. In addition, the digitized resection cavity was compared with early postoperative MRI scans to determine whether these scans can further inform tissue resection. The results demonstrate benefit in model correction despite not having resection explicitly modeled. However, results also indicate the challenge that resection provides for model-correction approaches. With respect to the digitization technology, it is clear that the conoprobe provides important real-time data regarding resection and adds another dimension to our noncontact instrumentation framework for soft-tissue deformation compensation in guidance systems.

I. Introduction

The success of an image-guided surgical intervention is contingent on the determination of the spatial relationship between the preoperative patient images and the intraoperative state of the patient in the operating theatre. In neurosurgery, this relationship is compromised by brain tissue deformation and shift that occurs during surgical resection. The nature and extent of the shift and how it affects resection is dependent on many factors such as the drainage of cerebrospinal fluid, gravity, edema, hyperosmotic drugs, the nature of the pathology, application of the retractor, and the resection process itself [24], [26], [28]. In the course of an intervention, the brain can deform over a centimeter in a nonuniform way [7], [10], [11], [20], [25], [26], [28], [38]. This deformation compromises the accuracy of surgical systems because the guidance display no longer corresponds to the physical reality in the operating room. The general conclusion from these studies is that brain deformation during surgery needs to be accounted for to maximize the effectiveness of image-guided neurosurgery systems.

Compensating for intraoperative brain shift remains a challenging task in image-guided neurosurgery. Predicting shift prior to surgery is difficult; hence, most techniques involve compensating for shift after it has occurred. The primary computational strategy for compensating for brain shift is by way of a nonrigid registration algorithm that maps intraoperatively acquired data to preoperative images. As an alternative to whole-brain intraoperative imaging, one approach uses low-cost readily available intraoperative data integrated into a framework called model-updated image-guided neurosurgery (MUIGNS) [29]. This framework combines the fidelity of computational models in conjunction with intraoperative data acquisition (by way of laser-range scanning (LRS) [3], [4], [8], [9], ultrasonography [17], [18], [29], or stereo reconstruction [29], [35]) as a means for updating high-resolution preoperative-based images to reflect current operative conditions. In this paradigm, intraoperative data that characterize brain deformation (i.e., cortical shift measurements) are used to formulate an inverse problem framework that uses patient-specific biomechanical models. The model calculations produce 3-D whole-volume displacement fields that are subsequently used to deform all forms of preoperative-based image data (for example, positron emission tomography, electroencephalography, functional magnetic resonance (MR) imaging, and MR spectroscopy). The outcome provides targeting assistance for surgical navigation in the presence of brain deformations toward more accurate localization near functionally important areas.

Much of the related work in MUIGNS has been focused on the development of computational models for brain deformation to include methods of retraction and the incorporation of patient specific properties and anatomical constraints [3], [6], [8], [9], [17], [18], [21], [23], [29], [35]. A critical challenge in this work is the intraoperative patient data to drive these models. Typically, modeling results are driven based on surface measurements. For example, closest-point distances between intraoperatively acquired stereo camera point clouds pre- and postresection are reported [35], [36]. Picking corresponding points on the pre- and postresection point clouds is a better option [9] but can typically only be done for a small number of identifiable points and still only captures surface shift. Some authors have attempted to use subsurface features derived from intraoperative ultrasound [13] but tissue deformation due to compression with the transducer and difficulty of localizing structures in images is a challenging task. If an intraoperative MRI or computed tomography (CT) unit were available, the true shift and resection could be determined to capture the evolution of surgery directly and then subsequently used to provide correspondence with other forms of preoperative data.

To date, the only methods to assess subsurface deformations have taken the form of intraoperative imaging. In this paper, we investigate the use of a low-cost acquisition method that relies on the principle of conoscopic holography for measuring resection changes. Conoscopic holography is a distance measurement method proposed by Sirat and Psaltis [33] traditionally used in industrial quality control. The technique relies on analyzing constructive and destructive interference patterns between emitted and reflected laser light. A method of optically tracking the device for noncontact surface characterization was first developed at Vanderbilt University in a laparoscopic port application [15]. In that work, the conoscopic holography sensor (Conoprobe Mark 3, Optimet Metrology Ltd., Jerusalem, Israel) was outfit with tracking targets. The tracked conoprobe system then reported the distance and direction from the laser source to the object being scanned. While some commercial guidance systems employ the use of laser-based digitization, the primary utilization is for digitizing the patient’s exterior anatomy for purposes of registration. For example, in the zTouch system (Brainlab, Munich, Germany), the laser dot is tracked by the tracking system so digitizing a tumor cavity would be impossible due to line of sight issues associated with tracking the laser dot, rather than the device itself.

We should note that our deformation correction approaches have been focused on intraoperative surface acquisition methods to include LRS [22], stereo-pair reconstruction [14], and now conoscopic holography. The advantage of these approaches is their ease of integration within the operating room workflow. The LRS is a fast noncontact method that collects surface data as a point cloud and 2-D texture of the scanned object. We have documented the geometric accuracy of our LRS approach as root mean squared (RMS) error of 0.47 mm and the RMS error of the tracked LRS as 2.4 mm [27]. We have similar accuracies with our stereo-pair work too [14]. While the latter method is more favorable to surgical microscope workflows, the former has the advantage of a direct measure of the field with no feature identification needed. The method in this investigation, conoprobe, has a distance measurement accuracy of less than 100 µm, and a tracked conoprobe error accuracy of 0.77 mm [2]. Further, using phantom and ex vivo tissue, the conoprobe consistently outperformed the LRS with respect to registration accuracy when compared to ground truth estimates [32]: for example, in five trials with an anthropomorphic brain phantom, target registration error (TRE) with the LRS-acquired data was 2.1 ± 0.2 mm, reduced slightly to 1.9 ± 0.4 mm with the conoprobe. Registration accuracy with an ex vivo porcine specimen using the LRS acquired data was 3.3±0.8 mm, reduced to 1.73±0.8 mm with the conoprobe. Although both devices are laser-based technologies, the LRS is based on the principal of triangulation which measures the angle of a single ray whereas conoscopic holography measurements are derived from a solid angle (cone of light consisting of many rays) [2]; hence, the accuracy improvements with the conoprobe.

As a result of this improved accuracy, we investigate in this paper the use of conoscopic holography as an intraoperative method to digitize the resection cavity for comparison to predictions based on our model as a quasi-validation scheme in an eight patient study. The intention in this paper is not to validate the correction scheme per se since that would require known correspondences, a characteristic only available with an intraoperative imaging unit. Rather, this paper investigates 1) how conoscopic holography can obtain meaningful subsurface measurements, 2) what the challenges associated with tissue resection are, and 3) how model compensation compares to these measurements. We employ the conoprobe as a secondary measurement system for assessment of our model correction scheme. Preliminary results from this study for one metric with two patients were presented at SPIE Medical Imaging [31].

II. Methods

The MUIGNS platform that we have constructed employs an LRS to acquire the brain surface before and after resection to generate shift measurements to drive a mathematical model. The pipeline of tasks in this process from the preoperative stages of mesh generation and boundary condition assignment to intraoperative data acquisition and image update has been reported in other work [4], [8], [9] and are summarized in the Appendix. While this framework is potentially powerful, the ability to characterize a resection cavity with a low-encumbrance device like the conoprobe during surgery may potentially inform this framework. This section details our methods using the conoprobe as an independent means to assess tissue resection cavities. Going further, our analysis of conoprobe data could have wider impact on other deformation compensation schemes that use stereoscopic images [29], [35] and ultrasound [17], [18], [29], reported by other research groups.

A. Patient Selection

Ten patients undergoing tumor resection at Vanderbilt University Medical Center were enrolled in the study. Patient consent was obtained prior to surgery as required by the Vanderbilt Institutional Review Board.

B. Data Collection

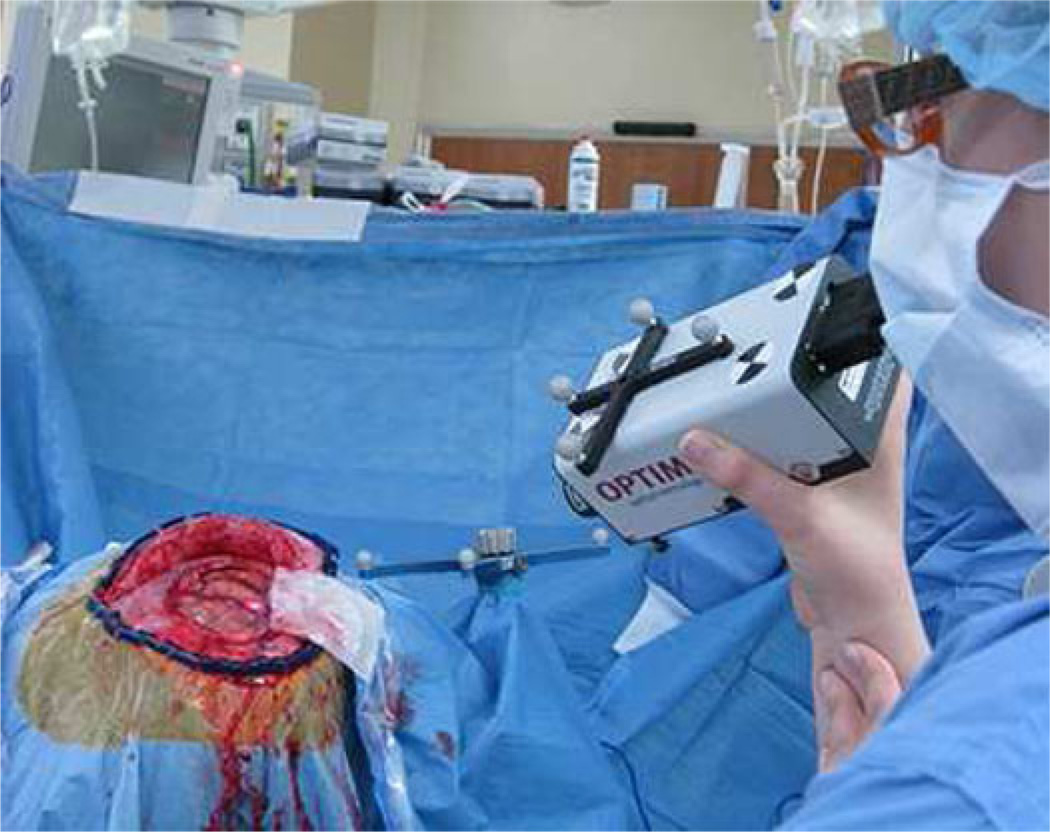
Preoperative MRI scans were acquired consistently with the standard of care at our institution. The images were segmented, tetrahedral models generated, and boundary conditions assigned as described in the Appendix. Intraoperatively, an optical tracking system (Polaris Spectra, Northern Digital Inc., Waterloo, ON, Canada) and navigation system were used for study data collection. An optical tracking rigid body (Medtronic, Minneapolis, MN, USA) was attached to the patient using the protocol established by the manufacturer so that all data could be referred to in a common coordinate frame. An optically tracked LRS (Pathfinder Therapeutics Inc., Nashville, TN, USA), conoprobe (Conoprobe Mark 10, Optimet Metrology Ltd., Jerusalem, Israel), and surgical instrument (Medtronic, Minneapolis, MN, USA) were used to acquire intraoperative data. The conoprobe is shown in Fig. 1 for use in the OR. The conoprobe was not sterilized since it was operated at a distance from the patient and required no physical contact with the tissue. After the postresection LRS was acquired, the conoprobe was used to swab the full extents of the inside of the resection cavity and the cortical surface. Postoperative MRI scans were obtained following surgery using the same imaging protocol as the preoperative MRI acquisitions.

Fig. 1.

Conoprobe surface acquisition of patient enrolled in our study undergoing resection surgery at Vanderbilt University Medical Center (Nashville, TN, USA). The single laser point is visible on the surface of the brain and the optical tracking target can be seen on the conoprobe.

C. Data Processing

Comparisons between model prediction and intraoperatively collected conoprobe points characterizing the resection cavity were performed retrospectively. From segmented MR images of the tumor volume, a discretized model surface was generated and then deformed using model predictions as derived from our inverse shift compensation approach.

The accuracy of the conoprobe is affected by the absorption properties of the tissue under interrogation. The conoprobe software reports the SNR as a percentage for every collected point. The manufacturer of the device suggests only using points with an SNR greater than 30% (supported by our own lab studies [32]); therefore, only these points were used for analyses. To address any issues with the fluid build-up in the cavity (which reduces SNR), the surgeon was asked to remove any fluid prior to conoprobe collection.

D. Evaluation Framework

The evaluation framework relies on the somewhat idealized scenario that conoprobe points describing the physical structure of the tumor cavity after resection would coincide with the MR-segmented tumor boundary, if the alignment and segmentation were correct. However, clinically, resection cavities are dynamic: decompression effects can shrink cavity volume, cavity walls may sag due to gravity and relative to location of the cortical surface while some maintain their shape. We assess this variability using the conoprobe by 1) visually comparing the conoprobe points and the resection cavity, 2) computing the distance from the deformed/undeformed tumor models to the conoprobe points, and 3) comparing the conoprobe points with very early postoperative MRI scans.

1) Distance From Tumor to Resection Cavity Using Nearest Neighbors Search

For each point in the conoprobe collection, the nearest neighbor to the deformed and undeformed tumor surface geometric models was calculated and the distances measured. The intuition is that the resection cavity defined by the conoprobe points will be closer to the deformed tumor surface model rather than the undeformed tumor. To test this hypothesis, for a surface model S and set of conoprobe points q, an approximate nearest neighbor search returns k distinct points of S corresponding to each point in q. For each point in q, the nearest triangle in the surface model is found using kd-tree search. The point is projected onto the triangle. The Euclidian distance between the points is determined based on the whether the projected point lies on an edge or vertex of the triangle. This ensures that the distance is calculated from point to surface model rather than from point to vertices of the surface model. The kd-tree search was implemented using the approximate nearest neighbor library.¹

2) Comparison of Conoprobe Points and Tumor Models With Postoperative MRI

MRI scans of patients were obtained following surgery. These postoperative scans were aligned to their preoperative counterparts so that all scans and computational model components were in a common coordinate frame for analysis. The matching of the postoperative to the preoperative scan was achieved using multiresolution mutual information registration [5], [37] from ITK Applications (Kitware Inc., Chapel Hill, NC, USA). The resection cavity was manually segmented from the postoperative scan using the ITK Snap application² and a surface model generated using the marching cubes algorithm [16]. The distances from the conoprobe points to the surface model of the resection cavity were measured using the nearest neighbor approach described in the previous paragraph. The rationale behind this test was to see whether early postoperative MRI scans could inform model correction evaluation.

III. Results

Two of the ten patients were excluded from analysis because the postresection cavity collapsed before conoprobe points could be acquired. Patient demographics and pathology are summarized in Table I. The accuracy results of the deformation correction scheme for all eight cases are summarized in Table II. These results include the root mean squared TRE after rigid registration, the number of nodes in the biomechanical mesh, the number of corresponding points selected from the pre- and postresection LRS (called shift vectors) used to drive the model, the measured shift (magnitude of the shift vectors), and the error corrected by the model. These values are automatically calculated at the conclusion of the correction scheme and presented here for comparison with the evaluation framework. Note that there were no corresponding points to drive the model in patients 1 and 7 so closest-point distances from the pre- and postresection LRS were used to drive the model (as described in the Appendix).

TABLE I.

Clinicopathological Factors

Patient	Age (yrs)	Gender	Tumor locationa	Tumor Size (cm3)
1	37	F	L, F	1.2
2	83	M	L, F	47.2
3	42	F	L, F	100.2
4	19	F	R, T	4.8
5	28	F	R, F	7.6
6	62	M	L, F	29.2
7	67	F	L, F	16.1
8	64	F	R, F	101.4

^aTumor locations: left (L) or right (R) signify the hemisphere, followed by lobe: frontal (F), pariental (P), or temporal (T).

TABLE II.

Shift Correction Results As Reported By Model

Patient	TRE Rigid (mm)	Mesh Nodes	Shift Vectors	LRS Measured Shift (mm)				Model Corrected Shift (mm)
				μ	σ	min	max	μ	σ	min	max
1	2.7	19844	-	6.6	-	5.3	8.6	2.4	0.9	0.8	4.2
2	4.1	27382	13	6.8	4.8	2.9	17.0	3.3	1.8	1.0	7.5
3	4.1	20995	20	7.1	4.8	2.7	22.3	2.5	1.3	1.0	6.7
4	3.5	23455	52	9.3	1.4	6.0	13.0	3.1	1.4	0.5	7.5
5	3.6	21960	11	11.9	2.2	6.7	14.7	3.3	1.5	0.9	5.2
5a	3.6	21960	10	8.4	3.5	3.4	13.0	3.1	1.1	2.0	5.4
6	2.4	23007	4	3.2	3.2	2.2	4.4	0.7	0.4	0.3	1.2
7	3.6	21247	-	2.5	1.0	0.4	4.9	1.6	0.8	0.2	3.7
8	4.2	22875	3	4.9	0.2	4.8	5.1	1.2	0.4	0.8	1.5

^aModel correction scheme was run with homologous points derived from the preoperative scan and early postoperative scan as described in Section III-B2.

A. Qualitative Results

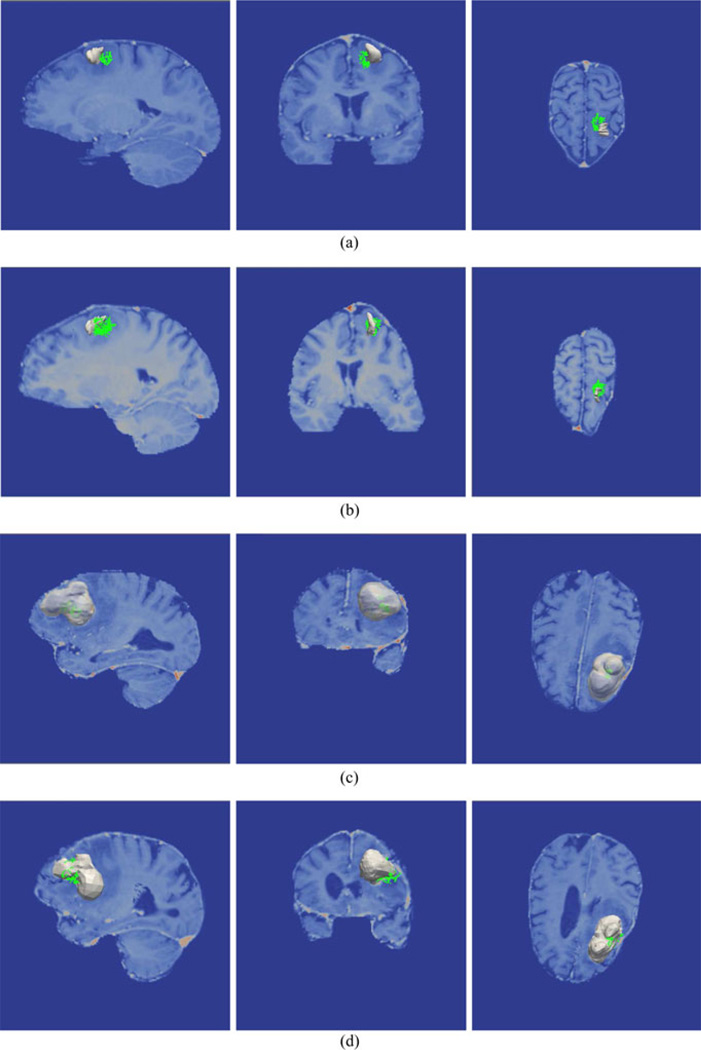
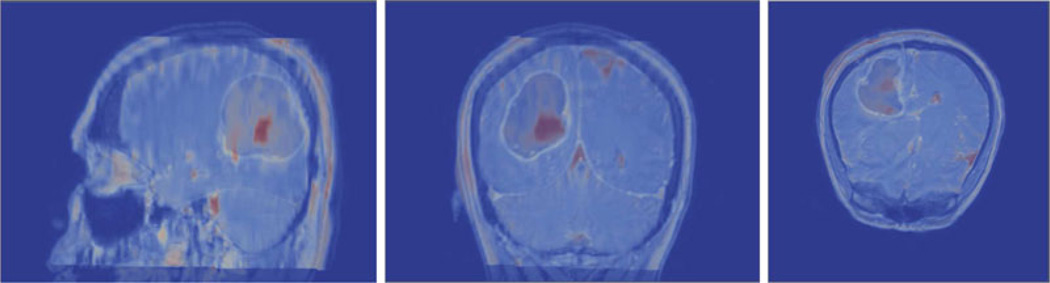
Conoprobe points (green) and the tumor (gray) are overlaid on the image volume in Figs. 2 and 3 for three representative patients illustrated before and after correction. The results for patient 1 from Table II indicate that the mean measured shift was 6.6 mm, which was reduced to a mean error of 2.4 mm after model correction. No corresponding points could be identified on the pre- and postresection LRS so the model was driven with the closest point distances from the scans. With respect to evaluation, the conoprobe points do not fully envelop the tumor prior to correction [see Fig. 2(a)], but after correction the tumor has shifted closer to the center of the points [see Fig. 2(b)]. This is an example of the conoprobe evaluation scheme under less than ideal correction (no corresponding points were used in the correction), where the model appears to be inconsistent in one of the shift directions.

Fig. 2.

Conoprobe points (green) and tumor (gray) tumor overlaid on the image volume in three views for two representative cases. Patient 1 is illustrated without correction (a) and with correction (b) representing a directional error due to a lack of corresponding points. Patient 2 is illustrated with without correction (c) and with correction (d) representing less than ideal correction results.

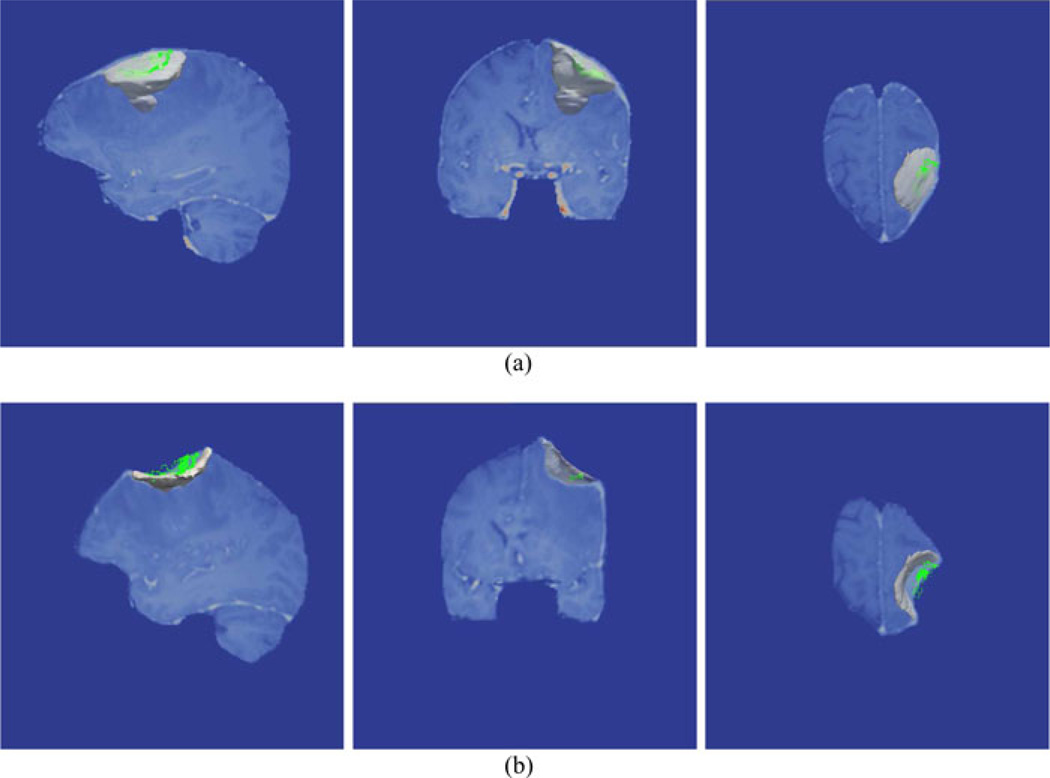
Fig. 3.

Conoprobe points (green) and tumor (gray) tumor overlaid on the image volume in three views for one representative case. Results for patient 6 are illustrated without correction (a) and with favorable correction (b).

For patient 2, the mean measured shift was 6.8 mm and after model correction, the mean error was reduced to 3.3 mm. Thirteen corresponding points were used to drive the model. In this example, the conoprobe points lie entirely inside the tumor prior to correction [see Fig. 2(c)] and envelop only the proximal tumor after correction [see Fig. 2(d)]; the conoprobe points support the correction results.

For patient 6, the mean measured shift was 3.2 mm, which was reduced to a mean error of 0.7 mm after model correction. Four corresponding points were used to drive the model. In this example, the conoprobe points lie inside the tumor model before correction [see Fig. 3(a)]. After correction [see Fig. 3(b)], the conoprobe points lie on the flattened tumor (the model does not remove nodes thus the flattening). In this example, the conoprobe evaluation supports that the modeling scheme performed well.

B. Quantitative Results

1) Distance From Tumor to Resection Cavity

The distances from the resection cavity characterized by the conoprobe points to the tumor before and after correction are summarized in Table III with the number of conoprobe points used in the evaluation. These numbers represent the average nearest neighbor distance between resection cavity measurement with the conoprobe and tumor boundary as determined from the preoperative image volume. In an ideal world, where Gadolinium enhancement represented tumor boundary exactly, where a surgeon could and only resect the border to voxel resolution level with no intraoperative judgment to resection extent based on visual information during surgery, and lastly no intraoperative shift, the average nearest neighbor distances between tumor and resection bed in Table III would be zero. The correction results in Table II are consistent with these distance metrics. In general, the magnitude of corrected shift (mean measured shift—mean corrected error) relates to distance: in patient 6, the mean magnitude of corrected shift was 2.5 mm (3.2–0.7 mm) while the corrected distance of the conoprobe points was 2.7 mm. In patient 3, mean magnitude of corrected shift was 4.6 mm (7.1–2.5 mm) while the corrected distance of the conoprobe points was 3.8 mm.

TABLE III.

Nearest Neighbor Distance Metric Results

Patient	# Conoprobe Points		Distance (mm)
			μ	σ	min	max
1	682	no correction	5.5	2.7	0.0	12.8
		correction	3.9	2.1	0.0	9.6
2	442	no correction	7.8	2.4	0.1	14.6
		correction	2.6	2.2	0.0	8.8
3	180	no correction	6.8	3.5	0.6	15.4
		correction	3.8	3.0	0.0	13.0
4	484	no correction	2.8	1.9	0.1	7.4
		correction	2.5	1.7	0.0	7.8
5	425	no correctiona	9.6	2.2	3.0	15.4
		correction	10.8	1.8	5.1	16.2
		correction	10.2	1.9	5.0	16.3
6	444	no correction	4.0	2.1	0.1	9.3
		correction	2.7	2.3	0.0	9.0
7	719	no correction	3.5	2.4	0.0	9.5
		correction	3.4	2.6	0.0	10.0
8	394	no correction	6.3	4.0	0.0	19.3
		correction	3.9	3.9	0.0	20.3

^aModel correction scheme was run with homologous points derived from the preoperative scan and early postoperative scan as described in Section III-B2.

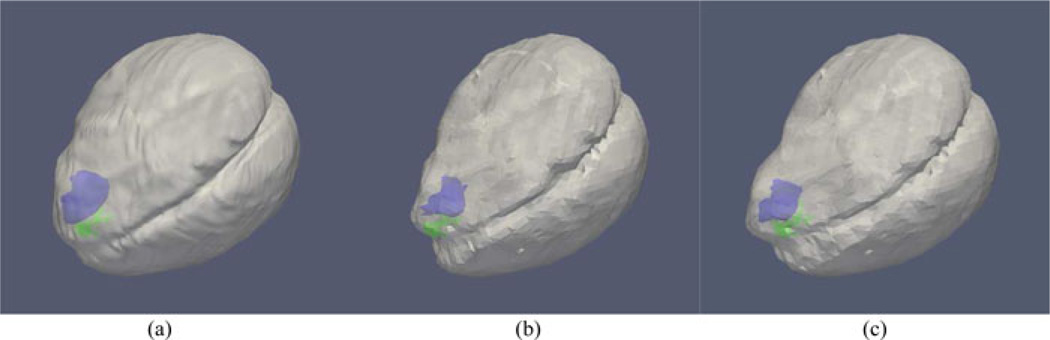
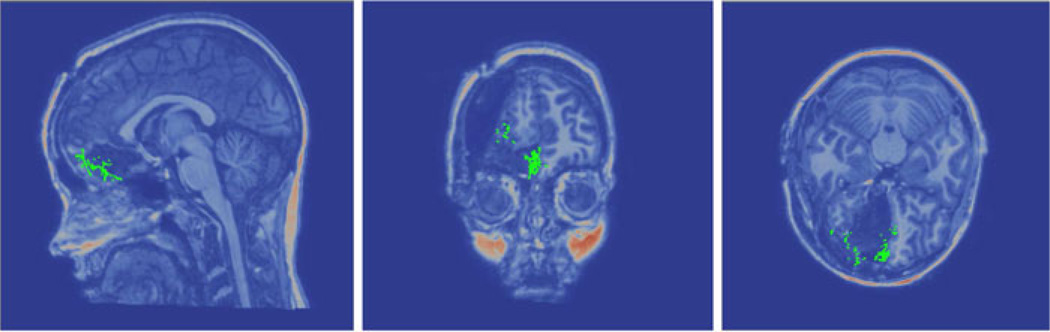
Overall, distances are lower after correction with the exception of patient 5. Fig. 4 illustrates the relationship of the conoprobe points to the tumor before and after correction. The green conoprobe points lie on the bed of the cavity, well below the tumor indicating that neither the uncorrected or corrected tumor accurately reflects the large intraoperative shift (measured shift was 11.9 mm). In this example, the modeling results are ambiguous though it may be that cortical surface points were not sufficient to drive correction for accurate subsurface deformations, only surface deformations.

Fig. 4.

Rendering of the conoprobe points (green), tumor (blue), and brain surface (gray) for patient 5 before (a) and after (b) correction. The conoprobe points lie well below the tumor, likely due to cavity collapse during surgery. For comparison, correction using homologous points from postoperative MRI scans described in Section III-B2. (a) Patient 5: No correction. (b) Patient 5: With correction. (c) Patient 5: With correction.

2) Comparison to Early Postoperative MRI Data

Postoperative MRI scans were acquired within 7.5 to 25 (mean 14) h of the postresection LRS to assess whether these scans could assess model correction. The distances from the resection cavity on the postoperative MRI to the intraoperatively acquired conoprobe points are summarized in Table IV. In general, the conoprobe points characterize the resection cavity well with the exception of patient 3. The distances reported for patient 3 are quite high likely due to the collapse of the tumor in the postoperative MRI which is illustrated in Fig. 5. The preoperative MRI is overlaid on the postoperative MRI such that the outline (white) of the 100.2 cm³ tumor prior or to surgery is shown with the postoperative cavity (red). In this example, the early postoperative MRI is likely unusable for retrospective evaluation of computation model solutions; however, the other seven cases reported here suggest that their use may add to an evaluation scheme.

TABLE IV.

Nearest Neighbor Distance Metric Results For postoperative Mri

Patient	Distance (mm)				Postop Scan hh:mm
	μ	σ	min	max
1	3.2	1.5	0.0	11.0	24:07
2	2.3	2.2	0.0	9.0	9:31
3	12.9	5.4	0.7	26.6	7:51
4	4.0	2.7	0.0	10.0	15:42
5	2.0	2.3	0.0	13.0	10:54
6	4.2	3.2	0.0	11.5	24:49
7	3.0	1.9	0.0	11.5	7:26
8	5.3	4.9	0.0	15.6	1:58

Fig. 5.

Preoperative MRI overlaid on the postoperative MRI for patient 3. The outline of the large tumor is visible in the preoperative scan as well as the resected tumor bed (red mass) in the postoperative scan. Significant shift occurred in this case due to the size and position of the tumor. The postoperative MRI demonstrates collapse of the tumor making the scan unusable for retrospective evaluation.

Revisiting patient 5 from Table III where the conoprobe distances suggested poor model performance, the degree of dynamic change due to the very large tumor (101.4 cm³) located deep in the frontal lobe and bound by the dural septa, makes for a very challenging model-based compensation task. Since the conoprobe points are consistent with the very deep resection cavity on the postoperative MRI in Fig. 6, this suggests that visual cues to the surgeon intraoperatively required additional resection which was not reflected on the image enhancement designating tumor in the preoperative images. As a result, the conoprobe points in this case do not provide a sense of extent of correction but rather provide evidence of a difference between proposed resection preoperatively (enhancing tumor region) and extent of resection intraoperatively (consistency between probe points and postoperative images). Still wanting to determine if correction had some potential value in this case, we selected homologous points from the brain surface in the preoperative and postoperative MRI scans and used these measurements to drive our correction pipeline. This approach has the added benefit that corresponding subsurface features can be designated between preoperative and postoperative scans and used as targets providing a somewhat indirect assessment of the value of correction. In Table II, the correction results in patient 5 driven by pre/postoperative MRI analysis (labeled patient 5^a) indicated a mean shift of 8.4 ± 3.5 mm reduced to 3.1 ±1.1 mm, quite different from the correction using homologous points from LRS (11.9±2.2 mm reduced to 3.3±1.5 mm). The magnitude of the deformations is quite reduced in the pre/post MRI analysis, a finding that is consistent with other work [4]. Interestingly in Table III, however, we note the conoprobe distance metric did not improve with the use of homologous surface points from MRI further suggesting resection differences. While these results are somewhat inconsistent, as noted, the pre/post MRI analysis does afford us the ability to identify subsurface corresponding features for further study. Twelve corresponding feature points from the pre- and postoperative MRI scans were chosen as prospective targets. Analyzing subsurface feature target error, the mean shift of subsurface feature targets near the tumor was 8.4 ± 1.2 mm with a remaining mean error of 3.2 ± 1.5 mm after correction. This is quite different than the poor correction suggested in Table III. This pre/post MRI analysis suggests that the conoprobe metric may not on its own indicate fidelity or value of correction and provides further impetus for intraoperative imaging validation methods for correction.

Fig. 6.

Conoprobe points (green) rendered with the postoperative MRI scan for patient 5. The conoprobe points lie on the extents of the resected tissue.

IV. Discussion

We proposed a low-cost solution that relies on conoscopic holography for intraoperative subsurface digitization of resection cavities and demonstrated use with eight patients undergoing tumor resection therapy at Vanderbilt University Medical Center. A limitation of our approach is that the conoprobe requires direct line of sight in order to characterize the resection cavity. Within the ten consecutive cases acquired for the study, two cases are not reported here because the cavity collapsed entirely after resection such that there was no cavity for conoprobe point acquisition. This further emphasizes the dynamic nature of tissue-cavity behavior during surgery.

The cases reported in this paper were chosen based on the presenting population, as evidenced by the variety of tumor sizes, magnitude of shift, and craniotomy size. Table V summarizes the shift correction results where the percentage of shift captured by the model was calculated by taking the mean across all remaining error and dividing by the average total shift, expressed as a percentage. The scale of the shift is based on the classification proposed by Bucholz et al. (low, 0–2.9 mm; moderate, 3.0–6.9 mm; high, > 7.0 mm) [1]. The correction impact score was generated based on the percentage of shift captured score (score of 0; 30–50% score of 1; 50–70% score of 2; and better than 70% score of 3) with the conoprobe distance metric scored similarly. The mean cumulative score was considered high impact (score of 2), moderate (score of 1.5), low (score of 1), negligible (score below 1). For patent 1, for example, the mean cumulative score was 1.5 or moderate value.

TABLE V.

Summary Of Shift Correction Results

Patient	Correction (%)				Summary scale of shift/correction impact
	μ	σ	min	max
1	63.4	14.4	32.6	86.8	moderate shift/moderate value
2	51.5	25.9	0.0	74.6	moderate shift/high value
3	65.0	18.5	30.6	86.6	high shift/moderate value
4	66.9	15.1	41.7	94.1	high shift/low value
5	70.6	13.3	43.7	92.4	high shift/low value
6	76.9	12.8	61.8	91.2	moderate shift/high value
7	37.5	30.9	0.0	90.8	low shift/negligible value
8	76.3	7.5	69.3	84.5	moderate shift/high value

In general, our model-based correction performed well in terms of surface shift with six of eight cases reporting better than 60% shift correction and Table V indicating moderate to high value in five cases. Results for patient 7, a case that generated low cortical surface shift with the reality being that shift-compensation approaches are likely of only negligible value to the practicing neurosurgeon (although the table indicates improvement if compensation was elected to be used). As for subsurface evaluation, the conoprobe points support the claim that correction is better than no correction (see Table III). The results for patient 1 are a good example of the need to drive computational models with known correspondences rather than closest point distances between points clouds. Fig. 2(b) indicates that the correction is off in one direction. The results demonstrate that the conoprobe can be an effective tool to digitize the resection bed. The results also demonstrate that resection cavities can be complex environments. With respect to model comparisons, the results show promise but certainly some ambiguity. One important aspect that we must recognize is that enhancing tumor regions in an MRI often do not represent the extent of resection. While difficult to confirm, this is likely the case in patient 5 whereby more tumor was identified intraoperatively and the surgical plan was modified. The aggressiveness versus conservativeness with which the tumor was segmented (in both the preoperative and postoperative scans) and subsequently resected may have further contributed to the complexity of the evaluation scheme.

It is interesting to note the high degree of agreement between the conoprobe points and the early postoperative MRI. This could be explained by the early timing of the postoperative scans (all scans were acquired within 25 h of surgery) (see Table IV). In some respects, this does lend credence to our previous investigations [8] where the correction approach was driven by cortical surface points extracted from pre- and postoperative MRI points and validated against subsurface corresponding target points.

The work presented here informs future developments necessary with respect to MUIGNS. The need to simulate cavity collapse is illustrated by Figs. 3 and 5; in both cases, significant collapse of the resection cavity affected the accuracy of our model-based correction strategy (even though resection is modeled in our framework by simulating no mechanical effect from tumor material). Intraoperative tomographic imaging methods clearly would have an advantage in capturing such an event; however, intraoperative volumetric imaging is not a perfect solution since nonrigid registration of intraoperative MRI to preoperative MRI in the resection region is a challenging problem and continual tissue changes compromise registration accuracy. In terms of validation of sparse data approaches, intraoperative MRI is often thought of as the only method to employ but the ability to simultaneously acquire forms of sparse data and MRI data at the same time points during the surgical intervention is not trivial. Depending on the measurement approach, patient orientation, data time points, interaction, and registration processes utilized, these approaches can be cumbersome to workflow. Our quasi-validation scheme is limited by the lack of correspondence between the model and the conoprobe points. The development of validation frameworks is a challenging endeavor: one advantage of the work in this paper is that measurements are at the same presentation and are highly temporally consistent. Modalities like intraoperative MRI usually incur overhead for patient preparation (clearing of the field, sometimes moving patients or magnets before and after imaging) and as a result, images obtained are not temporally consistent with the moment of surgical interaction. While the framework of measurement here also has some latency, it reduces that latency significantly when comparing to full intraoperative tomographic modalities.

Natural comparisons can be made between the conoprobe and LRS devices. The conoprobe is a hand-held unit with a single laser source that can be manipulated into a variety of positions to swab a cavity. The LRS is mounted on an arm for positioning and consists of a laser line that sweeps over the anatomy to produce a single scan. This can be compromised by large deviations from planarity that occur while attempting to sweep into a resection cavity. With a large enough cavity where sufficient tumor bed is visible, the laser range scanner can perform well. The conoprobe however does allow for significantly more versatility and ability to capture data in cases of high deviations from planarity and limited visible surfaces. While line of sight is still required, with the tracking approach we have adopted, we can get a great deal of complex geometric data. However, the conoscope does not currently acquire texture information (field of view digital image data), which provides corresponding points for our correction framework. We would suggest that the feedback provided by the conoprobe does seem to provide relevant information to study tissue resection. While cortical surface information provides some level of shift capture, the need to integrate an instrument such as the conoprobe does seem appropriate in these cases.

V. Conclusion

We proposed the use of an optically tracked conoscopic holography device for characterizing and evaluating the shape of the resection cavity during image-guided surgery. With eight surgical cases, we demonstrate positive benefits to the MUIGNS framework for shift correction but have also documented shortcomings when it comes to tissue resection cavity collapse as measured by the intraoperative digitizations. While clearly there are more developments needed, it is encouraging that a noncontact instrumentation platform (LRS, stereo-pair, and now conoscopic holography) can capture cortical surface deformations and complex subsurface events.

Appendix

Intraoperative Deformation Correction Pipeline

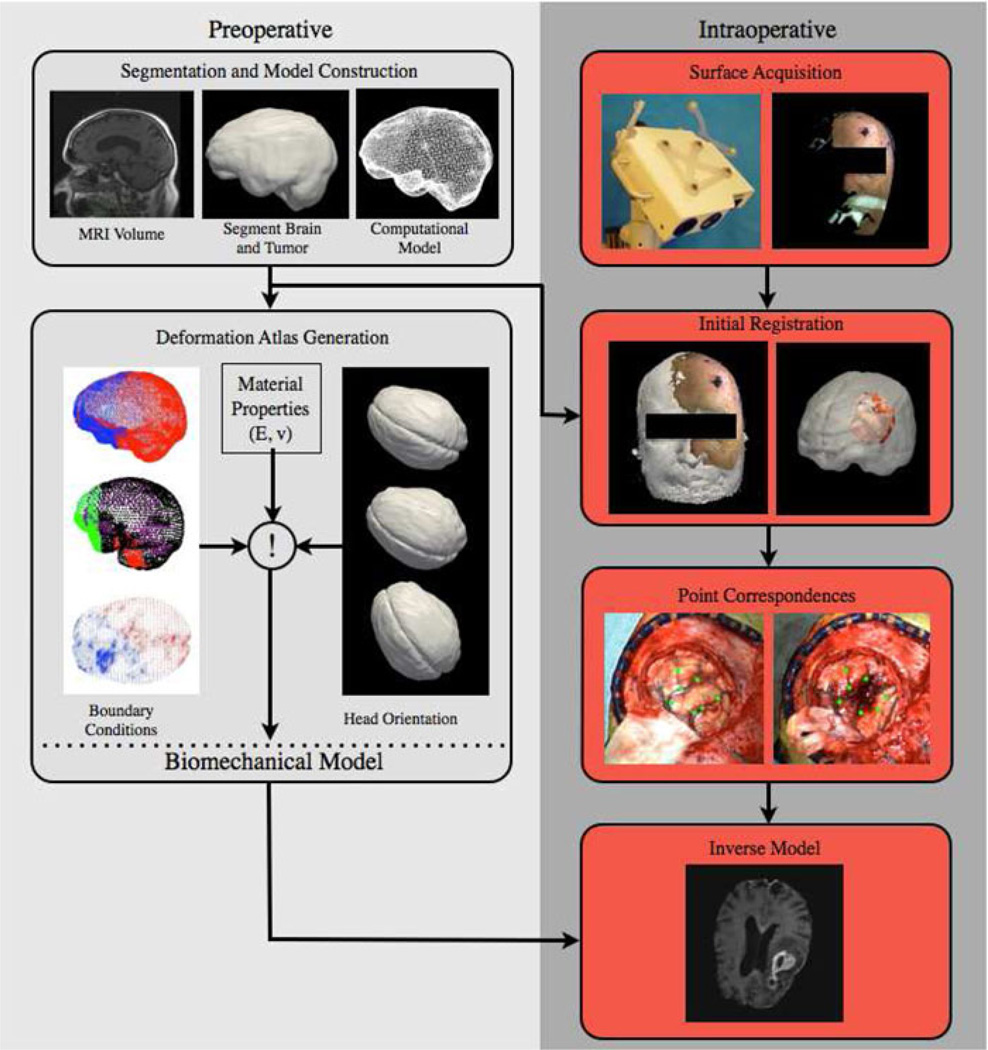
An illustration of the steps in our framework for compensation of deformation in the brain using mathematical models is provided in Fig. 7.

Fig. 7.

Deformation correction framework developed by our research group.

A. Preoperative Tasks

1) Patient Imaging

A MRI volume was acquired using a 1.5T scanner, a similar scan is required in conventional surgery that uses image guidance. The MR volumes were T1-weighted and gadolinium enhanced with a voxel size of 1 mm × 1 mm × 1.2 mm.

2) Image Segmentation

The brain was segmented from neighboring structures using an automatic method [30]. Manual refinements of the segmentation were sometimes required in the area of the tumor. The tumor was extracted using manual segmentation. A 3-D surface model was constructed of both the brain and tumor using the marching cubes algorithm [16]. A 3-D surface of the patient’s head was extracted from the MR volume using marching cubes.

3) Mesh Construction

Using 3-D surface model of the brain, a volumetric tetrahedral mesh was generated for use in the finite element model [34].

4) Atlas Generation and Boundary Condition Determination

In our terminology, an atlas consists of a collection of possible deformations predicted by our model. The deformations represented by the atlas included: volumetric deformations due to changes in vascular permeability (caused by mannitol, a hyperosmotic drug administered to reduce intracranial pressure), gravity-induced sag (determined by the head orientation of the patient in the OR and the amount of cerebrospinal fluid leakage in the procedure), and swelling (caused by a physiological response). Appropriate contact conditions between the brain and the skull are estimated for each set of conditions and applied as boundary conditions in a biomechanics finite element model of the patient’s brain built from the preoperative image set. Gray and white matter elements were assigned their own material property. The tumor region was assigned another material property. Tissue resection was simulated by removing nodes belonging to the tumor material type. As described in other work [8], [9], the atlas of deformation solutions is built, and the atlas-based correction approach can be run during surgery and a volumetric prediction of organ deformation generated.

B. Intraoperative Tasks

1) Patient Registration

A laser range scan (Pathfinder Therapeutics Inc., Nashville, TN, USA) [27] of the patient’s face was acquired prior to sterile field assembly. The LRS point cloud was initially aligned to the 3-D model of the patient using Horn’s method [12] and refined using an iterative closest point variant that is insensitive to spurious points [19]. This step provided the initial physical to image space transformation; all subsequent LRS acquisitions were in this space.

2) Point Correspondences

An LRS surface was acquired after the dura was opened and prior to tumor resection, the tumor was resected, an LRS surface was acquired after resection. The LRS point clouds were fit with a high-resolution surface using the FastRBF toolkit.³ Corresponding points were designated on the pre- and postresection bitmap images from the LRS acquisition. The corresponding 3-D point was determined from the LRS point cloud. The vectorial difference between the pre- and postresection points represented a full 3-D description of tissue shift. In cases where no corresponding points can be found, closest point distances between the pre- and postresection LRS surfaces represent shift for the model.

3) Inverse Model Update

An inverse model was solved using the atlas predictions built prior to surgery, driven by the homologous points picked in the point correspondences step. Simply stated, an inverse solution was obtained by the minimization of least-squared error between the predictions and the measured displacements. The details of this calculation can be found in Chen et al. [4]. Once the cortical shift data have been matched by assembling the best combination of atlas solutions, the complete displacement field was concurrently provided by the inverse model which was then used to deform the preoperative MR volume for updating the guidance display.