Automated 3D Segmentation of Intraretinal Surfaces in SD-OCT Volumes in Normal and Diabetic Mice

Abstract

Purpose

To describe an adaptation of an existing graph-theoretic method (initially developed for human optical coherence tomography [OCT] images) for the three-dimensional (3D) automated segmentation of 10 intraretinal surfaces in mice scans, and assess the accuracy of the method and the reproducibility of thickness measurements.

Methods

Ten intraretinal surfaces were segmented in repeat spectral domain (SD)-OCT volumetric images acquired from normal (n = 8) and diabetic (n = 10) mice. The accuracy of the method was assessed by computing the border position errors of the automated segmentation with respect to manual tracings obtained from two experts. The reproducibility was statistically assessed for four retinal layers within eight predefined regions using the mean and SD of the differences in retinal thickness measured in the repeat scans, the coefficient of variation (CV) and the intraclass correlation coefficients (ICC; with 95% confidence intervals [CIs]).

Results

The overall mean unsigned border position error for the 10 surfaces computed over 97 B-scans (10 scans, 10 normal mice) was 3.16 ± 0.91 μm. The overall mean differences in retinal thicknesses computed from the normal and diabetic mice were 1.86 ± 0.95 and 2.15 ± 0.86 μm, respectively. The CV of the retinal thicknesses for all the measured layers ranged from 1.04% to 5%. The ICCs for the total retinal thickness in the normal and diabetic mice were 0.78 [0.10, 0.92] and 0.83 [0.31, 0.96], respectively.

Conclusion

The presented method (publicly available as part of the Iowa Reference Algorithms) has acceptable accuracy and reproducibility and is expected to be useful in the quantitative study of intraretinal layers in mice.

Translational Relevance

The presented method, initially developed for human OCT, has been adapted for mice, with the potential to be adapted for other animals as well. Quantitative in vivo assessment of the retina in mice allows changes to be measured longitudinally, decreasing the need for them.

Introduction

Optical coherence tomography (OCT)¹ is a noninvasive imaging modality that acquires high-resolution images of layered structures such as the retina. The ability to quantitatively study retinal structures has led to its widespread use in the clinical detection and management of various ocular diseases as well as in research studies.² The automated segmentation and quantification of intraretinal layers seen in time-domain (TD-OCT)^3–8 and spectral-domain OCT (SD-OCT)^9–18 images acquired from human subjects is a well-studied problem. However, similar methods are not as readily available for the automated analysis of animal scans. Furthermore, the ability to discern and quantitatively measure retinal structures of interest in SD-OCT images of animal retinas,^19–22 such as mice,^23,24 has led to a pressing need for automated methods.

Automated methods^25,26 have been described for the segmentation of retinal layers in SD-OCT images in normal rats. However, these methods, are essentially two-dimensional (2D) methods and did not incorporate contextual information available in volumetric scans. Srinivasan et al.²⁷ described a graph-based method for the segmentation of surfaces in mice scans, where the proposed method was compared with the results provided by the Bioptigen SD-OCT scanner. We have also previously described the segmentation of mice scans, while incorporating learned textural²⁸ and topological information.²⁹ The reproducibility of thickness measurements, however, has only been described briefly³⁰ and was limited to the reproducibility of total retinal thickness.

In our previous work,^11–13 we described a fully automated three-dimensional (3D) graph-theoretic approach for the simultaneous segmentation of multiple intraretinal layers from human SD-OCT images, publicly available as the Iowa Reference Algorithms at http://www.biomed-imaging.uiowa.edu/downloads/. Here, we present an adaptation of this graph-theoretic approach for the automated segmentation of intraretinal layers in mouse SD-OCT volumes. The method is designed to segment 10 retinal surfaces, the accuracy of which is assessed by comparing the automated results to manual tracings obtained from two retinal specialists. As the method is ultimately intended to quantitatively measure structures in normal as well as diseased mice, the reproducibility of thickness measurements is statistically assessed in scans obtained from normal and diabetic mice. The purpose of this study is to assess the accuracy of the method and the reproducibility of thickness measurements in the mouse retina.

Methods

Data

All animal procedures in this study were approved by the Institutional Animal Care and Use Committee at the University of Iowa, and complied with the ARVO statement for the Use of Animals in Ophthalmic and Vision Research. Diabetes was induced in 8- to 10-week-old mice C57BL/6J (n = 10; Jackson Laboratory, Bar Harbor, ME) by intraperitoneal injection of streptozotocin 200 mg/kg (STZ; Sigma-Aldrich, St. Louis, MO) dissolved in sodium citrate buffer (pH 4.5). Age-matched C57BL/6J mice (n = 8) were assigned to the control group. Volumetric scans centered on the optic nerve head (ONH; 1.4 × 1.4 × 1.57 mm) were obtained from both eyes (right eye imaged first) of the mice using an R2200 UHR SD-OCT scanner (Bioptigen Inc., Morrisville, NC, USA) where the scans contained 400 × 400 × 1024 voxels. After the retina of the right and then left eye was imaged, the retina of the right eye was re-imaged using the same protocol listed above, giving us repeat scans of the right eyes. The diabetic mice were imaged at the onset of the study and 6 weeks after the induction of diabetes, while the normals were imaged once at the onset of the study. The scans obtained from the diabetic mice before induction of diabetes were grouped with the normal scans, providing a total of 18 and 10 repeat scans from the normal and diabetic mice, respectively.

Segmentation Algorithm

The segmentation of intraretinal layers in SD-OCT volumetric scans of human retinas is a well-studied problem. The graph-theoretic approach^31,32 is well suited to this problem as it allows for the simultaneous segmentation of multiple surfaces while ensuring the global optimality of the final solution. We have previously described the use of such a graph-theoretic method for the segmentation of intraretinal surfaces in SD-OCT obtained from human subjects.^11–13 The overall method (illustrated in Fig. 1, with labeled layers in Fig. 2) remains similar to our previous work where the outer surfaces, namely the internal limiting membrane (ILM), the external limiting membrane (ELM), the junction of the inner and outer segments, the retinal pigment epithelium (RPE), and the Bruch's membrane (BM), were segmented first using a multiresolution approach^12,13 followed by the segmentation of the inner surfaces, namely the nerve fiber ganglion cell complex (NF-GCL), the inner plexiform layer (IPL), the inner nuclear layer (INL), and the outer plexiform layer (OPL). However, some changes were made in order to accommodate the differences in anatomy between human and mice retinas.

Figure 1.

Overview of the automated 3D segmentation method. First, the outer surfaces, namely the ILM, the ELM, the bounding surfaces of the IS/OS, the RPE, and BM were segmented. Next, the inner surfaces, namely the bounding surfaces of the NF-GCL, IPL, and INL were segmented.

Figure 2.

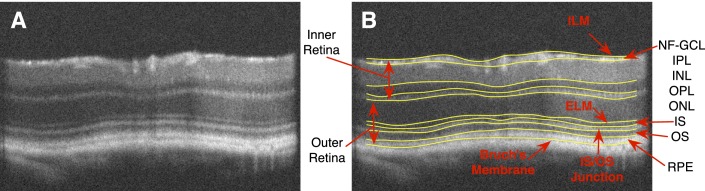
(A) A slice from a mouse SD-OCT image. (B) The same slice showing 10 intraretinal surfaces. Given the axial resolution of these scans (1.53 μm) the junction between the IS/OS appears, in fact, as a layer in these images.

The expected layer thicknesses, for instance, used to describe feasible retinal surfaces needed to be adjusted to meet the expected mouse retinal layer thicknesses. The nerve fiber layer (NFL) and ganglion cell layer (GCL) appear as a combined structure in mice retinas, while in humans the NFL is quite distinct. Moreover, the NF-GCL is significantly thinner than the NFL in healthy human subjects. The thickness values were empirically determined and incorporated into the graph-theoretic method. The optic nerve head region always poses a challenge, as it is a region where the layers are ill defined, and errors in this region could propagate into the paracentral regions as well. Although this structure is noticeably smaller in mice than in humans, it is not a characteristic that can be ignored. The scans themselves differed in quality as well, showing little to no motion artifact, which in human scans can frequently be quite large. This lack of motion artifact and the dense acquisition of the slices allowed us to filter the inherent noise in the images by averaging three adjacent slices, instead of employing more complex speckle noise filters. Once the images were smoothed, the cost functions were derived using Gaussian derivatives.³³ Positive and negative gradients can be detected through the selection of the parameters that define the Gaussians. The size of the scans also posed a challenge, as they are significantly larger than current volumetric scans obtained from human subjects (usually 312 MB, compared with the typical 39 MB for cubic scans from Cirrus SD-OCT scanners; Carl Zeiss Meditec, Dublin, CA, USA).

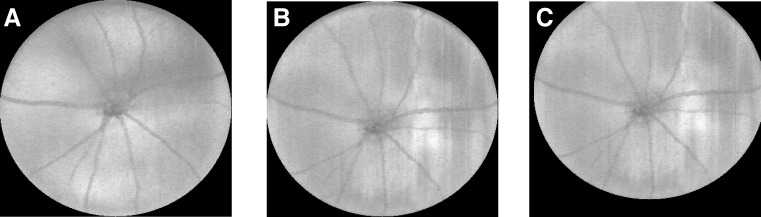
Some scans were not accurately centered on the ONH during acquisition and needed to be centered manually before the reproducibility could be assessed. For this, the automated segmentation of the inner/outer segment (IS/OS) junction was used to create projection images using a small number of A-scans near this layer. The center of the ONH was manually identified in the projection images and used to translate the volume into the correct location. Figure 3 shows projection images obtained from the repeat scans of the right eye of a mouse, where Figure 3A shows one that was acquired correctly, while Figure 3B shows an example of one that was off-center and needed to be corrected.

Figure 3.

Projection images were created from a number of slices near the IS/OS and used to center the scans when needed. The images here show (A) a well-centered scan, (B) an off-center scan, and (C) the manually corrected result.

Surface Accuracy Assessment

The accuracy of the segmentation method was assessed by comparing the automated segmentation results to the full manual tracings obtained from two retinal specialists (WJ, MDA). For this, 10 slices were extracted from 10 normal volumetric scans obtained from one eye of 10 normal mice. Each of the scans was divided into 10 evenly spaced subvolumes from which one slice was chosen at random. Up to 10 intraretinal surfaces (Fig. 2) were then manually traced on each of these slices independently by the two retinal specialists. The reference standard for each surface was defined as the average of the two tracings. Algorithm variability was calculated as the unsigned surface position errors with respect to the reference standard, in microns, for each surface on these slices. The interobserver variability of the two retinal specialists was computed similarly.

Algorithm variability and interobserver variability was compared using a paired t-test. These comparisons were performed in an annular region of the retina defined by two circles 0.2 and 1.2 mm in diameter centered on the ONH, so as to exclude the ONH region and the most peripheral regions of the scan.

Thickness Parameters

Thickness maps were calculated from the centered scans for four retinal layers, namely, (1) the combination of the NF-GCL and IPL, (2) the inner retina (Fig. 2), which is bounded by the ILM and the bottom of the OPL, (3) the outer retina which extends from the ONL to BM, and (4) the total retinal thickness (TRT) defined from the ILM to BM. The mean thickness was then computed for each of the layers in eight regions, namely, the central superior (CS), central nasal (CN), central inferior (CI), central temporal (CT), paracentral superior (PS), paracentral nasal (PN), paracentral inferior (PI), and paracentral temporal (PT) regions, as shown in Figure 4. The circles used were 0.2 mm, 0.6 mm, and 1.2 mm in diameter, respectively.

Figure 4.

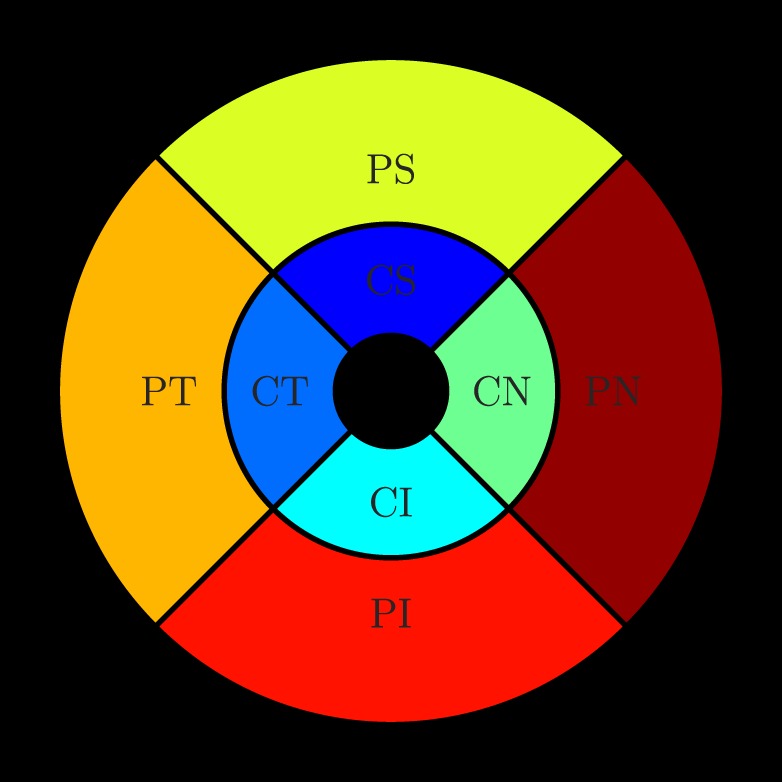
The reproducibility measures were computed in the eight regions shown above, namely, the CS, CN, CI, CT, PS, PN, PI, and PT regions. The inner, middle, and outer circles are 0.2, 0.6, and 1.2 mm in diameter, respectively.

Layer Thickness Reproducibility Analyses

The reproducibility of the four retinal layer thicknesses was computed in eight predefined regions (Fig. 4). The following were computed:

• 1.Intervisit reproducibility: mean difference and SD (μm) between each layer's thicknesses obtained from the two repeat scans;
• 2.Intervisit coefficient of variation (CV), expressed as the ratio of the SD of the difference of the thickness measurements to the mean thickness measurement obtained from the two repeats; and
• 3.The intraclass correlation coefficient (ICC) and the corresponding confidence intervals (CIs), computed in the statistical package R.^34,35

Results

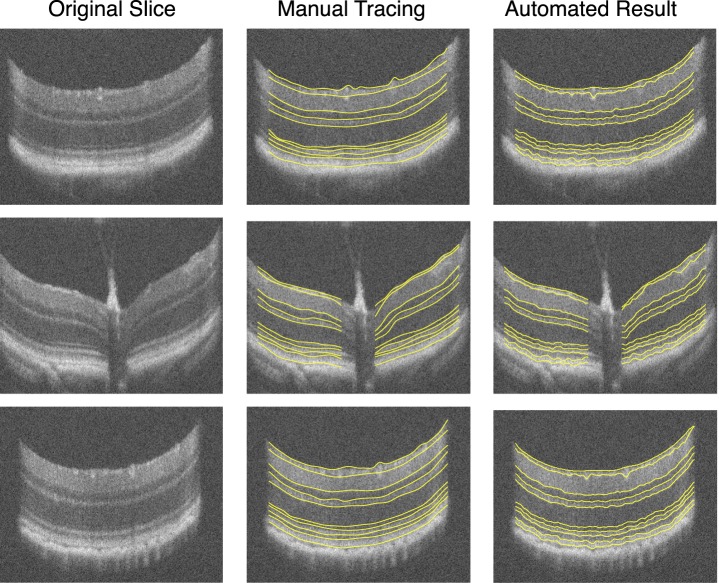
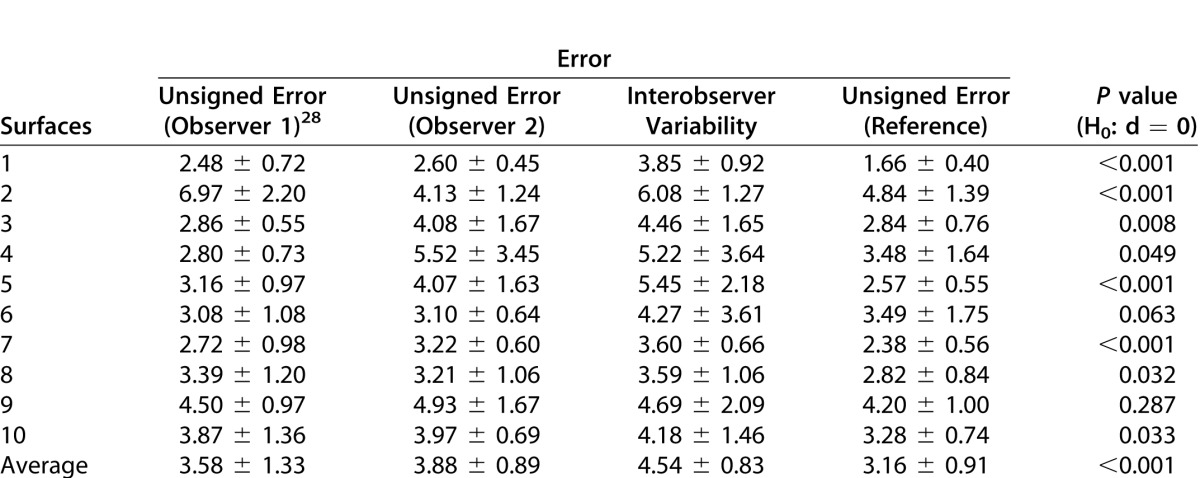
The automated segmentation results were compared with the manual tracings obtained on 97 slices from 10 scans (10 normal mice). Three slices from the original 100 were excluded, as one of the experts could not confidently trace all 10 surfaces on these slices. Figure 5 shows the manual tracings obtained from the expert and the automated segmentation result on three slices from a normal mouse scan. The mean error for each of the 10 surfaces across all 97 slices is summarized in Table 1. The errors (mean ± SD μm) were only computed within an annular region defined by two circles 0.2 mm and 1.2 mm in diameter. The errors were computed by comparing the automated segmentation to the manual tracings of each observer (columns 2 and 3) as well as the reference standard (column 5). The difference d between the interobserver variability (column 4) and the unsigned errors (column 5) were statistically compared using a paired t-test. The mean unsigned border position error of the algorithm compared with each expert and reference standard was 3.58 ± 1.33, 3.88 ± 0.89, and 3.16 ± 0.91 μm, respectively. The interobserver variability was 4.54 ± 0.83 μm, which was found to be significantly larger than the algorithm error (p < 0.01).

Figure 5.

Three slices from a normal mouse SD-OCT image. The original slices (left column) are shown alongside the manual tracings obtained by a retinal specialist (middle column) as well as the automated result (right column).

Table 1.

Unsigned Border Position Error (Mean ± SD in mm) for Each of the 10 Segmented Intraretinal Surfaces Computed on a Total of 97 Slices Obtained From 10 Normal Scans

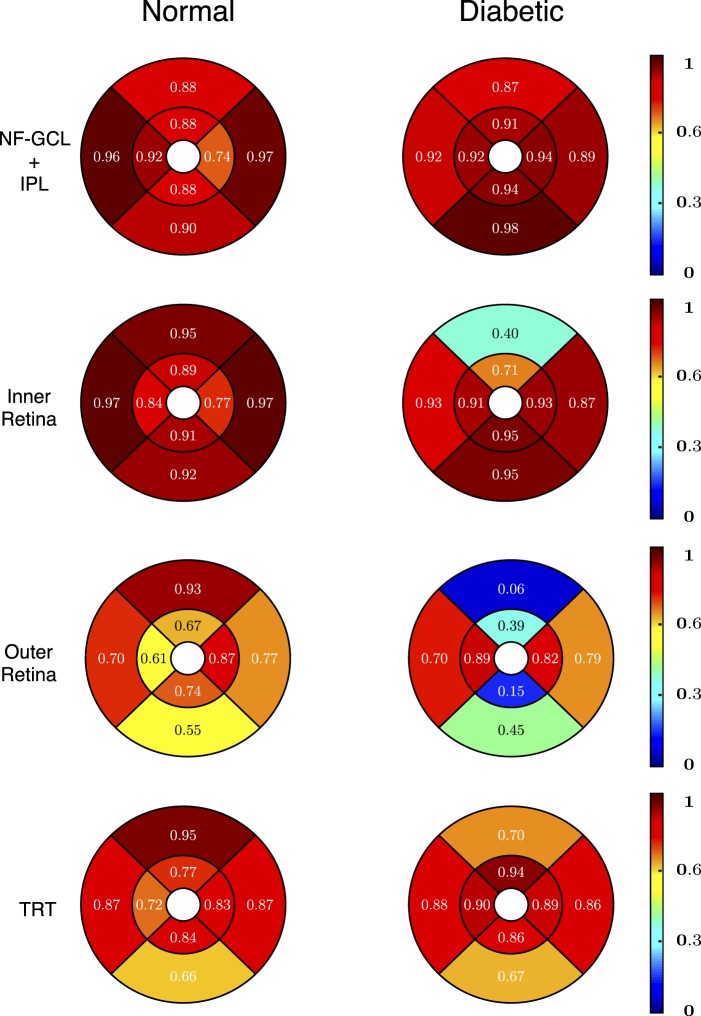
Reproducibility of thickness measurements based on these surfaces was assessed in 17 normal and 10 diabetic mice, with sufficient OCT signal strength in both first and repeat scans. The mean thickness of the NF-GCL+IPL and total retinal thickness in the normal and diabetic mice were 64.14 ± 1.17 and 211.04 ± 5.89 μm, and 62.33 ± 0.99 and 207.95 ± 4.16 μm, respectively, see Table 2. The mean thickness of the nine retinal layers in the normal and diabetic mice is also tabulated in Supplementary Table S1 ^{(48KB, doc)} .

Table 2.

Summary of the Reproducibility Analysis

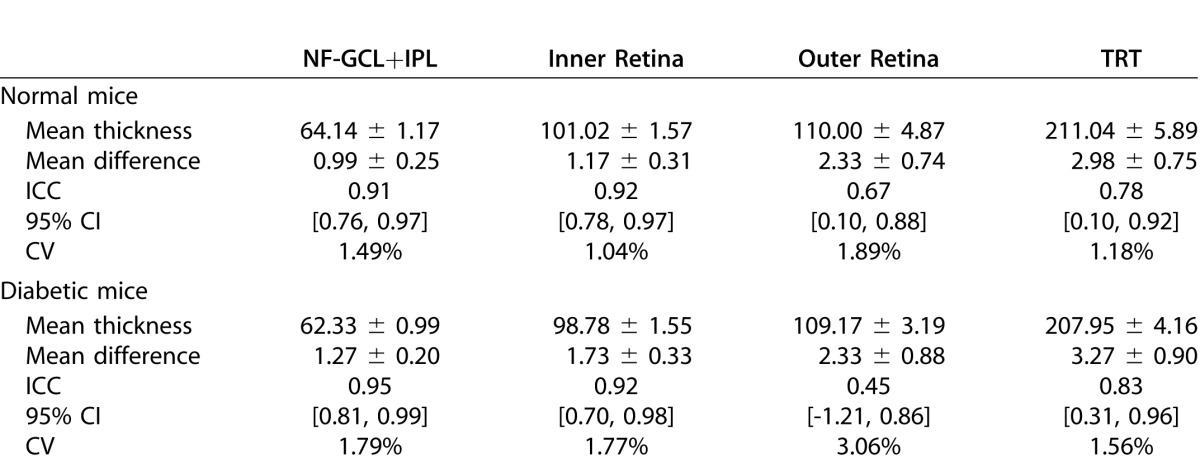
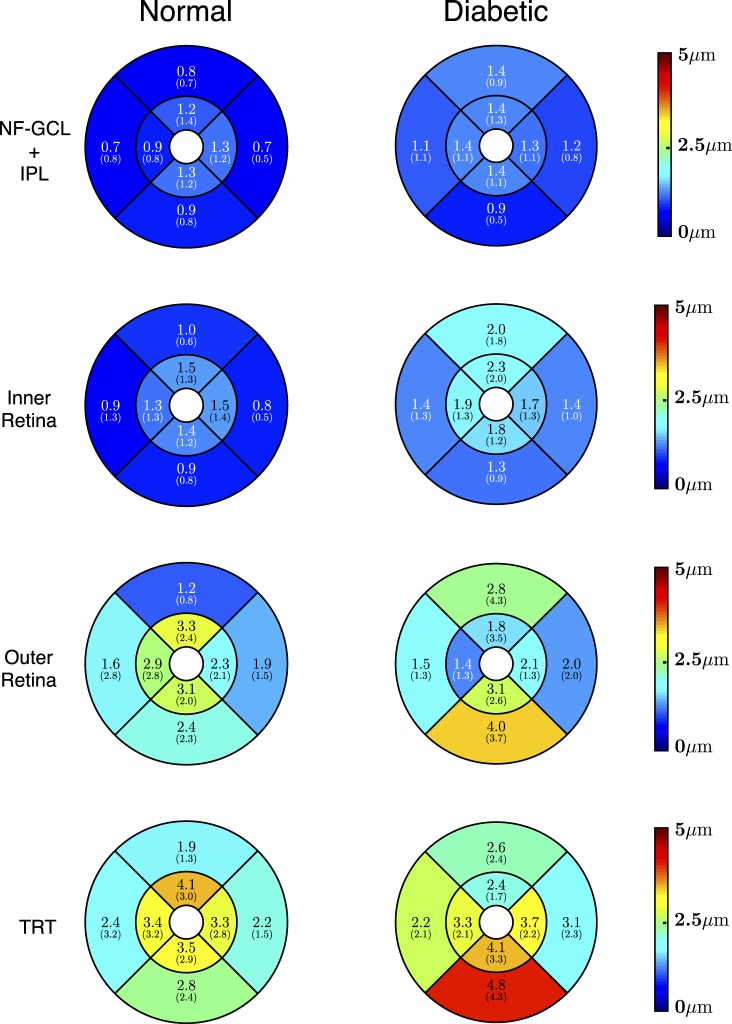
The regional intervisit difference in thickness measurements for the four layers (depicted in Fig. 6) were 0.99 ± 0.25, 1.17 ± 0.31, 2.33 ± 0.74, and 2.98 ± 0.75 μm, respectively. The largest thickness difference (under 5 μm) was noted in TRT in the central superior and paracentral inferior regions in the normal and diabetic mice, respectively. The overall mean thickness difference over the four retinal layers in the normal and diabetic mice was found to be 1.86 ± 0.95 and 2.15 ± 0.86 μm, respectively.

Figure 6.

The thickness differences computed (mean [SD] μm) within the NF-GCL+IPL (top row), the inner retina (second row), the outer retina (third row), and the total retinal thickness (last row) for the normal (left) and the diabetic (right) mice.

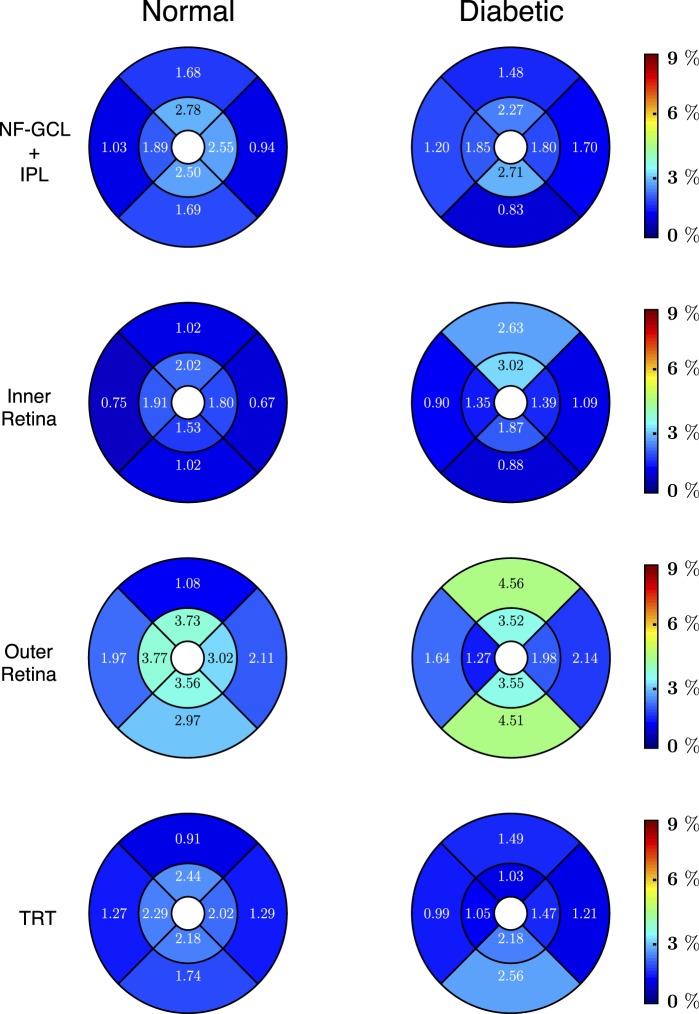
Regional CV for the normal and diabetic mice are shown in Figure 7. The CVs for all the layers are under 5% with the highest values being noted among the diabetic mice. The CV for the NF-GCL+IPL and total retinal thicknesses was found to be 1.49% and 1.18%, and 1.79% and 1.56% in the normal and diabetic mice, respectively.

Figure 7.

The CV (%) values computed within the NF-GCL+IPL (top row), the inner retina (second row), the outer retina (third row), and the total retinal thickness (last row) for the normal (left) and the diabetic (right) mice. The CV values were obtained by dividing the SD of the thickness difference per region by the mean thickness of the region.

Regional ICC for the normal and diabetic mice are shown in Figure 8 and are also summarized in Table 2. The ICC values (and the 95% CIs) for the NF-GCL +IPL layer, inner retina, outer retina and the TRT in the normal mice were 0.91 [0.76, 0.97], 0.92 [0.78, 0.97], 0.67 [0.10, 0.88], and 0.78 [0.10, 0.92], respectively. In the diabetic mice, the ICC values for these layers were 0.95 [0.81, 0.99], 0.92 [0.70, 0.98], 0.45 [−1.21, 0.86] and 0.83 [0.31, 0.96], respectively.

Figure 8.

The ICC values computed within the NF-GCL+IPL (top row), the inner retina (second row), the outer retina (third row), and the total retinal thickness (last row) for the normal (left) and the diabetic (right) mice. The ICC values were computed in the statistical package R.

The reproducibility analyses were also conducted for all nine layers and the results are summarized in the Supplementary Table S2 ^{(48KB, doc)} .

Discussion

The graph-theoretic approach^11–13 previously proposed for the segmentation of intraretinal surfaces in human SD-OCT images is an efficient algorithm that not only segments multiple surfaces in 3D, but also ensures the global optimality of the results with respect to the cost function. The ability to incorporate 3D contextual information in addition to localized features ensures its robustness in the presence of noise as well as disease induced disruptions.^13,36 Here, we have presented an adaptation of this graph-theoretic approach for the segmentation of intraretinal layers in mouse SD-OCT volumetric scans.

The results show that the method is accurate and reproducible. Algorithm surface segmentation variability was significantly lower than the interobserver variability between two retinal specialists. The reproducibility of the thickness measurements is of the same magnitude as the pixel length in tissue (1.53 μm) and is in fact, smaller than the scanner axial resolution (1.7 μm in tissue). The CV values are under 5% and the ICC values also indicate good reproducibility, especially given the small number of mice used in the study.

The accuracy assessment shows that the NF-GCL complex is the most difficult to segment, with a signed error indicating that the algorithm tends to overestimate this layer. This is not unexpected as the layer is quite thin, disappearing completely at the periphery of the scans and can even be quite difficult to visually discern in some locations. The incorporation of learned a priori information, such as expected thickness and topological information learned from a training set, does help prevent this as demonstrated in our associated works.^28,29 The reproducibility of the thickness measurements showed slightly larger errors in the diabetic mice. This is also not unexpected as the presence of disease does make it difficult to segment the layers, and it is also important to note that the total number of scans obtained in diseased mice were lower than the total number obtained from the normals. Nevertheless, the reproducibility is expected to be sufficient for the monitoring of pathophysiologically meaningful change over time (Jeong W, et al. IOVS. 2013;54:ARVO E-Abstract 4883).

SD-OCT imaging has been shown to be effective for the quantitative study of retinal structures in animal retinas. However, the delineation of these structures is often done manually^20,22 or obtained by correcting the automated results²⁴ obtained. A reliable automated segmentation method, such as the one presented here, could reduce the burden of delineating these structures manually, while providing volumetric analysis of the multiple layers. We have made the method publicly available as part of the Iowa Reference Algorithms at http://www.biomed-imaging.uiowa.edu/downloads/.

In conclusion, the adapted graph-theoretic approach described here shows a high degree of accuracy and reproducibility, thus, making it ideal for the noninvasive quantification of retinal layers in mice, and could be extended to analyze other animal scans as well.