Computational Investigation of [FeFe]-Hydrogenase Models: Characterization of Singly and Doubly Protonated Intermediates and Mechanistic Insights

Abstract

The [FeFe]-hydrogenase enzymes catalyze hydrogen oxidation and production efficiently with binuclear Fe metal centers. Recently the bioinspired H₂-producing model system Fe₂(adt)(CO)₂(dppv)₂ (adt=azadithiolate and dppv=diphosphine) was synthesized and studied experimentally. In this system, the azadithiolate bridge facilitates the formation of a doubly protonated ammonium-hydride species through a proton relay. Herein computational methods are utilized to examine this system in the various oxidation states and protonation states along proposed mechanistic pathways for H₂ production. The calculated results agree well with the experimental data for the geometries, CO vibrational stretching frequencies, and reduction potentials. The calculations illustrate that the NH···HFe dihydrogen bonding distance in the doubly protonated species is highly sensitive to the effects of ion-pairing between the ammonium and BF₄^– counterions, which are present in the crystal structure, in that the inclusion of BF₄^– counterions leads to a significantly longer dihydrogen bond. The non-hydride Fe center was found to be the site of reduction for terminal hydride species and unsymmetric bridging hydride species, whereas the reduced symmetric bridging hydride species exhibited spin delocalization between the Fe centers. According to both experimental measurements and theoretical calculations of the relative pK_a values, the Fe_d center of the neutral species is more basic than the amine, and the bridging hydride species is more thermodynamically stable than the terminal hydride species. The calculations implicate a possible pathway for H₂ evolution that involves an intermediate with H₂ weakly bonded to one Fe, a short H₂ distance similar to the molecular bond length, the spin density delocalized over the two Fe centers, and a nearly symmetrically bridged CO ligand. Overall, this study illustrates the mechanistic roles of the ammonium-hydride interaction, flexibility of the bridging CO ligand, and intramolecular electron transfer between the Fe centers in the catalytic cycle. Such insights will assist in the design of more effective bioinspired catalysts for H₂ production.

Short abstract

Theoretical calculations in conjunction with supporting experimental data are used to analyze the mechanistic pathway for hydrogen evolution catalyzed by the bioinspired model Fe₂(adt)(CO)₂(dppv)₂. This study elucidates the site of reduction and the pK_a values associated with formation of the singly and doubly protonated species, as well as the roles of the ammonium-hydride interaction, flexibility of the bridging CO ligand, and intramolecular electron transfer between the Fe centers in the catalytic cycle for H₂ production.

I. Introduction

The design of H₂ oxidation and production electrocatalysts is critical for the development of alternative renewable energy technologies. The [FeFe]-hydrogenase enzymes catalyze these reactions effectively with binuclear Fe metal centers, as depicted in Figure 1.¹⁻³ The detailed catalytic mechanism of these enzymes is still not completely understood. Fourier transform infrared spectroscopy (FTIR) and electron paramagnetic resonance (EPR) studies on the native enzyme have identified a mixed-valence oxidized state, H_ox, and a diamagnetic reduced state, H_red.⁴⁻⁶ The H_ox state is well-characterized and features an obvious site for binding the H₂ substrate on the distal Fe center, denoted Fe_d in Figure 1. The structure of the H_red state is less clear because X-ray crystallography of biological systems cannot easily resolve hydrogen atoms. Although hypothesized for more than a decade,^7,8 an azadithiolate bridgehead with an amine group pendant to the Fe metal center has only recently been confirmed experimentally.^9,10 This recent insight is guiding current modeling and computational efforts. Relative to biophysical studies, an advantage of model systems is that hydride and dihydrogen species are readily observed by ¹H NMR and, in some cases, X-ray crystallography.^11,12 Moreover, model systems are more computationally tractable, thereby providing additional structural and mechanistic insights.^8,13−33

Figure 1.

Oxidized (H_ox) and reduced (H_red) intermediates of the [FeFe]-hydrogenase enzyme’s active site with the azadithiolate (adt) cofactor.

A variety of H₂-producing model systems inspired by [FeFe]-hydrogenases have been synthesized.³⁴⁻³⁸ Many of these models suffer from high overpotentials (i.e., negative reduction potentials) for hydrogen production. The recent H₂-producing models Fe₂(xdt)(CO)₂(dppv)₂ (xdt = pdt, adt), depicted in Figure 2, rely on an electrode in place of the [Fe₄S₄] clusters that normally support electron transfer in the enzyme. Furthermore, in these models the CN and one of the CO ligands are replaced by diphosphine (dppv) ligands.³⁸ The presence of sterically crowded, electron-rich ligands on diiron carbonyl has been shown to stabilize the desired terminal hydride species.^35,39 Through this approach, key hydride intermediates have been crystallographically characterized.^35,38,40,41 The most recent advance has revealed a key intermediate wherein the hydride is dihydrogen bonded to the protonated azadithiolate cofactor.³⁸

Figure 2.

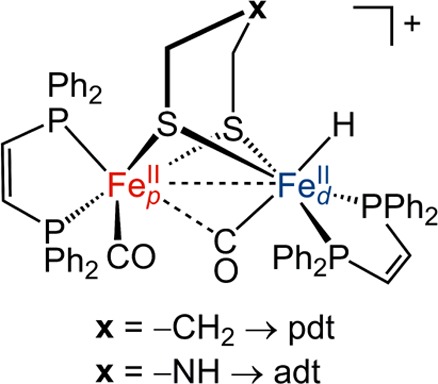
Model of the H_red state of the enzyme, where the role of the [Fe₄S₄]²⁺ cluster is replaced by an electrode and the other ligands are replaced by 1,2-bis(diphenylphosphino)ethylene (dppv). The x represents the heteroatom in the dithiolate bridge (xdt = pdt, adt). The configuration shown is the terminal hydride, [tH-(Fe^IIFe^II)xdt]⁺.

This paper analyzes computationally the recent advances in the models and chemistry of the [FeFe]-hydrogenases. This paper has two components: benchmarking the computational methodology for these model systems and providing insights into the mechanism of H₂ production. The benchmarking provides the validation that is necessary to support the more hypothetical mechanistic predictions. In the first part of this paper, the computational methods are benchmarked by comparing experimental and theoretical structures, infrared (IR) vibrational frequencies of the CO groups, reduction potentials, and relative pK_a values. The second part of this paper focuses on the mechanism for H₂ production. In particular, we examine these model systems in the various oxidation states and protonation states along proposed mechanistic pathways for H₂ production. Of particular interest, we aim to clarify the nature of the doubly protonated ammonium-hydride intermediate, which has been characterized crystallographically for this bimetallic system.³⁸ Such doubly protonated intermediates have not been observed in bioinspired monometallic Ni-based catalysts,^17,20,42 although a mono-Fe catalyst in the doubly protonated state has very recently been characterized by DuBois and co-workers.⁴³ We also present additional experimental data to validate the theoretical studies and to test predictions generated by the calculations.

An outline of this paper is as follows. In section II, we introduce the nomenclature for the species studied and describe the computational methods used to calculate the structures, CO vibrational frequencies, reduction potentials, and pK_a values for these species. Section III presents the results and analysis, starting with the geometries and vibrational frequencies, followed by the reduction potentials and an analysis of the spin densities to determine the oxidation states of the metal centers. The second part of this section focuses on the protonation states and relative pK_a values and presents an analysis of possible H₂ evolution mechanisms in the context of the experimental and computational data. Concluding remarks are presented in section IV.

II. Methods

A. Defining the Nomenclature

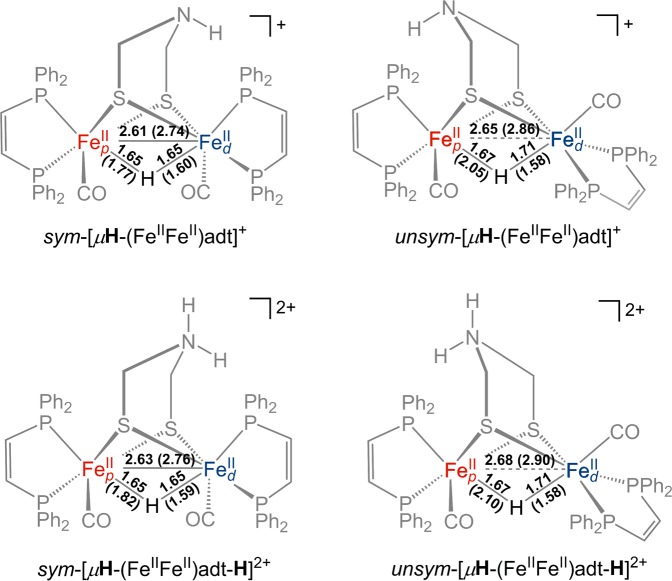
The diiron model systems can adopt numerous isomeric and geometric forms. Borrowing the nomenclature generally employed in enzymatic studies, the Fe center with the hydride is denoted distal (Fe_d) and the opposite Fe center is denoted proximal (Fe_p). Herein, we will abbreviate the (Fe_pFe_d)(xdt)(CO)₂(dppv)₂ catalysts as [(FeFe)xdt] for notational simplicity. Figure 2 depicts the electrocatalyst in the terminal hydride (tH) form with xdt representing either a propanedithiolate (pdt), [tH-(Fe^IIFe^II)pdt]⁺, or an azadithiolate (adt), [tH-(Fe^IIFe^II)adt]⁺. In this notation, the terminal hydride is always assumed to reside on the Fe_d center. Figure 3 depicts all of the protonation states of the [(FeFe)adt] species studied in this work. A similar scheme for the [(FeFe)pdt] species is available in the Supporting Information (Figure S17).

Figure 3.

Schematic depiction of the various [(FeFe)adt] species, where each row represents a different protonation state of the catalyst. Only the isomers with the lowest free energies are shown for each species in this figure. The dashed lines (P1, P2, P3, P4, and P5) correspond to pathways for which structural and electronic changes can be monitored by Δν_CO values; they do not necessarily correspond to reaction pathways.

Although the terminal hydride (tH) species are thermodynamically less stable than their associated bridging hydride (μH) isomers in model systems, experiments indicate that the terminal hydride species are much more catalytically active: they generate H₂ faster and at less negative potentials than their bridging hydride counterparts.^35,38 The dependence of the reduction potential on the regiochemistry of the hydride remains unexplained but appears to be catalytically relevant. Whereas the [(Fe^IFe^I)pdt] complex requires strong acids to form the terminal hydride species, [tH-(Fe^IIFe^II)pdt]⁺, the nearly isostructural [(Fe^IFe^I)adt] complex can be protonated with weak acids due to the proposed relay activity of the azadithiolate.³⁴ Specifically, the presence of the azadithiolate bridge permits the formation of the ammonium tautomer, [(Fe^IFe^I)adt-H]⁺, and subsequent intramolecular proton transfer to the Fe_d leads to the terminal hydride species, [tH-(Fe^IIFe^II)adt]⁺ (Figure 3). Both [tH-(Fe^IIFe^II)adt]⁺ and [tH-(Fe^IIFe^II)pdt]⁺ convert to their respective bridging hydride isomers irreversibly at room temperature.^38,44 Upon equilibration, two bridging hydride species form, sym-[μH-(Fe^IIFe^II)adt]⁺ and unsym-[μH-(Fe^IIFe^II)adt]⁺, which differ in the orientation of the dppv ring on the Fe_d center relative to the dppv ring on the Fe_p center (Figure 3).

The adt-containing hydride species can undergo a second protonation with stronger acids, leading to the doubly protonated species, [tH-(Fe^IIFe^II)adt-H]²⁺ (Figure 3). Again, [tH-(Fe^IIFe^II)adt-H]²⁺ isomerizes into two bridging hydrides, sym-[μH-(Fe^IIFe^II)adt-H]²⁺ and unsym-[μH-(Fe^IIFe^II)adt-H]²⁺, albeit at a slower rate than the singly protonated analog.³⁸ Although less thermodynamically stable than the bridging hydride species, the terminal hydride species, [tH-(Fe^IIFe^II)adt-H]²⁺, is poised for H₂ production due to the close proximity of the ammonium and Fe-hydride centers in the doubly protonated species.

B. Electronic Structure Methods

Density functional theory (DFT) calculations were performed to characterize the structural and energetic properties of the pertinent species in the catalytic scheme. All calculations were performed using the Gaussian 09 electronic structure program.⁴⁵ For geometry optimizations, the starting geometries were obtained from the corresponding crystal structures, which are available for the [(Fe^IFe^I)pdt]⁰,⁴⁰ [(Fe^IIFe^I)pdt]⁺,⁴⁶unsym-[μH-(Fe^IIFe^II)pdt]⁺,³⁵ and unsym-[μH-(Fe^IFe^II)pdt]⁰ species,⁴¹ as well as the [(Fe^IFe^I)adt]⁰ and [tH-(Fe^IIFe^II)adt-H]²⁺ species.³⁸ The starting geometries for species without crystal structures were obtained by manually altering the most closely related crystal structure. Optimizations in the gas phase and solution phase resulted in similar structures for several representative species, so gas phase optimizations were used herein for computational efficiency. A comparison of the structures optimized in the gas phase and solution phase for several representative species is available in the Supporting Information (Table S2).

The DFT calculations were performed using the B3P86 density functional^47,48 with the Stuttgart pseudopotential and associated basis set of Preuss and co-workers (SDD) for the Fe centers,⁴⁹ the 6-31G** basis set for the active hydrogens,⁵⁰ the 6-31+G* basis set for the BF₄^– counterions,⁵¹ and the 6-31G* basis set for all other atoms.^52,53 To obtain the solvation free energies, we used the conductor-like polarizable continuum model (C-PCM)^54,55 with the Bondi atomic radii⁵⁶ and included nonelectrostatic interactions, namely, the dispersion,^57,58 repulsion,^57,58 and cavitation energies.⁵⁹ The solvation free energies were calculated in dichloromethane (CH₂Cl₂) to coincide with the experiments unless otherwise stated.

C. Calculation of Vibrational Frequencies, Reduction Potentials, and ΔpK_a Values

The CO vibrational frequencies were calculated within the harmonic model and were scaled by a factor of 0.9850, as indicated by previous studies.⁶⁰ The vibrational frequency shifts, Δν_CO, were calculated for the dashed pathways shown in Figure 3. For the [tH-(Fe^IIFe^II)adt]⁺ and [tH-(Fe^IIFe^II)adt-H]²⁺ species, the presence of the semibridging CO ligand allows for the assignment of two distinguishable CO stretching frequencies: the higher ν_CO corresponds to the terminal CO attached to the Fe_p center, and the lower ν_CO corresponds to the semibridging CO. For all other species, both CO ligands are terminal, so their stretching frequencies are less separated.

In general, DFT does not consistently provide reliable absolute pK_a’s and reduction potentials because of limitations in the functionals, basis sets, and solvation models, as well as uncertainties in the free energies of the electron, proton, and electrode. As discussed previously,⁶¹ the calculation of pK_a’s and reduction potentials relative to related reference systems with known experimental values has been shown to be more reliable because many of the systematic errors cancel. For this reason, we discuss only relative reduction potentials and pK_a’s in this paper. The structures and energies of all complexes discussed herein are provided in the Supporting Information.

The reaction free energies associated with reduction and deprotonation were calculated using the Born–Haber thermodynamic cycle. The reaction free energy for reduction, ΔG_r^°(e^–), was calculated using the expression

1

In this expression, ΔG_s^°(Red) and ΔG_s(Ox) are the solvation free energies of the reduced and oxidized species, respectively, and ΔG_gas^° is the gas phase reaction free energy calculated using the standard relation ΔG_gas = ΔH_gas^° – TΔS_gas. A similar expression was used to calculate the reaction free energy for deprotonation, ΔG_r^°(H⁺).

For reasons mentioned above, the reduction potentials were calculated relative to a related reference reaction for which the experimental value is known. This procedure accounts for systematic errors associated with the selected theoretical method and basis set and avoids the determination of the free energies of the electron and the electrode because these terms cancel. Detailed descriptions of this methodology can be found elsewhere.^27,61−63 For our specific application, we used the following expression to calculate the reduction potentials:

2

Here, E° is the reduction potential of the [(FeFe)adt] species of interest, E_ref^° is the experimentally measured reduction potential of the reference species, which is the [(FeFe)pdt] species in this work, ΔΔG_r(e^–) is the calculated difference in reaction free energies (eq 1) for reduction of the species of interest and the reference, and F is the Faraday constant. All calculated and experimental reduction potentials are given in volts (V) relative to the ferrocene/ferrocenium (Fc⁰/Fc⁺) couple in CH₂Cl₂. The irreversible reduction potentials of the doubly protonated species are calculated relative to the reduction potentials of the corresponding singly protonated species and are labeled ΔE_prot^°. The cyclic voltammetry (CV) experiments were performed at 273 K, and the reduction potentials were also calculated at this temperature.³⁸

We used the standard relationship, pK_a = ΔG_r^°(H⁺)/(RT ln 10), to calculate the pK_a values. In this expression, ΔG_r(H⁺) corresponds to the calculated reaction free energy for deprotonation, R is the gas constant, and T = 233.15 K to coincide with experimental conditions. Due to the limited experimental pK_a data for the [(FeFe)pdt] systems and its inherent inability to doubly protonate, these complexes were not used as references. Instead, we calculated ΔpK_a, which is defined to be the difference between the pK_a values for two specified states of the [(FeFe)adt] complex. The reported ΔpK_a values were calculated in CH₂Cl₂ to coincide with experimental conditions and in acetonitrile (CH₃CN) to coincide with the reference pK_a values used in the interpretation of the experimental values because a pK_a scale is not well established for CH₂Cl₂.

III. Results and Discussion

A. Geometries, Free Energies, and Vibrational Frequencies

We optimized the geometries of the various species discussed above and compared the structures and key vibrational frequencies to available experimental data. The optimized geometries are in reasonable agreement with the X-ray crystal structures. Table 1 provides a comparison of the most relevant bond lengths for the various species. Structural and energetic information on all systems studied herein are provided in the Supporting Information. The relative free energies of the species depicted in Figure 3 are provided in Table 2. Moreover, the relative free energies of these species and other isomers of higher free energy are provided in Figures S15 and S16, Supporting Information.

Table 1. Selected Bond Lengths from DFT Calculations and X-ray Structures^a.

	Fep···Fed		Fep···CO		Fed···CO		Fep···H		Fed···H
species	expt	DFT	expt	DFT	expt	DFT	expt	DFT	expt	DFT
[(FeIFeI)pdt]0b	2.60	2.53	1.74	1.73	1.75	1.73	g	g	g	g
[(FeIIFeI)pdt]+c	2.59	2.59	1.75	1.76	1.79	1.78	g	g	g	g
unsym-[μH-(FeIIFeII)pdt]+d	2.66	2.66	1.78	1.75	1.74	1.74	1.69	1.68	1.65	1.71
unsym-[μH-(FeIFeII)pdt]0e	2.80	2.85	1.75	1.74	1.78	1.76	1.82	2.00	1.61	1.59
[(FeIFeI)adt]0f	2.60	2.53	1.74	1.73	1.75	1.73	g	g	g	g
[tH-(FeIIFeII)adt-H]2+f	2.62	2.65	2.52	2.50	1.79	1.78	g	g	1.44	1.53

^aValues given in Å.

^bExperimental data from ref (40).

^cExperimental data from ref (46).

^dExperimental data from ref (35).

^eExperimental data from ref (41).

^fExperimental data from ref (38).

^gNot applicable because the hydrogen is not present for certain species or the distance is not relevant for the doubly protonated species.

Table 2. Calculated Relative Free Energies (ΔG°)^a of Protonated Species.

species	ΔG°
[(FeIFeI)adt]0	0.00
[(FeIIFeII)adt-H]+	–279.32
[tH-(FeIIFeII)adt]+	–286.09
sym-[μH-(FeIIFeII)adt]+	–296.64
unsym-[μH-(FeIIFeII)adt]+	–294.70
[tH-(FeIIFeII)adt-H]2+	–553.02
sym-[μH-(FeIIFeII)adt-H]2+	–564.82
unsym-[μH-(FeIIFeII)adt-H]2+	–561.16

^aValues given in kcal/mol relative to the unprotonated species, [(Fe^IFe^I)adt]⁰, in CH₂Cl₂ at 298.15 K. The free energy of a solvated proton should be included to obtain free energies relevant to the protonation reactions.

The optimized geometry for the doubly protonated species, [tH-(Fe^IIFe^II)adt-H]²⁺, exhibited one key difference from the crystal structure, namely, the dihydrogen distance NH···HFe. This dihydrogen distance was d_H···H = 1.88 Å in the crystal structure and d_H···H = 1.40 Å in the optimized geometry. Thus, DFT leads to a significantly shorter dihydrogen distance that corresponds to a stronger dihydrogen bond.^64,65 A previous DFT study on a model of the [FeFe]-hydrogenase active site also showed an underestimation of the dihydrogen distance for a related doubly protonated species.⁸ This smaller dihydrogen distance in the [tH-(Fe^IIFe^II)adt-H]²⁺ species was found for a wide range of density functionals, as shown in Table S3, Supporting Information. However, dihydrogen bond distances have also been shown to be extremely sensitive to weak intra- and intermolecular interactions, such as ion-pairing.⁶⁶ Moreover, neutron diffraction experiments are expected to provide more reliable positions for hydrogen atoms than X-ray diffraction, which most likely overestimates this distance.⁶⁷ A recent neutron diffraction study on a monometallic Fe hydrogenase model using the noncoordinating counterion, BAr^F₄^–, found the NH···HFe dihydrogen bond to be 1.49 Å.⁴³ In contrast, the doubly protonated structure, [tH-(Fe^IIFe^II)adt-H]²⁺, was determined with X-ray crystallography and included BF₄^– ions that could exhibit significant ion-pairing effects.⁶⁸

Given the difference in the crystallographic and calculated dihydrogen bond length in [tH-(Fe^IIFe^II)adt-H]²⁺, we hypothesized that this discrepancy was due to the omission of the BF₄^– ions in the geometry optimizations. To test this hypothesis, we also optimized the structure including one or two of the BF₄^– ions closest to the azadithiolate bridge in the crystal structure. Figure 4 illustrates that the geometry optimizations including either one or two BF₄^– ions improved the agreement between DFT and experiment by shifting the amine bridgehead and elongating the dihydrogen distance. The bond lengths given in Table 3 show that including the ion-pairing interactions preserves the Fe···Fe and Fe···H distances while elongating the dihydrogen distance. Although the inclusion of counterions improves the agreement with the doubly protonated crystal structure, we omit the counterions in the calculations of other quantities, such as reduction potentials and spin densities, to maintain consistency among the various species studied under a range of experimental conditions.

Figure 4.

Superimposed structures of the doubly protonated species, [tH-(Fe^IIFe^II)adt-H]²⁺, illustrating the better agreement between the crystal structure and the optimized geometries when BF₄^– ions are included in the calculations. The phenyl groups have been removed, and the FeH···HN interaction is circled for clarity. Color Scheme: crystal structure (gray) and optimized geometry with no BF₄^– (red), one BF₄^– (blue), and two BF₄^– (green) counterions.

Table 3. Selected Bond Lengths from DFT Calculations and X-ray Structures for Doubly Protonated Species Optimized with and without BF₄^– Anions^a.

	Fep···Fed	Fed···H	N···H	H···H
exptb	2.62	1.44	1.00	1.88
no BF4–	2.65	1.53	1.07	1.40
solutionc	2.61	1.51	1.04	1.55
1·BF4–	2.62	1.51	1.04	1.65
2·BF4–	2.59	1.50	1.04	2.04

^aValues given in Å. All optimizations were conducted in the gas phase unless stated otherwise.

^bExperimental data from ref (38).

^cThis structure was optimized in solution (CH₂Cl₂) using C-PCM without any BF₄^– counterions.

The strong, distinctive absorptions at ∼2000 cm^–1 associated with CO stretching can be used to probe changes in the electronic structure due to protonation, isomerization, reduction, and oxidation.^13,23,69,70 We calculated the change in the CO frequencies, Δν_CO, for the five protonation reactions depicted by dashed lines in Figure 3. As shown in Table 4, the calculated Δν_CO values due to protonation are within ∼10 cm^–1 of the experimentally measured values. This level of agreement provides validation for the structures of species for which crystal structures are not available. Typically DFT calculations are more reliable for changes in frequencies than for absolute frequencies; a comparison between the calculated and experimental absolute frequencies is provided in Table S4, Supporting Information. For the present study, the previously reported³⁸ spectroscopic studies were repeated using the acid [H(OEt₂)₂]BAr^F₄ to eliminate the possibility of ion pairing arising from the coordination of BF₄^– when using HBF₄·Et₂O, which has been shown to participate in hydrogen-bonding interactions,⁷¹ particularly in complexes with protonated adt ligands.⁷² The agreement between calculated and experimental frequencies is better for the BAr^F₄^– salts; these spectra are provided in the Supporting Information (Figures S6 and S7).

Table 4. Experimental and Calculated Δν_CO Values^a upon Protonation.

reactionb	exptc	calcdd
P1	22, 22	31, 30
P2e	78, 46	86, 37
P3	82, 79	89, 77
P4e	24, 21	27, 34
P5	19, 17	29, 29

^aValues given in cm^–1.

^bThe P1, P2, P3, P4, and P5 protonation reactions are defined in Figure 3.

^cExperimental data from ref (38).

^dFrequencies scaled by a factor of 0.9850.

^eThe second Δν_CO value is assigned to the semibridging CO.

The Δν_CO values reflect the protonation sites, as indicated by both experimental measurements and theoretical calculations. The Δν_CO values associated with N-protonation are typically characterized by CO frequency increases of ∼20 cm^–1.⁷³⁻⁷⁵ The experimental and calculated Δν_CO values associated with N-protonation to form either the singly or doubly protonated species (P1, P4, and P5 protonations) exhibit this shift. While N-protonation is associated with a relatively small ν_CO shift, formation of the terminal and bridging hydrides (P2 and P3 protonations, respectively) is associated with much higher shifts of ∼70 cm^–1. In both cases, two well-resolved bands are observed in the spectra, but the bands are much more energetically separated for the terminal hydride species than for the bridging hydride species. The band at lower frequencies in the terminal hydride species is assigned to the semibridging CO, which exhibits a smaller ν_CO shift of ∼40 cm^–1. Our calculated Δν_CO values for the protonations leading to the terminal and bridging hydride species (P2 and P3 protonations, respectively) demonstrate this trend and agree well with the experimental values (Table 4). An analogous figure and table for the [(FeFe)pdt] complexes is provided in the Supporting Information (Figure S17 and Table S1).

B. Reduction Potentials

The calculated reduction potentials for the species in CH₂Cl₂ are presented in Table 5. Because the [(FeFe)pdt] species are used as the reference systems, these reduction potentials agree exactly with experiment by construction, and all other reduction potentials are calculated relative to these values. The agreement between theory and experiment for the [(FeFe)adt] species is reasonable for the singly protonated species with errors of ∼0.05 V vs Fc⁰/Fc⁺ in CH₂Cl₂. Additional calculated reduction potentials are provided in the Supporting Information (Table S5). A detailed analysis of the metal oxidation states of the reduced species in terms of the spin densities is provided in the next subsection.

Table 5. Experimental and Calculated Reduction Potentials^a.

species		E° [(FeFe)]+/0	E° [tH-(FeFe)]+/0	E° unsym-[μH-(FeFe)]+/0
[(FeFe)pdt]b	exptc	–0.94	–1.70d	–1.80
	calcd	–0.94	–1.70	–1.80e
[(FeFe)adt]	exptf	–0.76	–1.66g	–1.79
	calcd	–0.84	–1.69	–1.77h

^aValues given in volts vs Fc⁰/Fc⁺ in CH₂Cl₂. Experimental E_1/2 values given unless otherwise indicated.

^b[(FeFe)pdt] reactions were used as the reference reactions, so the calculated and experimental values agree by construction.

^cExperimental data from ref (79).

^dQuasi-reversible reaction, so E_p is reported.

^eE° = −1.82 V vs Fc⁰/Fc⁺ in CH₂Cl₂ if calculated using the symmetric bridging form.

^fExperimental data from ref (38).

^gIrreversible reaction, so E_p is reported.

^hE° = −1.83 V vs Fc⁰/Fc⁺ in CH₂Cl₂ if calculated using the symmetric bridging form.

Due to difficulties in determining a suitable reference system for the doubly protonated species, we calculated the difference between the reduction potentials for the doubly and singly protonated species (ΔE_prot^°). Using this formulation, we calculated ΔE_prot = 0.59 V vs Fc⁰/Fc⁺ in CH₂Cl₂. As expected from basic electrostatic arguments, the doubly protonated species has a less negative reduction potential than the singly protonated species. The experimentally measured difference in these reduction potentials was 0.39 V vs Fc⁰/Fc⁺ in CH₂Cl₂.³⁸ As discussed above, this error could be due to the neglect of BF₄^– in the calculations. Note that BF₄^– ions were present in the electrochemical measurements for the doubly protonated species but not for the singly protonated species. Furthermore, the effects of ion pairing on reduction potentials are known to be pronounced in solvents of low dielectric constants, such as CH₂Cl₂.^76,77 Thus, the difference in the counterions present for the electrochemical experiments of the singly and doubly protonated species could lead to discrepancies in the comparison between calculated and experimental results. Note that the experimentally measured reduction potentials for the terminal hydride species are for quasireversible couples, which could introduce additional discrepancies.

C. Analysis of Metal Oxidation States

For species with an unpaired electron, we analyzed the spin densities to determine the localization of the unpaired electron. The spin densities for the reduced species are presented in Table 6. For the reduced terminal hydride species, [tH-(Fe^IFe^II)adt]⁰, the unpaired spin density is localized entirely on the Fe_p center, suggesting that the Fe_p center is reduced. This localization on the Fe_p center is similar for the reduced terminal hydride species, [tH-(Fe^IFe^II)pdt]⁰, which is produced at a similar potential as the [tH-(Fe^IFe^II)adt]⁰ species, indicating that the dithiolate is not a major influence on the redox behavior for the terminal hydride species. The spin densities pertaining to the [(FeFe)pdt] complexes are provided in the Supporting Information (Table S6).

Table 6. Spin Densities of the Reduced Mixed-Valence Species^a.

species	ρ(Fep)	ρ(Fed)
[tH-(FeIFeII)adt]0	1.03	0.05
sym-[μH-(Fe1.5Fe1.5)adt]0	0.76	0.37
sym-[μH-(Fe1.5Fe1.5)adt-H]+	0.81	0.29
unsym-[μH-(FeIFeII)adt]0	0.98	0.15
unsym-[μH-(FeIFeII)adt-H]+	0.96	0.14

^aSee Figure 3 for definitions of Fe_p and Fe_d.

Previous studies also examined the metal oxidation states upon reduction of [μH-(Fe^IIFe^II)pdt]⁺ by analyzing the spin density with the BP86 functional and EPR spectra of the mixed-valence species.⁴¹ These studies showed that reduction of sym-[μH-(Fe^IIFe^II)pdt]⁺ resulted in a species with the unpaired electron delocalized between the Fe_p and Fe_d centers, sym-[μH-(Fe^1.5Fe^1.5)pdt]⁰. However, reduction of unsym-[μH-(Fe^IIFe^II)pdt]⁺ resulted in a species with the unpaired electron localized on the Fe_p center, unsym-[μH-(Fe^IFe^II)pdt]⁰. Our calculations revealed a similar trend with the bridging hydride species of the singly and doubly protonated [(FeFe)adt] (Table 6), although several important differences were observed.

In the singly protonated symmetric and unsymmetric [(FeFe)adt] bridging hydride species, sym-[μH-(Fe^IIFe^II)adt]⁺ and unsym-[μH-(Fe^IIFe^II)adt]⁺, the orientations of the dppv ligands on the two Fe centers dictate the overall symmetry of the system, as depicted in Figure 3. Furthermore, the hydride is located symmetrically between the two Fe centers in both isomers for the oxidized state. These distances are reported in Figure 5. Upon reduction, the bridging hydride is perturbed from this symmetric position. In the reduced unsymmetric bridging hydride species, the hydride is more closely bound to Fe_d (d_Fe···H = 1.58 Å) than to Fe_p (d_Fe···H = 2.05 Å) and resembles a terminal hydride. In the reduced symmetric bridging hydride species, the hydride is more symmetrically bound to the two iron centers (d_Fe···H = 1.60 Å for Fe_d and d_Fe···H = 1.77 Å for Fe_p). The observation that the reduction of sym-[μH-(Fe^IIFe^II)adt]⁺ maintains a more symmetric bridging hydride is consistent with the observation that the spin density is somewhat delocalized between the two Fe centers. In contrast, reduction of unsym-[μH-(Fe^IIFe^II)adt]⁺ leads to a much more asymmetric bridged hydride, and the spin density is localized on Fe_p, which does not have a bound hydride. Thus, unsym-[μH-(Fe^IIFe^II)adt]⁺ is similar to [tH-(Fe^IIFe^II)adt]⁺ in that reduction occurs at the Fe_p site, but reduction of unsym-[μH-(Fe^IIFe^II)adt]⁺ also involves motion of the bridged hydride toward the Fe_d site to resemble a terminal hydride. These observations are consistent with the observation that the terminal hydride species is reduced more easily (i.e., at a slightly less negative potential) than the unsymmetric bridging hydride species (Table 5).

Figure 5.

Bond lengths (Å) of symmetric and unsymmetric bridging hydrides. The bond lengths given without parentheses correspond to the oxidized species as drawn, while those given in parentheses correspond to the reduced mixed-valence species (not drawn). The spin densities of the reduced mixed-valence species are reported in Table 6.

The presence of the amine group in the azadithiolate bridgehead affects the degree of asymmetry observed upon reduction of the symmetric bridging hydride species. Although the bridging hydride is more symmetric in the sym-[μH-(Fe^IIFe^II)adt]⁺ species than in the unsym-[μH-(Fe^IIFe^II)adt]⁺ species, more asymmetry is exhibited in the sym-[μH-(Fe^IIFe^II)adt]⁺ than in the analogous sym-[μH-(Fe^IIFe^II)pdt]⁺ species. In the previous study of [(FeFe)pdt] bridging hydride species, reduction of sym-[μH-(Fe^IIFe^II)pdt]⁺ preserves the symmetry of the hydride position to a higher degree, with d_Fe···H = 1.68 Å and d_Fe···H = 1.70 Å for the Fe_p and Fe_d centers, respectively.⁴¹ We have confirmed these observations using the level of theory described within the present paper and various other basis sets. These results are given in the Supporting Information (Table S7). Moreover, these nearly symmetric Fe···H bond lengths are associated with nearly equal spin densities on the two Fe centers. As shown in Figure 5 and Table 6, the reduced symmetric protonated [(FeFe)adt] system, sym-[μH-(Fe^1.5Fe^1.5)adt]⁰, exhibits more asymmetry in these Fe···H bond lengths and unequal delocalized spin densities on the two Fe centers.

The reduction of the doubly protonated bridging hydride species, unsym-[μH-(Fe^IIFe^II)adt-H]²⁺ and sym-[μH-(Fe^IIFe^II)adt-H]²⁺, follows a similar trend but displays a slightly smaller degree of delocalization of the spin density, as shown in Table 6. According to the distances given in Figure 5, the asymmetry of the bridging hydride is slightly more pronounced in both the symmetric and unsymmetric forms for the doubly protonated species. Thus, reduction is expected to occur primarily at the nonhydride Fe_p center, as supported by the unpaired spin densities given in Table 6. This pattern for the electron localization is also seen in doubly protonated terminal hydride species, which will be discussed below.

D. Analysis of the Protonation Scheme and ΔpK_a

Previous experiments on the [(FeFe)adt] system estimated a small difference in the pK_a of the first and second protonation steps (ΔpK_a ≈ −2);³⁸ however, our calculated values indicated much larger differences, as seen from ΔpK_a(P4 – P2) in Table 7. This discrepancy between experiment and theory prompted a reinvestigation of the acid–base chemistry of the [(FeFe)adt] species. The pK_a values can be estimated by NMR measurements because each protonated species displays a unique ³¹P NMR spectrum. The experimental details and spectra are provided in the Supporting Information (Figures S12 and S13). According to these experiments, the protonation reactions leading to the formation of [(Fe^IFe^I)adt-H]⁺, [tH-(Fe^IIFe^II)adt]⁺, and [tH-(Fe^IIFe^II)adt-H]²⁺, defined as P1, P2, and P4 in Figure 3, correspond to pK_a values of >14.2, ∼15.5, and ∼6, respectively.

Table 7. Experimental and Calculated ΔpK_a Values^a.

		calcd
		CH2Cl2		CH3CN
	exptb	233.15 K	298.15 K	233.15 K	298.15 K
ΔpKa(P2 – P1)	>1.3	6	5	5	4
ΔpKa(P4 – P2)	–9.5	–18	–14	–12	–10
ΔpKa(P3 – P2)	>2.0	8	6	5	4

^aThe protonation pathways P1, P2, P3, and P4 are defined in Figure 3, and the pK_a is determined for the protonated species in each case.

^bThese experiments were performed in CH₂Cl₂ solvent, but the reference pK_a values pertain to CH₃CN solvent.

For reasons discussed in the Methods section, we calculated only the relative pK_a values for these species. This procedure accounts for systematic errors associated with the selected theoretical method and avoids the determination of the free energy of the solvated proton because this term cancels. Note that the experimentally measured values are only qualitatively meaningful because the experiments were performed in CH₂Cl₂, which does not have a well-defined pK_a scale, and the reference pK_a values of the acids pertain to CH₃CN. As a result, we calculated the relative pK_a values in both CH₂Cl₂ and CH₃CN. Additionally, the effects of homoconjugation in these experiments may distort the apparent pK_a measured. As discussed above in the context of comparing the crystal structure and optimized geometries, the impact of ion pairing is significant for the doubly protonated species. Furthermore, it has been shown experimentally that ion pairing between the BF₄^– counterion and the ammonium center can shift the equilibrium of the singly protonated species toward [(Fe^IFe^I)adt-H]⁺.³⁸

The experimental and calculated ΔpK_a values for these species are given in Table 7. The experimental ΔpK_a(P2 – P1) value indicates that the Fe_d site is more basic than the amine by at least ∼1.3 pK_a units; however, the amine is more readily protonated than the stereochemically crowded Fe site. The greater basicity of the Fe_d site than the amine is corroborated by our calculated ΔpK_a(P2 – P1) value of ∼6 in CH₂Cl₂. The large, negative ΔpK_a(P4 – P2) value measured experimentally indicates that N-protonation of [tH-(Fe^IIFe^II)adt]⁺ to form [tH-(Fe^IIFe^II)adt-H]²⁺ requires much stronger acids, as supported by our calculated large, negative ΔpK_a(P4 – P2). Note that this experimentally measured value of ΔpK_a(P4 – P2) is significantly more negative than the previously measured value.³⁸ Again, it is worth noting that the presence of the BF₄^– ions in the experiments may contribute to the remaining discrepancy between theory and experiment. Moreover, the theoretical calculation of pK_a differences for species with different charges (i.e., +2 and +1 for the doubly and singly protonated species) is more challenging. Turning our attention to the bridging hydride isomers, previous experiments have suggested that the conversion to the bridging hydride isomers is irreversible, and the bridging hydride is estimated to be at least ∼2 pK_a units less acidic than the terminal hydride.^35,38 This observation is supported by the large, positive calculated ΔpK_a (P3–P2) value and the thermodynamic stability of the bridging hydride isomers. These ΔpK_a trends are reproducible using different functionals, as indicated by additional data provided in the Supporting Information (Table S8).

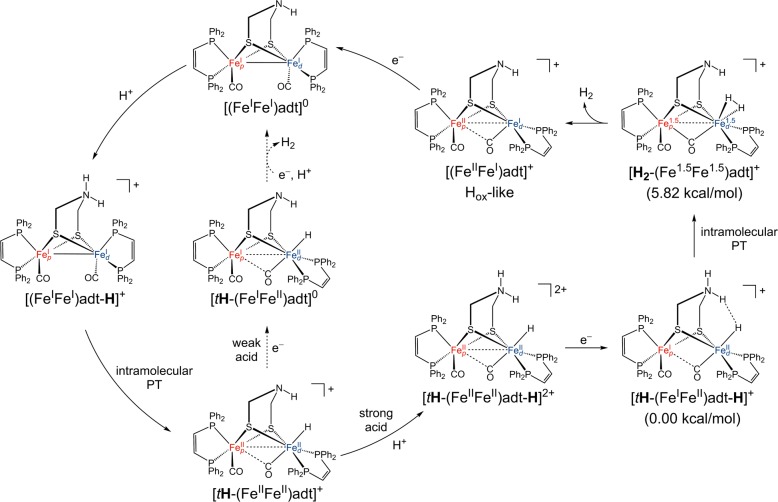
E. Analysis of the H₂ Evolution Mechanism

The proposed mechanisms for hydrogen evolution catalyzed by the [(FeFe)adt] system for weak and strong acids are depicted in Figure 6. Initially, the amine group on [(Fe^IFe^I)adt]⁰ is protonated to form the ammonium tautomer, [(Fe^IFe^I)adt-H]⁺. An intramolecular proton transfer occurs from the N to the Fe_d to form the terminal hydride, [tH-(Fe^IIFe^II)adt]⁺. For weak acids, the terminal hydride species, [tH-(Fe^IIFe^II)adt]⁺, is reduced prior to subsequent protonation and reduction to evolve H₂. This pathway is shown in dotted lines in Figure 6. For stronger acids, the intramolecular proton transfer is followed by another protonation at the amine group to generate [tH-(Fe^IIFe^II)adt-H]²⁺. Reduction of this doubly protonated species then evolves H₂. A possible mechanism for this process is indicated with solid lines on the right side of Figure 6. The values for the spin densities and bond distances for the species associated with this pathway are given in Table 8.

Figure 6.

Possible mechanisms for H₂ production with strong or weak acids. The steps indicated with solid lines along the perimeter represent the proposed pathway discussed in the main text. The steps indicated with dotted lines represent the pathway with a weak acid.

Table 8. Spin Densities and Bond Lengths of Doubly Protonated Species, Reduced Doubly Protonated Species, H₂ Adduct Intermediate, and H_ox-like Species^a.

species	ρ(Fep)	ρ(Fed)	Fep···Fed	Fed···H	H···H	Fep···CO	Fed···CO
[tH-(FeIIFeII)adt-H]2+	0.00	0.00	2.65	1.53	1.40	2.50	1.78
[tH-(FeIFeII)adt-H]+	1.02	0.05	3.03	1.56	1.30	2.84	1.78
[H2-(Fe1.5Fe1.5)adt]+	0.43	0.45	2.69	1.75b	0.79	2.06	1.89
[(FeIIFeI)adt]+	0.03	1.11	2.59	c	c	2.51	1.78

^aBond lengths given in Å. See Figure 6 for definitions of Fe_p and Fe_d.

^bThis bond length is the average of the two Fe_d···H distances.

^cNot applicable because the hydrogen is not present for this species.

Our calculations indicate that reduction of [tH-(Fe^IIFe^II)adt-H]²⁺ leads to the mixed-valence complex, [tH-(Fe^IFe^II)adt-H]⁺. The spin densities and bond distances of this species are given in Table 8. This mixed-valence species is characterized by the unpaired electron localized on the Fe_p center, which is in agreement with the reduction scheme exhibited by the [tH-(Fe^IIFe^II)adt]⁺ and [tH-(Fe^IIFe^II)pdt]⁺ species discussed previously. The NH···HFe distance is shorter in [tH-(Fe^IFe^II)adt-H]⁺ (d_H···H = 1.30 Å) than in [tH-(Fe^IIFe^II)adt-H]²⁺ (d_H···H = 1.40 Å) but is still larger than the distance in molecular H₂ (d_H···H = 0.74 Å). Although we were unable to locate a minimum-energy species with H₂ weakly bound to an Fe_d(I) center, we found another type of H₂ adduct intermediate with the unpaired electron delocalized between the Fe_p and Fe_d metal centers. This H₂ adduct, [H₂-(Fe^1.5Fe^1.5)adt]⁺, is higher in free energy than the mixed-valence doubly protonated species, [tH-(Fe^IFe^II)adt-H]⁺, by 5.82 kcal/mol but has several features that are potentially catalytically relevant, as will be discussed below. Note that previous theoretical studies on small models of the [FeFe]-hydrogenase active site found that reduction of a doubly protonated Fe_p(II)Fe_d(II) species could lead to the formation of a stable mixed-valence H₂ adduct intermediate, Fe_p(I)Fe_d(II), where the Fe_p center is the site of reduction and the H₂ ligand is loosely bound to the Fe_d(II) center.^8,19 These mixed-valence intermediates are similar to the [tH-(Fe^IFe^II)adt-H]⁺ species found herein; however, the [H₂-(Fe^1.5Fe^1.5)adt]⁺ species was not found in these previous studies.

In contrast to the [tH-(Fe^IFe^II)adt-H]⁺ species, the [H₂-(Fe^1.5Fe^1.5)adt]⁺ species features a much shorter NH···HFe distance (d_H···H = 0.79 Å), suggesting an activated H₂ molecule. In conjunction with the activated H₂ bond distance, the average distance between each hydrogen and the Fe_d center is elongated (d_Fe···H = 1.75 Å), suggesting that the H₂ ligand is weakly bound to the Fe_d center and poised for release. Another important structural feature is that unlike all terminal hydride species reported in the present paper, the semibridging CO ligand in this H₂ adduct is nearly symmetrically bridged between the Fe_p and Fe_d centers, where d_Fe···CO= 2.06 and 1.89 Å, respectively. The Fe_p···Fe_d distance contracts (d_Fe···Fe = 2.69 Å) to accommodate this bridging interaction. This structural property is reminiscent of the enzyme’s H_ox state, which features a nearly symmetrically bridged CO ligand (Figure 1). Moreover, the spin density is now delocalized between the Fe_p and Fe_d center, 0.43 and 0.45, respectively, warranting the [H₂-(Fe^1.5Fe^1.5)adt]⁺ assignment. This delocalization of the spin density suggests the possibility for intramolecular electron transfer to occur between the Fe_p and Fe_d centers concomitant with formation of a shorter H₂ bond. Note that the proposed mechanism in Figure 6 is similar to mechanisms proposed previously for [FeFe]-hydrogenases in terms of the reduction and protonation steps.^8,13−15,21 Our objective is to characterize the proposed intermediates and to analyze aspects such as dihydrogen bonding and electron delocalization or localization with respect to the metal centers.

Release of H₂ from [H₂-(Fe^1.5Fe^1.5)adt]⁺ would generate another mixed-valence state, the [(Fe^IIFe^I)adt]⁺ species shown in Figure 6. This mixed-valence species is closely related to the H_ox state of the enzyme shown in Figure 1. Interestingly, the spin densities for this species, which are given in Table 8, indicate Fe oxidation states that are opposite to the various other mixed-valence species discussed in this paper. Whereas the spin density was localized on the Fe_p center for the other purely mixed-valence species, such as [tH-(Fe^IFe^II)adt]⁰ and [tH-(Fe^IFe^II)adt-H]⁺, this H_ox-like species has the spin density entirely localized on the Fe_d center, suggesting that the Fe_d center is now more reduced than the Fe_p center. Upon formation of this [(Fe^IIFe^I)adt]⁺ species, the bridging CO ligand returns to the original asymmetric semibridging position. This analysis of the mechanism points to the importance of the bridging CO ligand, which seemingly behaves as a lever and indicator for intramolecular electron transfer between the Fe centers. Moreover, there is 0.16 spin density localized on the symmetric bridging CO ligand in the [H₂-(Fe^1.5Fe^1.5)adt]⁺ species, suggesting that it may be even more involved in the electron transfer process.

IV. Concluding Remarks

In this paper, we investigated a proton reduction catalyst, [(FeFe)adt], which is modeled after the [FeFe]-hydrogenase enzyme. This model is characterized by incorporation of the azadithiolate bridge, which facilitates the formation of a doubly protonated species through a proton relay. The calculated results agree well with the experimental data for the geometries, CO vibrational stretching frequencies, and reduction potentials for the systems studied. This agreement provides validation for the computational methods. The calculations illustrate that the NH···HFe dihydrogen bonding distance in the doubly protonated species is highly sensitive to the effects of ion-pairing between the ammonium and BF₄^– counterions, which are present in the crystal structure. Specifically, the inclusion of BF₄^– counterions leads to a significantly longer dihydrogen bond. Comparable weak interactions with the protein backbone might be expected to influence the H···H bonding in the enzyme. Analyses of spin densities provide insight into the oxidation states of the metal centers for the reduced singly and doubly protonated species. The non-hydride Fe center (Fe_p) was found to be the site of reduction for terminal hydride species and for unsymmetric bridging hydride species. In contrast, the reduced symmetric bridging hydride species exhibited a significant degree of spin delocalization between the Fe centers, although these species exhibited more asymmetry than the analogous [(FeFe)pdt] species. These differences in the degree of spin localization, as well as the movement of the hydride upon reduction of the unsymmetric bridging species, may be related to the experimental observation that the terminal hydride species are reduced at less negative potentials than their bridging hydride isomers.^35,41,78 This analysis suggests that the bridging hydrides may be considered to be quasi-terminal hydrides for the unsymmetric species.

A combined experimental and theoretical study of the relative pK_a values for the various species in the catalytic cycle provides further insights. The Fe_d site was found to be more basic than the amine, although the amine is more readily protonated. Moreover, the bridging hydride species was found to be more thermodynamically stable than the terminal hydride species. These observations are consistent with the initial protonation of the amine, followed by intramolecular proton transfer to the Fe_d site to produce a terminal hydride species, followed by isomerization to the bridging hydride species at room temperature but not at low temperatures. In terms of forming the doubly protonated species, the amine site is significantly less basic for the terminal hydride species than for the unprotonated species. Both the experimental and theoretical data indicate that a stronger acid is required for this second protonation.

In addition, these calculations implicate a possible pathway for H₂ evolution that involves an intermediate with H₂ weakly bonded to one Fe, a short H₂ distance similar to the molecular bond length, the spin density delocalized over the two Fe centers, and a nearly symmetrically bridged CO ligand. The short H₂ distance implies that the Fe–H₂ bonding is relatively weak and that the product H₂ is poised for release. Upon H₂ release, the mixed-valence species produced is closely related to the H_ox state of the enzyme. The key features of this proposed mechanism highlight the roles of the ammonium-hydride interaction, flexibility of the bridging CO ligand, and intramolecular electron transfer between the Fe centers in the catalytic cycle. While these bioinspired models are effective catalysts for H₂ production, the challenge of designing molecular electrocatalysts that can perform with weaker acids and lower overpotentials remains.¹ Further investigation of the effects of ligand substitution at the Fe centers will help guide the design of more effective H₂-producing catalysts.

Supporting Information Available

Details of experimental methods, ³¹P NMR, ¹H NMR, and FT-IR spectra of the species studied, experimental measurement of pK_a, relative free energies of all protonated [(FeFe)adt] species, protonation scheme, Δν_CO, and spin densities of [(FeFe)pdt] species, comparison of crystal structures and DFT optimized structures, expanded version of Table 5, ΔpK_a values calculated using different levels of theory and solvents, and coordinates of optimized structures. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Present Address

^† W.W.: School of Chemistry and Chemical Engineering, Shandong University, Jinan 250100, China.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States