Patient No-Show Predictive Model Development using Multiple Data Sources for an Effective Overbooking Approach

Summary

Background

Patient no-shows in outpatient delivery systems remain problematic. The negative impacts include underutilized medical resources, increased healthcare costs, decreased access to care, and reduced clinic efficiency and provider productivity.

Objective

To develop an evidence-based predictive model for patient no-shows, and thus improve overbooking approaches in outpatient settings to reduce the negative impact of no-shows.

Methods

Ten years of retrospective data were extracted from a scheduling system and an electronic health record system from a single general pediatrics clinic, consisting of 7,988 distinct patients and 104,799 visits along with variables regarding appointment characteristics, patient demographics, and insurance information. Descriptive statistics were used to explore the impact of variables on show or no-show status. Logistic regression was used to develop a no-show predictive model, which was then used to construct an algorithm to determine the no-show threshold that calculates a predicted show/no-show status. This approach aims to overbook an appointment where a scheduled patient is predicted to be a no-show. The approach was compared with two commonly-used overbooking approaches to demonstrate the effectiveness in terms of patient wait time, physician idle time, overtime and total cost.

Results

From the training dataset, the optimal error rate is 10.6% with a no-show threshold being 0.74. This threshold successfully predicts the validation dataset with an error rate of 13.9%. The proposed overbooking approach demonstrated a significant reduction of at least 6% on patient waiting, 27% on overtime, and 3% on total costs compared to other common flat-overbooking methods.

Conclusions

This paper demonstrates an alternative way to accommodate overbooking, accounting for the prediction of an individual patient’s show/no-show status. The predictive no-show model leads to a dynamic overbooking policy that could improve patient waiting, overtime, and total costs in a clinic day while maintaining a full scheduling capacity.

1. Background

The problem of a patient “no-show” in outpatient delivery systems has long been a recognized issue. A no-show is defined as occurring when a patient does not arrive for a previously scheduled clinic appointment, or cancels with such minimal lead time that the slot cannot be filled. The negative impacts of no-shows include underutilized medical resources, increased healthcare costs, decreased access to care, and reduced clinic efficiency and provider productivity. These anticipated but unpredictable idle times for physicians and support staff are often unrecoverable. A no-show can also deprive other patients from being seen, even when a ‘last minute’ opening is created. Hence, developing solutions to reduce clinic idle times resulting from no-shows is important for improving the efficiency and accessibility of health-care delivery systems, especially in primary care settings.

Prior studies have reported no-show rates generally ranging from 10% to 30%, although much variation exists depending on the clinic, location, and provider specialty [1–5]. Primary care general pediatric clinics are among those that tend to have the most no-shows [6]. While much effort has been made to reduce the rate of no-shows such as reminder letters [7], telephone calls [8, 9], text messages [10, 11] and even disincentives such as missed appointment fees [12] or termination of care [13], the problem continues for many clinics.

Various scheduling methods have attempted to reduce the negative impact of patient no-shows [14–19]. One of the solutions, called ‘open access’ uses the philosophy of “doing today’s work today” [20–25]. Rather than advanced scheduling, patients make appointments on the day of, or just a few days before, the desired visit. This approach seems to reduce no-show rates, but can create problems when demand on a specific day exceeds the supply of available openings. Research has demonstrated that open access works best when the patient load is relatively low [24] and found it is often difficult to achieve same-day access [26, 27].

Therefore, some have suggested that overbooking is a better general approach than open access [28] and could reduce physician idle time, and increase availability for patients as well as revenue for healthcare providers [29–32]. Overbook appointments, where more than one patient is scheduled at the same time slot, is a common solution to accommodate patient no-shows, and is often used for sustaining clinical productivity and ensuring provider availability despite the missed appointments [33]. This is similar to how airlines handle flight reservations, but also suffers from the airline industry problems that can occur when more than one person arrives for the same seat, referred to as a scheduling ‘collision’. But unlike airlines, clinics cannot ‘bump’ patients from their appointments; when clinic collisions occur waiting times often increase, affecting all downstream appointments. In general, clinic overbooking is done ‘blindly’, without consideration for when a no-show is likely to occur. It follows that a more robust process should consider overbooking a patient when the originally scheduled patient is highly likely to be a no-show. Indeed, airlines overbook flights at different rates depending on historic data of no-shows for specific routes and times [34].

Various approaches have been proposed that consider patient no-show rates to overbook appointment slots. However, these approaches have done little to address the issue of collisions. An early approach estimated the number of patients arriving to a clinic based on the average no-show rate, which did not take into account individual patients’ no-show probabilities [35]. Others have focused on minimizing the total cost including patient wait time, physician idle time, and overtime [30–32, 36], but did not include the likelihood of individual patient’s no-show rates when designing the scheduling schemes. Some approaches used the patient no-show rates to develop an ‘optimal’ scheduling sequence (e.g., all sick visits in the morning and all well visits in the afternoon) that either minimized costs or maximized profit [17, 37, 38]. Other researchers adopted the individual no-show probability to identify overbooking criterion, using a no-show threshold, by minimizing estimated costs [29, 39]. Despite these efforts, no-shows remain difficult to predict, and it is difficult to adjust patient arrivals once they are scheduled. Hence, it remains important to accurately predict the likelihood of individual patient no-shows.

One of the key tasks of building an accurate no-show predictive model is to study the contributing factors. Prior work has shown that factors can include gender, age [40, 41], social factors [42], patient perceptions of medical providers, direct patient costs, distance to the clinic, a lack of a personal relationship with the physicians [6], adherence to physician visits [43], the perception of long waiting times [44], the delay in scheduling appointments [45], the long lead time from scheduling date to appointment date [46], and the provider’s specialty [6]. Others estimated the no-show rate based on factors, such as purpose of visit, day of the week, and age using data mining techniques [47, 48] or logistic regression modeling [49, 50] and developed a predictive model for the probability of no-shows for groups of patients that shared common attributes, often in an attempt to minimize costs rather than predicting errors.

2. Objectives

The purpose of our study was to determine if it is possible to predict with reasonable accuracy when a patient is likely to no-show. Using such predictions to overbook appointments at those specific times is one approach to reduce the negative impact of patient no-shows for improving access with the smallest risk of schedule “collisions”. The goals of this study, therefore, are to (1) develop a statistical model to predict a patient’s show/no-show status based on factors that generally should be available to most clinics such as demographics, time of year, and prior no show history; (2) conduct a validation of the predictive model to ensure the accuracy; and (3) provide a demonstration of how the predictive model could be used to overbook patients in a scheduling template. We also present an alternative way of defining the no-show threshold by minimizing the weighted misclassification on both Type I and Type II errors between the actual no-show status from the data and the predicted no-show status. This study approach is demonstrated using an empirical dataset of over 100,000 scheduled appointments from a general pediatrics clinic.

3. Methods

Herein we describe the clinical setting, the dataset used for the analysis, the development and validation of the no-show predictive model, and the overbooking approach comparison. The study was reviewed and approved by the University of Michigan Medical School Institutional Review Board (IRB). A waiver of informed consent was obtained because the analysis only involved retrospectively collected data, and no patient contact occurred.

3.1 Clinical Setting

The data were obtained from a single general pediatrics clinic in the city of Livonia, located in a sub-urban area about 30 miles away from its affiliated institution, University of Michigan. According to 2010 census data, the city where the clinic is located has a population of approximately 97,000 in an area encompassing 36 square miles. Public transportation (bus service) is available in some areas, but is very limited and most residents rely on cars. The population is 92.0% White, 3.4% African American, 2.5% Asian and 2.1% other races. The median yearly income is about $65,000.

At the time the study was conducted there were five physicians attending in the clinic but generally two to three were present each day. The clinic left openings for near-day or same-day acute care ‘sick’ visits with varying frequency depending on the time of year. The same day appointments allow urgent patients in need of medical attention to be seen promptly. It was common at the time for visit types to be scheduled in blocks; that is, a morning of all acute care visits and an afternoon of all well child visits. Generally up to two overbooks per provider were permitted each day, often at the discretion of the physician and scheduling clerks. For previously scheduled well child exams, computer generated letters were sent via the United States Postal Service to all families five days before a scheduled appointment, and clerks also personally called families with a reminder one day before appointments, although not all phone numbers were valid. Reminders were not provided for same-day, or near same-day, appointments.

3.2 Description of Data

All historic clinic scheduling data for a ten-year period were obtained from our scheduling system. Associated demographic and registration data were obtained from our homegrown electronic health record (EHR) that was implemented in 1998. Data elements were chosen based on their availability in the EHR and consensus development among the research and clinical care teams, including support staff. For example, distance to the clinic was included based on a perception that patients further away were more likely to no-show, especially during inclement weather. Driving distance, rounded to the nearest mile, was calculated between each patient’s household and the clinic using ArcGIS ArcMap Version 9.3 (Esri, Redlands, CA). Additionally, number in household was selected based on the perception that families with multiple children often seem to no-show due to the complicated logistics of handling the varied needs of the family members. This latter variable was estimated by extracting the number of individuals in our EHR that shared the same address as the patient.

The final dataset included 17 variables that most health care clinics routinely collect or could derive, grouped into three major categories: (1) appointment characteristics including visit type, time to appointment, appointment month, appointment weekday, appointment time, and the count of prior no-shows; (2) demographic information such as age, language, religion, race, gender, number in household, distance to the clinic, and county (with respect to the clinic); and (3) insurance information including primary insurance, main insurance holder, and total insurance carriers. For the purposes of our study we used a broad definition for a no-show which included true no-shows (wherein a patient does not show for an appointment and provides no warning) as well as any cancellation within one week of a scheduled appointment, since it is often difficult to fill those appointment slots with such short notice. Detailed definitions for each variable are summarized in ▶ Table 1.

Table 1.

Variable definitions and their significance and frequency in the training and validation datasets

Variable	p-value	Training data (n = 84,928)	Validation data (n = 19,871)
Appointment Characteristics
Visit type	< 0.0001
• New patient		1,129 (1.3%)	267 (1.3%)
• Return visit		56,426 (66.4%)	12,413 (62.5%)
• Newborn		1,558 (1.8%)	380 (1.9%)
• New patient – well child exam		946 (1.1%)	302 (1.5%)
• Return visit – well child exam		24,869 (29.3%)	6,509 (32.8%)
Time to appointment	< 0.0001
• 1 day		39,159 (46.1%)	7,255 (36.5%)
• 1–2 weeks		22,628 (26.6%)	5,764 (29.0%)
• More than 2 weeks		23,141 (27.2%)	6,852 (34.5%)
Appointment month	< 0.0001
• January		7,502 (8.8%)	1,682 (8.5%)
• February		7,458 (8.8%)	1,682 (8.5%)
• March		8,015 (9.4%)	1,904 (9.6%)
• April		7,068 (8.3%)	1,595 (8.0%)
• May		7,027 (8.3%)	1,607 (8.1%)
• June		6,451 (7.6%)	1,597 (8.0%)
• July		6,341 (7.5%)	1,420 (7.1%)
• August		7,089 (8.3%)	1,747 (8.8%)
• September		6,987 (8.2%)	1,622 (8.2%)
• October		7,485 (8.8%)	1,684 (8.5%)
• November		6,851 (8.1%)	1,688 (8.5%)
• December		6,654 (7.8%)	1,643 (8.3%)
Appointment weekday	< 0.0001
• Monday		19,396 (22.8%)	4,797 (24.1%)
• Tuesday		14,980 (17.6%)	3,716 (18.7%)
• Wednesday		16,196 (19.1%)	3,478 (17.5%)
• Thursday		14,847 (17.5%)	3,753 (18.9%)
• Friday		15,209 (17.9%)	3,076 (15.5%)
• Saturday		4,300 (5.1%)	1,051 (5.3%)
Appointment time	< 0.0001
• Morning		42,237 (49.7%)	9,547 (48.0%)
• Afternoon		42,691 (50.3%)	10,324 (52.0%)
Count of prior no-shows	< 0.0001
• No history (first visit)		7,114 (8.4%)	874 (4.4%)
• None		42,090 (49.6%)	7,255 (36.5%)
• Once		18,106 (21.3%)	4,757 (23.9%)
• Twice		8,703 (10.2%)	2,843 (14.3%)
• Three and four times		6,405 (7.5%)	2,612 (13.1%)
• Five times and more		2,510 (3.0%)	1,530 (7.7%)
Demographic information
Age	< 0.0001
• 18 months old		23,197 (27.3%)	5,089 (25.6%)
• 5 years old		20,255 (23.8%)	4,182 (21.0%)
• 10 years old		19,453 (22.9%)	4,761 (24.0%)
• More than 10 years old		22,023 (25.9%)	5,839 (29.4%)
County to clinic location	< 0.0001
• Inside		70,087 (82.5%)	16,272 (81.9%)
• Adjacent		14,477 (17.0%)	3,547 (17.9%)
• Other		364 (0.4%)	52 (0.3%)
Language	< 0.0001
• English		76,037 (89.5%)	19,054 (95.9%)
• Other		8,891 (10.5%)	817 (4.1%)
Religion	0.249
• Christian		44,917 (52.9%)	10,567 (53.2%)
• Other		40,011 (47.1%)	9,304 (46.8%)
Race	< 0.0001
• Asian		2,830 (3.3%)	595 (3.0%)
• African American		4,480 (5.3%)	1,246 (6.3%)
• Hispanic		831 (1.0%)	240 (1.2%)
• Caucasian		68,193 (80.3%)	16,160 (81.3%)
• Other		8,594 (10.1%)	1,630 (8.2%)
Gender	0.381
• Male		44,436 (52.3%)	10,197 (51.3%)
• Female		40,492 (47.7%)	9,674 (48.7%)
Number in household	≤ 0.0001
• <3		33,014 (38.9%)	7,901 (39.8%)
• 4–5		33,709 (39.7%)	7,898 (39.7%)
• >5		18,205 (21.4%)	4,072 (20.5%)
Distance to the clinic	< 0.0001
• < 5 miles		38,957 (45.9%)	9,839 (49.5%)
• 5 – 10 miles		35,016 (41.2%)	7,921 (39.9%)
• 10 – 20 miles		8,153 (9.6%)	1,729 (8.7%)
• > 20 miles		2,802 (3.3%)	382 (1.9%)
Insurance information
Primary insurance	< 0.0001
• Blue Cross/ Blue Shield		46,003 (54.2%)	12,524 (63.0%)
• Medicaid/ Medicare		4,001 (4.7%)	1,222 (6.1%)
• HMO		20,670 (24.3%)	3,857 (19.4%)
• Other insurance		14,254 (16.8%)	2,268 (11.4%)
Main insurance holder	< 0.0001
• Parents		67,514 (79.5%)	14,261 (71.8%)
• Spouse		305 (0.4%)	69 (0.3%)
• Grandparent/ Legal guardian		306 (0.4%)	43 (0.2%)
• Patient		16,562 (19.5%)	5,480 (27.6%)
• Other		241 (0.3%)	18 (0.1%)
Total insurance carriers	< 0.0001
• One		79,001 (93.0%)	18,329 (92.2%)
• More than one		5,927 (7.0%)	1,542 (7.8%)

The entire dataset included 7,988 distinct patients and 104,799 visits over a ten-year time period (January 2002 – December 2011). The overall dataset contained 11,737 (11.2%) appointments that were no-shows, whereas the final two years of the dataset contained 19,871 appointments with 2,784 (14.0%) no-shows. It is worth noting that the dataset represented an entire 10-year ‘snapshot’ of scheduling activities for the clinic, and thus many patients had return visits. The mean number of scheduled visits per patient was 13 and the median was 10, with a range of 1 to 94. Further, some of the variables selected for the predictive model were dependent upon prior data. For example, prior no-show history was determined for each appointment with the data that was available at the time of the appointment. Thus, the third appointment for a patient would include the two prior show/no-show outcomes in the model whereas the tenth appointment for a patient would include the nine prior show/no-show outcomes.

3.3 Predictive model development

We used eight years of data (2002 – 2009) as our training set to build our model, which was then validated against two years of data (2010 – 2011). Our primary outcome variable was the no-show status for each scheduled appointment. We first determined which of the 17 variables demonstrated the greatest influence on the no-show rate by performing likelihood ratio chi-square tests with significance level of α = 0.05 as the inclusion threshold. If the p-values (▶ Table 1) were less than α, the variables were considered as candidates for the predictive model. After determining the most significant factors, we used logistic regression to develop a predictive model for the binary outcome of whether each patient arrived or no-showed for their appointment. All analyses were conducted using the R Project for Statistical Computing, version 2.9.0.

3.4 Determination of optimal no-show threshold

From the predictive logistic regression model, a no-show probability for a visit can be calculated. However, in reality, a visit will have only two outcomes, either show or no-show, excluding other modifiers such as late shows. In order for us to translate the probability to a predicted show or no-show, a threshold needs to be determined in order to separate the two. No-show thresholds have been determined in prior work with the objective of minimizing the costs of patient wait time, physician idle time and overtime [29]. In this paper, an alternative method is presented to determine the threshold so that the error (misclassification) count is minimized.

Let p be the threshold of the show probability, p̂_i be the predicted show probability from the regression model for patient i, and M̂_i be the predicted show (1) or no-show (0) derived from the training dataset and applied to patient i. Hence,

Let M_i be the actual show (1) or no-show (0) from the training dataset for patient i, and E_i be the error of misclassified (1) and accurately-identified (0) for patient i. Therefore,

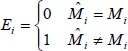Two types of error are considered here. A Type I error is when a patient is classified as a no-show when a patient’s actual status is a show. A Type II error is when a patient is classified as a show when the actual status is a no-show. In terms of ensuring greater patient satisfaction and avoiding scheduling “collisions”, we suggest that minimizing Type I errors is more critical than minimizing Type II errors. For these reasons, we assume that the c_no-show is less than c_show.

Let N_show be the total number of actual show patients in training dataset, N_no-show be the actual no-show patient population in training dataset; c_show is the cost of the Type I errors and c_no-show is the cost of the Type II errors. The Type I error probability can be presented as

and the Type II error probability is computed as

The goal is to determine a classification threshold that minimizes the weighted sum of Type I and Type II errors. Therefore, the objective function is to minimize

and obtain the optimal threshold p. This provides the assignment of either show or no-show to any given patient. Given these assumptions, we investigated two cost ratios, 2 and 3, to determine their impact on minimizing Type I errors at the expense of additional Type II errors.

3.5 Comparison of proposed overbooking approach to existing methods

There are various ways in which patient scheduling in a clinic can be modeled. [29, 51–52]. In this study, we adopted an overbooking model developed by Huang and Zuniga [29], and further adapted it with the addition of a prediction error rate. To demonstrate the effectiveness of the proposed overbooking approach (P), a comparison with two other approaches, random (R) and evenly-distributed (E) overbooking with a flat overbooking percentage, was conducted using simulation modeling techniques. The flat overbooking percentage is based on an average patient no-show rate and is used to overbook with the goal that the schedule, on average, will remain just at capacity [35, 53]. Random overbooking (R) allows for overbooking to occur at any point during the day without restrictions, and is one of the most commonly implemented approaches [29]. The evenly-distributed overbooking (E) approach spaces out the overbooked appointments at specific intervals during the day (e.g., 8:30 AM, 10:30 AM, 1:30 PM, 3:30 PM) to allow for a broad distribution of the overbooks throughout the entire day. This approach has been used to avoid patient congestion in the clinic [54] and has been shown to be cost-effective [18].

The performance measurements for the method comparisons are average patient wait time (W̅), average physician idle time (P̅), overtime at the end of day (O), and expected total cost (T). The expected total cost (T) consists of three elements: the cost of patient wait time, the cost of physician idle time, and the cost of overtime. In order to define costs, some assumptions of the unit cost are required. We assumed the cost of patient wait time is $10 per hour (c_w), the cost of physician idle time is $50 per hour (c_p), and the cost of overtime is 1.5 times that of physician idle time, or $75 per hour (c_o). The cost ratios between physician idle time and patient wait time have been reported to range widely (e.g., 1 to 100) depending on the specialty [31]. In our case, the chosen cost ratio is 5, which is expected to be reasonable for a general pediatric clinic. The total cost is calculated as: T=c_wW+c_pP+c_oO

The simulation was modeled using a Microsoft Excel macro function applied to a hypothetical physician’s daily clinic schedule using each of the three overbooking methods described above. For each method, 1600 replications were run. Additional assumptions in the model were that (1) all patients who arrived would do so on time; (2) all 30 schedule slots were 15 minutes long, with half in the morning and half in the afternoon; (3) inter-appointment time (e.g, time spent non-clinical activities) was not considered; and (4) only one overbook appointment was permitted for each time slot in which an overbook occurred. An example of such a daily schedule is displayed in ▶ Table 3. Variations in the actual length of appointment times were modeled using a Gamma distribution [29, 55-56] seeded with a random number generator, with a mean of 15 minutes and a standard deviation of 10 minutes. Random numbers were also used to vary the combinations of scheduling order and combinations of variables for each hypothetical patient in a daily schedule. The average no-show rate chosen for this modeling exercise was 14%. From the training data we also estimated the distribution of the predicted no-show rates for the predictive model using a right-skewed Gamma distribution, which is a common distribution found in scheduling scenarios [29]. A Goodness of Fit test with Anderson-Darling (AD) statistics was used to determine how well the training data fit a Gamma distribution, using a significance level of α = 0.05. This distribution was then modeled for the predictive no-show rates in our simulation.

Table 3.

An example of implementing overbooking for a clinic day at threshold of 0.74. Slots that have patients with a predicted show probability less than the threshold would be overbooked.

Appt Time	Age	Month of Year	Day	Time	Visit Type	Primary Insurance	Insurance Holder	Time to Appt	Total Insurance Carriers	County	Language	Race	Number in Household	Distance to Clinic	Prior No-show Count	Predicted Show Rate	Show/No-show Indicator	Overbook
8:00	18 months	Feb	Fri	AM	RV	HMO	Patient	1 day	1	Inside	English	Caucasian	<3	< 5 miles	1	0.95	1	No
8:15	5 years	Feb	Fri	AM	RV-WCE	BCBS	Parents	1 day	1	Inside	English	Other	<3	5–10 miles	0	0.99	0	No
8:30	10 years	Feb	Fri	AM	RV	Medicaid/ Medicare	Parents	> 2 weeks	1	Inside	English	African Amer ican	>5	5–10 miles	0	0.85	1	No
8:45	5 years	Feb	Fri	AM	RV-WCE	Other	Patient	>2 weeks	>1	Other	English	Caucasian	<3	> 20 miles	1	0.74	1	No
9:00	5 years	Feb	Fri	AM	RV	BCBS	Parents	1 day	1	Inside	English	Hispanic	>5	< 5 miles	3–4	0.97	1	No
9:15	10 years	Feb	Fri	AM	RV	HMO	Patient	>2 weeks	>1	Adjacent	English	Caucasian	>5	10–20 miles	0	0.71	0	Yes
9:30	> 10 years	Feb	Fri	AM	NP	BCBS	Parents	1 day	1	Inside	English	Caucasian	>5	5–10 miles	First Visit	0.97	0	No
9:45	18 months	Feb	Fri	AM	RV	BCBS	Parents	1 day	1	Adjacent	English	African Amer ican	4–5	10–20 miles	0	0.97	1	No
10:00	> 10 years	Feb	Fri	AM	RV	Medicaid/ Medicare	Grandparent/ Legal Guardian	1–2 week	1	Inside	Other	Caucasian	4–5	5–10 miles	3–4	0.86	1	No
10:15	18 months	Feb	Fri	AM	NP-WCE	HMO	Patient	>2 weeks	1	Inside	English	Caucasian	4–5	< 5 miles	First Visit	0.84	1	No
10:30	> 10 years	Feb	Fri	AM	RV	HMO	Parents	1 day	1	Inside	English	Other	4–5	< 5 miles	2	0.97	1	No
10:45	10 years	Feb	Fri	AM	RV	HMO	Patient	>2 weeks	1	Inside	English	Caucasian	4–5	5–10 miles	5+	0.61	0	Yes
11:00	5 years	Feb	Fri	AM	NP	BCBS	Spouse	1 day	1	Adjacent	English	Caucasian	4–5	10–20 miles	First Visit	0.97	1	No
11:15	5 years	Feb	Fri	AM	RV	BCBS	Parents	1 day	1	Inside	English	African Amer ican	>5	5–10 miles	2	0.95	1	No
11:30	10 years	Feb	Fri	AM	RV	BCBS	Parents	1 day	1	Inside	English	Caucasian	<3	< 5 miles	0	0.98	1	No
13:00	> 10 years	Feb	Fri	PM	NP-WCE	Medicaid/ Medicare	Grandparent/ Legal Guardian	1–2 weeks	1	Inside	English	Asian	<3	5–10 miles	First Visit	0.92	1	No
13:15	18 months	Feb	Fri	PM	RV	BCBS	Parents	1–2 weeks	1	Other	Other	Hispanic	4–5	> 20 miles	1	0.85	1	No
13:30	5 years	Feb	Fri	PM	RV-WCE	HMO	Patient	>2 weeks	>1	Inside	English	African Amer ican	4–5	5–10 miles	1	0.68	0	Yes
13:45	> 10 years	Feb	Fri	PM	RV	BCBS	Parents	1–2 weeks	1	Inside	English	Caucasian	4–5	5–10 miles	1	0.87	1	No
14:00	18 months	Feb	Fri	PM	NP	BCBS	Grandparent/ Legal Guardian	1 day	>1	Inside	English	Caucasian	4–5	5–10 miles	First Visit	0.98	1	No
14:15	> 10 years	Feb	Fri	PM	RV	BCBS	Parents	1–2 weeks	1	Inside	English	African Amer ican	>5	< 5 miles	5+	0.70	0	Yes
14:30	10 years	Feb	Fri	PM	RV-WCE	Other	Parents	1–2 weeks	1	Adjacent	English	Caucasian	>5	10–20 miles	1	0.91	1	No
14:45	5 years	Feb	Fri	PM	RV	BCBS	Parents	1–2 weeks	1	Inside	English	Caucasian	>5	< 5 miles	1	0.89	1	No
15:00	5 years	Feb	Fri	PM	RV	BCBS	Spouse	1 day	1	Inside	English	Caucasian	>5	< 5 miles	0	0.97	1	No
15:15	10 years	Feb	Fri	PM	RV	HMO	Parents	1–2 weeks	1	Inside	English	African Amer ican	>5	5–10 miles	1	0.81	1	No
15:30	> 10 years	Feb	Fri	PM	RV-WCE	BCBS	Parents	1–2 weeks	1	Inside	English	Caucasian	>5	< 5 miles	1	0.92	1	No
15:45	18 months	Feb	Fri	PM	RV	BCBS	Parents	1–2 weeks	1	Adjacent	English	Caucasian	4–5	> 20 miles	1	0.87	1	No
16:00	> 10 years	Feb	Fri	PM	NP	Other	Patient	1–2 weeks	1	Inside	English	Caucasian	>5	< 5 miles	First Visit	0.80	1	No
16:15	5 years	Feb	Fri	PM	RV-WCE	BCBS	Parents	1–2 weeks	1	Other	Other	Other	4–5	> 20 miles	1	0.90	1	No
16:30	> 10 years	Feb	Fri	PM	RV	BCBS	Parents	1 day	1	Inside	Other	Asian	4–5	5–10 miles	0	0.97	1	No

RV: return visit; WCE: well child exam; NP: new patient; HMO: health maintenance organization; BCBS: blue cross/blue shield

The performance of the three overbooking approaches were compared to each other using an analysis of variance (ANOVA) test with α = 0.05. ANOVA tests were run for each of the performance measures of wait time, physician idle time, overtime, and the total costs. We used 95% confidence intervals as a post hoc comparison rather than multiple comparison methods.

4. Results

4.1 Influence of variables

The Chi-square test results showed that gender and religion did not significantly impact the status of a no-show for a scheduled appointment and these were pruned from our model. The full logistic regression model was then built from the 15 remaining variables using the training dataset (▶ Table 2). ▶ Figure 1 displays a graphical presentation of the odd ratios (ORs) for each of the variables. The ORs provide an intuitive way to interpret the influence of each of the variables in predicting the likelihood of a patient showing up for a visit. In this case, ORs significantly different from and higher than 1 predict a greater likelihood of showing for a visit compared to the reference, whereas those significantly different and less than 1 predict a lower likelihood of showing for a visit. For example, patients coming to a newborn visit were more likely to show compared to all other visit encounter types. Additionally, children and adolescents greater than 10 years old were less likely to show for their visits compared to all of the younger age group categories. Prior no-show history also proved to be a significant predictive factor: those with 5 or more no-shows were least likely to show for a visit, followed by those with 3–4 prior no-shows.

Table 2.

Logistic regression model to predict the patient show rate. Each level for the categorical variables is assigned the values of either 0 or 1. The reference levels are chosen by the R software. The coefficients represent the relative ratio to the reference level.

Reference level in ()	Coefficient (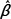)	Odds ratio (e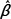)	Odds ratio 95% CI	p value
Intercept	1.77879			< 0.0001
Visit type (Newborn)
• Return visit	-0.98053	0.38	[0.28, 0.49]	< 0.0001
• New patient	-1.17604	0.31	[0.22, 0.43]	< 0.0001
• New patient – well child exam	-0.98053	0.38	[0.27, 0.52]	< 0.0001
• Return visit – well child exam	-0.45971	0.63	[0.47, 0.83]	0.0014
Time to appointment (1–2 weeks)
• 1 day	1.38889	4.01	[3.76, 4.28]	< 0.0001
• More than 2 weeks	-0.41509	0.66	[0.62, 0.71]	< 0.0001
Appointment month (April)
• January	0.11690	1.12	[1.00, 1.26]	0.0458
• February	0.13061	1.14	[1.01, 1.28]	0.0279
• March	-0.30591	0.74	[0.66, 0.82]	< 0.0001
• May	0.06925	1.07	[0.96, 1.20]	0.2296
• June	0.06681	1.07	[0.95, 1.20]	0.2547
• July	0.21308	1.24	[1.10, 1.39]	0.0004
• August	0.24301	1.28	[1.14, 1.43]	< 0.0001
• September	0.06525	1.07	[0.96, 1.19]	0.2502
• October	0.16892	1.18	[1.06, 1.33]	0.0033
• November	0.31265	1.37	[1.21, 1.54]	< 0.0001
• December	0.01766	1.02	[0.91, 1.14]	0.7640
Appointment weekday (Friday)
• Monday	0.10703	1.11	[1.03, 1.20]	0.0012
• Tuesday	0.09383	1.10	[1.02, 1.19]	0.0164
• Wednesday	0.05991	1.06	[0.99, 1.14]	0.1104
• Thursday	0.11382	1.12	[1.04, 1.21]	0.0033
• Saturday	0.24379	1.28	[1.10, 1.48]	0.0012
Appointment time (Morning)
• Afternoon	-0.14898	0.86	[0.82, 0.90]	< 0.0001
Count of prior no-shows (3 – 4 times)
• No history (first visit)	0.74934	2.12	[1.85, 2.42]	< 0.0001
• None	0.56375	1.76	[1.62, 1.91]	< 0.0001
• Once	0.21910	1.24	[1.14, 1.36]	< 0.0001
• Twice	0.14005	1.15	[1.04, 1.27]	0.0060
• 5 times or more	-0.33250	0.72	[0.63, 0.82]	< 0.0001
Age (more than 10 years old)
• 18 months old	0.24324	1.28	[1.19, 1.36]	< 0.0001
• 5 years old	0.19334	1.21	[1.14, 1.30]	< 0.0001
• 10 years old	0.18773	1.21	[1.13, 1.29]	< 0.0001
County to clinic location (Adjacent)
• Inside	0.03018	1.03	[0.97, 1.10]	0.3559
• Other	-0.00358	1.00	[0.74, 1.36]	0.9817
Language (English)
• Other	-0.17018	0.84	[0.74, 0.96]	0.0118
Race (African American)
• Asian	0.38749	1.47	[1.25, 1.75]	< 0.0001
• Hispanic	0.45747	1.58	[1.24, 2.03]	0.0003
• Caucasian	0.45925	1.58	[1.45, 1.73]	< 0.0001
• Other	0.43606	1.55	[1.33, 1.80]	< 0.0001
Distance to the clinic (10 – 20 miles)
• < 5 miles	0.21790	1.24	[1.15, 1.35]	< 0.0001
• 5 -10 miles	0.11418	1.12	[1.04, 1.21]	0.0045
• > 20 miles	-0.08125	0.92	[0.80, 1.06]	0.2453
Number in household (>5)
• ≤3	0.05776	1.06	[1.00, 1.13]	0.0683
• 4-5	0.10051	1.11	[1.04, 1.18]	0.0016
Primary insurance (BCBS)
• Medicaid/ Medicare	0.16248	1.18	[1.03, 1.34]	0.0155
• HMO	-0.03024	0.97	[0.90, 1.04]	0.4112
• Other insurance	-0.05279	0.95	[0.89, 1.02]	0.1279
Main insurance holder (Grandparents/ Legal guardian)
• Parents	-0.38714	0.68	[0.42, 1.04]	0.0937
• Spouse	-0.25427	0.78	[0.42, 1.43]	0.4185
• Patient	-0.77952	0.46	[0.28, 0.71]	0.0009
• Other	-0.27669	0.76	[0.40, 1.45]	0.3994
Total insurance carriers (more than one)
• One	0.16962	1.18	[1.08, 1.29]	0.0002

Fig. 1.

The relative ratio to the reference level for all 15 variables included in the logistic regression model

4.2 Practical application of the predictive no-show model

To demonstrate the practical use of this model from ▶ Table 2, let r̂ be the show probability, with the logistic regression model generalized as the following:

log[r̂/(1-r̂)]=1.77879 + (Visit type) + (Age) + (County to clinic location) + (Distance to the clinic) + (Appointment time) + (Appointment weekday) + (Appointment month) + (Time to appointment) + (Race) + (Language) + (Total insurance carriers) + (Primary insurance) + (Main insurance holder) + (Number in household) + (Count of prior no shows).

Then input the coefficient (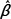) of the level selected for each factor and calculate r̂. If the selected level is the reference level, then the coefficient is zero. Assume a patient is scheduled as a return visit patient for a well-child exam ( 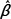= –0.45971), at the age of 18 years old (more than 10 years old, 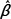= 0), from the same county as the clinic (Inside, 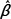= 0.03018) and driving distance from the clinic is between 5 to 10 miles ( 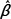= 0.11418). An afternoon appointment ( 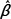= –0.14898) is scheduled on a Wednesday ( 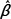= 0.05991) in March ( 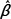= –0.30591) 5 hours ahead (1 day for time to appointment, 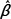= 1.38889). The patient is a Caucasian ( 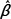= 0.45925) and speaks English ( 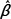= 0), who only has a primary insurance ( 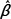= 0.16962) with HMO ( 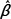= –0.03024) under her parents ( 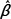= –0.38714) and has a total of four people (4–5, 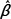= 0.10051) in her household with no prior no-shows on record ( 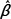= 0.56375). The calculation of the show rate for this patient is therefore the following:

log[ r̂ /(1– r̂)]=1.77879 – 0.45971 + 0 + 0.03018 + 0.11418 – 0.14898 + 0.05991 – 0.30591 + 1.38889 + 0.45925 + 0 + 0.16962 – 0.03024 – 0.38714 + 0.10051 + 0.56375 = 3.3331.

Thus, r̂ /(1– r̂) = e3^.3331 = 28.03 → r̂ = 28.03 × (1- r̂) → r̂ = 0.97 , which results in a show probability of 0.97. Conversely, the no-show probability is (1 – show probability), or 0.03 (3% no-show probability).

A hypothetical scenario in which the no-show probability is near the maximum predicted by the model contains the following elements: An fifteen year-old, English-speaking African American adolescent, with 6 people in her household and a history of five prior no-shows to the clinic. She made the appointment about two months in advance for a routine return visit, scheduled for a Friday afternoon in March. She lives in a county that is adjacent to the county in which the clinic resides, about 22 miles away. She has more than one insurance carrier, but her primary insurance is HMO under herself. The patient in this specific scenario has a predicted no-show probability of 79% for the appointment. This scenario, and others, can be worked out using the interactive, spreadsheet calculator (available as an online supplemental file).

4.3 No-show threshold determination and validation

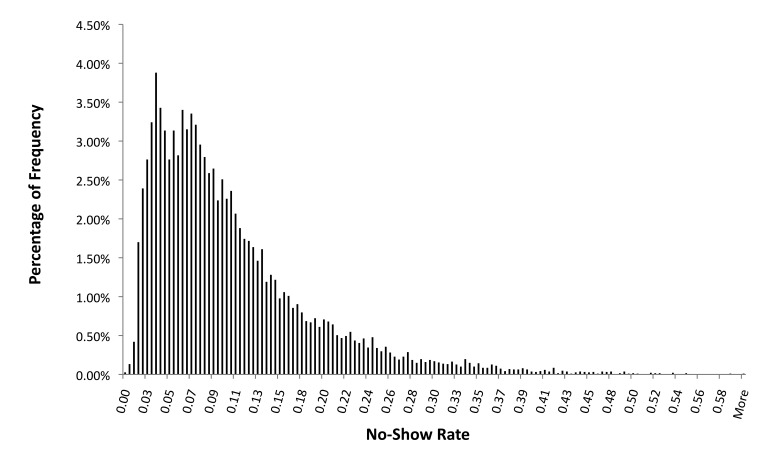
The results of the analysis determining the two cost ratios (2 and 3) for the Type I and Type II errors are shown in ▶ Figure 2. Given a cost ratio of 2, the weighted sum of Type I and Type II error is minimized at the threshold (p) of 0.86. For cost ratio of 3, the threshold (p) is at 0.74. This means that based on the training dataset, at cost ratio of 2, if the probability of show rate for a patient’s visit is calculated to be greater than or equal to 0.86, this visit is classified to be a “show” visit. This results in a Type I error of 11.3% and a Type II error of 68.1 %. For the cost ratio of 3, if the probability of show rate for a patient’s visit is calculated to be greater than or equal to 0.74, this visit is classified to be a “show” visit. This results a Type I error of 1.8% and a Type II error of 91.9 %. Applying this threshold of 0.74 to the validation dataset, among 19,871 visits, the model successfully predicts 17,104 cases, which translates to 86.1% of scheduled visits. The overall error rate is 13.9%, which consists of 3.9% Type I errors and 87.2% Type II errors. We also found that, with respect to the predicted no-show rates, the model did fit a Gamma distribution with a mean of 0.10 and a standard deviation of 0.16. The p-value for the Goodness of Fit test was 0.185, meaning that we could not reject the null hypothesis that the data follows such a distribution. ▶ Figure 3 displays a histogram of the relative frequency of the predicted no-show rates in the training data.

Fig. 2.

Threshold probability (p) determination for cost ratios of 2 and 3. The probability is determined to be at the minimum for the weighted sum of Type I and Type II errors.

Fig. 3.

The histogram of the predictive no-show rate and the Gamma distribution fit from Goodness of Fit test with Anderson-Darling (AD) statistic, based on the eight years of training data. For the curve above the AD statistic was 0.548 with a p-value of 0.185.

4.4 Example of overbooking implementation

Here we demonstrate how to implement the model into a scheduling system and how this model could improve overbooking over existing approaches that do not consider individual patient no-show rates. ▶ Table 3 displays a hypothetical schedule for a single provider for one clinic day. Thirty patients are scheduled in 15-minute intervals. The example shows that four appointment slots at 9:15 am, 10:45 am, 1:30 pm and 2:15 pm have a predicted show rates of less than the threshold of 74%, which suggests that these four slots are most appropriate for overbooking.

4.5 Comparison of the new overbooking approach to existing approaches

Based on an estimated overall no-show rate of 14% and a 30-patient clinic day, the expected number of no-shows for a given day is approximately four. Thus, the evenly-distributed (E) overbooking method would result in four overbooked slots at 8:30 AM, 10:30 AM, 1:30 PM, and 3:30 PM. The random (R) overbooking method would still have four slots overbooked based on the 14% no-show rate, but these times will vary randomly throughout the day and will differ for each of the 1600 replications to test each approach. Results of the ANOVA testing comparing the three overbooking methods are reported in ▶ Table 4. Based on our simulations, the proposed (P) approach, where overbooking occurs for the scheduled patients who were predicted to be no-shows, performs better in terms of average patient wait time, overtime, and total cost. No significant difference was found for average physician idle time between the three overbooking approaches.

Table 4.

ANOVA results comparing four performance measurements for the three overbooking methods.

Performance Measurement	Mean	Standard Deviation	95% C.I.	p-value*
Average patient wait time (minutes)				0.005
P	17.2	12.0	(16.6, 17.8)
R	18.8	13.6	(16.9, 20.7)
E	18.3	13.7	(16.4, 20.2)
Average physician idle time (minutes)				0.485
P	2.4	1.3	(2.2, 2.6)
R	2.4	1.4	(2.2, 2.6)
E	2.3	1.4	(2.1, 2.5)
Overtime (minutes)				< 0.0001
P	14.2	22.9	(13.1, 15.3)
R	19.0	28.2	(15.1, 23.0)
E	18.1	28.2	(14.1, 22.0)
Total cost (US $)				0.001
P	162.8	68.5	(159.4, 166.1)
R	173.5	81.4	(162.1, 184.8)
E	167.6	83.9	(155.9, 179.3)

P = proposed overbooking approach; R = random overbooking approach; E = evenly-distributed overbooking approach

*When the p-value for the ANOVA test is < 0.05 it can be interpreted that at least one of the mean values for a given performance measurement differs significantly from the others.

The proposed (P) approach results in 8.9% and 6.2% less average wait time compared to the random (R) and evenly-distributed (E) overbooking approaches, respectively, reducing wait times by about 1 to 1 ½ minutes per patient. Similarly, the proposed (P) approach results in 28.9% and 24.1% less overtime compared to the (R) and (E) approaches, respectively.

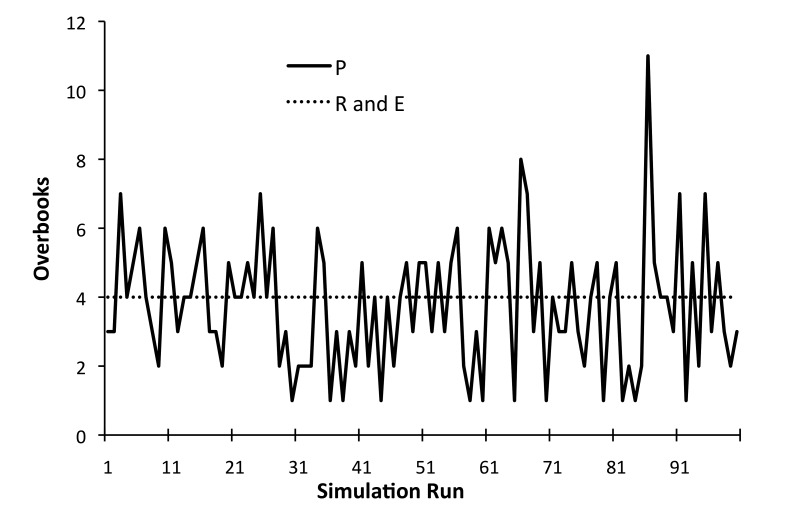
The mean number of overbooked patients from the 1600 simulation runs for the proposed approach (P) was 3.7 (standard deviation of 1.9; range 1–11), which was close to the flat overbooking rate of 4 patients. ▶ Figure 4 presents the first 100 simulation runs for the overbooked patients among three overbooking methods.

Fig. 4.

Comparison of overbooked patient frequencies per day among three overbooking methods for the first 100 runs of the 1600 run simulation. The horizontal dashed line represents a static no-show rate of 4 per day for the Random (R) and Evenly-distributed (E) overbooking approach, based on a 14% historic no-show rate. The variable solid line represents the proposed (P) approach for overbooking based on the specific characteristics of the patients created for each simulation run. This latter approach (P) can more flexibly accommodate the variable likelihood of no-shows each day compared to the standard approaches.

5. Discussion and Clinical Implications

This paper demonstrates an approach for predicting clinic no-shows using multiple data elements that are likely available at most health centers and clinics with an electronic health record and a scheduling system. Our proposed overbooking approach provides an alternative way of dynamically overbooking patients by taking into account an individual patient’s probability of a no-show based on his or her characteristics, including prior no-show history. Further, based on our simulations, the approach appears to have advantages over more standard overbooking approaches in terms of being cost-effective and providing shorter patient wait times and less clinician overtime.

Given the likely availability of the data elements used in our predictive model, it is worth considering how such a model could be implemented and applied to the daily operations of a clinic, where clerks who handle schedules must quickly consider the options for overbooking patients. While we are not aware of any EHR and scheduling systems that currently incorporate predictive algorithms for no-shows, there is no reason such functionality could not be built into these systems. In such a scenario the scheduling system could provide predictions that could guide schedulers to the best possible times for an overbook, should one be necessary. Further, the system could automatically update its model on a routine basis, incorporating new data and outcomes.

In situations where the predictive algorithms could not feasibly be incorporated in the system, another approach could be to simply have the predictive model built into an easily accessible web page or even a spreadsheet. In fact, to demonstrate the ease with which one could apply this approach, we have developed a simple calculator using Visual Basic in a Microsoft Excel spreadsheet (available as an online supplemental file).

It is important to note that our study developed a predictive model specific to a single practice. It is likely that other specialties or even the same specialty with a different patient mix would have to construct their own model to achieve optimal performance. Future work should test the portability of the model we constructed to other clinical domains (e.g., internal medicine, cardiology) and geographic regions (e.g., urban, rural).

The overbook approach proposed in this paper may provide advantages over current overbooking approaches, but it still does not make perfect predictions, especially on Type II errors. The factors we selected for our model were chosen because of their availability, but there are likely many other factors that also contribute to no-shows which are harder to quantify and which may be difficult to collect on a routine basis for all patients, such as weather conditions [39, 47]. Additionally, logistic regression is only one type of modeling possible. Future work should also test other modeling techniques such as artificial neural networks or support vector machines.

In our analysis we considered the impact of both Type I and Type II errors when predicting no-shows. For Type I errors (patients predicted to no-show but actually show), the most straightforward solution to accommodate the additional patients would be to extend the workday, which could result in overtime, higher costs, and patient dissatisfaction due to longer-than-expected wait times. In our case, Type I errors are at 3.9% based on the validation data. For a 30-patient clinic day, the phenomenon of two patients showing up at the same time is only about 1 in a clinic day. For Type II errors (patients predicted to show but actually no-show), the main downsides are increased physician idle time resulting in lost revenue, and lost opportunities for patients to be seen. From a clinic managerial perspective, overtime can be more costly than physician idle time, and our proposed dynamic overbooking method reduced the potential for overtime compared to other methods.

The proposed overbooking approach, itself, has limitations. For example patients in need of an overbooked appointment will have fewer choices for potential time slots if the scheduling clerks focus on filling only certain slots that are identified for overbooks. Additionally, while the model was built on 10 years of retrospective data, the approach has not yet been tested prospectively in a clinical setting. Future work should explore this.

6. Conclusion

This paper demonstrates an alternative approach for overbooking patients, using demographic data as well as scheduling system data, accounting for the prediction of an individual patient’s no-show rate. In simulations, the approach we proposed resulted in approximately 6 to 8% less average wait time, and 24 to 29% less overtime compared to the more traditional random and evenly-distributed overbooking approaches. Because the data used in the prediction model are already collected as part of routine clinical operations, no additional burden would be required to utilize these variables in the no-show model. Thus, while such an approach has not yet been built into existing scheduling systems, it should be feasible to implement. Further, using the predictive no-show model in designing an overbooking policy could reduce problems of patient waiting, overtime, and total costs compared to other common overbooking approaches, ultimately leading to improved patient access as well as provider productivity.