Thermodynamic insight into spontaneous hydration and rapid water permeation in aquaporins

Abstract

We report here a detailed thermodynamic description of water molecules inside a biological water channel. Taking advantage of high-resolution molecular dynamics trajectories calculated for an aquaporin (AQP) channel, we compute the spatial translational and rotational components of water diffusion and entropy in AQP. Our results reveal that the spontaneous filling and entry of water into the pore in AQPs are driven by an entropic gain. Specifically, water molecules exhibit an elevated degree of rotational motion inside the pore, while their translational motion is slow compared with bulk. The partial charges of the lining asparagine residues at the conserved signature Asn-Pro-Ala motifs play a key role in enhancing rotational diffusion and facilitating dipole flipping of water inside the pore. The frequencies of the translational and rotational motions in the power spectra overlap indicating a strong coupling of these motions in AQPs. A shooting mechanism with diffusive behavior is observed in the extracellular region which might be a key factor in the fast conduction of water in AQPs.

Permeation of water across the cell membrane is facilitated by specific water channels, called aquaporins (AQPs).^1–7 A single-file configuration of water, shown to be present in AQPs, exhibits interesting structural and dynamical properties with implications in key functional aspects, such as proton exclusion, selectivity, and change of dipole orientation.^1,8–11 AQPs are shown to be fast conductors of water¹² with a single-channel conductivity of about 10⁹ molecules per second. Water spontaneously fills the AQP pore despite its highly confining and tortuous pore.^1,3,13 Unlike carbon nanotubes (CNTs) with a constant radius and charge-free channel architecture, AQP channels have an hourglass shape with highly constricted/nozzle-like regions lined with various charged groups.^1,3,14 CNTs have also been proven to be fast transporters of water, a property primarily attributed to their smooth and slippery surface and the presence of a diffusive water layer at the CNT interface.^15,16 Even though AQPs have inspired development and application of synthetic nanopores (e.g., CNTs) for rapid water transport, the fundamental question of how AQPs can act as fast transporters of water, especially given their tortuous water permeation pathways, has not been answered. In spite of numerous studies on the mechanism, permeation dynamics, and selectivity of AQPs,^1,5,17 the fundamental physical/thermodynamical bases for spontaneous filling, fast water transport of AQPs, and the role of pore lining residues in water dynamics and motion are still lacking.

In this letter, we focus on the computation of thermodynamic properties, spatially varying as well as averaged, of water molecules in an AQP channel. The thermodynamic properties are computed by performing molecular dynamics (MD) simulations using NAMD 2.6¹⁸ with CHARMM27 force-field.¹⁹ Water molecules are described using the TIP3P²⁰ model. Initially, a tetramer of AQP1 (built using the 2.2 Å monomeric structure of bovine AQP1 reported in PDB 1J4N²¹) was inserted into a patch of POPE phospholipid bilayer. A tetramer with the central pore aligned along with the membrane normal (z-axis) was first constructed in Visual Molecular Dynamics (VMD)²² by using the transformation matrices provided in the PDB file and then embedded in a POPE lipid bilayer and solvated by a 25-Å thick slab of water on each side of membrane (Fig. 1(a)). The system was first equilibrated for 1 ns with the protein fixed under constant temperature (310 K) and constant pressure (1 atm) conditions (constant number, pressure, and temperature (NPT) ensemble). The protein was then released and another 1 ns of equilibration was performed under the same conditions. Finally, the production run was performed for 20 ns using 0.2 fs time steps and the data were collected every 1 fs for calculation of the autocorrelation function. The pressure was maintained at 1.0 atm using the Nosé-Hoover Langevin piston method²³ and the temperature at 310 K using Langevin dynamics with a damping coefficient of 0.5 ps⁻¹. Short-range interactions were truncated at 12 Å with a smoothing function applied after 10 Å, and long-range electrostatic forces were calculated using the particle mesh Ewald (PME) method²⁴ with a grid density of at least 1/ų.

FIG. 1.

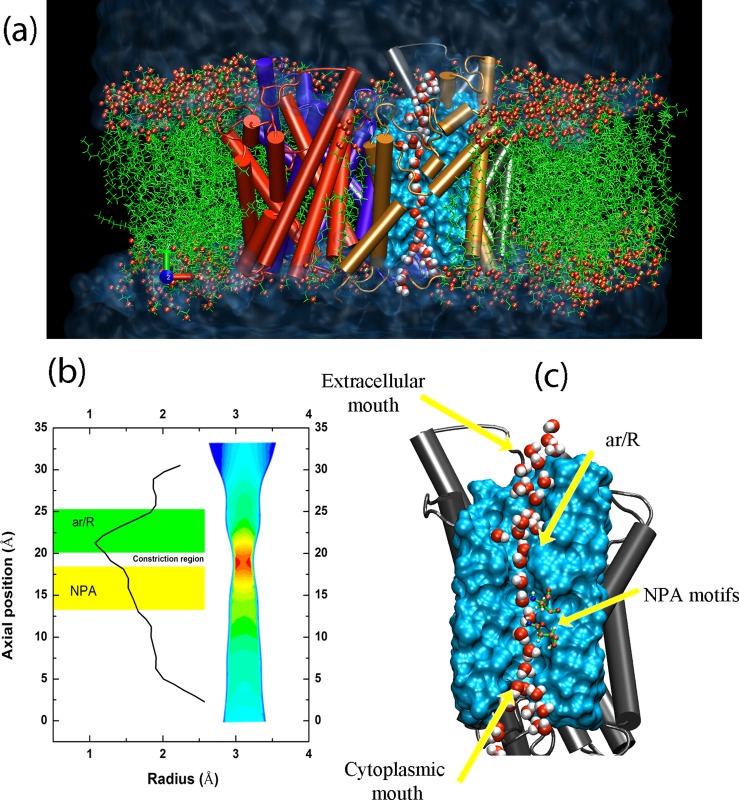
(a) Front view of the simulation system, including water reservoirs, lipid bilayer, and an AQP tetramer. Single-file water chains are formed in AQP monomer (only one shown). (b) The channel radius averaged over 20 ns production run and the designation of NPA and ar/R regions. Coarse-grained cross-section of the channel representing the hourglass topology of the AQP channel is also shown. (c) Single-file water formation in the pore with illustration of cytoplasmic, extracellular, and pore constriction regions labeled.

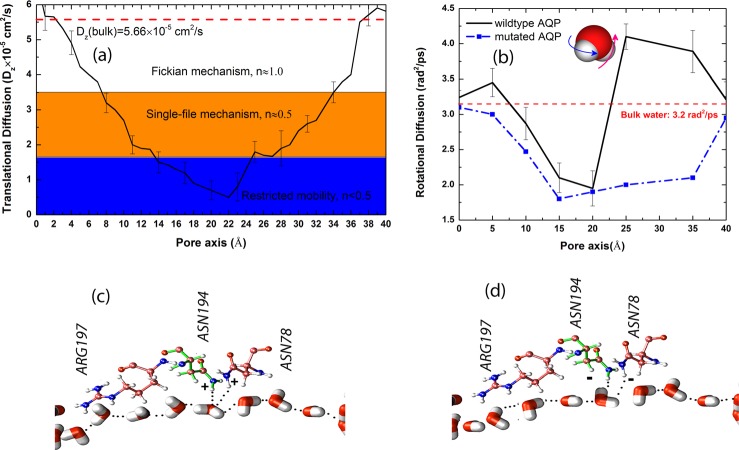
The HOLE program was used to calculate the pore radius profile (Fig. 1(b)). The pore is constricted most near the arginine/aromatic (ar/R) region with a minimum radius of 1.2 Å. Water molecules adopt a single-file configuration inside the AQP channel (Fig. 1(c)), as reported in previous simulation studies.^1,25 We evaluated the axial diffusion coefficient of water molecules, D_z, by computing the mean-squared displacement (MSD) of water molecules in different regions of the pore and fitting it to $MSD=2t^n$, where n defines the mechanism.¹⁶ The method is described in detail in our previous work.¹⁶ We also computed the axial translational diffusion by integrating the translational velocity (axial) autocorrelation function, $D_z={\int }_{t=0}^{\infty }⟨v_z(t).v_z(0)⟩dt$. Based on the diffusion coefficient, different mechanisms of diffusion¹⁶ are observed in different segments of the pore (Fig. 2(a)). Within the intracellular lumen, NPA (Asn-Pro-Ala), and the ar/R regions, a Fickian, single-file and low-mobility diffusion mechanism was observed. Right after the ar/R region (23 Å < z < 26 Å), a fast transition from low-mobility (n < 0.5) to single-file diffusion is observed. This fast transition from low mobility to single-file and then to Fickian diffusion regime can be referred to as a “shooting mechanism” in the extracellular segment of the lumen.

FIG. 2.

(a) Spatial variation of the axial translational diffusion coefficient of water molecules in AQP and the identification of different diffusion mechanisms inside the channel. (b) Spatial variation of the rotational diffusion coefficient of water molecules in AQP. (c) Water arrangement in wildtype AQP and the structure of ASN78, ASN194, and ARG197; the dipole flip is observed. (d) Mutated AQP with inversed charges of amino hydrogens in ASN78 and ASN194; the dipole flip is not observed.

To understand the rotational dynamics of water molecules inside the pore, the rotational diffusion coefficient was computed by obtaining the rotational mean-squared displacement (RMSD). The rotational mean-squared angular displacement was also calculated (averaged over all molecules) using $⟨\Delta {\varphi }^2(t)⟩=\frac{1}{N}\sum _i⟨|{\varphi }_i(t)-{\varphi }_i(0){|}^2⟩$ with ${\varphi }_i(t)$ being the total angular deflection of water dipole and N the number of water molecules. The rotational diffusion coefficient can be computed at the limit of long time by $D_{\mathit{r}\mathit{o}\mathit{t}}=\underset{t\to \infty }{\lim }\frac{1}{4t}⟨\Delta {\varphi }^2(t)⟩$. A detailed description of the RMSD method is provided in our previous work²⁶ and in Ref. 17. The spatial variation of the rotational diffusion coefficient inside the simulated AQP pore is depicted in Fig. 2(b). In both extracellular and intracellular mouths of the pore, a larger rotational diffusion is observed compared with bulk water. Interestingly, in the same region (20 Å < z < 28 Å) of transition from low-mobility to single-file diffusion, a significant rotational diffusion (4.0 rad²/ps compared with the bulk value of 3.2 rad²/ps) is also observed. The enhanced rotational diffusion coefficient is a strong indicator of the specific pore-lining charged groups on the surface of AQP helices that are responsible for the rotation of water.

Previous studies^1,27–29 suggested that the rotation of water molecules in AQPs is facilitated by hydrogen bonds between the oxygen of the permeating water molecule and the ASN side chains of the two signature NPA motifs in the middle of the channel (Fig. 2(c)). However, whether or not the rotation of water molecules has any biological significance is still debated. The resulting “bipolar” orientation of water molecules in AQPs was proposed to contribute to the barrier against proton transfer via the Grotthuss mechanism by breaking the optimal configuration of a proton wire, while still permitting a fast flux of water molecules.¹ Other studies characterized the importance of the electrostatic barrier in proton blockage.^28,30,31 In this view, the rotation of water molecules might be only viewed as an electrostatic barrier against proton transfer.²⁸ As will be described below, we demonstrate a high degree of correlation between the rotational motion of water inside the pore and its rate of permeation in the simulated AQP, therefore proposing a previously uncharacterized role for the enhanced rotational dynamics in AQPs.

To shed more light on the effect of pore lining residues on the local enhancement of rotational diffusion, we mutated the ASN78 and ASN194 residues (at the NPA motifs) by reversing the charge of the single amino hydrogen atom in each residue that forms hydrogen bond with permeating water molecules (Figs. 2(c) and 2(d)). Among all the lining residues of the AQP pore, ASN78 and ASN194, which are known to play an important role in determining the structure of water in AQPs, were selected for mutation in order to test their role on the orientation and rotation of water molecules within the AQP pore.^5,13 In wildtype (unmutated) AQP, the dipole flip is clearly observed near residues ASN78 and ASN194. To quantify the dipole flip, we binned the AQP water channel with 2 Å width bins. The water dipole vector is projected onto the transport axis (z) by a dot product of the dipole vector with the unity vector, (0,0,1).With mutated AQP, no water dipole flip is observed throughout the entire 20 ns of the simulation time, and the rotational diffusion of water molecules is significantly suppressed in this region when compared with wildtype AQP (Fig. 2(b)). Comparison of the rotational diffusion for mutated and wildtype AQPs in Fig. 2(b) also suggests that the effect of local reduction of rotational diffusion near the two mutated ASN residues propagates in both directions inside the pore, resulting in the decrease in the rotational diffusion in other segments of the pore. The reduction of the rotational diffusion in all regions of the mutated AQP channel demonstrates that the motion of water molecules is highly correlated and the reduction in the rotation of even one water molecule triggers a significant change in the rotation of other water molecules inside the pore.

We computed the pore water occupancy (the segment of channel with: 10 Å < z < 30 Å, averaged over 20 ns production run) for mutated and wild type AQPs to be 7 and 6, respectively, indicating that the pore remains hydrated in both cases. Nevertheless, there is a remarkable difference between the number of water molecules permeating these channels; while 19 water molecules were found to permeate the wild type channel (per monomer averaged over the four simulated monomers) during the 20 ns of the simulation time, no permeation events were observed in the mutated AQPs, indicating the significant role of dipole flipping and rotation on water permeation rate. We define a “permeation event” as complete translocation of a water molecule through the channel from one reservoir to the other (from one side of the membrane/channel to the other). In other words, a permeation event requires a water molecule to traverse all the way through the pore region of the channel protein. Out of the observed 19 permeation events, nine occur from the cytoplasmic mouth to extracellular one, and 10 in the opposite direction, which is expected as no chemical or mechanical gradient (osmotic or hydrostatic pressures), was applied across the membrane.

To investigate in more detail the translational and rotational characteristics of water dynamics in AQP, the VACF (velocity autocorrelation function) and RACF (rotational autocorrelation function) were computed for both bulk water and the water chain in AQP (Figs. 3(a) and 3(b)). VACF of water in AQP shows backscattering due to back and forth bouncing of water molecules inside the pore as imposed by neighboring water molecules and the pore lining residues. The negative part of VACF indicates a high probability of large angle deflections in particle collisions (here, collision of water molecules). Bulk water VACF damps in 1 ps, while the damping time for water molecules in the channel is around 2 ps. The motions of water molecules in AQP are more correlated compared with bulk. RACF shows a rotational correlation for t > 100 fs (Fig. 3(b)) which represents the orientation dependence of water molecules on each other.

FIG. 3.

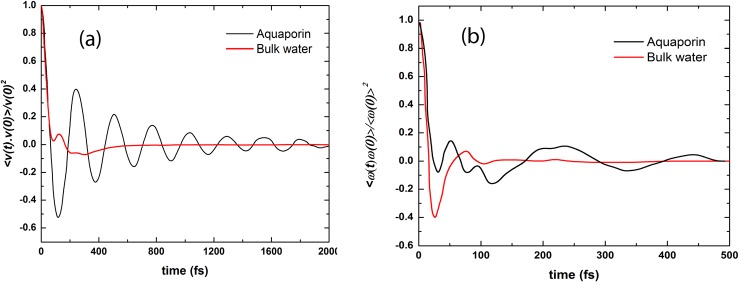
(a) Normalized VACF for AQP and bulk water. (b) Normalized RACF for AQP and bulk water.

The rotational and translational density of states (DOS) were computed by taking the Fourier transform of VACF and RACF, respectively (Figs. 4(a) and 4(b)). In the same plots, the power spectra of the bulk water are also shown. A Comparison of the translational and rotational DOS of wildtype AQP and bulk water reveals a substantial shift (200 cm⁻¹) in the rotational power spectra toward the translational DOS. The rotational and translational power spectra frequencies overlap in wildtype AQP suggesting coupling of the translational and rotational motions.³² In bulk, the two motions have a negligible correlation. Inside the channel, on the other hand, the rotation of water molecules facilitates their translational motion through the constriction region (the diameter of the constriction region in AQP is only 2.5 Å, whereas the size of the water molecule is σ = 3.4 Å).

FIG. 4.

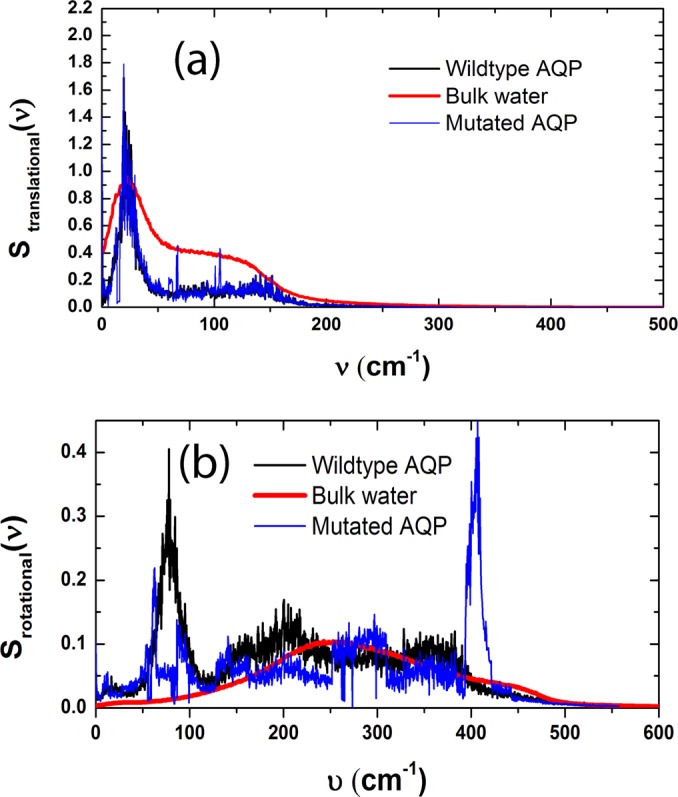
Power spectra of translational VACF (a) and RACF (b).

The comparison of rotational DOS for wildtype and mutated AQP reveals a significant shift in the frequency of rotation (Fig. 4(b)) and a non-significant shift for translation (Fig. 4(a)). For mutated AQP, rotation occurs with higher frequencies and lower amplitudes giving rise to lower rotational diffusion (Fig. 2(b)) and “quiver” like motion.

To understand the spontaneous filling of AQPs, we computed the translational, rotational, and total entropy (S = S_trans + S_rot) of water molecules inside the channel using the two phase thermodynamic (2PT) method.^17,33,34 2PT is a powerful method for calculation of free energies and the deconvolution of rotational, translational, and vibrational energy (entropy and enthalpy) components.³⁵ We computed the total entropy of bulk water (S_bulk) to be 61.32 J/mol K which is in good agreement with the experimental value.³³ The translational and rotational entropies are, S_trans,bulk = 53.1 J/mol K and S_rot,bulk = 8.22 J/mol K, respectively. For AQP, the computed entropy components are S_trans,AQP = 48.3 J/mol K and S_rot,AQP = 17.72 J/mol K, respectively, and the total entropy of the water chain is S_AQP = 66.02 J/mol K. Although the translational entropy of water in AQP (48.3 J/mol K) is less than the bulk value (53.1 J/mol K), its rotational entropy is two times larger than the bulk value.

The increase in the total entropy originating from water rotation in the pore can also explain the relevance of dipole flip and the existence of the bipolar water chain in the channel to the rate of water permeation. Without the flipping of the water dipole, permeation of the water molecule appears to be largely impeded in the AQP channel.

The comparison between entropy of water in wildtype and mutated AQP reveals that not only the total entropy of water in mutated AQP is less than wildtype, it is also lower than bulk water entropy (Table I). This result suggests that entropic barrier for water entry is lowered in the wildtype AQP compared with mutated AQP channel.

TABLE I.

Components of entropy and total enthalpy for water in bulk phase and in wildtype or mutated AQP channels. The uncertainties are computed by block averaging equilibrium trajectories (5 datasets each 2 ns).

	Translational entropy (J/mol K)	Rotational entropy (J/mol K)	Total entropy (J/mol K)	Total enthalpy kJ/mol
Bulk water	53.1 ± 0.72	8.22 ± 0.87	61.32 ± 1.29	−36.17 ± 0.1
Wildtype AQP	48.3 ± 0.99	17.72 ± 0.94	66.02 ± 1.44	−35.56 ± 0.34
Mutated AQP	44.91 ± 0.81	6.11 ± 0.77	51.02 ± 1.28	−36.43 ± 0.48

To investigate the effect of enthalpic components of free energy on water entry into AQP, we computed enthalpy of bulk water, water in wildtype and in mutated AQP. We did not observe a significant change in enthalpy of water in either mutated or wildtype AQP compared with bulk water (Table I). We therefore conclude that enthalpy is not a driving force for water entry in AQP.

The 5 J/mol K increase in the total entropy of water in AQP compared with bulk water is therefore, the driving force for spontaneous filling of the channel. The fast conduction of water in AQP can therefore be attributed to favorable entropic gain. In conclusion, the coupling of translational and rotational motions of water gives rise to enhanced transport/permeation of water molecule in AQPs. Water molecules rotate more freely compared with bulk in both extracellular/intracellular mouths of the channel giving rise to higher total entropy of water molecules in AQP compared with bulk.