Abstract
Purpose:
4D cone beam CT (4D-CBCT) has been utilized in radiation therapy to provide 4D image guidance in lung and upper abdomen area. However, clinical application of 4D-CBCT is currently limited due to the long scan time and low image quality. The purpose of this paper is to develop a new 4D-CBCT reconstruction method that restores volumetric images based on the 1-min scan data acquired with a standard 3D-CBCT protocol.
Methods:
The model optimizes a deformation vector field that deforms a patient-specific planning CT (p-CT), so that the calculated 4D-CBCT projections match measurements. A forward-backward splitting (FBS) method is invented to solve the optimization problem. It splits the original problem into two well-studied subproblems, i.e., image reconstruction and deformable image registration. By iteratively solving the two subproblems, FBS gradually yields correct deformation information, while maintaining high image quality. The whole workflow is implemented on a graphic-processing-unit to improve efficiency. Comprehensive evaluations have been conducted on a moving phantom and three real patient cases regarding the accuracy and quality of the reconstructed images, as well as the algorithm robustness and efficiency.
Results:
The proposed algorithm reconstructs 4D-CBCT images from highly under-sampled projection data acquired with 1-min scans. Regarding the anatomical structure location accuracy, 0.204 mm average differences and 0.484 mm maximum difference are found for the phantom case, and the maximum differences of 0.3–0.5 mm for patients 1–3 are observed. As for the image quality, intensity errors below 5 and 20 HU compared to the planning CT are achieved for the phantom and the patient cases, respectively. Signal-noise-ratio values are improved by 12.74 and 5.12 times compared to results from FDK algorithm using the 1-min data and 4-min data, respectively. The computation time of the algorithm on a NVIDIA GTX590 card is 1–1.5 min per phase.
Conclusions:
High-quality 4D-CBCT imaging based on the clinically standard 1-min 3D CBCT scanning protocol is feasible via the proposed hybrid reconstruction algorithm.
Keywords: computerised tomography, data acquisition, deformation, graphics processing units, image reconstruction, image registration, iterative methods, lung, medical image processing, optimisation, phantoms, radiation therapy
Keywords: 4D cone beam CT, reconstruction, GPU
I. INTRODUCTION
Respiratory motion is a major problem in lung and abdomen radiotherapy. While advanced 4D treatment planning and delivery techniques have been developed to deliver a highly conformal dose to the moving target, their efficacies are compromised by static in-room imaging guidance, e.g., 3D cone-beam CT (CBCT),1,2 which is registered to the 4D-CT image for patient setup. 4D image guidance is therefore needed for precise tumor targeting,3 particularly in the context of the increasingly used stereotactic body radio-surgery,2,4 where the high fractional dose makes it less forgiving to targeting error. Moreover, adaptive radiation therapy (ART) (Ref. 5) is currently an active research topic, which addresses interfractional variations of patients’ respiratory motion pattern6–8 and tumor shrinkage9,10 by adaptively developing new treatment plans based on the up-to-date anatomy. It calls for high-quality in-room 4D images with accurate Hounsfield Units (HU) to facilitate accurate deformable registration and dose calculation for plan adaptations.
In recent years, respiratory-phase resolved CBCT, or 4D-CBCT technique has been developed.4,11–16 However, current 4D-CBCT technique cannot fully satisfy the aforementioned clinical needs. Specifically, (1) Current 4D-CBCT needs a long scan protocol (typically 4–6 min, referred as 4-min scan hereafter) to provide enough number of projections per breathing phase for reconstruction. This inherently impedes the clinical workflow and elevates the imaging dose, greatly limiting its clinical use; (2) the overall image quality (e.g., signal-to-noise ratio, SNR) of 4D-CBCT is still inferior to that of a standard 3D-CBCT (referred as 1-min scan hereafter), let alone the planning CT; (3) 4D-CBCT usually adopts a full-fan mode to maximize the angular sampling. Nonetheless, the associated small field-of-view (FOV) (e.g., 25 cm in diameter) usually cannot cover the whole thorax/abdomen, leading to truncation problem,17,18 and the truncated 4D-CBCT images cannot serve the purpose of dose calculations due to missing anatomies outside the FOV; and (4) the HU of 4D-CBCT images is inaccurate due to scatter contaminations. The factors mentioned here are usually coupled together. Improving one factor may inevitably worsen another. For example, any attempt to reduce scanning time could speed up the workflow and save imaging dose, but would further introduce view-aliasing/streaking artifacts.19 Another example is adopting a half-fan mode to increase the FOV. Yet, because only half of the patient is covered at each view angle, the angular sampling rate is effectively reduced. In light of all of these facts, a fast, high-quality, low dose 4D-CBCT imaging technique is in great demand.20–42
One unique feature of radiotherapy is that a patients’ own planning CT (p-CT) is always available from the treatment simulation stage. In light of the availability of this prior information, 2D-3D matching-based reconstruction models have been proposed in a wide spectrum of imaging tasks, such as tomosynthesis, real-time volumetric imaging, and 3D/4D CBCT.27,36,37,39,43–45 These methods optimize a motion vector field (MVF) to deform the p-CT, such that its forward projections match the measurements. Brock et al. proposed to match the forward projections by adjusting the MVF control points, so that the forward projections have minimal mismatch with the measurements. They evaluated the algorithm via simulation and reported that it is sensitive to contrast mismatch errors between the measurements and the calculated projections.27 Ren et al. proposed to solve a MVF energy function using a nonlinear conjugate gradient (NCG) method. They investigated various scan protocols, suggesting that ∼57 projections over 360° are required to achieve acceptable accuracy.36 To mitigate the local minima problem associated with the NCG framework, Wang and Gu introduced a better initial image using a compressed sensing (CS) based iterative reconstruction algorithm. They tested it with one simulation case and one patient case of a 2-min scan.37 Recently, a multiple-step algorithm combing PCA modeling, optical flow based registration and reconstruction was proposed.39 It was validated with simulation studies and one patient data study and was compared with the state-of-the-art CS-based methods, such as TV (Ref. 46) and PICCS.21,22 The results show that it offers better overall compromise in the depiction of moving and stationary anatomical structures.
In spite of the success, there is still room for improvement. It is desirable to reconstruct 4D-CBCT based on projections acquired in a short scan time, e.g., 1-min as in the current clinical protocol for 3D-CBCT. In addition to the limited number of projections, practical issues such as intensity difference due to scatter, truncation, and noise also make this a challenging problem. The local-minima problem in 2D-3D registration is another issue. While standard gradient-based algorithm can be employed to solve the optimization problem, more comprehensive evaluations of reconstruction results in patient cases are needed to demonstrate the clinical utility of algorithms of this kind, particularly with respect to both the intensity accuracy and geometry accuracy. Finally, computation efficiency should be improved to render the algorithm in a clinically applicable form.
In this paper, we will present an alternative approach to the existing algorithms,36,37,39 called forward-backward splitting (FBS) algorithm, to solve the 2D-3D registration-based 4D-CBCT reconstruction problem. It splits the model into two well-studied subproblems, i.e., image reconstruction and deformable image registration (DIR). By alternatively solving these two problems in an iterative manner, FBS gradually yield 4D-CBCT images with satisfactory even with very sparsely acquired projections from a 1-min CBCT scan (e.g., ∼10–20 projections over a 200° arc for each phase). To achieve a clinically acceptable efficiency, all components along the whole reconstruction workflow have been implemented on graphic processing unit (GPU). The GPU implementation has substantially reduced the reconstruction time to 1–1.5 min per phase. As a comparison, hours of computation time are usually observed for those CPU based 2D-3D matching algorithms.39 Both phantom and multiple real patient data sets are used to test the efficacy of the proposed algorithm. For each case, comprehensive evaluations are conducted regarding the image quality, algorithm robustness, and computational efficiency.
II. METHODS AND MATERIALS
II.A. The hybrid 4D-CBCT reconstruction algorithm
II.A.1. Reconstruction model
The p-CT fp(x), in this study is chosen to be one phase of the 4D-CT image or a breath-hold CT image, in which there is minimal motion artifacts. We first reconstruct an average 3D-CBCT image using all projections in a 4D-CBCT scan via the conventional Feldkamp-Davis-Kress (FDK) (Ref. 47) algorithm. The p-CT is then rigidly aligned with it. Let us denote 4D-CBCT image at phase i as fi(x), which can be obtained by deforming fp(x) with an MVF vi(x), i.e., fi(x) = fp(x + vi(x)). In our study, it is our objective to restore vi(x) by solving the following optimization problem:
| (1) |
where ‖·‖2 represents l2 norm and ∇ is the gradient operator. Pi is the x-ray projection matrix for the phase i, and gi is the corresponding measured projections. The first term in the objective function is to ensure the fidelity between the reconstructed results and the projection measurements. c represents a correction step to address the intensity inconsistency between the measured x-ray projections gi and the calculated forward projections Pifp due to, e.g., x-ray scatter contaminations in the projection measurements. The second term is to enforce the MVF smoothness. λ is a penalty weight. Once Eq. (1) is solved, fi(x) can be obtained by deforming fp(x) via vi(x).
II.A.2. Forward-backward splitting algorithm
Let us first consider the optimality condition of the problem. By taking the derivative of Eq. (1), we arrive at
| (2) |
where fp is the simplified representation of denotes the matrix transpose of Pi, and Δ is the Laplacian operator. By introducing an auxiliary function si(x) and a term ∇fp[fp − si], we can get
| (3) |
Since we have the freedom to choose the function si(x), we would like to combine the first and the third term, and the second and the fourth term together, respectively, and split Eq. (3) into
| (4) |
| (5) |
For Eq. (4), assuming ∇fp ≠ 0, we can get
| (6) |
Interestingly, Eq. (6) is a typical gradient descent update step for a CBCT reconstruction problem, and meanwhile, Eq. (5) is essentially the Euler-Lagrange equation of , an energy function of the DIR problem between the moving image fp(x) and the static image si(x). Based on these observations, we propose a FBS algorithm to solve Eq. (1), by alternatively performing CBCT reconstruction as in Eq. (6) and DIR corresponding to Eq. (5).
Specifically, FBS can be summarized as three steps (S1)–(S3) shown in Table I. In the reconstruction step of (S1), we have heuristically substituted by FDK (Ref. 47) operator F, which has been found to improve the convergence of the reconstruction problem.48,49 Since si is obtained purely based on reconstruction, it contains the correct anatomy location information decoded from the CBCT projections, although it is contaminated by streak artifacts due to limited number of projections and inaccurate HU values due to scattering. In the subsequent steps S2 and S3, si serves as a guidance to deform the prior image fp. Steps S1–S3 are iteratively performed, gradually leading to a fusion of both correct anatomy location/motion information from si and accurate intensity values from fp.
TABLE I.
FBS algorithm solving the problem in Eq. (1).
| (S1) | |
| (S2) | |
| (S3) |
II.A.3. Implementation
Before FBS, all 4D-CBCT projections are sorted into ten respiratory phases by performing a projection-based sorting via local principle component analysis (LPCA).50 In principle, 4D-CT image at an arbitrary phase can serve as the p-CT fp. However, in order to minimize the motion blur in the p-CT, 0% (maximum inhale) or 50% (maximum exhale) phase of the 4D-CT is recommended. An average 3D-CBCT is reconstructed using the FDK algorithm and a mutual information-based rigid registration51 is performed to align the p-CT with the average 3D-CBCT image. In (S1), to realize the c operator, linear intensity equalization is implemented as in Ref. 45. To address the residual intensity inconsistency between CT and CBCT images, which is indeed an open problem existing in all 2D-3D matching-based methods,27 Demons with simultaneous intensity correction (DISC) (Ref. 52) is adopted for the DIR step in (S2) and (S3), instead of a conventional intensity-based registration algorithm, such as Demons algorithm.53 We have used a standard multiscale registration strategy in DISC.52 At each scale, the iteration stops when the MVF does not change anymore. The workflow of FBS is shown in details in Table II.
TABLE II.
FBS algorithm for hybrid 4D-CBCT reconstruction.
| Rigid registration from p-CT (fP) to the average 3D-CBCT image. |
| Repeat for each phase i (i = 0, 1, 2, …, 9) |
| Down-sample fP and CBCT projections gi to the coarsest resolution; |
| Initialize the moving vector vi to zero; |
| Repeat for each resolution level |
| While the stop criteria is not met, do |
| 1. Calculate forward projection ; |
| 2. Reconstruct the difference image from and |
| get si (S1); |
| 3. Deform toward si to obtain vi (S2 and S3); |
| Up-sample vi to a finer resolution level |
| Until the finest resolution is reached |
| Until all phases are done |
To yield a satisfactory efficiency, key components of FBS, including FDK reconstruction F,54 forward projection calculation P,55,56 and DISC,52 have been implemented under CUDA programming environment on a GPU platform with an NVIDIA GTX590 card.
II.B. Evaluation
II.B.1. Experimental data
The experiments include one moving phantom case and three patient cases. For all cases, the resolution of a CBCT projection is 512 × 384 with pixel size of 0.784 × 0.784 mm2. In each case, 4D-CBCT projection images are acquired. The respiratory signal is obtained by analyzing those projections using a LPCA method.50 Projections are then distributed to each breathing phase according to the obtained signal.
In the phantom case, a small ball is attached to a stick, which is then set on a QUASARTM respiratory motion platform. The platform motion follows a standard sinusoidal curve along the superior–inferior (SI) direction with an amplitude of ±7.5 mm. In order to mimic patient interfractional breathing variations, we have set the breathing period to 4 s for the 4D-CT simulation to obtain the p-CT and 6 s for the 1-min 4D-CBCT scan. The 4-s period is a typical value for a patient with normal breathing. The 6-s breathing period is selected to create a challenging yet realistic case to test our algorithm. In fact, for this case with a long breathing period, there are only 9–10 projections for each respiratory phase during the 1-min scan time. The purpose of this phantom study is to evaluate the accuracy of the target (moving ball) location, as we have the predefined tumor trajectory along the SI direction as the ground-truth.
Three patients (patients 1–3) were scanned with a 4D-CBCT protocol under a full fan mode with a slow gantry rotation in 5.8, 4.5, and 5.7 min over a 200° arc.15 Their breathing periods are 2.87 ± 0.65, 2.78 ± 0.26, and 4.45 ± 0.83 s, respectively. According to the breathing signal, we extract 121, 97, and 77 projections for each phase. These data sets are denoted as 4-min data here after. Furthermore, we select among the 4-min data 21, 20, and 13 projections per phase for the three patients, corresponding to 0.97, 0.93, and 0.96 min of scanning time over the 200° arc, to simulate scans of 1 min scan time (denoted as 1-min data). In these patient cases, we consider the 4D-CBCT images reconstructed by the FDK algorithm using all the 4-min data as ground truth.
II.B.2. Evaluations
For the moving ball phantom, besides the visual inspection, we determine its incremental shift in the SI direction between two adjacent phases by template matching, where the shift is indicated by the maximum cross correlation (CC) value between the shifted 4D-CBCT image at one phase and the image at the next phase. The ball location at each phase is then determined and compared with the ground truth ball trajectory set at the motion platform. Average and maximal location differences will be calculated. A region of interest (ROI) is also selected to calculate the intensity differences.
For patients’ cases, in addition to directly compare the images visually, we have conducted quantitative evaluations on both geometry and image quality accuracy. For geometry accuracy evaluation, the reference is the 4D-CBCT images reconstructed by the FDK algorithm using the 4-min data, denoted as FDK-4D (4-min). Test images are (1) Hybrid-4D: 4D-CBCT images reconstructed by the proposed hybrid method using the 1-min data, (2) FDK-4D: 4D-CBCT images reconstructed by the FDK algorithm using the 1-min data, (3) 3D-CBCT: CBCT image reconstructed by the FDK algorithm using all projections, and (4) p-CT: the image used as the input of the proposed hybrid method. A ROI containing the tumor has been selected. We have used the derivative of the ROI images to highlight the structure edges in this test in order to minimize the impacts of intensity differences between the reference and some of the test images. We have used two metrics that are robust to the intensity discrepancies to a certain degree. The first metric is the spatial shift corresponding to the maximum CC (denoted by S). Specifically, we shift the test image pixel by pixel along the SI direction until the maximum CC value between the test and the reference images is achieved. The smaller this shift S is, the better the alignment between the two images is, indicating a good reconstruction with correct anatomical structure locations. The purpose of using this quantity is to test the anatomical structure location accuracy with respect to the reference. The second one is feature similarity index (FSIM),57,58 a novel human-perception based metric, with a higher value reflecting a better similarity between the test and reference images. FSIM ranges in [0, 1], with 1 being the best. To evaluate images from intensity accuracy aspect, intensity differences and SNR are calculated. In this study, a ROI has been selected, which is located at the center of the tumor. p-CT is considered as the reference image, which has the highest image quality. The test images are (1) Hybrid-4D, (2) FDK-4D, (3) 3D-CBCT, and (4) FDK-4D (4-min). Absolute image intensity difference averaged in the ROI between each of the test images and the reference image is calculated. For SNR calculation, no reference is needed. SNR = μ/σ is used, where μ and σ represent the mean and the standard deviation of the ROI image.
III. RESULTS
III.A. Phantom case
Figure 1 summarizes the moving phantom results. While the average 3D-CBCT image [Fig. 1(a)] shows significant blurring and the FDK-based 4D-CBCT images suffer from streaking artifacts [Figs. 1(b) and 1(c)], the proposed hybrid method yields 4D-CBCT images with superior quality [Figs. 1(e)–1(g)]. Compared with the p-CT, the average 3D-CBCT and the FDK based 4D-CBCT images attain intensity difference of ∼–270 and ∼185 HU; the images from the proposed hybrid method yield a negligible HU difference, since it is deformed from the p-CT. Satisfactory agreements have been observed in terms of motion trajectory. Comparing the reconstructed ball trajectory with ground truth, our result achieves 0.204 mm average and 0.484 mm maximum differences [Fig. 1(h)].
FIG. 1.

Results of the moving phantom experiment. Display window: [−1000, 250] HU. (Upper-left) the transverse and sagittal images of (a) 3D-CBCT image, (b) FDK based 4D-CBCT image at 0% phase, (c) FDK based 4D-CBCT image at 50% phase, (d) p-CT image, (e) and (f) 4D-CBCT image at 0% and 50% phases reconstructed by the proposed hybrid algorithm, respectively. Arrows indicate the mean HU values inside the ball. In each group the two rows are transverse view and sagittal view, respectively. (g) Sagittal views at all phases of the results from the proposed hybrid algorithm. (h) Comparison of the motion trajectories derived from the results of the proposed algorithm and from ground truth.
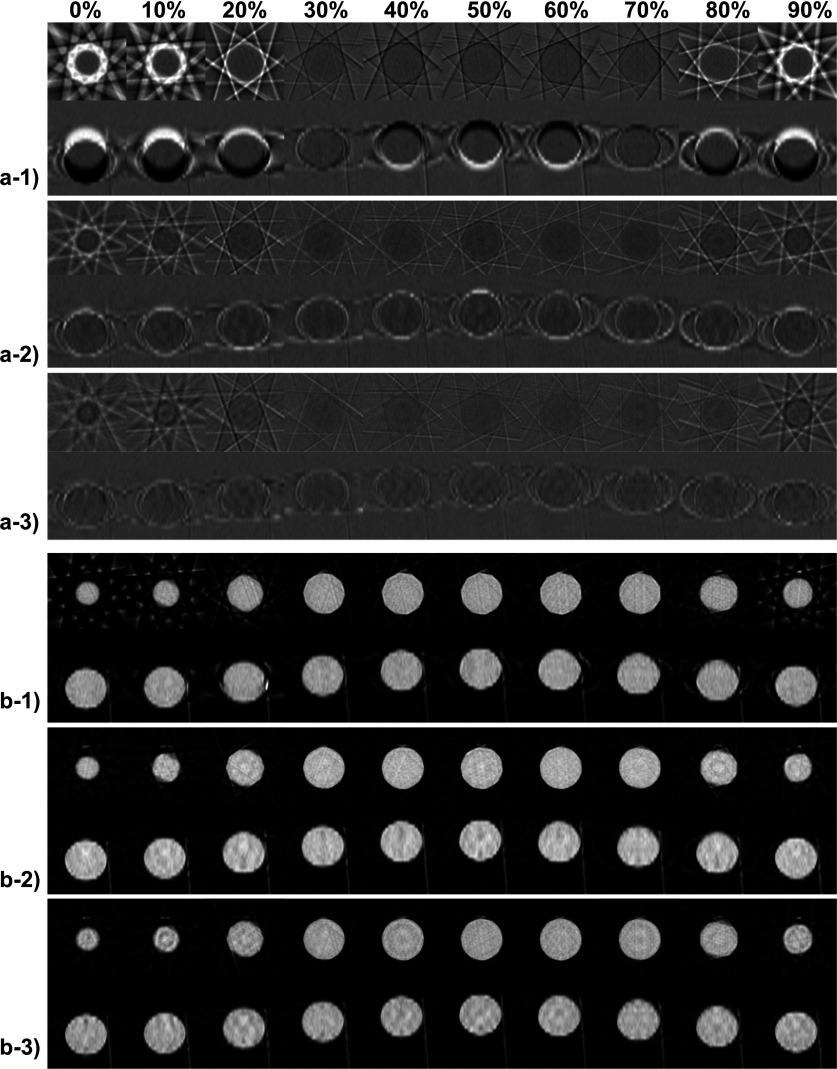
To investigate the iteration process of our algorithm in detail, we present the intermediate results of the moving phantom at all ten phases in Fig. 2. From the difference images for k = 1, 2, 3 shown in Fig. 2(a-1)–(a-3), we can see that the difference decreases quickly. After 3 iterations, the resulting has been deformed to a status such that its projections match well with the measurements c(gi), indicated by the small difference at this stage. From the corresponding siimages shown in Fig. 2(b-1)–(b-3), we observe that these images always give the correct anatomical information derived from the projection measurements. When registering with them in the DIR step, the correct MVF can be generated. It is this fact that leads to the successful estimations of the MVF and hence the reconstruction of 4D-CBCT images.
FIG. 2.
Intermediate results of the moving ball experiment (all ten phases): (a-1)–(a-3): the difference images after 1, 2, and 3 iterations. Display window: [−500, 500] HU; (b-1)–(b-3): si image after 1, 2, and 3 iterations. Display window: [−1000, 250] HU. In each subfigure, the upper and the bottom rows show the transverse and the sagittal view, respectively.
III.B. Patients case
III.B.1. Visual inspections
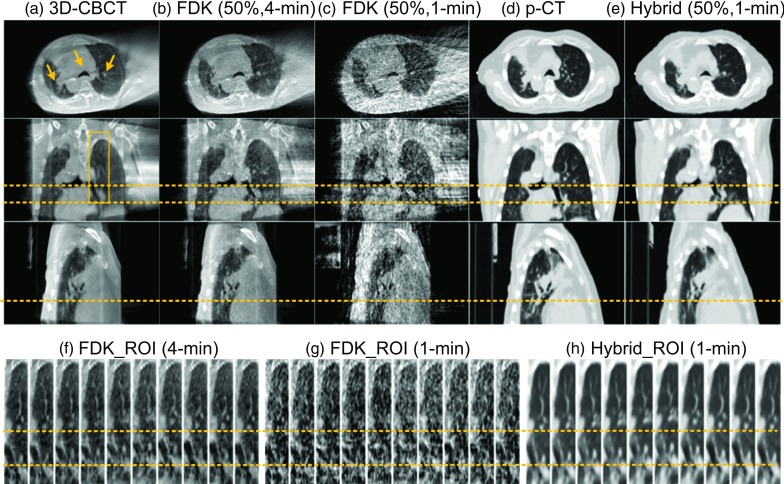
The results of the patient 1 are shown in Figs. 3 and 4. From Fig. 3, we have the following observations: (1) FDK based average 3D-CBCT image [Fig. 3(a)] shows minimal noise but blurred anatomies; (2) FDK based 4D-CBCT images from the 4-min data [Fig. 3(b)] can greatly reduce motion artifacts, but the image quality is inferior to the average 3D-CBCT because of amplified streaks; (3) FDK based 4D-CBCT images from the 1-min data [Fig. 3(c)] shows amplified noise and severe undersampling streaking artifacts; (4) Truncation exists in all the FDK-based images [Figs. 3(a)–3(c)], which will lead to inaccurate dose calculations in radiation therapy due to the missing tissue information outside the FOV; (5) With the 1-min projection data and a p-CT image [Fig. 3(d)], the proposed method yields 4D-CBCT images with much better quality for tumor delineation, i.e., accurate anatomy location and accurate HU value [Fig. 3(e)]. The images are also free of truncation artifacts, facilitating dose calculations. Detailed comparisons of image quality inside ROI are also shown in Figs. 3(f)–3(h).
FIG. 3.
Experimental results for Patient 1. Display window: [−1000, 250] HU. (Upper) Transverse, coronal, and sagittal views of (a) FDK-based 3D-CBCT image, (b) FDK-based 4D-CBCT image at 50% phase using 4-min data, (c) FDK-based 4D-CBCT image at 50% phase using 1-min data, (d) p-CT image, (e) 4D-CBCT image at 50% phase reconstructed by the proposed algorithm using 1-min data. (f)–(h) Sagittal ROI 4D-CBCT images corresponding to (b), (c), and (e), respectively. ROI is indicated by the box in (a). Arrows in transverse views highlight structures with relatively large motions. Horizontal dashed lines are plotted to help comparing the anatomy locations.
FIG. 4.
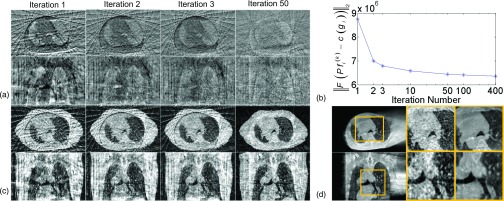
Intermediate results during reconstructing the 0% phase of 4D-CBCT using the 0% phase of p-CT (Patient 1). (a) The difference images after 1, 2, 3, and 50 iterations. Display window: [−700, 700] HU. (b) as a function of iteration steps, with the x-axis in a log scale. (c) The si images after 1, 2, 3, and 50 iterations. (d) Zoomed-in ROIs to compare the si image after 50 iterations and the FDK-based 4D-CBCT (4-min scan). ROIs are indicated by the box. The three columns are FDK image, zoomed-in view of si, and the zoomed-in view of FDK image. In subfigures (a), (c), and (d), the upper and the bottom rows show the transverse and the sagittal view, respectively.
Figure 4 shows intermediate results during the 4D-CBCT reconstruction for the 0% phase by using the 4D-CT image of 0% phase [Fig. 3(d)] as p-CT. Similar observations to those in Fig. 2 are made. From the difference images shown in Fig. 4(a), it can be seen that the contents of image are gradually deformed to the correct locations during the iterations, and the mismatch between and the measured c(gi) is reduced gradually. Figure 4(b) uses calculated after 1, 2, 3, 10, 50, 100, and 400 iterations to quantify this fact. It can be seen that the first several iterations dramatically reduce the mismatch, and this decrease becomes gradual in later iterations. Note that this plot only illustrates the gradual reductions of the mismatches between the reconstructed results and the measurements, rather than demonstrating the algorithm convergence. From Fig. 4(c), we can see that the quality of si images is also improved during the iteration. For example, the streaking artifacts and the evident boundary around the original FOV are eliminated greatly after 50 iterations. We have also shown in Fig. 4(d) a zoomed-in ROI to demonstrate that si provides correct anatomy information compared to that in the ground-truth, despite the intensity variations. These facts help guiding the deformations of the p-CT toward a correct location.
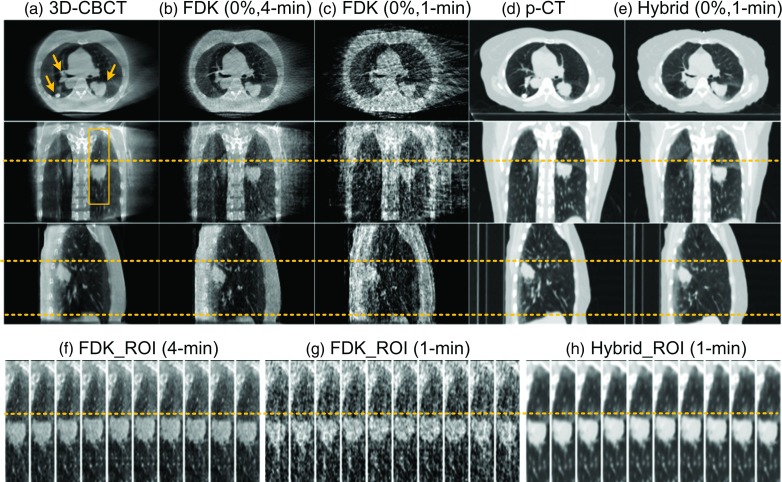
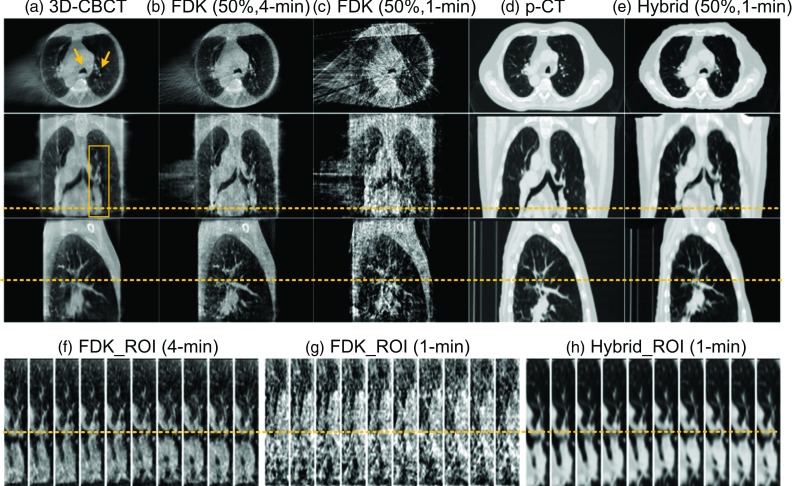
We have observed the same performance of our algorithm in patients 2 and 3 shown in Figs. 5 and 6, respectively. In general, the 1-min FDK reconstructed images are not suitable for the tumor delineation due to the obvious streaks, especially for patient 3 where only 13 projections are available for each phase [Fig. 6(g)] because of the long breathing period. In contrast, the proposed hybrid method is able to reconstruct images with better quality for both cases.
FIG. 5.
Experimental results of Patient 2. Subfigure arrangement is the same as that in Fig. 3 except that the upper part shows 0% phase.
FIG. 6.
Experimental results of Patient 3. Subfigure arrangement is the same as that in Fig. 3.
III.B.2. Quantitative evaluations
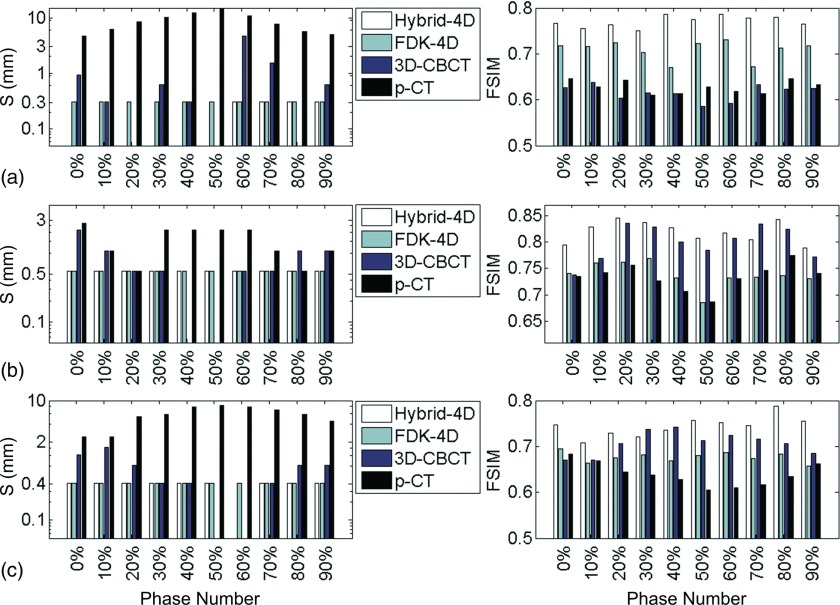
Figure 7 summarizes the quantitative evaluation results regarding the geometry accuracy for all the three patient cases. We have the following observations: (1) Hybrid-4D method has the smallest shift S and the highest FSIM scores in almost all cases, indicating the high quality of our reconstruction results. This is also consistent with the visual inspections performed above. (2) FDK-based 4D-CBCT using the 1-min scan data also has small S values for all cases. It indicates that these images have correct anatomy locations, although the images are full of streaking artifacts; however, for patients 2 and 3, the FSIM scores are lower than those of our results, implying that visualization-based tasks, e.g., soft-tissue/tumor delineations are significantly affected by the artifacts. (3) 3D-CBCT image generally has large S values and low FSIM scores. There are a few cases where the 3D-CBCT has slightly better numbers in these two metrics, e.g., lower S values for patient 2 at 40% and 50% phases and patient 3 at 50% phase, and higher FSIM scores for patient 2 at 70% phase and patient 3 at 30% and 40% phases. Since there is only one static average 3D-CBCT for a patient, when the structure location in it happens to be close to that in one breathing phase, the corresponding S value may be very low. For the FSIM scores, not only does it compare structures, it also considers intensity difference. Because our reference images are reconstructed by the FDK algorithm, the FSIM score is actually biased toward those images reconstructed by this algorithm due to the similar HU values. It is this fact that leads to higher FSIM scores to the average 3D-CBCT image sometimes. (4) p-CT always has the largest S value and the lowest FSIM scores. This is due to both mismatched structural information and different image intensities between the p-CT and the reference images. It implies that only using rigid registration cannot guarantee accurate soft-tissue alignment. Yet, using p-CT as an input, the proposed method is able to generate high quality outputs.
FIG. 7.
Comparisons of S (left) and FSIM (right) of different methods. The results of patients 1–3 are shown in (a)–(c), respectively. For S value, absence of a bar corresponds to zero.
Quantitative evaluations regarding the intensity accuracy have also been conducted. An example result is shown in Fig. 8 for patient 2 and similar results have been observed in other patient cases. Our Hybrid-4D method has the smallest intensity difference (from 14.76 to 18.21 HU for different phases, 16.70 HU on average) and the highest SNR (from 60.94 to 83.35 for different phases, 69.55 on average) in all phases. In contrast, all three FDK based reconstructions have large intensity differences [254.96, 288.68, and 286.43 HU on average for FDK-4D, 3D-CBCT, and FDK-4D (4-min)]. As for SNR, FDK-4D using the 1-min scan data has the lowest ones (5.46 on average), due to the streaking artifacts and amplified noise with limited data. For FDK-4D (4-min), SNR is improved (13.58 on average) yet still lower than the regular 3D-CBCT (30.65 on average). The underlying reason for such observations is that using the Hybrid-4D method, high image quality is inherited from the p-CT, while FDK-based reconstruction results have inferior quality due to scatter (causing large intensity differences) and the limited data induced streaking artifacts and noise (causing low SNRs).
FIG. 8.
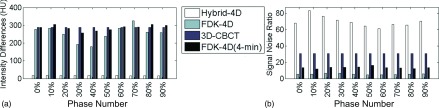
Comparisons of different methods in terms of (a) intensity difference and (b) signal-noise-ratio based on the results of patient 2.
III.B.3. Impacts of scanning time
The above experiments were focused on 1-min scan time. We would also like to understand how the scan time impacts on the results in our method. As such, we have extracted multiple subsets of projection data of patient 1 to simulate cases with different scan time. To evaluate the results, we consider the one reconstructed by the hybrid method using all the 4-min scan data as ground truth. S and FSIM are calculated with respect to it. Figure 9 shows the results. Along the x-axis, the scanning time is increased from 0.39 min (∼7 projections per phase) to 2.90 min (∼61 projections per phase). Vertical black line indicates the case with 1-min scan time studied previously. It is interesting to see that neither metric is significantly affected by the scan time over a large range, until the time is reduced to ∼0.53 min (∼9 projections per phase). The existence of a margin from 1 min scan time to ∼0.53 min scan time indicates the robustness of our algorithm against the projection number reduction. The range of this margin is certainly dependent on the patient breathing period. For those patients with a long breathing period, e.g., patient 3, there are less number of projections per phase for a given scan time. It is therefore harder to reconstruct images for them, and the margin is expected to be smaller.
FIG. 9.
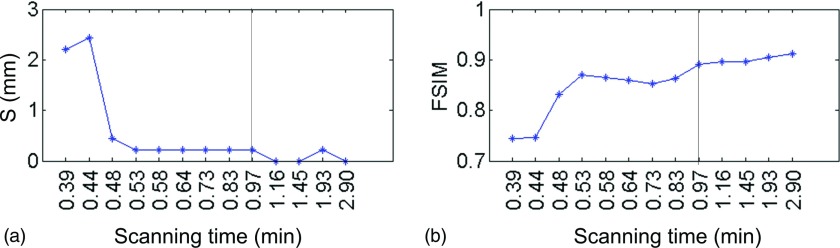
S and FSIM as the functions of scan time (patient 1, phase 0%). The vertical black lines indicate the scanning time in Fig. 3 (0.97 min).
III.B.4. Impacts of deformation size
Another aspect of the algorithm robustness is the dependence on deformation size, since it is very challenging to address cases with large deformations. To test our algorithm in this regard, we have also reconstructed all the ten phases of 4D-CBCT for patients 1–3 using different p-CTs (0% or 50% phase of 4D-CT). No observable difference is found in the results compared with those shown in Figs. 3–6. As an example, Fig. 10 shows the results of patient 1, when reconstructing the 50% phase of 4D-CBCT using the 0% phase of p-CT. Due to the large deformation (∼17 mm of diaphragm motion), this case is more challenging than that shown in Fig. 4. In such a case, FBS algorithm still performs very robust. As indicated by Figs. 10(a) and 10(b), image is deformed to the correct locations, and the mismatch between and the measurement is reduced gradually. Figure 10(c) shows that through two iterations, diaphragm in si image has already been seen in the correct location, and small structures are gradually refined in the following iterations. This guides the deformable registration to generate a good final image.
FIG. 10.
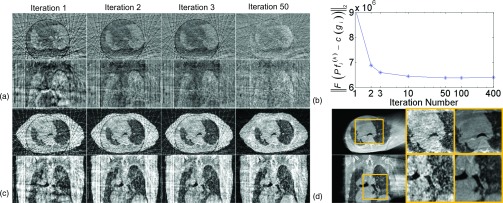
Intermediate results during reconstructing the 50% phase of 4D-CBCT using the 0% phase of p-CT (Patient 1). Figure layout is the same as in Fig. 4.
The maximum motion amplitude in our patient cases is ∼23 mm at diaphragm. While good results have been achieved using p-CT at one phase (e.g., 0% phase) to reconstruct the 4D-CBCT at another phase that is far away (e.g., 50% phase), it does not exclude the possibility that registration may fail when the respiration deformation is extremely large. We currently do not have patient data with larger deformations to test this. Yet, this concern is associated with all registration-based algorithms. To prevent such a problem, a feasible solution is to use the p-CT at a certain phase to reconstruct the 4DCBCT at the same or close phase, to ensure that the deformation is within a reasonable range.
III.C. Efficiency
The entire reconstruction process has been implemented on a GPU platform with a NVIDIA GTX590 card. Two resolution levels are used in our studies in all cases. The corresponding reconstruction time and the iteration number for each multiresolution level are listed in Table III. It can be seen that the computational time depends on the complexity of the cases tested. Currently, for the typical clinical patient cases shown here, the runtime is about 1–1.5 min for each phase.
TABLE III.
Iteration number and computational time per phase.
| Test cases | Moving phantom | Patient 1 | Patient 2 | Patient 3 | |
|---|---|---|---|---|---|
| Iterations | Level 0 | 5 | 77 | 72 | 78 |
| Level 1 | 3 | 53 | 57 | 53 | |
| Time (s) | 2.16 | 83.90 | 81.38 | 67.33 | |
IV. DISCUSSIONS AND CONCLUSION
In this paper, we have developed a 4D-CBCT reconstruction method to facilitate fast and accurate 4D-CBCT imaging for lung and abdomen radiotherapy. The method has been thoroughly evaluated in terms of efficacy and efficiency in both phantom and real patients’ cases. By using this method, we have obtained 4D-CBCT images with correct motion information and good image quality inherited from p-CT, namely, high SNR, correct intensities, and free of truncation artifacts. We have also investigated algorithm robustness with respect to scan time and deformation size. High computational efficiency (1–1.5 min per phase) has been observed due to GPU implementations.
Despite the success in those cases studied here, we would like to point out that there is no theoretical proof regarding the convergence of the algorithm. In addition, the local-minima issue associated with this and all other 2D-3D registration-based reconstruction method may lead to geometrical inaccuracy in the results to a certain extent. There have been active researches to solve this problem in deformable image registration context, such as using multiple resolution levels. These methods may be employed here to maximally mitigate the problem. Using p-CT at the same phase to the 4D-CBCT to be reconstructed will also reduce the deformation amplitude and therefore help preventing this problem.
We would like to further comment on the reconstruction image quality. For the moving phantom case, the results show a certain amount of blurring at the superior and inferior boundaries [Fig. 1(g)]. This can be ascribed to the blurring in the p-CT at the same area [Fig. 1(d)]. Because of the smoothness of the MVF, this blurring originated in the p-CT will be transfer to the resulting images. Practical solution to this problem will be using high quality p-CT images, e.g., those obtained with fast CT gantry rotations. Another interesting observation is that, even though the hybrid method yields the best “similarity” with respect to the reference images, the FSIM scores are still relatively low [Fig. 7]. This is because FSIM method considers both structural and intensity similarity between the test and the reference images. Since our reference images are reconstructed by FDK algorithm, which have different HU values from the p-CT, the FSIM score underestimated the image quality to a certain extent.
While high computational efficiency has been achieved in this work, further efficiency boost is still necessary for routine clinical applications. For example, it may be possible to use less strict stopping criteria to terminate the iteration early, as it is observed in Fig. 4(b) that the later iterations only improve the deformation marginally. Yet, this will inevitably impact on the accuracy of deformation. Since clinically acceptable tolerance of deformation accuracy definitely depends on specific applications, the termination stopping criteria will tie to the applications as well, which will be investigated in our future studies. Another direction to accelerate the computations is to take advantages of the advanced hardware, such as multi-GPU implementation.59
ACKNOWLEDGMENTS
This work is supported in part by NIH (1R01CA154747-01), Varian Medical Systems, Inc., and the National Natural Science Foundation of China (Nos. 30970866 and 81301940). The authors would also like to thank Yan Jiang Graves and Quentin Gautier for the assistance in CUDA implementation.
Presented at the 55th Annual Meeting of the American Association of Physicists in Medicine, Indianapolis, Indiana, August 4–8, 2013.
REFERENCES
- 1.Jaffray D. A., Siewerdsen J. H., Wong J. W., and Martinez A. A., “Flat-panel cone-beam computed tomography for image-guided radiation therapy,” Int. J. Radiat. Oncol., Biol., Phys. 53, 1337–1349 (2002). 10.1016/S0360-3016(02)02884-5 [DOI] [PubMed] [Google Scholar]
- 2.Sweeney R. A., Seubert B., Stark S., Homann V., Müller G., Flentje M., and Guckenberger M., “Accuracy and inter-observer variability of 3D versus 4D cone-beam CT based image-guidance in SBRT for lung tumors,” Radiat. Oncol. 7, 81 (2012). 10.1186/1748-717X-7-81 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Korreman S., Persson G., Nygaard D., Brink C., and Juhler-Nottrup T., “Respiration-correlated image guidance is the most important radiotherapy motion management strategy for most lung cancer patients,” Int. J. Radiat. Oncol., Biol., Phys. 83, 1338–1343 (2012). 10.1016/j.ijrobp.2011.09.010 [DOI] [PubMed] [Google Scholar]
- 4.Purdie T. G., Moseley D. J., Bissonnette J. P., Sharpe M. B., Franks K., Bezjak A., and Jaffray D. A., “Respiration correlated cone-beam computed tomography and 4DCT for evaluating target motion in stereotactic lung radiation therapy,” Acta Oncol. 45, 915–922 (2006). 10.1080/02841860600907345 [DOI] [PubMed] [Google Scholar]
- 5.Yan D., Vicini F., Wong J., and Martinez A., “Adaptive radiation therapy,” Phys. Med. Biol. 42, 123–132 (1997). 10.1088/0031-9155/42/1/008 [DOI] [PubMed] [Google Scholar]
- 6.Bortfeld T., Jokivarsi K., Goitein M., Kung J., and Jiang S. B., “Effects of intra-fraction motion on IMRT dose delivery: Statistical analysis and simulation,” Phys. Med. Biol. 47, 2203–2220 (2002). 10.1088/0031-9155/47/13/302 [DOI] [PubMed] [Google Scholar]
- 7.Hugo G. D., Yan D., and Liang J., “Population and patient-specific target margins for 4D adaptive radiotherapy to account for intra-and inter-fraction variation in lung tumour position,” Phys. Med. Biol. 52, 257–274 (2007). 10.1088/0031-9155/52/1/017 [DOI] [PubMed] [Google Scholar]
- 8.Harsolia A., Hugo G. D., Kestin L. L., Grills I. S., and Yan D., “Dosimetric advantages of four-dimensional adaptive image-guided radiotherapy for lung tumors using online cone-beam computed tomography,” Int. J. Radiat. Oncol., Biol., Phys. 70, 582–589 (2008). 10.1016/j.ijrobp.2007.08.078 [DOI] [PubMed] [Google Scholar]
- 9.Ben-Josef E., Normalle D., Ensminger W. D., Walker S., Tatro D., Ten Haken R. K., Knol J., Dawson L. A., Pan C., and Lawrence T. S., “Phase II trial of high-dose conformal radiation therapy with concurrent hepatic artery floxuridine for unresectable intrahepatic malignancies,” J. Clin. Oncol. 23, 8739–8747 (2005). 10.1200/JCO.2005.01.5354 [DOI] [PubMed] [Google Scholar]
- 10.Keall P. J., Mageras G. S., Balter J. M., Emery R. S., Forster K. M., Jiang S. B., Kapatoes J. M., Low D. A., Murphy M. J., and Murray B. R., “The management of respiratory motion in radiation oncology report of AAPM Task Group 76,” Med. Phys. 33, 3874–3900 (2006). 10.1118/1.2349696 [DOI] [PubMed] [Google Scholar]
- 11.Sonke J. J., Zijp L., Remeijer P., and van Herk M., “Respiratory correlated cone beam CT,” Med. Phys. 32, 1176–1186 (2005). 10.1118/1.1869074 [DOI] [PubMed] [Google Scholar]
- 12.Kriminski S., Mitschke M., Sorensen S., Wink N. M., Chow P. E., Tenn S., and Solberg T. D., “Respiratory correlated cone-beam computed tomography on an isocentric C-arm,” Phys. Med. Biol. 50, 5263–5280 (2005). 10.1088/0031-9155/50/22/004 [DOI] [PubMed] [Google Scholar]
- 13.Li T., Xing L., Munro P., McGuinness C., Chao M., Yang Y., Loo B., and Koong A., “Four-dimensional cone-beam computed tomography using an on-board imager,” Med. Phys. 33, 3825–3833 (2006). 10.1118/1.2349692 [DOI] [PubMed] [Google Scholar]
- 14.Dietrich L., Jetter S., Tücking T., Nill S., and Oelfke U., “Linac-integrated 4D cone beam CT: First experimental results,” Phys. Med. Biol. 51, 2939–2952 (2006). 10.1088/0031-9155/51/11/017 [DOI] [PubMed] [Google Scholar]
- 15.Lu J., Guerrero T. M., Munro P., Jeung A., Chi P. C. M., Balter P., Zhu X. R., Mohan R., and Pan T., “Four-dimensional cone beam CT with adaptive gantry rotation and adaptive data sampling,” Med. Phys. 34, 3520 (2007). 10.1118/1.2767145 [DOI] [PubMed] [Google Scholar]
- 16.Sonke J. J., Rossi M., Wolthaus J., Van Herk M., Damen E., and Belderbos J., “Frameless stereotactic body radiotherapy for lung cancer using four-dimensional cone beam CT guidance,” Int. J. Radiat. Oncol., Biol., Phys. 74, 567–574 (2009). 10.1016/j.ijrobp.2008.08.004 [DOI] [PubMed] [Google Scholar]
- 17.Yu H. and Wang G., “Compressed sensing based interior tomography,” Phys. Med. Biol. 54, 2791–2805 (2009). 10.1088/0031-9155/54/9/014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wang G. and Yu H., “The meaning of interior tomography,” Phys. Med. Biol. 58, R161–R186 (2013). 10.1088/0031-9155/58/16/R161 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ahmad M. and Pan T., “Target-specific optimization of four-dimensional cone beam computed tomography,” Med. Phys. 39, 5683–5696 (2012). 10.1118/1.4747609 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Li T., Koong A., and Xing L., “Enhanced 4D cone-beam CT with inter-phase motion model,” Med. Phys. 34, 3688–3695 (2007). 10.1118/1.2767144 [DOI] [PubMed] [Google Scholar]
- 21.Chen G. H., Tang J., and Leng S. H., “Prior image constrained compressed sensing (PICCS): A method to accurately reconstruct dynamic CT images from highly undersampled projection data sets,” Med. Phys. 35, 660–663 (2008). 10.1118/1.2836423 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Leng S., Tang J., Zambelli J., Nett B., Tolakanahalli R., and Chen G. H., “High temporal resolution and streak-free four-dimensional cone-beam computed tomography,” Phys. Med. Biol. 53, 5653–5673 (2008). 10.1088/0031-9155/53/20/006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Leng S., Zambelli J., Tolakanahalli R., Nett B., Munro P., Star-Lack J., Paliwal B., and Chen G. H., “Streaking artifacts reduction in four-dimensional cone-beam computed tomography,” Med. Phys. 35, 4649–4659 (2008). 10.1118/1.2977736 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bergner F., Berkus T., Oelhafen M., Kunz P., Pan T., and Kachelrieß M., “Autoadaptive phase-correlated (AAPC) reconstruction for 4D CBCT,” Med. Phys. 36, 5695–5706 (2009). 10.1118/1.3260919 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Rit S., Wolthaus J. W. H., van Herk M., and Sonke J. J., “On-the-fly motion-compensated cone-beam CT using an a priori model of the respiratory motion,” Med. Phys. 36, 2283–2296 (2009). 10.1118/1.3115691 [DOI] [PubMed] [Google Scholar]
- 26.Bergner F., Berkus T., Oelhafen M., Kunz P., Pan T., Grimmer R., Ritschl L., and Kachelrieß M., “An investigation of 4D cone-beam CT algorithms for slowly rotating scanners,” Med. Phys. 37, 5044–5053 (2010). 10.1118/1.3480986 [DOI] [PubMed] [Google Scholar]
- 27.Brock R. S., Docef A., and Murphy M. J., “Reconstruction of a cone-beam CT image via forward iterative projection matching,” Med. Phys. 37, 6212–6220 (2010). 10.1118/1.3515460 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Zhang Q., Hu Y. C., Liu F., Goodman K., Rosenzweig K. E., and Mageras G. S., “Correction of motion artifacts in cone-beam CT using a patient-specific respiratory motion model,” Med. Phys. 37, 2901–2909 (2010). 10.1118/1.3397460 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ahmad M., Balter P., and Pan T., “Four-dimensional volume-of-interest reconstruction for cone-beam computed tomography-guided radiation therapy,” Med. Phys. 38, 5646–5656 (2011). 10.1118/1.3634058 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Brehm M., Berkus T., Oehlhafen M., Kunz P., and Kachelrieß M., presented at the IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC), 2011 (unpublished).
- 31.Gao H., Cai J.-F., Shen Z., and Zhao H., “Robust principal component analysis-based four-dimensional computed tomography,” Phys. Med. Biol. 56, 3181–3198 (2011). 10.1088/0031-9155/56/11/002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Park J. C., Park S. H., Kim J. H., Yoon S. M., Kim S. S., Kim J. S., Liu Z., Watkins T., and Song W. Y., “Four-dimensional cone-beam computed tomography and digital tomosynthesis reconstructions using respiratory signals extracted from transcutaneously inserted metal markers for liver SBRT,” Med. Phys. 38, 1028–1036 (2011). 10.1118/1.3544369 [DOI] [PubMed] [Google Scholar]
- 33.Staub D., Docef A., Brock R. S., Vaman C., and Murphy M. J., “4D Cone-beam CT reconstruction using a motion model based on principal component analysis,” Med. Phys. 38, 6697–6709 (2011). 10.1118/1.3662895 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zheng Z., Sun M., Pavkovich J., and Star-Lack J., “Fast 4D cone beam reconstruction using the McKinnon-Bates algorithm with truncation correction and nonlinear filtering,” Proc. SPIE 7961, 79612U (8pp.) (2011). 10.1117/12.878226 [DOI] [Google Scholar]
- 35.Jia X., Tian Z., Lou Y., Sonke J.-J., and Jiang S. B., “Four-dimensional cone beam CT reconstruction and enhancement using a temporal nonlocal means method,” Med. Phys. 39, 5592–5602 (2012). 10.1118/1.4745559 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ren L., Chetty I. J., Zhang J., Jin J.-Y., Wu Q. J., Yan H., Brizel D. M., Lee W. R., Movsas B., and Yin F.-F., “Development and clinical evaluation of a three-dimensional cone-beam computed tomography estimation method using a deformation field map,” Int. J. Radiat. Oncol., Biol., Phys. 82, 1584–1593 (2012). 10.1016/j.ijrobp.2011.02.002 [DOI] [PubMed] [Google Scholar]
- 37.Wang J. and Gu X., “High-quality four-dimensional cone-beam CT by deforming prior images,” Phys. Med. Biol. 58, 231–246 (2013). 10.1088/0031-9155/58/2/231 [DOI] [PubMed] [Google Scholar]
- 38.Zhang H. and Sonke J. J., “Directional interpolation for motion weighted 4D cone-beam CT reconstruction,” Medical Image Computing and Computer-Assisted Intervention–MICCAI 2012, Lecture Notes in Computer Science, Vol. 7510 (Nice, France, 2012), pp. 181–188 [DOI] [PubMed] [Google Scholar]
- 39.Christoffersen C., Hansen D., Poulsen P., and Sørensen T. S., “Registration-based reconstruction of four-dimensional cone beam computed tomography,” IEEE Trans. Med. Imaging 32(11), 2064–2077 (2013). 10.1109/TMI.2013.2272882 [DOI] [PubMed] [Google Scholar]
- 40.Cooper B. J., O’Brien R. T., Balik S., Hugo G. D., and Keall P. J., “Respiratory triggered 4D cone-beam computed tomography: A novel method to reduce imaging dose,” Med. Phys. 40, 041901 (9pp.) (2013). 10.1118/1.4793724 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.O’Brien R. T., Cooper B. J., and Keall P. J., “Optimizing 4D cone beam computed tomography acquisition by varying the gantry velocity and projection time interval,” Phys. Med. Biol. 58, 1705–1723 (2013). 10.1088/0031-9155/58/6/1705 [DOI] [PubMed] [Google Scholar]
- 42.Fast M. F., Wisotzky E., Oelfke U., and Nill S., “Actively triggered 4d cone-beam CT acquisition,” Med. Phys. 40, 091909 (14pp.) (2013). 10.1118/1.4817479 [DOI] [PubMed] [Google Scholar]
- 43.Ren L., Zhang J., Thongphiew D., Godfrey D. J., Wu Q. J., Zhou S. M., and Yin F. F., “A novel digital tomosynthesis (DTS) reconstruction method using a deformation field map,” Med. Phys. 35, 3110–3115 (2008). 10.1118/1.2940725 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Li R., Jia X., Lewis J. H., Gu X., Folkerts M., Men C., and Jiang S. B., “Real-time volumetric image reconstruction and 3D tumor localization based on a single x-ray projection image for lung cancer radiotherapy,” Med. Phys. 37, 2822–2826 (2010). 10.1118/1.3426002 [DOI] [PubMed] [Google Scholar]
- 45.Li R., Lewis J. H., Jia X., Gu X., Folkerts M., Men C., Song W. Y., and Jiang S. B., “3D tumor localization through real-time volumetric x-ray imaging for lung cancer radiotherapy,” Med. Phys. 38, 2783–2794 (2011). 10.1118/1.3582693 [DOI] [PubMed] [Google Scholar]
- 46.Sidky E. Y. and Pan X., “Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization,” Phys. Med. Biol. 53, 4777–4807 (2008). 10.1088/0031-9155/53/17/021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Feldkamp L., Davis L., and Kress J., “Practical cone-beam algorithm,” JOSA A. 1, 612–619 (1984). 10.1364/JOSAA.1.000612 [DOI] [Google Scholar]
- 48.Lalush D. S. and Tsui B. M., “Improving the convergence of iterative filtered backprojection algorithms,” Med. Phys. 21, 1283–1286 (1994). 10.1118/1.597210 [DOI] [PubMed] [Google Scholar]
- 49.Zeng G. L. and Gullberg G. T., “Unmatched projector/backprojector pairs in an iterative reconstruction algorithm,” IEEE Trans. Med. Imaging 19, 548–555 (2000). 10.1109/42.870265 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Yan H., Wang X., Yin W., Pan T., Ahmad M., Mou X., Cerviño L., Jia X., and Jiang S. B., “Extracting respiratory signals from thoracic cone beam CT projections,” Phys. Med. Biol. 58, 1447–1464 (2013). 10.1088/0031-9155/58/5/1447 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Ruchala K. J., Olivera G. H., Kapatoes J. M., Reckwerdt P. J., and Mackie T. R., “Methods for improving limited field-of-view radiotherapy reconstructions using imperfect a priori images,” Med. Phys. 29, 2590–2605 (2002). 10.1118/1.1513163 [DOI] [PubMed] [Google Scholar]
- 52.Zhen X., Gu X., Yan H., Zhou L., Jia X., and Jiang S. B., “CT to cone-beam CT deformable registration with simultaneous intensity correction,” Phys. Med. Biol. 57, 6807–6826 (2012). 10.1088/0031-9155/57/21/6807 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Gu X., Pan H., Liang Y., Castillo R., Yang D., Choi D., Castillo E., Majumdar A., Guerrero T., and Jiang S. B., “Implementation and evaluation of various demons deformable image registration algorithms on a GPU,” Phys. Med. Biol. 55, 207–219 (2010). 10.1088/0031-9155/55/1/012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Sharp G., Kandasamy N., Singh H., and Folkert M., “GPU-based streaming architectures for fast cone-beam CT image reconstruction and demons deformable registration,” Phys. Med. Biol. 52, 5771–5783 (2007). 10.1088/0031-9155/52/19/003 [DOI] [PubMed] [Google Scholar]
- 55.Folkerts M., Jia X., Choi D., Gu X., Majumdar A., and Jiang S., “SU-EI-35: A GPU optimized DRR algorithm,” Med. Phys. 38, 3403–3416 (2011). 10.1118/1.3611608 [DOI] [Google Scholar]
- 56.Jia X., Yan H., Folkerts M., and Jiang S., “GDRR: A GPU tool for cone-beam CT projection simulations,” Med. Phys. 39, 3890–3890 (2012). 10.1118/1.4735880 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Zhang L., Zhang L., Mou X. Q., and Zhang D., “FSIM: A feature similarity index for image quality assessment,” IEEE Trans. Image Process 20, 2378–2386 (2011). 10.1109/TIP.2011.2109730 [DOI] [PubMed] [Google Scholar]
- 58.Yan H., Cervino L., Jia X., Jiang S. B., “A comprehensive study on the relationship between the image quality and imaging dose in low-dose cone beam CT,” Phys. Med. Biol. 57, 2063–2080 (2012). 10.1088/0031-9155/57/7/2063 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Yan H., Wang X., Folkerts M., Cervino L., Jiang S. B., and Jia X., “Towards the clinical implementation of iterative low-dose cone-beam CT reconstruction in image guided radiation therapy: Solutions for image quality improvement and efficiency boost,” Med. Phys. (submitted). [DOI] [PMC free article] [PubMed]