Reconstruction and Feature Selection for Desorption Electrospray Ionization Mass Spectroscopy Imagery

Abstract

Desorption electrospray ionization mass spectrometry (DESI-MS) provides a highly sensitive imaging technique for differentiating normal and cancerous tissue at the molecular level. This can be very useful, especially under intra-operative conditions where the surgeon has to make crucial decision about the tumor boundary. In such situations, the time it takes for imaging and data analysis becomes a critical factor. Therefore, in this work we utilize compressive sensing to perform the sparse sampling of the tissue, which halves the scanning time. Furthermore, sparse feature selection is performed, which not only reduces the dimension of data from about 10⁴ to less than 50, and thus significantly shortens the analysis time. This procedure also identifies biochemically important molecules for pathological analysis. The methods are validated on brain and breast tumor data sets.

1. DESCRIPTION OF PURPOSE

The development of the technique of desorption electrospray ionization mass spectrometry (DESI-MS) has provided a highly sensitive technique for molecular imaging in the ambient environment with short tissue sample preparation time. This enables greatly improved identification and characterization of the given tissue. In particular, for the critical decisions necessary during intra-operative tumor resection, it is crucial to understand the boundary and infiltration of the tumor with its surrounding tissue. In such cases, DESI-MS can provides a superior discrimination for the assessment of tumor cell concentration, tumor type, and grade.^1–3

The goal is to infer the tissue type and cancer grade with MS scan in the intra-operative environment. The imaging and data analysis time are still critical factors for it to be ultimately used in the intra-operative situation so that such data acquisition and processing time is critical. Moreover, the data acquired from the DESI-MS imaging is huge: roughly 10⁴ numbers are obtained at a single voxel. This ”Big Data” problem constitutes a great opportunity for data analysis and classification, as well as a challenge for handling such data in a near real-time fashion. Hence the necessity to select or extract the important information from such big data sets, and perform the computation in a sparse manner. In addition to reducing the computational load, identifying a sparse sub-set in the rich spectrum of DESI-MS would naturally link with exploring the biochemical significance of the MS data. Indeed, among the 10⁴ values at a single voxel, only less than 10² render themselves as the key chemical substances that differentiate the normal and cancerous tissue. Hence, determining the sparse spectral features would provide indications on which mass/charge ratios (m/z values) are significantly different among various tissues.

2. METHOD

In this work, we propose to address the needs described in the Introduction by employing the compressive sensing (CS) framework. CS and sparse signal representation have been actively studied in the past few years.^{4, 5} They provide an efficient methodology for the purpose of combining data capacity and efficiency for solving problems in big data. In sparse representation theory, it is observed that the many signals are often sparse when represented in a certain basis or dictionary. Such an idea of sparse representation and the related research have now drawn much attention in image restoration,⁶ segmentation,⁷ face detection,⁸ etc. In this work, we propose to use the CS and sparse representation for the reconstruction of DESI-MS spectra and feature selection.

2.1 DESI-MS image reconstruction

When acquiring a DESI-MS image for a tissue sample, the sample is prepared and scanned on an approximately 25 × 25 grid. For each point on the grid, a mass spectrum is acquired. As a result, a DESI-MS image may be described as a function f : Ω ⊂ ℝ² → ℝ^D where D is the number of samples of the m/z values with a typical value of D ≈ 10⁴. For aiding interventional tumor infiltration detection and decision purposes, it is of great advantage to reduce the scanning time of DESI-MS imaging. To that end, we perform sparse scanning and then reconstruct the spectra on the entire domain using the CS technique. Specifically, only a random subset of Ω is scanned and the corresponding spectra are obtained. The entire DESI-MS image is then found via a certain reconstruction technique, which is essentially an l₁ optimization process as formulated below.

Mathematically, M random samples are drawn from {1, 2, …, Q} ≕ ℚ where Q = 25² in the current case. Denote the index set of the M random samples as 𝕄 ≔ {m₁, m₂, …, m_M} ⊂ ℚ and their corresponding positions in Ω as ℙ ≔ {p_i ∈ Ω; i = 1, 2, …, M}. Then, the DESI-MS is only performed on ℙ instead of on the entire Ω. Based on the values f(p_i) ∈ ℝ^D; i = 1, 2, …, M, we can reconstruct the f(Ω) via l₁-norm minimization. Specifically, set ${\mathit{x}}^i={(x_1^i,x_2^i,\dots ,x_M^i)}^{\top }\in {ℝ}^M$ with $x_j^i=f^i({\mathit{p}}_j)$, i = 1, …, D. We wish to find sparse coefficients yⁱ with respect to the basis Ψ ∈ ℝ^Q×Q:

$$\text{min}{\Vert {\mathit{y}}^i\Vert }_1\text{such that}A\mathrm{\Psi }{\mathit{y}}^i={\mathit{x}}^i$$ (1)

where A ∈ ℝ^M×Q is constructed from the Q × Q identity matrix by removing all its i-th rows where i ∉ 𝕄. That is, assuming m_i < m_j; ∀_i < j, A(i, j) = 1 if j = m_i and A(i, j) = 0 otherwise. At convergence, the reconstructed image is computed as f̂ⁱ = Ψyⁱ. The optimization of Equation (1) is repeated for all the i = 1, 2, …, D and the entire spectra on Ω is reconstructed.

2.2 Spectrum feature extraction

The DESI-MS image has a high dimensional (D ≈ 10⁴) range. Such high dimensional data pose computational difficulties in tissue characterization and classification. As a result, extracting fewer “important” features from the raw data will reduce the data analysis load, facilitating the intra-operative usefulness of the method. Furthermore, certain molecules are characteristic for cancerous tissue, which need to be extracted from the entire spectrum. To address both needs, a sparse feature selection is performed. Mathematically, among N spectra g_i ∈ ℝ^D; i = 1, 2, …, N, some are sampled from the cancerous tissue and the others are from normal tissue. The tissue types are recorded as a class variable l = {l₁, l₂, …, l_N} ∈ {−1, 1}^N where l_i = −1 indicates that gi is from normal tissue and l_i = 1 for g_i being from cancerous region. Then, we solve the optimization problem:

$$\mathit{a},b=\underset{\mathit{a}\in {ℝ}^D,b\in ℝ}{\text{arg min}}E(\mathit{a},b);\text{where}E(\mathit{a},b)≔\sum _{i=1}^N\text{max}(0,1-l_i({\mathit{a}}^{\top }{\mathit{g}}_i-b))+\lambda {\Vert \mathit{a}\Vert }_1$$ (2)

In the equation a and b defines the hyperplane separating the two groups and λ > 0 is a regularizing factor.^9–11 Being convex, the above problem can be solved efficiently with global optimality. The resulting a is a sparse vector in which the non-zero locations indicate significant contributions of the spectrum at those m/z values. These selected m/z values and their corresponding weights (a_i values) should provide key insights for chemists and biologists who can further investigate the presence (or lack thereof) of specific chemical substances.

3. EXPERIMENTS AND RESULTS

The proposed methods have been validated on both brain and breast tumor samples. The brain tissue samples were from grade IV astrocytomas obtained from the Brigham and Women's Hospital (BWH) Neurooncology Program Biorepository collection under an IRB approved protocol.¹ The DESI-MS experiments were performed in both the negative and positive ion mode with a 5kV spray voltage, 175 psi N₂ pressure and 1.5 µL/min ow rate. The solvent system has methanol:water=1:1.

3.1 DESI-MS image reconstruction

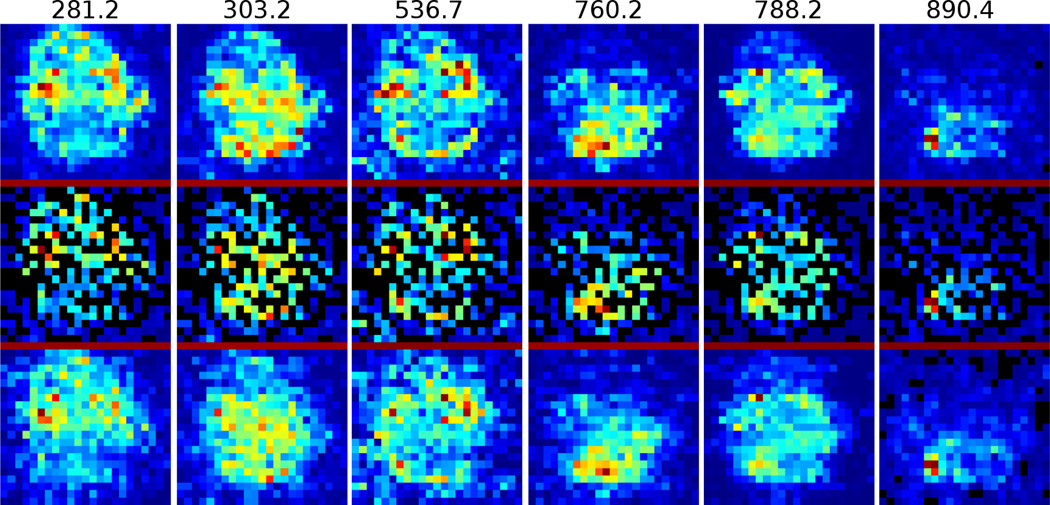
In this experiment, we reconstruct the brain DESI-MS image using only half of the sampling points (pixels) in the original images, that is, M = Q/2. The Ψ in Equation (1) is chosen as the inverse discrete cosine transform matrix. In total, 10 data sets are tested and one is shown in Figure 1. The top figure of each column is the original DESI-MS image. After randomly down-sampling by a half, the figures are shown in the middle row. The reconstructed images are in the bottom row. It can be observed that the bottom row is almost identical to the top row.

Figure 1.

Reconstruction of brain DESI-MS at m/z values from 281.2 to 890.4. Top row: original DESI-MS at the m/z value above; Middle row: random sampled positions; Bottom row: reconstructed images are very close to the original ones at the top.

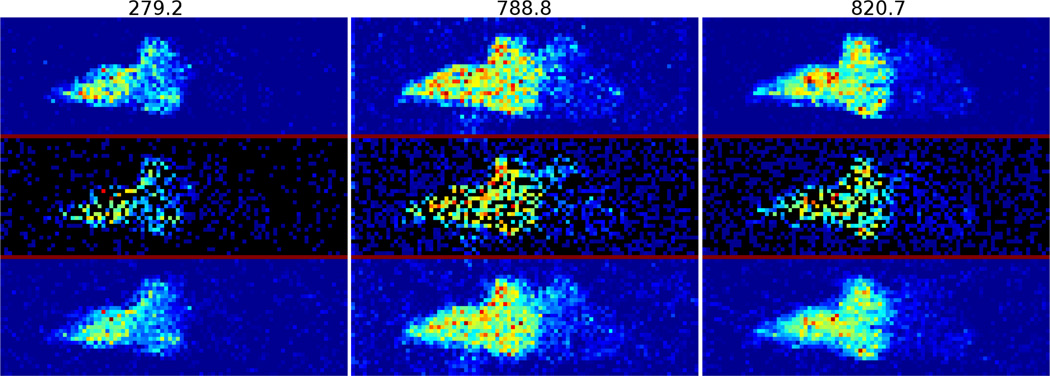
Applying the method to a total of 9 breast DESI-MS data sets, the reconstructed images of one data set at some key m/z values are shown in Figure 2.

Figure 2.

Reconstruction of breast DESI-MS at m/z values from 279.2 to 820.7.

3.2 Feature extraction and validation on brain DESI-MS data

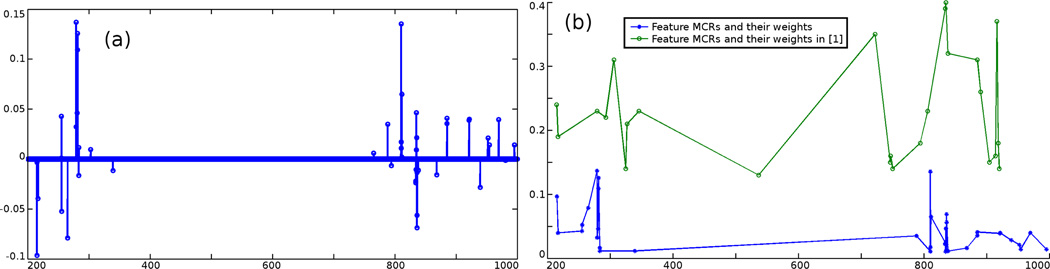
Among the 10⁴ mass/charge ratios, only a few of them are significant for differentiating cancerous and non-cancerous tissues. In order to extract these m/z values, N = 1000 spectra are used for the feature selection among which 500 are from the high tumor concentration region, and the other 500 are from the low tumor concentration region, each determined by histopathological analysis. The λ in Equation (2) is set to 0.01 in all the tests. The extracted feature m/z values are shown in Figure 3. It can be seen that only very few (less than 40) m/z values are identified as “important” for tumor detection purpose among approximately 10⁴ m/z values. Moreover, the computed m/z values and their weights in the classification match quite closely with those verified by chemists and pathologists.¹ This demonstrates the capability of identifying the chemically significant m/z values employing the proposed method.

Figure 3.

(a) The computed vector a: only very few components are non-zero. (b) Feature m/z values and their weights (contributions for differentiating the two classes) computed using the proposed method and those in,¹ in which the chemical significance of the m/z values have been verified by chemists and pathologists.

3.3 Feature extraction and testing on breast DESI-MS data

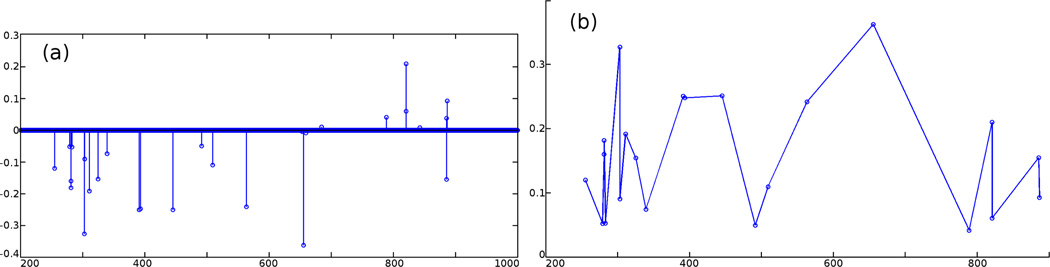
Feature selection has also been applied to breast tumor cases. N = 800 spectra (400 in the tumor region and 400 in the non-tumor region) are used, which give the selected m/z values and their weights for the classification as shown in Figure 4. For breast tumors, no a priori m/z locations have been identified as with the brain case. As a result, the computed results offer a useful indication of the key substances contrasting the normal and cancerous tissues. In fact, the validation of the biochemical significance of the m/z values is one of our key ongoing projects. Furthermore, it is noted that the m/z values shown in Figure 2 for reconstruction are all computed using the preceding selection method. As a result, for the ultimate purpose of online cancer margin delineation, one need only perform the reconstruction at these “important” m/z values. This effectively reduces the image reconstruction task from the entire spectrum of dimension 10⁴ to 40, and significantly increases the imaging and data analysis speed to reduce the critical time in intra-operative tumor resection procedures.

Figure 4.

(a) The computed vector a: only few components are non-zero. (b) Feature m/z values and computed weights.

4. CONCLUSION AND FUTURE RESEARCH DIRECTIONS

In this note, we utilized the CS technique for the reconstruction and feature selection in mass spectrometry imaging. Not only it is able to reduce the imaging time, but also a small number of mass/charge ratios can be identified for the purpose of differentiating between cancerous and non-cancerous tissue. Such techniques will assist in creating a fast and accurate computation framework to be employed in intra-operative DESI-MS imaging for online tumor delineation.

Future research directions include finding the optimal basis/dictionary for reconstruction so that the DESI-MS spectrum is represented as sparsely as possible. Another topic will be to further validate the m/z values identified using the proposed method with chemists. As a result, we will provide a better biochemical interpretation of the data for the specific clinical purpose of interest in this work.

The work has not been submitted for publication or presentation elsewhere.