Integrating Structural and Functional Imaging for Computer Assisted Detection of Prostate Cancer on Multi-Protocol In Vivo 3 Tesla MRI

Abstract

Screening and detection of prostate cancer (CaP) currently lacks an image-based protocol which is reflected in the high false negative rates currently associated with blinded sextant biopsies. Multi-protocol magnetic resonance imaging (MRI) offers high resolution functional and structural data about internal body structures (such as the prostate). In this paper we present a novel comprehensive computer-aided scheme for CaP detection from high resolution in vivo multi-protocol MRI by integrating functional and structural information obtained via dynamic-contrast enhanced (DCE) and T2-weighted (T2-w) MRI, respectively. Our scheme is fully-automated and comprises (a) prostate segmentation, (b) multimodal image registration, and (c) data representation and multi-classifier modules for information fusion. Following prostate boundary segmentation via an improved active shape model, the DCE/T2-w protocols and the T2-w/ex vivo histological prostatectomy specimens are brought into alignment via a deformable, multi-attribute registration scheme. T2-w/histology alignment allows for the mapping of true CaP extent onto the in vivo MRI, which is used for training and evaluation of a multi-protocol MRI CaP classifier. The meta-classifier used is a random forest constructed by bagging multiple decision tree classifiers, each trained individually on T2-w structural, textural and DCE functional attributes. 3-fold classifier cross validation was performed using a set of 18 images derived from 6 patient datasets on a per-pixel basis. Our results show that the results of CaP detection obtained from integration of T2-w structural textural data and DCE functional data (area under the ROC curve of 0.815) significantly outperforms detection based on either of the individual modalities (0.704 (T2-w) and 0.682 (DCE)). It was also found that a meta-classifier trained directly on integrated T2-w and DCE data (data-level integration) significantly outperformed a decision-level meta-classifier, constructed by combining the classifier outputs from the individual T2-w and DCE channels.

1. INTRODUCTION

Prostate cancer (CaP) is the second leading cause of cancer-related deaths among males in the US with an estimated 186,320 new cases in 2008 alone, with 28,660 fatalities^*. The current protocol for CaP detection is a screening test based on elevated levels of the Prostate Specific Antigen (PSA) in the blood. High PSA levels typically call for a blinded sextant transrectal ultrasound (TRUS) guided symmetrical needle biopsy. However, TRUS biopsies have been associated with a significantly lower CaP detection accuracy due to (a) the low specificity of the PSA test, and (b) poor image resolution of ultrasound.¹

1.1 Use of multimodal MRI for CaP detection

Recently, Magnetic Resonance Imaging (MRI) has emerged as a promising modality for CaP detection with several studies showing that 3 Tesla (T) endorectal in vivo T2-weighted (T2-w) imaging yields significantly higher contrast and resolution compared to ultrasound.² An additional advantage offered by MRI is the ability to capture information using different protocols within the same acquisition. Dynamic-Contrast Enhanced (DCE) MRI³ aims to provide complementary information to the structural data captured by T2-w MRI, by characterizing the uptake and washout of paramagnetic contrast agents over time within an organ. Cancerous tissue is known to possess increased vascularity and therefore exhibits a significantly differing uptake profile as compared to normal tissue.³

1.2 Challenges in building an integrated multi-protocol CAD system

Recently several clinical studies have shown that the combination of DCE MRI and T2-w MRI results in improved CaP localization compared to any individual modality.^2–5 The ability to quantitatively integrate multiple MR protocols to build a meta-classifier for CaP detection is impeded by significant technical challenges (described below).

• Data alignment

The different imaging modalities ${\mathcal{C}}^A$ and ${\mathcal{C}}^B$ considered in a multi-protocol system require to be brought into the same spatial plane of reference via image registration. This is especially challenging when the two modalities are structurally different (e.g. histology and T2-w MRI). The aim of multimodal image registration is to find a mapping ψ between ${\mathcal{C}}^A$ and ${\mathcal{C}}^B$ which will bring them into alignment and overcome issues related to modality artifacts and/or deformations.

• Knowledge representation

Following image alignment of the 2 modalities ${\mathcal{C}}^A$ and ${\mathcal{C}}^B$, the objective is to integrate the corresponding feature vectors f^A(x) and f^B(x), where x is a single spatial location (pixel) on ${\mathcal{C}}^A$, ${\mathcal{C}}^B$. However in certain cases, it may not be possible to directly concatenate f^A(x) and f^B(x), owing to dimensionality differences in f^A(x) and f^B(x). For instance f^A(x) may correspond to scalar image intensity values and f^B(x) may be a vector of values (e.g. if ${\mathcal{C}}^A$ and ${\mathcal{C}}^B$ correspond to T2-w and Magnetic Resonance Spectroscopy (MRS) data respectively). One possible solution is to apply a transformation Ω to each of ${\mathcal{C}}^A$ and ${\mathcal{C}}^B$ yielding data mappings Ω(f^A(x)) and Ω(f^B(x)) respectively, such that |Ω(f^A(x))| = |Ω(f^B(x))| , where |S| is the cardinality of any set S. The direct concatenation of Ω(f^A(x)) and Ω(f^B(x to result in a new feature vector f^AB(x) = [Ω(f^A(x)), Ω(f^B(x))] could then be used to train a classifier h^AB(x) to identify x as belonging to one or two of several classes. An alternative approach is to develop individual classifiers h^A(x) and h^B(x) and then combine the individual decisions. Note that h^AB(x), h^A(x), h^B(x) could represent posterior class conditional probabilities regarding class assignment of x or could represent actual class labels (0 and 1 in the 2-class case).

• Fusion approaches

As suggested by Rohlfing et al.,⁶ data fusion could either be via data level integration (creating a consolidated feature vector f^AB(x) and then the meta-classifier h^AB(x)) or via decision level integration (combining h^A(x) and h^B(x) via one of several classifier fusion strategies - product, average, or majority voting).

1.3 Previous work in computer-aided diagnosis of CaP from multi-protocol MRI

Madabhushi et al.⁷ presented a weighted feature ensemble scheme that combined multiple 3D texture features from 4 Tesla ex vivo T2-w MRI to generate a likelihood scene in which the intensity at every spatial location corresponded to the probability of CaP being present. We have presented unsupervised computer-aided diagnosis (CAD) schemes for CaP detection from in vivo T2-w⁸ and DCE-MRI⁹ respectively. In spite of using only single protocols, our CAD systems yielded CaP detection accuracies of over 80%, when evaluated on a per-pixel basis. Vos et al.¹⁰ have described a supervised CAD scheme for DCE MRI prostate data which used pharmacokinetic features and SVM classifiers while examining the peripheral zone of the prostate alone. In [11], a multimodal classifier which integrated texture features from multi-protocol 1.5 T in vivo prostate MRI (including T2-w, line-scan diffusion, and T2-mapping) was constructed to generate a statistical probability map for CaP. We have also presented an unsupervised meta-classifier for the integration of T2-w MRI and MRS data¹² which yielded a higher CaP detection rate compared to either modality alone. Vos et al.,¹³ also recently presented a supervised CAD system to integrate DCE and T2-w intensities, however they reported no improvement in CaP detection accuracy.

1.4 Our solution

In this paper, we present a novel comprehensive CAD scheme which integrates structural and functional prostate MR data for CaP detection. Our methodology seeks to provide unique solutions for each of the challenges in multimodal data integration (data alignment, knowledge representation, and data fusion). Our scheme comprises dedicated prostate segmentation, data alignment, and multi-classifier modules. A novel active shape model (ASM), called MANTRA (Multi-Attribute, Non-initializing, Texture Reconstruction based ASM)¹⁴ is used to to segment out the prostate boundary on the T2-w and DCE MRI images. Bias field correction¹⁵ and MR image intensity standardization¹⁶ techniques are then applied to the image data. T2-w and DCE MRI data are aligned via a novel multimodal registration scheme, COLLINARUS (Collection of Image-derived Non-linear Attributes for Registration Using Splines).¹⁷ COLLINARUS is also applied to align corresponding histological sections from ex vivo prostatectomy specimens to the T2-w and DCE imagery to enable mapping of CaP extent onto T2-w/DCE MRI. The CaP extent thus determined on T2-w and DCE MRI is then used for classifier training and evaluation on the MR imaging protocols. Multiple texture feature representations of T2-w MRI data⁷ which we have previously shown to better discriminate between CaP and benign areas are then extracted from the image scene. We construct meta-classifiers for CaP by (a) fusing the structural T2-w and functional DCE information in the data space and (b) performing decision level integration via fusing classifiers trained separately on the T2-w and DCE data (Figure 1). The classifier that we consider here is the random forest¹⁸ obtained by bagging multiple decision tree classifiers.¹⁹ A basic overview of the system is presented in Figure 2.

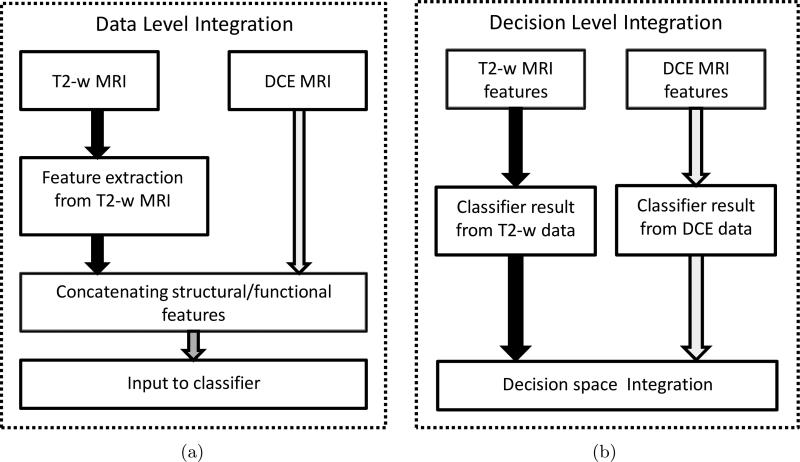
Figure 1.

Constructing a meta-classifier for CaP detection by combining functional and structural data at the (a) data-level, and at the (b) decision-level.

Figure 2.

Flowchart showing different system components and overall organization. Note the convention of using blue arrows to represent the T2-w MRI data flow and red arrows to represent the DCE MRI data flow.

2. EXPERIMENTAL DESIGN

2.1 Data Acquisition

A total of 6 patient studies were obtained using a 3 T Genesis Signa MRI machine at the Beth Israel Deaconess Medical Center. Each of the patients was confirmed to have prostate cancer via core needle biopsies. These patients were then scheduled for a radical prostatectomy. Prior to surgery, MR imaging was performed using an endorectal coil in the axial plane and included T2-w and DCE protocols. The DCE-MR images were acquired during and after a bolus injection of 0.1 mmol/kg of body weight of gadopentetate dimeglumine using a 3-dimensional gradient echo sequence (3D-GE) with a temporal resolution of 1 min 35 sec. Prostatectomy specimens were later sectioned and stained with Haematoxylin and Eosin (H & E) and examined by a trained pathologist to accurately delineate presence and extent of CaP. A pathologist and radiologist working in consort, visually identified 18 corresponding whole mount histological sections (WMHS) and T2-w MRI sections from these 6 studies. Correspondences between T2-w and DCE images were determined via the stored DICOM ^† image header information.

2.2 Notation

We represent a single 2D slice from a 3D MRI T2-w scene as ${\stackrel{‒}{\mathcal{C}}}^{T2}=(C^{T2},f^{T2})$, where C^T2 is a finite 2D rectangular array of pixels c^T2 and f^T2(c^T2) is the T2-w MR image intensity at every c^T2 ∈ C^T2. Similarly ${\mathcal{C}}^{T1,t}=(C,f^{T1,t})$ represents a single planar slice from a spatio-temporal 3D DCE scene where f ^{T 1,t(c)} assigns an intensity value to every pixel c ∈ C at time point t, t ∈ {1, . . . , 7}. A whole mount histological section (WMHS) is similarly denoted as ${\stackrel{‒}{\mathcal{C}}}^H=(C^H,f^H)$. Following image registration via COLLINARUS to DCE-MRI and hence the 2D grid C, T2-w MR images are denoted as ${\mathcal{C}}^{T2}=(C,f^{T2})$ and WMHS are denoted as ${\mathcal{C}}^H=(C,f^H)$. We thus data analyze all image at the DCE-MRI resolution (256 × 256 pixels).

2.3 Prostate boundary segmentation via MANTRA

We have recently developed a Multi-Attribute, Non-initializing, Texture Reconstruction based Active shape model (MANTRA) algorithm¹⁴ for automated segmentation of the prostate boundary on in vivo endorectal MR imagery. MANTRA requires only a rough initialization (such as a bounding-box) around the prostate to be able to segment the boundary accurately. Unlike traditional active shape models (ASMs), MANTRA makes use of local texture model reconstruction as well as multiple attributes with a combined mutual information²⁰ metric to overcome limitations of using image intensity alone in constructing an ASM. MANTRA is applied to segment the prostate boundary for all images ${\stackrel{‒}{\mathcal{C}}}^{T2}$ and ${\mathcal{C}}^{T1,t},t\in \{1,\dots ,7\}$. The main steps involved in MANTRA are,

Step 1 (Training)

Landmarks on the prostate boundary are selected from expert prostate boundary segmentations. A statistical shape model is then constructed by performing Principal Component Analysis (PCA) across the landmarks. Texture features are calculated on training images, and regions of pixels sampled from areas surrounding each landmark point are used to construct a statistical texture model via PCA.

Step 2 (Segmentation)

Regions within a new image are searched for the prostate border and potential boundary landmark locations have pixels sampled from around them. The pixel intensity values within a region associated with a landmark are reconstructed from the texture model as best as possible, and mutual information is maximized between the reconstruction and the extracted region to test whether the location associated with this region may be a boundary location. An ASM is fit to a set of locations selected in this manner, and the process repeats until convergence.

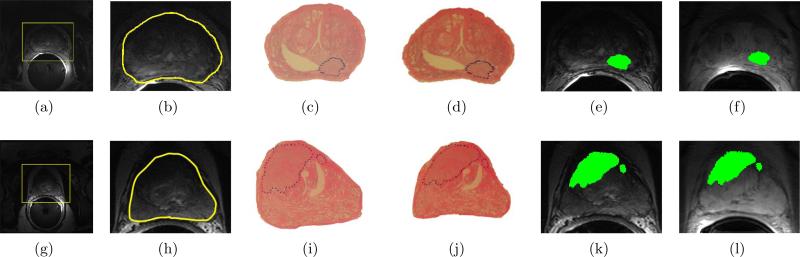
Figure 3 shows sample results of prostate boundary segmentation using MANTRA on 3 T T2-w endorectal in vivo MR images. The original 3 T T2-w images ${\stackrel{‒}{\mathcal{C}}}^{T2}$ are shown in Figures 3(a) and 3(g) with the initializing bounding box in yellow. The final segmentations of the prostate boundary via MANTRA (in yellow) for each image are shown in Figures 3(b) and 3(h).

Figure 3.

(a), (g) 3 T in vivo endorectal T2-w prostate MR images ${\stackrel{‒}{\mathcal{C}}}^{T2}$ for two different patient studies (in each row), with manually placed bounding-boxes (in yellow) which serves as model initialization for MANTRA; (b), (h) resulting prostate boundary segmentations via MANTRA (in yellow). The WMHS ${\stackrel{‒}{\mathcal{C}}}^H$ corresponding to the MRI sections in (a), (g) with CaP extent outlined in blue by a pathologist are shown in (c) and (i), respectively. The result of registration of ${\stackrel{‒}{\mathcal{C}}}^H$ ((c), (i)) to ${\stackrel{‒}{\mathcal{C}}}^{T2}$ ((b), (h)) via COLLINARUS are sh ${\stackrel{‒}{\mathcal{C}}}^{T2}$ own in (d) and (j) respectively. Note the warped appearance of the WMHS in (d) and (j), which is now in spatial correspondence with ${\stackrel{‒}{\mathcal{C}}}^{T2}$ in (b) and (h) respectively. (e) and (k) show the mapping of the CaP extent (in green) from ${\mathcal{C}}^H$ onto ${\mathcal{C}}^{T2}$, following alignment to ${\mathcal{C}}^{T1,5}$ . (f) and (1) show the corresponding mapping of spatial CaP extent (in green) from the newly aligned ${\mathcal{C}}^H$ to ${\mathcal{C}}^{T1,5}$.

2.4 Correct bias field artifacts and intensity non-standardness

We used the ITK BiasCorrector algorithm¹⁵ to correct each of the 2D MR images, ${\stackrel{‒}{\mathcal{C}}}^{T2}$ and ${\mathcal{C}}^{T1,t},t\in \{1,\dots ,7\}$ for bias field inhomogeneity. Intensity standardization¹⁶ was then used to correct for the non-linearity in MR image intensities on ${\stackrel{‒}{\mathcal{C}}}^{T2}$ to ensure that the T2-w intensities have the same tissue-specific meaning across images within every patient study, as well as across different patient studies.

2.5 Multimodal registration of multi-protocol prostate MRI and WMHS

Registration of multimodal imagery is complicated by differences in both image intensities and shape of the underlying anatomy from scenes corresponding to different modalities and protocols. We have previously addressed these challenges in the context of rigid registration using our feature-driven registration scheme, COmbined Feature Ensemble Mutual Information (COFEMI).²⁰ The goal of the COFEMI technique is to provide a similarity measure that is driven by unique low level image textural features to result in a registration that is more robust to intensity artifacts and modality differences, compared to traditional similarity measures (such as MI) which are driven by image intensities alone. However, our specific problem, namely alignment of WMHS and T2-w MRI, is complicated by non-linear differences in the overall shape of the prostate between in vivo T2-w and DCE MRI and ex vivo WMHS as a result of (1) the presence of an endorectal coil during MR imaging and (2) deformations to the histological specimen due to fixation and sectioning.²¹ Consequently, achieving correct alignment of such imagery requires elastic transformations to overcome the non-linear shape differences. Our new COLLINARUS non-rigid registration scheme¹⁷ allows us to make use of the robustness of COFEMI to artifacts and modality differences²⁰ in combination with fully automated non-linear image warping at multiple scales via a hierarchical B-spline mesh grid optimization scheme. Registration by COLLINARUS is critical to account for local deformations that cannot be modeled by any linear coordinate transformations. This technique is used to align all 18 corresponding ${\stackrel{‒}{\mathcal{C}}}^H$, ${\stackrel{‒}{\mathcal{C}}}^{T2}$ and ${\stackrel{‒}{\mathcal{C}}}^{T1,t},t\in \{1,\dots ,7\}$. The main steps involved in COLLINARUS are described below:

1. Initial affine alignment of ${\stackrel{‒}{\mathcal{C}}}^H$ to the corresponding ${\stackrel{‒}{\mathcal{C}}}^{T2}$ via COFEMI²⁰ which enables correction of large scale translations, rotations, and differences in image scale.

2. Automated non-rigid registration of rigidly registered ${\stackrel{‒}{\mathcal{C}}}^H$ from step 1 to ${\stackrel{‒}{\mathcal{C}}}^{T2}$ using our automated feature-driven COLLINARUS technique to correct for non-linear deformations caused by the endorectal coil on ${\stackrel{‒}{\mathcal{C}}}^{T2}$ and histological processing on ${\stackrel{‒}{\mathcal{C}}}^H$.

3. Affine registration of ${\stackrel{‒}{\mathcal{C}}}^{T2}$ to ${\mathcal{C}}^{T1,5}$ (chosen due to improved contrast) via maximization of mutual information (MI) to correct for subtle misalignment and resolution mismatch between the MR protocols, thus bringing all modalities and protocols into spatial alignment. It is known that the individual DCE time point images ${\mathcal{C}}^{T1,t},t\in \{1,\dots ,7\}$, are in implicit registration and hence require no additional alignment step.

4. Calculate combined transformation Φ₁ based on Steps 1-3 to apply to ${\stackrel{‒}{\mathcal{C}}}^H$ resulting in new WMHS scene ${\mathcal{C}}^H=(C,f^H)$, bringing it into alignment with ${\mathcal{C}}^{T1,5}$.

5. Calculate transformation Φ₂ based on Step 3 to apply to ${\stackrel{‒}{\mathcal{C}}}^H$ resulting in new T2-w MR scene ${\mathcal{C}}^{T2}=(C,f^{T2})$, also bringing it into alignment with ${\mathcal{C}}^{T1,5}$.

The CaP extent on ${\mathcal{C}}^H$ is mapped via Φ onto ${\mathcal{C}}^{T1,5}$, yielding the set of CaP pixels G(C), which then corresponds to CaP extent at DCE MRI resolution. Figures 3(b)-(c) and Figures 3(h)-(i) show corresponding ${\stackrel{‒}{\mathcal{C}}}^H$ and ${\stackrel{‒}{\mathcal{C}}}^{T2}$ slices. The results of registering ${\stackrel{‒}{\mathcal{C}}}^H$ and ${\stackrel{‒}{\mathcal{C}}}^{T2}$ in Step 2 are shown in Figures 3(d) and 3(j). Figures 3(e) and 3(k) show the result of mapping CaP extent from ${\mathcal{C}}^H$ (Figures 3(d) and 3(j)) onto ${\mathcal{C}}^{T2}$ (Figures 3(b) and 3(h)) after transforming ${\stackrel{‒}{\mathcal{C}}}^H$ and ${\stackrel{‒}{\mathcal{C}}}^{T2}$ to be in alignment with ${\mathcal{C}}^{T1,5}$. Figures 3(f) and 3(l) show the mapping of CaP extent from ${\mathcal{C}}^H$ onto ${\mathcal{C}}^{T1,5}$.

2.6 Knowledge Extraction

2.6.1 Structural attributes from T2-w MRI

We have previously demonstrated the utility of textural representations of T2-w MR data in discriminating CaP regions from benign areas, as compared to using T2-w MR image intensities alone.⁷ A total of 6 texture features are calculated for ${\mathcal{C}}^{T2}$ and denoted as ${\mathcal{F}}_{\varphi }^{T2}=(C,f_{\varphi }^{T2})$, where $f_{\varphi }^{T2}\left(c\right)$ is the feature value associated with each pixel c ∈ C, and feature operator φ ∈ {1, . . . , 6}. We define a κ-neighborhood centered on c ∈ C as ${\mathcal{N}}_{\kappa }\left(c\right)$ where $\forall e\in {\mathcal{N}}_{\kappa }\left(c\right)$, ∥ e − c ≤ κ, $c\notin {\mathcal{N}}_{\kappa }\left(c\right)$, |S| is the cardinality of any set S, and ∥ . ∥ is the Euclidean distance operator. The 6 texture features that we extract include,

1. First order statistical features (standard deviation operator): This is defined as the standard deviation of the gray level distributions of pixels within local neighborhoods ${\mathcal{N}}_{\kappa }\left(c\right)$ centered about each c C. Figure 4(b) shows the result of applying this operator to the T2-w MR image shown in Figure 4(a).

2. Non-steerable features (Sobel-Kirsch operator): This is used to detect the strength of horizontal edges via the convolution of the following linear operator ${\oint }_1=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 2\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -1\hfill & \hfill -2\hfill & \hfill -1\hfill \end{array}\right]$ with the image ${\mathcal{C}}^{T2}$. Figure 4(c) shows the resulting image upon applying this operator to the T2-w scene shown in Figure 4(a).

3. Second order statistical (Haralick) features: To calculate the Haralick feature images, we first compute a $\mathcal{G}\times \mathcal{G}$ co-occurrence matrix P _d,c,κ within each ${\mathcal{N}}_{\kappa }\left(c\right)$, c ∈ C, such that the value at any location [g₁, g₂] in P_d,c,κ represents the frequency with which two distinct pixels $a,b\in {\mathcal{N}}_{\kappa }\left(c\right)$ with associated image intensities f(a) = g₁, f(b) = g are separated by distance d, where $\mathcal{G}$ is the maximum gray scale intensity in ${\mathcal{C}}^{T2}$ and $g_1,g_2\in \{1,\dots ,\mathcal{G}\}$. A total of 4 Haralick features including intensity average, entropy, correlation, and contrast inverse moment are calculated with $\mathcal{G}=128$, d = 1, κ = 1. Figure 4(d) shows the Haralick feature image (contrast inverse moment) corresponding to the image shown in Figure 4(a).

The extracted T2-w texture features and the T2-w intensity values are concatenated to form a feature vector ${\mathbf{F}}^{T2f}\left(c\right)=[f^{T2}\left(c\right),f_{\varphi }^{T2}\left(c\right)\mid \varphi \in \{1,\dots ,6\}]$ associated with every pixel c ∈ C.

Figure 4.

(a) ${\mathcal{C}}^{T2}$ with CaP extent G(C) superposed in green. Feature scenes for ${\mathcal{C}}^{T2}$ in (a) corresponding to (b) first order statistics (standard deviation), (c) Sobel-Kirsch, and (d) second order statistics (contrast inverse moment). (e) Corresponding time-intensity curves for CaP (red) and benign (blue) regions are shown based on DCE MRI data. Note the significant differences in the uptake and wash-out characteristics.

2.6.2 Functional attributes from DCE MRI

The wash-in and wash-out of the contrast agent within the gland is characterized by varying intensity values across the time-point images ${\mathcal{C}}^{T1,t}$, t ∈ {1, . . . , 7 . Figure 4(e) shows typical time-intensity curves associated with pixels belonging to cancerous (red) and benign (blue) regions respectively.³ It can be seen that cancerous regions have a distinctly steeper uptake and wash-out as compared to the more gradual uptake of benign regions, in turn reflecting the increased vascularity of the CaP regions. The time-point information is concatenated to form a single feature vector F^T1(c) = [f^T1,t(c)|t ∈ {1, . . . , 7}] associated with every pixel c ∈ C.

2.7 Knowledge representation and integration

2.7.1 Data level integration

In this work we adopt the approach of Braun et al.,²² to achieve data level integration of structural and functional attribute vectors F^T1(c) and F^T2f(c) by directly concatenating features in the original high-dimensional feature space. This results in an integrated attribute vector F^T1T2f(c) = [F^T1(c), F^T2f(c)], for c ∈ C. Additionally we consider data level integration in intensity space as F^T1T2(c) = [F^T1(c), f^T2(c)], whereby only the original untransformed protocol intensity values are combined.

2.7.2 Decision level integration

Decision integration refers to the combination of weak classifiers (based on individual modalities) via some pre-decided rule such as averaging or majority voting. Any c ∈ C is assigned to one of several classes (Y = {0, 1} in the 2 class case) via multiple weak classifiers h_n(c), n ∈ {1, . . . , N}. For the 2 class case, h_n(c) {0, 1}. A meta-classifier h(c) is then achieved via one of the several rules mentioned below. For instance, assuming that all h_n(c), c ∈ C, n ∈ {1, . . . , N} are independent, we can invoke the product rule as

$${\mathbf{h}}_{Ind}\left(c\right)=\prod _{n=1}^N{h}_n\left(c\right).$$ (1)

We formulate the averaging rule as

$${\mathbf{h}}_{Avg}\left(c\right)=\frac{1}{N}\sum _{n=1}^N{h}_n\left(c\right).$$ (2)

Another strong classifier h_OR(c) is defined as,

$${\mathbf{h}}_{OR}\left(c\right)=\underset{n}{\mathrm{OR}}\left[h_n\left(c\right)\right],\text{where the logical operator OR is stated as}{\mathbf{h}}_{OR}\left(c\right)=\{\begin{array}{cc}0\hfill & \text{when}\forall n,h_n\left(c\right)=0,\hfill \\ 1\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$ (3)

2.8 Description of classifier ensembles

In the following subsections we describe some of the classifier schemes employed to generate weak and strong classifiers.

2.8.1 Naive Bayes classifier

Consider a set of labeled instances C, where for each c ∈ C, Y (c) ∈ {0, 1}. For all c ∈ C, such that Y (c) = 1, a distribution D¹ is obtained. Similarly ∀c ∈ C such that Y (c) = 0, distribution D ⁰ can be obtained. The posterior conditional probability that c belongs to class Y, given the value of c, can then be calculated as

$$P(Y,D^Y\mid c)=\frac{p(c\mid Y,D^Y)p\left(Y\right)}{\sum _{Y\in \{0,1\}}p(c\mid Y,D^Y)p\left(Y\right)},$$ (4)

where p(c|Y, D^Y ) is the posterior conditional probability for the occurrence of c given class Y , p(Y) is the prior probability of class Y, and the denominator is a normalizing constant. For the T2-w intensity feature set f^T2(c), c ∈ C we can define a naive Bayesian classifier such that Y (c) {0, 1}, where 1 represents the cancer class (∀c ∈ G(C), Y (c) = 1). Then, h^T2(c) = P (Y, D^Y |f^T2(c)), Y = 1, is the posterior class conditional probability that c belongs to class Y , given its T2-weighted image intensity f^T2(c).

2.8.2 Random forests of decision trees

A random forest¹⁸ refers to a classifier ensemble of decision trees based on bootstrap aggregation (or bagging) and uses averaging to combine the results of multiple weak classifiers such that the overall bias and variance across all classifiers is reduced. For a given training set of labeled instances C, we have for each c ∈ C, Y (c) ∈ {0, 1}. We construct subsets of C asĈ , _n ∈ {1, . . . , N} such that ${\widehat{C}}_n\subset C$, $C={\cup }_n{\widehat{C}}_n$. These Ĉ_n are bootstrap replicates so that ${\widehat{C}}_v\cap {\widehat{C}}_w\ne \varnothing ,v,w\in \{1,\dots ,N\}$. From each Ĉ_n we construct a decision tree classifier (C4.5 algorithm¹⁹) as h_n(c) ∈ {0, 1}, n ∈ {1, . . . , N} for all c ∈ C. The final Random Forest classifier result is obtained via Equation (2) as h_Avg(c) ∈ [0, 1].

2.8.3 Classifier prediction results

Given a classifier h, we can obtain a binary prediction result at every c ∈ C by thresholding the associated probability value h(c) ∈ [0, 1]. We define h_ρ(c) as this binary prediction result at each threshold ρ ∈ [0, 1] such that

$${\mathbf{h}}_{\rho }\left(c\right)=\{\begin{array}{cc}1\hfill & \text{when}\mathbf{h}\left(c\right)>\rho ,\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$ (5)

3. EXPERIMENTAL RESULTS AND DISCUSSION

3.1 Description of Experiments

The different feature vectors that are formed from ${\mathcal{C}}^{T1,t}$, ${\mathcal{C}}^{T2}$ and ${\mathcal{F}}_{\varphi }^{T2},\varphi \in \{1,\dots ,6\}$, the associated classifier outputs and resulting binary predictions employed for the specific application considered in this paper are summarized in Table 1. Labeled data ∀c ∈ C for the classifiers are generated based on G(C) such that ∀c ∈ G(c), Y (c) = 1 and Y (c) = 0 otherwise. Decision-level fusion (Section 2.7.2) is performed at every threshold ρ and ∀c ∈ C. This results in two decision level classifiers $({\mathbf{h}}_{Ind,\rho }^{T1,T2f}={\mathbf{h}}_{Avg,\rho }^{T1}\times {\mathbf{h}}_{Avg,\rho }^{T2f})$ and $({\mathbf{h}}_{OR,\rho }^{T1,T2f}=\mathrm{OR}[{\mathbf{h}}_{Avg,\rho }^{T1},{\mathbf{h}}_{Avg,\rho }^{T2f}])$, obtained by invoking the independence assumption and the logical OR operation.

Table 1.

Notation corresponding to different types of data and decision fusion approaches.

Description		Data decision vectors	Classifier outputs	Binary prediction
Data-level fusion	Structural intensity	FT2(c) = [fT2(c)]	hT2(c)	${\mathbf{h}}_{\rho }^{T2}\left(c\right)$
	Functional intensity	FT1(c) = [fT1,t(c)|t ∈ {1,..., 7]	${\mathbf{h}}_{Avg}^{T1}\left(c\right)$	${\mathbf{h}}_{Avg,\rho }^{T1}\left(c\right)$
	Derived structural features	${\mathbf{F}}^{T2f}\left(c\right)=[f^{T2}\left(c\right),f_{\varphi }^{T2}\left(c\right)\mid \varphi \in \{1,\dots ,6\}]$	${\mathbf{h}}_{Avg}^{T2f}\left(c\right)$	${\mathbf{h}}_{Avg,\rho }^{T2f}\left(c\right)$
	Integrated intensities	FT1T2(c) = [FT1(c), FT2(c)]	${\mathbf{h}}_{Avg}^{T1T2}\left(c\right)$	${\mathbf{h}}_{Avg,\rho }^{T1T2}\left(c\right)$
	Integrated structural, textural, functional	FT1T2f(c) = [FT1(c), FT2f(c)]	${\mathbf{h}}_{Avg}^{T1T2f}\left(c\right)$	${\mathbf{h}}_{Avg,\rho }^{T1T2f}\left(c\right)$
Decision-level fusion	Independent classifiers	${\mathbf{h}}_{Avg,\rho }^{T1}\times {\mathbf{h}}_{Avg,\rho }^{T2f}$	${\mathbf{h}}_{Ind}^{T1,T2f}\left(c\right)$	${\mathbf{h}}_{Ind,\rho }^{T1,T2f}\left(c\right)$
	Majority voting of classifiers	$\mathrm{OR}[{\mathbf{h}}_{Avg,\rho }^{T1},{\mathbf{h}}_{Avg,\rho }^{T2f}]$	${\mathbf{h}}_{OR}^{T1,T2f}\left(c\right)$	${\mathbf{h}}_{OR,\rho }^{T1,T2f}\left(c\right)$

3.2 Evaluation of classification schemes

Based on the binary prediction results β(c), $\beta \in \{{\mathbf{h}}_{\rho }^{T2},{\mathbf{h}}_{Avg,\rho }^{T1},{\mathbf{h}}_{Avg,\rho }^{T2f},{\mathbf{h}}_{Avg,\rho }^{T1T2},{\mathbf{h}}_{Avg,\rho }^{T1T2f},{\mathbf{h}}_{Ind,\rho }^{T1,T2f},{\mathbf{h}}_{OR,\rho }^{T1,T2f}\}$, ∀c ∈ C, Receiver Operating Characteristic (ROC) curves representing the trade-off between CaP detection sensitivity and specificity can be generated. The vertical axis of the ROC curve is the true positive rate (TPR) or sensitivity, and the horizontal axis is the false positive rate (FPR) or 1-specificity and each point on the curve corresponds to the sensitivity and specificity of detection of the classification for some ρ ∈ [0, 1]. For any scene , the CaP detection result obtained by the classifiers described in Table 1 is given as ${\Psi }_{\rho }^{\beta }\left(C\right)=\{c\mid \beta \left(c\right)=1\}$, c ∈ C. For each ${\Psi }_{\rho }^{\beta }\left(C\right)$ and corresponding CaP extent G(C), sensitivity (SN) and specificity (SP{) are calculated

$$S{N}_{\beta ,\rho }=1-\frac{\mid G\left(C\right)-{\Psi }_{\rho }^{\beta }\mid }{\mid G\left(C\right)\mid }\text{and}S{P}_{\beta ,\rho }=1-\frac{\mid {\Psi }_{\rho }^{\beta }-G\left(C\right)\mid }{\mid C-G\left(C\right)\mid }.$$ (6)

A 3-fold randomized cross-validation procedure is used when testing the system, whereby from the 18 images, 3 sets of 6 slices each are formed. During a single cross-validation run, 2 out of the 3 sets are chosen (corresponding to 12 MR images) as training data while the remaining set of 6 images are used as testing data. The final result is generated for each test image based on the feature sets and procedures as described previously. This process is repeated until all 18 images are classified once within a cross-validation run. Randomized cross-validation is repeated 25 times for different sets of training and testing slices.

Average ROC curves for each classifier were generated by fitting a smooth polynomial through the ROC curve generated for each image to allow averaging over all 18 images, and then averaging across all 25 cross-validation runs. Mean and standard deviation of Area Under the ROC (AUC) values for each of the classifiers was calculated over 25 runs. The operating point θ on the ROC curve is defined as value of ρ which yields detection SN, SP that is closest to 100% sensitivity and 100% specificity (the top left corner of the graph). The accuracy of the system at the threshold θ corresponding to the operating point, as well as the AUC values for each of the average curves generated previously is used in our quantitative evaluation.

3.3 Qualitative Results

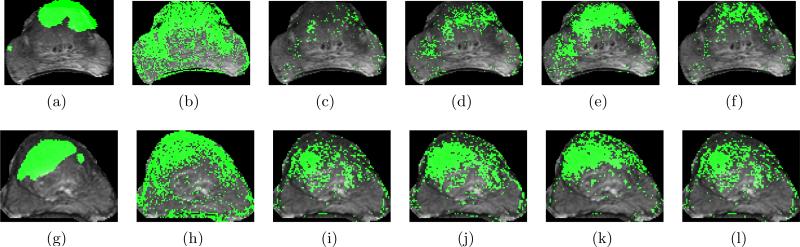
Sample detection results are shown in Figure 5 with each row corresponding to a different study. Figures 5(a) and 5(g) show overlays of G(C) in green on ${\mathcal{C}}^{T2}$ (obtained via COLLINARUS, Section 2.5). In Figures 5(b)-(f) and Figures 5(h)-(l) the binary prediction for CaP at the operating point threshold θ via different classifiers has been overlaid on ${\mathcal{C}}^{T2}$ and shown in green. The results in Figures 5(e) and 5(k) corresponding to the integration of structural T2-w texture features and the functional intensity features $\left({\mathbf{h}}_{Avg,\theta }^{T1T2f}\right)$ show accurate segmentations of CaP when compared to the ground truth in Figures 5(a) and 5(g) respectively. Compare this result (Figures 5(e) and 5(k)) with that obtained from the individual modalities (Figures 5(b), (h) for ${\mathbf{h}}_{\theta }^{T2}$, Figures (c), (i) for ${\mathbf{h}}_{Avg,\theta }^{T1}$), data level fusion in intensity space (Figures 5(d), 5(j) for ${\mathbf{h}}_{Avg,\theta }^{T1T2}$) as well as decision level fusion of these modalities (Figures 5(f), 5(l) for ${\mathbf{h}}_{OR,\theta }^{T1,T2f}$).

Figure 5.

(a) and (g) G(C) superposed on ${\mathcal{C}}^{T2}$ and highlighted in green. CaP detection results (in green) are shown corresponding to (b), (h) ${\mathbf{h}}_{\theta }^{T2}$; (c), (i) ${\mathbf{h}}_{Avg,\theta }^{T1}$ ; (d), (j) ${\mathbf{h}}_{Avg,\theta }^{T1T2}$ ; (e), (k) ${\mathbf{h}}_{Avg,\theta }^{T1T2f}$; (f), (l) ${\mathbf{h}}_{OR,\theta }^{T1,T2f}$ at the operating-point threshold θ, where θ ∈ [0, 1]. Note the significantly improved CaP detection via the integrated structural, functional classifiers in (e) and (k) as compared to the others.

3.4 Quantitative Results

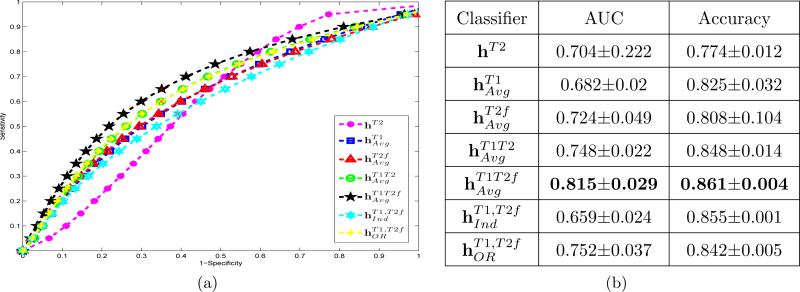
Figure 6(a) shows average Receiver-Operating Characteristic (ROC) curves obtained via averaging corresponding results across 18 slices and 25 cross-validation runs. The highest AUC value corresponds to the classifier ${\mathbf{h}}_{Avg}^{T1T2f}$ (shown in black), while the lowest is for h^T2 (shown in purple). AUC values averaged over 18 slices and 25 cross validation runs for each of the different classifiers are summarized in Table 6(b) with corresponding standard deviations. Paired student t-tests were conducted using the AUC and accuracy values at the operating point of the average ROC curves corresponding to each of 25 cross validation runs, with the null hypothesis being no improvement in performance of ${\mathbf{h}}_{Avg}^{T1T2f}$ when compared to the remaining classifiers (Table 2). The significantly superior performance (p < 0.05) when using ${\mathbf{h}}_{Avg}^{T1T2f}$ suggests that integrating structural textural features and functional information directly at the data level offers the most optimal results for CaP detection.

Figure 6.

(a) Average ROC curves across 18 slices and 25 cross validation runs. different colors correspond to different classifiers. The best performance corresponds to the classifier based on integration of structural and functional data $\left({\mathbf{h}}_{Avg}^{T1T2f}\right)$, in black. (b) Average and standard deviation of AUC and accuracy values for different classifiers averaged over 18 slices and 25 cross-validation runs.

Table 2.

p values for a paired student t-test comparing the improvement in CaP detection performance (in terms of AUC and accuracy) of ${\mathbf{h}}_{Avg}^{T1T2f}$ with the other classifiers (Table 1) across 25 cross-validation runs and over 18 slices.

	hT2	${\mathbf{h}}_{Avg}^{T1}$	${\mathbf{h}}_{Avg}^{T2f}$	${\mathbf{h}}_{Avg}^{T1T2}$	${\mathbf{h}}_{Ind}^{T1,T2f}$	${\mathbf{h}}_{OR}^{T1,T2f}$
Accuracy	1.742e-40	2.282e-19	4.421e-4	2.960e-13	1.233e-54	4.306e-07
AUC	0.013	9.281e-23	4.689e-11	1.255e-17	1.811e-18	5.894e-13

4. CONCLUDING REMARKS

In this paper we have presented an integrated system for prostate cancer detection via fusion of structural and functional information from multi-protocol (T2-w and DCE) 3 T in vivo prostate MR images. Our solution provides a comprehensive scheme for prostate cancer detection, with different automated modules to handle the individual tasks. The prostate region of interest is extracted via our automated segmentation scheme, MANTRA. Our recently developed multimodal image registration scheme, COLLINARUS, is used to register whole-mount histological sections and the multi-protocol MR data, as well as align T2 and DCE protocols prior to integration. Texture features are used to quantify regions on T2-w MRI and functional intensity information is used from DCE MRI. Detection results using multiple combinations of structural and functional MR data are quantitatively evaluated against ground truth estimates for cancer presence and extent. Additionally we have compared the performance of classifiers generated via data-level and decision-level integration. The fusion of DCE-MR functional information with extracted T2-w MR structural information in data space was found to perform statistically significantly better as compared to all other decision and data level classifiers, with an average AUC value of 0.815 and an accuracy value of 0.861. Future work will focus on validating these results on a larger cohort of data.