Relative object detectability (ROD): a new metric for comparing x-ray image detector performance for a specified object of interest

Abstract

Relative object detectability (ROD) quantifies the relative performance of two image detectors for a specified object of interest by taking the following ratio: the integral of detective quantum efficiency of a detector weighted by the frequency spectrum of the object divided by that for a second detector. Four different detectors, namely the micro-angiographic fluoroscope (MAF), the Dexela Model 1207 (Dex) and Hamamatsu Model C10901D-40 (Ham) CMOS x-ray detectors, and a flat-panel detector (FPD) were compared. The ROD was calculated for six pairs of detectors: (1) Dex/FPD, (2) MAF/FPD, (3) Ham/FPD, (4) Dex/Ham, (5) MAF/Ham and (6) MAF/Dex for wires of 5 mm fixed length, solid spheres ranging in diameter from 50 to 600 microns, and four simulated iodine-filled blood vessels of outer diameters 0.4 and 0.5 mm, each with wall thicknesses of 0.1 and 0.15 mm.

Marked variation of ROD for the wires and spheres is demonstrated as a function of object size for the various detector pairs. The ROD of all other detectors relative to the FPD was much greater than one for small features and approached 1.0 as the diameter increased. The relative detectability of simulated small iodine-filled blood vessels for all detector pairs was seen to be independent of the vessel wall thickness for the same inner diameter. In this study, the ROD is shown to have the potential to be a useful figure of merit to evaluate the relative performance of two detectors for a given imaging task.

1. INTRODUCTION

Metrics help us to quantify image receptor performance in a reliable and comprehensive manner. Modulation transfer function (MTF) and detective quantum efficiency (DQE) are commonly used to characterize and compare the performance of x-ray imaging detectors. They indicate the essential measures of detector performance but are not sufficient to assess the relative performance of detectors for a specified imaging task. In this work, we present a metric that quantifies the relative performance of two detectors regarding detectability of specified objects and that could be used as a figure of merit for relative performance evaluation of the two detectors for a given imaging task. Other entirely experimental direct measurements of specific task relative detector performance in terms of contrast signal to noise comparisons are also being investigated by our group¹.

2. METHODS AND MATERIALS

The noise equivalent quanta (NEQ), which gives the output signal-to-noise ratio squared (SNR²_out) as function of spatial frequency, provides an absolute measure of output image quality by taking both the signal and noise transfer characteristics of the detector into account. If the NEQ is weighted at each frequency with the square of the absolute value of the Fourier Transformation of an object [OBJ(u,v) where ‘u’ and ‘v’ are frequency domain variables], the output SNR could be designated as the ‘weighted (SNR²_out)’.

The detectability² of the object in the radiographic image is proportional to the ‘weighted (SNR²_out)’ or

$$\mathit{Detectability}\propto \iint {\mid \mathit{OBJ}(u,v)\mid }^2\times \mathit{NEQ}(u,v)$$ (1)

The NEQ in Eq. 1 can be replaced by the DQE to quantify the efficiency of the detectability for the detector relative to the input signal to noise ratio squared. Thus, taking the ratio of two such detectabilities corresponding to two different detectors for a specified object gives the metric of Relative Object Detectability (ROD) (Eq. 2), which quantifies the relative detectability performance of two x-ray imaging detectors for a given object detection task.

$$\mathit{ROD}=\frac{\iint {\mid \mathit{OBJ}(u,v)\mid }^2{\mathit{DQE}}_1(u,v)dudv}{\iint {\mid \mathit{OBJ}(u,v)\mid }^2{\mathit{DQE}}_2(u,v)dudv}$$ (2)

An object function ‘obj(x,y)’ is defined here corresponding to an object in air as shown in Eq. 3, which is the subject position-dependent difference signal relative to the background. Although for this work an attenuation coefficient is used for a single energy equal to the mean energy of the RQA5 spectrum (54 keV), the derived position-dependent signal may more accurately be obtained by using a complete beam spectrum and the object’s energy dependent attenuation coefficient. By taking the Fourier Transform of this object function, the frequency spectrum of that object distribution is obtained (Eq. 4).

$$\mathit{obj}(x,y)=\frac{(\mathit{background}-\mathit{signal})}{\mathit{background}}=\frac{(N_0-N_0{e}^{-\mu t(x,y)})}{N_0}=(1-e^{-\mu t(x,y)})$$ (3)

$$\mathit{OBJ}(u,v)=\iint \mathit{obj}(x,y)e^{-i2\pi (ux+vy)}dxdy$$ (4)

Using this formulation, frequency spectra were generated for 5 mm long Al wires and solid spheres of blood ranging in diameter from 50 to 600 μm. The figures 1(a) to 2(b) show the frequency spectrum of a few selected objects. The frequency spectra of the objects are shown up to 12 cycles/mm in the figures because the amplitude becomes negligible beyond that, especially for diameters beyond 0.25 mm. It is very clear from figures 1(b) and 2(b) that as the size of the object increases the low frequency content of the object increases.

Figure 1.

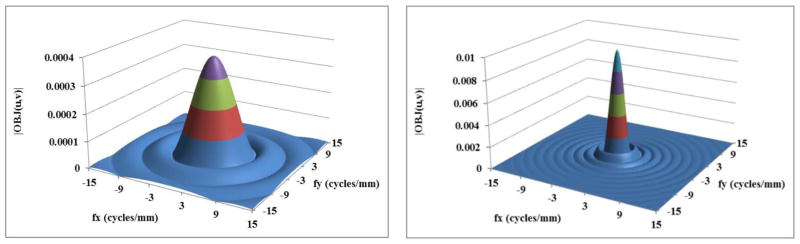
Figure 1(a) Frequency spectrum of a sphere of diameter 0.2 mm; (b) sphere of diameter 0.6 mm.

Figure 2.

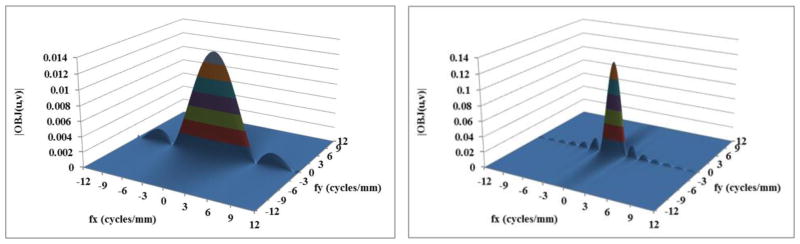
Figure 2(a) Frequency spectrum of a wire of length 5 mm and diameter 0.2 mm; (b) wire of length 5 mm and diameter 0.6 mm.

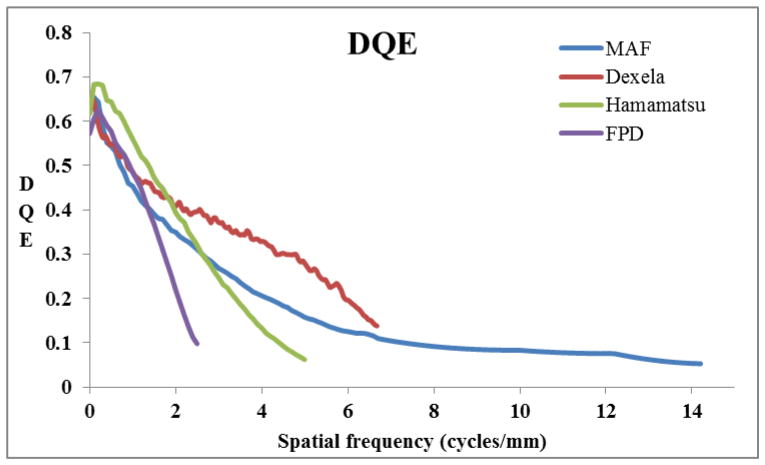
Four different detectors, namely the micro-angiographic fluoroscope (MAF³) (pixel size 35 μm), Dexela 1207 CMOS x-ray detector (Dex) (pixel size 75 μm), Hamamatsu C10901D-40 CMOS x-ray detector (Ham) (pixel size 100 μm) and a flat panel detector (FPD), Paxscan 2020 (pixel size 194 μm) were used to evaluate their relative performance regarding detectability of the simulated objects. The DQE of each detector is shown in Fig. 3. The ROD was calculated for the following six pairs of detectors having the DQE of the first one in the numerator: (1) Dex/FPD, (2) MAF/FPD, (3) Ham/FPD, (4) Dex/Ham, (5) MAF/Ham and (6) MAF/Dex.

Figure 3.

DQE of four detectors evaluated for relative performance

For calculating the integrals shown in equation (2), the product of the two-dimensional DQE of the detector, which was obtained by rotating the one-dimensional DQE of the detector in the frequency domain, and the power spectrum of the object (|OBJ(u,v)|² ) was integrated up to the Nyquist frequency of each detector. The ROD for a pair of detectors was calculated by taking the ratio of two such integrals for two different detectors for a given object. This whole methodology was tested by using objects for which the results are well known. The first object was a uniform background and the second was a delta impulse function. The predicted results were respectively the ratio of DQEs at zero frequency and ratio of the area under the DQE curves.

Once it was verified that the calculation was working, more complex objects were considered such as solid wires and spheres. Although not shown in detail in this paper, previous calculations had shown that the shape rather than the specific material had the greatest effect on the ROD calculation. In this work the wire was taken to be aluminum and the sphere was of blood. The ROD was next used to determine the relative performances of the pairs of detectors regarding detectability of four simulated blood vessels of fixed length of 10 mm filled with iodine where the outer diameters were 0.4 mm and 0.5 mm each with wall thicknesses of 0.1 mm and 0.15 mm. Mass attenuation coefficient values for aluminum, blood and iodine were taken from the NIST website⁴.

3. RESULTS

Figures 4(a) and 4(b) show the ROD for solid spheres and figures 5(a) and 5(b) show the ROD for wires. For the MAF/FPD, MAF/Ham, Dex/Ham and MAF/Dex ratios, the ROD starts with a value greater than one at 50 microns and decreases monotonically with diameter and goes below one after a certain value of diameter (say D₀) for a particular pair of detectors in the case of spheres. For the other two pairs, Dex/FPD and Ham/FPD, the ROD curve shows the same general shape approaching a value of 1 as the diameter is increased. This implies that the detector in the numerator performs better relative to the detector in the denominator up to a given D₀ which marks the reversal of better performance for the same pair of detectors. But this reversal of better performance beyond D₀ is not as dramatic as it is for the values less than D₀.

Figure 4.

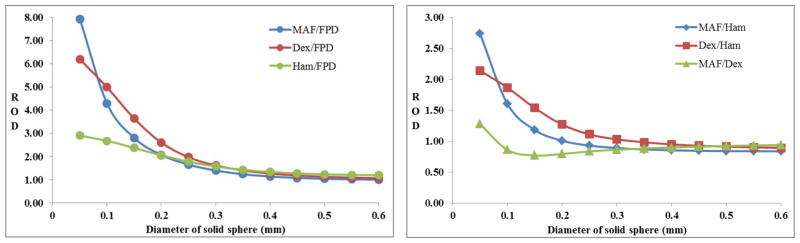
Figure 4(a): ROD vs. diameter of solid sphere for MAF, Dexela and Hamamatsu compared to the FPD; (b) same for the other three pairs of detectors.

Figure 5.

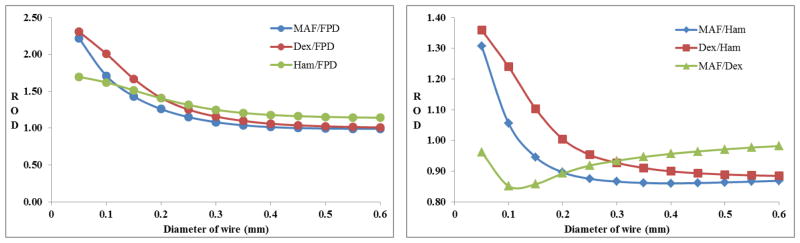
Figure 5(a): ROD vs. diameter of wire for MAF, Dexela and Hamamatsu compared to the FPD; (b) same for the other three pairs of detectors.

In the case of the wire we observe a similar trend for ROD curves for all the pairs of detectors except one difference. The ROD for the MAF/Dex pair is less than one at 50 microns which was greater than one in the case of sphere. If the size gets larger and larger, the ROD tends to the limit of the ratio of DQEs at zero frequency for each pair but showing the same upward trend with decreasing diameter. This is evident from the ROD plot for the MAF/Ham in the case of the wire (Fig 5b) which shows an upward trend after reaching the minimum as the ratio of DQEs of the MAF and Hamamatsu at zero frequency is one.

Table 1 shows the ROD values for the same pairs of detectors regarding detectability of four different simulated vessels (A, B, C and D) and indicates the relative performance of a detector compared to the other regarding relative visibility of blood vessels. The relative performances of detectors are very similar for the same inner diameter even if the wall thickness increases by 50 % (compare A to D).

Table 1.

The ROD for all six pairs of detectors for four different iodine-filled blood vessels.

Blood vessel	Diameter		Thickness	ROD
	Outer (mm)	Inner (mm)	of wall(mm)	$\frac{\mathit{MAF}}{\mathit{FPD}}$	$\frac{\mathit{Dex}}{\mathit{FPD}}$	$\frac{\mathit{Ham}}{\mathit{FPD}}$	$\frac{\mathit{MAF}}{\mathit{Ham}}$	$\frac{\mathit{Dex}}{\mathit{Ham}}$	$\frac{\mathit{MAF}}{\mathit{Dex}}$
A	0.4	0.2	0.10	1.21	1.34	1.36	0.89	0.98	0.91
B	0.4	0.1	0.15	1.55	1.81	1.53	1.01	1.18	0.86
C	0.5	0.3	0.10	1.06	1.12	1.22	0.87	0.92	0.94
D	0.5	0.2	0.15	1.20	1.33	1.36	0.89	0.98	0.91

4. DISCUSSION

The ROD depends upon how the DQEs of the detectors get weighted by the power of the object (|OBJ(u,v)|²). As the size of the object decreases the power (|OBJ(u,v)|²) contained in the high frequency range of the spectrum increases, therefore, the high resolution detectors (MAF and Dexela) having nonzero DQE in high frequency range perform better than the Hamamatsu and the FPD. As the size of the object increases the power (|OBJ(u,v)|²) contained in the low frequency range of the spectrum increases giving more weight to DQE values in the low frequency range; therefore, the detector with high DQE in the low frequency range compared to the other would perform better. This is the reason why there was reversal of the performance for the pairs MAF/FPD, MAF/Ham and Dex/Ham at a particular diameter, D₀. But the reversal was not dramatic because the DQE of these four detectors has no dramatic variation in the low frequency range. This also explains why the ROD decreases with diameter because power contained in the high frequency range becomes negligible; therefore, the performance of the detectors in the numerator (having higher Nyquist compared to the detector in the denominator) started approaching the performance of the detector in the denominator whose performance was dominated mainly by its low frequency DQE. It is noteworthy that the ROD for the MAF/Dex was greater than one for the 0.05 mm sphere whereas it became less than one in the case of the wire of the same diameter or the blood vessels. The case of the MAF/Dex is an interesting case of two detectors where one has very high Nyquist (14.2 cycles/mm) but lower DQE (MAF) while the other one has lower Nyquist (6.67 cycles/mm) but higher DQE (Dexela) for all frequency ranges except for a small overlap in the very low frequency range (0–1 cycle/mm). The metric of ROD may be helpful to predict the relative performances regarding detectability of small objects; however, the effect of aliasing for the Dexela on detectability of these small objects may have to be considered in more detail.

5. CONCLUSIONS

The metric of ROD is capable of assessing the relative performance of two detectors regarding detectability of specific objects. It has the following benefits:

1. ROD gives a quantitative measure of relative performance of two detectors regarding detectability of an object of interest for a given set of imaging conditions.

2. The results depend primarily upon the geometry of the object and the DQE of the detectors.

3. The relative performance evaluation done by this metric is very comprehensive as it makes use of the frequency domain which contains comprehensive information about both the object and the detectors.

4. It may be useful to make predictions regarding the relative detectability of specific objects and conditions such as the ones shown in this study, i.e. blood vessels, and endovascular devices.

In endovascular image-guided interventions, better visibility of devices and pathology is crucial for effective treatment. The ROD enables the relative performances of detectors to be compared with respect to the specific object frequencies and this may help in selecting the appropriate detector for a clinical task. A G-ROD (a generalized ROD) could further be developed for the whole imaging system to compare the relative performance of detectors in a real clinical situation by using the metric generalized detective quantum efficiency (GDQE)⁵ which includes the effect of scatter and geometrical un-sharpness. Thus the potential for the ROD and G-ROD to become valuable figures of merit when comparing the relative performance of two detectors regarding detectability of an object of interest warrants further investigation.