Recent development and application of constant pH molecular dynamics

Abstract

Solution pH is a critical environmental factor for chemical and biological processes. Over the last decade, significant efforts have been made in the development of constant pH molecular dynamics (pHMD) techniques for gaining detailed insights into pH-coupled dynamical phenomena. In this article we review the advancement of this field in the past five years, placing a special emphasis on the development of the all-atom continuous pHMD technique. We discuss various applications, including the prediction of pK_a shifts for proteins, nucleic acids and surfactant assemblies, elucidation of pH-dependent population shifts, protein-protein and protein-RNA binding, as well as the mechanisms of pH-dependent self-assembly and phase transitions of surfactants and peptides. We also discuss future directions for the further improvement of the pHMD techniques.

1 Introduction

A change in solution acidity or pH is a driving force for many important biological processes. For example, ATP synthase utilizes a transmembrane pH gradient to synthesize cellular ATP [1]. Driven by the trans-membrane proton gradient, the multidrug efflux pump in gram-negative bacteria undergoes conformational changes to extrude antibiotics out of the cell [2]. The influenza M2 proton channel is activated by the low pH in the endosome to initiate viral uncoating [3]. The prion protein can misfold under low pH conditions to form infectious prion particles [4].

Traditional molecular dynamics (MD) simulations are performed with fixed protonation states, whereby solution pH is approximately taken into account by assigning the protonation states based on a comparison between the pH and model pK_a’s (pK_a’s of model compounds in solution) or the predicted values using empirical methods such as PROPKA [5] and H++ [6]. The former is not accurate because the pK_a’s in protein can significantly differ from the model values. The latter relies on a static structure and often give large error if the protein is flexible [7] or the residues are highly buried [8]. In addition, by fixing the protonation states, dynamical processes coupled to a change in protonation states cannot be directly studied. Lastly, the condition of coexisting protonated and deprotonated states cannot be simulated with fixed protonation states.

To more accurately include pH effects, a class of methods known as constant pH molecular dynamics (pHMD) emerged over the past decade, which allow the protonation states of titratable sites to be determined during the dynamics simulation at a specified pH [9, 10, 11, 7]. These methods opened a door to detailed mechanistic studies of pH-dependent conformational processes. In this review article we will discuss the development of the field as well as application studies in the past five years giving more emphasis to the work from our group.

2 Recent development of discrete constant pH molecular dynamics

Based on the representation of protonation states and the way they are sampled, pHMD methods can be categorized into two types: discrete pHMD (DpHMD) and continuous pHMD (CpHMD). In the DpHMD (also known as stochastic pHMD), dynamics is periodically interrupted by the Monte Carlo (MC) sampling to update the protonation states of titratable sites. The idea of DpHMD was first proposed by Baptista and coworkers, where they applied Poisson-Boltzmann continuum electrostatics calculation to estimate the energies for the MC move while running molecular dynamics in fully explicit solvent [12]. Following this work, several versions of DpHMD methods have been developed, which mainly differ in the solvent models used for the MC and MD steps. Of particular note is the method implemented in the AMBER package [13] originally developed by the McCammon group [14] and later extended by the Roitberg group [15], which employs the Generalized-Born (GB) implicit-solvent model for the Monte-Carlo step and molecular dynamics. Below we will discuss recent improvement of the DpHMD methods, while directing the reader to the previous reviews for the breadth of these methods [9, 10, 11, 7].

Due to the microscopic coupling between conformational dynamics and protonation-state sampling in pHMD, macroscopic pK_a values converge slowly [9]. This issue was first addressed by the Brooks group by incorporating the temperature replica-exchange (TREX) protocol to promote conformational sampling in the CpHMD method [16] (see discussion of CpHMD below). Using nine diverse proteins as a test bed, the TREX-CpHMD technique was demonstrated to deliver more accurate pK_a values that converge within 500 ps – 1 ns per replica [16]. The TREX protocol was later adopted by the Roitberg group in DpHMD [15]. McCammon and coworkers coupled DpHMD with accelerated MD, demonstrating faster convergence and more accurate pK_a calculation for several residues in the hen egg-white lysozyme (HEWL) [17]. More recently, Itoh et. al. developed the pH-based replica-exchange method for the DpHMD, which exchanges solution pH to directly enhance sampling of the protonation states [18]. This method was implemented by the Roitberg group in the GB-based DpHMD module in the AMBER package [13] and tested on the pK_a calculation for HEWL [19].

3 Recent development of continuous constant pH molecular dynamics

In contrast to the MC/MD protocol used in DpHMD, CpHMD first introduced by Brooks and coworkers [20, 21], draws the idea from the λ-dynamics approach for free-energy simulations [22]. In CpHMD, each titratable site of the protein is assigned a λ variable, also known as the titration coordinate, which continuously evolves between 0 and 1, representing the protonated and deprotonated states, respectively [20, 21]. The underlying coordinate θ, which is assigned a fictitious mass and propagated simultaneously with the spatial coordinates, is related to λ via the functional form, λ = sin²θ. The coupling between conformational dynamics and protonation-state sampling is enabled through the linear interpolation of partial atomic charges as well as van der Waals interactions between the protonated and deprotonated forms. The original version of the CpHMD method employs the GB implicit-solvent model for propagation of both spatial and titration coordinates [20, 21] and was implemented in the CHARMM package [23]. Below we will discuss new versions of CpHMD developed recently (Table I).

Table I.

Comparison of the CpHMD methods

CpHMD	Solvent model	Advantage	Drawback
GB-based [20, 21, 16]	GB for both spatial and protonation space	Rapid pKa convergence (500 ps)	Less accurate conformational dynamics; effects due to explicit ions neglected
Hybrid-solvent [24]	Explicit solvent for spatial space and GB for protonation space	Rapid pKa convergence (1 ns); more accurate conformational dynamics	Mismatch of implicit and explicit solvent; effects due to explicit ions neglected
Explicit-solvent [25, 26]	Explicit solvent for both spatial and protonation space	Accurate conformational dynamics; accounts for effects due to explicit ions; simulation system is charge neutral	Slow pKa convergence (10 ns for most residues); complicated electrostatic treatment (Chen and Shen, unpublished data)

3.1 Continuous constant pH molecular dynamics based on a hybrid-solvent scheme

To take advantage of the higher accuracy of the explicit-solvent model for conformational dynamics and the efficiency of the GB model for calculating solvent forces on titration coordinates, our group developed a mixed-solvent CpHMD method [24]. We also developed a pH-based replica-exchange (pHREX) protocol [24] to accelerate convergence of the pK_a’s in the hybrid-solvent CpHMD. We note that the TREX protocol implemented for the GB-based CpHMD [16] is not feasible for explicit-solvent simulations. In the pHREX protocol, independent replicas are subject to constant temperature and pressure/volume simulations in parallel at different pH conditions. At a given frequency, for example, every 100 or 500 dynamics steps, 3 exchanges are attempted between two adjacent replicas in the pH ladder, where the acceptance probability is given by the Metropolis criterion [24]

$$P_{1\leftrightarrow 2}=min\left(1,e^{-ln10({\text{pH}}^1-{\text{pH}}^2)({\sum }_i{\lambda }_i^1-{\sum }_i{\lambda }_i^2)}\right),$$ (1)

where the superscripts 1 and 2 refer to the two replicas and the summation runs through all λ variables for that replica. Compared to the GB version, the hybrid-solvent CpHMD offers improved pK_a prediction and conformational dynamics for proteins [24] and surfactant micelles [27]. Nevertheless, several limitations remain due to the use of the GB model for calculating forces on titration coordinates. For example, the effects due to explicit ions, which in some instances can be significant (see for example our work on the proton titration of a cationic micelle [27]), cannot be accounted for. Also, because of the lack of a formal Hamil-tonian, the total energy is not conserved, which may result in potential artifacts with prolonged simulation time.

3.2 Development of all-atom continuous constant pH molecular dynamics

Recently, we and two other groups have made efforts to extend the CpHMD framework to fully explicit-solvent simulations. Grubmüller and coworkers implemented CpHMD in the GROMACS package [28] using an alternative functional form for λ. The implementation was tested on the titration of single amino acids and a dipeptide [29]. Brooks and coworkers employed the multi-site λ-dynamics technique [30] for fully explicit-solvent constant pH simulation of RNA nucleotides [31]. Later the method was also applied to the pK_a calculation of lead-dependent ribozyme [32] (see more discussions later). Most recently, the multi-site λ-dynamics was combined with the pHREX protocol [24], which showed improved accuracy for the calculated pK_a values of a GAAA tetraloop [33].

3.3 Introducing a charge-leveling technique to maintain charge neutrality

A fully explicit-solvent version of CpHMD has also been developed by our group [25, 26]. A major difference between our method and those by Grubmüller group [29] and Brooks group [31] is a charge-leveling technique [25]. In a pHMD simulation, regardless of the discrete or continuous methods used, since the titratable groups are allowed to protonate and deprotonate, the total charge of the system fluctuates with time and varies at different pH. The charge-leveling technique keeps the net charge of the simulation system constant by coupling the ionization of so-called co-ions to the proton titration of ionizable sites [25]. Specifically, an acidic site is paired with a negative co-ion to maintain a total net charge of −1,

$$\text{AH}+{\stackrel{\sim }{\mathrm{I}}}^{-}\rightleftharpoons {\mathrm{A}}^{-}+{\stackrel{\sim }{\mathrm{I}}}^0,$$ (2)

while a basic site is paired with a positive co-ion to maintain a total net charge of +1,

$${\text{BH}}^{+}+{\stackrel{\sim }{\mathrm{I}}}^0\rightleftharpoons {\mathrm{B}}^0+{\stackrel{\sim }{\mathrm{I}}}^{+}.$$ (3)

where Ĩ represents a co-ion. Thus, the charge-leveling technique when combined with the addition of counter-ions allows the simulation system to be kept charge-neutral. We tested the fully explicit-solvent CpHMD with co-ions on a series of aliphatic dicarboxylic acids [25] and proteins (Shen and coworkers, unpublished data). The accuracy for the calculated pK_a’s of a series of aliphatic dicarboxylic acids is on par with the GB-based CpHMD simulations [25]; however, the deviations from experimental data are slightly larger for the proteins (Shen and coworkers, unpublished data). We attribute the latter to the slow convergence. Even with the simulation length of 10 ns per replica, which is an order of magnitude longer than the typical GB or hybrid-solvent CpHMD simulations (1 ns per replica), the pK_a’s of some residues ( deeply buried ones or those involved in salt-bridges) are not fully converged. Despite these limitations, explicit-solvent CpHMD is promising as it captures details not included in other methods (see addition discussion below).

3.4 Introducing titratable water to further improve physical realism

Inclusion of co-ions allows the simulation system to be kept charge neutral. However, when the co-ions become neutral, they may aggregate causing artifacts. To address this issue and to further improve the physical realism of CpHMD simulations, we replaced the co-ions with titratable water molecules [26], which can convert to a hydroxide upon losing a proton,

$${\mathrm{H}}_2\mathrm{O}\rightleftharpoons {\text{OH}}^{-}+{\mathrm{H}}^{+}$$ (4)

or a hydronium upon gaining a proton.

$${\mathrm{H}}_2\mathrm{O}+{\mathrm{H}}^{+}\rightleftharpoons {\mathrm{H}}_3{\mathrm{O}}^{+}$$ (5)

The titration of a hydroxide is coupled with that of an acidic site,

$$\text{HA}+{\text{OH}}^{-}\rightleftharpoons {\mathrm{A}}^{-}+{\mathrm{H}}_2\mathrm{O}$$ (6)

while the titration of a hydronium (Eq. 5) is coupled with that of a basic site

$${\text{BH}}^{+}+{\mathrm{H}}_2\mathrm{O}\rightleftharpoons {\mathrm{H}}_3{\mathrm{O}}^{+}+\mathrm{B}$$ (7)

Thus, the total charge of a coupled acid-hydroxide (or base-hydronium) pair is maintained constant. The titratable water model has been tested in the CpHMD simulations of several proteins (see Figure 1). The resulting accuracy of the calculated pK_a’s is comparable to the GB-based CpHMD [26].

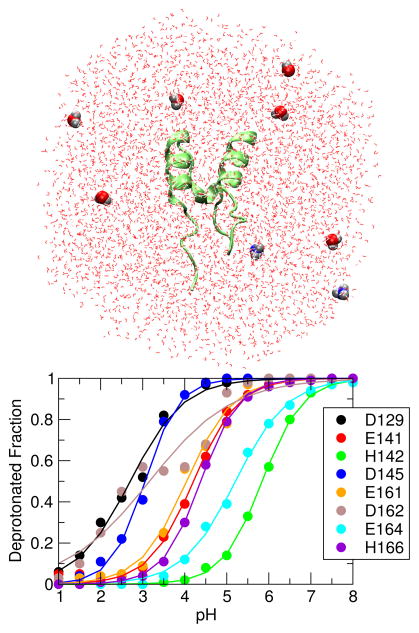
Figure 1.

All-atom CpHMD simulation of BBL protein. Upper : BBL in the simulation box filled with water. Titratable water molecules are highlighted in the van der Waals representation. Lower : Simulated titration curves for carboxyl and histidine sidechains.

3.5 Proper treatment of long-range electrostatic forces on titration coordinates

To properly account for long-range electrostatics in explicit-solvent simulations, particle-mesh Ewald (PME) and generalized reaction field (GRF) methods are the two most widely used options (see descriptions of CHARMM [23], AMBER [13] and GROMACS [28]). In principle, PME can be used to evaluate long-range electrostatic forces on the λ coordinates in CpHMD simulations of periodic systems; however, the implementation of the forces beyond the real-space cutoff is non-trivial. A simple truncation leads to not only inaccurate results but also large fluctuation in the forces acting on the titration coordinates[25]. [29, 31] In the development of Grubmüller and coworkers, PME was used; however, they did not make clear how long-range electrostatics forces on the titration coordinates are treated [29]. In the implementation of Brooks and coworkers, the force-shifting (FSh) potential was used [31]. In our implementation we resorted to the GRF method[34]. We are currently investigating the impact of different large-range electrostatic methods on the accuracy of CpHMD simulations.

4 Recent applications of constant pH molecular dynamics

4.1 Predicting pK_a shifts for proteins

In the context of pK_a calculations, a pK_a shift refers to the difference between the pK_a value of a titratable group in the solute environment, such as a protein, and that of the corresponding model compound in solution. A major application area of pHMD is to calculate the pK_a shifts of protein side chains, which informs their protonation states at a specified pH condition, thereby allowing the identification of acid or base for delineating the mechanism of acid-base catalysis [35] or the pathway for proton translocation. Comparison to experimental values allows one to assess the accuracy of the technique. In the first blind prediction exercise, the pK_a values of 87 engineered mutants of staphylococcal nuclease (SNase) were calculated by many groups using both structure- and MD-based methods [36]. The accuracy of the GB-based DpHMD method was put to the test by McCammon and coworkers [37]. Based on the data of 11 residues from the engineered mutants as well as the wild-type variant of SNase, McCammon and coworkers concluded that while the accuracy of the DpHMD method for predicting the pK_a’s of surface sidechains is high (root-mean-square error of 1.2 units), challenge remains for interior and coupled sites which require increased sampling and accelerated convergence [37]. To address this issue, the Roitberg group and others applied the pH-REX protocol to revisit the pK_a calculation of hen egg white lysozyme (HEWL) [19] and small peptides [38, 39]. For more detailed discussion of the blind prediction results we direct the reader to the review article by Alexov et al [36].

In the blind prediction exercise, the Shen group applied the GB-based TREX-CpHMD to predict the pK_a values of all 87 residues of the SNase mutants with an overall root-mean-square (RMS) error of 1.7 units [8]. The same CpHMD method was also tested by the Brooks group using a variant of wild-type SNase as well as several mutants yielding an average unsigned error of 1.5 units [40]. These data revealed that, while the pK_a values are converged due to the enhanced sampling protocol, outliers are due to the limitations of the underlying GB model, i.e., less accurate desolvation free energy for deeply buried sites and distorted local conformational environment of sidechains close to the protein-water interface. To circumvent this and other problems (see more discussion below) due to the implicit-solvent models, we developed the hybrid-solvent CpHMD technique together with the pHREX protocol [24]. Validation study based on the pK_a calculations for five proteins (HP36, NTL9, BBL, HEWL and SNase) gave an RMS deviation of 0.74 units compared to experiment [24]. Although the RMS error from the hybrid-solvent simulation is only slightly below that from the GB-based simulations (0.82), the correlation with experiment is greatly improved due to the significant reduction of errors for the outliers [24]. Another strength of the hybrid-solvent pHREX-CpHMD is fast convergence. For most proteins we have studied, 1 ns per replica is sufficient to yield converged pK_a’s (Ref [24] and unpublished data from the Shen group). Most recently, the fully explicit-solvent pHREX-CpHMD method with titratable water models was applied to the same benchmark set of proteins (HP36, BBL and HEWL), yielding an RMS error of 0.9 based on 10-ns sampling per replica, which is slightly worse than the GB-based simulations (RMS error of 0.7) [26]. Despite the slightly larger errors due to the longer sampling time required as compared to the GB- or hybrid-solvent based techniques, the fully explicit-solvent CpHMD is promising as it is physically more sound and captures details such as the interaction with explicit ions, the effect of which may be significant for some systems such as charged micelles [27].

4.2 Predicting pK_a shifts for nucleic acids, surfactant and lipid assemblies

Knowledge of pK_a shifts is relevant not only for protein systems but also for other macromolecular assemblies such as nucleic acids, surfactant micelles and lipid membranes. As discussed earlier, application of pHMD techniques to such systems requires conformational sampling in explicit solvent, as the GB model is not sufficiently accurate for highly-charged systems or those with large hydrophobic regions. Brooks and coworkers applied explicit-solvent CpHMD to calculate the pK_a values of adenine and cytosine bases in the lead-dependent ribozyme [32]. The calculation reproduced the direction of the experimental measured pK_a shifts. Later they showed that the error for the poorly predicted residue in the GAAA tetraloop can be reduced from 2.9 to 1.2 units by incorporating the pHREX protocol [33]. Combined with NMR measurements, the same technique was employed to determine the protonation state of cytosine in a transient Hoogsteen base pair at biological pH [41].

Predicting pK_a shifts for lipid and surfactant assemblies is particularly challenging, as the flexibility of such systems renders the structure-based methods practically ineffective. We applied the GB-based REX-CpHMD to the calculation of the pK_a shift of a fatty acid embedded in anionic, cationic and neutral surfactant micelles [27]. Although the calculation agreed well with experiment for the anionic and neutral micelles, the calculated pK_a shift was in the wrong direction for a cationic micelle, where the balance between electrostatic stabilization and desolvation is biased towards the former [27]. We attributed the discrepancy to the micelle being more compact and rigid in the GB-based conformational sampling [42, 27]. Indeed, using the hybrid-solvent pHREX-CpHMD, which utilizes explicit-solvent model for conformational sampling, the calculated pK_a shift was greatly improved [27]. The shift from the GB-based CpHMD is −3.0, which is in the opposite direction compared to the experimental shift of 0.1/0.9 (in the presence of chloride or bromide ions). By contrast, the shift from the hybrid-solvent simulation is 1.5 units, which is in the same direction as the experimental shift. The residual error is mainly due to the lack of explicit treatment of ions. Most recently, a pK_a shift of 0.8 was obtained using the fully explicit-solvent pHREX-CpHMD simulation in the presence of explicit chloride ions (Shen group, unpublished data). This result demonstrates that by incorporating more detailed physics, the all-atom CpHMD is superior in accuracy and can be applied to a wider range of problems such as the coupled dynamics and proton titration of surfactant or lipid bilayers [43, 44].

4.3 Modeling coupled protonation and conformational dynamics

Constant pH molecular dynamics can be applied to study the pH-dependence of conformational variability and ionization-coupled conformational transitions. Using the PB-based DpHMD method [12], the Baptista and Machuqueiro groups investigated the pH-dependent conformational change of the prion protein [45, 46] as well as small peptides [47]. Using the GB-based DpHMD method [14], the Roitberg group studied the pH-dependent conformational variability of the Nitrophorin proteins [48, 49]. Applying the GB-based TREX-CpHMD simulations, Huo and coworker explored the folding free energy landscape of a mini-protein BBL [50]. Most recently, Brooks and coworkers combined the GB-based pHREX-CpHMD in implicit membrane [16] and the harmonic Fourier Beads method [51] to gain insight into the coupled structural rearrangement and protonation-state change of a critical residue in the activation event of rhodopsin [52].

4.4 Interpretation of macroscopic pK_a’s involving pH-dependent population shift

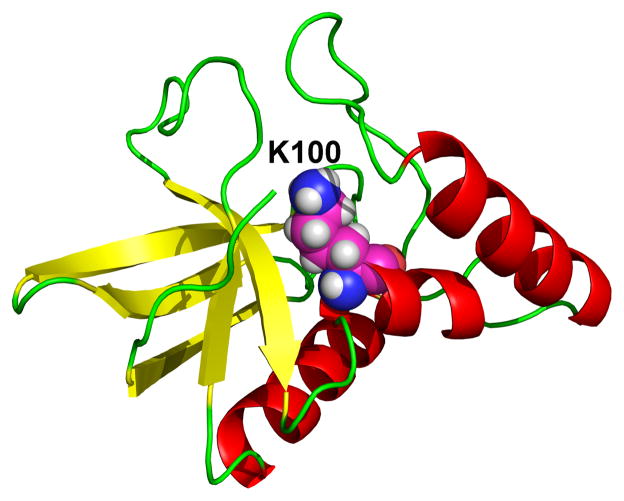
Ionization-induced conformational transitions are ubiquitous in biology. These processes are often associated with a significant change in the microscopic pK_a values, which makes the macroscopic or apparent pK_a seemingly difficult to interpret. One example is the unexpected pK_a value of Lys100 in the mutant N100K of SNase [53]. Lys100 is deeply buried in the hydrophobic core and not in the vicinity of other ionizable residues (Figure 2). Experimental data based on the stability measurements at different pH conditions gave a vof 8.6±0.2, [54, 53] corresponding to a down-shift of less than 2 units relative to the model value of 10.4. This was unexpected, as internal residues far from other charged groups generally have much larger pK_a shifts [8]. Thus, it was not surprising that most methods in the blind prediction exercise severely overestimated the shift of N100K [36]. Our calculation using the GB-based TREX-CpHMD simulations overpredicted the shift by 5 units, which was the largest deviation in the entire data set. Later we revisited the problem using the hybrid-solvent pHREX-CpHMD simulations [55]. We found that the protein exists in a pH-dependent equilibrium between open and closed states. At high pH such as pH 10, the site of Lys100 is closed. However, as pH is lowered, Lys100 becomes protonated and the site opens up allowing the entrance of water molecules. Thus, a four-state thermodynamic cycle as in Figure 3 was obtained comprising a conformational equilibrium between the closed and open states, each of which is subject to a protonation equilibrium with microscopic pK_a values of 5.8±0.4 and 10.3±1.2, respectively. The calculated apparent pK_a is 6.9±0.7, which is an improvement of over 3 units relative to the GB-based prediction. The remaining discrepancy from the experimental value of 8.6±0.2 can be attributed to the underestimation of the closed-state pK_a due to the limitation of the GB model which does not capture the effect of discrete water molecules.

Figure 2.

Structure of the N100K mutant of SNase protein. Lys100 is shown in the van der Waals representation.

Figure 3.

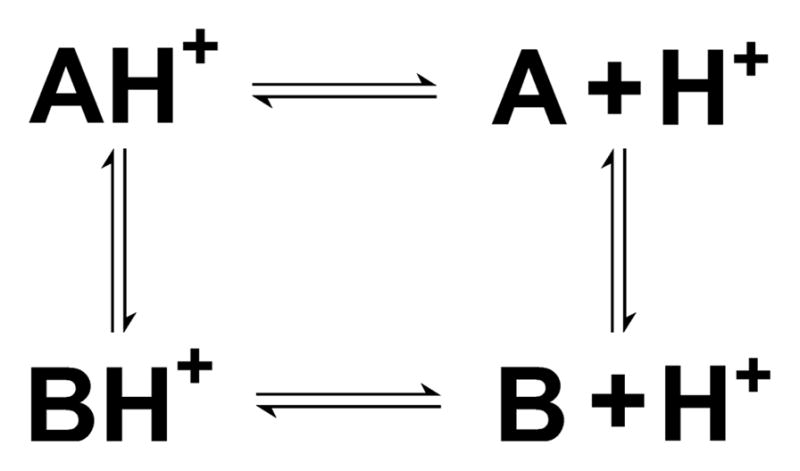
Coupling of protonation equilibria with conformational exchange. A and B refer to the closed and open states of the N100K mutant of SNase, respectively. AH⁺ and BH⁺ refer to the respective charged forms when Lys100 is protonated.

Another example of pH-dependent population shift in conformational states is Nitrophorin 4 protein (NP4), which undergoes conformational exchange between a closed and an open state upon binding or releasing nitric oxide (NO) in a pH-dependent manner [49]. Using the GB-based DpHMD simulation and the four-state model [55], Roitberg and coworkers found that the modest pK_a shift (about 2.5 units) as determined by experiment is a result of two distinct microscopic pK_a shifts (4.5 and 0.3) of Asp30, corresponding to the closed and open states [49].

4.5 Mechanisms of pH-dependent protein-protein and protein-RNA binding

Exploiting the Wyman-Tanford linkage equation [56], constant pH molecular dynamics can be used to predict the contributions of ionizable residues to the pH-dependent stability change upon protein-protein binding. An example of this application is our study of the pH-induced dimerization of the spider silk protein based on hybrid-solvent pHREX-CpHMD simulations [57]. Our data revealed that at pH 4–6 the dimer interface is stabilized by salt-bridges between two aspartates, Asp39 and Asp40, and basic residues in the opposite subunit. When the pH is increased above 6, however, two other residues, Asp79 and Glu119, become deprotonated, introducing excessive negative potential at the binding interface which leads to water entrance and dissociation of the dimer [57]. These predictions are supported by a later experimental work which found that D39N and D40N mutants do not dimerize and that E119Q mutation stabilizes the dimer at pH 6 [58].

Acidic environment can also induce dissociation of dimeric proteins such as the acid stress chaperone HdeA. Using umbrella sampling in the context of GB-based CpHMD simulations, Brooks and coworkers calculated the potential of mean force as a function of the monomer-monomer distance, which revealed a significant decrease in stability upon a pH change from 4 to 3.5 [59]. Through pK_a calculations of the monomers and dimer, they also identified key residues responsible for the stability of the HdeA dimer [59, 60]. A similar study was also conducted by Brooks and coworkers to find specific residues in control of the pH-dependent binding of P19 protein to siRNA [61].

4.6 pH-dependent self-assembly and phase transition of surfactants and peptides

As a generalization of titration of a single fatty acid in micelles, we simulated the self-assembly of 20, 30 and 40 fatty acids in the presence of proton titration of all molecules using hybrid-solvent pHREX-CpHMD [43, 44]. The simulations captured the formation of a micelle at high pH conditions and a bilayer at intermediate and low pH conditions. The bulk pK_a value (7.5) of the 40-mer aggregate represents a shift of 2.5 units relative to a single fatty acid in solution, which is in exact match with experiment [44]. The calculated pH at the micelle-to-bilayer transition is underestimated by 1–2 units as compared to experiment, possibly due to the lack of ions in the hybrid-solvent simulations.

In a similar study but in the absence of the de novo assembly, Tieleman and coworkers conducted titration simulations of a micelle comprising 20 oleic acids using the fully explicit-solvent CpHMD implementation in GROMACS [29] in conjunction with the coarse-grained MARTINI model [62]. The resulting bulk pK_a value was in good agreement with experiment [62]. The phenomenon of pH-dependent self-assembly also occurs for peptides. In an ongoing study, we found that both hybrid- and explicit-solvent pHREX-CpHMD simulations can be applied to accurately predict the pH condition of the transition between the β-sheet and random-coil state for peptides with a sequence such as IAAAEEEE (Cote and Shen, unpublished data). With an alkyl chain attached to the N-terminus, these peptides can self assemble into nano fibers in a pH-dependent manner [63].

5 Outlook

In recent years the major advance in constant pH molecular dynamics has been the extension of the CpHMD formalism to all-atom simulations [29, 24, 31, 25]. This advance is critical because it enables us to simulate pH-dependent processes of systems that cannot be accurately described by implicit-solvent models such as nucleic acids, surfactants and lipid assemblies. The all-atom CpHMD has been applied to proteins [26] and RNAs [32, 33], demonstrating its ability for predicting pK_a’s and revealing pH-dependent conformational dynamics. Nevertheless, there are several remaining challenges related to convergence, ways to allow water titration, and long-range electrostatics.

Even with the pH replica-exchange protocol [24], some of the pK_a values do not converge with 10-ns sampling per replica. An example is Asp162 in BBL (Figure 1). By contrast, the GB and hybrid-solvent CpHMD simulations, both using the implicit-solvent model for propagation of protonation states, usually converge within one ns per replica. The main reason for the speedup in the latter case is the direct calculation of the solvation free energy for deriving forces on particles in contrast to the calculation of free energy by sampling the explicit-solvent degrees of freedom. One straightforward way to accelerate convergence is to combine temperature and pH replica-exchange to a two-dimensional protocol. Test simulations with such a protocol showed improved pK_a calculations for residues that are involved in salt-bridge inter-actions (Shen and coworkers, unpublished data). However, two-dimensional REX simulations require an excessively large number of compute nodes, which is often times not feasible. A second area of future improvement is related to the titratable water model. Although the inclusion of titratable water to the simulation system enables charge neutrality and opens a door to modeling of solvent-solute proton exchange, the concentration of hydronium and hydroxide ions may become very high in a small simulation volume, which may lead to potential artifacts. Another critical factor for the fully explicit-solvent CpHMD is the proper treatment of long-range electrostatics. We employed the generalized reaction field (GRF) method [25], while the Brooks group used the force-shifting (FSh) potential [31]. However, the relative deviation from the exact force on the titration coordinates is quite large with either option (Shen and coworker, unpublished data). Since particle-mesh Ewald (PME) is most widely used in explicit-solvent simulations of periodic systems, we anticipate the next step to be the implementation of full PME forces for the titration coordinates. Finally, we note that while significant efforts have been made in the development of all-atom constant pH techniques, methods for incorporating pH effects in coarse-grained simulations are emerging [62, 64]. Together, these developments will soon allow solution pH condition to be rigorously controlled in standard molecular dynamics simulations.