The Basic Mechanics of Bipedal Walking Lead to Asymmetric Behavior

Abstract

This paper computationally investigates whether gait asymmetries can be attributed in part to basic bipedal mechanics independent of motor control. Using a symmetrical rigid-body model known as the compass-gait biped, we show that changes in environmental or physiological parameters can facilitate asymmetry in gait kinetics at fast walking speeds. In the environmental case, the asymmetric family of high-speed gaits is in fact more stable than the symmetric family of low-speed gaits. These simulations suggest that lower extremity mechanics might play a direct role in functional and pathological asymmetries reported in human walking, where velocity may be a common variable in the emergence and growth of asymmetry.

I. Introduction

Gait asymmetry is a commonly observed phenomenon in both impaired [1]–[3] and able-bodied human walking [4]–[8]. Many methods exist for quantifying or defining asymmetry between the right and left sides of the human body, using variables such as stride/step length, joint range of motion, velocity profiles, and ground reaction forces [9]. However, the underlying causes of these forms of asymmetry in various populations are still the subject of debate [4].

The hypothesis of functional asymmetry in able-bodied walking distinguishes the primary role of each leg as vertical support/control and anterior-posterior (AP) propulsion [7]. These differences have been attributed to leg dominance (see [4] for a review), whereas asymmetries reported in athletic race walking are often assumed to be the result of shoe differences or training on curved tracks [8].

Unilateral deficits observed in stroke gait are thought to be the manifestation of abnormal co-activation between muscle groups on the paretic side of the body [10]–[12]. For example, the stereotypical behavior of leg circumduction has been attributed to torque coupling between hip adduction and knee extension [10], [11]. Asymmetries also result from apparent bilateral impairments, a common example being cerebral palsy [3]. Gait symmetry and speed are common outcome metrics in clinical rehabilitation, but symmetry has not been shown to enable faster walking for stroke subjects [1]. In fact, variables for asymmetry are highly correlated with speed in hemiparetic stroke gait, where asymmetric leg motion accompanies increases in stride length/velocity [1]. Attempts at enforcing symmetry using an orthosis to induce knee flexion have resulted in new asymmetries such as exaggerated frontal-plane motion from hip adductor coupling [2]. The underlying mechanisms behind gait asymmetry must be understood in order to effectively treat such deficits.

In the context of robot walking, asymmetries naturally arise in computational simulations of symmetrical “passive walking” models that use only momentum and gravity to propel forward motion down a shallow slope [13]. Although the dynamical equations of motion may yield a stable solution corresponding to a symmetric walking gait, varying model parameters may cause a structural instability at a bifurcation point, after which a new (stable) asymmetric solution emerges from the (unstable) symmetric solution. The symmetrical mechanics of these walking machines admit two families of solutions, one symmetric and one asymmetric.

This paper examines previously unaddressed kinetic and stability variables in the planar compass-gait biped to better understand the cause, function, and benefit of gait asymmetry. We show that changes in both environmental and physiological parameters naturally facilitate the emergence and growth of asymmetry in gait energy, impact dissipation, and ground reaction forces. We find that walking speed is a common variable in both parametric cases, where the symmetric family of walking gaits is stable at low speeds and the asymmetric family is stable at high speeds. These results show that asymmetric gaits can be beneficial for stability and efficiency and suggest that lower extremity mechanics might play a direct role in functional and pathological asymmetries previously observed in human walking.

We begin by describing our simple computational model of bipedal walking in Section II. This model is simulated in Section III to show the evolution of its walking gait when varying an environmental parameter and a physiological parameter. We offer interpretations of these results in the context of able-bodied and impaired human walking in Section IV and provide closing remarks in Section V.

II. The Compass-Gait Biped Model

The planar compass-gait biped of Fig. 1 has point feet that coincide with the ankle joints. This simple model's 2-DOF configuration is given by the vector θ = (θ_s, θ_ns) in the configuration space $\mathcal{Q}={\mathbb{T}}^2$, representing the stance angle at the ankle and the non-stance/swing angle at the hip.

Fig. 1.

Model diagram for the planar compass-gait biped.

The single-support phase dynamics are represented by the continuous 2nd-order differential equation

$$M\left(\theta \right)\ddot{\theta }+C(\theta ,\stackrel{.}{\theta })\stackrel{.}{\theta }+N\left(\theta \right)=\tau ,$$ (1)

where M is the n × n mass/inertia matrix, n × n-matrix C contains the Coriolis/centrifugal terms, N is the vector of potential torques, and τ is the vector of torque inputs. These matrices are given symbolically by

$$\begin{array}{c}\hfill M\left(\theta \right)=\left(\begin{array}{cc}\hfill \frac{{\ell }^2}{4}(5m+4m_{\mathrm{h}})\hfill & \hfill -\frac{{\ell }^{2}m}{2}\cos ({\theta }_{\mathrm{s}}-{\theta }_{\mathrm{ns}})\hfill \\ \hfill -\frac{{\ell }^{2}m}{2}\cos ({\theta }_{\mathrm{s}}-{\theta }_{\mathrm{ns}})\hfill & \hfill \frac{{\ell }^{2}m}{4}\hfill \end{array}\right)\hfill \\ \hfill C(\theta ,\stackrel{.}{\theta })={\ell }^{2}m2\left(\begin{array}{cc}\hfill 0\hfill & \hfill -{\stackrel{.}{\theta }}_{\mathrm{ns}}\sin ({\theta }_{\mathrm{s}}-{\theta }_{\mathrm{ns}})\hfill \\ \hfill {\stackrel{.}{\theta }}_{\mathrm{s}}\sin ({\theta }_{\mathrm{s}}-{\theta }_{\mathrm{ns}})\hfill & \hfill 0\hfill \end{array}\right)\hfill \\ \hfill N\left(\theta \right)=\left(\begin{array}{c}\hfill -g\ell (3m+2m_{\mathrm{h}})\sin \left({\theta }_{\mathrm{s}}\right)∕2\hfill \\ \hfill g\ell m\sin \left({\theta }_{\mathrm{ns}}\right)∕2\hfill \end{array}\right).\hfill \end{array}$$

We choose human-like parameters, grouping the trunk masses at the hip: m_h = 31.73 kg, m = 13.5 kg, and $\ell =0.856$ m. The total mass is M_tot = 58.73 kg.

The continuous-time single-support phase is defined by constraint h(θ) ≥ 0, where scalar

$$h\left(\theta \right)=\ell ((\cos \left({\theta }_{\mathrm{s}}\right)-\cos \left({\theta }_{\mathrm{ns}}\right))+(\sin \left({\theta }_{\mathrm{s}}\right)-\sin \left({\theta }_{\mathrm{ns}}\right))\tan \left(\gamma \right))$$

gives the height of the swing foot above ground with slope angle γ. The instantaneous impact event from foot-ground strike is indicated by the guard condition/switching surface¹

$$G=\{(\theta ,\stackrel{.}{\theta })\mid h\left(\theta \right)=0,\stackrel{.}{h}=\left({\nabla }_{\theta }h\right)\stackrel{.}{\theta }<0\}\subset T\mathcal{Q}.$$

We model these impulsive events as perfectly plastic (inelastic) collisions, so any solution trajectory intersecting the ground plane is subjected to the discontinuous impact map $\Delta :G\to T\mathcal{Q}$. Thus, we have the impulsive dynamical system

$$\begin{array}{cc}\hfill M\left(\theta \right)\ddot{\theta }+C(\theta ,\stackrel{.}{\theta })\stackrel{.}{\theta }+N\left(\theta \right)=\tau & \text{for}(\theta ,\stackrel{.}{\theta })\notin G\hfill \\ \hfill ({\theta }^{+},{\stackrel{.}{\theta }}^{+})=\Delta ({\theta }^{-},{\stackrel{.}{\theta }}^{-})& \text{for}({\theta }^{-},{\stackrel{.}{\theta }}^{-})\in G.\hfill \end{array}$$

For brevity we defer the details regarding map Δ to [13].

Bipedal walking gaits correspond to solutions $x\left(t\right)=(\theta \left(t\right),\stackrel{.}{\theta }\left(t\right))$ of the above system that are periodic, i.e., x(t) = x(t + T) for some T > 0 and all t. These solutions define isolated orbits in state space known as hybrid limit cycles, which correspond to equilibria of the Poincaré return map P : G → G. The return map represents an impulsive dynamical system as a discrete-time system between impact events, sending state x_j ∈ G ahead one step by the discrete system x_j+1 = P(x_j). A symmetric periodic solution x(t) has a fixed point x* ∈ G such that x* = P(x*). A periodic solution that is asymmetric has a period greater than one, i.e., x* ≠ P(x*), requiring multiple compositions of the return map to find a fixed point x* = P^k(x*), for k > 1. In the case of 3D bipeds with bilateral symmetry about the sagittal plane, asymmetric gaits are those with consecutive step cycles that are not the mirror image of the other.

Although we cannot analytically calculate the return map, we can verify orbital stability from k-step fixed point x*, k ≥ 1, by approximating the linearized map ∇_xP^k(x*) through simulation [13]. This yields a discrete linear system that is exponentially stable if and only if the complex eigenvalues of ∇_xP^k(x*) are strictly within the unit circle (absolute values are less than one). An unstable solution also corresponds to cyclic walking, but any perturbation causes permanent deviation from the nominal trajectory (e.g., falling).

III. Simulation Results

Biped mechanics in this modeling construct admit a symmetric and asymmetric family of gaits depending on certain types of parameters [13]. We will examine how gait kinetics change between the families of solutions parameterized by the environmental ground slope and the physiological mass distribution between the hip and legs.

A. Varying an Environmental Parameter

A biped is said to be passive when propelled solely by ballistic momentum and gravity, without applying any control torques, i.e., τ = 0 in (1). Passive walking gaits arise from a balanced exchange between potential energy introduced on an inclined slope and kinetic energy dissipated at impact. When walking passively down a shallow slope, the planar compass-gait biped may fall into one of two cyclic gaits, one stable and one unstable [13], [15].

For a range of moderate slope angles, the steady-state gait is symmetric and stable, repeating exactly every step cycle. The symmetric gait becomes unstable on large slopes beyond a bifurcation point at slope γ = 0.073 rad, splitting into a stable asymmetric gait. These gaits are cyclic every two steps with one long stride and one short stride, which is stereotypical of unilateral impairments. We then observe 4-step asymmetric gaits after the second bifurcation point at γ = 0.0843 rad. Our simulations no longer exhibit cyclic behavior beyond 0.0853 rad.

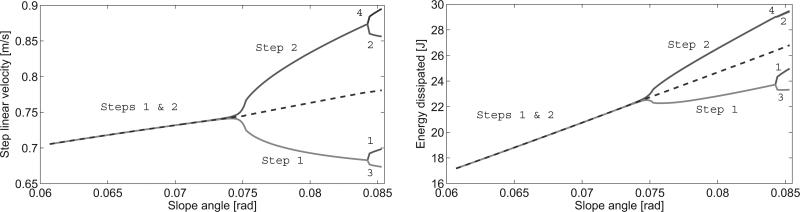
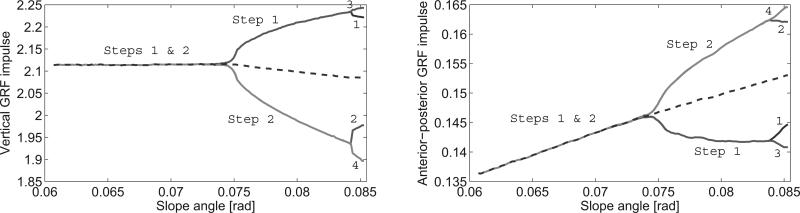
This period-doubling behavior is illustrated by bifurcation diagrams in which the steady-state evolution of so-called “gait descriptors” (variables of the steady gait) is shown over the range of slopes. Gait descriptors of stable solutions are given in solid lines and (approximate) unstable solutions in dashed lines, where asymmetric solutions have two or more branches showing the descriptor for each step cycle in the gait. We see in Fig. 2 that step velocity and impact energy dissipation of the symmetric gait evolve monotonically with slope, and the same holds for the asymmetric descriptors averaged over the gait cycle. This trend is also true of total mechanical energy at the end of each step cycle. Integrating the ground reaction forces (GRF) for each step cycle, we find in Fig. 3 that the AP impulse (midstance to foot strike) follows a monotonic trend whereas the vertical impulse of the symmetric solution remains close to constant. We interpret the function of these relationships in Section IV.

Fig. 2.

Passive steady-state step velocity (left) and impact energy dissipation (right) over slope angle. Solution is solid if stable and dotted if unstable.

Fig. 3.

Passive steady-state vertical GRF impulse (left) and anterior-posterior GRF impulse (right) over slope angle. Step cycle impulses are calculated by integrating the GRF vector (over the entire step period for vertical, after midstance for AP) and normalizing by $M_{\mathrm{tot}}g\sqrt{\ell ∕g}$ to be dimensionless.

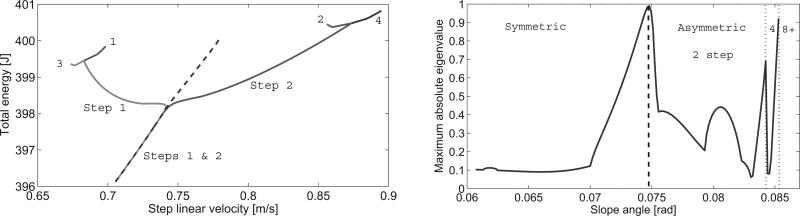
The eigenvalues of the return map between steps characterize a mathematically meaningful definition of gait stability. In fact, the maximum absolute eigenvalue is an inverse scale for stability between zero and one: a smaller value implies faster attenuation of perturbations in some local region around the nominal joint trajectory. We find in Fig. 4 that some asymmetric gaits after the bifurcation point are more stable than symmetric gaits before the bifurcation point (e.g., maximum absolute eigenvalue of 0.061 at 0.083 rad versus 0.09 at 0.066 rad). The maximum absolute eigenvalue of the 4-step asymmetric gait also drops significantly after the 2-step gait becomes unstable at the second bifurcation point. We see that there are multiple local stability minima within the range of walking gaits, where in this case the global minima resides in the 2-step asymmetric family.

Fig. 4.

Passive steady-state gait energy over linear velocity (left) and maximum absolute eigenvalue over slope angle (right). For the sake of comparison between families of solutions, eigenvalues are calculated with the period-4 return map.

Similar behavior for passive hopping models was observed in [16], where some asymmetric gaits appeared to have larger regions of attraction than symmetric gaits. This phenomenon can be explained by the presence of multiple orbital branches in the asymmetric solution, by which these gaits can occupy greater volume in the state space.

B. Varying a Physiological Parameter

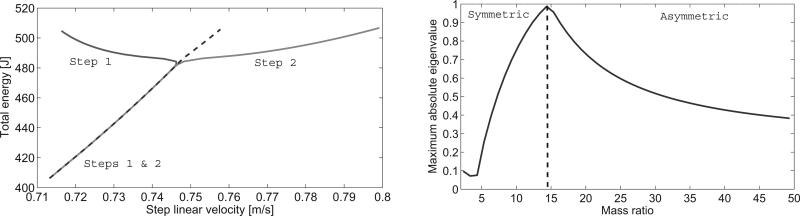
We now consider a controlled case of walking on flat ground when varying a physiological parameter corresponding to the biped's mass distribution. We first produce walking using a control law that virtually rotates the gravity vector to map a passive downhill gait to a “pseudo-passive” gait on level ground [17]. Letting total mass M be fixed, we vary distribution parameter μ = m_h/m corresponding to hip mass m_h = μM/(2 + μ) and leg mass m = M/(2 + μ). This bifurcation parameter was originally studied in [13].

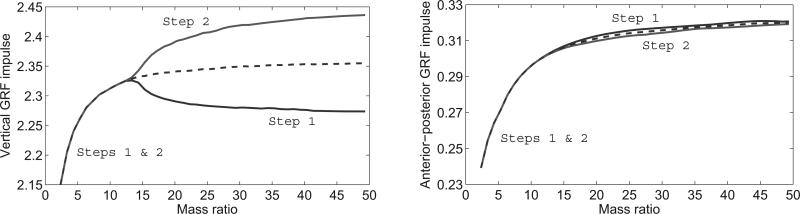
We find that the symmetric gait is stable as we increase the mass ratio from μ = 2.35 until μ = 12.35, at which point the symmetric gait becomes unstable and bifurcates into a stable asymmetric gait. The bifurcation diagrams for gait descriptors of vertical and AP impulses are given in Fig. 6, showing that vertical impulse differs substantial between legs whereas AP impulse does not (see [13] for other descriptors). The period-two asymmetric gait appears to remain stable in the limit as μ → ∞. Upon inspection of the maximum absolute eigenvalue in Fig. 7, we find that in this case the symmetric family of solutions is locally more stable than the asymmetric family. However, this might not be the case when comparing volumes of the regions of attraction.

Fig. 6.

Controlled steady-state vertical GRF impulse (left) and anterior-posterior GRF impulse (right) over slope angle. Step cycle impulses are calculated by integrating the GRF vector (over the entire step period for vertical, after midstance for AP) and normalizing by $M_{\mathrm{tot}}g\sqrt{\ell ∕g}$ to be dimensionless.

Fig. 7.

Controlled steady-state gait energy over linear velocity (left) and maximum absolute eigenvalue over slope angle (right). For the sake of comparison between families of solutions, eigenvalues are calculated with the period-2 return map.

Varying μ in the opposite direction (decreasing to zero), the symmetric solution exhibits a different period-doubling bifurcation at μ = 0.025, which is not shown in the above figures due to its smaller scale. This family of asymmetric gaits corresponds to walking speeds less than 0.564 m/s, which may be more representative of stroke pathology than the high-speed family of asymmetric gaits. In summary, the biped mechanics facilitate symmetry for a middle range of walking speeds and asymmetry in the extremes.

IV. Discussion

Although the simple model of Section II neglects many of the complexities of human locomotion, the period-doubling behavior observed in Section III is a generic manifestation of structural instabilities in discrete or impulsive dynamical systems [18]. Bifurcations have been observed in kneed models [19] and three-dimensional models that include stabilizing functions outside the sagittal plane [20]. Even different forms of locomotion such as hopping [18], [21] and climbing [22] exhibit this behavior. Therefore, the simulations of our simple biped mechanics offer some meaningful observations.

A. Asymmetry and Causality

The simulations of Section III show that both environmental and physiological parameters can directly cause asymmetry to emerge from bipedal mechanics. However, it would be useful to determine if a single unifying variable is likely responsible for both bifurcation cases.

We notice common monotonically increasing (one-to-one) relationships between bifurcation parameters and the gait descriptors of step length, velocity, and energy. In the case of slope variation, the first bifurcation point corresponds to a step length of 0.522 m, velocity of 0.742 m/s, and energy of 398.1 J. The first bifurcation point in the mass ratio case corresponds to a step length of 0.563 m, velocity of 0.746 m/s, and energy of 482.2 J. Both cases bifurcate at approximately the same linear velocity, suggesting that walking speed plays a fundamental role in the emergence of asymmetry. This could explain the experimentally observed correlations between asymmetry and walking speed in both pathological [1] and able-bodied [7] studies. However, a causal relationship is difficult to prove because multi-period solutions to nonlinear hybrid dynamics generally cannot be solved analytically, even when further simplification yields an analytical return map [15].

We therefore plot linear velocity against the gait descriptor of total energy in Figs. 4 and 7. We again see a monotonically increasing relationship for the symmetric solution. COM energy appears to increase proportionally to the square of COM velocity and inner-leg angle as we would expect from [23]. Asymmetry may be a natural way for the body mechanics to compensate for an excess of energy at fast walking speeds, where long strides perform a propulsion/accelerating function and short strides perform a support/control function. We now explore this concept of functional asymmetry.

B. Interpretations for Able-Bodied Gait

Asymmetry in able-bodied human walking has been attributed to differing biomechanical functions of the legs, where one leg contributes more to propulsion and the other is mainly responsible for body-weight support/transfer and motion control [4]–[7]. This is supported by the asymmetric family of solutions in Figs. 2, 3, and 6, where each leg contributes different impulses per step cycle and dissipates different energy at double-support transitions. These functions are manifested in the reaction forces as seen in the passive asymmetric gait of Fig. 5. The first stance phase provides support with a vertical impulse 15% greater than the second, whereas the second stance phase performs propulsion with an AP impulse 14.3% greater than the first. However, the only functional difference observed in the physiological case of Fig. 6 is in vertical impulse, suggesting that these roles need not be mutually exclusive (reaffirming observations in [7]).

Fig. 5.

Phase portrait (left) and vertical ground reaction forces (right) for the passive period-2 asymmetric gait on slope angle 0.0838 rad. Note that the second step cycle is shifted to coincide with the first step cycle in the reaction force figure for visual comparison.

Passive walking requires no energy contribution from the biped, so the existence of passive asymmetric gaits shows that asymmetry can be very energetically efficient. For walking speeds beyond the first bifurcation point (Figs. 4 and 7), the asymmetric solution is trivially more stable than the unstable symmetric solution. Both correspond to cyclic walking motion, but the biped can employ the asymmetric gait at no cost, allowing the lower extremity mechanics to naturally attenuate perturbations. Walking symmetrically at the same speeds requires active stabilization from the motor control system, which must apply torques at some cost to counteract destabilizing perturbations. The maximum eigenvalue plots similarly show that high-speed asymmetric gaits can be more stable than low-speed symmetric gaits under certain physical and environmental conditions.

If these characteristics indeed hold for human walking, asymmetries observed in able-bodied studies might be explained in part by humans self-selecting walking speed to maximize stability and/or efficiency. The leg corresponding to each biomechanical function may relate to limb dominance, but debate still surrounds the underlying reasons for this motor control strategy [4], [9]. Our simulations suggest that this walking strategy is dynamically beneficial for stability and efficiency, and human neurophysiology might have developed to exploit this fact.

However, healthy motor control systems appear to limit or delay the emergence of asymmetry as walking speed increases. A study on able-bodied children and young adults did not find any noticeable changes in kinematic and temporal symmetry variables as a function of age or walking speed [24]. The functional asymmetry hypothesis was tested in [7] and asymmetry was observed in AP impulses only during fast walking. The motor control system may enforce symmetry in all but the most challenging tasks for more than aesthetic reasons – unbalanced strain on joints and muscles

C. Interpretations for Pathological Gait

The basic mechanics of the lower limb apparatus may also play a role in gait asymmetries observed after impairment. The range of physiological parameters examined in Section III-B can be interpreted as a range of bilateral impairments (e.g., abnormal mass distributions associated with prosthetic legs). These simulations suggest that an impairment may alter the biomechanics in such a way that abnormal asymmetry improves stability and efficiency and enables faster walking.

A neurological impairment such as stroke² corresponds to a state change in the motor control system. This change might render the asymmetric family of solutions more optimal than the symmetric family (e.g., Fig. 4), pushing the biomechanics toward asymmetric behavior. If we assume that healthy motor control systems prevent the natural growth of asymmetry, this state change might instead render the motor control system unable to compensate for the tendency of biped mechanics to facilitate asymmetry. A third possibility is that impaired biomechanics admit an entirely different family of asymmetric gaits from that of able-bodied walking. Further studies are needed to determine which of these pathophysiologies is most likely.

V. Conclusions

We examined the kinetic properties of biped mechanics to investigate why asymmetry, whether functional or pathological, commonly appears in human locomotion. Our computational evidence suggests that environmental and physiological changes can cause gait asymmetry, even when the biomechanics remain perfectly symmetric. Walking speed appears to be a common variable related to the emergence and growth of asymmetry, where high-speed gaits are naturally asymmetric. Simulation results indicate that asymmetric gaits can be more stable (and efficient) than symmetric gaits, and similarly, high-speed gaits can be more stable (and efficient) than low-speed gaits. These observations suggest that biped mechanics might play a direct role in facilitating asymmetry in both able-bodied and impaired walking.

This paper motivates a new line of inquiry into the role of human motor control in suppressing gait asymmetry. Bilateral symmetry may be a desirable outcome in locomotor rehabilitation for aesthetic or musculoskeletal reasons, but we have found benefits to asymmetry such as improved walking speed, efficiency, and stability. This suggests a number of hypotheses for the pathophysiology of abnormal asymmetry, which may inform treatments to restore symmetry (e.g., constraining or challenging the subject's control system so the asymmetric family of gaits is no longer optimal). Future work will investigate these hypotheses with experiments.