Nanoparticle Counting: Towards Accurate Determination of the Molar Concentration

Summary

Innovations in nanotechnology have brought tremendous opportunities for the advancement of many research frontiers, ranging from electronics, photonics, energy, to medicine. To maximize the benefits of nano-scaled materials in different devices and systems, precise control of their concentration is a prerequisite. While concentrations of nanoparticles have been provided in other forms (e.g., mass), accurate determination of molar concentration, arguably the most useful one for chemical reactions and applications, has been a major challenge (especially for nanoparticles smaller than 30 nm). Towards this significant yet chronic problem, a variety of strategies are currently under development. Most of these strategies are applicable to a specialized group of nanoparticles due to their restrictions on the composition and size ranges of nanoparticles. As research and uses of nanomaterials being explored in an unprecedented speed, it is necessary to develop universal strategies that are easy to use, and compatible with nanoparticles of different sizes, compositions, and shapes. This review outlines the theories and applications of current strategies to measure nanoparticle molar concentration, discusses the advantages and limitations of these methods, and provides insights into future directions.

1. Introduction

Properties of solid materials with size in the macroscopic and microscopic scales are well studied and characterized. But when their sizes shrink to dimensions of approximately 1–100 nanometers, the materials’ properties, such as melting point, fluorescence, electrical conductivity and magnetic permeability, change significantly, ruled by quantum mechanical effects.^{1, 2} For example, metallic nanostructures in the presence of electromagnetic radiation exhibit electron density oscillations, which are highly sensitive to environmental perturbations and can be used for chemical and biological sensing. Iron oxide nanoparticles become superparamagnetic and can be used as imaging contrast agents. Carbon nanotubes with remarkable tensile strength and controllable electrical conductivity are widely used in mechanical parts and thin-film electronics. Similarly, semiconductor nanoparticles are outstanding wavelength-tunable light absorber and fluorescence emitter for solar energy harvesting and optical imaging. With recent advances in materials sciences and chemistry, these nanostructures have been synthesized in a variety of shapes and sizes with remarkable uniformity. More importantly, the theoretical framework explaining the unique optical, chemical and electronic properties of nanomaterials has also been established. Indeed, these functional nanomaterials have emerged as a new generation of building blocks beyond conventional chemicals, and are being incorporated in a variety of agents and devices, enabling exciting opportunities in electronics, photonics, energy, catalysis, computing, and medicine.

Despite these advances in the past several decades, some basic issues still remain to be tackled. One of these challenges is how to accurately determine the number or molar concentration of nanoparticles. The significance of this simple question is obvious. To incorporate these tiny yet powerful nanoparticles into electronic devices, the first question to ask is how many of them are needed. The number/molar concentration is typically available for conventional chemical molecules, but has puzzled nanotechnologists for decades. In most research laboratories, nanoparticles’ molar concentrations, particularly for novel structures, can only be estimated roughly. As a result, for downstream modification, functionalization and application, they are often formulated or used based on empirical data rather than accurate analytical measurements. Similarly, in the field of nanomedicine, the concentration of nanoparticles (e.g., drug delivery vehicles) administered in vivo needs to be precisely controlled in order to maximize the efficacy and minimize the toxicity of nanomaterials. Although different forms of concentrations (e.g., weight, total ions etc) have been reported by literatures, the size effect of nanomaterials is not taken into consideration. The fundamental source of this problem is nanoparticle heterogeneity, which also highlights a key distinction between chemistry and nanotechnology. In nanotechnology, although sometimes nanoparticles are referred to as artificial atoms or artificial molecules, individual nanoparticles are as unique as people’s fingerprints. Even made in the same synthetic reaction, these complex structures composed of hundreds to thousands of atoms and various surface ligands do not share a common molecular weight, as pure chemical compounds do.

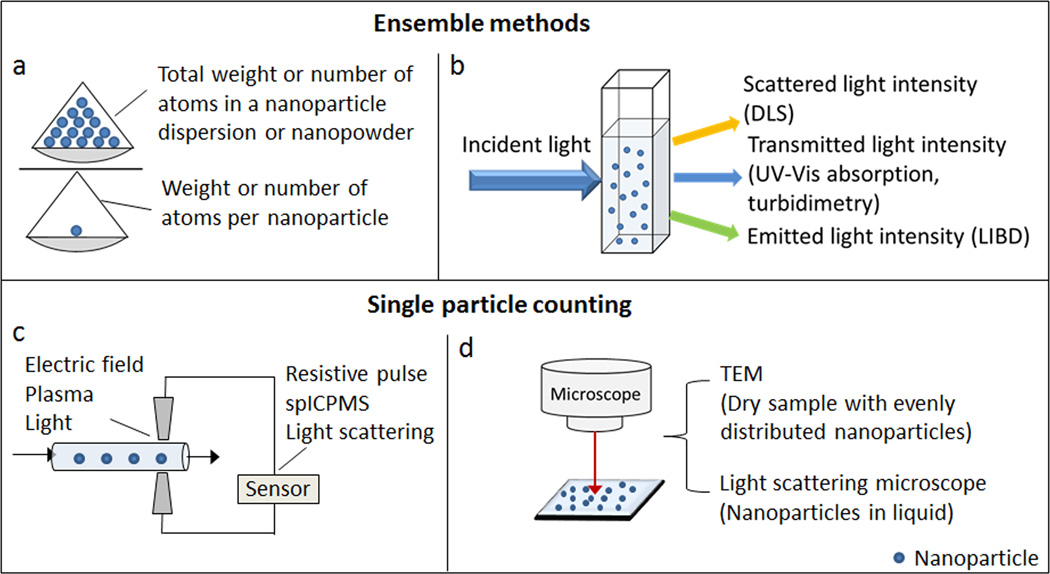
The importance of accurate determination of nanoparticle numbers, or molar concentration, has been realized by many scientists. Towards this goal, a number of analytical methods are currently under development. Some of the methods calculate concentrations based on ensemble physical properties of nanoparticle dispersions (e.g., light absorption), while others such as microscopy and sensors directly count individual particles (Fig. 1). As these methods adopt different mechanisms, they have limitations on nanoparticle sizes and compositions. Considering the diversity of existing nanoparticles and the fast pace that novel nanoparticles are being produced, it is of critical importance to develop universal and simple methods suitable for nanoparticle concentration measurements over a broad size range (in particular for particles <30 nm). In this review, we will summarize the state-of-art technologies for measuring nanoparticle molar concentration, and will provide insights into the features of new technologies that are applicable to various types of nanoparticles regardless of their compositions and sizes.

Figure 1.

Schematic summary of methods to measure nanoparticle molar concentration.

2. Ensemble measurements

2.1 Gravimetric measurement

The introduction of molar mass of atoms and the Avogadro constant provided a simple method to calculate the molar quantity of molecules. Based on this concept, assuming one nanoparticle as an artificial molecule, the number of nanoparticles in a colloidal suspension can be determined by measuring the ensemble quantities of nanoparticle suspensions and the unit quantity of one nanoparticle (Eq.1), and the molar concentration of nanoparticles can be subsequently calculated based on Eq.2.

$$N=\frac{N_{\mathit{\text{total}}}}{N_{\mathit{\text{particle}}}}=\frac{m_{\mathit{\text{total}}}}{m_{\mathit{\text{particle}}}}$$ (1)

$$c=\frac{N}{N_{A}V}$$ (2)

Where N is the number of nanoparticles in a colloidal suspension; N_total and m_total are the ensemble quantities of nanoparticles in a suspension,(N_total is the total atoms and m_total is the total weight of nanoparticles); N_particle and m_particle are the unit quantities of one nanoparticle (N_particle is the average number of atoms per nanoparticle and m_particle is the weight of one nanoparticle); c is the molar concentration; N_A is the Avogadro constant and V is the volume of the colloidal suspension.

In Eq.1–2, the ensemble quantifies and unit quantities of nanoparticles must be measured experimentally. For inorganic nanoparticles which are synthesized from precursor ions, N_total can be determined from the amount of initial reactants used for synthesis. For example, the quantity of HAuCl₄, which is the precursor for synthesizing gold nanoparticles, has been assumed to be equal to the total amount of gold atoms in the final colloidal suspension and used as N_total to calculate gold nanoparticle concentrations.³ Despite high yields in nanoparticle synthesis, the simple assumption of 100% yield is not always satisfied. An improved method is to quantify the total number of atoms in nanoparticle suspensions. This method involves digesting nanoparticles and analyzing the dissolved ions. For instance, nanocrystals made of CdSe, PbSe and Fe₃O₄ have been dissolved in acid and the concentrations of Cd, Pb and Fe are determined by analytical techniques, such as atomic absorption spectroscopy, inductively coupled plasma atomic emission spectrometry (ICP-AES), inductively coupled plasma mass spectrometry (ICPMS) and UV-Vis spectroscopy.^4–6 These analytical methods can detect metals with high sensitivity, leading to more accurate measurements of total atoms in a nanoparticle suspension. An alternative simpler approach to quantify the total weight of nanoparticles using analytical balance, provided sufficient amount of nanoparticle sample after vacuum dry, is available. For small sample size, ultrasensitive balance is needed. Reipa et al. recently demonstrated the use of Quartz Crystal Microgravimetry (QCM), a nanogram resolution mass sensing technique, to resolve the weight of 20 µl drop of Si nanocolloids and further estimate the concentration of Si nanoparticles using Eq.1–2.⁷ The weight measurement approach to determine total sample quantity is applicable to many types of nanoparticles, but a key requirement is that the nanoparticle must be ‘pure’, especially free of surface ligands.

Generally, measurement of nanoparticle total weight is relatively easy. The difficulty comes from the other critical quantity in Eq. 1, the average number of atoms per nanoparticle (N_particle), which can only be estimated from the size and crystal structures of nanoparticles. For example, Liu et al. assumed gold nanoparticles possess spherical shapes and uniform face-centered cubic (fcc) structures and used Eq.3 to calculate the number of gold atoms per particle:³

$$N_{\mathit{\text{particle}}}=\frac{\pi \rho d^3}{6M}{N}_A$$ (3)

Where ρ is the density of fcc gold (g/nm³), M is the atomic weight of gold (g/mole), d is the diameter of gold nanoparticles (nm), N_A is the Avogadro constant. For other nanoparticles with defined crystal structures (e.g., Ag, Si, and CdSe), Eq.3 is also applicable. However, the assumption that the crystal structures and associated physical properties of nanoparticles (e.g., density) equal to their bulk material counterparts does not hold for many types of nanoparticles. Dai et al. reported that PbSe nanocrystals exhibit a PbSe core with a Pb-rich shell, thus the Pb/Se atomic ratio is not equal to the bulk PbSe material.⁸ They further used atomic absorption measurement to quantify the ratio of Pb and Se atoms in a nanoparticle and used this number to adjust the concentration of PbSe nanocrystals.⁸ For nanoparticles with single chemical elements, the density of nanoparticles still varies due to atoms close to nanoparticle surface⁹. Similarly, for polymeric nanoparticles, the unit quantity is usually expressed as the weight of one nanoparticle m_particle and can be approximated from Eq. 4.

$$m_{\mathit{\text{particle}}}=\frac{\pi d^3}{6}\rho$$ (4)

Where ρ is the density of bulk polymer (g/nm³) and d is the diameter of polymeric nanoparticles (nm). Using this equation, the concentration of commercial polystyrene nanoparticles, which are provided by solid percentage, can be estimated.

As stated above, the method using ensemble weight divided by unit weight of nanoparticles is a simple and straightforward strategy, but experimental errors are easily introduced in the process of determining the weight or number of atoms of single nanoparticles (even for nanoparticles of regular shapes). For example, in Eq. (3) and (4), the diameter of nanoparticles must be known in order to calculate the unit quantity of nanoparticles. A number of techniques have been developed to accurately measure the size of individual nanoparticles (e.g., transmission electron microscopy (TEM) and scanning electron microscope (SEM)). However, due to the intrinsic polydispersity of nanoparticles, an averaged size has to be used for concentration determination. Thus, the accuracy of the unit quantity largely relies on the size distribution of nanoparticles. In addition, it is also very difficult to completely remove nanoparticle surface ligands that add errors to both total nanoparticle weight measurement as well as single particle weight calculation. Due to these challenges, this method is mostly applicable to rough concentration estimation for easy-to-purify nanoparticles with narrow size distribution and resolved crystal structures or known solid density. Future analytical technique advances and theoretical calculations may be able to reduce the errors for improved results.

2.2 Light absorption

Nanoparticles made from certain types of materials, such as noble metals and semiconductors, strongly interact with light at specific wavelength. Their unique extinction peaks on ultraviolet-visible (UV-Vis) spectra can be utilized to calculate nanoparticle concentrations via Beer-Lambert law (Eq.5).

$$A=\epsilon bc$$ (5)

where A is absorbance, ε is the molar extinction coefficient with unit of M⁻¹ cm⁻¹, b is the path length of the sample (cm), c is the concentration of nanoparticles in solution (M). To accurately derive the concentration from Eq.5, it is a prerequisite to know the molar extinction coefficient of specific nanoparticles. This parameter has been obtained for a few common nanoparticles.

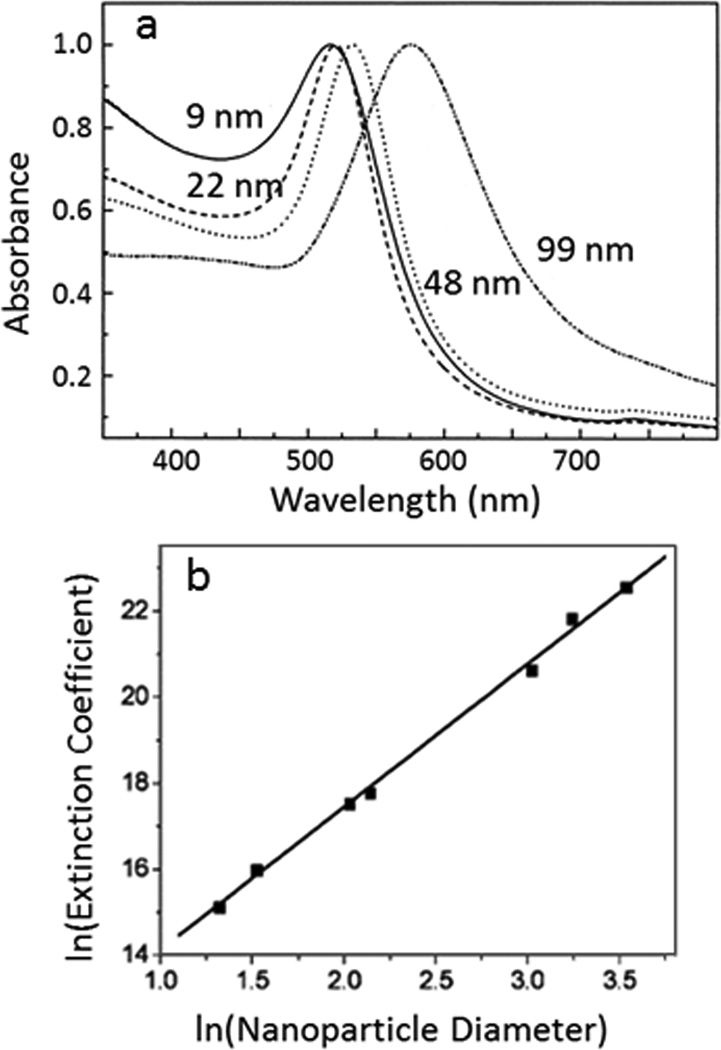
The molar extinction coefficient of gold nanoparticles has been estimated by both theoretical calculation and experimental measurement. El-sayed and co-workers did pioneer work on calculating the absorption and scattering properties of gold nanoparticles based on Mie theory and discrete dipole approximation.^{10, 11} They demonstrate that the resonance wavelength and extinction cross-section of gold nanoparticles are dependent on the size of nanoparticles (Fig. 2a). To further quantify the relationship between absorption coefficient and gold nanoparticle size, Liu et al. calculated the extinction coefficient of a series of spherical gold nanoparticles with diameters from 4 nm to 40 nm and established a linear relationship between lnε and lnd (Eq.6, Fig. 2b).³

$$\mathit{\text{ln}}\epsilon =3.32\mathit{\text{ln}}d+10.8$$ (6)

where ε is the molar extinction coefficient at the wavelength of maximum extinction (M⁻¹ cm⁻¹) and d is the diameter (nm) of gold nanoparticles.

Figure 2.

Relationship of UV-Vis extinction and size of gold nanoparticles. (a) UV-Vis spectra of gold nanoparticles with different diameters. The wavelength of maximum extinction depends on the size of gold nanoparticles. Reprinted with permission from ref. 11. Copyright (1999) American Chemical Society. (b) Linear relationship of the natural logarithm of extinction coefficients (L mole⁻¹ cm⁻¹) vs. logarithm of average gold nanoparticle core diameters (nm). Reprinted from ref. 3, with permission from Elsevier.

A similar linear relationship has also been established through theoretical calculations of gold nanoparticles in the size range of 5 nm to 50 nm.¹² However, this linear relationship is not always applicable for gold nanoparticles with larger sizes. Navarro et al. calculated the extinction coefficients of gold nanoparticles from 5 nm to 150 nm based on Mie theory and fit power laws to the curve of log(ε)-log(d). They found that one power law cannot fit the entire curve and a transition occurs around d=85 nm. Therefore, they refined the parameters in Eq.6 and derived a more accurate relationship between molar extinction coefficient and gold nanoparticle sizes (Eq.7):¹³

$$\epsilon =A{d}^{\gamma }$$ (7)

where A = 4.7 × 10⁴ M⁻¹ cm⁻¹, γ = 3.30, d ≤ 85 nm A = 1.6 × 10⁸ M⁻¹ cm⁻¹, γ = 1.47, d > 85 nm.

Similar to gold nanoparticles, silver nanoparticles also exhibit strong UV-Vis extinction due to their surface plasmon resonance feature. The relationship of their extinction coefficients and diameters has been reported to follow Eq.8:¹³

$$\epsilon =A{d}^{\gamma }$$ (8)

where A = 2.3 × 10⁵ M⁻¹ cm⁻¹, γ = 3.48, d ≤ 85 nm A = 4.2 × 10⁸ M⁻¹ cm⁻¹, γ = 0.77, d > 38 nm.

For semiconductor quantum dots (QDs), extensive research has been conducted to determine their extinction coefficients at the first exciton peaks. In several reports, general relationships between the extinction coefficient and QD particle size have been formulated (e.g., Eq.9).^{14, 15}

$$\epsilon =A{d}^{\beta }$$ (9)

where ε is the molar extinction coefficient at the first excitonic absorption (M⁻¹ cm⁻¹), d is the diameter of nanocrystals in cm, β is a constant (2<β<3 for larger particles, β tends toward 4 for smaller particles).¹⁵ Due to the sensitivity of the first excitonic wavelength on QD size and the intrinsic size distribution of QDs, alternative strategies based on QD absorption at shorter wavelengths rather than the first excitonic peak^16,17 or combination of absorptions at the first excitonic peak and shorter wavelengths^{4, 18} have also been investigated. For example, the extinction coefficients of CdTe with diameter from 3.1 nm to 11 nm can be summarized into Eq. 10.¹⁶

$${\epsilon }_{410}=(0.0106\pm 0.0002)\times d^3$$ (10)

where ε₄₁₀ is the extinction coefficient at 410 nm (L µmole⁻¹ cm⁻¹), d is the diameter of nanocrystals in nm.

Given the known extinction coefficients, UV-Vis spectroscopy is a highly efficient and simple strategy to measure nanoparticle concentrations. However, one needs to be careful to apply known parameters to newly-developed nanoparticles. First, none of the reported values are fully validated, and they are constantly being refined. Discrepancies between reported extinction coefficient-particle size relations and variations in exact values between different studies suggest that further investigations are needed to establish reliable coefficient values. Second, most of the known extinction coefficients of QDs are calculated based on the semiconductor core (e.g., CdSe, CdS). But the widely used QDs are often coated with a second layer of semiconducting materials (e.g., ZnS) with higher band gap to improve the quantum yield and the stability of QDs. Therefore, the concentration of core-shell QDs cannot be derived from the known QD extinction coefficients. Third, as novel nanoparticles with various chemical compositions, crystal structures, and shapes are being produced at a very fast pace, procedures of determining extinction coefficients must be simplified in order to facilitate measurement of nanoparticle concentrations using UV-Vis spectroscopy.

2.3 Turbidimetry

The turbidimetry method measures decreases in the intensity of the incident light caused by light scattering of nanoparticle suspensions.¹⁹ For a monodisperse system with nonabsorbing particles, the turbidity of colloidal suspensions is proportional to the number concentration of nanoparticles (Eq. 11).¹⁹

$$\tau =\frac{1}{4}\pi K{d}^{2}C$$ (11)

where τ is the turbidity (cm⁻¹), C is the number concentration of nanoparticles (particles/cm³), d is the particle diameter (cm), and K is the scattering coefficient, which is a function of nanoparticle size, the wavelength of the incident light and the relative refractive index of nanoparticles to the medium. If the scattering coefficient and the size of nanoparticles are known, turbidimetry is a facile method to calculate nanoparticle concentrations. Previous research has reported using turbidimetry to measure concentrations of latex, silica and poly (ethylene glycol)–poly (lactic acid) nanoparticles.^19–21 The concentrations calculated from turbidity data are in good agreement with those calculated from weight percentage.

Measurement of the refractive index and the scattering coefficient of different nanoparticles are, however, complex, limiting the applicability of this method to several non-absorbing nanoparticle suspensions. In addition, the sensitivity of turbidimetry depends on the scattering intensity of nanoparticles, which decreases as the size of particles becomes smaller.²² The smallest polymeric nanoparticles that have been quantified by turbidimetry are around 70 nm.²¹

2.4 Dynamic light scattering (DLS)

DLS measures the intensity of scattered light by nanoparticle suspensions.²³ As nanoparticles undergo Brownian motion in solution, the intensity of scattered light demonstrates a time-dependent fluctuation pattern. The fluctuations are related with the diffusion rate of nanoparticles in solution, which is subsequently dependent on the size of nanoparticles. Therefore, DLS can be used to determine the size distribution of nanoparticles. In addition to size, concentration of nanoparticles also affects the scattered light intensity. For a monodispersed nanoparticle solution, the scattered light intensity is proportional to the number of nanoparticles.²⁴ Indeed, a number of literatures have explored the feasibility of using DLS for determination of nanoparticle concentrations.

One method based on DLS uses photon count rate as an indicator of nanoparticle concentration. The photon count rate is defined as the number of photons detected per second by the DLS machine and has a unit of kilo counts per second (kCPS). At a certain concentration range, photon count rate is proportional to the scattered light intensity of colloidal dispersions (Eq. 12).^{24, 25}

$$I=BP$$ (12)

where I is the scattered light intensity, B is a constant and P is the photon count rate. The scattered light intensity is related to both size and concentrations of nanoparticles. If nanoparticles are sufficiently small compared to the wavelength of the incident light, Rayleigh scattering can be applied to describe the relation of scattered light intensity and the concentration of nanoparticles (Eq. 13).²⁵

$$I=I_0\frac{{\pi }^4(1+{\mathit{\text{cos}}}^2\theta )}{8R^2{\lambda }^4}{\left(\frac{m^2-1}{m^2+2}\right)}^2{d}^{6}C$$ (13)

where I₀ is the incident light intensity, θ is the scattering angle, R is the distance between the point of observation and the particle, λ is the wavelength of the incident light, m is the refractive index ratio of particles to the medium, d is the diameter of the nanoparticle, C is the number concentration of nanoparticles. As θ, R and λ are preset constants of a DLS instrument, Eq. 13 can be reduced to Eq.14:

$$I=I_0\alpha {\left(\frac{m^2-1}{m^2+2}\right)}^2{d}^{6}C$$ (14)

where α is an instrument coefficient. Taken Eq. 12–14 together, it is clear that the photon count rate P is proportional to the nanoparticle number concentration C.^{25, 26} If a standard colloidal sample is available, a linear calibration curve can be established between P and C. Thus, the concentration of an unknown sample could be derived based on its photon count rate and the calibration curve. It should be noted that applying this method has several prerequisites. First, the nanoparticles and the solvent in the standard and unknown samples should be the same in order to cancel out the effects of refractive index m and nanoparticle size d on the photon count rate. Second, many DLS instruments (e.g., Malvern Zetasizer) automatically optimize the attenuation factor and the measurement position to get a measurable count rate. Therefore, these two parameters also need to be consistent when the unknown and the standard samples are compared. Alternatively, the actual count rate can be calculated from the reported count rate divided by the attenuation factor, which is generated by the DLS instrument in the process of automatic adjustment.

To help eliminate the influence of instrumental parameters on measuring photon count rate, Xie et al. employed Triton X-100 micelles as an internal reference to calculate the concentration of gold nanoshells in blood samples.²⁷ They first mixed Triton X-100 with a standard gold nanoshell solution and measured the DLS signal of the mixed solution. Due to the size difference between Triton X-100 (10 nm) and the gold nanoshells (120–130 nm), DLS showed two distinct peaks which correspond to each of the nanoparticle populations in solution. By plotting the ratio of the integrated scattering intensity of these two peaks and the known concentration of standard gold nanoshells, they established a linear relationship between these two parameters and used this linear curve to measure unknown samples. Their results from DLS measurements are consistent with the results calculated from the number of total gold atoms. The limitation of this method is mainly from the selection of an appropriate internal reference. As DLS cannot distinguish two types of particles with diameter difference smaller than 3 fold,²⁸ caution is needed to select the right nanoparticles as reference.

DLS is convenient and simple to get the concentration information if a reference sample is available. Ideally, the standards should contain the same nanoparticles as the unknown sample does, but this type of standards is generally unavailable. Often nanoparticle concentrations are only estimated by assuming a series of nanoparticles with the same composition and surface ligand sharing the same refractive index. Therefore, if the standards are made from the same materials but have different sizes, concentration of unknown samples can be estimated using Eq. 15.

$$\frac{P_1}{P_2}=\frac{d_1^6}{d_2^6}\frac{C_1}{C_2}$$ (15)

where P₁ and P₂ are the photon count rate of standard and unknown samples respectively, C₁ and C₂ are the number concentrations, and d₁ and d₂ are the diameters of these two samples (d₁, d₂ need to fit Rayleigh scattering criteria). In this way, one standard sample can be used to measure the concentration of a series of nanoparticles, which simplifies and broadens the application of the DLS method. One thing should be noted is that standard DLS measurements assume that nanoparticles are spherical and scatter light isotropically. For particles with more complex structures, DLS analysis may not be useful or at least the algorithms have to be adjusted.

2.5 Laser-induced breakdown detection

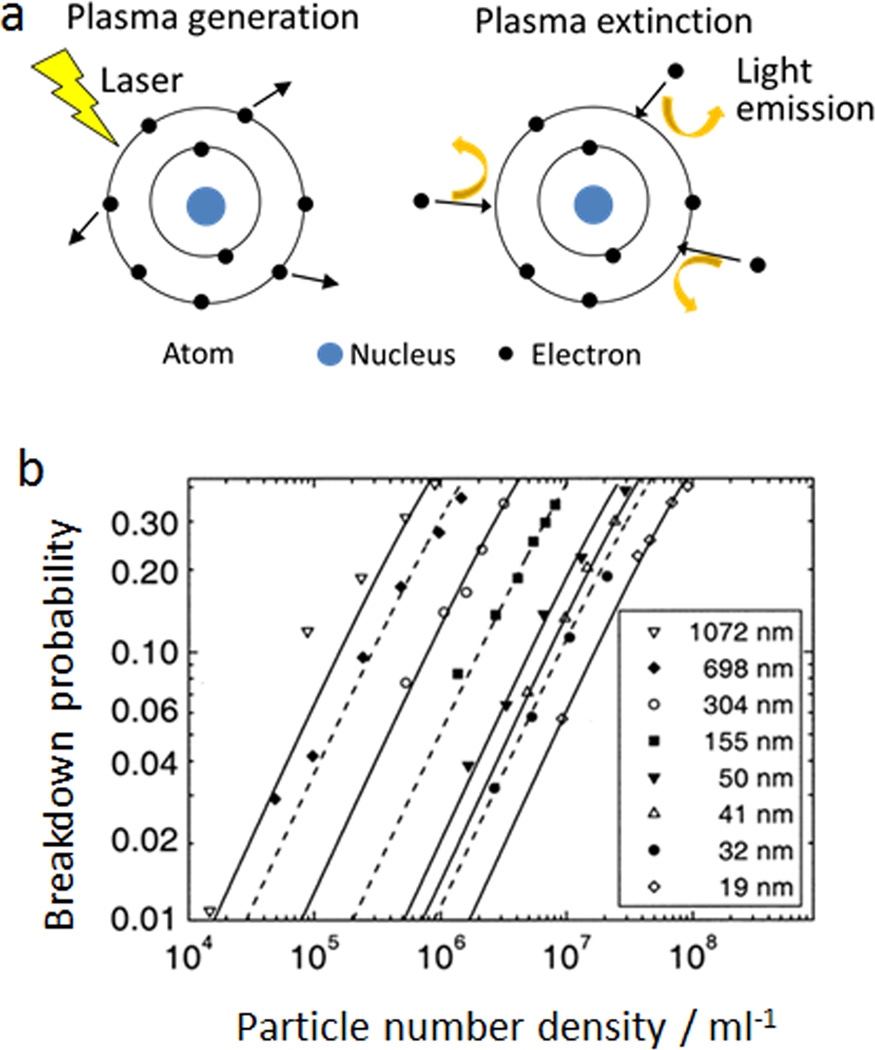
Laser-induced breakdown detection (LIBD) is based on the generation of plasma from nanoparticles irradiated by a focused intense laser.²⁹ The process of plasma generation, also referred as the breakdown of dielectric properties of a given medium, is shown in Fig. 3a.³⁰ When a pulsed laser interacts with molecules, the electrons of the molecules can be knocked out if the intensity of laser reaches a certain threshold. The released electrons further absorb energy from the radiation source and induce an electron avalanche, resulting in the generation of plasma. As the laser pulse diminishes, the excited electrons return to their initial state by emission of light, leading to the extinction of plasma. The breakdown threshold—minimal laser intensity required for plasma generation is dependent on the state of matter. Solid has the lowest threshold, followed by liquid and gas. To detect solid colloids in a suspension, LIBD adjusts the threshold of laser intensity and selectively breakdowns nanoparticles while leaving the solvent intact. The breakdown events can be detected by a piezoelectric sensor or a microscope charge-coupled device (CCD) camera system.³¹ The probabilities of breakdown, which is the number of breakdown events divided by the number of laser pulses for each measurement, have a linear relationship with the number concentration of nanoparticles (Fig. 3b).³¹ The concentration of unknown samples can be calculated based on a calibration curve derived from a standard sample. The minimal size of nanoparticles detectable by LIBD relies on the laser system. It has been reported that excimer-dye laser can detect nanoparticles with radius around 10 nm, while a more powerful Nd-YAG laser can reduce the detection limit to less than 1 nm in radius.³¹ In addition to low size limit, another advantage of LIBD is its applicability to most types of nanoparticles. Any inorganic, organic and microorganisms can be detected by LIBD as long as the laser intensity is adjusted above the particle breakdown threshold and below the solvent breakdown value. Furthermore, LIBD can detect colloids with very low concentrations, which may not be detectable by light scattering methods. Because of these excellent characteristics, LIBD has been widely used to characterize colloids in natural aquatic systems and detect impurities in ultrapure water.

Figure 3.

Illustration of the laser-induced breakdown detection method (LIBD) for nanoparticle quantification. (a) Scheme of laser-induced breakdown mechanism, adapted from ref. 30, with permission from John Wiley and Sons. (b) The linear relationship between breakdown probabilities of LIBD and polystyrene particle concentrations, reprinted from ref. 31, with permission from Elsevier.

Regardless of the detection mechanism (e.g., by measuring mass, light scattering, or light absorbance), these approaches based on readings of the collective properties of suspended nanoparticles share similar strengths and weaknesses. They are easy to perform. Unfortunately, obtaining absolute molar concentrations of unknown samples are contingent upon standards with known molar concentrations or individual nanoparticle characteristics with known values. The a priori information is generally unavailable or difficult to obtain particularly for novel nanomaterials.

3. Single particle counting

Unlike measuring ensemble quantities of nanoparticle dispersions, a number of techniques enable counting individual nanoparticles under direct visualization. Although it is generally laborious to count a large number of nanoparticles that can represent the overall particle population, these approaches can potentially provide absolute molar concentration without the need of standards. Here we summarize current strategies that realize unbiased counting and provide statistically significant information on nanoparticle concentrations.

3.1 Detecting one particle at a time

One general approach is to focus nanoparticles through an orifice or microfluidic channel and count them one at a time (Fig. 1c). With advances in analytical chemistry, a number of detecting mechanisms, such as electrical, chemical, and optical sensing, offer sufficient sensitivity to detect single nanoparticles.

Resistive-pulse sensing

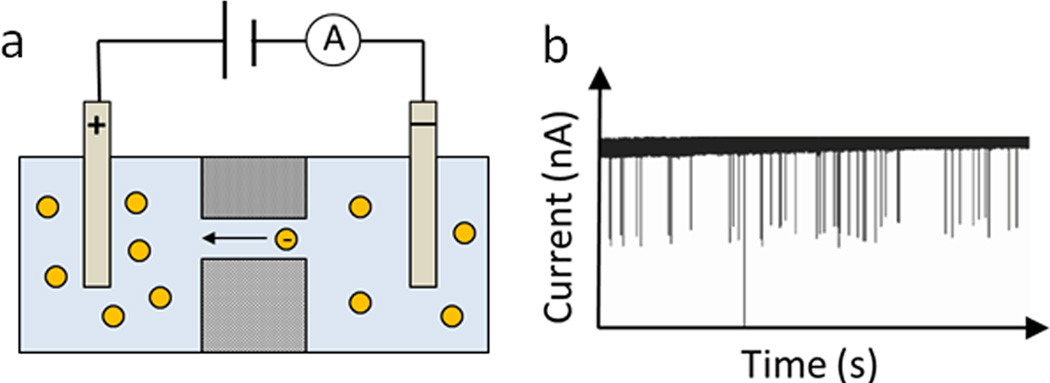
Resistive-pulse sensors detect changes in current or resistance when particles pass through an electric field. It is worth mentioning that this detection mechanism dates back to the 1950s when W.H. Coulter invented the Coulter counter that has been widely adopted for microparticle (e.g., cells) counting and sizing.^{32, 33} The setup of resistive-pulse sensors consists of two main parts, an insulating membrane that contains a single channel and an electric cell filled with electrolyte solution and divided by the insulating membrane (Fig. 4).³⁴ When a particle passes through the single channel, a transient change of ionic current in the channel is recorded as a signal pulse.³⁴ Charged particles can migrate through the channel by electric force, while neutral particles are driven by pressure or vacuum. Through a detailed analysis of the signal pulse, a wealth of information can be obtained about the size, shape, charge and concentration of nanoparticles. A comprehensive review on resistive-pulse sensors has been published.³⁵ Here we want to emphasize its application in determining nanoparticle concentration. The frequency of resistive pulses is related with the number of particles passing through a channel, thus the concentration of nanoparticles can be calculated if the volume of the solution is known.³⁴ It has been demonstrated that the resistive pulse frequency has a linear relationship with nanoparticle concentration.³⁶ By calibrating the pulse frequency with a known concentration standard, the concentration of unknown samples can be easily derived. Alternatively, if the geometry of the channel is well characterized, it is possible to calculate nanoparticle concentration by estimating the fluid flow rate and volume during the measurement period.³⁷

Figure 4.

Mechanism of resistive-pulse sensors for nanoparticle counting. (a) Schematic setup of one type of resistive-pulse sensors; charged particles migrate through the channel by electric force, adapted from Ref. 34, with permission from The Royal Society of Chemistry. (b) Typical current-time recordings when nanoparticles pass through the channel, adapted with permission from ref. 36. Copyright (2001) American Chemical Society.

The sizing range of resistive-pulse sensors is highly dependent on the geometry of the channel that particles pass through. For example, the commercial coulter counter resistive-pulse analyzer uses channels with diameter larger than 1 µm, which limits its application to particles larger than 400 nm. In recent years, advances in nanopore technologies have dramatically pushed down the size of detectable particles to 10 nm. These nanopores are fabricated by various methods, including ion-beam etching, rapid prototyping in polydimethylsiloxane (PDMS), mechanical puncturing in elastomeric membranes, nanotube-based and protein channels. Due to easy fabrication and tunability of nanopore technologies, the application of nanopore-based resistive-pulse sensing has been expanded to different types of nanoparticles as well as single DNA and protein molecules.^38–40 Izon qNano is one of the recent commercialized nanopore-based resistive-pulse sensors. It employs tunable nanopores fabricated on elastomeric membranes and enables detection of particles with sizes from 50 nm to 10 µm.⁴¹

In addition to nanopore technologies, a high-throughput electrical readout has also been integrated with resistive-pulse sensors to further improve its sensitivity and efficiency of detection. Fraikin et al. developed a microfluidic chip embedded with a nanoconstriction and a wide-bandwidth electrical detector and improved the analysis rate to 500,000 particles per second.⁴² This analyzer can determine concentrations of standard polystyrene nanoparticles as well as bacteriophage and viruses, and the analysis time of biological samples is in seconds rather than in hours required for traditional biological titre.

Resistive-pulse sensing technologies have demonstrated great advantage in determining nanoparticle concentrations. Due to the tunability of nanopores and the electric sensing modality, this method is compatible with a variety of nanoparticle sizes and materials (inorganic, polymeric and biological samples). One limitation of this method is that a standard nanoparticle sample is usually needed to calibrate the pulse count to the known nanoparticle concentration. Roberts et al. has reported a calibration-free method, which requires labor-intensive measurement of the pore dimensions under microscopy.³⁷

Inductively Coupled Plasma Mass Spectrometry (ICPMS)

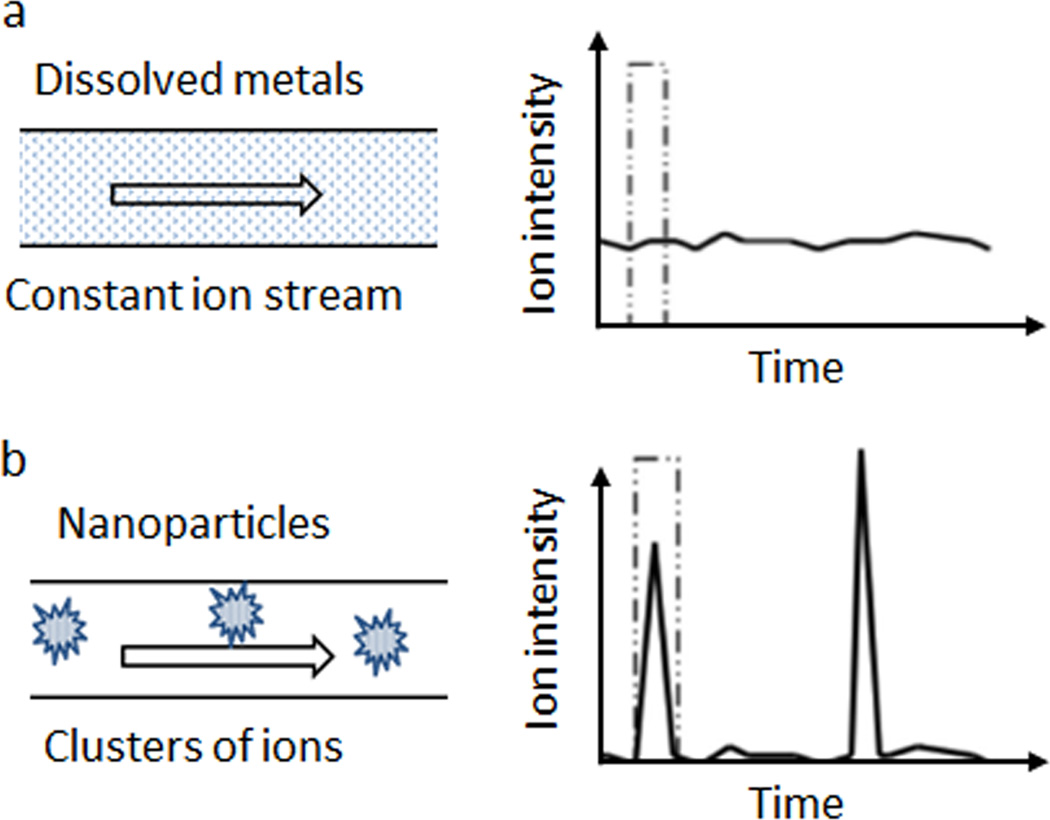
ICPMS is a highly sensitive and rapid analytical technique for elemental analysis at ultralow concentrations.⁴³ The samples in traditional ICPMS are usually metal ions dissolved in solution and the concentration of total metal can be calculated based on the averaged intensity of the ion peak over a measuring period. As metal ions are homogeneously distributed in a sample before entering ICPMS plasma, the intensity of ion peaks keeps relatively constant during the analysis interval. However, if a solution containing metal nanoparticles enters the ICPMS analyzer, the metal ions are no longer homogeneously distributed after plasma treatment, but form clusters of ions and produce an instantaneous increase of ion intensity (Fig. 5).⁴⁴ Single particle ICPMS (spICPMS) captures each pulse in intensity and correlates the number of pulses to the quantity of nanoparticles passing through the analyzer. To ensure each intensity pulse corresponds to one individual particle, spICPMS uses a much shorter detection interval (≤ 10 ms) than traditional ICPMS (0.3–1 s), and requires a low concentration of nanoparticle solution.⁴³

Figure 5.

Diagram of single particle Inductively Coupled Plasma Mass Spectrometry (spICPMS) principle, adapted from ref. 44, with permission from John Wiley and Sons. (a) Dissolved metal ions are homogeneously distributed in a sample and the intensity of ion peaks keeps relatively constant during the analysis interval. (b) Metal nanoparticles form ion clusters after plasma treatment and produce an instantaneous increase of ion intensity.

The accuracy of nanoparticle concentration measured by spICPMS relies on several parameters of the instrument. The most important one is the transport efficiency, which is the ratio of the amount of nanoparticles entering the plasma to the amount of nanoparticles aspirated into the spray chamber.⁴³ As a volume loss always happens when a sample transported through the spray chamber, the quantity of nanoparticles analyzed by ICPMS is not equivalent to that of the original nanoparticles aspirated into the ICPMS spray chamber. Therefore, the effect of transport efficiency on estimating nanoparticle concentrations must be considered (Eq. 16):⁴³

$$N=\frac{f}{q\eta }$$ (16)

where N (particles/ml) is the number concentration, f (number of pulses/ms) is the frequency of signal pulse, q (ml/ms) is the sample flow rate and η is the transport efficiency. The transport efficiency η can be calculated by using a well-characterized reference nanoparticle sample with known concentration.⁴³

spICPMS has been used to characterize various types of metal nanoparticles (e.g., Au, Ag, TiO₂, Al₂O₃ and ZrO₂) and demonstrated good linear relationship between intensity pulse frequency and nanoparticle concentration. The size of nanoparticles detectable by spICPMS is dependent on nanoparticle composition and the sensitivity of ICPMS instrument. It has been reported that spICPMS can detect silver nanoparticles with 20 nm and gold nanoparticles as small as 15 nm.^{44, 45}

Optical sensing

Single particle detection in microfluidic channels has been well-established in particular for fluorescent nanomaterials.⁴⁶ For non-fluorescent nanoparticles, optical detection often employs a photodetector to measure the flash of scattered light.⁴⁷ By counting the number of flashed light pulses, the number of particles can be quantified. This method is suitable for analyzing samples with low concentration (10⁴ – 10⁸particles/ml) and has been commercialized (e.g., particle measuring systems, Boulder, CO) to characterize particles in ultrapure water or monitor contamination in a manufacturing process.⁴⁷ For colloids with higher concentrations, measurement errors could be introduced during several dilution steps. In addition, smaller nanoparticles are difficult to detect mainly due to their low scattering efficiency. Therefore, calibration of the instrument using standard samples is usually required in order to improve the accuracy of measurement. In recent years, a high-sensitivity flow cytometer has been developed to quantify nanoparticles with nearly 100% detection efficiency.⁴⁸ This technology measures side scattered light signals from gold nanoparticles at a very high counting rate (100–200 particles per second) and correlates the number of scattered pulses with the nanoparticle concentration. As this flow cytometer is able to count all particles in a defined volume, the absolute concentration of nanoparticles can be derived accurately. The current size limit of this technique depends on the scattering property of nanoparticles. For gold nanoparticles with strong surface plasmon resonance scattering, the detectable size can be as small as 24 nm. Because many engineered nanoparticles are smaller than this size, and most of them do not scatter incident light as much as gold nanoparticles, the detection sensitivity of this technique requires further development. Besides improvement of the detectors, an alternative is to encapsulate small nanoparticles with a shell layer (e.g., silica shell, polymer shell, or aerosol droplet). Converting small nanoparticles into larger particles increases their scattering capability and consequently their visibility in optical sensors, while the nanoparticle encapsulation step must be simple, general, and clean (without introducing nanocontaminates such as self-nucleated nanoparticles made of the shell material).

3.2 Tracking and imaging nanoparticles

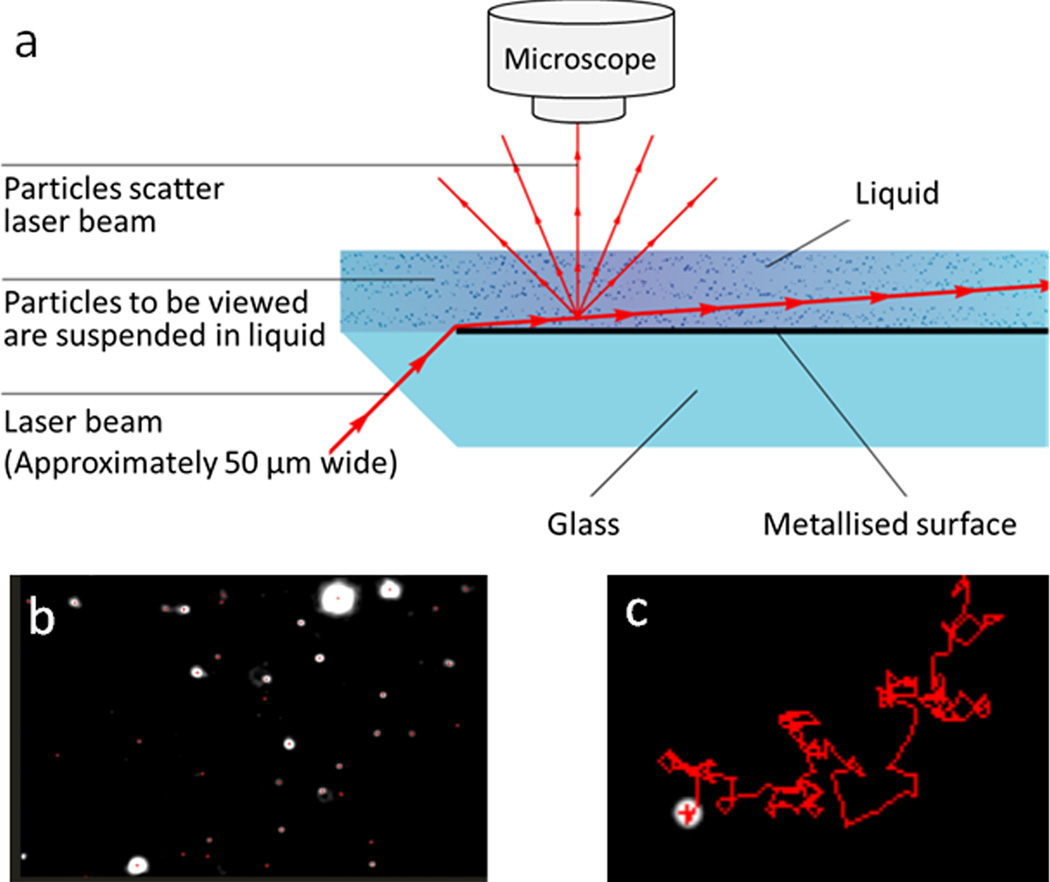
As aforementioned, scattering-based detection mechanism has been explored to measure bulk solutions and individual nanoparticles. This approach has also been expanded to nanoparticle imaging. Nanosight, a nanoparticle tracking analysis (NTA) system, is one of the commercial products that can track and count nanoparticles in liquid. This technology is based on a laser light scattering microscopy that can visualize nanoparticles under Brownian motion. As shown in Fig. 6a, a focused laser beam illuminates a nanoparticle suspension at a low angle and the scattered light of particles in the liquid is collected by a conventional optical microscope.⁴⁹ The movement of each nanoparticle is recorded by a CCD camera and analyzed by NTA software, which can track and analyze each particle in a moving mode (Fig.6b and 6c). There are many literatures using Nanosight to characterize different types of nanoparticles, including polystyrene nanoparticles, gold nanoparticles, viruses, and cellular vesicles. For monodispersed nanoparticles, the concentration measured by Nanosight is close to their real value. However, in polydispersed colloidal suspensions the number of larger particles tends to be overestimated. The reason is that Nanosight detects the light scattered from particles but not the particles themselves. To visualize both the small and large particles in a polydispersed suspension, the instrument settings are adjusted to ensure that the scattered light from small particles is detectable. But at this setting, larger particles may scatter multiple points of light, which are interpreted as multiple particles by the software.⁵⁰ In addition to the limitation of colloidal polydispersity, the minimal size of nanoparticles detectable by Nanosight is also restricted by the refractive index of particles. For biological (e.g., exosomes, liposomes) and polymer nanoparticles (e.g., polystyrene), the smallest size reliably analyzed by Nanosight is ~40nm in diameter; whereas for metal or semiconductor nanoparticles, the smallest size analyzed has gone down to 10–15 nm.⁴⁹

Figure 6.

Illustration of the nanoparticle tracking analysis (NTA) system, adapted from ref. 49, with permission from Nanosight Ltd. (a) Scheme of Nanosight configuration. (b) One frame from a video captured by Nanosight; each bright spot represents one nanoparticle in liquid. (c) Typical moving motion of one nanoparticle tracked by NTA software.

Overall, the detection limits of the single particle analysis approaches discussed above are determined by the signal-to-noise ratio, which decreases as nanoparticle sizes decrease. As a result, nanoparticles greater than 40–50 nm with strong scattering capability can be analyzed quite reliably, whereas counting small nanoparticles is much more difficult. In addition, manually setting a threshold to distinguish signals scattered by nanoparticles of interest and background signals originated from instrument fluctuation and impurities can impact the concentration values substantially. To tell apart nanoparticles of interest from impurities and background noises, imaging approaches with higher imaging contrast and capability to analyze nanoparticles in details are needed.

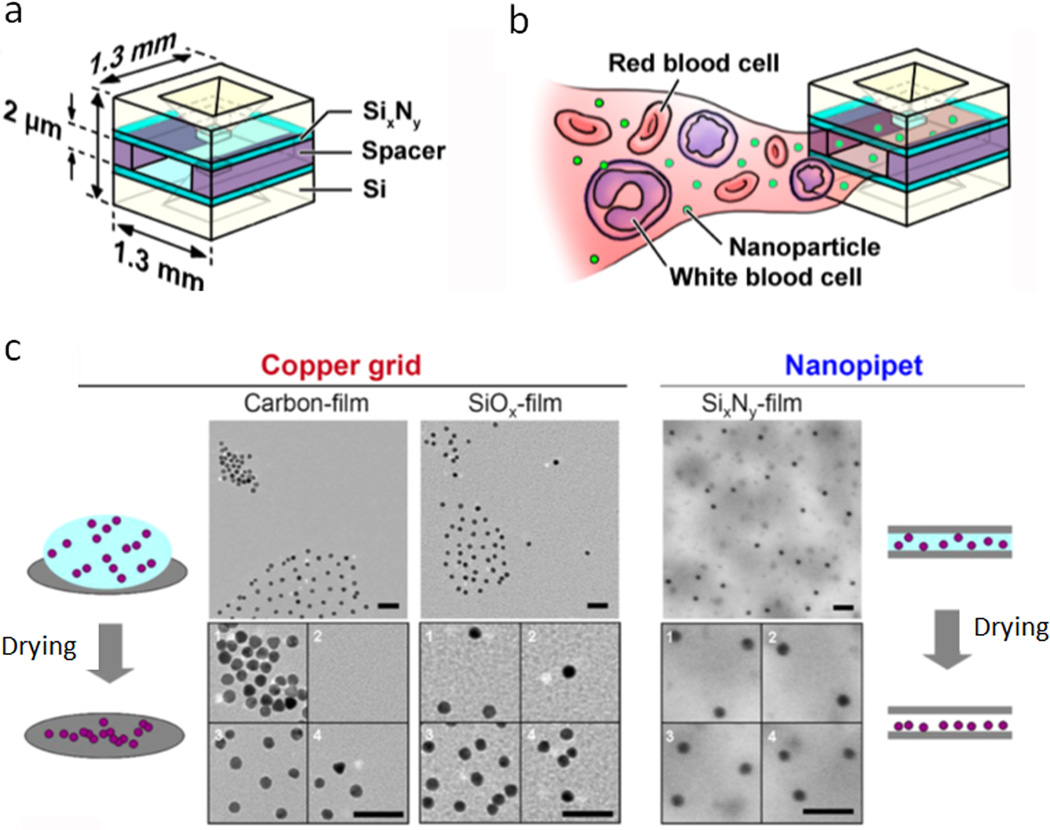
In this context, despite low throughput, TEM is well suited. The resolution of TEM is in sub-nanometer, which is sufficient to visualize most nanoparticles consisting of heavy metals.⁵¹ For organic samples with low electron density, high atomic number stains have been employed to increase their contrast. Although TEM is a powerful tool for characterizing nanoparticles, challenges still exist to measure nanoparticle concentrations. The main reason is that nanoparticles tend to aggregate during the drying process on TEM grids, leading to uneven distribution and biased counting of nanoparticles on the grid.⁵² To solve this problem, Tai et al. fabricated a microchip nanopipet on a hydrophilic Si_xN_y film using semiconductor processing.⁵² As shown in Fig. 7a, the nanopipet has a very small size (1.3 mm × 1.3 mm) and a narrow chamber width (2 µm). This setup can break the surface tension of the sample droplet and suppress the capillary flow during the vacuum drying process, resulting in uniformly dispersed nanoparticles on a substrate (Fig. 7c). The nanoparticle numbers can be easily counted on each TEM image and the concentration of nanoparticles is calculated based on a fixed and well-defined volume of the nanopipet chamber (< 1 µl). In addition to preventing aggregation of nanoparticles on TEM grids, the nanopipet can also act as a prefilter to inhibit large substances entering the chamber (Fig. 7b). Taking this advantage, the authors demonstrated that blood cells and other large components in blood samples can be easily sorted out, leaving gold nanoparticles on the TEM grid for concentration measurement. The results from TEM counting showed no significant difference from those calculated from total gold atoms. The method based on nanopipet and TEM is a promising strategy for measuring nanoparticle concentrations, especially in biological-relevant media. With the development of semiconductor processing techniques, nanopipet can potentially be mass-produced, making the nanopipet-TEM method accessible to many research labs.

Figure 7.

Counting nanoparticles using nanopipet and TEM. (a) Scheme of the TEM microchip nanopipet. (b) Illustration of nanopipet preventing larger substances in the blood entering the chamber. (c) Comparison of nanoparticle TEM images generated by normal drying process (gradual evaporation of solvent on copper grids) and vacuum drying process in a nanopipet. Normal drying leads to aggregation of nanoparticles on copper grids coated with either hydrophobic carbon or hydrophilic SiOx film; vacuum drying in the nanopipet results in homogeneous distribution of nanoparticles on a hydrophilic SixNy film. Adapted with permission from ref. 52. Copyright (2012) American Chemical Society.

In addition to nanopipet, a fractionator sampling strategy has also been employed to eliminate biased counting of nanoparticles in cells.⁵³ This method utilizes traditional cell fixation and embedding techniques to embed nanoparticle-tagged cells in epoxy resin. The resin sample is further sectioned into 200-nm thin films and placed on TEM grids for imaging. To ensure unbiased estimation of nanoparticles in the entire cell population, each 200-nm section is selected randomly from a sample pool and a fraction of each sample on the TEM grid is analyzed. By using a fractionation equation, the total number of nanoparticles and the number of particles in a single cell or in subcellular organelles can be calculated. Despite the relatively labor-intensive procedure, this fractionation method is a promising strategy to achieve accurate and precise counting of nanoparticles in cells and tissues. Moreover, this method has great potential to be generalized to measure nanoparticle concentrations in liquid. For instance, if nanoparticles can disperse well in the solvent used in the embedding process, it is possible to generate a resin sample which retains the spatial distribution of nanoparticles in solution. Therefore, the concentration of nanoparticles can be measured using the fractionator principle.

All the microscopic techniques discussed above demonstrate advantages in measuring nanoparticle concentrations. As the limitation of size and type of nanoparticles varies among different techniques, it is important to evaluate the property of nanoparticles and select the appropriate microscopy. With the improvement of counting efficiency and the elimination of biased counting, these counting methods hold great promise to generate accurate and statistically significant information of nanoparticle concentrations.

4. Summary and outlook

Molar/number concentration of nanoparticles is a critically important quantity that needs to be measured for nanoparticle fabrications, modifications, and downstream applications. Considering the fast growing number of nanoparticles with a wide range of sizes and materials, it is essential to develop simple and versatile methods that are compatible to various types of nanoparticles. The technologies summarized in this review adopt different mechanisms and demonstrate strengths as well as limitations (Table 1). The methods using the ensemble quantity divided by unit quantity represent the simplest concept and can be applied to all types of nanoparticles, in theory. However, it is challenging to accurately measure the unit quantity of nanoparticles (e.g., number of atoms per nanoparticle or weight of one nanoparticle). Therefore, this method is usually used as a crude estimation of nanoparticle concentration unless precise measurement of unit quantity is available. UV-Vis spectroscopy, turbidimetry, DLS are three optical methods that measure intensity of light upon absorption or scattering by nanoparticles. The values measured by these methods are ensemble properties of nanoparticle suspensions, which can reflect averaged concentrations with statistical significance. The limitations of these three methods lie in the complexity of measuring extinction/scattering coefficient or employing a reference sample with a known concentration. LIBD is another method measuring the plasma generation from nanoparticles in a suspension. It has a wide application in a variety of particles with different sizes, but a special laser system is required to ensure breakdown of nanoparticles. Resistive-pulsed sensing, spICPMS, and light scattering particle counter are three methods that can count particles. They provide concentration information based on the signal pulses from a sensor and a standard reference sample is usually required for calibration, unless sample volume and nanoparticle detection efficiency can be accurately determined. Microscopic techniques enable direct visualization of nanoparticles on a surface. These methods are straightforward, but it is critical to ensure unbiased counting as the number of nanoparticles on one image may not represent the overall density of nanoparticles in solution.

Table 1.

Summary of methods for measuring nanoparticle molar concentration

Methods	Types of nanoparticles	Size limitation (diameter)	Prerequisites
Gravimetric measurement (ensemble quantity/quantity per nanoparticle)	Nanoparticles with known density and regular shape	No restriction	Precise measurement of average weight or number of atoms per nanoparticle
UV-Vis spectroscopy	Strong extinction on UV-Vis spectra (e.g., gold, silver and cadmium selenide)	No minimal limitation	Accurate determination of molar extinction coefficient of nanoparticles
Turbidimetry	Non-absorbers at detection wavelength (e.g., polystyrene at 350 nm)	≥ 70 nm21	Accurate determination of scattering coefficient of nanoparticles
Dynamic light scattering (DLS)	No absorbance/fluorescence at laser wavelength	Ultimately sub-nanometer54	Calibration with a standard nanoparticle solution
Laser-induced breakdown detection (LIBD)	No specific restriction	1–2 nm31	Powerful laser system; Calibration with a standard nanoparticle solution
Resistive-pulse sensor	No specific restriction	Izon qNano: ≥ 50 nm41	Calibration with a standard nanoparticle solution
Single Particle Inductively Coupled Plasma Mass Spectrometry (spICPMS)	Metal nanoparticles	Depends on type of nanoparticles. Gold nanoparticles: ≥ 15 nm45 Silver nanoparticles: ≥ 20 nm44	Calibration with a standard nanoparticle solution
Optical sensing (light scattering particle counter)	Nanoparticles with strong scattering	24 nm for gold nanoparticles48	Calibration with a standard nanoparticle solution, or accurate determination of sample volume and detection efficiency
Laser-illuminated light scattering microscopy (Nanosight)	Any types of nanoparticles with high scattering coefficient	Depends on type of nanoparticles: Organic nanoparticles: ≥ 50 nm Metal and semiconductor: ≥ 10 nm49	Optimize nanoparticle concentrations to ensure all particles are analyzed by the NTA software
Transmission electron microscopy (TEM)	High electron density (metal nanoparticles); organic nanoparticles with staining	Depends on image contrast, many inorganic nanoparticles can be imaged at sub-nanometer sizes	Uniform distribution on TEM grids and unbiased counting

To meet the need of accurately measuring nanoparticle molar/number concentrations, we envision that new technologies should simultaneously possess the following features: 1) applicability to all types of nanoparticles with low size limitation (1 nm); 2) simple setup and ease to operate; 3) capability to measure unknown samples without the need of standards or measurement of complicated physical properties (e.g., extinction/scattering coefficients); and 4) statistical significance. With improvements to the methods discussed above and invention of new technologies, these criteria will likely be met in the near future. Simple and accurate measurement of molar concentration will help transform the way nanoparticles are made, functionalized, assessed, and used, and will significantly expand the impact of nanotechnology on many fields such as electronics, photonics, energy, catalysis, computing, and medicine.

Key learning points.

1. Knowing the molar concentration of nanoparticles is important for their modification, application, and toxicity assessment.

2. Current strategies for determination of nanoparticle molar concentration adopt a broad spectrum of mechanisms, with different strengths and limitations.

3. General and simple approaches are urgently needed for characterization of diversified and novel nanoparticles.