Working Memory Contributions to Reinforcement Learning Impairments in Schizophrenia

Abstract

Previous research has shown that patients with schizophrenia are impaired in reinforcement learning tasks. However, behavioral learning curves in such tasks originate from the interaction of multiple neural processes, including the basal ganglia- and dopamine-dependent reinforcement learning (RL) system, but also prefrontal cortex-dependent cognitive strategies involving working memory (WM). Thus, it is unclear which specific system induces impairments in schizophrenia. We recently developed a task and computational model allowing us to separately assess the roles of RL (slow, cumulative learning) mechanisms versus WM (fast but capacity-limited) mechanisms in healthy adult human subjects. Here, we used this task to assess patients' specific sources of impairments in learning. In 15 separate blocks, subjects learned to pick one of three actions for stimuli. The number of stimuli to learn in each block varied from two to six, allowing us to separate influences of capacity-limited WM from the incremental RL system. As expected, both patients (n = 49) and healthy controls (n = 36) showed effects of set size and delay between stimulus repetitions, confirming the presence of working memory effects. Patients performed significantly worse than controls overall, but computational model fits and behavioral analyses indicate that these deficits could be entirely accounted for by changes in WM parameters (capacity and reliability), whereas RL processes were spared. These results suggest that the working memory system contributes strongly to learning impairments in schizophrenia.

Introduction

Patients with schizophrenia (SZ) demonstrate deficits across a wide range of measures of executive control/working memory (WM; Barch and Ceaser, 2012) and reinforcement learning (RL; Gold et al., 2008; Deserno et al., 2013) paradigms, including the Iowa Gambling Task (Shurman et al., 2005), the Wisconsin Card Sorting Test (Prentice et al., 2008), probabilistic reinforcement, and reversal learning (Waltz and Gold, 2007; Waltz et al., 2007, 2011; Schlagenhauf et al., 2013). However, the specific underlying cognitive and neural mechanisms remain uncertain: most tasks involve multiple cognitive and neural processes, including the striatal dopamine system, which is involved in signaling prediction errors and integrating them over trials (Frank et al., 2004; Dayan and Daw, 2008), and the prefrontal cortex, which is involved in using WM to test hypotheses and represent values of prospective outcomes to guide choice.

Patients with SZ consistently exhibit deficits in tasks involving learning (Paulus et al., 2003; Kim et al., 2007), but a better understanding of these deficits necessitates parsing the contribution of different neurocognitive processes. Since most learning paradigms confound contributions of two separable cognitive processes, WM and RL, it remains unclear whether patient impairments arise from core changes in the RL process per se (where “RL” is used to signify the incremental accumulation of values based on reward prediction errors).

Computational models of RL afford trial-by-trial quantification of choices (O'Doherty et al., 2007; Daw, 2011) and are thought to reflect dopamine-mediated corticostriatal synaptic plasticity (Frank et al., 2007). However, computational modeling by itself does not solve the problem of task impurity: other cognitive functions involved in RL tasks (such as working memory) may contaminate the inferred RL processes.

Collins and Frank (2012) developed a task to disentangle WM and RL contributions to learning by explicitly manipulating potential WM load. They also presented a hybrid model that included a model-free RL process, reflecting the striatum-dopaminergic system; and a capacity-limited, decay-sensitive WM process. They showed that classical RL models overestimated learning rates but that the hybrid model was able to separately estimate the contribution of WM from RL. Furthermore, once WM processes were controlled, individual differences in the RL learning rate were related to genetic variants in GPR6, a protein selectively expressed in the striatum (Lobo et al., 2007). Conversely, WM capacity estimates were related to COMT, a gene that preferentially affects prefrontal function (Gogos et al., 1998; Huotari et al., 2002; Matsumoto et al., 2003; Frank et al., 2007; Slifstein et al., 2008).

We apply a similar experimental and modeling strategy to investigate whether learning impairments in SZ patients are more closely related to WM processes or to core aspects of the RL system. Based on recent studies (Waltz and Gold, 2007; Strauss et al., 2011; Gold et al., 2012; Doll et al., 2014), we hypothesized that patients would exhibit deficits in WM processes with relative sparing of incremental, model-free RL processes (Waltz et al., 2009; Dowd and Barch, 2012).

Materials and Methods

Patient-related methods

A total of 49 people (35 males and 14 females) with a DSM-IV (American Psychiatric Association, 2000) diagnosis of schizophrenia (n = 44) or schizoaffective disorder (n = 5) participated. All were clinically stable outpatients recruited from the MPRC Outpatient Research Program or from other nearby outpatient clinics. Diagnosis was determined by the Structured Clinical Interview for DSM-IV Axis I Disorders (SCID; First et al., 1997), past medical records, and clinician reports. At the time of testing, all participants had been on stable medications (same type and dose) for a minimum of 4 weeks. Duration of illness was also recorded.

A total of 36 healthy volunteers (25 males and 11 females), matched to the patient group in terms of important demographic variables (Table 1), were recruited through a combination of random telephone number dialing, Internet advertisements, and word of mouth among recruited controls. All were screened with the SCID and the Structured Clinical Interview for DSM-IV Personality Disorders (First et al., 1997; Pfohl et al., 1997) and were free of a lifetime history of psychosis, current Axis I disorder, and Axis II schizophrenia spectrum disorders. All denied a family history of psychosis in first-degree relatives. All control participants denied a history of medical or neurological disease, including current or recent substance abuse or dependence that would likely impact cognitive performance.

Table 1.

Demographics and clinical characteristics of patients with schizophrenia and healthy control comparison participants

	Schizophrenia (n = 49)		Healthy control (n = 36)		Group comparison
	Mean	(SD)	Mean	(SD)
Demographics
Age	39.46	(10.66)	41.36	(9.85)	F = 0.7; p = 0.40
Gender (% males)	71		69		χ2 (1, n = 85) = 0.0; p = 0.84
Race and ethnicity (% Cauc:% AA:% other)	53:35:12		61:31:8		χ2 (5, n = 85) = 2.0; p = 0.85
Personal education	12.73	(2.16)	15.17	(2.01)	F = 27.9; p < 0.001
Mother's education	14.00	(2.79)	13.83	(2.55)	F = 0.1; p = 0.78
Father's education	14.86a	(3.11)	14.41b	(3.19)	F = 0.4; p = 0.54
Neuropsychology measures
WASI	101.20	(14.72)	118.26	(11.53)	F = 34.1; p < 0.001
WRAT4	95.47	(14.63)	111.03	(11.50)	F = 24.8; p < 0.001
WTAR	97.51	(17.26)	111.67	(10.90)	F = 18.7; p < 0.001
MCCB	32.94	(13.76)	54.14	(10.47)	F = 59.8; p < 0.001
Clinical variables
SANS total	25.91	(13.41)
BNSS total	21.33	(14.11)
BPRS total	32.20	(6.21)
LOF total	21.9	(5.81)
Illness duration (years)	19.6	(11.4)

Cauc, Caucasian; AA, African American; WASI, Wechsler Abbreviated Scale of Intelligence; WRAT, Wide Range Achievement Test Reading; WTAR, Wechsler Test of Adult Reading; LOF: Level of Function.

^a n = 43.

^b n = 34.

All participants received the Wechsler Abbreviated Scale of Intelligence (Wechsler, 1999) and the MATRICS Consensus Cognitive Battery (MCCB; Nuechterlein and Green, 2006) to assess the overall level of cognitive ability, as well as a measure of working memory performance that we used in correlational analyses with model-based estimates of WM. Participants with SZ also received the Scale for the Assessment of Negative Symptoms (SANS; Andreasen, 1983), the Brief Negative Symptom Rating Scale (BNSS; Kirkpatrick et al., 2011), and the Brief Psychiatric Rating Scale (BPRS; Overall and Gorham, 1962) to assess symptom severity. The patients were mild-moderately symptomatic as seen on the clinical rating scales. The healthy controls scored significantly higher on measures of word reading, estimated IQ, and general neuropsychological ability as is typical in the literature.

Experimental design

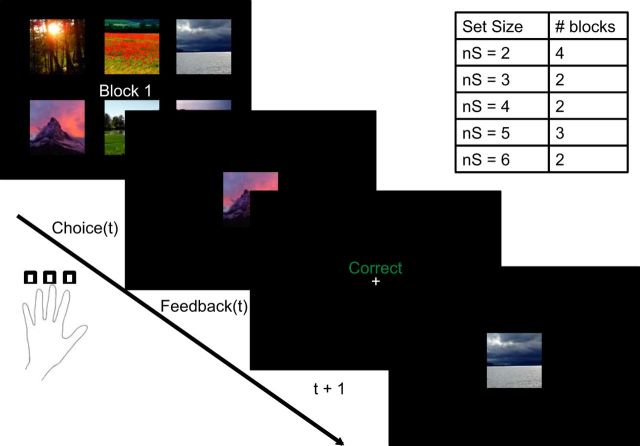
The task was modified from a classic conditional associative learning paradigm (Petrides, 1985; Fig. 1) in which, on each trial, a single stimulus was presented to which subjects could respond with one of three responses (button presses on a response pad). Subjects had to learn over time which of those responses was the correct one to select for each stimulus, based on the binary deterministic feedback they received (Collins and Frank, 2012).

Figure 1.

Experimental protocol. At the beginning of each block, subjects were presented the set of stimuli they would have to learn the correct actions for in that block. Each trial included a 3.5 s presentation of a stimulus during which time subjects pressed one of three responses. Feedback indicating correct or incorrect followed. Block set sizes varied between two and six, and the order was randomized across subjects.

To manipulate working memory demands separately from RL components, we systematically varied the number of stimuli (denoted as set size n_s) for which subjects had to learn the correct actions within a block. There were four blocks with n_S = 2, two blocks each with n_S = 3 or n_S = 4, three blocks with n_S = 5, and two blocks with n_S = 6 for a total of 13 blocks, requiring ∼35 min to complete. The number of blocks per set size was determined by a trade-off between three constraints: equating the overall number of stimuli per set size, obtaining sufficient blocks of higher set size to ensure taxing of the RL system, and the overall experiment length. Each block corresponded to a different category of visual stimulus (such as sports, fruits, places, etc.), with stimulus category assignment to block set size counterbalanced across subjects. Block ordering was also counterbalanced within subjects to ensure an even distribution of high/low load blocks across the duration of the experiment.

At the beginning of each block, subjects were shown the entire set of stimuli for that block and encouraged to familiarize themselves with them. They were then asked to answer as quickly and accurately as possible after each individual stimulus presentation. Within each block, stimuli were presented in a pseudo-randomly intermixed order, with a minimum of 9 and a maximum of 15 presentations of each stimulus, up to a performance criterion of at least four correct responses of the five last presentations of each stimulus.

Stimuli were presented in the center of the screen for up to 3.5 s, during which time subjects could press one of three keys. Binary deterministic auditory feedback ensued (high tone for correct and low tone for incorrect, as well as the words “correct” or “incorrect,” presented for 1 s). A 0.75 s dark screen followed this, before the next stimulus.

Subjects were instructed that finding the correct action for one stimulus was not informative about the correct action for another stimulus. This was enforced in the choice of correct actions, such that, in a block with n_S = 3, for example, the correct actions for the three stimuli were not necessarily three distinct keys. This procedure was implemented to ensure independent learning of all stimuli (i.e., to prevent subjects from inferring the correct actions to stimuli based on knowing the actions for other stimuli).

Computational modeling

RLWM model

To better account for subjects' behavior and disentangle roles of working memory and reinforcement learning, we fitted subjects' choices with our RLWM computational model. Previous research showed that a model allowing choice to be a mixture between a classic δ rule reinforcement learning process and a fast capacity-limited working memory process accounted best for learning (Collins and Frank, 2012). The model used here is a variant of the previously published model. We first summarize its key properties.

1. RLWM includes two modules, a classic incremental RL module with learning rate α and a WM module that can learn in a single trial (learning rate 1) but is capacity limited (with capacity K).

2. Both RL and WM modules are subject to forgetting [decay parameters φ_RL and φ_WM and noise in the choice policy (directed: softmaxβ, undirected: ε)]. We also include a perseveration parameter pers to account for potential tendencies to repeat actions in the face of negative feedback.

3. The final action choice is controlled by weighing the contributions of the RL and WM modules' policies. How much weight is given to WM relative to RL (the mixture parameter) depends on two factors. First, it depends on what the probability is that a stimulus is stored in WM of capacity K. If there are fewer stimuli than WM can hold (n_S ≤ K), then that probability is 1. Otherwise, only K out of n_S can be stored. Second, the overall reliance of WM versus RL is scaled by factor 0 < ρ < 1, with higher values reflecting relative greater confidence in WM function. Thus, the weight given to the WM policy relative to the RL policy is w = ρ × min(1, K/n_S).

We conducted extensive comparisons of multiple models to determine which fit the data best (penalizing for complexity) so as to validate the use of this model in interpreting subjects' data. In particular, we fit several other models that include or leave out various properties of the RLWM model.

Learning model details

Reinforcement learning model.

All models include a standard RL module with simple δ rule learning. For each stimulus s and action a, the expected reward Q(s,a) is learned as a function of reinforcement history. Specifically, the Q value for the selected action given the stimulus is updated after observing each trial's reward outcome r_t (1 for correct, 0 for incorrect) as a function of the prediction error between expected and observed reward at trial t, as follows:

where δ_t = r_t − Q_t(s,a) is the prediction error and α is the learning rate. Choices are generated probabilistically with greater likelihood of selecting actions that have higher Q values, using the following softmax choice rule:

Here, β is an inverse temperature determining the degree with which differences in Q values are translated into a more deterministic choice and the sum is over the three possible actions a_i.

Undirected noise.

The softmax temperature allows for stochasticity in choice in an oriented way, by making more valuable actions more likely. We also allow for “slips” of action (“irreducible noise,” i.e., even when Q value differences are large). Given a model's policy π = p(a|s), adding undirected noise consists of defining the new mixture policy as follows:

where U is the uniform random policy (U(a) = 1/n_A, n_A = 3) and the parameter 0 < ε < 1 controls the amount of noise (Collins and Koechlin, 2012; Guitart-Masip et al., 2012; Collins and Frank, 2013).

Forgetting.

We allow for potential decay or forgetting in Q values on each trial, additionally updating all Q values at each trial, according to the following:

where 0 < φ < 1 is a decay parameter pulling at each trial the estimates of values toward initial value Q₀ = 1/n_A.

Perseveration.

Previous studies have shown differential treatment of positive and negative outcomes in patients in probabilistic learning tasks, as well as perseveration (neglect of negative outcomes) in adaptive cognitive tasks such as the Wisconsin Card Sorting Test (Kim et al., 2007; Prentice et al., 2008). To allow for potential neglect of negative, as opposed to positive, feedback, we estimate a perseveration parameter pers such that for negative prediction errors (δ < 0), the learning rate α is reduced by α = (1 − pers) × α. Thus, values of pers near 1 indicate perseveration with complete neglect of negative feedback, whereas values near 0 indicate equal learning from negative and positive feedback. Note that this notion of perseveration is focused on the failure to use negative feedback to avoid repeating an error, rather than to shift away from a previously reinforced option, as is often implied in the Wisconsin Card Sorting Test (Kim et al., 2007; Prentice et al., 2008).

Working memory.

To implement an approximation of a rapid updating but capacity-limited WM, this feature assumes a learning rate α = 1 but includes capacity limitation such that only, at most, K stimuli can be remembered. At any time, the probability of a given stimulus being in working memory is p_WM = ρ × min(1,K/n_S). As such, the overall policy is as follows:

where π_WM is the WM softmax policy and π_other is another module's policy. In the WM-only model, this is the random uniform policy: π_other = U. In the RLWM model, this is π_other = π_RL: the softmax policy from the RL module without capacity limitation. Note that this implementation assumes that information stored for each stimulus in working memory pertains to action–outcome associations. Furthermore, this implementation is an approximation of a capacity-/resource-limited notion of working memory. It captures key aspects of working memory such as (1) rapid and accurate encoding of information when a low amount of information is to be stored and (2) decrease in the likelihood of storing or maintaining items when more information is presented or when distractors are presented during the maintenance period. Because it is a probabilistic model of WM, it cannot capture specifically which items are stored, but it can provide the likelihood of storing and maintaining items given task structure (set size, delay, etc.).

Models considered

We combined the previously described features into different learning models and investigated which ones provided the best fit of subjects' data. For all models we considered, adding undirected noise, forgetting, and perseveration features significantly improved the fit, accounting for added model complexity (see model comparisons).

This left three interesting classes of models to consider.

1. RL: This model combines simple δ rule RL, with forgetting, perseveration, and undirected noise features. It assumes a single system that is sensitive to delay and asymmetry in feedback processing. This is a five-parameter model (learning rate α, sofmax inverse temperature β, undirected noise ε, decay φ_RL, and pers parameter).

2. RLWM: This is the main model, consisting of a mixture of RL and working memory. RL and WM modules have shared softmax β and pers parameters but separate decay parameters, φ_RL and φ_WM. Working memory capacity is 0 < K < 6, with reliance 0 < ρ < 1 on working memory for items potentially stored in working memory. Undirected noise is added to the RLWM mixture policy. This is an eight-parameter model (capacity K, WM reliance ρ, WM decay φ_WM, RL learning rate α, RL decay φ_RL, perseveration pers, sofmax inverse temperature β, undirected noise ε).

3. WM: This is the WM-only model. It is equivalent to the previous one with RL learning rate α = 0, RL decay φ_RL = 0. It assumes that any choice not made by working memory is made randomly (uniform). It is a six-parameter model.

RLWM fitting procedure

Parameters were fit using Matlab optimization under the constraint function fmincon. This was iterated with 50 randomly chosen starting points to increase the likelihood of finding a global rather than local optimum. For models including the discrete capacity parameter, this fitting was performed iteratively for capacities n = {0,1,2,3,4,5,6}, then inferring capacity and other parameters that gave the best fit.

Softmax β temperature was fit with constraints [0 500]. All other parameters were fit with constraints [0 1]. We considered sigmoid-transforming the parameters to avoid constraints in optimization and obtain normal distributions, but whereas fit results were similar, distributions obtained were actually not normal. Thus, all statistical tests on parameters were nonparametric.

Model comparison

We used the Akaike Information Criterion (AIC) to penalize model complexity (Burnham and Anderson, 2002). Indeed, we previously showed that AIC was a better approximation than the Bayesian Information Criterion (Schwarz, 1978) at recovering the true model from generative simulations of the WMRL model and variants (Collins and Frank, 2012). We used the Matlab spm_bms function to compute Bayesian model evidence over AIC (Stephan et al., 2009) for Bayesian model selection over the group. Models WM-only and RL-only were strongly nonfavored, with probability 0 over the whole group. This was also true when investigating separately each group, with evidence in favor of RLWM > 0.97.

Results

Data were successfully collected for 49 patients (SZ) and 36 healthy controls (HCs). All subjects reached asymptotic performance above chance in set sizes of two to three. Although three patients did not show improvement for higher set sizes, we chose to not remove any subjects from the analysis as they did learn in lower set sizes. Exclusion of these three subjects did not change the effects of interests, however.

We first investigated learning curves per stimulus in different set sizes. These analyses (Fig. 2, top) revealed that both healthy controls and patients learned to select the correct action for each stimulus in all set sizes and that both groups showed an effect of set size. Importantly, learning slowed when there were more stimuli to be learned in parallel, with healthy controls reaching asymptotic performance by iteration 3 in set size two (corresponding to “perfect memory” performance).

Figure 2.

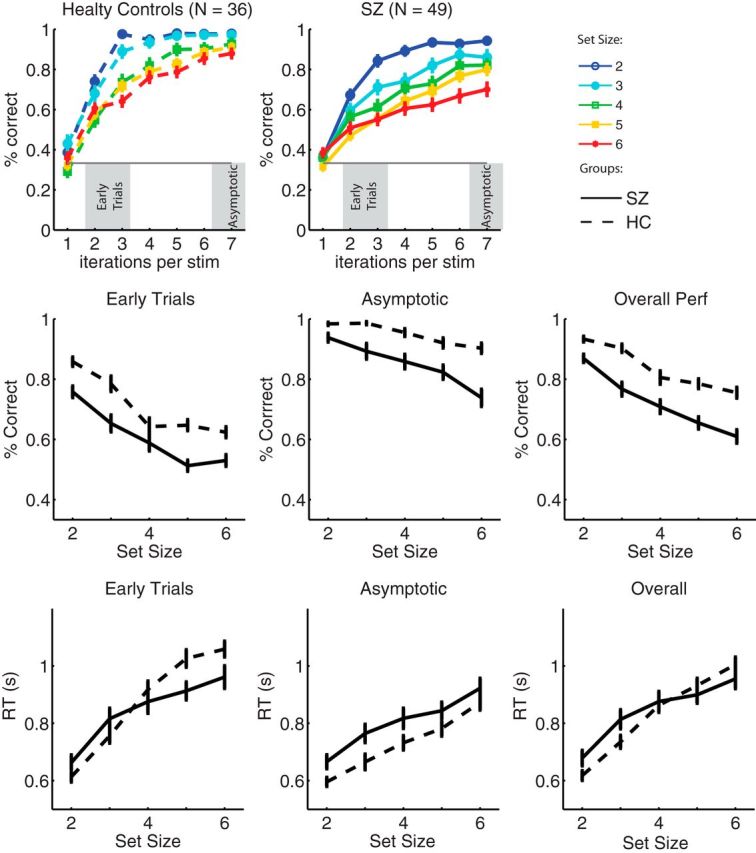
Learning effects. Top, Learning curves per set size and group (SZ, patients; HC, healthy controls, dashed lines). Learning curves indicate the probability of a correct response at the nth presentation of a single stimulus (stim). Middle, Average performance for early trials (presentations 2 and 3 of each stimulus), for asymptotic trials (last 2 presentations of each stimulus), and over the whole block. Bottom, Reaction times (RT) for early trials, asymptotic trials, and the whole block. Error bars indicate SEM.

To compare learning performance across groups and conditions, we first entered average performance in a multiple regression analysis, with factors set size (two to six), group (SZ vs HC), and time (early vs asymptotic trials; Fig. 2, top). Results showed main effects of all three factors (all p values <10⁻⁴) and interactions of set size with group and with time (p = 0.005 and p = 0.04, respectively) but no interaction of group with time (p = 0.95) or three-way interaction. We thus performed a separate analysis within early trials and within asymptotic trials. In early trials, we observed main effects of group and set size (both p values <10⁻⁴), indicating lower performance for patients and higher set sizes, but no interaction. In contrast, in late trials, both main effects (p values <10⁻⁴) were qualified by interactions (p = 0.01), indicating that the effect of set size was larger for the SZ group.

We also investigated reaction times across the same factors (figure 2, bottom). There was a main effect of set size, indicating slower reaction times for higher set sizes (p < 10⁻⁴); a main effect of time, indicating slower reaction times at the beginning of a learning block (p < 10⁻⁴); but no main effect of group, indicating that controls and patients were, on average, as fast to respond (p = 0.11). However, there was an interaction of group with set size, indicating a stronger effect of set size on healthy controls (p = 0.006), and an interaction of group with time, indicating a stronger effect of learning on healthy controls (p = 0.002). Specifically, patients' reaction times were less sensitive to difficulty or learning. However, restricting the analysis to the SZ group, we found a main effect of set size and time (both p values <10⁻³), indicating that their reaction times were sensitive to those factors, even if less so than controls and without interaction (p = 0.5). In contrast, within the HC group, we observed both main effects (both p values <10⁻⁴), as well as an interaction (p = 0.02), showing that the effect of set size decreased with time.

In these analyses, set size is confounded with delay effects: indeed, each stimulus is seen, on average, every 1/n_S trials so that time-dependent forgetting could cause slower learning in higher set sizes, independently of load effects. However, on a trial-by-trial basis, these effects are dissociable: since stimulus order within each block was randomized, we can make use of the variability of delay between repetitions of a single stimulus to disentangle set-size and delay effects. We thus performed for each subject a logistic regression including three factors (inverse of set size, number of trials since last correct choice for the current stimulus, and number of previous correct choices for current stimulus) and analyzed regression weights across subjects. We hypothesized that set-size and delay factors should be indicative of a capacity-limited working memory process, whereas iteration should be representative of a RL-like slow, cumulative learning process.

Regression weights across the whole group were significantly nonzero for all three main effects (binomial test, all p values <10⁻⁴), as well as set-size interaction with delay (p < 10⁻⁴) and with correct iterations (p = 0.002) and delay interaction with correct iterations (p < 0.05). Although set-size and iteration effects confirmed previous analysis indicating worse performance for higher set sizes and learning effects, delay effect showed that subjects were more likely to make an error when more trials intervened before a stimulus from a successful trial was presented again. Positive interaction of set size with delay indicated that this was more pronounced in higher load conditions, whereas negative interaction of delay with iterations indicated that the effect of delay decreased over time.

The previous effects all remained true when considering only the SZ group (all p values <0.05), indicating that similarly to controls, patients' learning was determined not exclusively by feedback accumulation over time (as predicted by a single RL process), but also by set size and delay, hinting at their concurrent use of capacity-working memory to learn the associations. Logistic regression weights differed significantly between control and patients groups only for the fixed-effect β weight (t₍₈₃₎ = 4.7; p < 10⁻⁴) and the set-size β weight (t₍₈₃₎ = 2.7; p = 0.008), indicating a stronger effect of set size in SZ. No other weights differed (p values > 0.12), and in particular, there was no difference between the groups in the effect of iteration number. These results are consistent with previous evidence suggestive of a role for WM in RL deficits in SZ. To separate more explicitly the effects of working memory, we fit subjects' data with reinforcement learning models.

Model fitting and model comparisons (see Materials and Methods) confirmed that subjects' learning was best represented by a mixture of two separate processes, one learning slowly and incrementally for all stimuli and the other storing information rapidly but with capacity limitations.

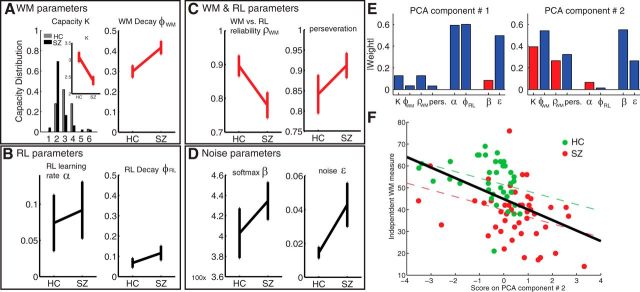
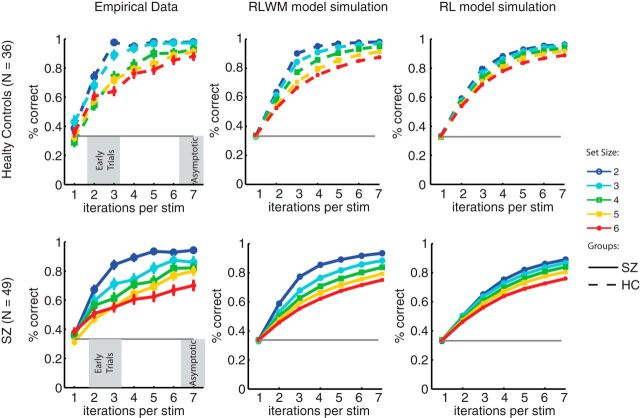
We next investigated the values of parameters obtained to confirm that they produced values for which the model was valid. First, the model fitting was successful in recovering two distinct processes. Indeed, across all subjects, the mean fit learning rate for the RL process was 0.084 (SD, 0.25) compared with the fixed learning rate of 1 for the WM memory process (Fig. 3). The mean fit decay rate for the RL process was 0.096 (SD, 0.21) compared with 0.37 (SD, 0.21) for the WM process (binomial test, p = 10⁻¹¹). This shows that the two modules had distinct learning dynamics, slow accumulation and nearly no forgetting for RL and fast learning but stronger forgetting for WM. Furthermore, both processes were indeed used: average WM reliability was ∼0.83 +/− 0.24, showing that it was efficiently used when a stimulus was stored, but capacity was found mostly within the two to four range (consistent with the WM literature), showing that RL was increasingly used to compensate for increasing failure of WM in higher set sizes when capacity was exceeded. Second, it is interesting to note that negative feedback was strongly neglected, as indicated by the high value of the perseveration parameter. Figure 4 shows simulation of the RLWM model with fitted parameters, as well as with the best-fitting pure RL models (see Material and Methods). This indicates that although both models can account for the qualitative effect of slower learning curves for higher set sizes, RLWM captures much better the learning dynamics exhibited in different sessions for each group.

Figure 3.

RLWM model fit parameters. Parameters fit on subjects' behavior with the RLWM model, for the HC group and patients (SZ). Red indicates a significant difference between groups. Error bars indicate SEM. A, WM-specific parameter rates show less robust WM for patients (lower capacity N and faster decay rate φ_WM). B, RL-specific parameters (learning rate α and decay φ_RL) show no difference. C, Patients rely a priori less on WM (ρ_WM) and perseverate more than controls. D, Despite worse performance in patients, noise parameters show no difference between groups, indicating that this is attributable to deficit in learning more than deficit in choice. E, Absolute value of the weights on model parameters for the first two principal components. Blue bars indicate a positive weight and red bars a negative weight. The first component loads strongly on the two RL parameters, whereas the second component loads strongly on the four WM parameters. pers., Perseverate. F, The second component is correlated with an independent classic measure of working memory across all subjects (black regression line) and within each group.

Figure 4.

Learning curves and model simulations. Left, Empirical data per group (SZ, patients; HC, healthy controls, dashed lines). Middle, RLWM model simulation. Right, RL model simulation (δ rule learning model including undirected noise, forgetting, and perseveration mechanisms). Learning curves indicate the probability of a correct response at the nth presentation of a single stimulus (stim). For each subject's fitted parameters, one set of learning curves was obtained by averaging over 100 simulations of the model with those parameters. Overall learning curves were then obtained by averaging across subjects.

We have shown that the recovered parameters are reasonable within the model hypothesis and that the fit model can adequately account for observed behavior. This allowed us next to use the model to better understand subjects' individual behaviors by summarizing individual differences into meaningful model parameters and comparing them across groups. Since most fit parameter distributions were non-normally distributed (see Materials and Methods), we compared results across groups with a nonparametric unpaired test (Wilcoxon rank sum test). We found (Fig. 3A) that both working memory-specific parameters were impaired in SZ compared with HC: patients showed lower working memory capacity (median of two vs three for controls; p < 10⁻⁴) and more forgetting in WM (φ_WM, p = 0.005). Furthermore, the reliance on WM use was lower in SZ (Fig. 3C; ρ_WM, p = 0.04). The parameter accounting for neglect of error information (or perseveration) in both WM and RL was significantly stronger in patients than controls (Fig. 3C; pers, p = 0.001). In contrast, RL-specific parameters showed no difference between groups (Fig. 4B; α, φ_RL, p > 0.3). The same was true of the noise parameter, β (Fig. 3D; p = 0.25), though undirected noise was marginally higher for patients (ε, p = 0.06).

To investigate further the role of the different processes summarized by the fit model parameters, we performed a principal component analysis (PCA) on the z-scored fit parameters. We investigated the first two components, which accounted for 52% of the variance, and compared them to the MCCB working memory domain measure as an established measure of working memory performance. The first component loaded only on RL parameters (Fig. 3E) and undirected noise, did not differ significantly between groups (p = 0.49; t = 0.69), and did not relate to a direct measure of WM (see Materials and Methods; ρ = 0.13; p = 0.21). On the contrary, the second component loaded on all WM parameters (Fig. 3E) and noise parameters, with higher value corresponding to lower capacity, higher forgetting, less WM use, and more perseveration. This encompasses all aspects of the WM process, and thus, as expected, SZ subjects had a significantly higher score than controls (Fig. 3F; t = 3.8; p = 0.0003). Notably, this score was significantly negatively correlated with the direct WM measure (ρ = −0.52; p < 10⁻⁶), and this remained true within each group (both p values <0.05; ρ < −0.29).

These results confirmed our hypothesis that the observed learning impairment in patients was related to a deficit in the working memory component of the model, rather than in reinforcement learning or in choice selection. We next investigated whether positive or negative symptoms of schizophrenia impacted any aspect of behavior. Based on prior work (Waltz et al., 2007, 2011), we had hypothesized that negative symptom severity might be related to the WM parameters. Correlations between symptoms and fit model parameters, as well as PCA components or the MCCB working memory measure, yielded no significant associations (BPRS, BNSS, and SANS scales; all p values > 0.1; Spearman ρ < 0.24). This lack of association with negative symptoms might reflect the fact that the current task more closely relates to the sort of rule-based working memory process that would involve lateral prefrontal cortex, whereas prior associations with negative symptoms involved representing specific reward values for each stimulus or action, functions attributed to more limbic portions of prefrontal cortex hypothesized to be related to negative symptoms, such as orbitofrontal cortex (Gold et al., 2012).

We also investigated the effects of drug dose on performance. We found a significant correlation between a Haloperidol equivalent dose and RL learning rate parameter α_RL (Spearman ρ = − 0.37; p = 0.009) as well as error neglect parameter pers (Spearman ρ = 0.46; p = 0.001), indicating more error neglect and slower learning for higher antipsychotic doses. Importantly, there was no effect on the working memory capacity parameter (p = 0.97) or any other parameter (all p values > 0.11). Finally, we found no effect of duration of illness on any parameters.

Discussion

These behavioral and modeling analyses provide a new perspective on the genesis of reinforcement learning deficits in people with schizophrenia. Our basic behavioral result that patients are overall less able than controls to use feedback to guide optimal response selection is consistent with many other reports in the literature (Waltz and Gold, 2007; Polli et al., 2008; Murray et al., 2008b; Somlai et al., 2011). Indeed, this body of behavioral work, combined with functional neuroimaging evidence suggesting abnormalities in the signaling of prediction errors in both cortical (Corlett et al., 2007) and striatal (Murray et al., 2008a; Koch et al., 2010) regions and abnormal striatal dopamine (Abi-Dargham et al., 1998; Howes et al., 2012), has led to a renewed focus on the role of reward-related dopaminergic mechanisms in both the positive and negative symptoms of schizophrenia (Kapur et al., 2005; Howes and Kapur, 2009; Ziauddeen and Murray, 2010; Deserno et al., 2013).

Our behavioral results and modeling strategy indicate, however, that learning impairments in SZ stem primarily from a core deficit in working memory, which may be responsible for what appears to be a reinforcement learning impairment. Specifically, we found robust evidence that patients had reduced working memory capacity, as well as faster working memory decay, coupled with normal reinforcement learning rates. This was observable in terms of a stronger detrimental effect of set size on learning in patients than in controls, together with a diminished effect of set size on reaction time. Assuming that the increased reaction time with set size arises from greater taxing of WM processes, the latter result is convergent with the modeling finding, not only of WM capacity and forgetting limitations, but also of less overall reliance on WM, among patients (even with their limited capacity). In contrast, the slow, incremental learning that is thought to be driven by dopaminergic prediction error signaling appears to be intact in schizophrenia, consistent with several recent reports from our group (Gold et al., 2012).

Note that we are not suggesting that reinforcement learning as a behavioral construct is normal in schizophrenia; the evidence for a behavioral deficit is clear (Waltz and Gold, 2007; Polli et al., 2008; Murray et al., 2008b; Somlai et al., 2011). Patients fail to learn from outcomes, and thus, functionally, patients show failures in reinforcement learning. This learning impairment, however, appears to arise primarily as a consequence of WM deficits.

This conclusion was substantially aided by the use of computational modeling to estimate contributions of distinct processes. Much as it did for healthy participants (Collins and Frank, 2012), model fitting revealed that behavior is better accounted for by a mixture of WM and RL processes than by single process models, for both controls and patients. Moreover, our prior work showed that two of the key parameters characterizing WM and RL systems are related to genetic variations in prefrontal versus striatal function, respectively. The use of computational modeling for teasing apart the purported neural and psychological processes governing motivational deficits in learning and decision making may be particularly useful with disorders, such as schizophrenia, that involve multiple cognitive deficits (Montague et al., 2012; Wiecki et al., 2014). Indeed, it is difficult to isolate the role of specific processes in a quantifiable fashion using behavioral or imaging methods alone. Computational modeling methods, however, provide a method to parse out different contributions to behavior.

It is interesting to note that the patient group did not differ from controls in noise parameters. This is important evidence that the patients did not simply have a noisier decision strategy in the face of a challenging task: their impairment is in learning the associations, not in using the learned associations to make a decision.

Deficits in working memory have long been considered a central feature of schizophrenia (Lee and Park, 2005; Barch et al., 2009). Indeed, one reason working memory has been such a focus of the schizophrenia literature is that it is a critical resource for many other aspects of cognition, ranging from fluid reasoning to language comprehension (Just and Carpenter, 1992; Johnson et al., 2013). Thus, working memory impairments could reasonably provide a principled account of many of the cognitive deficits characteristic of schizophrenia. Here, we show that this same impairment has consequences for reinforcement learning, thereby having broad implications for motivational processes.

A potential limitation of our study is that, contrary to many published studies, our experiment uses deterministic rather than probabilistic reinforcement feedback. Although this allows more straightforward interpretation and modeling of the potential content of working memory, it may weaken the sensitivity to the contribution of “RL” mechanisms to overall performance: in the absence of probabilistic feedback, prediction errors are less variable over time and the integration process of RL less critical. In principle, probabilistic tasks may be more sensitive to gradual RL mechanisms, whereas WM mechanisms may be more useful with deterministic feedback. Thus, we do not mean to suggest that our account of the data from this experiment can be confidently generalized to the larger clinical literature. However, it is interesting to note that patients sometimes demonstrate more severe learning impairments on nearly deterministic stimulus pairs (e.g., in the case of 90% validly reinforced responses, which, in principle, should be easier to learn), but more “normal” performance on less deterministic pairs (e.g., in the case of 80% validly reinforced responses, which are more slowly acquired; Gold et al., 2012). This suggests a role for WM in some probabilistic learning environments (Kim et al., 2007). Thus, we suspect that WM impairments may well play an important and previously unknown role in the learning, decision making, and motivational deficits observed in people with schizophrenia.

Several other results deserve discussion. First, we found that both patients and controls tended to neglect errors but that patients were more likely to do so and persist with prior response choices. This is consistent with numerous prior reports of perseveration in the schizophrenia literature, beginning with studies using the Wisconsin Card Sorting Test (Goldberg, 1987; Prentice et al., 2008). Interestingly, there are now multiple reports of relatively normal feedback error-related negativity in schizophrenia (Morris et al., 2011; Horan et al., 2012), suggesting that the error information is processed but fails to fully impact behavior.

Second, model fits showed that patients relied less on the working memory process relative to RL process, as indicated by a significantly lower reliability parameter, ρ_WM. One possible interpretation is that storage of any individual stimulus into working memory is less reliable (even within capacity) and is thus less likely to be used by patients, highlighting another limitation of their working memory system. However, another interpretation is in the arbitration between the use of the WM and RL systems. Indeed, the WM system is capacity limited, so that if subjects completely rely on it, their best performance will be constrained by capacity. But they could also decide to not rely on WM as much even if within their capacity, e.g., because they have learned over the course of their life that WM is not likely to be successful in producing the right behaviors. This could arise because capacity is lower and thus more often unhelpful, or because of more noise within WM even when under capacity. Thus, they might generalize that to all situations regardless of whether that situation could actually be solved within their capacity. Although the current results cannot distinguish between those two possibilities, they both support the interpretation of impaired working memory as a source of slower learning.

Finally, as noted above, we found a negative relationship between antipsychotic dose and RL learning rate. Whereas it is tempting to conclude that substantial blockade of striatal dopamine receptors is responsible for this association, this result should be regarded with caution. Recall that the patients and controls did not differ on RL learning rate, and that all of the patients were taking antipsychotic medications. Thus, if antipsychotics had a dose-dependent effect on RL, one would expect robust between-group differences. Furthermore, close examination of the data revealed that the performance correlations were primarily driven by a small number of patients who were taking very high doses of antipsychotics (>20 mg of haloperidol equivalents). Thus, this association could exist either because a high degree of D₂ blockade is needed to ”overcompensate” for excess striatal DA levels, and thus impair RL, or it could also simply reflect the possibility that those patients taking very high doses were the most ill and least treatment responsive. In the absence of random assignment to antipsychotic drug, the interpretation of drug dose correlations with behavioral or modeling parameters is necessarily confounded. However, the notion that very high doses of antipsychotic medication might interfere with RL is clearly plausible (Beninger et al., 2003). Indeed, it would be somewhat surprising if this were not the case.

In summary, through the use of a novel behavioral task and computational model, it appears that working memory impairments may be critically implicated in the reinforcement learning deficits found in schizophrenia. It remains for future work to determine whether this understanding generalizes to other types of learning and decision-making tasks.