Early Monocular Defocus Disrupts the Normal Development of Receptive-Field Structure in V2 Neurons of Macaque Monkeys

Abstract

Experiencing different quality images in the two eyes soon after birth can cause amblyopia, a developmental vision disorder. Amblyopic humans show the reduced capacity for judging the relative position of a visual target in reference to nearby stimulus elements (position uncertainty) and often experience visual image distortion. Although abnormal pooling of local stimulus information by neurons beyond striate cortex (V1) is often suggested as a neural basis of these deficits, extrastriate neurons in the amblyopic brain have rarely been studied using microelectrode recording methods. The receptive field (RF) of neurons in visual area V2 in normal monkeys is made up of multiple subfields that are thought to reflect V1 inputs and are capable of encoding the spatial relationship between local stimulus features. We created primate models of anisometropic amblyopia and analyzed the RF subfield maps for multiple nearby V2 neurons of anesthetized monkeys by using dynamic two-dimensional noise stimuli and reverse correlation methods. Unlike in normal monkeys, the subfield maps of V2 neurons in amblyopic monkeys were severely disorganized: subfield maps showed higher heterogeneity within each neuron as well as across nearby neurons. Amblyopic V2 neurons exhibited robust binocular suppression and the strength of the suppression was positively correlated with the degree of hereogeneity and the severity of amblyopia in individual monkeys. Our results suggest that the disorganized subfield maps and robust binocular suppression of amblyopic V2 neurons are likely to adversely affect the higher stages of cortical processing resulting in position uncertainty and image distortion.

Introduction

The maturation of the primate visual brain depends on normal visual experience and requires precise matching of images in the two eyes. Experiencing interocular decorrelation of cortical input signals early in life, because of early ocular misalignment (strabismus) or monocular defocus (anisometropia), is known to cause amblyopia, a disorder of spatial vision. Amblyopic subjects typically show reductions in contrast sensitivity and visual acuity in their affected eye (Hess and Howell, 1977; Levi and Harwerth, 1977; Kiorpes et al., 1998), but also exhibit a broad range of far more complex vision deficits (Hess et al., 1999; Kovács et al., 2000; Chandna et al., 2001; Kozma and Kiorpes, 2003; Levi, 2008). For example, amblyopic humans exhibit difficulties in global perceptual tasks that require precise pooling of neighboring local stimulus feature information. These deficits in spatial integration tasks are closely associated with increased position uncertainty, i.e., confusion between neighboring positions of local feature elements (Levi and Klein, 1983, 1985; Levi et al., 1987; Watt and Hess, 1987), and/or excessive crowding, i.e., the deleterious influence of nearby contours on visual discrimination (for review, see Levi, 2008, 2013), resulting in spatial distortion (Bedell and Flom, 1981; Barrett et al., 2003).

The neural basis of position uncertainty or distortion has not been directly investigated with electrophysiological or imaging techniques. Numerous perceptual studies suggest that the deficits of amblyopes in complex spatial tasks result from “abnormal pooling” of local stimulus information by neurons beyond the striate cortex (V1; Hess et al., 1999; Mussap and Levi, 2000; Chandna et al., 2001; Kozma and Kiorpes, 2003; Simmers and Bex, 2004; Levi, 2008, 2013). Extrastriate neurons with relatively large receptive fields (RFs) can act as integrators of local stimulus information processed by V1. However, there are only two studies in the literature that quantitatively analyzed the RF properties of extrastriate neurons in amblyopic primates (El-Shamayleh et al., 2010; Bi et al., 2011).

Neurons in V2 receive the major feedforward projections from V1 and are an integral part of the “ventral pathway” subserving “form” vision (Lund et al., 1981; Van Essen et al., 1986; Sincich and Horton, 2005; El-Shamayleh et al., 2013). The RFs of individual V2 neurons are much larger than those of V1 neurons and consist of multiple subfields that are thought to reflect V1 inputs. Therefore, V2 neurons are capable of encoding the spatial relationship between local stimulus features such as orientation and spatial frequency as an initial processing of complex visual images (Ito and Komatsu, 2004; Anzai et al., 2007; Willmore et al., 2010; El-Shamayleh and Movshon, 2011; Tao et al., 2012). In this study, we show that the spatial maps of RF subfields of multiple nearby V2 neurons are severely disorganized in amblyopic monkeys, and as a result, the ability of these neurons to accurately encode geometric relationships among neighboring local stimulus features over space is compromised.

Materials and Methods

All experimental and animal care procedures were in compliance with the Guiding Principles for Research Involving Animals and were approved by the Institutional Animal Care and Use Committee of the University of Houston.

Subjects

The subjects were 11 rhesus monkeys (Macaca mulatta), eight males and three females. Six monkeys served as normally reared controls; a substantial proportion of the normal control data come from the monkeys in which previously published experiments were conducted (Tao et al., 2012; Zhang et al., 2013). Five monkeys served as amblyopic subjects (Table 1). Of these, four monkeys were subjected to procedures to simulate anisometropia, a significant interocular difference in refractive errors. One monkey had a naturally occurring anisometropia (see below). The procedures for creating anisometropia by optical means were previously described in detail (Wensveen et al., 2003, 2006). Briefly, all infant monkeys were reared in our primate nursery that was maintained on a 12 h light/dark cycle. To simulate anisometropia, experimental infant monkeys wore a light weight helmet containing a defocus lens (−3 or −10 D lens) over one eye and a plano lens over the other eye. This rearing procedure began at 3 weeks of age and ended at 3 months of age. Around 18–24 months of age, behavioral testing began to measure their monocular visual capacities. Upon the completion of behavioral testing ∼4 years of age, the microelectrode recording experiments were conducted in V2 of each monkey.

Table 1.

The rearing history, refractive errors, and visual acuity/contrast sensitivity of the experimental subjects

Subject (age, years)	Rearing history	Amblyopic index	Grating acuity (c/d)	Vernier acuity (arcmin)	Vernier acuity loss (db)	Refractive error
MK-401	R: no lens	0.82	12.0	3.53 ± 1.37	2.93	R: +4.00 DS
(5)	L: no lens		17.7	3.13 ± 1.07	2.06	L: +2.00 DS
MK-403	R: −3 D	0.53	15.9	1.55 ± 0.28	−0.65	R: +1.75 DS
(4)	L: plano		24.1	1.83 ± 0.72	−0.28	L: +2.25 DS
MK-404	R: −10 D	0.54	19.0	No data	—	R: −1.75, −0.50 × 135
(3)	L: plano		22.6	No data	—	L: +2.00, −0.50 × 045
MK-405	R: −3 D	0.38	14.6	6.34 ± 3.71	5.47	R: +2.00 DS
(4)	L: plano		21.7	5.48 ± 2.11	4.48	L: +2.00 DS
MK-411	R: −3 D	0.51	19.4	2.27 ± 0.72	1.01	R: +2.00 DS
(5)	L: plano		24.9	2.42 ± 0.66	0.93	L: +2.50, −0.25 × 045

Behavioral testing

Spatial contrast sensitivity functions were obtained separately for each eye when the monkeys were at least 18 months of age using operant procedures described previously (Harwerth et al., 1980; Smith et al., 1985; Wensveen et al., 2006). Briefly, the monkeys were placed in a primate chair inside a dark sound-attenuating chamber. The animal's optimal spectacle correction determined by subjective refraction was held in a facemask at ∼14 mm vertex distance. The visual stimuli (Gabor patches) were generated on a 20 inch video monitor (Nano Flexscan 9080; Eizo Nanao) that operated at 100 Hz by using a graphic board (VSG; Cambridge Research Systems). The usable display subtended a visual angle of 11 × 14° at the 114 cm viewing distance and had a space average luminance of 60 cd/m². The behavioral paradigm was a temporal-interval detection task that required the monkey to press and hold down the response lever to initiate a trial and then release the lever within a criterion response interval (900 ms) after presentation of the Gabor stimulus to score a hit and receive juice reinforcement. The Gabor stimuli, which consisted of carrier gratings presented in sine phase at the center of the display and that had contrasts attenuated by a 2D Gaussian envelop with a 4° SD, were presented for durations of 500 ms, with uniform probability density between 250 and 6000 ms after the initial lever press. Contrast detection thresholds were measured as a function of spatial frequency from 0.25 to 16 c/° in 0.5 octave steps using an adaptive decreasing contrast staircase procedure. Contrast sensitivity functions were generated from the geometric means of a minimum of 10 threshold measurements at each spatial frequency.

Amblyopia index (AI) values (Kiorpes et al., 1998; Wensveen et al., 2006) were calculated for each monkey to determine the depth of amblyopia by integrating the area between the contrast sensitivity functions for the affected and fellow eyes and dividing it by the area under the function for the fellow eye. This index ranges from 0 (no deficit) to 1.0 (no measurable sensitivity in the operated eye). For our experimental monkeys, the AI ranged from 0.38 to 0.82 (Table 1). Unlike other experimental monkeys raised with a defocusing lens, MK-401 was not reared with a defocusing lens but was born with very high hyperopic refractive errors in both eyes and did not develop anisometropia until 3 months of age, near the end of the known critical developmental period for binocular functions in macaque monkeys (Harwerth et al., 1990). Consequently, this monkey exhibited amblyopia for both eyes. For this monkey, we calculated AI values for both the amblyopic and the fellow eye against the mean AI value for normal monkeys.

The method to measure Vernier acuity was previously described in detail (Harwerth et al., 1995). Briefly the stimuli were two square-wave nonius lines which appeared as dark bars 5.5 arcmin wide × 55 arcmin high separated by 2 arcmin, presented at the center of the monitor and flanked by high contrast 1c/° gratings to maintain a fusion lock. The method of constant stimuli was used where the lower test bar was presented at five offsets to the left and five offsets to the right of the upper reference bar. Monkeys were trained to press on a lever when a tone signaled the beginning of a trial. The upper reference bar and flanking gratings were presented for 1 s, followed by a 250 ms presentation of the lower test bar. Monkeys released the lever if the test bar appeared to the right of the reference and held the lever down for an additional 1 s through the trial if the test bar appeared to the left of the reference. Monkeys were rewarded with a conditioned reinforcing tone, and on a percentage basis with orange drink. In a single daily 2 h session monkeys performed ∼500 total trials, interleaved by eye and offset. The data for each session were fitted with a logistic function to determine the alignment errors in arcmin for each eye (Berkson, 1953). All experimental monkeys except one (MK-403) had significantly worse Vernier acuities than normal monkeys (Table 1). In addition, we had no Vernier acuity data for one monkey (MK-404). Note that the Vernier acuity deficits were present for both eyes. The differences between Vernier acuity of the amblyopic eye or fellow eye and that of normal monkeys were statistically significant (t test, p < 0.05). Note that the Vernier acuities of normal monkeys in this study (1.87 ± 0.07 arc min) is three to four times worse than that published by Kiorpes et al. (1993). The differences in measurement methods (e.g., stimulus) and more importantly the analysis methods between the two studies might have contributed to this difference. However, it is important to keep in mind that the lower Vernier acuities of amblyopic monkeys in this study were found using the same stimulus and analysis method as that for our normal monkeys; there was a significant loss of Vernier acuity for our experimental monkeys relative to that in our normal controls (“Vernier acuity loss in db” in Table 1).

Surgical preparation

The surgical preparation and the recording and stimulation methods were previously described in detail (Maruko et al., 2008; Tao et al., 2012; Zhang et al., 2013). Briefly, monkeys were anesthetized initially with an intramuscular injection of ketamine hydrochloride (15–20 mg/kg) and acepromazine maleate (0.15–0.2 mg/kg). The animals were paralyzed by an intravenous infusion of vecuronium bromide (a loading dose of 0.1–0.2 mg/kg followed by a continuous infusion of 0.1–0.2 mg/kg/h) and artificially respired with a mixture of 59% N₂O, 39% O₂, and 2% CO₂. Anesthesia was maintained by the continuous infusion of a mixture of sufentanyl citrate (0.05 μg/kg/h) and propofol (4 mg/kg/h). The core body temperature was kept at 37.6°C. Cycloplegia was produced by 1% atropine sulfate, and the animals' corneas were protected with rigid, gas-permeable, extended-wear contact lenses. Retinoscopy was used to determine the contact lens parameters required to focus the eyes on the stimulus screen. The use of anesthesia and paralysis was necessary to ensure that quantitative analyses of monocular and binocular responses could be obtained from a large number of units for each monkey.

Recording and stimulation

Electrode penetrations were confined to a parasagittal plane, and the angle of the penetration was typically 15° from vertical. The penetrations were started right behind the blood vessels running along the lunate sulcus and 15–17 mm lateral to the midline. Unit activity was isolated at intervals of 50–100 μm steps. The penetrations ended when the electrode exited V2. For each penetration, we made records of the cortical depth for each isolated unit. This approach allowed us to sample units consistently from similar regions of V2 for both infants and adults. Nearly all receptive-fields were located within 5° of the center of the projected fovea.

A monitor (Vision Research Graphics) with ultra-short persistence (frame rate = 140 Hz, 800 × 600 pixels) was used to present visual stimuli. The viewing distance was set to 114 cm where the display subtended a visual angle of 20° (horizontal) × 15° (vertical). Multiunit or single-unit activities were extracellularly recorded with tungsten-in-glass microelectrodes (Fredric-Haer). Action potentials from individual cortical neurons were amplified, digitized at 25 kHz, and stored using the data acquisition components in our workstation (Tucker-Davis Technology/TDT). For each isolated neuron, handheld stimuli were initially used to map the receptive fields in each eye and to qualitatively determine the neuron's ocular dominance and preferred stimulus orientation. Quantitative measurements using drifting gratings followed these procedures.

Spike sorting.

During recording experiments, the spike-sorting software in our data acquisition system (TDT-system 3) was used to maintain the quality of isolation and to ensure we were recording from the same units throughout each run. Following the completion of the entire experiment for a given animal, we used our custom made spike-sorting software off-line to isolate spiking activity from as many as three nearby units for subsequent data analyses (Fig. 2).

Figure 2.

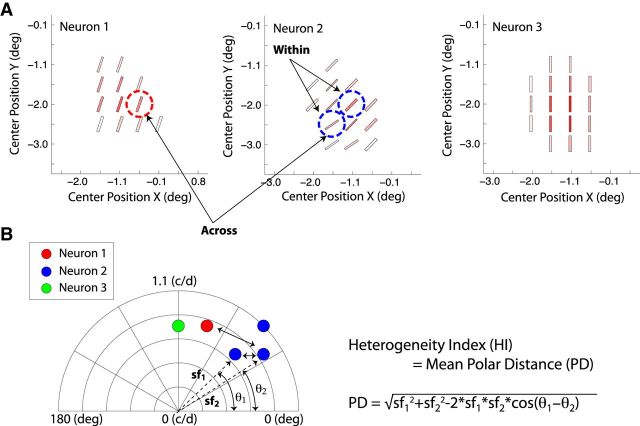
Methods to quantify the heterogeneity of RF subfield maps. A, Schematic diagrams showing the preferred orientation (bar angle) and spatial frequencies (width), and the maximum Z-scores (saturation) of the subfields in three nearby V2 neurons. B, The preferred orientation and the optimal spatial frequency of each subfield were first expressed as a polar coordinate value and illustrated with colored circles (θ = orientation, sf = spatial frequency). The difference in the preferred orientation and the optimal spatial frequency between a pair of subfields was quantified by calculating a polar distance (double arrows) between the pair with the following equation: PD = √ sf₁² + sf₂² − 2sf₁ × sf₂ × cos (θ1 − θ2). This calculation was repeated for all possible pairs of subfields and obtained the average polar distance, which was defined as the H-index. H-index was calculated within a given neuron (HI-within) and across all three nearby units (HI- across). Note that in neurons 1 and 3, there was no measurable difference in preferred orientation or spatial frequency between any pair of subfields within each RF, resulting in a single data point for each neuron.

Measurements with drifting sine wave gratings

Neurons' responses to drifting sine-wave gratings were sampled at a rate of 140 Hz (7.14 ms bin widths) and compiled into peristimulus time histograms (PSTHs) that were equal in duration to, and synchronized with, the temporal cycle of the grating. The amplitude and phase of the temporal response components in the PSTHs were determined by Fourier analysis. The stimuli were presented to the right or left eye in a randomly ordered sequence for relatively short periods (3.22 s). Rerandomized stimulus sequences were repeated three to six times during a given experiment. Blank stimuli (i.e., zero contrast control) were included in each repeat to provide a measure of the neuron's maintained firing rate. For each neuron, the orientation, spatial frequency, and size-tuning functions were first obtained using sine wave gratings (80% contrast and temporal frequency = 3.1 Hz).

Ocular dominance.

The “ocular dominance index” (ODI) of a neuron was quantitatively determined from the spatial frequency tuning functions using the following formula (Chino et al., 1997; Smith et al., 1997): ODI = (R_l − noise)/[(R_r − noise) + (R_l − noise)], where R_l is the peak response amplitude for left eye stimulation, R_r is the peak response amplitude for right eye stimulation, and “noise” is the spontaneous maintained activity. ODI values range from 0.0 (right eye response alone) to 1.0 (left eye response alone) with 0.5 indicating perfect binocular balance. An ocular imbalance index (OII) was quantified for all units using the formula OII = 2 × |ODI - 0.5| (DeAngelis and Newsome, 1999). The OII value ranges from 0.0 (no imbalance) to 1.0 (complete monocular dominance) and shows the difference in relative strength of the two eyes in driving a unit. Because the OII value does not indicate which eye is dominant, each unit was assigned according to ODI value to be dominated by the amblyopic (right in normal monkeys) eye (ODI <0.5) or the fellow (left) eye group (ODI ≥0.5). Then all OII values of units dominated by each eye were summed. The relative ratio (log₂) of the summed OII value for units dominated by the nonamblyopic eye (left eye in normal monkeys) over that dominated by the amblyopic eye (right eye in normal monkeys) was defined as the relative ocular dominance index (ROII). Therefore, if ROII is 0.0, there is no shift in ocular dominance distribution and positive ROII values indicate an ODI shift away from the amblyopic eye.

Spatial frequency tuning.

Each cell's optimal spatial frequency was determined by fitting the response data with the following Gaussian functions (DeAngelis et al., 1993a,b):

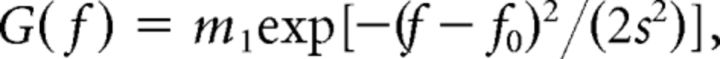where m₁ is the response amplitude, f is spatial frequency, f₀ is preferred spatial frequency, and s is the SD of the Gaussian function.

RF center and surround size.

To determine the position and extent of a neuron's receptive field center, we measured area-summation functions with drifting high-contrast (80%) sinusoidal gratings of optimized orientation, spatial frequency, and temporal frequency (Zhang et al., 2005). The neuronal responses were measured as a function of the diameter of the grating patch. The measured area response functions were fitted by the following formula:

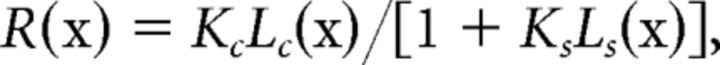where L_c(x) = [w_c × erf(x/w_c)]²; L_s(x) = [w_s × erf(x/w_s)]², erf is the error function, x is the stimulus diameter, K_c and K_s are the gains of the center and surround, L_c and L_s are the summed squared activities of the center and surround mechanisms; w_c and w_s represented the spatial extents of the center and surround components; and w_c is always constrained to be less than w_s during our curve-fitting procedures. The receptive field center size was determined by searching for the smallest center stimulus diameter at which neuronal discharges reached 95% of the peak firing rate. The border of the surround was the point at which further increases in stimulus diameter did not alter the response amplitude. The surround suppression strength was quantified for each neuron by calculating a surround suppression index (SSI): SSI = (peak response − suppressed responses)/peak response for the unit's area summation function.

Orientation bias.

Orientation bias was calculated by using the vector summation methods (Levick and Thibos, 1982; Smith et al., 1990). Briefly, the response of a given cell to a given orientation was expressed as the following complex number:

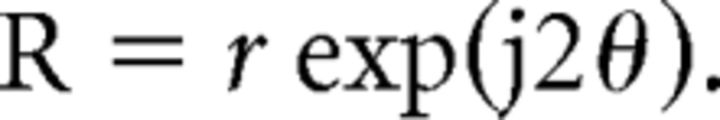The response amplitude for a grating of orientation θ is described by a vector with a length of r at an angle coordinate of 2θ, where j is the square root of −1. The orientation bias is expressed as the mean response vector for a series of equally spaced stimulus orientations: R_mean = ΣR/N, where N = number of orientations. The mean response vector was then normalized with respect to the average amplitude of the vectors for all orientations, that is, Σr/N. A normalized phasor for all stimulus orientations was computed by the following formula:

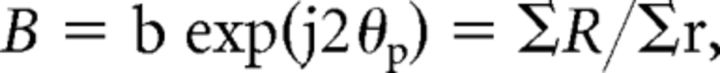where ΣR is the vector sum for all 12 orientations and Σr is the scalar sum of the amplitudes of all the response vectors. The normalized phasor b represents orientation bias, which varied between 0 (no orientation bias) and 1.0 (responsive to only one orientation). The term 2θ_p signifies the angular coordinates of the resultant vector and the angle θ_p is the preferred stimulus orientation of the unit. It is important to emphasize that the above normalization procedure minimizes the sensitivity of the measure to the responsiveness of the cell (Thibos and Levick, 1985).

Binocular interactions.

To determine the strength and the nature of binocular interactions, responses were collected for dichoptic sine-wave gratings of the optimal spatial frequency, orientation, and direction of drift as a function of the relative interocular spatial phase disparity of the grating pair. The sensitivity to relative interocular spatial phase disparities was quantified using a “binocular interaction index” (BII) that was calculated from the sine function fit to the binocular phase tuning data (BII = amplitude of the fitted sine wave/the average binocular response amplitude; Ohzawa and Freeman, 1986a,b; Smith et al., 1997). To characterize whether binocular signal interactions were facilitatory or suppressive in nature, the “peak binocular response amplitude/dominant monocular response amplitude” ratios (peak B/M) were calculated for each unit and expressed in terms of relative strength (db), that is, 10 log peak B/M. Negative peak B/M values signify binocular suppression, and positive values indicate binocular facilitation.

LSRC method

The details of visual stimulation and data analysis for the local spectral reverse correlation (LSRC) method were described previously (Nishimoto et al., 2006; Tao et al., 2012; Zhang et al., 2013). Briefly, the control functions and the stimulus routines were performed using custom software on two Windows-based personal computers. A dynamic two-dimensional noise array (51 × 51 elements) that covers an area three times larger in width and height (typical ranges were from 1° × 1° to 12° × 12°) than the classical receptive field was used as the stimulus for each isolated V2 neuron (Fig. 1Aa). The luminance of each element in the noise array was bright (99 cd/m²), dark (1 cd/m²), or equal to the mean luminance of the display (50 cd/m²). The noise array was redrawn with a new noise pattern every 28 ms (four video frames). Typically, 15 blocks of the noise arrays (a total of 62,565 frames) were presented to obtain a sufficient number of spikes for subsequent data analysis. This measurement took 30 min for each neuron.

Figure 1.

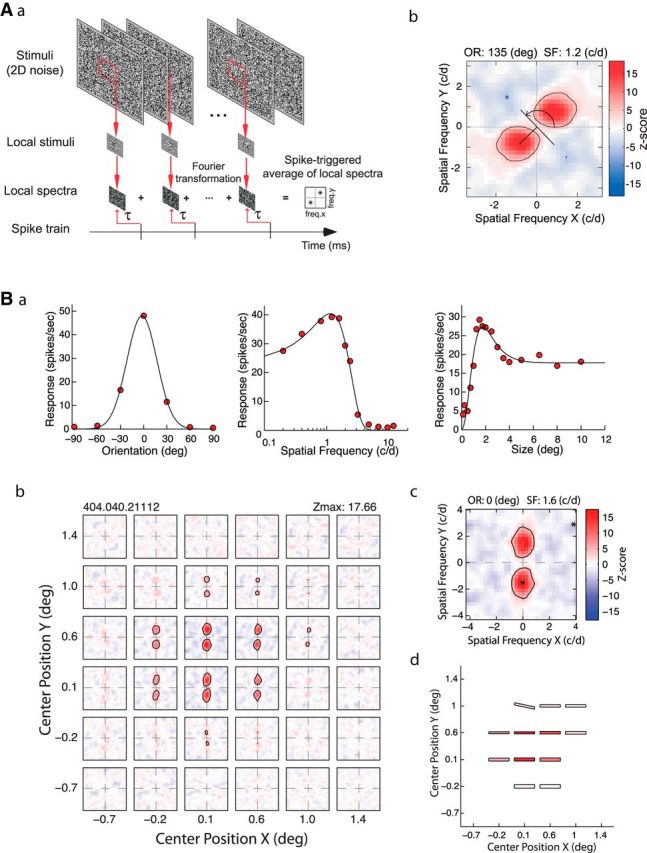
A, Schematic diagram of the LSRC analysis (see Materials and Methods for details). Aa, The visual stimuli and analysis procedure used to derive LSRC subfield maps. We calculated a cross-correlation between the spike train and the amplitude spectra of Gaussian-windowed stimuli to obtain a two-dimensional frequency tuning function for the given subfield. Ab, An example of the spike-triggered average of local spectra (local spectral selectivity map or subfield). The x- and y-axes show vertical and horizontal spatial frequency in cycle/degree (c/d). The facilitations and suppressions are indicated by red and blue, respectively. Asterisks show the location of the highest and lowest Z-scores that correspond to the frequency of the maximum facilitation and suppression, respectively. The scale bar with Z-scores is illustrated on the right. The distance from the origin to the peak of the excitation indicated the optimal spatial frequency for the local subfield of the RF. The angle perpendicular to the line connecting the origin and the excitation peak (with the horizontal axis) depicted the optimal orientation for the local subfield (curved arrow). Ba, Orientation, spatial frequency and size tuning functions of a V2 neuron from a normal monkey obtained with grating stimuli. Bb, A spatial matrix of subfields with facilitatory profiles in a V2 neuron from a normal adult monkey that exhibited spatial homogeneity of orientation and spatial frequency within its RF. Bc, Detail profile of the subfield with the maximum Z-score. Bd, Schematic diagram showing the preferred orientation (bar angle) and spatial frequencies (width), and the maximum Z-scores (saturation) of the subfields. Note that vertical orientation in spatial frequency space is equivalent to horizontal orientation in positional space.

We calculated the spike-triggered average of the amplitude spectra produced by the noise array for a given subfield to obtain the subfield's two-dimensional frequency tuning function. The subfields were windowed by a two-dimensional Gaussian function, and the frequency spectra were calculated by a standard fast Fourier transform algorithm with zero padding (Press et al., 1992). The center of the window was stepped typically by 1 SD of the Gaussian function. A joint spatial frequency and orientation profile was obtained by interpreting the two-dimensional frequency-tuning plot as a polar coordinate representation. The distance from the origin to the peak of the excitation represented the optimal spatial frequency for the local subfield of the RF. The angle perpendicular to the line connecting the origin and the excitation peak (with the horizontal axis) represented the optimal orientation for the local subfield (Fig. 1Ab). By systematically changing the positions of the subfield for calculating the spectra, a spatial matrix of subfields was obtained (Fig. 1Bb). Therefore, the final matrix describes the tuning profile of the neuron as a function of position (x, y) as well as spatial frequency and orientation in a joint manner. We optimized the number of positions/spacing for each unit depending on the spatial frequency tuning of the unit; for neurons with bandpass spatial frequency (SF) tuning profiles, the analysis window covered at least half of the period for the optimal spatial frequency within 1 SD of the Gaussian. In rare cases where neurons had low-pass SF tuning functions, we used the SD value corresponding to one-fifth of the mapped area.

Optimal delays.

We calculated spike-triggered averages of stimulus local spectra for correlation delays from 0 to 150 ms in 15 ms steps. Then, the optimal correlation delay was determined as the delay at which the maximal signal amplitude was found. Typical optimal correlation delays varied from 45 to 90 ms. The average number of spikes per recording for our population of neurons was ∼10,000 spikes.

Z-scores.

To evaluate the significance of the spike-triggered signals, we calculated the average and SD (noise level) of signals using shuffled correlations. We obtained the shuffled correlations by calculating cross-correlations between spike trains and shifted (unpaired) stimulus blocks. The mean and SD of the shuffled correlations were then used to normalize the original spike-triggered signals into Z-score representations (Figs. 1Ab,Bc). To reduce the computational burden, we assumed that the noise level was identical for a sequence of random patterns for any given subfield and spatial frequency. The Z-scores were used to represent the response strength in the spectral receptive field profiles, taking variability and statistical significance of responses into account. The Z-scores were sometimes negative, which was interpreted as a reduction of activities below the baseline level. The statistical significance of signals was examined by the Z-score, corrected for multiple comparisons by Bonferroni's method. The degree of freedom for the Bonferroni's correction was set to the number of subfields multiplied by the number of noise elements within ±1SD of the analyzing Gaussian window. Black lines in the LSRC plot indicate contours for p = 0.05. Finally, a schematic diagram, which shows the preferred orientation (bar angle) and spatial frequency (width), and the maximum Z-scores (saturation) of the subfields for the matrix, summarizes the similarities and differences between subfields for a given V2 neuron (Fig. 1Bd).

Anatomical methods

To identify recording sites, small electrolytic lesions were produced at three locations along the electrode track (at the end of each penetration, at the midpoint of the penetration, and near the cortical surface) by passing current through the electrode (5 μA for <5 s, electrode tip negative). At the end of the recording experiments, an overdose of sodium pentobarbital (100 mg/kg) was administered intravenously to induce a deep level of anesthesia and the animals were killed. The animals were perfused through the heart with an aldehyde fixative (2% paraformaldehyde and 0.5% glutaraldehyde in 0.1 m phosphate buffer, pH 7.4). The brains were removed immediately and kept overnight in fixative with 20% sucrose. The tissues were cut in 40 μm sections on a freezing microtome in parasagittal planes. The sections were used to confirm that we recorded from comparable sites in amblyopic and normal monkeys by analyzing the location of the three lesions along electrode tracks and the depth information for each recording site.

Statistical analyses

Unless specified otherwise, one-way ANOVA was applied to test if the difference among the mean values of normal, amblyopic and fellow-eye groups was significant. Bonferroni test was applied for post hoc multiple comparisons between specific pairs of groups. For three pairwise comparisons, the pairwise α was set at 0.017 (0.05/3) or 0.003 (0.01/3) to keep the familywise α value at 0.05 or 0.01, respectively.

Results

Studies of amblyopia traditionally compare the perceptual or neuronal deficits of the amblyopic eye to those of the fellow eye. However, an increasing number of perceptual studies have documented that the visual performance of the fellow “normal” eye of amblyopic humans is not always normal (Wong et al., 2001; Simmers et al., 2003; Simmers and Bex, 2004; Ho et al., 2005, 2008; Mansouri et al., 2005; Norcia et al., 2005; Wong and Levi, 2005; Hayward et al., 2011). The spatial contrast sensitivity (Kiorpes et al., 1993, 1998) and contour integration (Kozma and Kiorpes, 2003) of the fellow eye in some amblyopic monkeys are also subnormal, as was in one of our anisometropic monkeys (MK-401). Vernier acuity was lower in both eyes of our experimental monkeys compared with that in normal monkeys (Table 1). Therefore, for the subsequent analysis, we compared the responses of V2 neurons driven by the amblyopic eye, those driven by the nonamblyopic eye, and neurons from normal monkeys that were recorded under identical recording conditions and in similar recording sites. The receptive fields of the great majority of V2 neurons (>95%) in both amblyopic and normal monkeys were located within 5° of the center of the projected fovea.

Subtle monocular and robust binocular response deficits measured with gratings

Using high-contrast sine wave gratings, we first quantitatively analyzed the ocular dominance distribution, the strength and nature of binocular interactions, and the monocular RF properties including the orientation, spatial frequency, and size tuning functions of each neuron (Table 2). Some of the data obtained with gratings will be compared with the results on the RF subfield maps.

Table 2.

Binocular and monocular responses of V2 neurons to grating stimuli

Grating response	Normal (n)	Fellow (n)	Amblyopic (n)
Monocular
Orientation bias	0.49 ± 0.01 (298)	0.34 ± 0.01 (593)	0.37 ± 0.01 (640)
Optimal spatial frequency (c/d)	1.52 ± 0.06 (246)	1.28 ± 0.05 (509)	1.48 ± 0.06 (603)
RF center size (deg)	2.06 ± 0.07 (247)	1.88 ± 0.04 (559)	2.26 ± 0.07 (456)
RF surround size (deg)	7.31 ± 0.17 (247)	7.17 ± 0.10 (559)	7.55 ± 0.12 (456)
SSI	0.51 ± 0.02 (217)	0.60 ± 0.01 (380)	0.60 ± 0.01 (375)
Binocular
ROII	0.45	−0.05
BII	0.40 ± 0.02 (193)	0.21 ± 0.05 (259)
Binocular suppression (%)	15 (193)	36 (259)

Binocular properties

The relative strength of the amblyopic eye to drive cortical neurons is generally weak in V1 of monocularly form-deprived monkeys (Hubel et al., 1977; Sakai et al., 2006; for review, see Wong, 2012) and in monkeys reared with severe monocular defocus (Movshon et al., 1987), which in turn could affect the ocular dominance distribution of V2 neurons (Zhang et al., 2011). Because the magnitude of monocular defocus for the experimental monkeys in this study was very mild (−3D except MK-404) compared with more severe defocus or monocular form deprivation, the great majority of the V2 neurons retained robust signals from each eye; overall the strength of signals from the two eyes was relatively well balanced. The ROII (see Materials and Methods for details) values were similar for amblyopic and normal monkeys (if ROII is 0.0, the ocular dominance distribution is perfectly balanced and if it is negative, the distribution is shifted away from the amblyopic eye; Table 2).

In sharp contrast, when two eyes were stimulated together with dichoptic sine-wave gratings, we found that the ability of the amblyopic neurons to combine signals from the two eyes (BII) was significantly reduced in V2 neurons of amblyopic monkeys (t test, p < 0.005). More important for this study was that the prevalence of V2 neurons exhibiting binocular suppression, defined as units exhibiting 10 log Peak Binocular/Monocular spiking rate <0.0 (db), was much higher in our amblyopic monkeys (36%) compare with that for normal control monkeys (15%; χ² test, p < 0.001; see below for the significance of elevated binocular suppression).

Orientation tuning

The orientation bias was significantly lower in neurons driven by the amblyopic eye compared with those driven by the fellow eye or neurons from normal monkeys (p < 0.01). The reduced orientation bias in amblyopic monkeys was a result of substantial responses to stimulus orientations far away from the cell's preferred orientation. This result represents, to best of our knowledge, the first demonstration of how early defocus can lead to abnormal orientation tuning of individual extrastriate neurons in macaque monkeys.

Spatial frequency tuning

Similarly, the optimal spatial frequency of V2 neurons was significantly lower in those neurons driven by either the amblyopic eye or the fellow eye compared with that for normal control units (p < 0.05).

RF center and surround

The size of the RF center for a given V1 neuron depends on the relative strength (“gain”) of both the feedforward excitatory inputs and suppressive signals from the RF surround (Cavanaugh et al., 2002). Chronic defocus shortly after birth can disrupt the functional circuitry supporting the RF center and surround of individual V2 neurons. We analyzed the size of the RF center and surround, and the strength of surround suppression (SSI). The RF centers of neurons driven by the amblyopic eye were significantly larger than those driven by the fellow eye or for neurons from normal monkeys (p < 0.01). The RF surround sizes of V2 neurons for the amblyopic eye were not significantly different from those driven by the fellow eye or normal control units (p > 0.05). However, surround suppression was stronger in V2 neurons driven by the amblyopic or fellow eyes of experimental monkeys compared with suppression in units from normal monkeys (p < 0.01).

The experiments with drifting high contrast gratings revealed subtle abnormalities in the monocular RF properties of V2 neurons and robust deficits in binocular signal interactions. The results are consistent with the nature of the early visual experience (relatively small defocus) for our experimental monkeys.

Disorganized spatial maps of RF subfields

The RFs of V2 neurons in normal monkeys consist of multiple subfields each of which has its preferred orientation and spatial frequency. The term “subfields” refers to the subunits of the RFs that were experimentally revealed by the LSRC method (Nishimoto et al., 2006; Tao et al., 2012; Zhang et al., 2013). Previously some heterogeneity in the subfield maps of normal V2 neurons has been observed and these neurons are thought to be capable of encoding nonlinear contours (Ito and Komatsu, 2004; Anzai et al., 2007; Willmore et al., 2010; El-Shamayleh and Movshon, 2011; Tao et al., 2012). The extent to which heterogeneity is higher in amblyopic monkeys provides a measure of their abnormality. Here we tested the idea that the spatial organization of RF subfields (RF structure) of individual V2 neurons was disrupted in amblyopic monkeys, and as a result, encoding the orientation, spatial frequency, and spatial position information was disrupted in amblyopic primates. We studied the responses of V2 neurons to dynamic two dimensional noise stimuli in 296 units driven by the amblyopic eye, 281 units driven by the nonamblyopic eye of the anisometropic monkeys, and in 242 units from normally reared monkeys. We analyzed the heterogeneity of the RF subfield map of each V2 neuron. We also examined whether multiple nearby V2 neurons in amblyopic monkeys recorded with a single electrode, hence viewing virtually identical small regions of the visual field, are capable of accurately encoding geometric relationships of local stimulus features over space.

To assess the heterogeneity of the RF subfield map, the overall differences in the spatial maps of subfields were quantified by calculating the heterogeneity index (H-index) for each unit (Fig. 2). The preferred orientation and the optimal spatial frequency of each subfield were first expressed as a polar coordinate value (θ = orientation, sf = spatial frequency). The difference in the preferred orientation and the optimal spatial frequency between a pair of subfields was quantified by calculating a polar distance between the pair with the following equation: polar distance (PD) = √ sf₁² + sf₂² − 2sf₁ × sf₂ × cos (θ1 − θ2). This calculation was repeated for all possible pairs of subfields and obtained the average polar distance, which was defined as the H-index. H-index was calculated within a given neuron (HI-within) and across nearby units (HI-across).

High heterogeneity of subfield maps in amblyopic monkeys

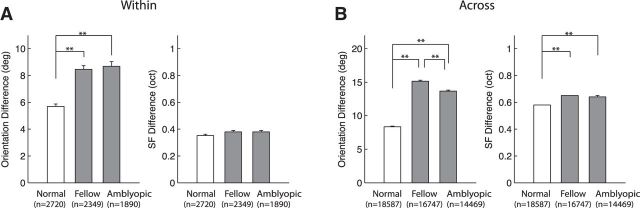
The spatial organization of RF subfields for individual V2 neurons was disrupted in amblyopic monkeys. This “disruption” of the subfield maps was found for neurons driven by the amblyopic eye and those by the fellow eye (Fig. 3). Specifically the frequency distribution of heterogeneity index values shows that those units driven by both the amblyopic eye and the fellow eye had significantly more heterogeneous subfield maps (higher H-index within unit) compared with those from normal monkeys (p < 0.01; Fig. 3A). Moreover, the H-index (within) of V2 neurons in amblyopic monkeys was slightly but significantly higher for the amblyopic eye than for the fellow eye (p < 0.01). The subfield maps of nearby neurons recorded simultaneously in amblyopic monkeys were significantly different from those in normal control units, showing huge heterogeneity (HI-across; p < 0.01; Fig. 3B). The small differences in H-index (across) between the amblyopic and fellow eyes were not significant (p > 0.05). In addition, the spread of the H-index values was more substantial for both eyes of amblyopic monkeys compared with that in normal monkeys. The observed higher heterogeneity of the RF subfield maps for amblyopic monkeys reflects both orientation and spatial frequency differences between subfields. However, the above analysis does not give any information about the relative weight of the variability in preferred orientation and spatial frequency. Therefore, instead of comparing H-index values, we separately calculated the actual differences in preferred orientations and optimal spatial frequencies between all pairs of subfields (Fig. 4). For the within-unit comparisons (Fig. 4A), there was no significant difference in the average SF between those neurons driven by either eye of amblyopic monkeys and normal control neurons (p > 0.05). However, for the across-unit comparisons, we found small, but significant differences between neurons driven by either eye of amblyopic monkeys compared with normal control units (p < 0.01).

Figure 3.

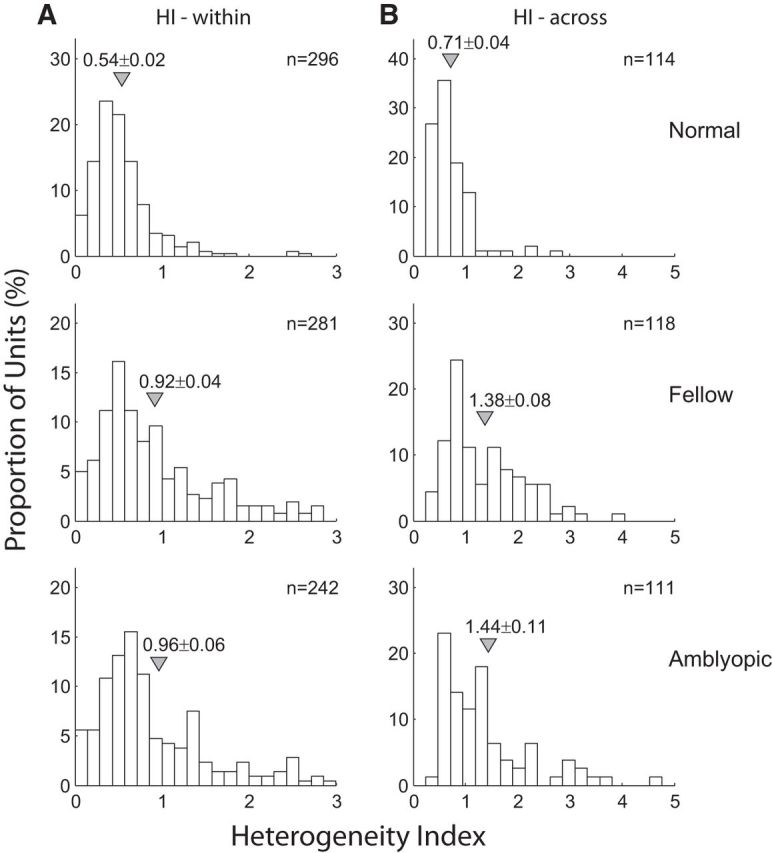
Frequency distributions of H-index values of V2 neurons in normal monkeys (top), and the fellow (middle), and amblyopic eye of amblyopic monkeys (bottom). A, Frequency distributions of H-index values within RFs. B, Frequency distributions of H-index values across RFs of nearby multiple neurons. Arrows and attached numbers indicate the means and SEM; n indicates the number of neurons for within unit-comparisons and the number of recording sites for across unit comparisons.

Figure 4.

Mean (±SE) orientation and spatial frequency differences between pairs of subfields in amblyopic and normal V2 neurons. A, Mean differences in orientation (left) and spatial frequency (right) differences between pairs of subfields for within-cell comparisons. B, Mean differences in orientation (left) and spatial frequency (right) differences between pairs of subfields for across-cell comparisons. The numbers at the bottom indicate the sample size (pairs of subfields) for each cell group. **p < 0.01.

Importantly, the differences in the preferred orientations between pairs of subfields were significantly greater for amblyopic neurons than those for normal control neurons. This difference was found for neurons driven by both the amblyopic and fellow eyes and for both the within-unit and across-unit comparisons (p < 0.01). Finally, the effective size of abnormal increases in the orientation differences between subfields of amblyopic neurons was much larger than that for the spatial frequency differences for both within-unit and across-unit comparisons. Together, the orientation differences between subfields within a given unit or across multiple nearby neurons had a much larger impact on the disruption of V2 subfield maps in amblyopic monkeys, i.e., abnormally higher H-index values.

Relation to data obtained with gratings

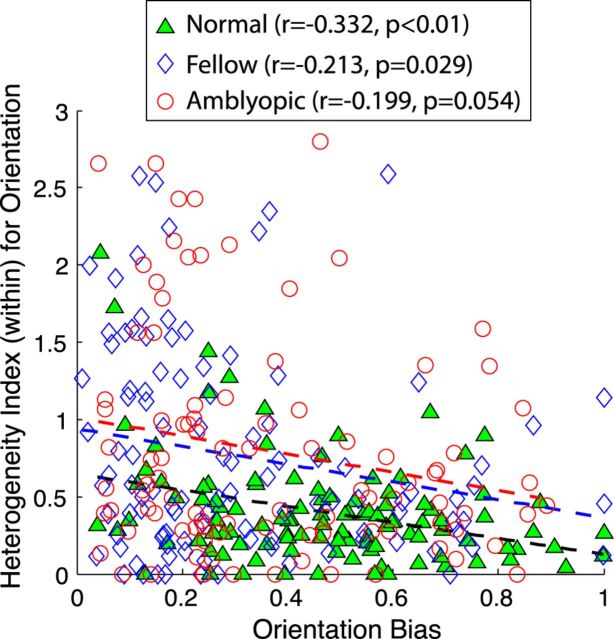
The large differences in preferred orientations in the subfield maps of amblyopic monkeys were related to their reduced orientation biases revealed by grating stimuli (Fig. 5). For both amblyopic and normal monkeys, there was a mild but significant negative correlation between orientation biases determined with gratings and H-index (within) values calculated just for orientation differences in subfield maps; V2 neurons having higher H-index values (within) for orientation tend to have lower orientation biases. This relationship was slightly tighter for normal monkeys (r = −0.33, p < 0.001) compared with that for amblyopic monkeys (r = −0.21, p < 0.01 for fellow eye; r = −0.20, p = 0.054 for amblyopic eye). Note that this correlation did not reach statistical significance for neurons driven by the amblyopic eye. These results suggest that the overall orientation tuning of individual V2 neurons depend, at least in part, on how multiple feedforward V1 input signals having specific information about preferred orientation are combined in V2 neurons and that this relationship is weaker in amblyopic monkeys.

Figure 5.

Scatter plot relating H-index (within) for each V2 neuron with its orientation bias determined with grating stimuli. Note that if orientation bias is 0, neuron has no orientation selectivity, whereas 1.0 signifies that cell is sensitive to only one orientation. Green filled triangles indicate normal control units, blue open diamonds signify units driven by fellow eye and red open circles show units driven by amblyopic eye.

Subfield maps with suppressive profiles

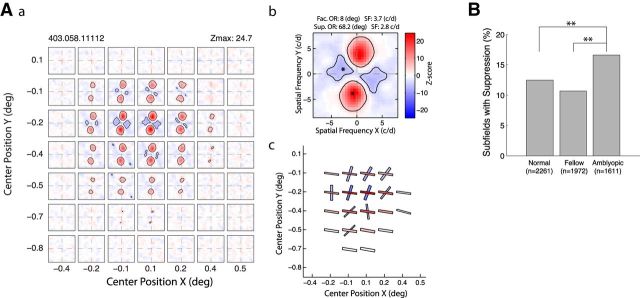
In V2 of normal monkeys, a substantial proportion of RF subfield maps contain suppressive profiles (Tao et al., 2012; Zhang et al., 2013). Suppressive profiles can interact with facilitatory profiles and make the spiking output of subfield maps more complex compared with maps without suppressive profiles (Nishimoto et al., 2006; Anzai et al., 2007; Willmore et al., 2010; Tao et al., 2012; Zhang et al., 2013). Some subfields showed suppression that resembles cross orientation suppression in V1 neurons (Fig. 6Aa,Ac). We examined all subfield maps and counted the number of subfields containing suppressive profiles. There were significantly higher percentages of subfields with suppressive profiles for those units driven by the amblyopic eye than those driven by the fellow eye in amblyopic monkeys or units from normal monkeys (χ² test, p < 0.0005; Fig. 6B). Thus, the spiking output of the abnormally heterogeneous subfield maps of V2 neurons in amblyopic monkeys, revealed solely based on facilitatory profiles, can be further “modified” by the presence of suppressive profiles, at least for those units driven by the amblyopic eye. It is important to keep in mind that the LSRC method calculates the net sum of facilitation and suppression for each frequency, and, therefore, it can only visualize whichever is stronger (Nishimoto et al., 2006; Tao et al., 2012). However, the summed information reflects the spiking output of neurons that is transmitted to the next neurons in the cascade of cortical processing.

Figure 6.

A, V2 neuron from an amblyopic monkey having subfields with both facilitatory and suppressive profiles. Aa, Spatial matrix of subfields with both profiles. Ab, Detailed profile of the subfield with the maximum Z-scores. Location of the highest and lowest Z-scores is indicated with asterisks. Ac, Schematic diagram of the preferred orientations (bar angles) and spatial frequencies (widths) of subfields with the facilitatory (red) and suppressive (blue) profiles. B, Prevalence of suppressive profiles in subfields of V2 neurons driven by the amblyopic eye, fellow eye, and in normal monkeys. **p < 0.01.

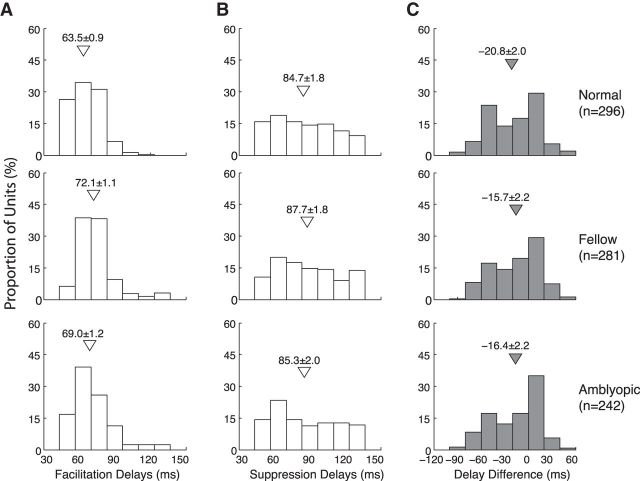
Dynamics of facilitatory and suppressive profiles

Previously we showed that the mean optimal delay (“latency”) for suppressive profiles for V2 neurons of 4-week-old infant monkeys was longer compared with that in adults, whereas the optimal delays for facilitatory profiles for the infants and adults were similar (Zhang et al., 2013). To investigate how experiencing defocus in one eye between 3 weeks and 3 months of age alters such dynamics of facilitation and suppression, we compared the optimal correlation delays for facilitatory profiles with that of suppressive profiles (Fig. 7). The mean optimal delay for the facilitatory profiles was longer for both eyes of amblyopic monkeys compared with those in normal monkeys (p < 0.01). Although the mean optimal delay for the fellow eye was slightly longer than that for the amblyopic eye, there was no statistical difference between the two eyes of amblyopic monkeys (p > 0.05). Unlike in infant monkeys, the optimal correlation delays of suppressive profiles for units driven by either the amblyopic or nonamblyopic eye were not different from those in normal adult monkeys (p > 0.05). Consequently, the latency difference between the facilitatory and suppressive profiles for amblyopic monkeys was less than that for the normal monkeys. For this analysis, it is important to keep in mind that since the correlation delays were calculated in 15 ms steps, the real timing difference could be off by ±7.5 ms (see Materials and Methods). Therefore, the dynamics of the RF subfield maps is abnormal in V2 for both eyes of amblyopic monkeys. Similar temporal processing deficits were recently reported for the amblyopic and the “fixing” fellow eye of amblyopic humans (Huang et al., 2012).

Figure 7.

Differences in optimal correlation delays (‘latency’) between the facilitatory and suppressive subfields in V2 neurons from normal monkeys (top), those driven by the fellow eye (middle), and amblyopic eye (bottom). A, Distribution of the correlation delays (latency) for facilitatory subfields. B, Distribution of the optimal correlation delays for suppressive subfields. C, Differences in the distribution of optimal correlation delays between facilitatory and suppressive profiles. Open triangles indicate means (±SE).

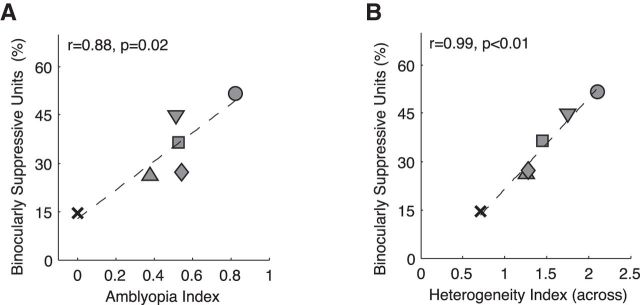
Relationships between binocular suppression, high heterogeneity, and amblyopia index

Experiencing early monocular defocus resulted in both a loss of cortical neurons' ability to combine binocular signals (BII) and a high prevalence of cortical neurons exhibiting binocular suppression (peak B/M; Table 2). Previously we reported that in monkeys showing strabismic amblyopia, the depth of amblyopia for individual monkeys was highly correlated with the proportion of V1 and V2 neurons exhibiting binocular suppression (Bi et al., 2011). Here we examined whether the magnitude of binocular suppression in individual monkeys of this study is related to the depth of their amblyopia. We also asked whether the higher heterogeneity of subfield maps among nearby units (HI-across) has any relation to the prevalence of binocularly suppressive V2 neurons. There was a positive correlation between the prevalence of binocularly suppressive V2 neurons and the depth of amblyopia (amblyopia index) of individual amblyopic monkeys (Fig. 8A). Moreover, the degree of heterogeneity in the subfield maps of individual monkeys was correlated with the strength of their binocular suppression in V2 (Fig. 8B). Together, these results indicate that there is a potential link between binocular suppression, disruption of RF subfield maps, and the depth of amblyopia (for review, see Birch, 2013; Hess et al., 2014).

Figure 8.

A, Relationship between the prevalence of binocularly suppressive units and the depth of amblyopia (amblyopia index) for individual monkeys. B, Relationship between the prevalence of binocularly suppressive units and the mean H-index (across) in individual monkeys. Different symbols indicate the data for individual monkeys.

Spike count, Z-max, and H-index

The observed higher H-index values in amblyopic V2 neurons could be a result of poor spiking and/or lower signal-to-noise ratios (SNR). To examine these possibilities we further analyzed spike counts and Z-max scores for amblyopic and normal neurons. The scatter plots relating spike count and Z-max score of each neuron (Fig. 9A) indicate that there is a mild but significant correlation between the spike count and the Z-max score of individual neurons for all groups. In addition, the mean spike counts of amblyopic V2 neurons were similar or even slightly higher than that for normal monkeys. Therefore, spike counts had very little to do with the observed “disorganization” of the RF subfield maps of amblyopic V2 neurons.

Figure 9.

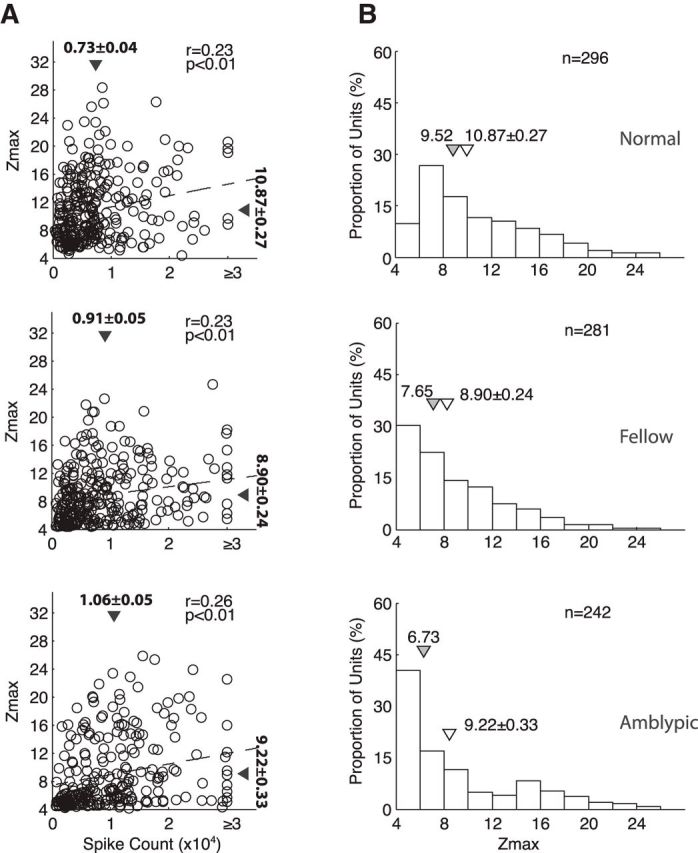
A, Scatter plots relating the Z-max score of each neuron with its spike count. Triangles indicate mean (±SE). B, Frequency distributions of Z-max scores of V2 neurons from normal monkeys (top), those driven by the fellow eye (middle), and those driven by the amblyopic eye (bottom). Filled triangles indicate median values and open triangles show mean values (±SE).

However, the mean Z-max scores of V2 neurons were clearly lower for both eyes of amblyopic monkeys than those for normal monkeys. The frequency distributions of Z-max scores further illustrate that there were more V2 neurons with Z-max scores lower or equal to 6.0 in amblyopic monkeys than in normal monkeys (Fig. 9B). This made the mean Z-max scores for both eyes of amblyopic monkeys significantly lower than Z-max scores for normal monkeys (p < 0.01). However, there was no significant interocular difference in amblyopic monkeys (p > 0.05).

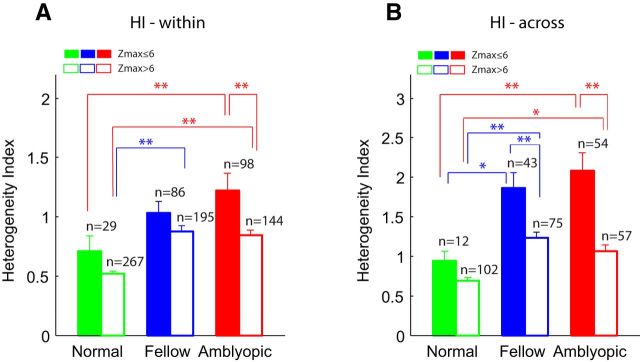
The frequency distribution of Z-max scores was relatively similar in all cell groups beyond Z-max = 6.0. Therefore, we divided all units into two subgroups, units with Z-max ≤6.0 and those with Z-max >6.0, and compared the mean (±SE) H-index for the amblyopic eye, the nonamblyopic eye, and normal monkeys (Fig. 10). The heterogeneity of subfield maps was abnormally elevated in amblyopic V2 neurons regardless of whether Z-max scores were high or low (two-way ANOVA with Bonferroni correction on post hoc analyses, p < 0.05). For example, Figure 10A shows that the mean (±SE) H-index values (within) for neurons driven by either eye of amblyopic monkeys and having Z-max scores >6.0 were significantly higher than comparable units with high Z-max scores from normal monkeys (two-way ANOVA, p < 0.01). In addition, the mean H-index value for those neurons with Z-max scores equal to or lower than 6.0 and driven by the amblyopic eye was significantly higher than comparable units with low Z-max scores from normal monkeys (two-way ANOVA, p < 0.01).

Figure 10.

A, Effects of Z-max scores on H-index values. A, Comparisons of the mean (±SE) H-index (within) values of neurons with high (>6.0) and low (≤6.0) Z-max scores for units driven by the amblyopic eye, the fellow eye of experimental monkeys, and normal control units. B, Similar comparisons of the mean (±SE) H-index values for across-unit comparisons. *p < 0.05; **p < 0.01.

Figure 10B shows the results of a similar analysis relating Z-max scores with H-index values across units. Note that we used the highest Z-max score among nearby multiple units at each site. The heterogeneity of subfield maps across nearby multiple neurons was abnormally elevated in amblyopic V2 neurons regardless of whether Z-max scores were high (>6.0) or low (≤6.0). The specific differences in H-index (across) between-subject groups and between units with high and low Z-max were significant (two-way ANOVA, p < 0.01). Together, the abnormally elevated H-index of V2 neurons in amblyopic monkeys cannot be explained simply by lower Z-max scores, i.e., the lower SNR in amblyopic monkeys.

Amblyopia index, Vernier acuity loss, and high H-index of V2 neurons

Our amblyopic monkeys exhibited a range of spatial contrast sensitivity and Vernier acuity losses (Table 1). Figure 11A indicates that the depth of amblyopia (AI) of individual monkeys was correlated with H-index (across) but far less with H-index (within). A key question is how the Vernier acuity loss of individual monkeys, a sign of position uncertainty, is related to the abnormally increased heterogeneity of RF subfield maps of amblyopic V2 neurons. Although not all of our experimental monkeys were tested for Vernier acuity, monkeys exhibiting a larger Vernier acuity loss tended to have higher heterogeneity in the RF subfield maps of V2 neurons (Fig. 11B). Together, some, but not all, of these acuity losses in our amblyopic monkeys can be explained by abnormal development of RF subfield maps of V2 neurons.

Figure 11.

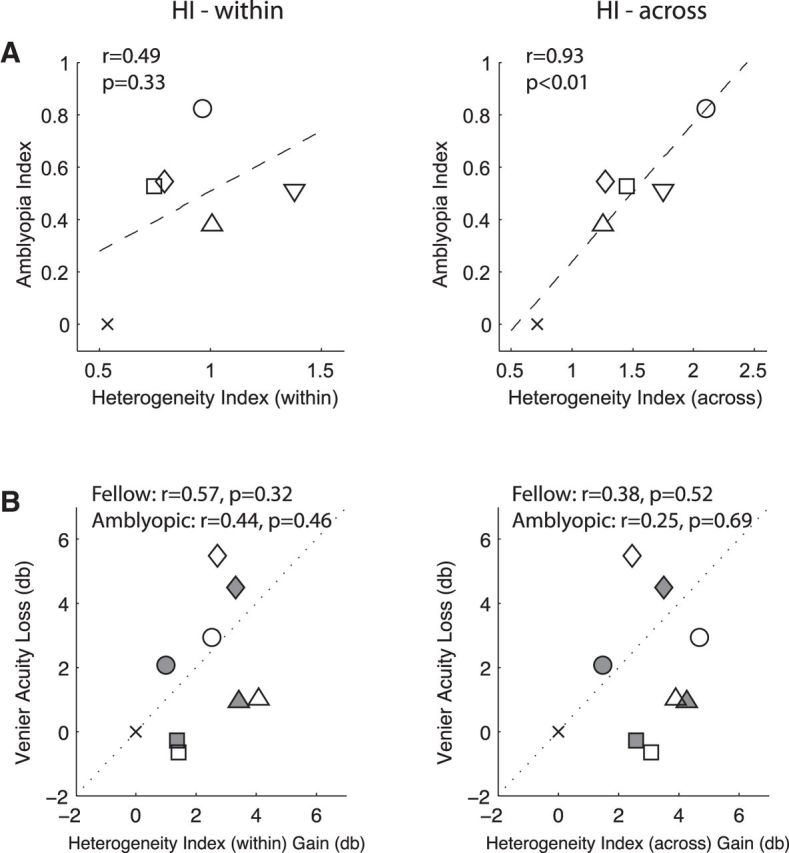
A, Relationship between depth of amblyopia (AI) of individual monkeys and their mean HI-within values (left) and HI-across values (right). B, Relationship between vernier acuity of individual monkeys and their mean HI-within values (left) and HI-across values (right). Vernier acuity loss of our experimental monkeys relative to that for normal control monkeys in db is shown in this figure.

Discussion

This study investigated how early chronic anisometropia alters the development of RF subfield maps of V2 neurons. The important findings were that (1) the subfield maps of a given V2 neuron from monkeys with anisometropic amblyopia are less homogeneous and the subfield maps of nearby V2 neurons are often very different, (2) the differences in preferred orientations between pairs of subfields were largely responsible for the observed high heterogeneity of subfield maps in amblyopic monkeys, (3) these neuronal deficits were found in neurons driven by the amblyopic eye and those driven by the fellow eye, (4) the degree of heterogeneity in RF subfield maps was correlated with the overall strength of binocular suppression in individual amblyopic monkeys, and (5) the degree of Vernier acuity loss in individual amblyopic monkeys paralleled the increase in the heterogeneity of RF subfield maps in their V2 neurons.

Methodological considerations

We analyzed the subfield maps of multiple nearby V2 neurons recorded with a single electrode, as previously performed in cat area 17 (DeAngelis et al., 1993a,b; Martin and Schröder, 2013) and monkey MT (Bair et al., 2001). The advantage of this approach is that the RFs of these nearby units extensively overlap around the local region of visual space and therefore, we can study how efficiently local feature information, such as preferred orientation and spatial frequency would be pooled by a neuron in the next stage of processing. More efficient pooling is thought to improve the quality of stimulus feature information by reducing noise (DeAngelis et al., 1993a,b; Shadlen et al., 1996; Mazurek and Shadlen, 2002). In the case of our amblyopic monkeys, the highly heterogeneous stimulus feature information encoded by nearby amblyopic neurons would be pooled at the next stage of processing. This is likely to result in higher noise in the system and perceptual difficulties in visual tasks that require integrating neighboring local stimulus features over space. This study indicates that the magnitude of the disruption in the RF spatial structure of V2 neurons generally paralleled the perceptual loss of Vernier acuity among our experimental monkeys (Fig. 11).

Recording spikes from multiple nearby neurons with a single electrode can be potentially limited by the effectiveness of spike sorting and other associated problems (Bair et al., 2001). To minimize problems with spike sorting, we used the spike sorting software in our data acquisition system (TDT, System-3) during all experimental runs, to isolate and keep track of units that we were working on. Moreover, for the off-line data analyses after the completion of experiments, we performed spike-sorting routines using a custom algorithm that allows us to reliably discriminate the amplitude and waveform of spikes from multiple neurons. Regardless, it is difficult to explain how less than optimal spike sorting, if any, could have selectively affected the data showing the heterogeneous subfield maps of V2 neurons in amblyopic monkeys but not the data demonstrating highly homogeneous subfield maps in normal monkeys.

The subnormal Z-max score (SNR) of amblyopic V2 neurons was ruled out as a primary source of the observed high heterogeneity in amblyopic neurons (Fig. 10). However it is unclear why the overall Z scores (SNR) of these amblyopic neurons were significantly lower than in normal V2 neurons (Fig. 9B). Low spike counts could result in lower Z scores. However, spike counts of amblyopic V2 neurons were as high as or higher than those in normal monkeys (Fig. 9A). Another possibility is that amblyopic V2 neurons have abnormality in some of their nonlinear response properties (e.g., nonlinear spatiotemporal summation across local spectral energy, or static nonlinearity) that are averaged out using our LSRC method. It is beyond this study to explore whether “extraordinary” nonlinearity exists in amblyopic V2 neurons: if it does, what is the source of the nonlinearity, how does such nonlinearity emerge after experiencing early anisometropia, or how it would affect the results of our LSRC methods?

Robust suppression and bilateral V2 deficits

It is unclear how experiencing anisometropia soon after birth causes a substantial disorganization of subfield maps for both eyes of amblyopic monkeys. As mentioned above, an increasing number of perceptual studies on amblyopia report the bilateral nature of vision deficits that are thought to involve neurons beyond V1. This is at least in part because the great majority of extrastriate neurons are known to process information from both eyes and therefore, the connections from either eye are equally vulnerable to abnormal visual experience during very early development (McKee et al., 2003; Simmers and Bex, 2004; Ho et al., 2005; Levi et al., 2011; Levi, 2013; Zhou et al., 2013). The results of this study represent the first electrophysiological evidence for this line of thought.

We propose that binocular suppression during a critical period may play a key role in the bilateral nature of disruptions in RF subfield maps. We previously found that experiencing ocular misalignment for as brief a period as 2 weeks near birth can devastate the ability of V1 or V2 neurons to combine binocular signals (Kumagami et al., 2000; Mori et al., 2002; Zhang et al., 2008), and only 3 d of strabismus can initiate robust binocular suppression in V1 neurons that is comparable in strength to binocular suppression found in adult strabismic monkeys (Zhang et al., 2008). It is reasonable to think that binocular suppression in our anisometropic amblyopic monkeys caused not only a breakdown of binocular connections, but also weaker and noisier spiking of V1 neurons for stimulation of either eye. Chronically weak or noisy input signals from V1 could have disrupted the maturation of the functional circuitry responsible for the RF subfield maps of V2 neurons for both eyes.

We found that V2 of amblyopic monkeys is dominated by suppression. Three different aspects of anomalous suppression were revealed in this study: the increased prevalence of binocularly suppressive neurons (Table 2), the stronger RF surround suppression (Table 2), and the higher prevalence of subfields with suppressive profiles (Fig. 6B). Although the relationship between these suppressive responses is not immediately clear, each of these suppressive responses has a substantial impact on the orderliness of RF subfield maps (heterogeneity). More specifically, the mean heterogeneity index of V2 neurons in individual amblyopic monkeys was directly correlated with the prevalence of binocularly suppressive neurons (Fig. 8B). Also there was a significant correlation between the depth of amblyopia and the strength of binocular suppression in V2 (Fig. 8A), as was previously found in strabismic/amblyopic monkeys (Bi et al., 2011).

The structure of the RF center for a given V2 neuron in normal monkeys critically depends on the orderly convergence of feedforward inputs from neighboring V1 neurons (Hegdé and Van Essen, 2003; Ito and Komatsu, 2004; Anzai et al., 2007; Tao et al., 2012; El-Shamayleh et al., 2013). Neighboring neurons tend to have similar RF structures in V1 (DeAngelis et al., 1993a,b; Martin and Schröder, 2013), in V2 (this study) and MT (Bair et al., 2001). The results of this study indicate that the normal development of the fine circuitry supporting the feedforward connections from V1 to V2 are functionally disrupted in amblyopic monkeys, and as outlined above, robust binocular suppression is likely to have been involved in these deficits. In contrast to the present findings, the neuronal projections from V1 to V2, studied anatomically with CTB tracer injections in V2, were found normal in form deprived monkeys (Sincich et al., 2012). However, as the authors suggested, synaptic connections in V2 of form-deprived monkeys might have been corrupted in various ways but their anatomical technique was not sufficiently sensitive to detect such developmental changes. Therefore, even if one could record responses of V2 neurons to stimulation of the deprived eye in form deprived monkeys, their RF subfield maps could be disorganized.

In addition to the feedforward projections to individual V2 neurons, there are long-range intrinsic connections and the feedback connections from higher order visual areas that can adversely affect the development of the RF structures across multiple nearby V2 neurons in our experimental monkeys. Although the RF center size of V2 neurons was abnormally enlarged in our amblyopic monkeys, the surround suppression, presumably mediated by the long-range intrinsic connections and/or the feedback connections (Shushruth et al., 2009), was significantly stronger, not weaker (Table 2). Thus, the known relationship between RF center size and the strength of surround suppression for V1 and V2 neurons of normal monkeys (Cavanaugh et al., 2002; Zhang et al., 2005; Shushruth et al., 2009) was largely absent in amblyopic V2 neurons. Together, the intrinsic and feedback connections of V2 neurons may have been functionally compromised in our amblyopic monkeys, resulting in abnormal increases in heterogeneity index values (across) of amblyopic neurons.

Perceptual implications

The observed abnormal subunit maps and robust binocular suppression of nearby amblyopic V2 neurons are likely to create substantial difficulties for downstream neurons in decoding incoming signals. Consequently, perceptual difficulties that amblyopes have in accurately localizing the position of nearby stimulus elements, i.e., position uncertainty, may reflect RF subfield abnormalities like those observed in our monkeys with anisometropic amblyopia.