Characterization of microfluidic shear-dependent epithelial cell adhesion molecule immunocapture and enrichment of pancreatic cancer cells from blood cells with dielectrophoresis

Abstract

Current microfluidic techniques for isolating circulating tumor cells (CTCs) from cancer patient blood are limited by low capture purity, and dielectrophoresis (DEP) has the potential to complement existing immunocapture techniques to improve capture performance. We present a hybrid DEP and immunocapture Hele-Shaw flow cell to characterize DEP's effects on immunocapture of pancreatic cancer cells (Capan-1, PANC-1, and BxPC-3) and peripheral blood mononuclear cells (PBMCs) with an anti-EpCAM (epithelial cell adhesion molecule) antibody. By carefully specifying the applied electric field frequency, we demonstrate that pancreatic cancer cells are attracted to immunocapture surfaces by positive DEP whereas PBMCs are repelled by negative DEP. Using an exponential capture model to interpret our capture data, we show that immunocapture performance is dependent on the applied DEP force sign and magnitude, cell surface EpCAM expression level, and shear stress experienced by cells flowing in the capture device. Our work suggests that DEP can not only repel contaminating blood cells but also enhance capture of cancer cell populations that are less likely to be captured by traditional immunocapture methods. This combination of DEP and immunocapture techniques to potentially increase CTC capture purity can facilitate subsequent biological analyses of captured CTCs and research on cancer metastasis and drug therapies.

I. INTRODUCTION

Circulating tumor cells (CTCs) are cells that have been shed into the circulatory system from a tumor source, and it is hypothesized that a subpopulation contributes to cancer metastasis by forming secondary tumors elsewhere in the body.¹ Genetic and pharmacological evaluation of captured CTCs can lead to a better understanding of cancer metastasis as well as improved drug therapies.^2–5 In particular, a high CTC capture purity—the percentage of all captured cells that are actually CTCs—can facilitate numerous subsequent biological analyses by reducing the amount of time and money that is potentially wasted on analyzing contaminating blood cells. For example, the yield from analyses that require single-cell sequencing, such as RNA sequencing to identify distinct CTC gene expression patterns^4,6–8 and copy number variation analysis to characterize CTC provenance,^9,10 is directly proportional to purity; a higher sample purity leads to more CTCs per sample that are analyzed, which results in less time and money spent per analysis of a single CTC.

Microfluidic techniques have been used successfully to capture rare CTCs from whole blood with high efficiency, although reported purities are often relatively low because of the nonspecific adhesion of leukocytes to capture surfaces.^4,11–14 A majority of immunocapture techniques use the epithelial marker EpCAM (epithelial cell adhesion molecule), which has been reported to have oncogenic potential,¹⁵ is correlated with proliferation in cancer cell lines,¹⁶ and has been used to identify CTCs in many cancers.^{11,13,17–23} However, EpCAM varies in expression level between cancers and potentially fails to capture more invasive CTCs that have undergone the epithelial-to-mesenchymal transition (EMT).^24–26 Despite differences in cell surface antigen expression levels, a majority of cancer cells are vastly different from blood cells in cellular composition and morphology, which leads to their distinct electrical properties and dielectrophoretic response.²⁷ Therefore, we hypothesize that dielectrophoresis (DEP) can potentially be used to capture cancer cells that are less likely to be isolated by traditional immunocapture methods with epithelial markers such as EpCAM. In this work, we aim to study how cancer cell capture performance can be improved by (1) characterizing EpCAM capture as a function of flow conditions (e.g., shear stress) and cancer cell surface expression levels, and (2) incorporating dielectrophoretic effects to enhance cancer cell capture while reducing nonspecific adhesion of leukocytes.

DEP is widely used in microfluidics to separate cell populations based on differences in their electrical properties.^22,28,29 Within certain applied electric field frequency ranges, majority of cancer cells exhibit a positive DEP (pDEP) response, are attracted to regions of high electric field gradients, and can be separated from blood cells, which exhibit a negative DEP (nDEP) response and are repelled from regions of high electric field gradients.^27,30–36 For applications in CTC capture, however, the use of DEP techniques alone have typically been limited by low capture efficiency and throughput owing to the rarity of CTCs in whole blood, as well as by restrictions of device and electrode design and difficulties with applying large enough electric field gradients near rare cells to capture them.²²

Given that existing immunocapture techniques typically report high capture efficiencies but low capture purities, and DEP methods have the potential for high-purity separation by cancer cells' pDEP and blood cells' nDEP responses but are limited by low capture efficiencies in rare cell capture applications, we hypothesize that DEP may work best as a complement to existing immunocapture devices to act only near immunocapture surfaces where electric fields are strongest and antibody interactions occur to improve capture purity. We previously characterized how a hybrid DEP-immunocapture approach can enrich prostate cancer cells from blood cells by attracting cancer cells to immunocapture surfaces while repelling contaminating peripheral blood mononuclear cells (PBMCs).^35,37 However, these studies used an antibody, J591, that is highly specific to the prostate-specific membrane antigen (PSMA) expressed on the surface of prostate cancer cells.³⁸ As many cancers (e.g., pancreatic) do not have an organ-specific biomarker and therefore are more difficult to capture with EpCAM,^20,21 CTC immunocapture can be further optimized by characterizing capture performance as a function of EpCAM expression level and evaluating the potential benefits of incorporating DEP effects. We have also recently reported on a capture probability model that can be used to inform simulations of capture as a function of shear stress in existing immunocapture device geometries;³⁹ by characterizing immunocapture with DEP effects, we can predict enhanced CTC capture performance in a future hybrid DEP-immunocapture system.

In the current study, we characterized the DEP response of a panel of pancreatic cancer cell lines (Capan-1, PANC-1, BxPC-3)—which, to our knowledge, has not been described before—with varying levels of EpCAM expression and evaluated their immunocapture performance as a function of the local shear stress experienced by the cells. This work was performed using a Hele-Shaw flow cell and a protocol designed to make nonspecific adhesion of PBMCs readily apparent.³⁵ In addition, by precisely tuning the applied electric field frequency, we enriched the pancreatic cancer cells from blood cells by attracting cancer cells to and repelling PBMCs from immunocapture surfaces with pDEP and nDEP, respectively. In comparing immunocapture performance with and without DEP effects, we also evaluated capture probability as a function of shear stress, cell surface chemistry, and normal force using the previously reported capture probability model.³⁹ We demonstrate that DEP can enhance immunocapture of cancer cells with lower EpCAM expression and that immunocapture purity can potentially be improved by repelling PBMCs with nDEP; this work informs the design of future hybrid DEP-immunocapture devices with increased CTC capture purity, which will facilitate subsequent functional and genetic analyses to elucidate cancer progression and develop more effective treatment options.

II. MATERIALS AND METHODS

A. Device fabrication and antibody functionalization

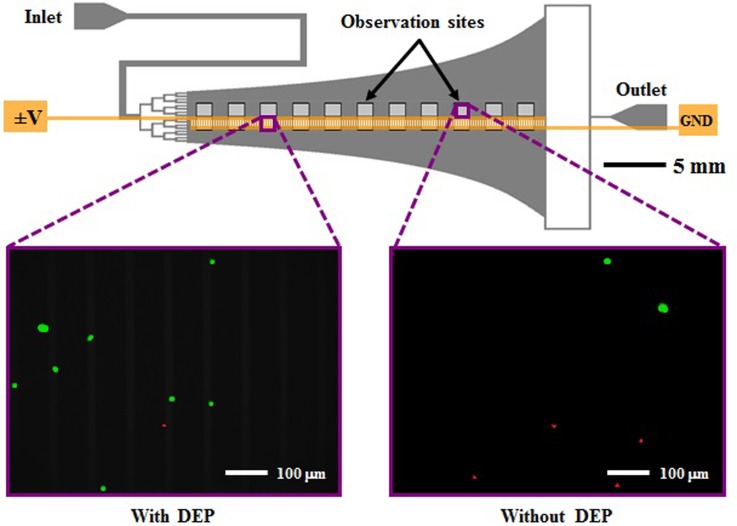
A Hele-Shaw flow cell with interdigitated gold electrodes, depicted in Figure 1, was used to characterize immunocapture with DEP effects as a function of shear stress. The design and fabrication of this Hele-Shaw DEP device is detailed in our previous work.^35,37,40 One major change to the device geometry from previous iterations is an elongation of the straight inlet channel to 45 mm, which allows for all cancer cells and PBMCs to settle to the bottom of the channel before entering the main chamber, and ensures that all cells are rolling on the immunocapture surface in the shear stress range where data are taken. This condition allows for cell capture to be quantified as a fraction of total cells entering the main chamber in subsequent data analysis steps.

FIG. 1.

Schematic of the Hele-Shaw flow cell and its interdigitated electrodes with lead connections to an applied voltage (±V) and ground (GND), and elongated straight inlet channel compared to previous designs.^35,37 The elongated straight inlet channel was 500 μm wide, the smaller branching channels were 156 μm wide, and all channels were 48 μm tall. The main chamber geometry leads to a monotonically decreasing shear stress along the device centerline, which allows for cell capture to be measured as a function of shear stress.^40–42 Inset images show fluorescently labeled PANC-1 cells (green) and PBMCs (red) adhered to the antibody-functionalized surface with and without DEP effects. These example images show that at an applied AC electric field frequency of 200 kHz, more PANC-1 cells and fewer PBMCs were captured with DEP compared to without DEP. Captured cells in each pair of 1-mm² observation windows were enumerated and compared at a series of observation sites corresponding to a range of shear stresses found in typical immunocapture devices.^4,12,39,43

The bottom surface of the Hele-Shaw DEP device was functionalized with NeutrAvidin (Thermo Fisher Scientific) following previously reported protocols,^12,40 then incubated with 10 μg/ml biotinylated goat anti-mouse antibody (Santa Cruz Biotechnology) for 1 h, followed by incubation with 10 μg/ml anti-EpCAM antibody (Clone 158206, R&D Systems) for 1 h.²⁰ All antibodies were prepared in 1% bovine serum albumin (BSA) in phosphate buffered saline (PBS).

B. Cell culture and preparation

Pancreatic cancer cell lines Capan-1, PANC-1, and BxPC-3 were purchased from the American Type Culture Collection and cultured at 37 °C in a 5% CO₂ humidified environment. Capan-1 cells were cultured in 20% fetal bovine serum (FBS) in Iscove's Modified Dulbecco's Medium (IMDM), PANC-1 cells were cultured in 10% FBS in Dulbecco's Modified Eagle Medium (DMEM), and BxPC-3 cells were cultured in 10% FBS in RPMI. All culture media was also supplemented with 1% penicillin-streptomycin. To prepare for experiments, cancer cells at >80% confluency were trypsinized from their culture flasks and incubated with 5 μM CellTracker™ Green CMFDA (Invitrogen) for at least 30 min.

PBMCs were isolated from the blood of consenting colonoscopy screening patients with Institutional Review Board (IRB) approval from the University of Michigan Medical School. Whole blood was collected in BD Vacutainer^® CPT™ Cell Preparation Tubes with Sodium Heparin^N, and PBMCs were isolated after centrifugation and incubated with 5 μM CellTracker™ Orange CMRA (Invitrogen) for at least 30 min.

After incubation with their respective fluorescent probes, pancreatic cancer cells and PBMCs were washed twice and resuspended in PBS diluted 20 times by volume in an isotonic sugar in deionized (DI) H₂O solution consisting of 9.5% sucrose and 0.3% dextrose with conductivity 0.07 S/m; this medium was chosen for its isotonic properties to cause minimal damage to cells as well as for the observed pDEP response of cancer cells and nDEP response of blood cells in the conductivity and applied electric field frequency ranges used in this study.^35,37 The final cell densities were approximately 5 × 10⁵ cancer cells per ml and 2 × 10⁶ PBMCs per ml; the two populations were mixed together before injection into the Hele-Shaw DEP device for all experiments except for those with BxPC-3 cells and an applied electric field frequency of 200 kHz, in which blood samples were unavailable and only cancer cell capture was characterized.

C. Characterization of pancreatic cancer cells' DEP response

In order to separate cancer cells from blood cells, the DEP response of both populations must be characterized as a function of applied electric field frequency. In this study, as with our previous characterization of prostate cancer,^35,37 we measured the approximate DEP crossover frequency of each pancreatic cancer cell line and extrapolated electrical properties to predict their DEP responses. The sign and magnitude of the time-averaged DEP force, $⟨{\mathbf{F}}_{\text{DEP}}⟩$, on a spherical particle in an infinite domain with a weakly varying electric field and homogeneous and isotropic complex permittivities is determined by the real part of the Clausius-Mossotti factor, $\Re ({\tilde{f}}_{\text{CM}})$

$$⟨{\mathbf{F}}_{\text{DEP}}⟩=\pi {\epsilon }_{\mathrm{m}}{a}^3\Re ({\tilde{f}}_{\text{CM}})\nabla ({\mathbf{E}}_0·{\mathbf{E}}_0),$$ (1)

$${\tilde{f}}_{\text{CM}}=\frac{{\tilde{\epsilon }}_{\mathrm{p}}-{\tilde{\epsilon }}_{\mathrm{m}}}{{\tilde{\epsilon }}_{\mathrm{p}}+2{\tilde{\epsilon }}_{\mathrm{m}}},$$ (2)

where a is the particle radius, E = E₀ cos(ωt) is the externally applied AC electric field, ω is the angular frequency of the electric field, $\tilde{\epsilon }=\mathrm{\epsilon }-\mathrm{i}\sigma /\omega$ is the complex permittivity, i = (−1)^1∕2, ε is the electrical permittivity, σ is the electrical conductivity, the subscripts p and m denote the particle and the medium, respectively, and bolded letters denote vectors.⁴⁴ The frequency at which $\Re ({\tilde{f}}_{\text{CM}})=0$, i.e., when the particle transitions from nDEP to pDEP, or vice versa, is termed the crossover frequency.

To determine the crossover frequency range of the pancreatic cancer cell lines, each cell population was manually flowed through the Hele-Shaw DEP device and observed above the interdigitated electrodes region on a Nikon LV100 upright microscope. The electrodes were energized by an Agilent 33200A function generator at 6 V peak-to-peak (V_pp) and frequencies ranging from 100 kHz to 1 MHz, and the DEP response was determined at each applied frequency by observing if the cells were attracted to or repelled from the electrodes by pDEP and nDEP, respectively. The DEP response of PBMCs in our setup was characterized in a previous study.³⁵ After determining each cell population's crossover frequency, we predicted the magnitude of its DEP response as a function of frequency by modeling the cell as a single-shelled dielectric sphere; this approach facilitates the description of a cell's extrinsic electrical properties, as they are often difficult to infer directly from experimental measurements.^28,30,31,45 The effective permittivity of the particle, ${\tilde{\epsilon }}_{\mathrm{p}}$, in Eq. (2), was replaced by an effective permittivity of the cell, ${\tilde{\epsilon }}_{\text{cell}}$, that describes its electrical properties in terms of a specific membrane capacitance, C_membrane, and the cytoplasmic permittivity and conductivity^35,37,44

$${\tilde{\epsilon }}_{\text{cell}}=\frac{C_{\text{membrane}}\hspace{0.17em}a\hspace{0.17em}{\tilde{\epsilon }}_{\text{cytoplasm}}}{C_{\text{membrane}}\hspace{0.17em}a+{\tilde{\epsilon }}_{\text{cytoplasm}}}.$$ (3)

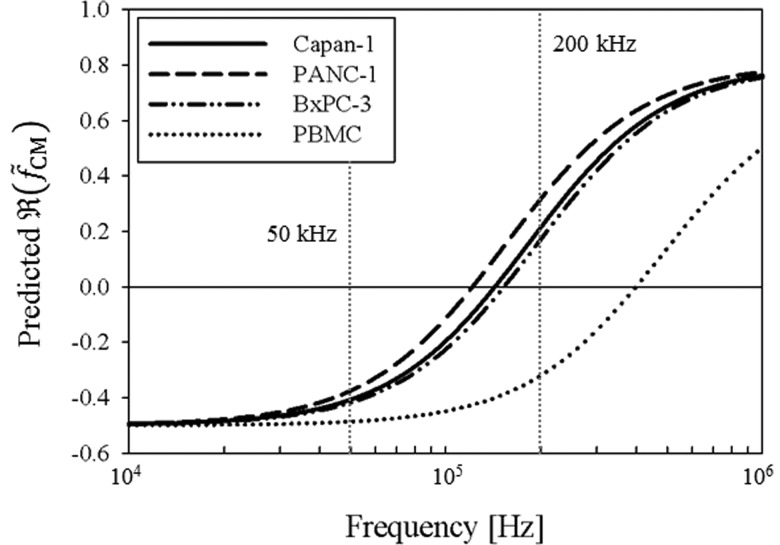
Figure 2 shows the predicted DEP responses of Capan-1, PANC-1, BxPC-3, and PBMCs as a function of frequency as described by the dielectric shell model. We fixed the cytoplasmic permittivity and conductivity to 50ε₀ (ε₀ = 8.85 × 10⁻¹² F/m) and 1 S/m, respectively, because these values are within previously reported ranges^27,30,45,46 and varying them did not significantly change the magnitude of $\Re ({\tilde{f}}_{\text{CM}})$ under our experimental conditions. The average cell diameters of Capan-1, PANC-1, and BxPC-3 were previously measured to be 15.8 ± 3.2 μm, 17.3 ± 2.7 μm, and 13.3 ± 2.9 μm, respectively,²⁰ and PBMCs were measured to have an average diameter of 10.1 ± 2.1 μm. We selected 50 kHz and 200 kHz as the frequencies to apply in characterizing nDEP and pDEP effects on cell adhesion as a function of shear stress. As shown in Figure 2, both cancer cells and PBMCs exhibit a nDEP response at 50 kHz, whereas at 200 kHz, cancer cells exhibit a pDEP response while PBMCs exhibit a nDEP response.

FIG. 2.

Predicted DEP response, as described by $\Re ({\tilde{f}}_{\text{CM}})$, of Capan-1 (solid line), PANC-1 (dashed line), BxPC-3 (dashed-dotted line), and PBMCs (dotted line) as a function of applied electric field frequency. Cells were modeled as single-shelled dielectric spheres, described by Eqs. (2) and (3). In a diluted PBS suspending medium with σ_m = 0.07 S/m, the crossover frequency was experimentally determined to be approximately 140 kHz for Capan-1, 120 kHz for PANC-1, 140 kHz for BxPC-3, and 400 kHz for PBMCs. Because the DEP force is weak in these frequency ranges and therefore difficult to observe, our crossover frequency estimates all have an uncertainty of ±10 kHz. These empirical measurements, combined with Eq. (3), corresponded to specific membrane capacitance values of C_membrane = 13.5 mF/m² for Capan-1, C_membrane = 14.5 mF/m² for PANC-1, and C_membrane = 15 mF/m² for BxPC-3, and C_membrane = 7.5 mF/m² for PBMCs in the dielectric shell model. At 50 kHz, cancer cells and blood cells both exhibit a nDEP response; at 200 kHz, however, cancer cells exhibit a pDEP response whereas PBMCs still exhibit a nDEP response.

D. Characterization of EpCAM immunocapture with DEP

Capan-1, PANC-1, and BxPC-3 cells were each mixed with PBMCs, and each mixture was flowed through the Hele-Shaw DEP device in separate experiments at 0.2 ml/h for 10 min using a Chemyx Fusion 400 syringe pump. The electrodes were energized at 6V_pp and two frequencies (50 kHz and 200 kHz), with 3 to 4 experimental replicates each. Fluorescent images of cancer cells and PBMCs were taken with FITC and Texas Red^®/Cy3.5™ Chroma filter cubes, respectively, at the observation window closest to the main chamber entrance every minute to quantify the amount of cells coming into the device (that are all rolling on the immunocapture surface). The total number of cells that entered the main chamber over the course of an experiment lasting t minutes was estimated as

$${\int }_0^t\frac{\#\hspace{0.17em}\text{of}\hspace{0.17em}\text{cell}\hspace{0.17em}\text{sat}\hspace{0.17em}\text{time}\hspace{0.17em}t}{\text{area}\hspace{0.17em}\text{of}\hspace{0.17em}\text{observation}\hspace{0.17em}\text{window}}\mathrm{d}t\times (\text{width}\hspace{0.17em}\text{of}\hspace{0.17em}\text{observation}\hspace{0.17em}\text{window})\times (\text{velocity}\hspace{0.17em}\text{in}\hspace{0.17em}\text{the}\hspace{0.17em}\text{channel}\hspace{0.17em}\text{at}\hspace{0.17em}\text{cell}\hspace{0.17em}\text{height}),$$ (4)

where the width of an observation window was 1 mm, the area of an observation window was 1 mm², and the integral was evaluated as a Riemann sum with the difference between upper and lower bounds equal to the number of subdivisions (i.e., the number of cells was counted at every minute)

$${\int }_0^{t}f(t)\mathrm{d}t=\sum _{i=0}^{t}f(t_i).$$ (5)

After each capture experiment, non-adherent cells were washed away with PBS, and images of captured cancer cells and PBMCs were taken at each observation window pair along the Hele-Shaw DEP device's central axis to directly compare capture with and without DEP as a function of shear stress. Captured cells were enumerated in each observation window and multiplied by a correction factor that was a function of shear stress to normalize for streamline divergence in the device.^35,37 The number of cells captured in spaces between two adjacent capture windows was estimated as the average number of captured cells in the two adjacent windows and also multiplied by the correction factor. The local capture probability was calculated by dividing the number of cells captured in a capture window (i.e., at a given shear stress value) by the number of cells that entered that particular window, which in turn was calculated by subtracting the number of cells captured in previous windows and those in the spaces between windows from the total number of cells that entered the device (determined by Eqs. (4) and (5)).

E. Derivation of exponential capture model

An exponential fit was used to convert experimental data collected in the Hele-Shaw DEP device into a probabilistic model, suitable for use in immunocapture simulations. This model predicts the probability of adhesion, P_capture, as a function of receptor and ligand surface densities, m_r and m_a; the receptor–ligand association constant at zero load, $K_a^0$; the contact area, A_c; the characteristic receptor–ligand bond length, λ; the thermal energy, k_BT; and the dislodging force, F_dislodge^47,48

$$P_{\text{capture}}=m_r{m}_l{K}_a^0{A}_c\hspace{0.17em}\text{exp}\left(-\frac{\lambda }{k_{B}T}\frac{F_{\text{dislodge}}}{m_r{A}_c}\right).$$ (6)

As values for these terms are often unavailable for rare cells in circulation, we grouped them into two lumped parameters, A and B, took F_dislodge as proportional to the shear stress τ, and discretized the equation as reported previously³⁹

$$\mathrm{d}{P}_{\text{capture}}(\tau )=A\hspace{0.17em}\text{exp}(-B\tau )\mathrm{d}t.$$ (7)

We identified values for A and B as a function of cell type and the frequency of the applied electric field by integrating the discrete equation over the length of each Hele-Shaw observation window

$$P_{\text{capture}}(\tau )={\int }_{x_1}^{x_2}A\hspace{0.17em}\text{exp}(-B\tau )\mathrm{d}t.$$ (8)

Noting the relationship between distance x, characteristic velocity U, shear stress τ, and characteristic time t as t = x/U = x/τa (where a is the cell radius), and discretizing as dt = dx/τa, we found

$$P_{\text{capture}}(\tau )={\int }_{x_1}^{x_2}\frac{A}{\tau a}\hspace{0.17em}\text{exp}\left(-B\tau \right)\mathrm{d}x.$$ (9)

Integrating over each observation window with τ approximated as uniform yielded

$$P_{\text{capture}}(\tau )=\frac{A\Delta x}{\tau a}\text{exp}\left(-B\tau \right),$$ (10)

where Δx is the length of each observation window (i.e., 1 mm) and P_capture (τ) is the fraction of cell captured that roll through each observation window. We fit our capture fraction versus shear stress data to a simple exponential model of the form

$$P_{\text{capture}}(\tau )\tau =A\prime \hspace{0.17em}\text{exp}(-B\tau ),$$ (11)

calculating B directly from our fit, and deriving A algebraically as $A=A\prime a/\Delta x$. Inserted into Eq. (10), A and B provide a fit to our experimental data; used in Eq. (7), A and B can be used to predict capture as cells are advected along a simulated capture surface.³⁹

III. RESULTS AND DISCUSSION

The immunocapture of pancreatic cancer cells and PBMCs was characterized with and without DEP effects as a function of shear stresses corresponding to those experienced by cells in typical immunocapture device geometries.^{4,35,37,39,40,43} We chose to characterize the cell lines Capan-1, PANC-1, and BxPC-3 because of differences in their tumor origin (Capan-1 from liver metastasis; PANC-1 and BxPC-3 from primary pancreatic tumors), differentiation state (Capan-1 is well differentiated; PANC-1 and BxPC-3 are moderately to poorly differentiated),⁴⁹ and EpCAM expression as measured by antibodies bound per cell.²⁰ In addition, although Pethig et al. previously measured the membrane capacitance and conductance of pancreatic beta cells⁵⁰ and Shim et al. recently made DEP crossover frequency measurements of all NCI-60 cell lines,²⁷ to our knowledge, the DEP response of these pancreatic cancer cells has not been characterized before. Therefore, in contrast to our previous work with prostate cancer and the highly organ-specific biomarker PSMA,^35,37,40 we aim to study in this work how DEP and normal forces affect immunocapture of pancreatic cancer cells that have no organ-specific biomarker and varying levels of EpCAM expression with an exponential capture model.

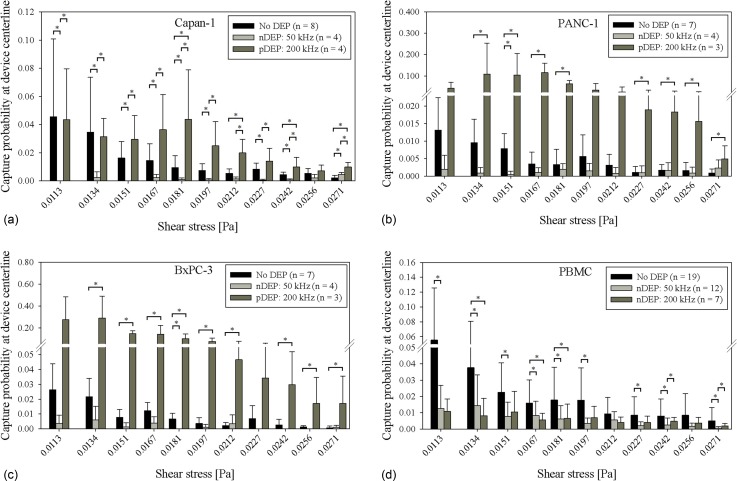
Shear-dependent immunocapture was characterized in a Hele-Shaw flow cell, and cell concentrations were chosen to be high enough to make nonspecific adhesion of PBMCs readily apparent and facilitate comparison with cancer cell capture.³⁵ In addition, elongation of the straight inlet channel from previous designs^35,37 led to all cells entering the main chamber to be rolling in contact with the immunocapture surface (Figure 1). This initial condition allowed for cell capture along the length of the device to be quantified as a fraction of the number of cells that entered a particular shear stress region (here termed the “capture probability”), which normalizes the data for variations in cell densities between experimental replicates. Figures 3(a)–3(d) show the capture probability of cells at the Hele-Shaw DEP device's central axis (along which the shear stress is monotonically decreasing and observation windows are located) for Capan-1, PANC-1, BxPC-3, and PBMCs, respectively. With no DEP applied, capture across all cell types generally decreased with increasing shear stress; these trends are in line with our previous characterization work in a Hele-Shaw flow cell^35,37,40 as well as in a three-dimensional immunocapture device geometry.^20,39 In addition, more Capan-1 cells were captured than PANC-1 and BxPC-3 cells at a majority of shear stress values. Previously measured EpCAM antibodies bound per cell (ABC) values by Thege et al.,²⁰ as listed in Table I, show that Capan-1 cells have a higher expression of EpCAM, which explains the current study's higher Capan-1 capture without DEP effects.

FIG. 3.

Capture probability of Capan-1 cells, 3(a), PANC-1 cells, 3(b), BxPC-3 cells, 3(c), and PBMCs, 3(d), at the central axis of the Hele-Shaw DEP device as a function of shear stress under experimental conditions of no DEP (black bars), 50 kHz (light gray bars), and 200 kHz (dark gray bars). Bars represent the mean capture of the indicated number of experimental replicates (n), and error bars represent standard deviation. A Wilcoxon rank-sum test was used to compare between each pair of DEP conditions, and asterisks (*) indicate significance of differences (P < 0.05).

TABLE I.

Ratios of pancreatic cancer cell capture probabilities with DEP to without DEP effects averaged across all reported shear stresses shown in Figure 3. Ratios are reported as mean ± standard error of the mean. EpCAM ABC data were previously reported in Ref. 20.

Cell line	EpCAM ABC	nDEP (50 kHz) to no DEP	pDEP (200 kHz) to no DEP
Capan-1	71 807	0.33 ± 0.17	2.58 ± 1.04
PANC-1	21 247	0.63 ± 0.69	12.72 ± 7.59
BxPC-3	28 197	0.38 ± 0.55	15.21 ± 8.09

At an applied electric field frequency of 50 kHz, pancreatic cancer cells and PBMCs both exhibit a nDEP response (Figure 2). For PBMCs, whose nonspecific adhesion to the immunocapture surface was purposely amplified by the device's geometric design and high input cell concentration to facilitate relative comparisons between capture with and without DEP, fewer cells were captured with nDEP at 50 kHz repelling them from the capture surface as compared to without DEP at a majority of shear stresses (Figure 3(d)). Similarly, for the cancer cells, capture with nDEP was lower at a majority of shear stresses, as cells were repelled from immunocapture surfaces (Figure 3). Table I lists the ratios of cancer cell capture probabilities with DEP to without DEP averaged across all reported shear stresses shown in Figure 3. The ratio of capture with nDEP to without DEP was less than 1 for all three cell lines, although the errors were larger for PANC-1 and BxPC-3 cells, which indicate that in these cell lines, there were smaller differences between capture with nDEP and without DEP; this result can be explained by PANC-1 and BxPC-3 cells' low EpCAM expression, which already led to a low amount of capture without DEP.

At an applied electric field frequency of 200 kHz, pancreatic cancer cells exhibit a pDEP response whereas PBMCs exhibit a nDEP response (Figure 2). For PBMCs, there was a general trend of less capture with nDEP at 200 kHz repelling cells from the immunocapture surface compared to without DEP. For cancer cells, capture with pDEP attracting cells to the immunocapture surface was higher compared to without DEP (Figure 3). Interestingly, for PANC-1 and BxPC-3 cells, the magnitude of capture with pDEP was higher than that of Capan-1 cells. Table I shows that the ratio of capture with pDEP to without DEP is much higher for PANC-1 and BxPC-3 cells compared to Capan-1 cells, which is expected, as Capan-1 cells have a higher EpCAM ABC count and, therefore, higher capture without DEP. However, the magnitude of Capan-1 capture with pDEP is much lower than that of PANC-1 and BxPC-3 cells, which cannot be attributed to differences in EpCAM ABC counts or DEP response magnitude, as our dielectric model predicts similar magnitudes of $\Re ({\tilde{f}}_{\text{CM}})$ for all three cell lines (Figure 2). We hypothesize that differences in Capan-1 cells' tumor origin, differentiation state, mutation status of key oncogenes,⁴⁹ and other biophysical and physiological properties from those of PANC-1 and BxPC-3 cells may contribute to its observed weaker pDEP response. Such differences may lead to changes in cell membrane properties (e.g., thickness, capacitance, conductivity, and permittivity) that are difficult to measure or infer from crossover frequency measurements alone. A more robust technique for measuring a cell's electrokinetic response is electrorotation,^51–55 which can potentially be used to investigate the magnitudes of each cell line's DEP response as a function of frequency but is beyond the scope of this study.⁵⁶ Nevertheless, our results show that pDEP enhances capture of all three pancreatic cancer cell lines, especially for PANC-1 and BxPC-3 cells, which are less differentiated; this suggests that DEP can potentially be used to enhance immunocapture of CTCs that (1) have lower EpCAM expression and are, thus, less likely to be captured without DEP, and (2) are less differentiated and metastatic, possibly leading to earlier detection of CTCs.

In comparing cancer cell capture with pDEP at 200 kHz to capture with nDEP at 50 kHz, there were more cancer cells captured across a majority of shear stresses for all three cell lines (Figures 3(a)–3(c)), showing that DEP can be tuned to enhance or diminish cancer cell immunocapture by pDEP and nDEP, respectively. For PBMCs, capture with nDEP at 200 kHz and capture with nDEP at 50 kHz were similar across all shear stresses (Figure 3(d)), indicating that there was not a significant difference in the magnitude of the nDEP force experienced by PBMCs at 200 kHz and 50 kHz, as confirmed by the predicted $\Re ({\tilde{f}}_{\text{CM}})$ magnitudes in Figure 2 and calculated $⟨{\mathbf{F}}_{\text{DEP}}⟩$ values in Table II.

TABLE II.

Exponential capture model fit values for A [Pa] and B [Pa⁻¹], described by $P_{\text{capture}}(\tau )=\frac{A\Delta x}{\tau a}\text{exp}\left(-B\tau \right)$ (Eq. (10)), as a function of cell type and normal force, F [N], to the immunocapture surface. In a typical obstacle-array immunocapture geometry, the normal force (Stokes' drag, F_Stokes = 6πμaU, where μ is the fluid viscosity, a is the cell radius, and U is the velocity of the cell normal to the obstacle) on a cell in contact with the obstacle varies from approximately zero to a maximum value reported in the table. With no DEP effects applied in the Hele-Shaw DEP device, the only normal force present is gravitational, F_g. With DEP effects applied, however, the normal force is dominated by the time-averaged DEP force, $⟨{\mathbf{F}}_{\text{DEP}}⟩$, described by Eqs. (1) and (2), with predicted $\Re ({\tilde{f}}_{\text{CM}})$ values taken from Figure 2 at 50 kHz and 200 kHz and the gradient of the electric field calculated by COMSOL simulation at a height equivalent to the cell radius above the immunocapture surface and electrodes. A positive force represents attraction to the immunocapture surface, whereas a negative force represents repulsion.

		No DEP			50 kHz			200 kHz
Cell type	FStokes	Fg	A	B	$⟨{\mathbf{F}}_{\text{DEP}}⟩$	A	B	$⟨{\mathbf{F}}_{\text{DEP}}⟩$	A	B
Capan-1	1.40 × 10−11	2.10 × 10−11	2.58 × 10−5	108.97	−1.48 × 10−9	1.99 × 10−6	108.97	1.25 × 10−9	4.21 × 10−5	108.97
PANC-1	1.62 × 10−11	2.75 × 10−11	5.53 × 10−6	76.29	−1.76 × 10−9	1.44 × 10−6	76.29	9.70 × 10−10	5.97 × 10−5	76.29
BxPC-3	1.06 × 10−11	1.25 × 10−11	1.80 × 10−5	130.46	−1.31 × 10−9	3.83 × 10−6	130.46	5.44 × 10−10	2.29 × 10−4	130.46
PBMC	6.66 × 10−12	5.43 × 10−12	1.24 × 10−5	73.98	−1.14 × 10−9	3.93 × 10−6	73.98	−7.45 × 10−10	3.96 × 10−6	73.98

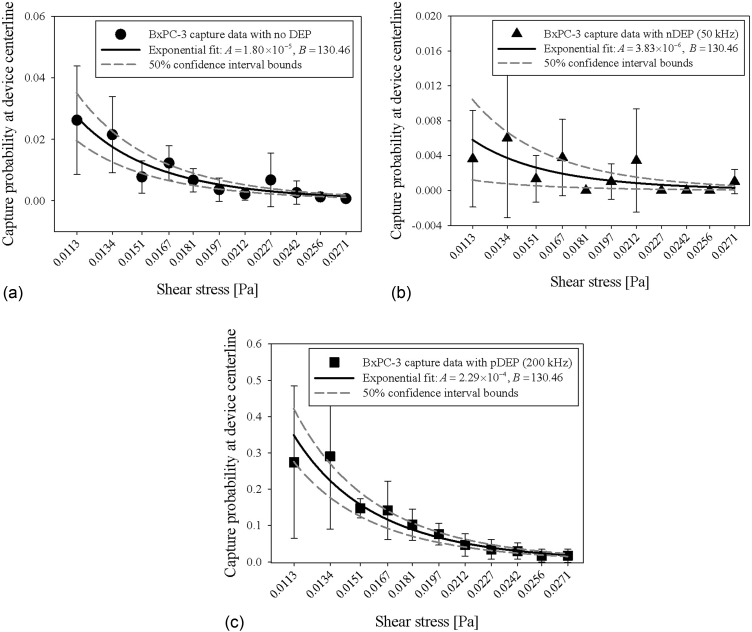
To further characterize capture probability as a function of shear stress, we fit our shear-dependent capture data for pancreatic cancer cells and PBMCs (Figure 3) to an exponential capture model described in Sec. II E and previously published work.³⁹ Curve fits to BxPC-3 capture data with no DEP, nDEP at 50 kHz, and pDEP at 200 kHz are shown in Figure 4; fit values for the other cell types are listed in Table II. In the capture model, A represents the magnitude of capture, and B represents the shear dependence. In our analysis, we found that fitting B as a free parameter under each separate DEP condition did not significantly change the quality of the fit (as measured by residual sum of squares and coefficient of determination calculations) when compared with fixing B to the same value for every DEP condition. Therefore, for each cell type, we fixed B for all DEP conditions to the same value obtained from fitting the capture data with no DEP effects applied (Table II). This result suggests that although our capture data can be described by an exponential function that has a unique decay (determined by B) for each cell type, the decay was not significantly affected by DEP effects in the shear stress range that we tested, and, therefore, does not require further characterization for our purposes of rare cell capture applications. In this work, we characterize DEP's effect on the relative magnitudes of immunocapture and translate these data to capture probabilities that decay exponentially with increasing shear stress; this exponential capture model can then be used in simulations of a hybrid DEP-immunocapture device to predict capture performance as a function of applied DEP force and shear stress.³⁹

FIG. 4.

Exponential fits (solid line) to shear-dependent BxPC-3 capture data (symbols) shown in Figure 3(c) for experimental conditions with no DEP, 4(a), nDEP at 50 kHz, 4(b), and pDEP at 200 kHz, 4(c). The exponential capture model derivation is detailed in Sec. II E. A [Pa] and B [Pa⁻¹] values are calculated from the exponential fit described by $P_{\text{capture}}(\tau )=\frac{A\Delta x}{\tau a}\text{exp}\left(-B\tau \right)$ (Eq. (10)), and 50% confidence interval upper and lower bounds for the A values are plotted as dashed lines. These fit values for Capan-1, PANC-1, BxPC-3, and PBMC capture data are also listed in Table II.

Figure 4 shows representative capture model fits to cancer cell (BxPC-3) capture data as a function of shear stress. For experimental conditions without DEP and especially with pDEP at 200 kHz (Figures 4(a) and 4(c)), cancer cell capture was generally high across the length of the device, resulting in good exponential fits to the data. The capture data with nDEP at 50 kHz (Figure 4(b)) was also fit well by an exponential function, but was noisier because there was comparatively lower capture compared to the other two experimental conditions (nDEP repelled cells across a majority of shear stresses). The magnitude of cancer cell capture with and without DEP effects is represented by A in the capture model, listed for each cell type under each DEP condition in Table II. In general, A values were highest for cancer cell capture with pDEP at 200 kHz and lowest for cancer cell capture with nDEP at 50 kHz, as expected. For PBMCs, A was highest for capture with no DEP and similar for capture with nDEP at both 50 kHz and 200 kHz. In addition, we found that B values were unique for each cell type, indicating that the capture performance of each cell type was different and dependent on EpCAM expression levels and electrical properties.

To interpret our capture data as a function of normal force to an immunocapture surface (which is the key information needed for future simulation work on capture probability in a hybrid DEP-immunocapture device), we calculated the Stokes drag on each cell type when in contact with an obstacle in a typical obstacle-array immunocapture device (such as the one described in Refs. 4, 12, 39, and 57) from the normal component of the cell's velocity. In addition, we calculated each cell type's weight (gravitational force, F_g, with no DEP effects) and predicted DEP response, $⟨{\mathbf{F}}_{\text{DEP}}⟩$; these normal forces are all listed in Table II. Although the equation for $⟨{\mathbf{F}}_{\text{DEP}}⟩$ (Eq. (1)) assumes a linearly varying electric field (which is not the case near the electrodes in our device geometry) and is derived by only retaining the first term of a linear multipole expansion, Eq. (1) provides a reasonable first-order approximation of the DEP force if the electric field is approximately axisymmetric on the length scale of the cell and if the characteristic length scale of the electric field non-uniformity is large compared to the cell size.²⁹ For simplicity and to only compare normal forces directly, we also ignored tangential DEP forces that are present in the system, but acknowledge that such forces can potentially change immunocapture's shear dependence. The calculated $⟨{\mathbf{F}}_{\text{DEP}}⟩$ values for all cell types were approximately 1 to 2 orders of magnitude larger than F_Stokes and F_g, suggesting that under similar experimental conditions, DEP can be made the predominant normal force in a hybrid DEP-immunocapture geometry and actuate cell motion toward or away from immunocapture surfaces in the presence of other weaker fluid mechanical forces.

Interestingly, the cell size (whose cube is proportional to $⟨{\mathbf{F}}_{\text{DEP}}⟩$ magnitude) does not appear to correlate with the amount of capture increase with pDEP or decrease with nDEP. For example, BxPC-3 cells are the smallest of the three cancer cell lines, had the lowest predicted $⟨{\mathbf{F}}_{\text{DEP}}⟩$ magnitude, and expressed lower EpCAM levels than Capan-1 cells (Table I), but had the highest A and B values with DEP (Table II). These results show that BxPC-3 cells had higher capture with pDEP on average (which was unexpected given its lower EpCAM expression), but that this capture performance decayed faster with increasing shear stress compared to other cell lines, suggesting that pDEP enhancement may only work optimally at lower shear stresses and also depend on other factors such as differences in tumor origin, differentiation state, and mutation status of key oncogenes whose effects on DEP response are difficult to infer from our current measurements. Importantly, however, our data demonstrate that DEP can enhance the immunocapture of cancer cells regardless of their surface antigen expression levels, and therefore, DEP has the potential not only to increase capture purity when used in combination with traditional immunocapture methods, but also to isolate cancer cells that are less likely to be captured by these immunocapture methods with epithelial markers. DEP-enhanced capture of cancer cells that have undergone the EMT, for example, can provide access to a subpopulation of CTCs that is currently difficult to isolate and facilitate studies on EMT's role in cancer progression.^58,59

IV. CONCLUSIONS

This work characterizes shear-dependent EpCAM immunocapture of pancreatic cancer cells enhanced by pDEP and nonspecific adhesion of PBMCs reduced by nDEP. We interpret our capture data using an exponential capture model, and show that capture performance is dependent on the applied DEP force magnitude, cell surface EpCAM expression level, and shear stress experienced by cells flowing in the capture device. Importantly, our results show that DEP enhances immunocapture of cancer cells, regardless of their surface epithelial antigen expression levels. Our characterization of DEP-controlled immunocapture inform the simulation of cancer cell and blood cell capture probabilities in a proposed hybrid DEP-immunocapture system for CTC capture, which we expect will increase capture purity and facilitate subsequent biological analyses of captured CTCs to better understand cancer metastasis and improve drug therapies.