Methodology for Developing and Evaluating the PROMIS^® Smoking Item Banks

Abstract

Introduction:

This article describes the procedures used in the PROMIS^® Smoking Initiative for the development and evaluation of item banks, short forms (SFs), and computerized adaptive tests (CATs) for the assessment of 6 constructs related to cigarette smoking: nicotine dependence, coping expectancies, emotional and sensory expectancies, health expectancies, psychosocial expectancies, and social motivations for smoking.

Methods:

Analyses were conducted using response data from a large national sample of smokers. Items related to each construct were subjected to extensive item factor analyses and evaluation of differential item functioning (DIF). Final item banks were calibrated, and SF assessments were developed for each construct. The performance of the SFs and the potential use of the item banks for CAT administration were examined through simulation study.

Results:

Item selection based on dimensionality assessment and DIF analyses produced item banks that were essentially unidimensional in structure and free of bias. Simulation studies demonstrated that the constructs could be accurately measured with a relatively small number of carefully selected items, either through fixed SFs or CAT-based assessment. Illustrative results are presented, and subsequent articles provide detailed discussion of each item bank in turn.

Conclusions:

The development of the PROMIS smoking item banks provides researchers with new tools for measuring smoking-related constructs. The use of the calibrated item banks and suggested SF assessments will enhance the quality of score estimates, thus advancing smoking research. Moreover, the methods used in the current study, including innovative approaches to item selection and SF construction, may have general relevance to item bank development and evaluation.

INTRODUCTION

The PROMIS^® Smoking Initiative identified six conceptual assessment domains to be represented as item banks in the PROMIS framework (i.e., nicotine dependence, coping expectancies, emotional and sensory expectancies, health expectancies, psychosocial expectancies, and social motivations for smoking). The items representing these domains were identified through a first phase that included literature review (concerning key constructs measured in smoking-related research), analyses of existing instruments (including item content), and extensive qualitative study (focus groups, cognitive interviews, and item review) to develop an item pool for field testing. The item pool was fielded to a large, nationally representative sample of smokers in the second phase, and a modern measurement theory approach was utilized to analyze the field test data. The quantitative analyses began with extensive exploratory factor analytic modeling of the entire item pool to identify the six distinct domains that would be represented as item banks in the PROMIS framework (see Edelen, Tucker, Shadel, Stucky, & Cai, 2012).

This article describes some of the more nuanced and detailed features of the methodological approach we employed to finalize the contents of the six item banks and evaluate their properties. The subsequent articles in this volume discuss the conceptual rationale for each of these smoking-related domains and present detailed information about their psychometric properties. Here, we focus on the common methods used for all the domains, with particular emphasis on the more technically innovative aspects of our approach.

Item bank development typically begins with a large pool of relevant items and proceeds by following a detailed series of analytic steps that reduce the number of items until a core subset of items are identified, which most accurately and precisely represent the theoretical construct. Although this item reduction process necessarily involves some subjective judgment, as it should, the methodological specifics we employed were adopted to provide as much empirical information as possible to inform item selection. We believe use of these innovative features, including the augmentation of standard results from exploratory item factor analyses, the application of new indices to quantify item bias, and the implementation of a novel approach to short form development that is well suited to assessment of psychological and health-related constructs, greatly enhanced the quality of information available to our study team and aided our decision-making process.

In what follows, we first provide a brief description of the study sample and data collection activity. Then each methodological step in developing and evaluating the item banks is described in turn. Illustrative examples from the development of one of the smoking banks are provided, with additional details for each of the item banks presented in their respective articles in this issue. We end with a discussion section describing the strengths and limitations of our approach. Much of the process we implemented follows standard practices for item bank development (both generally and within the PROMIS initiative, in particular). However, we take some time to discuss the more innovative aspects of the methods we implemented. We also identify some planned next steps in the evaluation and application of the smoking item banks.

METHODS AND RESULTS

Study Participants

Study participants were recruited by Harris Interactive through its online survey panel membership. Individuals were eligible if they were 18 years or older, had been smoking cigarettes for at least 1 year, had smoked a cigarette within the past 30 days, and were not planning to quit within the next 6 months. On the basis of the reported number of days smoked in the past 30 days (which smokers seem to report with reasonable accuracy; see, e.g., Harris et al., 2009), participants were classified as either daily (28–30 days) or nondaily (<28 days) smokers. Similar grouping have been used previously (see Fish et al., 2009; Shiffman, Kirchner, Ferguson, & Scharf, 2009), although of course alternative definitions of smoker type are possible. Of the 5,384 total participants, 4,201 were designated as daily cigarette smokers, and 1,183 were nondaily smokers.

Data Collection and Measures

All data were collected through a self-administered, web-based survey. A total of 277 smoking items were administered. To reduce respondent burden, these items were organized into blocks that were distributed across 26 overlapping forms. The average form length was 147 items. Each participant was randomly assigned to receive one of these forms, as well as one of eight established health-related PROMIS short forms. In addition, background characteristics were collected, including demographic information and reported past and present smoking behaviors.

General Analytic Approach

Previous research suggested that the constructs might manifest differently in daily and in intermittent or nondaily smokers (Shiffman, Ferguson, Dunbar, & Scholl, 2012; Shiffman & Paty, 2006). Put another way, the meaning of the constructs might vary across these groups such that the items that best differentiate individuals could be different across the smoker types. Accordingly, data for daily and nondaily smokers were analyzed separately.

Our initial focus was on generating item banks for daily smokers. For these analyses, a random subset of 3,201 daily smokers was selected for exploratory purposes. This subset was used in analyses that identified the six domains for which item banks would be developed (Edelen et al., 2012) and in the dimensionality assessment procedures reported here. A smaller random subset of 1,180 daily smokers was set aside to confirm (cross-validate) the exploratory findings (specifically, the fit of unidimensional models to the reduced item sets). When near-final item bank contents were identified for the daily smokers, we conducted corresponding analyses to identify bank contents for the nondaily smokers (the full sample of 1,183 nondaily smokers was used in these analyses, due to its smaller size). This resulted in the development of two item banks for each domain, with some differences in item content for daily and nondaily smokers. The methods for item selection described below were applied to both daily and nondaily smokers.

All items in these analyses utilized ordered response categories. Accordingly, a logistic graded response model (Samejima, 1969)—and its multidimensional extension (e.g., Muraki & Carlson, 1995; Gibbons et al., 2007)—was used in these analyses, following the standard practice for PROMIS item bank development (Reeve et al., 2007). Full-information estimation was used in estimating the various unidimensional and multidimensional item response theory (IRT) models. This estimation approach is particularly appropriate in a context such as this, in which there is extensive planned missingness (due to the assignment of respondents to forms with varying item content).

Dimensionality Assessment and Initial Item Selection

Analyses of the underlying dimensionality of the item sets for each of the six smoking domains were undertaken with the goal of identifying subsets that could form item banks that are essentially unidimensional in structure. Although the items comprising each domain were expected to be strongly related to a common underlying dimension, there were many more items than were needed to form each item bank, and we expected that the item sets would still contain clusters of items with excess dependence (i.e., not accounted for by the model) that would undermine the assumptions of the unidimensional IRT model to be used in subsequent item calibration and applications of the item banks. For example among the items measuring coping expectancies of cigarette smoking, some items relate to anxiety (“Smoking helps me deal with anxiety”; “I rely on smoking to deal with stress”), whereas others relate to feelings of anger (“When I go too long without a cigarette I lose my temper more easily,” “If I try to stop smoking I’ll be irritable”). Items sharing these more narrow content features are expected to be associated (beyond the level that would be expected simply due to the common influence of a general “coping expectancies” dimension).

Thus, our general approach to reduce the number of items in each domain was to (a) identify these item clusters, (b) specify a multidimensional model to account for and characterize the influence of the excess dependence in these clusters, (c) select item subsets that would remove or substantially reduce the excess dependence and collectively conform more closely to a unidimensional structure, and (d) test the fit of a unidimensional model to the reduced item set.

Identification of Item Clusters

Item clusters were identified using separate methodologies. First, we fit a series of exploratory item factor analysis models (which are multidimensional IRT models), extracting up to 15 latent dimensions (i.e., clusters) for each item set. An oblique rotation method was used (oblique CF-quartimax; see, e.g., Browne, 2001), consistent with our expectation that clusters should be correlated due to the influence of a strong general dimension. Full-information estimation of these relatively high-dimensional models was facilitated by the use of the Metropolis-Hastings Robbins-Monro algorithm (Cai, 2010b), which is implemented in the IRTPRO software (Cai, du Toit, & Thissen, 2011).

To obtain an alternative representation of the item clusters, we next fit a unidimensional IRT model and examined the standardized Chen & Thissen (1997) local dependence χ ² indices. These statistics, available in the IRTPRO output, are based on discrepancies between the observed and model-implied bivariate marginal response frequencies. Unmodeled dimensions (i.e., clusters) often manifest as residual associations between items, which may be detected by the local dependence indices.

To illustrate this process, results from the multidimensional exploratory item factor analysis model and unidimensional model-based local dependence indices for the 23 items in the social motivations for smoking domain are shown in Table 1. The left side of the table includes the factor loadings from the 5-factor model, and the right side of the table displays the local dependence indices. Boxes are drawn around clusters of items that appear to be locally dependent. Of particular note, Table 1 is a substantially augmented version of that provided in the standard IRTPRO output. The reorganization of rows and columns, deletion of ignorable table entries, and highlighting and boxing serve to emphasize the influence and size of the item clusters. This information is used to inform the specifications of the next modeling steps described below.

Table 1.

Assessment of Underlying Dimensionality: Exploratory Factor Analysis and Local Dependence Diagnostics

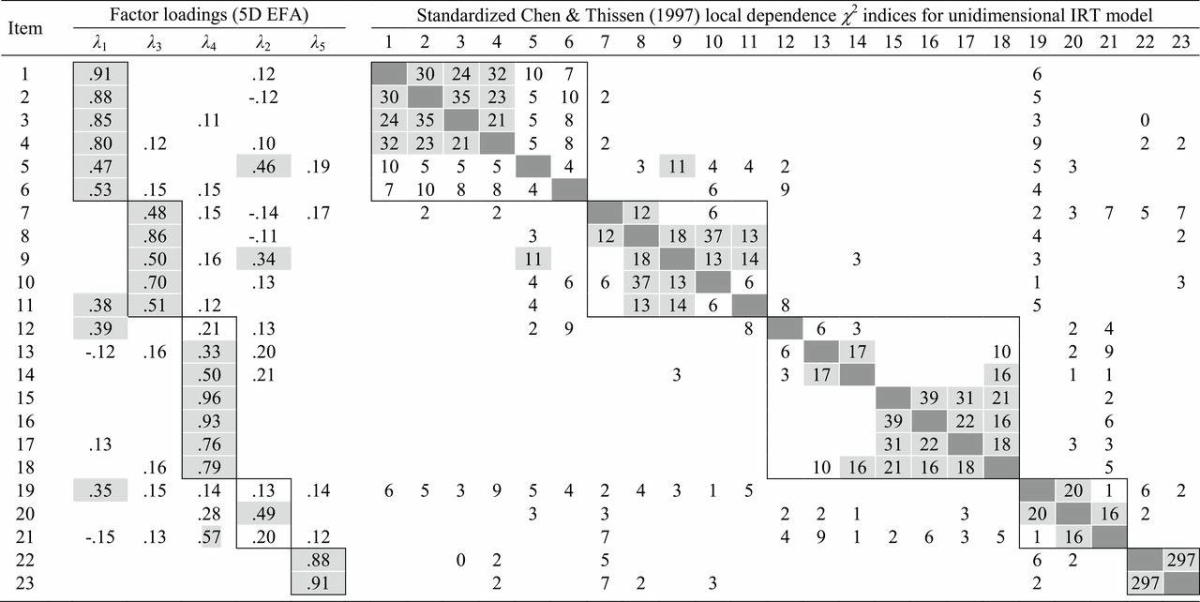
Note. EFA = exploratory factor analysis; IRT = item response theory.

The results were obtained from the analysis of the 23 items in the social motivations domain in a sample of daily smokers. For simplicity, only standardized factor loadings with absolute value less than 0.10 are shown in exploratory factor analysis (EFA) columns, and loadings above 0.30 are shaded gray. Only indices for positive local dependence are shown. Factor and positive local dependence indices above 10 are shaded gray in order to highlight the primary item clusters (boxes have also been drawn around these clusters).

Confirmatory Item Factor Modeling

Taken together, the exploratory factor analysis results and the local dependence diagnostics provided evidence of item clustering within each of the six domains. We used this information to specify confirmatory item bifactor models (Gibbons & Hedeker, 1992), which are constrained multidimensional IRT models in which the common variance of each item is decomposed into contributions from a general dimension (influencing all items in the domain) and a group-specific dimension (influencing only the items within a cluster). We evaluated the fit of the item bifactor models through comparisons with the more constrained unidimensional model. In addition, we compared the local dependence indices from the bifactor models with those from the unidimensional model to determine whether the incorporation of additional dimensions provided improved fit.

Based on the exploratory results of our illustrative example in Table 1, we fit a 6-factor item bifactor model to the same data. The item bifactor model posits a general dimension corresponding to the domain of interest. Five additional group-specific factors were included in the model to account for the clustering (local dependence) observed in Table 1. The standardized factor loadings for the fitted item bifactor model and corresponding local dependence indices are presented in Table 2. These indices, based on the bifactor specification, demonstrate that the addition of the five group-specific dimensions largely accounts for the dependence in the item clusters. Further, a likelihood ratio test and information-based fit criteria indicate that the item bifactor model fits substantially better than the unidimensional model.

Table 2.

Assessment of Underlying Dimensionality: Item Bifactor Model

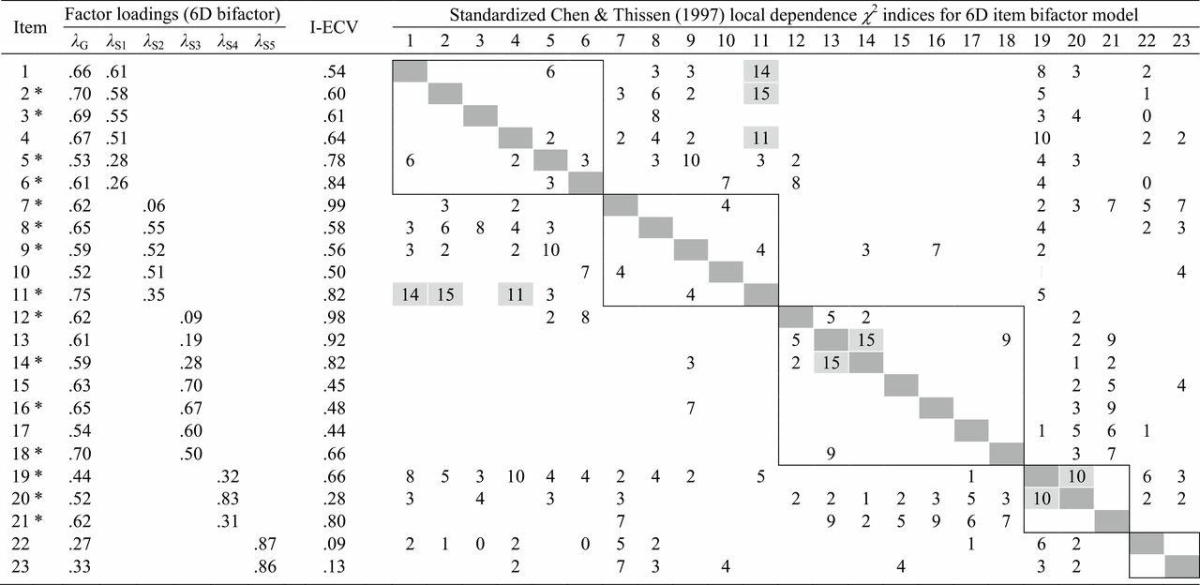
Note. The empty cells of the factor loading table have values fixed to zero. Only indices for positive local dependence are shown, and those with values above 10 are shaded gray. Boxes are drawn around the item clusters represented by the group-specific dimensions in the fitted model. I-ECV is the item-specific proportion of common variance explained by the general dimensions. Items with asterisk were retained (i.e., were considered for inclusion in final item banks).

Item Selection

After identifying a suitable bifactor model for each domain as illustrated, we were then faced with the task of reducing each item set to something essentially unidimensional, psychometrically strong, and containing adequate breadth of content. To help with these decisions, we used the standardized factor loading estimates from the bifactor models to calculate Explained Common Variance for a single Item (I-ECV; Stucky, Thissen, & Edelen, 2013), which describes the proportion of an item’s common variance that is explained by the general dimension. Generally speaking, items with higher I-ECVs would be favored over those with low values, as the higher value indicates minimal unique variance and a stronger relationship to the overall construct that is being measured by the general factor (and the eventual item bank). For item bifactor models, the I-ECV index is simply the square of an item’s loading on the general dimension, divided by the sum of the squared general and group-specific loadings:

$${\text{I-ECV}}_i=\frac{\lambda {}_{iG}^2}{\lambda {}_{iG}^2+\lambda {}_{is}^2}.$$

In order to identify subsets of unidimensional items, we carefully examined the estimated item factor loadings on the general dimension (λ _iG), I-ECV indices, and local dependence indices. Item content was also considered, as we sought to retain items identified by smoking researchers as important indicators of the domain. In general, our approach was to retain items strongly related to the general dimension (e.g., λ _iG > 0.5), and only weakly influenced by a group-specific dimension (e.g., I-ECV > 0.8). Although items with lower I-ECV values were considered for inclusion, we took care to limit the number of such items retained from a single item cluster.

Table 2 lists the I-ECV values, based on the fitted item bifactor model from our example. The values for this model ranged from 0.09 (Item 22) to 0.99 (Item 7). Based on the available information, 8 of the 23 items were excluded (the retained items are indicated in Table 2 by asterisks). The average I-ECV value of retained items was 0.70, whereas the average for the excluded items was 0.46.

Evaluation of Reduced Item Sets

In order to evaluate the effectiveness of the selection process for each domain, we computed an overall (test-level) ECV measure, which describes the proportion of total common variance (across all items) that is explained by the general dimension (ten Berge & Sočan, 2004). Like the I-ECV index, overall ECV may be computed from the estimated standardized factor loadings. For the bifactor model, in which each item loads on the general dimension and at most one of the group-specific dimension,

$$\text{ECV}=\frac{{\displaystyle \sum _{i=1}^I{\lambda }_{iG}^2}}{{\displaystyle \sum _{i=1}^I{\lambda }_{iG}^2}+{\displaystyle \sum _{s=1}^S{\displaystyle \sum _{i\in s}{\lambda }_{is}^2}}},$$

where I is the total number of items considered (either the number in the initial set or the number retained), S is the total number of group-specific dimensions, and $i\in s$ indicates the items loading on group-specific dimension s. Finally, we fit unidimensional IRT models to the initial and retained items using the Mplus software (Muthén & Muthén, 1998–2010). A limited-information estimation approach was used (mean- and variance-adjusted weighted least squares) to obtain standard confirmatory factor analysis goodness-of-fit indices (comparative fit index, Tucker Lewis Index, root mean squared error of approximation). These indices provided a basis for judging whether unidimensional models provided acceptable fit to the response data for the reduced item subsets.

Returning to our example in Table 2, the overall ECV based on the initial set of 23 items was 0.56, and ECV for the reduced set of 15 items was 0.64. Finally, the unidimensional model fit to the 15 items using limited-information methods produced improvements in each goodness-of-fit index compared with the results with 23 items (0.92 vs. 0.85 for comparative fit index; 0.91 vs. 0.84 for Tucker Lewis Index; 0.09 vs. 0.10 for root mean squared error of approximation). These results suggest that our item reduction process, guided by the I-ECV and local dependence values, yielded a set of items conforming much more closely to a unidimensional structure.

Evaluation of Differential Item Functioning

Items retained on the basis of the dimensionality assessment were then evaluated for differential functioning across demographic subgroups including age (18–30 vs. 31–50, 18–30 vs. 51+, and 31–50 vs. 51+), race/ethnicity (White vs. Black, White vs. Hispanic, and Black vs. Hispanic), and gender. We conducted differential item functioning (DIF) analyses separately for daily and nondaily smokers (DIF between these two smoker groups was considered at a later stage; see “Item Bank Calibration”). Our analyses consisted of three steps: (1) initial screening of items to identify DIF candidates, (2) formal DIF testing of the candidate items, and (3) an examination of severity or impact of statistically significant DIF. Items found to exhibit substantial bias for one or more comparisons were excluded from the final item banks.

Initial DIF Screening

In the first step, we utilized a two-stage Wald χ ² procedure (Langer, 2008; Woods, Cai, & Wang, 2013) to designate items as either anchors (those displaying no evidence of DIF) or candidates (showing some initial evidence of DIF). The two-stage procedure allows for tests of item parameter differences without prior identification of anchor items to link the groups being compared. The linkage was achieved by first fitting two-group IRT models to estimate the differences in the distributions of the latent trait in the groups being compared. A second series of models were then fit in which parameters for the group distributions were fixed and item parameters estimated without any equality constraints. Finally, the Wald χ ² for DIF (Lord, 1980; Langer, 2008) was used to test for differences in the parameter estimates for each item. In order to control the overall (familywise) error rate, we adjusted the critical p values for the test statistics using the Benjamini–Hochberg procedure (Benjamini & Hochberg, 1995; Thissen, Steinberg, & Kuang, 2002) with an overall alpha level of 0.05. This adjustment was applied to the set of tests obtained for all items in a given smoking domain and for a particular reference-focal group comparison.

Final DIF Tests

Items with significant group differences in the initial screening were viewed as DIF candidates. The second step in our DIF evaluation was to formally test these candidates, which was done by fitting another series of two-group IRT models. Items that were free of significant DIF in the screening step were used as anchors, with parameters constrained to be equal across groups. The availability of these anchors allowed the parameters of the latent trait distribution of one of the groups to be estimated, along with the group-specific parameters of the candidate items. Once again, we used the Wald χ ² (with Benjamini–Hochberg adjustment of critical values) to test the equality of the item parameters across groups.

Evaluation of DIF Severity

Even with the use of adjusted p values to determine statistically significant DIF, the DIF detection approach we utilized is very powerful; especially with such large samples, DIF that is identified as statistically significant with this approach can often be rather negligible in impact. Although we want to avoid problematic item bias in our banks, we do not want to remove items with negligible or ignorable bias; thus, we need some way to reduce the number of items considered for deletion due to DIF. It is often helpful to examine expected score curves and category response functions that provide a visual representation of the “size” of the identified DIF to determine whether the DIF is problematic. Still, the decision to retain or remove DIF items can be difficult without further numeric information as to the severity of the DIF impact.

We calculated two measures of DIF severity to augment our interpretation of the DIF plots. These numeric values provided tangible information that allowed us to develop “rules-of-thumb” and contributed to our decisions regarding removal or retention of items with significant DIF. The first was based on the weighted area between the expected score curves (wABC), following an approach similar to Rudner, Getson, & Knight (1980) and Raju (1988). Expected score curves relate the level of the underlying trait (represented here as θ) to the average response, given the probability of response in each available category. For an item i with K response categories, scored k ={0,1, …, K-1},

$${\text{ES}}_i(\theta )={\displaystyle \sum _{k=0}^{K-1}k\cdot \text{P}(x_i=k|\theta }),$$

where $\text{P}(x_i=k|\theta )$ is the probability of response x _i = k, given θ. This probability depends on the item parameters, and biases across groups (i.e., DIF) result in different expected score curves. We used wABC to quantify these differences. The index was obtained by integrating the absolute difference between the expected score functions of the reference and focal groups over the distribution of the latent trait:

$${\text{wABC}}_i={\displaystyle \underset{\theta }{\int }|{\text{ES}}_i^{(F)}(\theta )-{\text{ES}}_i^{(R)}(\theta )|g^{(R+F)}(\theta )d\theta .}$$

We approximated the integral by computing differences in expected score at discrete values of θ. The latent trait distribution, g ^{(R + F)}(θ), was the density of the mixed normal distributions of the reference and focal groups, with the mixing proportions based on the observed sizes of the groups being compared.

As a second index of DIF severity, we calculated the average differences in the expected a posteriori (EAP) scores for individual items, given the observed response category frequencies and the differences between the item parameter estimates in the reference and focal groups (dEAP). First, we obtained an EAP score for each response category by multiplying the category response likelihood by a standard normal prior (such that differences in EAP scores could be attributed entirely to the differences in estimated item parameters). We then calculated an overall difference in EAP, weighting the individual (within category) differences by the observed proportion of respondents within the category across both the reference and focal groups:

$${\text{dEAP}}_i={\displaystyle \sum _{k=0}^{K-1}{P}_{\text{obs}}(x_i=k)({\text{EAP}}_{ik}^{(R)}-{\text{EAP}}_{ik}^{(F)}}).$$

We examined the plotted expected item score functions and the wABC and dEAP indices for all comparisons demonstrating significant DIF. Decisions to retain or exclude items for the final item banks were based on consideration of all available information. In general, wABC values above 0.3 were deemed to represent possibly problematic DIF and were examined further for potential item bias. In general, however, most items removed for DIF had wABC values greater than 0.4. Items retained following these DIF analyses comprised the final item banks.

Illustrative Example

The features of our DIF evaluation are illustrated in Figure 1. Figure 1 shows three items from the nondaily smoker nicotine dependence domain. The first row of Figure 1 shows the category response curves, which produce the expected score functions in the second row. The wABC values, based on the area between the expected score curve, are also shown in the panels in row 2. The remaining rows of Figure 1 show the likelihood density curves for responses in each of the five categories, obtained by multiplying the category response curves (in row 1) by a standard normal prior distribution. These curves, along with the observed proportions of respondents in each category, serve as the basis for the expected dEAP scores resulting from differences in the item parameters.

Figure 1.

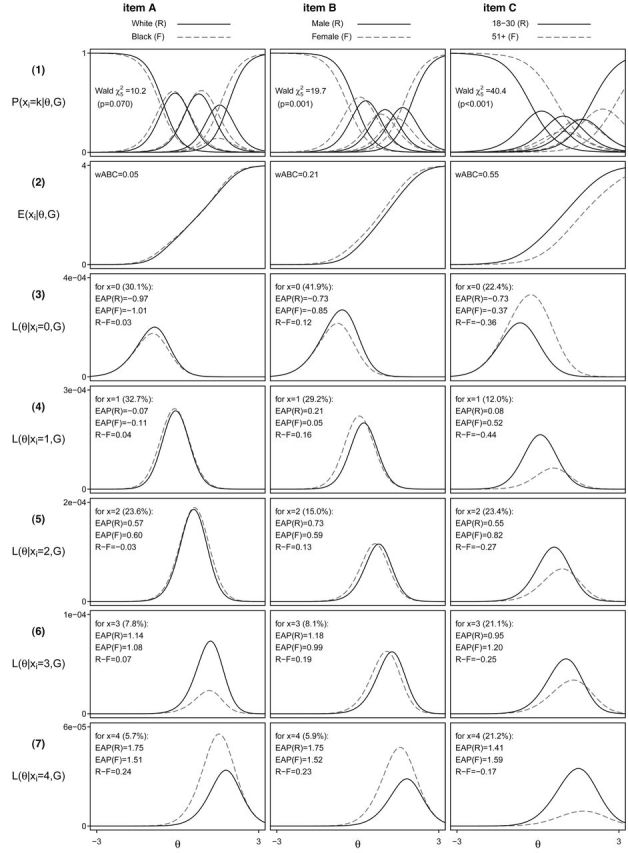
Analysis of three differential item functioning candidate items. Illustrative results for three items belong to the nicotine dependence domain. Separate parameter estimates were obtained for reference and focal group in the nondaily smoker sample. The Wald χ ² (shown in row 1 with the category response curves) is a test of equality for these estimates across the groups. wABC is the weighted area between the expected score curves (row 2). Posterior likelihoods (rows 3–7) were obtained for each response category (xi = 0,1,2,3,4) by multiplying the appropriate category response curve with a standard normal prior. The percentages of respondents in each category (combining the reference and focal groups) are shown, along with the expected a posteriori (EAP) scores.

For the first item (left column), the expected score functions for Black and White nondaily smokers are shown. Consistent with the nearly overlapping expected score functions for these groups, the Wald test was not significant (p =.07), and the item was thus retained. For the second and third items (middle and right columns, respectively), the DIF comparisons are between male and females and between the youngest (18–30) and the oldest (51+) age groups, respectively. For both of these items, the Wald tests indicated significant differences in the item parameters for these two groups (p < .001 for both comparisons). Despite this result, it appears that these differences produce much greater divergence for the third item than for the second. In fact, on the basis of the nearly coincident expected score curves, and wABC and dEAP measures, we might be quite willing to include the second item in the final item bank, despite statistically significant DIF. In contrast, the rather large shift in the response curves for the third item (and consequently the large values in the severity indices) would support the exclusion of this item.

Item Bank Calibration

Having finalized the composition of the banks, the next step was to calibrate the items with IRT modeling. Up until this point, the daily and nondaily samples had been treated separately. This resulted in the development of two item banks for each domain, with some differences in item content for daily and nondaily smokers. Despite the potential qualitative differences in these groups, it is still desirable to establish a basis for linking the scales across the daily and nondaily banks. To accomplish this, we performed concurrent calibrations of the item banks for the two smoker groups through a nonequivalent anchor test design (Dorans, 2007).

Concurrent calibration required the identification of items with equivalent functioning for both smoker groups to serve as anchor items. Thus, within each domain, we tested the common items from the daily and nondaily item banks (i.e., those items appearing in both banks) for DIF following an approach similar to that used for the demographic group DIF analyses described above. To be conservative, items with wABC values greater than 0.25 were allowed to vary across groups in the final calibrations, whereas all other common items were treated as anchors (with values constrained to be equal across the daily and nondaily groups). In these analyses and in the final calibration, daily smokers were treated as a reference group (with an assumed standard normal distribution). The final calibration models, thus, provided estimates of item parameters for all the items in each item bank, as well as estimates of the domain means and variances for the nondaily smoker group. These estimates are presented in subsequent articles in this volume.

Development, Scoring, and Evaluation of Short Forms

Given the calibrated item banks, researchers could assemble and score tests using any combination of items. However, in some clinical and research settings, it is far more practical to use a predetermined set of items that can be administered to all respondents. Ideally, this set of items would be substantially smaller than the full item bank, yet preserve (as much as possible) the conceptual breadth of the domain and provide good measurement precision across the distribution of potential respondents. In this section, we describe the methods we used to (a) identify such short form assessments for each of the six smoking domains, (b) score the selected short forms, and (c) evaluate the performance of the short forms, relative to the full item banks.

Short Form Selection

Within each smoking domain, forms of various lengths were considered. Our goal was to create forms that could be administered to any smoker, regardless of daily or nondaily status. Accordingly, only those items that were used as anchors in the item calibration were considered for inclusion. For a given domain, then, the possible short forms consisted of all unique combinations of anchor items. The minimum short form length we considered was four items, and the maximum length was equal to the number of anchor items in the domain. Without any restrictions, the total number of possible forms is generally rather large, and we are once again faced with a difficult decision-making process. To inform our decisions concerning the number and content of items comprising the short form for each bank, we first applied three criteria to reduce the number of short forms under consideration: (a) balance in the item format (i.e., frequency vs. quantity), (b) balance in item content, and (c) preference based on content expert ratings.

Across all item banks, two different sets of response labels were used. One set of labels related to frequency (never, rarely, etc.) and another related to amount (not at all, a little bit, etc.). The goal of the first criterion was to avoid selecting a short form with any unnecessary and sudden switch in the response category labeling across items. Thus, we eliminated candidate forms in which both sets of response labels were used, but one response set was used for only a single item (e.g., three frequency items and one amount item in a four-item short form).

The second criterion required that the short forms be balanced in item content. Balance was defined with respect to the item clusters identified previously in the exploratory item factor analyses and modeled in the confirmatory item bifactor models. Based on the number of clusters and the number of items identified within each cluster, we specified for each form length a minimum and maximum number of items allowed for each cluster. This allowed us to eliminate from consideration any candidate forms that did not reflect the conceptual breadth of the full item bank. For example, forms comprised entirely of items from a single cluster were excluded from consideration.

The third criterion gave preference to forms that included items favored by content experts. We asked three experts in smoking research to review the anchor items within each domain and nominate items that should be included in a short form for the domain (the number of items they were asked to select from each domain ranged from 4 to 8, depending on the total number of anchor items). Forms that failed to include items identified by multiple experts were eliminated. Among the expertise brought by these reviewers was knowledge of previous qualitative analyses of test items (see Edelen et al., 2012) and feedback from translators regarding items that could potentially prove difficult to translate in future studies, in addition to their experience with existing instruments and understanding of the domain definitions.

With the set of candidate short forms thus reduced, we next considered the psychometric properties of each candidate short form. Marginal reliability estimates were compared across the various short form lengths for each domain to identify test lengths for each domain that would allow for reasonable measurement precision while still capturing much of the conceptual breadth of the original item banks. The guiding questions in selecting these short form lengths were the following: Would the addition of one or more items produce a meaningful gain in reliability or in conceptual breadth? Could a shorter form be constructed that would provide scores with nearly the same reliability and without much loss in breadth?

Finally, we compared the test information curves (an indication of score precision) of the candidate forms to a target information function corresponding to a score reliability of 0.80 for respondents up to three SDs above and below the daily smoker population mean. This target favored item combinations that provided good measurement precision across a broad range of scores (and not only at the center of the distribution, for example). For each candidate form, we calculated a discrepancy measure d, which is a weighted sum of the difference between the estimated test information function and the target. Only test information levels below the target contributed to the discrepancy measure (i.e., forms were not penalized for exceeding the target level of test information). For test form f,

$$d_f={\displaystyle \underset{-3}{\overset{3}{\int }}\max [{(0.2{\sigma }^2{}_{D+\text{ND}})}^{-1}}-I_f(\theta ),0]g^{(D+\text{ND})}(\theta )d\theta ,$$

where ${(0.2{\sigma }^2{}_{D+\text{\hspace{0.17em}ND}})}^{-1}$ is the target information function for marginal reliability of 0.8, given the variance of the combined population of daily and nondaily smokers, ${\sigma }^2{}_{D+\text{\hspace{0.17em}ND}}$. Candidate short forms of the selected form length were ranked according to the discrepancy measure. For each item bank, the 10 highest ranking forms (those with the smallest discrepancy values) were presented to content experts for review (differences in the discrepancy measure and in marginal reliability were generally negligible). The content experts selected a single form from this group of candidates.

The results of our process of short form selection are shown in Table 3. As described previously, we considered all possible combinations of anchor items (those items both present and found to function equivalently in the daily and nondaily item banks). As seen in the first row of Table 3, the total number of possible forms of any given length (see rows labeled “Unrestricted”) is generally quite large. Applying the selection criteria related to content coverage, scale balance, and expert judgments resulted in a much reduced set of candidates. We used estimates of test information and marginal reliability to settle on a single form for each of the six domains.

Table 3.

Possible Smoking Domain Short Forms With and Without Restrictions

	4 Items		5 Items		6 Items		7 Items		8 Items
	No.	(Rel.)	No.	(Rel.)	No.	(Rel.)	No.	(Rel.)	No.	(Rel.)
Nicotine Dependence (20 common items)
Unrestricted	4845	(.900)	15504	(.915)	38760	(.926)	77520	(.934)	125970	(.940)
Reduced set	790	(.896)	3280	(.911)	4562	(.923)	7206	(.930)	14093	(.937)
Recommended forms	1	(.811)							1	(.905)
Emotional and Sensory Expectancies (15 common items)
Unrestricted	1365	(.860)	3003	(.883)	5005	(.897)	6435	(.907)	6435	(.916)
Reduced set	85	(.844)	244	(.872)	155	(.887)	120	(.899)	267	(.910)
Recommended form					1	(.861)
Coping Expectancies (11 common items)
Unrestricted	330	(.898)	462	(.913)	462	(.923)	330	(.931)	165	(.936)
Reduced set	26	(.883)	56	(.904)	79	(.918)	43	(.928)	17	(.934)
Recommended form	1	(.854)
Social Motivations (7 common items)
Unrestricted	35	(.813)	21	(.833)	7	(.842)	1	(.845)	0	(—)
Reduced set	9	(.813)	4	(.833)	2	(.842)	1	(.845)	0	(—)
Recommended form	1	(.812)
Psychosocial Expectancies (14 common items)
Unrestricted	1001	(.836)	2002	(.860)	3003	(.878)	3432	(.891)	3003	(.901)
Reduced set	43	(.826)	44	(.849)	133	(.870)	175	(.884)	67	(.895)
Recommended form					1	(.852)
Health Expectancies (13 common items)
Unrestricted	495	(.867)	792	(.887)	924	(.899)	792	(.908)	495	(.915)
Reduced set	84	(.857)	20	(.869)	290	(.895)	158	(.903)	80	(.909)
Recommended form					1	(.873)

Note. Values in parentheses indicate the highest marginal reliability (for EAP score estimates based on full response pattern) attained among a set of candidate forms.

Comparisons of the marginal reliabilities of the final short forms to the maximum reliabilities reported in the rows above (“Reduced set” or “Unrestricted”) emphasize the fact that our selection procedure did not select forms that were optimal in terms of marginal reliability (although the differences were generally quite small). This is to be expected, as selection based on marginal reliability alone would tend to favor forms that were narrow in content and with test information peaked near the mean of the population distribution. Instead, the procedure sought to identify those forms that displayed good measurement precision for a broad range of trait levels adequately represented the conceptual breadth of the domains and were acceptable in the view of content experts. We regard the balance of content and technical quality as a more desirable approach to short form selection than one focusing on reliability alone. The psychometric properties of the short forms selected for our six item banks, provided in detail in other articles in this volume, are excellent.

Short Form Scoring and Evaluation of Short Form Performance

Following standard PROMIS procedures, we obtained short form score estimates based on the sum of the coded responses over the items in the short form, rather than using the full response pattern as in traditional IRT scoring. The minor loss in precision from this method may be an acceptable cost given the substantial gain in the ease of scoring. We used the Lord and Wingersky (1984) algorithm implemented in both IRTPRO (Cai et al., 2011) and flexMIRT (Cai, 2012) to generate summed score to EAP conversions. Following PROMIS conventions (see Reeve et al., 2007), EAP scores were placed on a T-score metric. Daily smokers continued to serve as the reference population with M of 50 and SD of 10 for each domain. Subsequent articles in this volume present results comparing the marginal reliabilities of these short forms along with item bank and short form correlations.

Computerized Adaptive Test Administration of Item Banks

In computerized adaptive test (CAT) applications, items are selected based on what is already known about the respondent based on their responses to earlier items. Because items are tailored to the particular respondent, adaptive tests are capable of characterizing a person’s standing on the latent construct with enhanced efficiency, often achieving high levels of score precision with many fewer items than a fixed-length test (e.g., Gibbons et al., 2008).

Adaptive administration of the smoking item banks was investigated through a simulation study using the Firestar program (Choi, 2009). Item responses were simulated for 20,000 daily and 20,000 nondaily smokers in each domain. We investigated two methods of item selection (see Choi & Swartz, 2009). The first, termed maximum Fisher information, identifies the item with greatest information at the current score estimate. The second method, minimum expected posterior variance, requires calculation of the expected item responses (given the current score estimate) for all candidate items. These expected responses are then used to obtain the expected posterior distribution for each candidate. The item with the smallest expected posterior variance is selected and administered to the respondent.

For each item bank and sample of simulated respondents, we conducted multiple simulations in which the test was terminated if either the SE of measurement was less than some designated threshold or a maximum number of items was reached. SE thresholds of 2, 3, 4, and 5 (on the T-score metric) were examined, and the maximum number of items was varied from 1 to the total number of items in the bank.

For each condition, we examined the average number of items administered, the proportion of examinees who were administered the maximum number of items, marginal reliability, and the correlations of the CAT-based score estimates with the generating scores and scores based on the full bank.

Table 4 illustrates the progression of three simulated respondents through an adaptive test. Here, the items are selected from the daily smoker Nicotine Dependence item bank, and the maximum number of items to be administered is 10. Responses to this first item are used to update the score estimates, the SEs of measurement, and to identify the next item to administer. In the example shown, the sequence of item selection, administration, and score updating is continued until either the SE of measurement is less than 3 (which happens after three items for the first respondent and after six items for the second respondent) or a total of 10 items have been administered (which is the case for the third respondent). The full item bank EAP scores and SEs of measurement are shown in the final row of Table 4 for comparison with the CAT-based estimates and generating values.

Table 4.

Illustration of an Adaptive Test for Three Simulated Respondents (Nicotine Dependence Item Bank for Daily Smokers)

Total no. items administered	Simulated respondent A (true T = 50.3)				Simulated respondent B (true T = 45.8)				Simulated respondent C (true T = 79.2)
	Items administered	T	SE(T)	Next item	Items administered	T	SE(T)	Next item	Items administered	T	SE(T)	Next item
0		50.0	10.0	4		50.0	10.0	4		50.0	10.0	4
1	4	48.2	4.5	2	4	61.3	6.3	7	4	61.3	6.3	7
2	4,2	49.1	3.4	6	4,7	50.4	6.1	6	4,7	66.1	5.5	8
3	4,2,6	48.5	2.9	None	4,7,6	44.1	4.7	2	4,7,8	68.3	5.3	15
4					4,7,6,2	43.8	3.5	1	4,7,8,15	69.7	5.1	10
5					4,7,6,2,1	45.2	3.1	3	4,7,8,15,10	68.6	4.2	18
6					4,7,6,2,1,3	45.0	2.7	None	4,7,8,15,10,18	69.1	4.1	16
7									4,7,8,15,10,18,16	67.7	3.6	19
8									4,7,8,15,10,18,16,19	68.1	3.5	1
9									4,7,8,15,10,18,16,19,1	68.4	3.5	24
10									4,7,8,15,10,18,16,19,1,24	69.0	3.5	None
27	1–27 (all items)	51.0	1.6		1–27 (all items)	44.6	1.6		1–27 (all items)	71.8	3.2

Across the various adaptive test conditions, the CAT-based scores were correlated with the generating scores nearly as well as the scores obtained using the full item banks.

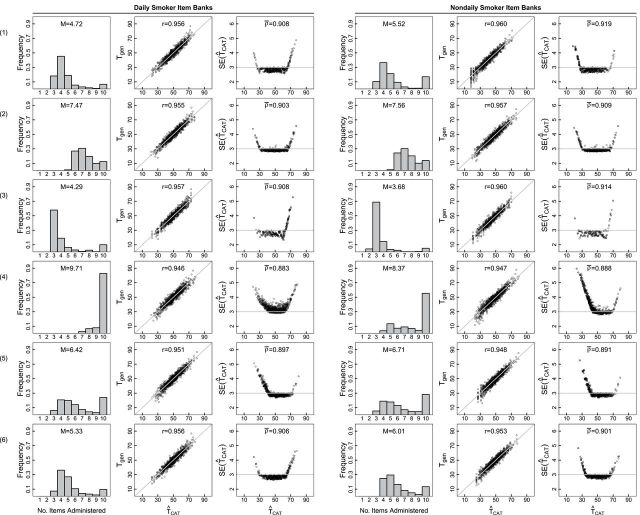
Figure 2 presents illustrative results for the simulated tests with a 10-item maximum and 3.0 SE target. Three panels are shown for each item bank: (a) a histogram showing the proportions of respondents administered 1–10 items, (b) a comparison of score estimates from the CAT simulation and from the full bank, and (c) the SEs of measurement plotted against the CAT-based scores. For most domains, only a small proportion of respondents receive the maximum number of items. The exceptions are the psychosocial expectancies and social motivations domains. These were the domains with the lowest average marginal item information, so the need for a greater number of items was expected.

Figure 2.

Selected results: computerized adaptive test simulations. Three panels are presented for each domain (1–6) and group (daily or nondaily). The first panel displays the proportions of respondents receiving 0–10 items. The middle panel compares the CAT-based scores to the true or data-generating values. The final panel shows the SEs of measurement plotted against the CAT-based score estimate. Domains: (1) nicotine dependence, (2) emotional and sensory expectancies, (3) coping expectancies, (4) social motivations, (5) psychosocial expectancies, and (6) health expectancies.

DISCUSSION

In this study, we have described the methods used in the development and evaluation of item banks for six self-reported smoking domains. Additional articles in this volume discuss the process and results for each domain in turn. The procedures used across all domains included the use of exploratory and confirmatory IRT models to characterize the underlying dimensionality of item sets. The results of these analyses were used to select, for each item bank, a subset of items that was largely unidimensional. The items in these subsets were then evaluated for bias (DIF) across several respondent groups, and items with severe bias were excluded. Once the item banks were finalized, we conducted final calibrations, utilizing anchoring items to link the scales of daily and nondaily smokers. The parameters obtained from these final calibrations were used in the development of short forms and in the simulated adaptive tests. Simulation studies demonstrated that short forms and CAT administration may allow for particularly efficient measurement of the six smoking domains; scores obtained with even a handful of carefully selected items produce scores that are highly similar to those obtained using all the items in each item bank.

Innovative Features of the Approach

Although the approach we took shares much in common with previous item banking efforts, there were some unique steps in our analyses that are important to highlight. First, the initial item selection, conducted with the goal of minimizing local dependence, followed a rather extensive examination of the dimensionality of each item set. This examination combined in a novel way high-dimensional exploratory item factor analysis results with limited-information goodness-of-fit indices, which guided the specification of item bifactor models. The I-ECV statistics based on those confirmatory bifactor models provided quantitative information about multidimensionality that informed item selection.

In our evaluation of DIF, we utilized measures of severity to complement the results of the Wald χ ² DIF tests. This approach is useful because the statistical tests for DIF are quite powerful, identifying some differences in item functioning with no practical impact. The wABC index is analogous to other area-based measures (Raju,1988; Rudner, Getson, & Knight, 1980) but extends this general approach to the sorts of polytomous items that are commonly used in assessments of patient-reported outcomes. To our knowledge, the dEAP index is also novel, providing a measure of expected change in score estimates due to DIF. A helpful feature of the DIF severity indices is that—unlike the Wald χ ² DIF tests—they are not influenced by sample size. Thus, values of these indices from the daily and nondaily samples could be compared and interpreted in the same ways.

In assembling short forms, the number of items under consideration was small enough that it was feasible to consider every possible combination and to evaluate each form with respect to content representation, balance in response scale, and the item preferences of content experts (with attention to test information only after these criteria were applied). This sort of census approach to form assembly may be appropriate when measuring patient-reported outcomes, given that item banks are limited in size, experts may not view those items as interchangeable, and there is little concern about test security.

Study Limitations

Some limitations and caveats regarding this approach should be noted. First, the performance of both short forms and CAT were evaluated using simulated respondents. Thus, simulated item responses followed the data-generating model perfectly. The reason for using simulated data is that complete response data were not available for item banks (and even short forms), due to the randomized blocks design used in administering the smoking items. This prevented direct comparisons of scores obtained from full bank responses and those based on CAT or short form summed scores. Thus, it is unclear how closely results in practice will resemble those presented based on simulation.

Our evaluation of CAT performance focused on the termination criteria, based on target SEs of measurement with varying constraints on the maximum test length. Of course, additional design manipulations are possible, including other-item selection methods, interim and final score estimators, and other termination rules. Constraints might also be placed on item content over the course of an adaptive test (see, e.g., Stocking & Swanson, 1993; van der Linden & Reese, 1998). Content balance was explicitly considered in our construction of short forms but ignored in our CAT simulations.

It should also be noted that our item bank calibrations and CAT simulations were based on unidimensional IRT models only. Scores based on multidimensional models might perhaps be estimated with substantially improved precision if two or more domains were considered simultaneously due to the correlations between domains (e.g., Cai, 2010a). A potentially useful variation on the administration of adaptive tests for the smoking domains would be the application of multidimensional IRT models. In this context, we still assume unidimensionality within each item bank. However, when an item from one bank is administered, that item provides information not only about the domain to which it belongs; some information is gained about any other correlated domain (Segall, 2010). Thus, in studies in which multiple correlated domains are to be measured, the efficiency of the adaptive test might be further enhanced.

The data used in this study were obtained through an internet survey panel via a self-administered survey. It is possible that item responses would differ if surveys were administered in another format or setting.

The development of separate item banks in each domain for daily and nondaily smokers adds some amount of complexity to the use of the banks. As noted previously, this approach was taken due to previous research suggesting that the constructs to be measured might differ qualitatively across these groups. Indeed, our item selection process yielded banks that differed in item content, and many items included in both item banks were found to function differently in the two groups. The separate analyses, thus, seem to accommodate the reality of such differences in these two groups. The particular smoker groups we used (i.e., designating as daily smokers those who smoked at least 28 of the past 30 days and nondaily smokers those smoking 27 or fewer days) have some basis in previous smoking research, although alternative definitions might have been used and would likely have led to differences in item bank content (as well as item parameter estimates and group parameters used in scoring). Thus, in future applications of the item banks (e.g., in CAT administrations), the same smoker group definitions should be used. That said, the linking of the scales across the item banks for the two groups should minimize the consequences of using alternative definitions (e.g., administering the items from the nondaily item bank to individuals who smoked 28 or 29 of the past 30 days) and the influence of misclassification due to incorrect self-reporting of days smoked. Finally, it should be noted that the fixed short forms may be administered and scored without differentiating between smoker groups.

Planned Next Steps

Studies are currently underway to examine the extent to which the performance of the short forms and the progression of real respondents through adaptive tests resemble the results obtained here using simulated examinees. These studies will also provide opportunities to directly examine relationships between scores on the six smoking domains and other variables of interest.

Planned studies also include administration of the smoking short forms to daily and nondaily smokers recruited from a community setting. This study will include random assignment to paper–pencil or computerized administration to enable comparison of modes and evaluate the smoking item banks’ performance in a community sample. The study will also include a test–retest substudy in which subjects will be administered the smoking short forms twice over a brief interval (about 1 week), thus providing estimates of the stability of responses over time. This is an important consideration since our current estimates of test information and marginal reliability depend only on internal consistency (the stability of responses over many items). Thus, the planned study will offer a more complete perspective on how the item banks are likely to perform in practice.

Of course, a goal of the PROMIS Smoking Initiative is the dissemination of standardized assessments to be used in clinical and research settings. To that end, a free online tool for administering adaptive tests has been developed and is maintained by the initiative (http://www.assessmentcenter.net). The smoking item banks and short forms developed in this study are now available for public use via the project Web site (http://www.rand.org/health/projects/promis-smoking-initiative.html) as well as through inclusion in the larger PROMIS item library, allowing researchers to measure the six smoking domains using tools appropriate to the needs of their particular study—fixed short forms, adaptive tests, or alternative forms assembled by the researchers. Thus, it is hoped that others will utilize these resources and contribute to the evaluation of the smoking item banks.

FUNDING

This work was supported by the National Institute on Drug Abuse (R01DA026943 to MOE). Additionally, MH was supported by the Institute for Education Sciences with a predoctoral training grant (R305B080016), and LC was supported by the National Institute on Drug Abuse (R01DA030466).

DECLARATION OF INTERESTS

None declared.