Learning to Rank Atlases for Multiple-Atlas Segmentation

Abstract

Recently, multiple-atlas segmentation (MAS) has achieved a great success in the medical imaging area. The key assumption is that multiple atlases have greater chances of correctly labeling a target image than a single atlas. However, the problem of atlas selection still remains unexplored. Traditionally, image similarity is used to select a set of atlases. Unfortunately, this heuristic criterion is not necessarily related to the final segmentation performance. To solve this seemingly simple but critical problem, we propose a learning-based atlas selection method to pick up the best atlases that would lead to a more accurate segmentation. Our main idea is to learn the relationship between the pairwise appearance of observed instances (i.e., a pair of atlas and target images) and their final labeling performance (e.g., using the Dice ratio). In this way, we select the best atlases based on their expected labeling accuracy. Our atlas selection method is general enough to be integrated with any existing MAS method. We show the advantages of our atlas selection method in an extensive experimental evaluation in the ADNI, SATA, IXI, and LONI LPBA40 datasets. As shown in the experiments, our method can boost the performance of three widely used MAS methods, outperforming other learning-based and image-similarity-based atlas selection methods.

I. Introduction

With the development of modern imaging techniques, imaging-based studies become more and more important in the medical science area. For example, many neuroscience and clinical studies have investigated the shapes of certain structures, such as hippocampus, for their close relation to certain brain diseases, such as Alzheimer's disease [1–6]. However, manual delineation of the structures of interest is a tedious task, especially for the studies involving large datasets. Therefore, the development of automatic segmentation tools is critical to facilitate the current medical imaging studies. A technique which has recently gained popularity is called multiple-atlas segmentation (MAS) [7–11]. It consists in segmenting an unknown target image by transferring the labels from a population of annotated exemplars (i.e., the atlases), through image registration. In the atlas-based segmentation, we assume that, if two anatomical structures have similar location and show similar intensity appearance, they should bear similar label (or tissue type). Since a population of atlases often encompasses large anatomical variability, MAS has a greater chance of accurately labeling a new target image with appropriate atlases than the use of only a single atlas.

Two main steps are involved in MAS, namely, image registration and label fusion. In the step of image registration, each atlas is non-rigidly warped onto the target image with non-linear registration methods [12–21]. Then, in the step of label fusion, the labels from the registered atlases are transferred onto the target image for producing the final result. A critical step in label fusion is how to measure the fidelity of each atlas or atlas patch in labeling the target image. The simplest strategy, known as majority voting (MV), treats each atlas equally by assigning each target location with the label appearing most frequently [22, 23]. More advanced methods use the appearance information of local image patches to guide the label fusion. For example, the local-weighted voting strategy (LWV) uses patch-wise similarity between the target and each registered atlas to determine the voting weight [8]. Moreover, in order to alleviate the possible registration errors, the non-local weighted voting strategy (NLWV) has also been proposed to examine not only the same-location patches but also the neighboring patches, thus improving both accuracy and robustness of the labeling results [24, 25].

Essentially, MAS methods leverage the information from multiple atlases to accommodate the possible complex anatomical variations in the target images. However, their performances highly depend on the set of atlases selected for labeling each target image, since the inclusion of misleading atlases will undermine the labeling performance. Most atlas selection methods employ image similarity measures, such as mutual information (MI) [26], to select suitable atlases. For example, in [7], it is shown that the use of atlases selected with the normalized MI leads to improved segmentation performance, compared to the random selection of atlases. In [27], authors selected the atlases based on the normalized MI between the regions of interest (ROIs), containing the structure to be segmented. More advanced methods used the distance in the manifold, instead of the original Euclidean space, to select the most similar atlases [11, 28]. However, these manifold-distance-based methods simply used the pairwise image similarity to learn the manifolds.

All of the aforementioned atlas selection methods have two limitations. Firstly, their selection accuracy highly depends on the performance of the non-rigid registration algorithm in aligning the atlases to the target image. Although we eventually select only a small set of best atlases for labeling of target image, we have to non-rigidly register all the atlases to the target image for atlas selection, which is very time-consuming. Secondly, image similarity (e.g., mutual information) is a surrogate and indirect measure for atlas selection, which is not closely related to the final labeling performance for the target image.

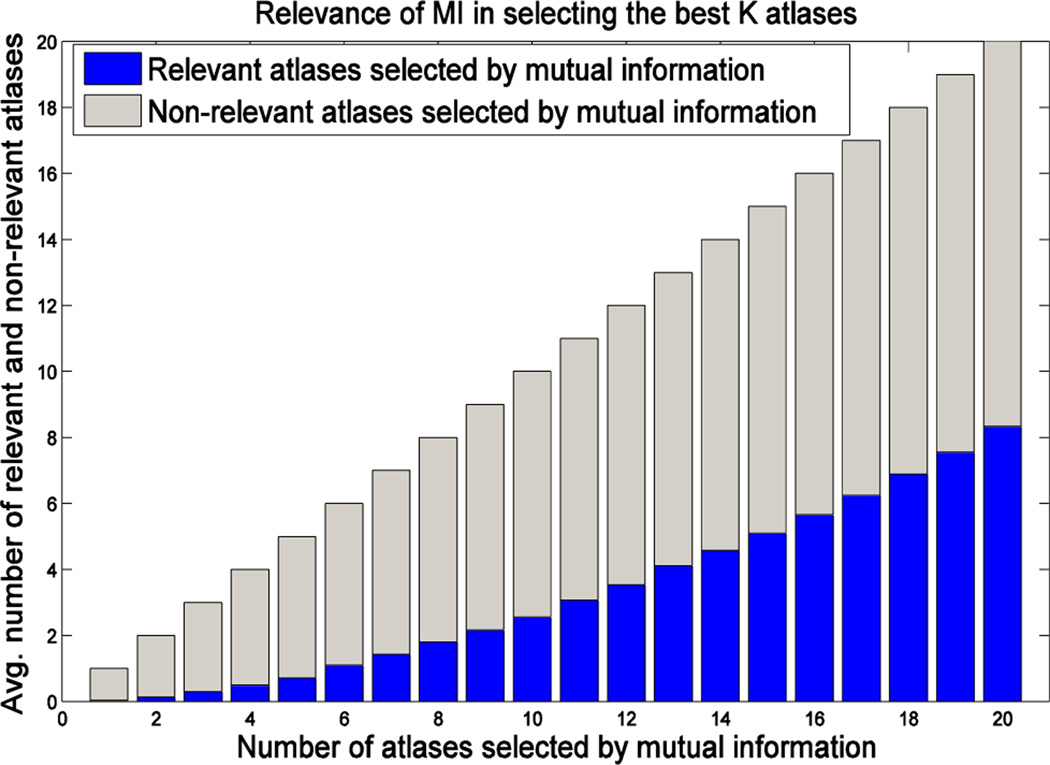
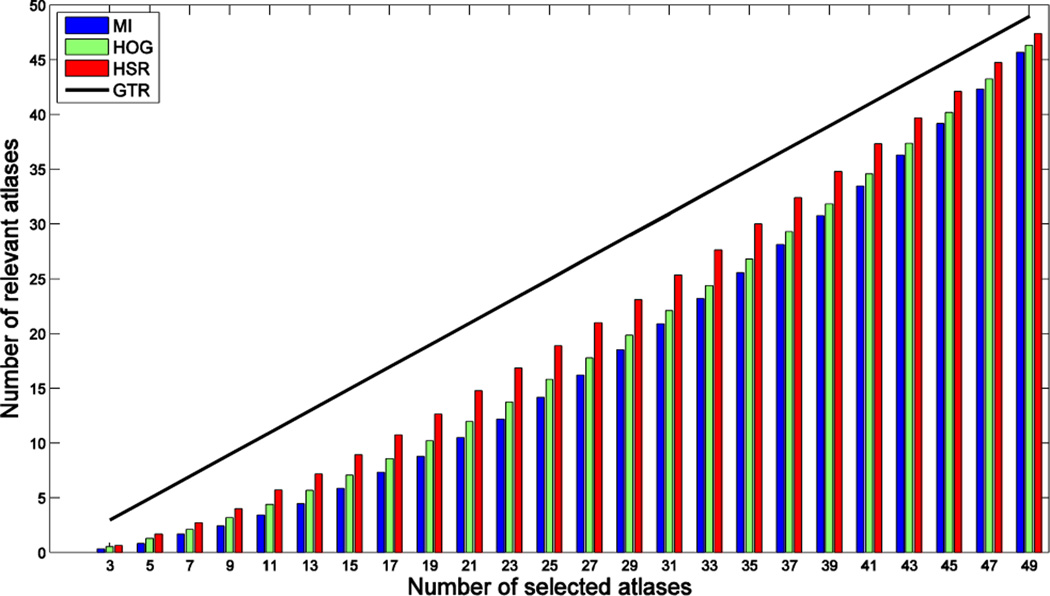
To better explain the second limitation, we examine the relevance of the atlases selected by mutual information (MI) based image similarity in labeling the target image. Specifically, we measure the number of common atlases included in the set of top K atlases selected by MI and the set of K atlases having the highest label overlap ratio w.r.t. the target labels after non-linear warping to the target (by assuming that we know the ground-truth target labels). If the number of common atlases is equal to K, it means that MI perfectly selects the K best performing atlases. Fig. 1 shows the average number of relevant (blue) and non-relevant (gray) atlases selected by MI for labeling the left and right hippocampi, where 65 images are used as atlases to label one target image. The different bars in the plot show the selection results for different numbers of selected atlases (K). As we can see from the figure, atlases selected by MI always contain less than 50% of the best performing atlases, especially when using small sets of atlases.

Fig. 1.

Number of relevant (blue) and non-relevant (gray) atlases selected by MI. Each bar shows the average results of 132 leave-one-out experiments in labeling the left and right hippocampi from 66 subjects. Specifically, at each leave-one-out experiment, we used one subject as the target subject and the remaining 65 as the atlases. We compute the MI between the ROIs (containing hippocampus) in the target image and each linearly-aligned atlas for selecting the top K atlases. Each selected atlas is considered relevant for labeling the target subject if it is included in the set of top K atlases with the highest label overlap ratio (Dice ratio) after non-linear warping to the target subject.

To overcome the aforementioned limitations, we propose a supervised learning approach to explore the relationship between pairs of images (i.e., atlas and target images) and the relevance of each atlas in segmenting the target image. Our method needs only to linearly register the target image to the atlas space, thus avoiding the computationally demanding non-rigid registrations. Also, our method directly employs the segmentation performance, instead of simple image similarity (e.g. mutual information), as a criterion for atlas selection.

In a similar line of work, Konukoglu et al. [29] presented Neighborhood Approximation Forests (NAF), a supervised learning method that use random forests to predict the neighborhood of an image under arbitrary distance metrics. The most related application to the task of atlas selection presented in their work is the prediction of the most similar images in terms of the amount of non-rigid deformation. Although the relationship between the amount of non-rigid deformation and segmentation performance is not shown in their work, their method can be easily adapted for the task of atlas selection by using the segmentation performance as similarity metric, as done by our method. NAF uses a training set, composed of the features extracted from each individual image, to learn the model. This approach suffers from the small-sample-size problem when applied to the atlas selection task due to the limited number of atlases available in the multiple-atlas segmentation datasets (typically ranging from N = 30 to N = 50 atlases). On the contrary, our approach alleviates this problem by focusing on triplets instead of individual atlases in the training set, where each triplet consists of a potential target image, a relevant atlas and a non-relevant atlas. Specifically, the final number of training samples becomes N × K × (N − K), where N is the number of atlases and K is the number of the desired best atlases.

We show the advantages of our proposed method compared to both learning-based and image similarity-based atlas selection methods after integrating them into the widely used label fusion methods majority voting [22, 23], local weighted voting [8], and non-local weighted voting [24, 25]. Validation is performed in the ADNI, SATA, IXI and LONI-LPBA40 databases.

The remainder of this paper is organized as follows. In Section II, we describe the proposed method. In Section III, we provide experimental results and comparisons. Finally, in Section IV, we give some concluding remarks.

II. Method

A. Overview

Assume that we have a set of atlases, composed of (1) intensity images A = {A_i, i ∈ I = {1, …, N}} and (2) their corresponding label images L = {L_i, i ∈ I = {1, …, N}}. Also, assume that all these atlases have been linearly aligned onto a common space with a certain population template. For each voxel x in the domain of a given atlas, x ∈ Ω_i, its intensity value can be denoted as A_i(x), while its label can be denoted as L_i(x) ∈ {0,1}, with L_i(x) = 1 indicating the presence of the structure of interest in the current voxel Our method can be extended to the case of multiple structures by applying it to each structure independently, as will be done in the experiments.

Given a target image T, the goal of MAS is to locate the expected structure in the target image T by transferring the labels from the aligned atlases onto the target image. This process often consists of two steps. First, spatial correspondence between each atlas and target image is obtained by a non-rigid registration algorithm [12–14]. In this way, we can obtain a set of registered atlases à = {Ã_i, i ∈ I}, along with a set of deformed label images L̃ = {L̃_i, i ∈ I}. Second, a label fusion procedure is performed to determine the label on each voxel of the target image by fusing the labels from all registered atlases L̃.

The accuracy of MAS largely depends on the ability of selecting suitable atlases, i.e., atlases that are anatomically similar to the target image. Therefore, atlas selection is a critical issue, which affects not only to the labeling accuracy, but also to the labeling speed. Although using a small subset of atlases can lead to faster labeling, it can potentially lead to a large inaccuracy since relevant information from other atlases may be left out. On the other hand, using a large subset of atlases can potentially increase the chance of including more relevant atlases at the expenses of including more ambiguous atlases and spending longer computational time. The most common atlas selection strategy consists in using an image similarity measurement such as mutual information (MI) [26] to select the K most similar atlases to the target image T. Although these image-similarity-based atlas selection methods perform significantly better than random atlas selection [7], the image similarity metric used is not directly related to the final labeling performance. Mathematically, given a target image T and a set of atlases (A, L), the whole process of MAS can be formulated as:

$$L_T=MAS(T;{\mathit{A}}_{S_T},{\mathit{L}}_{S_T})$$ (1)

where L_T is the resulting segmentation for the target image T, and (A_ST, L_ST) with selected index-set S_T ⊆ I, is the subset of selected atlases for segmenting the target image T.

Dice ratio (DR) is widely used to measure the degree of overlap between two segmentations, such as the resulting/expected segmentation L_T and the individual segmentation of each registered atlas L̃_i. It is defined as:

$$DR(L_T,{\tilde{L}}_i)=\frac{2\times vol(L_T\cap {\tilde{L}}_i)}{vol(L_T)+vol({\tilde{L}}_i)}$$ (2)

where vol(·) denotes volume. Suppose that we know the ground-truth label map for the target image, which we denote as $L_T^{*}$. We can use the Dice ratio between the ground-truth target labels and each registered atlas labels (i.e., DR ($L_T^{*}$, L̃_i)), to select the set of K best atlases for the given target image T, denoted as $S_T^{*}$, where the set of best atlases satisfies the following requirement:

$$DR(L_T^{*},{\tilde{L}}_i)>DR(L_T^{*},{\tilde{L}}_j),\forall i\in S_T^{*}\forall j\notin S_T^{*}$$ (3)

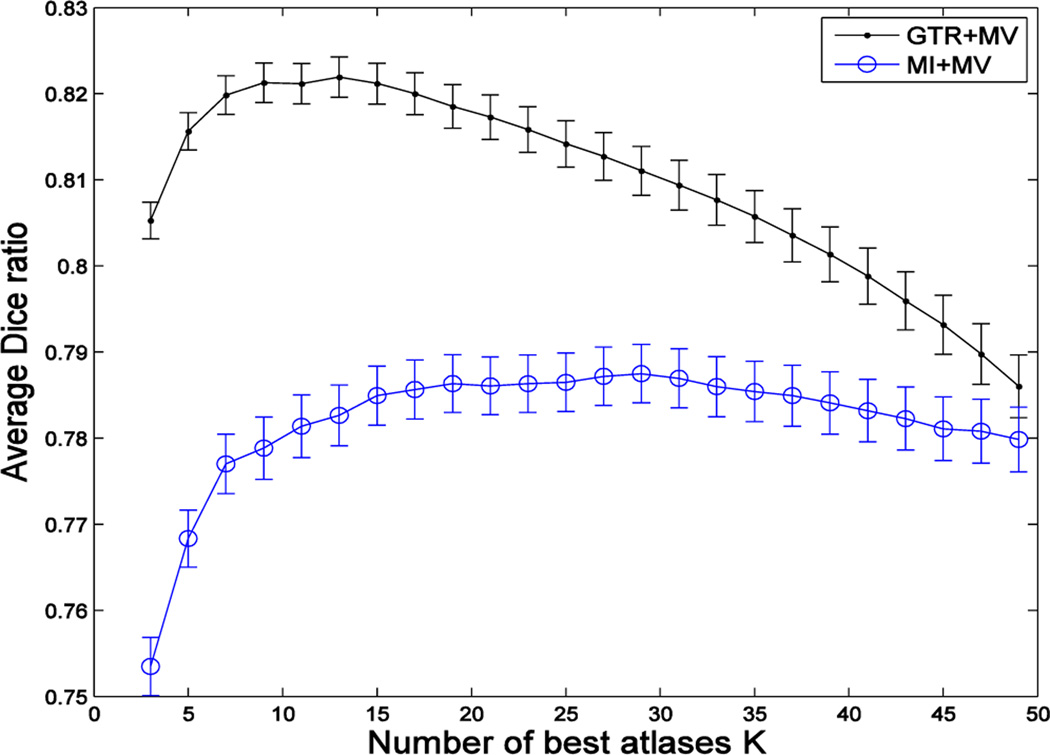
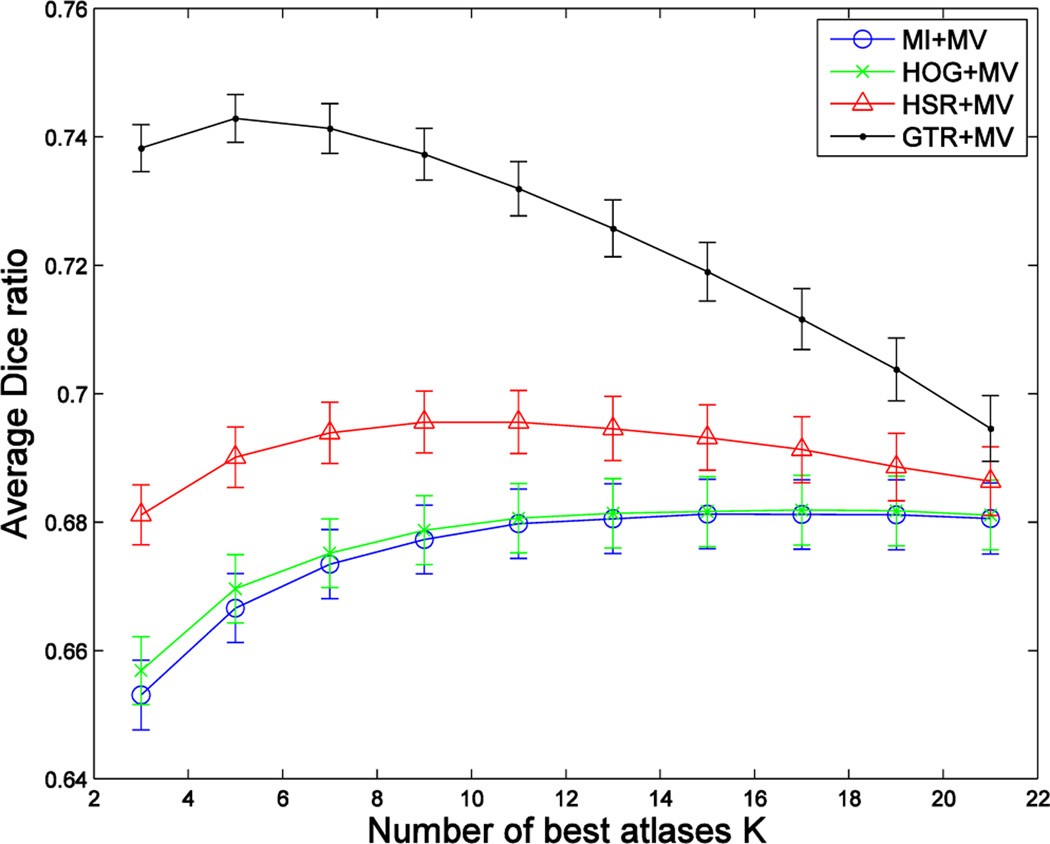
where the cardinality of the selected atlas set $S_T^{*}$ equals to K, i.e., $|S_T^{*}|=K$. Fig. 2 demonstrates the superiority of using the ground-truth Dice ratio (GTR), compared to mutual information (MI), for the task of selecting the best atlases for MAS, where the black and blue curves show the segmentation performances (assessed by the Dice ratio) with respect to the increase of the number of the best atlases selected by Equation (2) and mutual information, respectively. This figure shows a potentially large room for improvement of the atlas selection strategy targeted at Equation (2), compared to the widely-used, simple image-similarity-based atlas selection. Another interesting observation is that, for ground-truth DR-based selection, a small and accurate set of atlases leads to a considerably better segmentation performance than using all the atlases. This highlights the negative impact of including ambiguous atlases and motivates the importance of an accurate atlas selection.

Fig. 2.

Average segmentation accuracy of 66 images in the ADNI dataset, with respect to the use of an increasing number of atlases selected by using ground-truth Dice ratio (GTR) and mutual information (MI), respectively. Here, we show the results of applying the majority voting (MV) based label fusion for labeling the left and right hippocampi.

The scoring function proposed in Equation (3) presents two problems to be used for atlas selection in our method: (1) the target label map $L_T^{*}$ is unknown, and (2) the deformed atlas label map L̃_i is also unknown since one of our goals is to avoid warping atlases with the computationally-expensive non-rigid registration method before atlas selection.

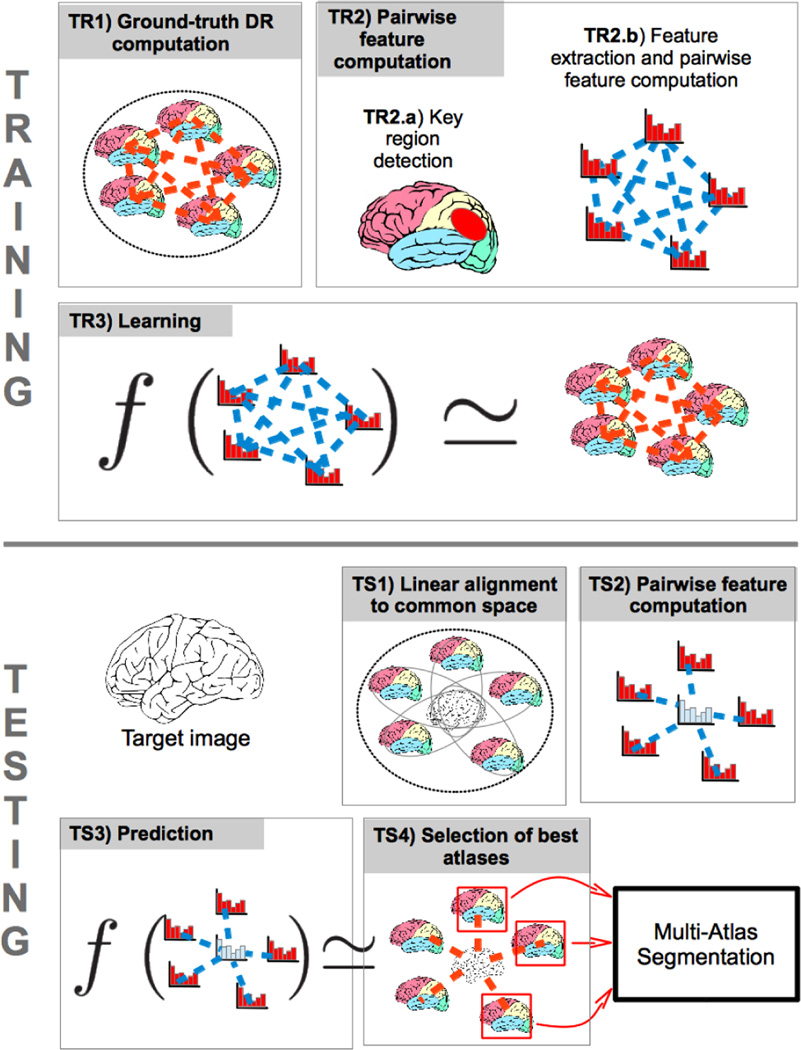
Our goal in this paper is to learn a scoring function f that can correlate the pairwise appearances of target image and each unregistered atlas image with the segmentation performance measured by Dice ratio. Fig. 3 provides an overview of our proposed method.

Fig. 3.

Overview of our proposed method. Training: TR1) computation of ground-truth Dice ratio between each pair of atlas label maps after non-rigid registration, TR2) computation of pairwise features from the key regions between each pair of atlas images after affine alignment, and TR3) learning of the relationship between pairwise features and ground-truth DR. Testing: TS1) affine alignment of the target image to the common space, TS2) computation of pairwise features between the target and all the atlas images, TS3) prediction of the segmentation performance by using the learned model, and TS4) selection of atlases with the highest scores for multiple-atlas segmentation.

In our proposed method, all atlases have been affinely aligned onto a common space, i.e., a population template. In the training stage, we first compute the ground-truth segmentation score between any pair of atlases, by non-rigidly aligning them to obtain the Dice ratio (DR) of their warped label maps using Equation (2) (shown as TR1 in Fig. 3). Next, for efficient representation, we identify a number of key regions in the entire image domain (TR2.a). Then, we extract HOG features (Histogram of Oriented Gradients) [30] to characterize the anatomical information in these key regions and further compute the pairwise features between each pair of atlas images (TR2.b). Finally, we can employ SVM-Rank [31] to learn the latent relationship between the pairwise HOG features and the ground-truth segmentation score (TR3), which will be detailed below. In the testing stage, we first affinely align the new target image to the common space (TS1). Next, we extract the selected HOG features from the key regions and compute the pairwise feature vectors between the new target image and each atlas (TS2). Finally, we evaluate the potential segmentation performance of each atlas by using the learned SVM-Rank model (TS3), and select the best atlases for MAS according to the obtained scores (TS4).

The main intuition behind our approach is to learn the relationships between affine registration errors (encoded in the pairwise HOG features) and the final segmentation performance (in terms of Dice ratio). Or, equivalently, we learn which affine registration errors are critical in determining the final segmentation performance after non-rigid registration. To make our learning approach tractable, we use a linear model for mapping the pairwise representations obtained by the feature extraction process to our final score f, as stated below:

$$f(T,A_i)={\overrightarrow{w}}^{\top }\Phi (T,A_i)$$ (4)

where Φ(·,·) is the vector of pairwise features derived from a pair of images (TR2 in Fig. 3) and w⃗ is the weighting vector modeling the relationship between the pairwise features and the ground-truth segmentation score (TR3 in Fig. 3). Each element in this weighting vector measures the importance of a particular pairwise feature in predicting the segmentation score.

In the next two subsections, we will describe the process of learning the weighting vector w⃗ and computing the pairwise features Φ(·,·), respectively. Table I shows a summary of the notation used in the rest of the paper.

TABLE I.

Summary of notation

Symbol	Description
(Ai, Li)	Intensity and label images of the i-th atlas
(Ãi, L̃i)	Intensity and label images of the i-th atlas after non-rigid warping to a particular target
(T, LT, $L_T^{*}$ )	Target intensity image, estimated label image (by MAS) and ground-truth label image, respectively.
I	Index-set of the N atlases
t	Index to denote the atlas acting as target image in the training set
K	Scalar denoting the number of selected atlases to be used for MAS
$S_t^{*}$	Set of indexes of the K best atlases for segmenting target image At, according to ground-truth
ST	Set of indexes of the K best atlases for segmenting target image T
f (·,·)	Scoring function that maps a pair of affinely registered images to their expected segmentation performance
w⃗	Weighting vector learned by SVM-Rank
θ⃗i	Vector with the HOG features extracted from i-th image in the training set
M	Scalar denoting the total number of features
Θ⃗k	Vector with the k-th pairwise feature from all atlas-target pairs in the training set
Ψ⃗	Vector with the ground-truth DR from all atlas-target pairs in the training set
Φ(·,·)	Compact vector of pairwise features from a pair of target and atlas images
m′	Scalar denoting the size of the compact set of features

B. Learning the Relationships Between Pairwise Features and Segmentation Score

Here, we focus on the computation of the weighting vector w⃗ by assuming that we already have the pairwise features between the images (which we will explain in Section II.C).

Consider an atlas in the training set as the target image, e.g., A_t, t ∈ I, and the rest as the atlases, i.e., {A_i, i ≠ t}. According to Equation (3), we focus on the separation between the set of the K best atlases, denoted as $S_t^{*}$, and the rest (i.e., $I\backslash \{S_t^{*}\cup \{t\}\}$). That is, we want to find the weighting vector w⃗ that satisfies the following inequalities:

$${\overrightarrow{w}}^{\top }\Phi (A_t,A_i)>{\overrightarrow{w}}^{\top }\Phi (A_t,A_j),\forall i\in S_t^{*},\forall j\notin \{S_t^{*}\cup \{t\}\}$$ (5)

It is worth noting that Φ(A_t, A_j) denotes the features extracted from a pair of linearly aligned intensity images without applying any non-rigid registration between them. This type of problem, in which we seek to satisfy certain order relationships between pairs of elements (A_i, A_j) with respect to a given reference A_t, is known as learning to rank and there exist several algorithms in the literature aimed at solving this problem [31–33]. We use SVM-Rank¹ [31] because it has superior performance than other methods [34]. Accordingly, we compute a set of constraints for each target image A_t, to constrain the pairs of atlases (A_i, A_j) so that the i-th atlas should be ranked higher than the j-th atlas according to their ground-truth Dice ratios. Considering $S_t^{*}$ as the ground-truth selection of the K best atlases for segmenting the target image A_t, as defined in Equation (3), the set of specific constraints for the target image A_t can be now defined as follows:

$$r_t^{*}=\{(i,j)|\forall i\in S_t^{*},\forall j\notin \{S_t^{*}\cup \{t\}\}\}$$ (6)

where $S_t^{*}$ is the set of indices of the best atlases for segmenting the target image A_t, and $(i,j)\in r_t^{*}$ means that the i-th atlas should be ranked higher than the j-th atlas for segmenting A_t. By using the SVM-Rank, we pose this problem as a constrained optimization problem, in which we want to find the weighting vector w⃗ that maximizes the margin between the scores of the relevant and non-relevant atlases. We can mathematically formulate it as:

• minimize: $\frac{1}{2}{\Vert \overrightarrow{w}\Vert }^2+\eta \sum _{t,i,j}{\xi }_{t,i,j}$

• subject to:

  $$\begin{array}{cc}\hfill \forall t\forall (i,j)\in r_t^{*}& :{\overrightarrow{w}}^{\top }\Phi (A_t,A_i)\ge {\overrightarrow{w}}^{\top }\Phi (A_t,A_j)+1-{\xi }_{t,i,j}\hfill \\ \hfill \forall t,i,j& :{\xi }_{t,i,j}\ge 0\hfill \end{array}$$ (7)

where the objective function represents a trade-off between a regularization term and the margin size, controlled by the parameter η. The margin is dynamically set to 1 − ξ_t,i,j, with ξ_t,i,j as the slack variable controlling the amount of margin violation regarding each triplet (A_t, A_i, A_j).

The constraints of Eq. (7) can be equivalently expressed as w⃗^⊤ Γ_t,i,j > 1 − ξ_t,i,j, ∀ Γ_t,i,j, where each Γ_t,i,j = Φ(A_t, A_i) − Φ(A_t, A_j) can be considered as an individual training sample regarding the triplet (A_t, A_i, A_j). Therefore, the final number of training samples used by our method becomes N × K × (N − K), where N is the number of atlases and K is the number of the desired best atlases. This represents an advantage in the case of small training sets as is usually the case in multiple-atlas segmentation. For example, in the case of learning to select the best K= 20 atlases from a set of N = 40 atlases, this would correspond to 16000 training samples in our method.

As part of the training process, we need to perform (N − 1)² pairwise non-rigid registrations between the atlases in order to compute the constraints of Equation (6). It is worth noting that this is done in the training stage, which will not affect the speed of the testing stage.

C. Pairwise Feature Computation

As mentioned in Equation (4), our relevance score f is a function of the pairwise features between target image T and atlas image A_i. In order to find a more compact and accurate representation for describing the connection between T and A_i, the calculation of Φ(T, A_i) consists of three steps, namely, (1) key region detection, (2) pairwise HOG computation, and (3) feature selection, as detailed below one by one. It is worth noting that we compute the pairwise features only after affine registration, both in the training and testing stages. However, the Dice ratio in the training stage (Section II.B) is computed based on the non-rigid registration results, which essentially reflects the goal of our approach to predict the segmentation score based only on the affine registration results.

1) Key Region Detection

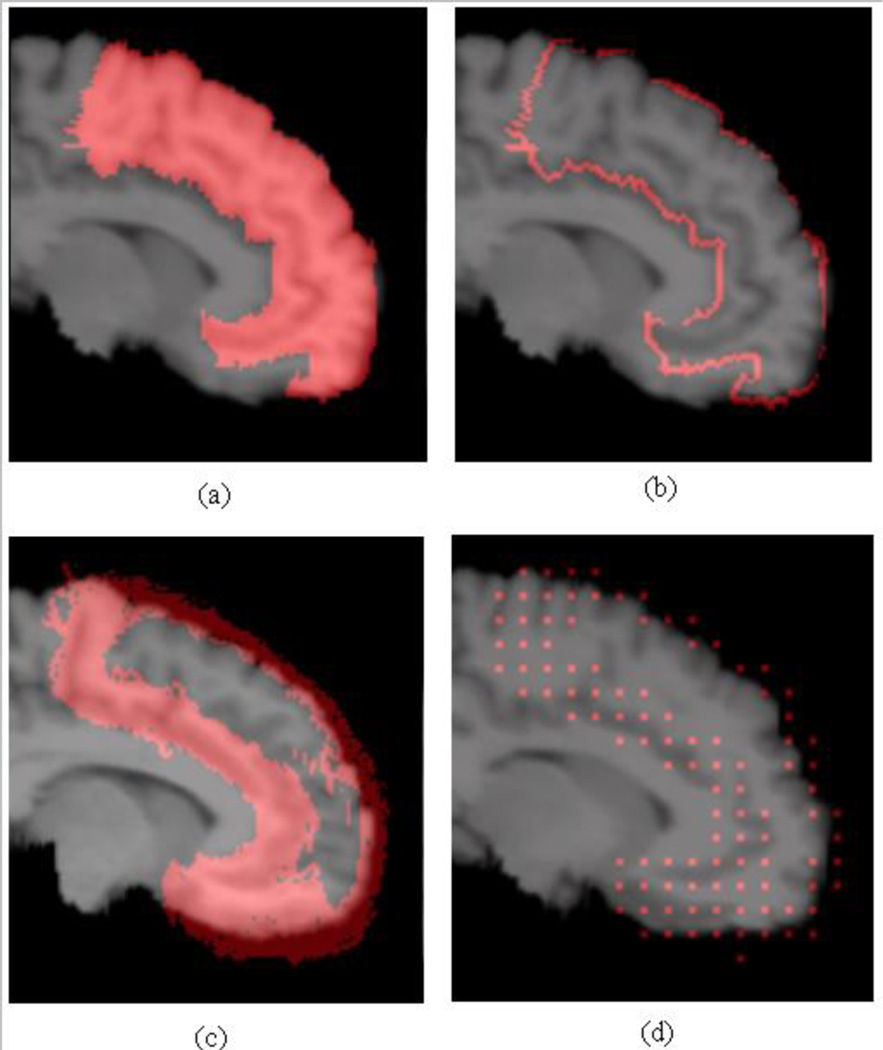
In MAS, the segmentation label at each point in the target image is determined by the labels of the aligned atlases at that point. Regions with high label variability, such as label boundaries, are the source of most labeling errors. Therefore, we use the appearance in these regions as cues to predict the segmentation performance. Since we already know the label information in the training set, we can obtain the set of boundary locations B(L_i) ⊂ Ω_i from the label map L_i, where Ω_i is the set of locations in the whole volume of the i-th atlas. We further define the set of sensible locations as the union of all boundary locations in all the training set, B = ∪_i B(L_i). Fig. 4 shows an example structure, its boundary, and the union of all boundaries from all pre-registered atlases (with affine transformation).

Fig. 4.

(a) Frontal gyrus from one example, (b) its boundary, (c) the union of the boundaries from the affine aligned atlases, and (d) centers of the spatial bins for computing HOG features in the boundary region.

2) Pairwise HOG Computation

HOG descriptors provide a histogram of local edge orientations in the image. Pairwise HOG features in our method are computed as the squared differences of the HOG features. Therefore, they convey information about edge orientation differences after affine alignment. Intuitively, high feature values at certain locations indicate large edge discrepancy between the two images. Many works have demonstrated that the registration accuracy depends on the shape discrepancies between two images, while label fusion performance (measured by the Dice score), depends on the non-rigid registration accuracy along the boundaries of the structures. Since HOG features are good indicators of the shape discrepancies, then HOG features extracted in the boundary regions provide useful clues to predict the final segmentation performance.

We initially extract the HOG features from the whole rectangular ROI containing the structure to be segmented. The rectangular ROI is computed as the rectangular bounding box containing the union of all the labels in the training set, and then enlarged by 20 voxels on each side. Computation of the HOG features establishes a partition of the ROI into spatial bins, with each spatial bin containing the feature values of all the orientation bins at that location. We concatenate the features at spatial bins within a distance ρ to the nearest boundary point in B, to construct a feature vector θ⃗. We use the locations of the spatial bin centers to compute the distance to the boundary region. Overlaid on the intensity image, Fig. 4 (d) shows the centers of the selected bins in the boundary region of Fig 4 (c). Note that the location of the selected HOG features is fixed for all the images since it depends on the union of boundaries in the whole training set. After this process, for each individual image, we obtain a vector θ⃗ containing a number M of selected HOG features in the boundary region. We use the squared difference between the features from the individual images to compute the pool of pairwise features between each target and atlas images, as follows:

$${\overrightarrow{\Theta }}_{t,i}(k)={({\overrightarrow{\theta }}_t(k)-{\overrightarrow{\theta }}_i(k))}^2$$ (8)

where k denotes the k-th feature, and t and i denote the indices of the target image A_t and the atlas image A_i, respectively. Finally, we denote the vector containing the k-th features from all the target-atlas pairs as follows:

$${\overrightarrow{\Theta }}_k=vec\left(\right\{{\overrightarrow{\Theta }}_{t,i}(k),\forall t,i\left\}\right)$$ (9)

where the operator vec(·) is used to represent a set of values into vector form.

In the following, we describe how to select the final set of compact features Φ(A_t, A_i) that will be used for both training and testing.

3) Feature Selection

To select a compact set of features, we sort each feature in the pool according to the maximum-relevance minimum-redundancy criterion (MRmR) [35]. This criterion encourages the selection of features that are highly correlated with the target score while maintaining a low redundancy. After sorting, we obtain a sequence F₁ ⊂ F₂ ⊂ ⋯ F_m … ⊂ F_M−1 ⊂ F_M, such that F_m contains the indices of the best m features according to MRmR. Suppose we already know F_m−1. The m-th feature to be added to F_m−1 for creating F_m can be determined according to the following formula:

$${\mathit{\text{max}}}_{k\notin F_{m-1}}\left(\mathit{\text{Rel}}\right({\overrightarrow{\Theta }}_k,\overrightarrow{\Psi })-\frac{1}{m-1}{\sum }_{k\prime \in F_{m-1}}\mathit{\text{Red}}({\overrightarrow{\Theta }}_{k\prime },{\overrightarrow{\Theta }}_k\left)\right)$$ (10)

where Θ⃗_k is the vector containing the k-th feature from all the target-atlas pairs, as defined in Equation (9), and similarly, Ψ⃗ = vec({DR(L_t, L̃_i), ∀t, i}) is the vector containing the ground-truth DRs between all target-atlas pairs. As for the relevance function Rel(·,·), we use the absolute value of the Spearman's rank correlation coefficient which measures the correlation between the ranks induced by the features and the ground-truth score. This measure is appropriate to assess the correlation with the ground-truth score, since it only takes into account the rank induced by the feature value, instead of the value itself, which is what we are interested in. As for the redundancy function Red(·,·), we use the absolute value of the Pearson correlation coefficient which measures the correlation between the values of pairs of features. This formula encourages the selection of features that induce the rankings correlated with the ground-truth ranking and further penalizes the features with values correlated with the already-chosen features. This will usually lead to more compact feature-sets for classification, since redundant features are filtered-out.

Finally, we select the best m′ features according to MRmR to obtain the compact set of features Φ(A_t, A_i) representing a pair of target and atlas images, as follows.

$$\Phi (A_t,A_i)=vec\left(\right\{{\overrightarrow{\Theta }}_{t,i}(k),k\in F_{m\prime }\left\}\right)$$ (11)

where F_m′ is the index-set of the best m′ features according to MRmR. In the experiments section, we give details about the number of features used in our experiments.

D. Summary

In the following, we provide a brief summary of our proposed method.

In the training stage:

1. Compute the ground-truth segmentation score for each pair of target and atlas images in the training set (A_t, A_i), thus obtaining the following elements:

   1. A vector of ground-truth segmentation scores Ψ⃗ = vec({DR(L_t, L̃_i), ∀t, i}), and
   2. the ground-truth sets of best K atlases $S_t^{*}$ for segmenting each target image A_t, as defined in Equation (3).

2. Extract the HOG features and compute the pairwise feature-vectors Θ⃗_t,i between each pair of images (A_t, A_i) in the training set, as defined in Equation (8).

3. Obtain a compact feature-vector Φ(A_t, A_i) for each pair of target and atlas images in the training set using the ground-truth segmentation scores Ψ⃗, as defined in Equations (10) and (11).

4. Learn a scoring function f(A_t, A_i) that predicts the segmentation performance of a pair of affinely aligned images (A_t, A_i), using the ground-truth selection-sets $S_t^{*}$ and the compact feature-vectors Φ(A_t, A_i), as defined in Section II.B.

In the testing stage:

1. Affinely align a new target image T onto the common space.

2. Extract HOG features from the affinely aligned target image T and obtain compact vectors of pairwise features between the target image and all the atlases, i.e., {Φ(T, A_i), ∀i ∈ I}.

3. Determine the set of K atlases (S_T) with the highest expected performance for segmenting target image T, such that f(T, A_i) > f(T, A_j), ∀i ∈ S_T, ∀j ∉ S_T, and |S_T| = K.

4. Segment target image T using the selected atlases (A_ST, L_ST), as defined in Equation (1).

It is worth noting that we need to learn a different scoring function f(·) for each different value of K.

III. Experiments

We have evaluated the performance of our atlas selection method in four datasets, namely, ADNI², SATA³, IXI⁴ and LONI-LPBA40⁵ [36] datasets. Segmentation performance is assessed by the Dice ratio between the estimated segmentations and the ground-truth label annotations.

In the ADNI, IXI and LONI-LPBA40 dataset we conducted the following three pre-processing steps on all images: (1) Skull stripping by a learning-based meta-algorithm [37]; (2) N4-based bias field correction [38]; (3) ITK-based histogram matching for normalizing the intensity range. We use nonrigid registration with diffeomorphic demons [14] for both ground-truth Dice ratio computation and multi-atlas segmentation of new target images. The images in the SATA dataset were already skull-stripped and their pairwise nonrigid deformations were also provided. We use FLIRT [39] to affinely align all atlases to a population image, prior to feature extraction.

We perform our segmentation experiments by combining different atlas selection methods with different label fusion methods. Specifically, we use the following atlas selection methods: (1) our proposed method, denoted as HSR (HOG plus SVMRank), (2) a degraded version of our proposed method that selects atlases according only to the distance between the HOG features, denoted as HOG, and (3) a baseline method which selects the best atlases by mutual-information-based image similarity, denoted as MI. We also include a comparison with the state-of-the-art Neighbourhood Approximation Forests (NAF) method [29], which uses random forests to predict the neighborhood in a population of training samples under arbitrary similarity measurements.

The degraded version of our method for atlas selection (i.e., HOG) uses the squared differences between the pools of HOG features from two images in order to select the best atlases. This can be expressed by the new scoring function $f(T,A_i)=-{\sum }_{k=1}^M{({\overrightarrow{\theta }}_T(k)-{\overrightarrow{\theta }}_{A_i}(k))}^2$, where θ⃗_T(k) and θ⃗_Ai(_k) are the k-th features in the vectors of M HOG features extracted from the key regions of the target image T and the atlas image A_i, respectively. This scoring function corresponds to the sum of local edge discrepancies between the atlas and the target image and can be used as reference to elucidate the benefit of the learning component in our method for effective atlas selection.

NAF is a state-of-the-art learning-based method for predicting neighborhoods given arbitrary distance metrics. One of the applications of NAF is the prediction of the most similar training images to a given testing one in terms of the amount of non-rigid deformation necessary to align them. Although there is no direct relationship between the amount of deformation and the final segmentation performance, it is straightforward to adapt NAF for the task of atlas selection. To that end, we define the new ground-truth dissimilarity metric between two training images A_i and A_j as 1 − DR(A_i, A_j), where DR(·) is the ground-truth Dice ratio as defined in Eq. (2). By using this dissimilarity measurement, selection by NAF is directly motivated by the final segmentation performance (as in our method). We use the implementation provided by the authors⁶.

Segmentation experiments are run on each anatomical structure independently. We use a region of interest containing the anatomical structure to be segmented as input for the three selection methods. All the methods use the affinely aligned images as input. The three label fusion methods used are, respectively, (1) majority voting (MV) [22, 23], (2) local weighted voting (LWV) [8], and (3) non-local weighted voting (NLWV) [24, 25]. MV-based label fusion assigns each target voxel with the label occurring most frequently among all the candidate atlas voxels. LWV- and NLWV-based label fusions use the image patch similarity measure to estimate the local relevance of each atlas patch to segment the target image. The difference between LWV and NLWV is that LWV-based label fusion only takes into account the corresponding atlas patches, whereas NLWV-based label fusion searches similar patches within a local neighborhood.

Each segmentation variant is named as ‘the atlas selection method + the label fusion method’. This is, ‘MI+MV’ represents the segmentation variant using mutual information for atlas selection and majority voting for label fusion.

In the ADNI, IXI and LONI-LPBA40 datasets, we conduct 5-fold cross-validation experiments. That is, we partition each dataset into 5 subsets and, at each fold, we use the images in one subset as the target images and all the images in the remaining subsets as the atlases. In the SATA dataset, we use the pre-defined training and testing sets.

A. Parameter Setting

HOG features have two parameters, namely, the number of orientation bins O and cell size C (in voxels) of the spatial bins. We found our method not very sensitive to the values of these parameters. Since different structures often have different sizes, setting these parameters to fixed values will cause larger structures to generate an unnecessarily high number of features. To trim the number of features to a manageable size, we adaptively fix the HOG parameters C and O to get a reasonable number (M) of features. Specifically, we start with C = 5 and O = 9, and iteratively increase the cell size C and decrease the number of orientation bins O until the number of resulting features is less than or equal to M, or we reach the pre-defined values C = 7 and O = 3. Therefore, the final values for these two parameters C and O are fixed for each structure. The number of features, M, is set to M = 10⁴ in all experiments. The final size of the selected features as used in all experiments is set to m = 1000. The distance threshold for selecting the features in the boundary regions is set to ρ = 0. That is, we use only the HOG features inside the boundary region. We set the parameters for the LWV- and NLWV-based label fusion methods according to the values given in [24].

B. Feature Comparison

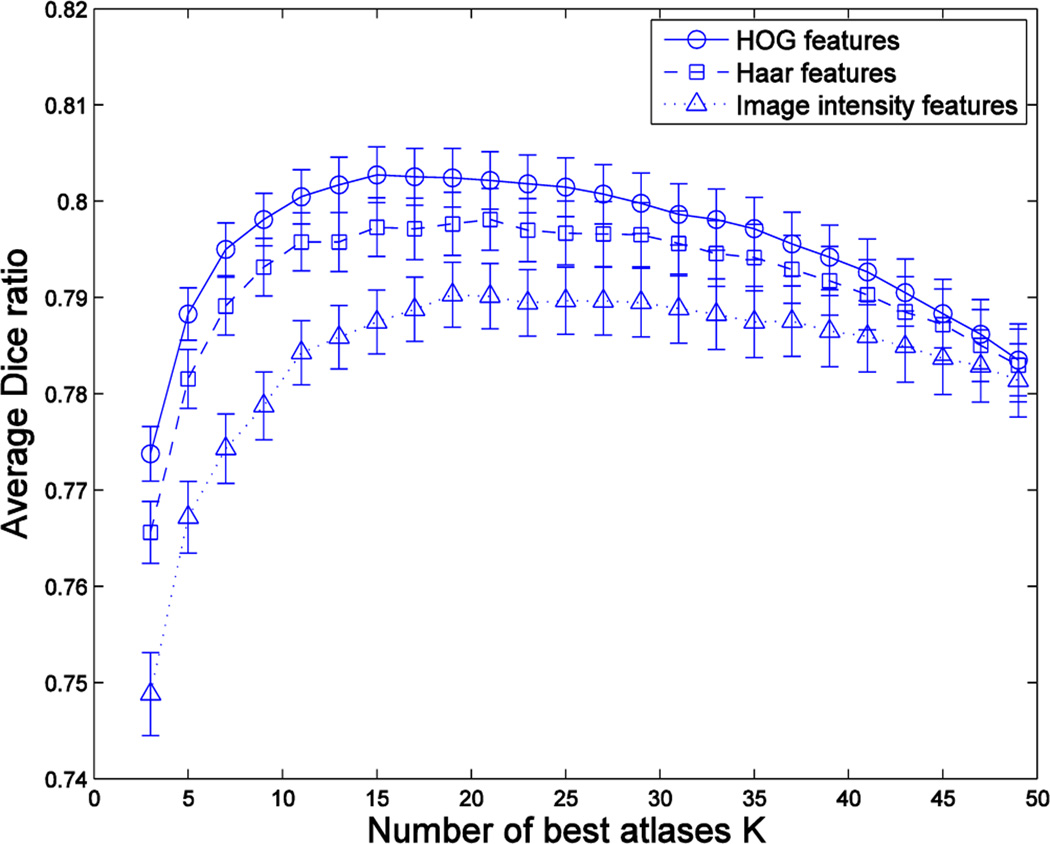
In order to see the advantages of using HOG features, we perform experiments to compare three different types of features, namely, HOG, Haar and image intensities. In all three cases, we follow the regular pipeline of our method: (1) feature extraction from boundary regions, (2) pairwise feature computation, (3) feature selection and (4) learning. In the case of image intensities, we use the mean intensity in a patch, which is more robust to noise than the values at single voxels. In the case of Haar features, we compute the intensity differences between pairs of patches at random locations, as done in [29]. As for Haar and image intensity features, we used cubic patches of different sizes (i.e., 3,5,8,12) and then report the best results. Regarding the number of features, we extract M = 10⁴ features from the boundary locations for HOG and Haar features, respectively. In the case of image intensities, we use all values at the boundary locations (which are nearly 10⁴ in the case of the hippocampus). For each feature type, we select the best m = 1000 features according to the MRmR criterion. Fig. 5 shows the average Dice ratios obtained in the segmentation of the hippocampus from 66 subjects in the ADNI dataset by using the different feature types in the pipeline of the proposed atlas selection method. As we can see, the local edge information conveyed by the HOG features is the most appropriate for the task of predicting good atlases, thus justifying its use in the subsequent experiments.

Fig. 5.

Segmentation performance by the proposed atlas selection method using different types of features. We use MV label fusion.

C. Results on the ADNI Dataset

The ADNI dataset contains the segmentations of the left (L) and right (R) hippocampi, which were obtained by a commercial brain mapping tool [40]. The size of each ADNI image is 256 × 256 × 256. We use 66 randomly selected ADNI subjects to test the performance of the 9 different segmentation methods. Due to the random selection, the prevalence of disease in our samples is similar to that in the original dataset, which is approximately $\frac{1}{4}$ of Alzheimer’s disease patients, $\frac{1}{4}$ of healthy subjects, and $\frac{1}{2}$ of subjects with mild cognitive impairment. To validate the segmentation performance of each target image, we use the Dice ratio between the automated segmentations by MAS and the manual ground-truth segmentations on the target image.

In the following, we compare the following four atlas selection methods in hippocampus segmentation experiments in the ADNI dataset: (1) the proposed method, denoted as HSR; (2) the degraded version of the proposed method, denoted as HOG; (3) Neighborhood Approximation Forests [29], denoted as NAF ; and (4) atlas selection by mutual information, denoted as MI.

Originally, NAF uses 1000 randomly picked Haar features from a pool of 10⁴ features in order to train 1500 trees. For a fair comparison, we similarly use 1000 randomly picked features from the pool of 10⁴ HOG features in the boundary regions for training each tree. Note, that in Fig. 5 we showed the superiority of HOG features for the task of predicting good atlases, thus we also use HOG features for NAF. In order to use the best parameters for NAF, we have tested the maximum tree depth values [3,4,5,7] and minimum number of samples at each leaf [1,3,5,7]. We report results for the best values of these parameters, i.e., the maximum tree depth of 4, the minimum number of samples of 3.

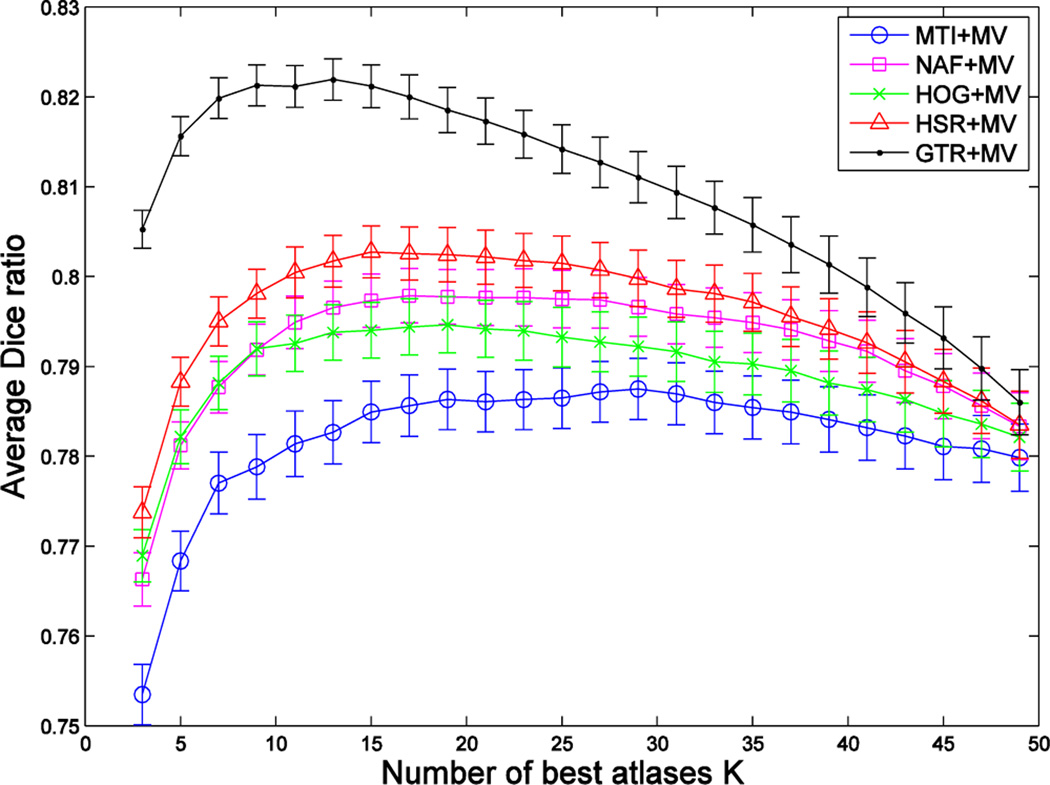
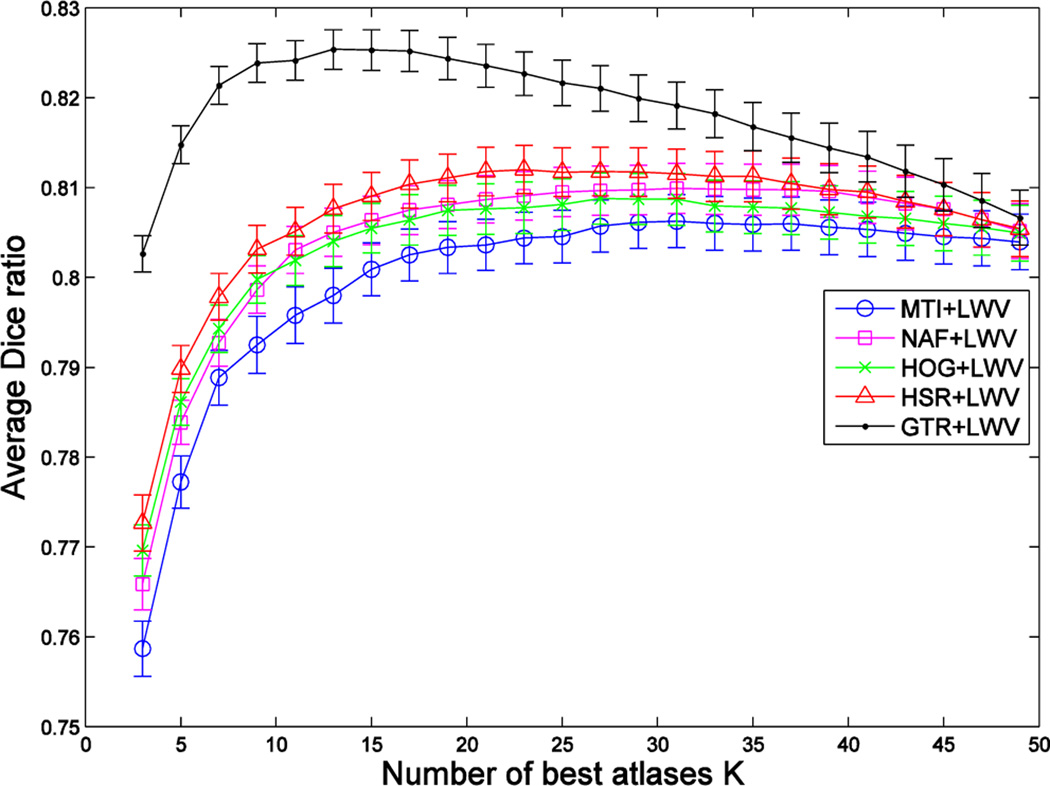
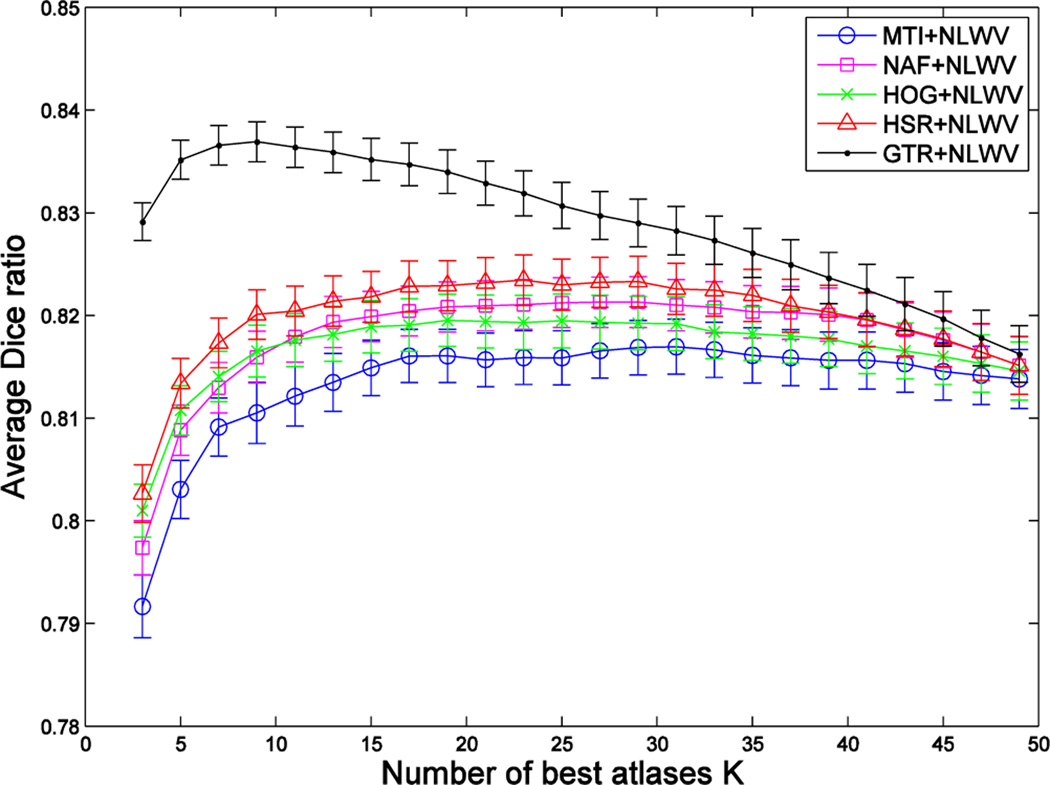
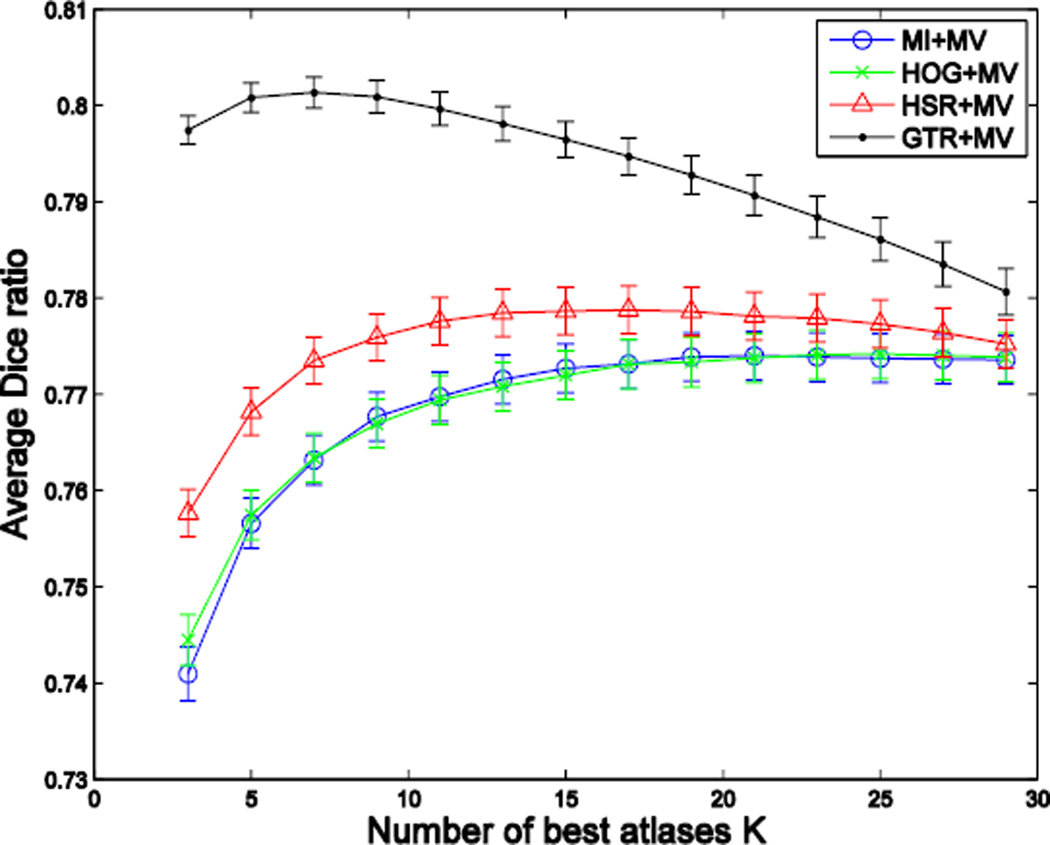
Fig. 6, Fig. 7 and Fig. 8 show, respectively, the Dice ratios achieved by the four atlas selection methods (MI, NAF, HOG, HSR) with respect to the use of three label fusion methods (MV, LWV, NLWV). We also include results of selection by the ground-truth DR (GTR) to show the upper-bound in the case of an ideal atlas selection. Vertical axes show the segmentation accuracy averaged over all target images in the 5 folds of cross validation, and horizontal axes show the number of atlases used.

Fig. 6.

Blue, magenta, green, red and black curves show the segmentation performance achieved by combining MV-based label fusion with five different atlas selection methods (MI, NAF, HOG, HSR and GTR) on the ADNI dataset. Vertical axis shows the segmentation performance, and horizontal axis shows the number of atlases used. Results show the average segmentation performance on both hippocampi.

Fig. 7.

Blue, magenta, green, red and black curves show the segmentation performance achieved by combining LWV-based label fusion with five different atlas selection methods (MI, NAF, HOG, HSR and GTR) on the ADNI dataset. Vertical axis shows the segmentation performance, and horizontal axis shows the number of atlases used. Results show the average segmentation performance on both hippocampi.

Fig. 8.

Blue, magenta, green, red and black curves show the segmentation performance achieved by combining NLWV-based label fusion with five different atlas selection methods (MI, NAF, HOG, HSR and GTR) on the ADNI dataset. Vertical axis shows the segmentation performance, and horizontal axis shows the number of atlases used. Results show the average segmentation performance on both hippocampi.

Both HSR- and NAF-based selections achieve their nearly optimal performance at K = 19 atlases for all label fusion methods, whereas MI-based selection achieves its nearly optimal performance at K = 29 atlases. Nearly optimal performance is decided as a trade-off between accuracy and computational time. Specifically, we choose K so that the average performance across all label fusion modalities has reached 99.95% of its best result. For the optimal number of atlases, the proposed atlas selection method consistently outperforms the other selection methods in all the label fusion modalities. Specifically, it achieves an improvement of ~ 1.5% compared to the MI-based selection when combined with MV label fusion, and ~0.6% when combined with LWV and NLWV label fusions. It achieves so by using $\frac{1}{3}$ fewer atlases than MI-based selection, thus representing a save of ~ 30% in computational time in deploying non-rigid registration and label fusion. Compared with NAF-based selection, our method achieves an improvement of ~ 0.5% when combined with MV label fusion, ~ 0.3%, when combined with LWV label fusion and ~ 0.2% when combined with NLWV label fusion. The performance of NAF is closer to HOG when only a few atlases are selected and closer to the proposed method (HSR) when many atlases are selected. This suggests that NAF is good at correctly identifying the neighborhood at a large scale rather than at a small scale. This could be because the amount of training data is not enough for NAF to capture the relevant patterns necessary for a fine discrimination. The combination of our atlas selection method and NLWV-based label fusion, HSR+NLWV, achieves the overall best performance. The combination of our proposed atlas selection method and the simplest label fusion method, i.e., HSR+MV, achieves comparable results to MI+LWV. Note that, as the number of selected atlases (K) increases, the performance of the different methods approach to the same value. Obviously, all selection methods are equivalent when selecting all available atlases.

Results of the degraded version of our method (all green curves in Fig. 6, Fig. 7 and Fig. 8) clearly show that the sum of edge discrepancies computed by HOG are more useful than the simple mutual information in selecting the best atlases. Comparing the results of the two versions of our method (HOG and HSR), we conclude that (1) the ground-truth DR is a good metric for atlas selection, and (2) the machine learning component successfully captures the relationships between the data and the ground-truth DR.

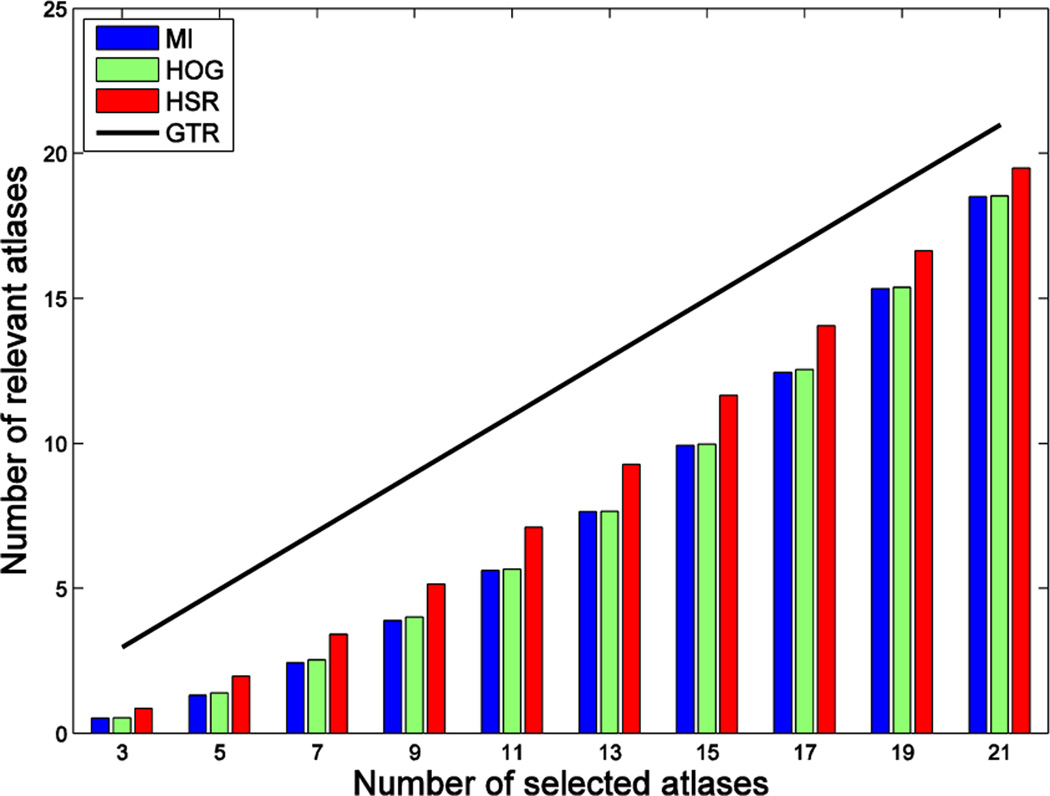
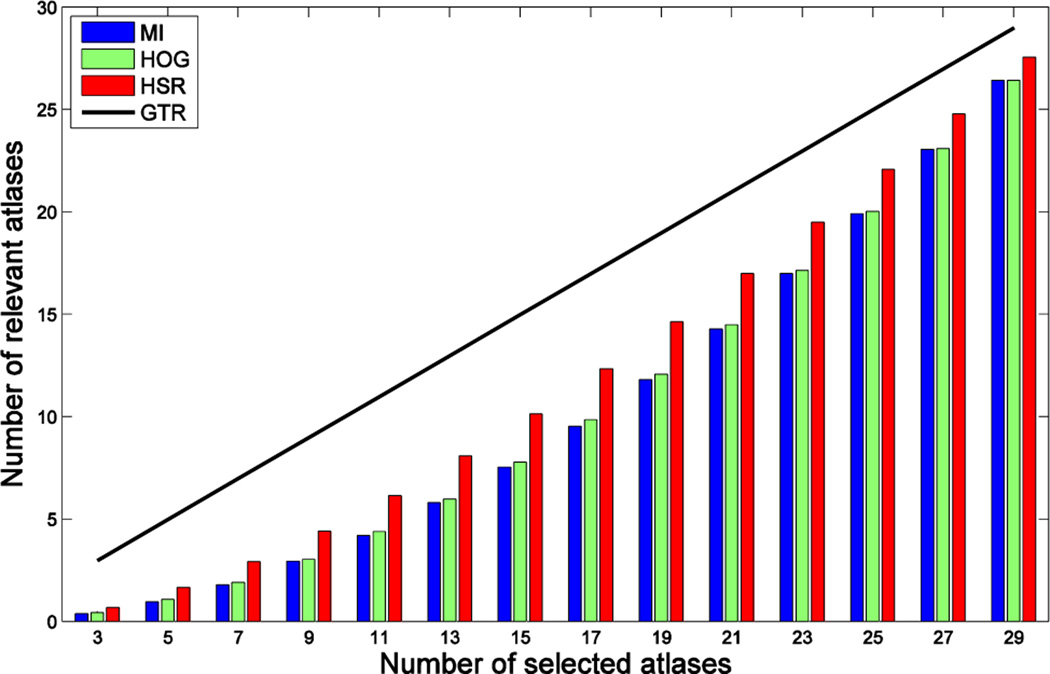
Results by GTR show that the nearly optimal segmentation performance in the case of ideal selection is achieved by using K = 13 atlases. This justifies the importance of selecting good atlases. Differences in segmentation performance with the rest of the methods are basically due to differences in atlas selection. To get a better insight about the performance of each method in selecting good atlases, Fig. 9 shows the number of relevant atlases selected by MI, HOG and HSR. The theoretical upper bound in the case of a perfect selection (i.e., GTR) is displayed as a black line. As we can see, the proposed method always selects the highest number of relevant atlases, followed by HOG. However, there is still some gap with respect to the ideal selection case, which has significant impact in segmentation performance, especially when using only a few atlases. For example, in the case of using K = 13 atlases, our method correctly selects 7 atlases in average, and thus the 6 incorrectly selected atlases are responsible for the segmentation performance differences observed in Fig. 6, Fig. 7 and Fig. 8.

Fig. 9.

Number of relevant atlases selected by each method in the ADNI dataset. Vertical axis shows the number of relevant atlases, and horizontal axis shows the number of selected atlases. The black line denotes the number of relevant atlases in the case of a perfect selection (GTR).

To further validate our proposed method, in Table II we show the average surface distance errors (in mm), computed as defined in [41], for all the different segmentation methods. For a fair comparison we use the optimal value of K for each method. That is, we use K = 19 atlases for our method (HSR) and K = 29 atlases for the MI-based selection method. In order to evaluate the benefit of the machine learning component, the degraded version of our method (HOG) uses the same number of atlases as our method (i.e., K = 19).

TABLE II.

Mean and standard deviation of the average surface distances (in mm) obtained in segmenting the left and right hippocampi by using K = 19 atlases for both HOG- and HSR-based selection methods and K = 29 atlases for the MI-based selection method.

Segmentation variant	Overall
MI+MV	0.4293 ± 0.1321
HOG+MV	0.3942 ± 0.1217
HSR+MV	0.3776 ± 0.1145
MI+LWV	0.3670 ± 0.1110
HOG+LWV	0.3522 ± 0.1031
HSR+LWV	0.3465 ± 0.0992
MI+NLWV	0.3221 ± 0.0987
HOG+NLWV	0.3187 ± 0.0952
HSR+NLWV	0.3102 ± 0.0898

As we can see, by using only K = 19 atlases, our proposed atlas selection can consistently achieve lower mean surface distances and standard deviations than HOG- and MI-based atlas selection. This suggests that our atlas selection method can lead to better and more stable segmentations in lower computational time than MI-based selection. HOG-based selection requires 30% fewer atlases than MI-based selection to achieve a better performance. As already noted in the previous results with Dice ratio, the more advanced label fusion method (NLWV) outperforms the simpler ones (MV and LWV).

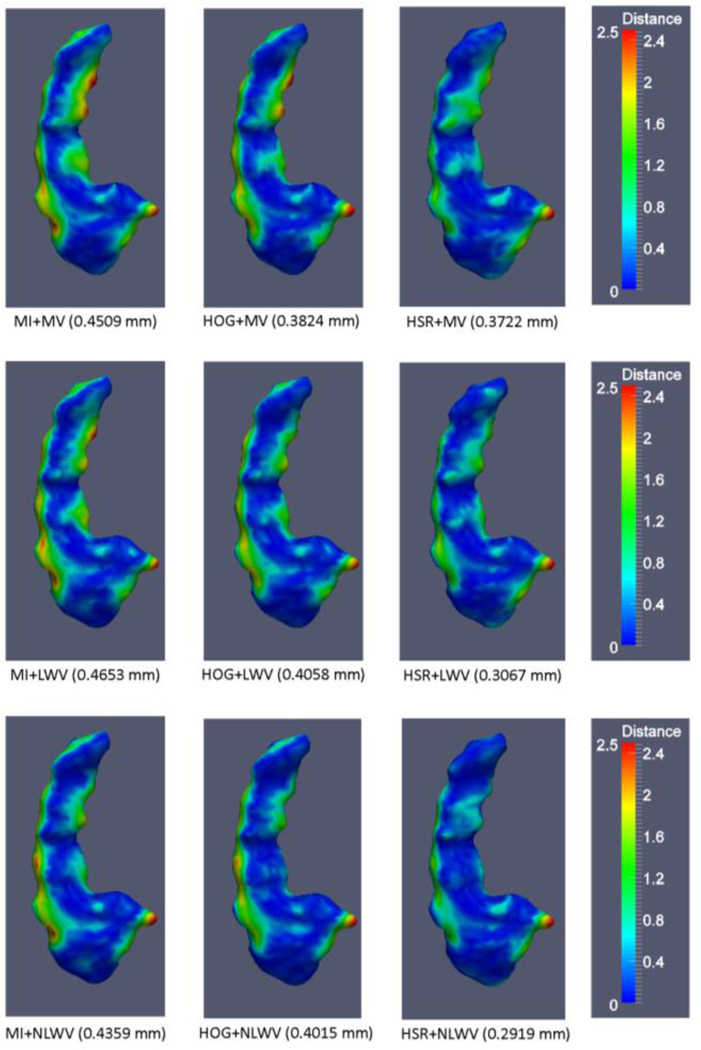
In order to further evaluate the effects of different atlas selection and label fusion methods, in Fig. 10 we show the segmentation error maps (in terms of surface distance error) incurred by different combinations of atlas selection and label fusion methods in segmenting the left hippocampus of one example subject.

Fig. 10.

Surface distance error map on the hippocampus by each method. At the bottom of each map, the segmentation method and its average surface distance error are provided.

By comparing the results across the columns in Fig. 10, we can see performance differences due to the use of the different selection methods. Specifically, HOG-based atlas selection requires only K = 19 atlases to outperform MI-based selection, that needs K = 29 atlases (see the first and second columns in Fig. 10). The proposed atlas selection method outperforms the rest of the methods in all the label fusion modalities (rightmost column), by using only K = 19 atlases. On the other hand, by comparing the results across the rows, we can observe the benefits of using more advanced label fusion methods (LWV and NLWV). Finally, the proposed atlas selection in combination with NLWV-based label fusion, HSR+NLWV, achieves the overall lowest surface distance errors, as can be seen in the bottom-right map.

D. Results on the SATA Dataset

The SATA dataset contains training and testing sets of 35 and 12 brain MR scans, respectively. The training set contains both intensity and label images with the annotations of 14 different ROIs. The testing set contains only the intensity images. Pairwise non-rigid registrations are provided among the training samples and also between training and testing samples. We will use these pairwise registrations for the purposes of training and testing our method, respectively. We applied two versions of our method: a baseline version using MV label fusion and also an advanced version using NLWV label fusion. In both cases, we compare the proposed atlas selection strategy (HSR) with mutual information (MI). For each method, we select a number of atlases in the range K = [7,11,15,19,25,35] and then report the best results obtained by each method, along with their corresponding best K value. Results after integrating the two atlas selection methods with MV and NLWV label fusion are reported in Table III and Table IV, respectively.

TABLE III.

Segmentation performance of MI- and HSR-based atlas selection after integrating with MV label fusion.

Selection method	Best atlas number	Mean DR (± s.d.)
MI+MV	K = 15	0.8326(± 0.0386)
HSR+MV	K = 15	0.8371(± 0.0396)

TABLE IV.

Segmentation performance of MI- and HSR-based atlas selection after integrating with NLWV label fusion.

Selection method	Best atlas mini	Mean DR (± s.d.)	Rank
MI+NLWV	K = 35	0.8581(± 0.0280)	4th
HSR+NLWV	K = 19	0.8593(± 0.0274)	2nd

For the baseline version, our atlas selection method achieves an improvement of 0.5% with respect to MI-based selection. It is worth noting that the baseline result reported by the SATA website⁷ using MV label fusion is 0.8280 ± 0.0460, which is 0.9% worse than the proposed method.

For the advanced version, we include an additional column indicating the overall ranking in the SATA challenge. Our atlas selection method boosts the standard NLWV-based label fusion from the 4^th to the 2^nd position in the SATA Challenge ranking (as of March 27^th, 2014), with a corresponding improvement in the mean DR of ~ 0.1%. This improvement is achieved by using approximately a half of the atlases required by MI.

E. Results on the IXI Dataset

We use a subset of 30 images in the IXI dataset containing the manual annotations of 83 structures [42, 43]. The size of each image is 128 × 128 × 99. Because the high amount of structures contained in this dataset, we focus on the 30 smallest ones which are usually the most challenging for labeling. We determine the number of atlases (K) to be used by each method based on the segmentation results for all possible values of K, using MV label fusion. Due to the high computational demands of the label fusion procedure, it is not feasible to run such exhaustive search on this dataset using the LWV and NLWV label fusion methods. However, as previously shown in the ADNI dataset, it is reasonable to extrapolate the choice of the number of atlases (K) for LWV and NLWV label fusions based on the results of MV label fusion. In Fig. 11 we show the average Dice ratio among the 30 structures achieved by the different selection methods combined with MV label fusion. We also include results of selection by ground-truth DR (GTR) to indicate the upper-bound in the case of an ideal atlas selection. Based on these results we choose the value of K = 13 for all the methods. Therefore, we can compare their performance under the same conditions.

Fig. 11.

Average segmentation performance achieved by the different selection methods combined with MV label fusion on the 30 smallest structures of the IXI dataset. Vertical axis shows the average performance, assessed by the Dice ratio, and horizontal axis shows the number of atlases used.

In Table V we show the average Dice ratios obtained when selecting the best K = 13 atlases by each selection method. As we can see, the proposed atlas selection method achieves an improvement of > 1% in all label fusion modalities with respect to MI-based selection.

TABLE V.

Average mean Dice ratios among all the ROIs in the IXI dataset by selecting the best K = 13 according to each selection method. Different atlas selection methods are arranged row-wise, and different label fusion modalities are arranged column-wise.

	MV	LWV	NLWV
MI	0.6839 ± 0.1532	0.6887 ± 0.1507	0.6935 ± 0.1583
HOG	0.6839 ± 0.1522	0.6878 ± 0.1500	0.6929 ± 0.1585
HSR	0.6984 ± 0.1387	0.7008 ± 0.1374	0.7079 ± 0.1431

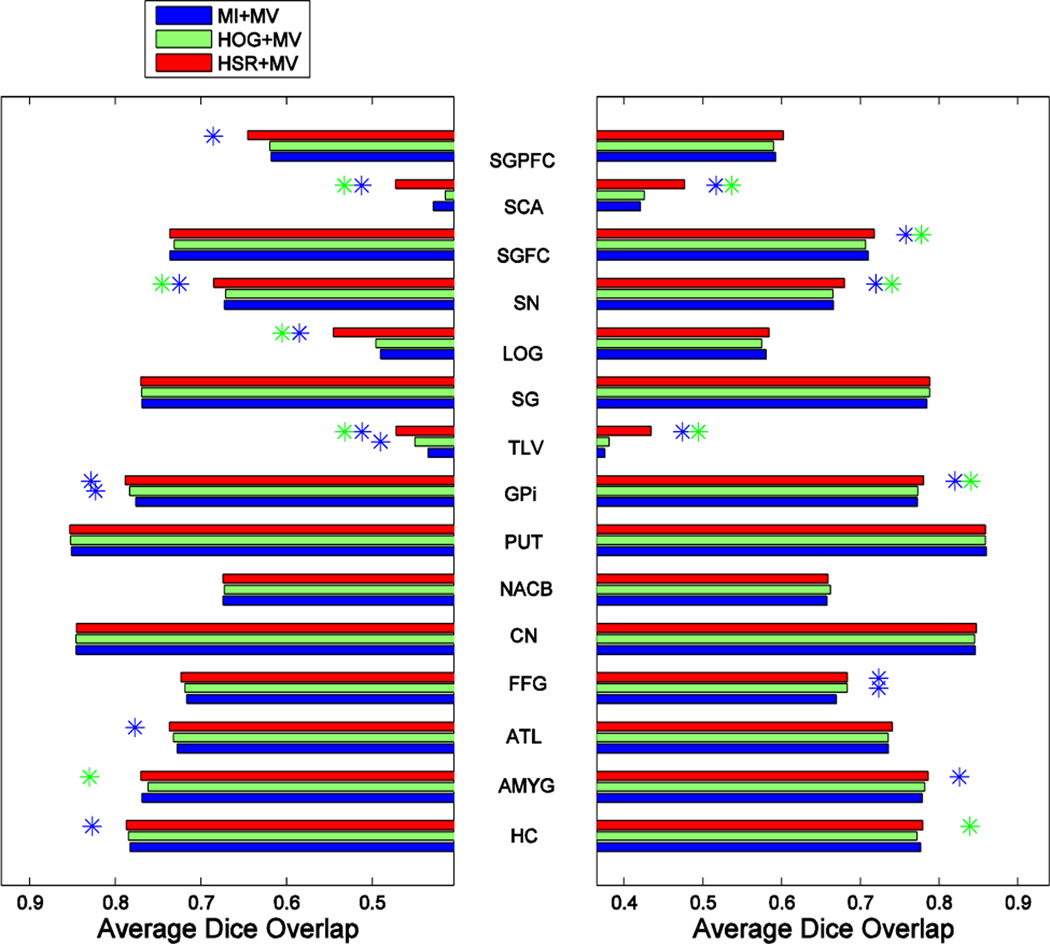
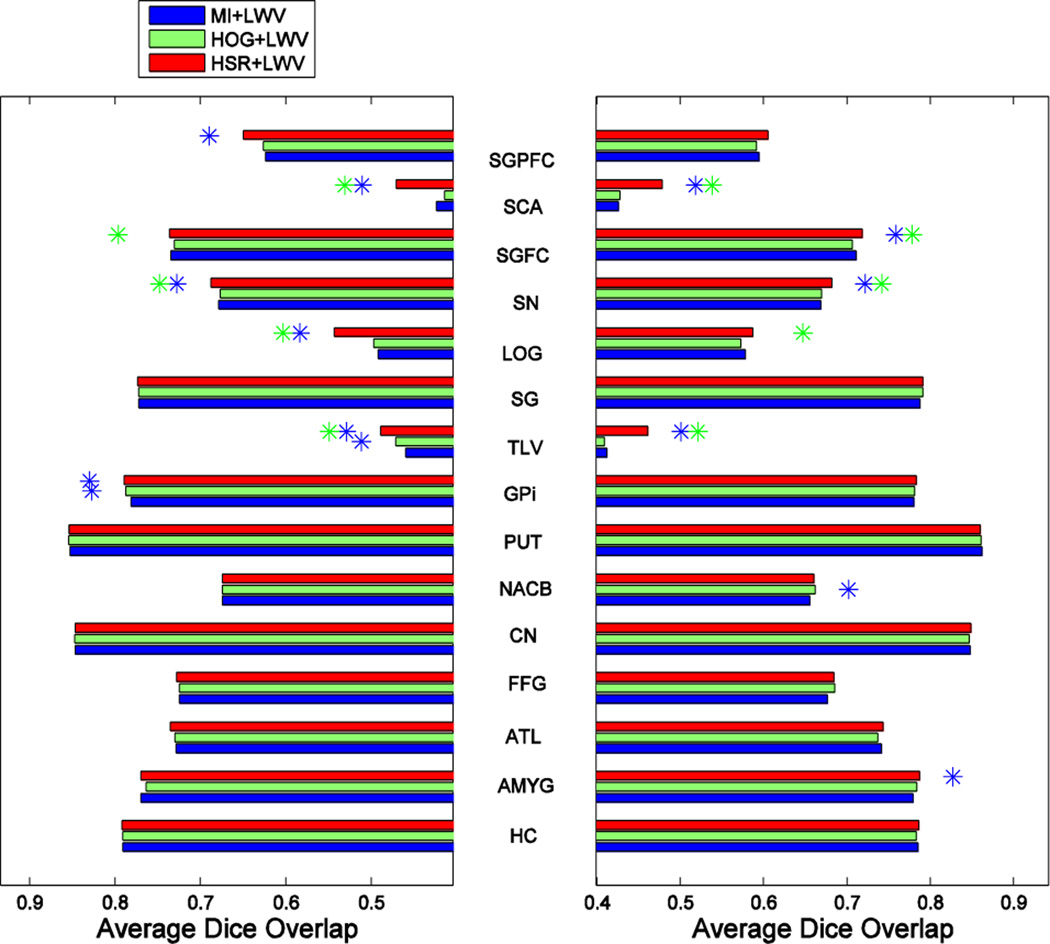
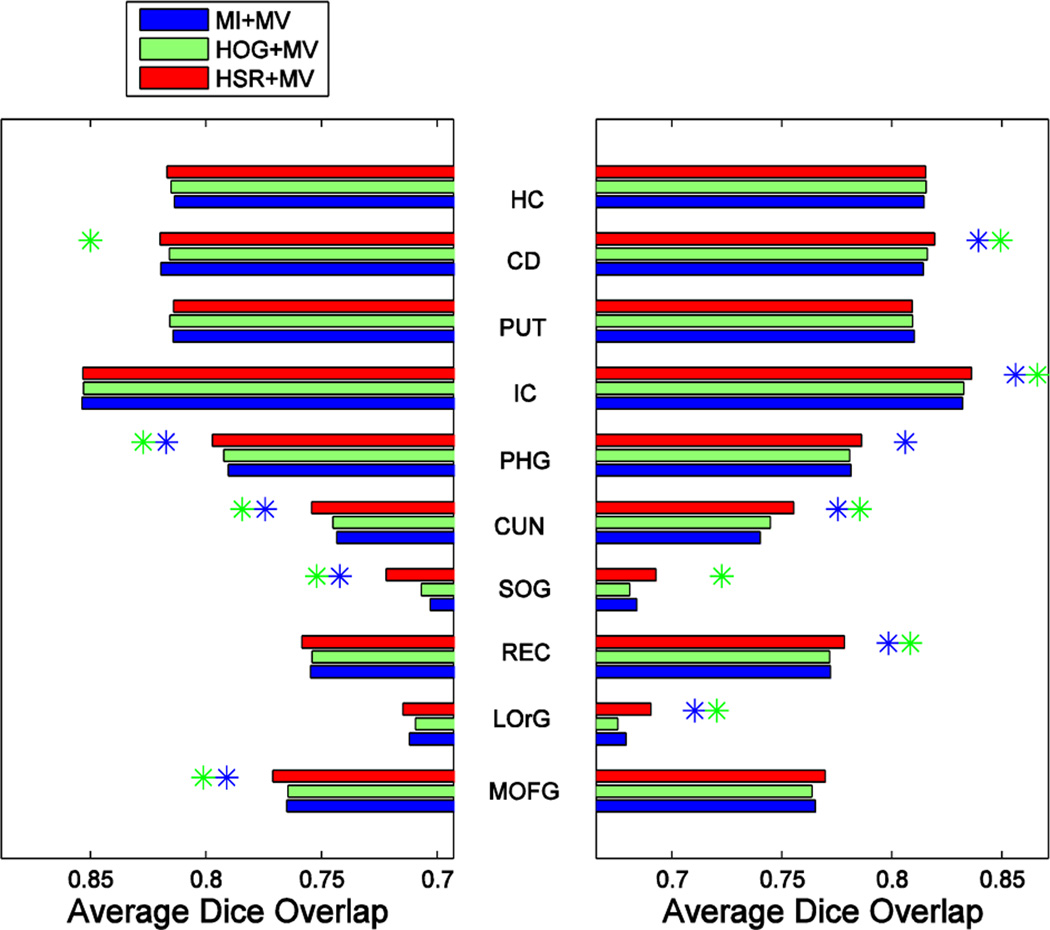
Fig. 12, Fig. 13 and Fig. 14 show the segmentation performance achieved by the different selection methods using K = 13 atlases for the three different label fusion modalities. Left and right plots show the results on the left and right parts of each structure, respectively, with the name shown in the middle. Blue and green asterisks at the end of each bar represent a significant improvement of the respective atlas selection method, according to a paired t-test with p ≤ 0.05, with respect to the MI- and HOG-based atlas selection methods, respectively.

Fig. 12.

Blue, green and red bars show the segmentation performance, assessed by the Dice ratio, obtained by combining MV-based label fusion with different atlas selection methods on the labeling of 30 structures in the IXI dataset. Left and right plots show the results for the left and right parts of each structure, respectively, with the structure names shown in the middle. A blue and green asterisk represent significant improvement with respect to MI- and HOG-based selection, respectively.

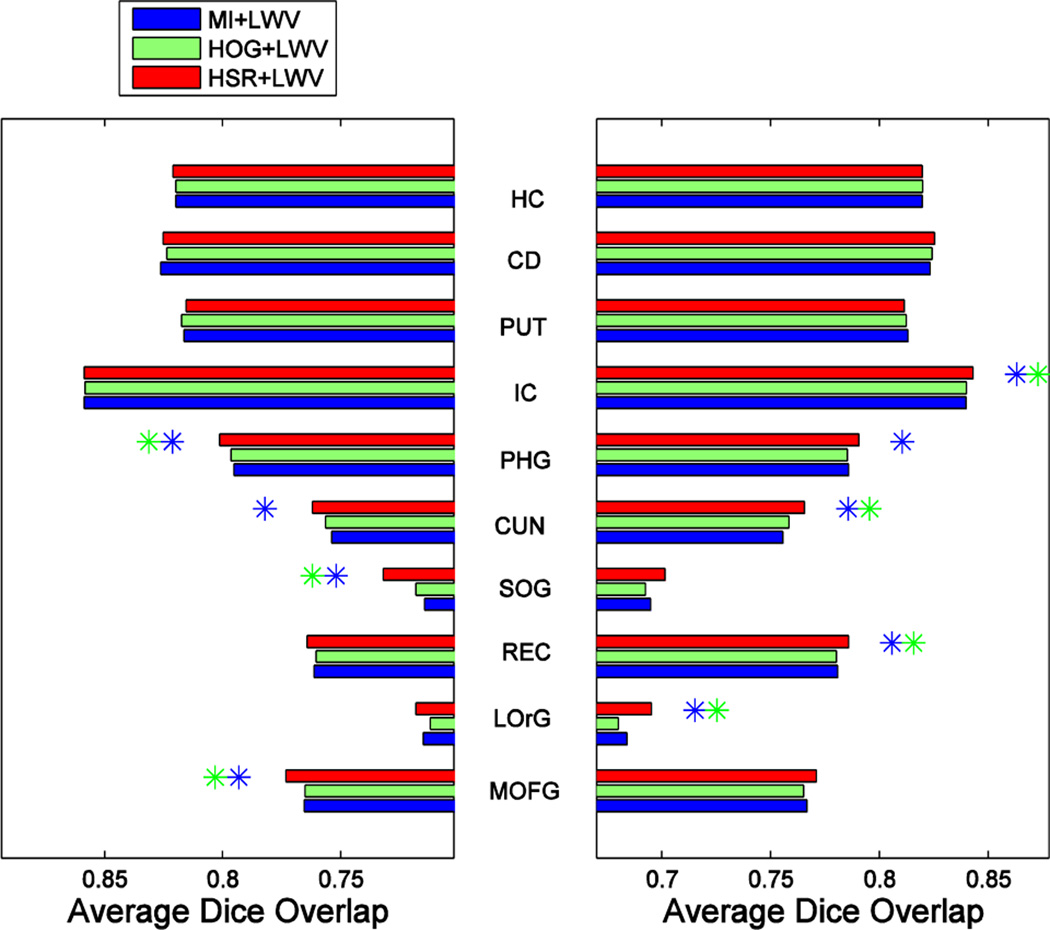
Fig. 13.

Blue, green and red bars show the segmentation performance, assessed by the Dice ratio, obtained by combining LWV-based label fusion with different atlas selection methods on the labeling 30 structures in the IXI dataset. Left and right plots show the results for the left and right parts of each structure, respectively, with the structure names shown in the middle. A blue and green asterisk represent significant improvement with respect to MI- and HOG-based selection, respectively.

Fig. 14.

Blue, green and red bars show the segmentation performance, assessed by the Dice ratio, obtained by combining NLWV-based label fusion with different atlas selection methods on the labeling 30 structures in the IXI dataset. Left and right plots show the results for the left and right parts of each structure, respectively, with the structure names shown in the middle. A blue and green asterisk represent significant improvement with respect to MI- and HOG-based selection, respectively.

As we can see from these 3 figures, our atlas selection method achieves a significant improvement with respect to the MI-based atlas selection method, according to a paired t-test with p ≤ 0.05, in 15, 11 and 11 structures (out of 30 structures) by MV-, LWV- and NLWV-based label fusions, respectively. This trend of results is consistent with what we observed on the ADNI dataset, which showed a more significant improvement when using the simpler label fusion modalities. Our atlas selection method achieves a significant improvement with respect to the HOG-based selection in 11, 10 and 11 structures (out of 30 structures) for the three different label fusion modalities, respectively. On average, compared to the MI-based selection, our atlas selection method achieves improvements of 1.29%, 1.13% and 1.29% for the three different label fusions modalities, respectively.

To get better insight about performance of each method in selecting good atlases, Fig. 15 shows the number of relevant atlases selected by MI, HOG and HSR in the IXI dataset. The theoretical upper bound in the case of a perfect selection (i.e., GTR) is displayed as a black line. Similarly as in the ADNI database, the proposed method selects the highest number of relevant atlases. However, in this case the improvement of HOG over MI is not so evident. This highlights the importance of the machine learning component of our method for selecting good atlases.

Fig. 15.

Number of relevant atlases selected by each method in the IXI dataset. Vertical axis shows the number of relevant atlases and horizontal axis shows the number of selected atlases. A black line indicates the number of relevant atlases in the case of a perfect selection (GTR).

To further evaluate the performance of the different atlas selection methods, in Table VI we show the average surface distance errors incurred by the 9 different segmentation methods in segmenting the 30 smallest structures of the IXI database.

TABLE VI.

Mean and standard deviation of the average surface distances (in mm) incurred by the different methods in segmenting the 30 smallest structures in the IXI dataset by using K = 13 atlases

Atlas selection method	Overall surface distance
MI+MV	0.7767 ± 0.5052
HOG+MV	0.7761 ± 0.4996
HSR+MV	0.7437 ± 0.4536
MI+LWV	0.7504 + 0.4831
HOG+LWV	0.7542 ± 0.5036
HSR+LWV	0.7275 ± 0.4550
MI+NLWV	0.7539 + 0.5089
HOG+NLWV	0.7643 ± 0.5767
HSR+NLWV	0.7220 + 0.5028

Similar to what we have observed in the ADNI dataset, our atlas selection technique achieves lower surface distance errors and lower standard deviations than the other methods in all the three label fusion modalities. LWV and NLWV label fusions achieve similar performances in this dataset. Our proposed atlas selection method in combination with NLWV-based label fusion, HSR+NLWV, achieves the lowest mean surface distances compared to the other 8 segmentation methods in Table VI.

F. Results on the LONI Dataset

The LONI-LPBA40 dataset is provided by the Laboratory of Neuro Imaging (LONI) at UCLA and contains 40 brain images of size 220 × 220 × 184, each one with 56 manually labeled structures. We focus on the 20 smallest ones since they are usually the most challenging ones to segment. Similarly as we did in the case of the IXI dataset, we choose the number of atlases (K) for each selection method based on the results of the MV label fusion, which are shown in Fig. 16. We also include results of selection by ground-truth DR (GTR) to indicate the upper-bound in the case of an ideal atlas selection. Based on these results we choose the value of K = 17 for all the atlas selection methods.

Fig. 16.

Average segmentation performance achieved by the different selection methods combined with MV label fusion on the 20 smallest structures of the LONI dataset. Vertical axis shows the average performance, assessed by the Dice ratio, and horizontal axis shows the number of atlases used.

In Table VII we show the average Dice ratios obtained when selecting the best K = 17 atlases by each selection method. As we can see, the proposed atlas selection method achieves an improvement of ~ 0.5% in all label fusion modalities with respect to MI-based selection.

TABLE VII.

Average Dice ratios among all the ROIs in the LONI dataset by selecting the best K = 17 according to each selection method. Different atlas selection methods are arranged row-wise, and different label fusion modalities are arranged column-wise.

	MV	LWV	NLWV
MI	0.7731 ± 0.0715	0.7795 ± 0.0697	0.7915 ± 0.0697
HOG	0.7719 ± 0.0723	0.7779 ± 0.0709	0.7901 ± 0.0712
HSR	0.7786 ± 0.0694	0.7835 ± 0.0684	0.7955 ± 0.0687

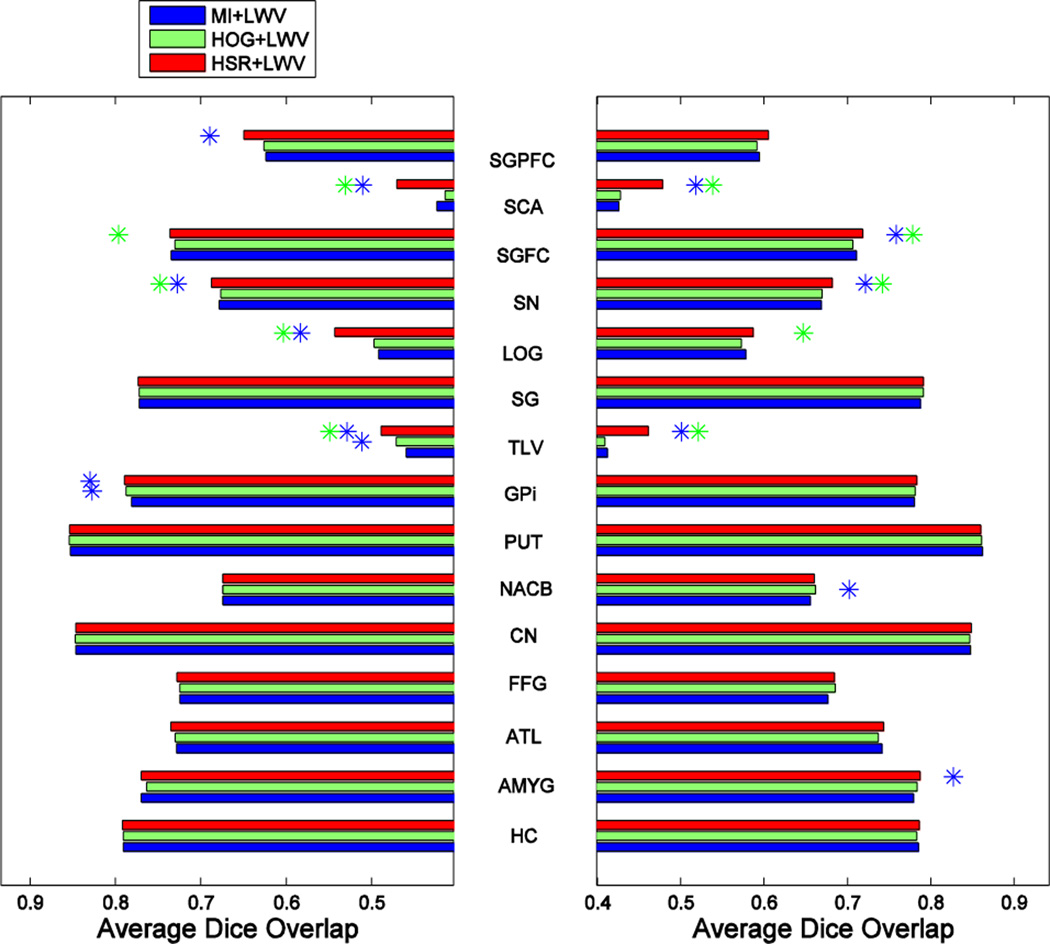
Fig. 17, Fig. 18 and Fig. 19, show, respectively, the average segmentation results, assessed by the Dice ratio, achieved by the different segmentation methods using K = 17 atlases. The left and right plots show the results for the left and right parts of each structure, with the name of each structure shown in the middle. Blue and green asterisks at the end of each bar represent a significant improvement of the respective method, according to a paired t-test with p ≤ 0.05, with respect to the MI- and HOG-based atlas selection methods, respectively.

Fig. 17.

Blue, green and red bars show the segmentation performances obtained by combining MV-based label fusion with different atlas selection methods on labeling the smallest 20 structures of the LONI dataset. Left and right plots show the results for the left and right parts of each structure, respectively, with the structure names shown in the middle. A blue and green asterisk represent significant improvement with respect to MI- and HOG-based selection, respectively.

Fig. 18.

Blue, green and red bars show the segmentation performances obtained by combining LWV-based label fusion with different atlas selection methods on labeling the smallest 20 structures of the LONI dataset. Left and right plots show the results for the left and right parts of each structure, respectively, with the structure names shown in the middle. A blue and green asterisk represent significant improvement with respect to MI- and HOG-based selection, respectively.

Fig. 19.

Blue, green and red bars show the segmentation performances obtained by combining NLWV-based label fusion with different atlas selection methods on labeling the smallest 20 structures of the LONI dataset. Left and right plots show the results for the left and right parts of each structure, respectively, with the structure names shown in the middle. A blue and green asterisk represent significant improvement with respect to MI- and HOG-based selection, respectively.

As we can see in these 3 figures, our atlas selection method achieves significant improvements with respect to MI-based atlas selection in 10, 9 and 7 (out of the 20 structures) for the MV-, LWV- and NLWV-based label fusions, respectively. Compared to HOG-based atlas selection, our method achieves significant improvements in 11, 7 and 7 structures, respectively. The average Dice ratio improvement of our atlas selection method, compared to the MI-based atlas selection method, is 0.59%, 0.45% or 0.42% when using MV-, LWV- or NLWV-based label fusions, respectively. Following a similar trend as in the ADNI and IXI databases, the proposed atlas selection method achieves larger improvement with respect to the MI-based atlas selection method for the simpler label fusion method (MV). The reason is that the simpler label fusion method (MV) offers more room for improvement to the atlas selection method.

To get better insight about performance of each method in selecting good atlases, Fig. 20 shows the number of relevant atlases selected by MI, HOG and HSR in the LONI dataset. The theoretical upper bound in the case of a perfect selection (i.e., GTR) is displayed as a black line. As we can see, the proposed method clearly outperforms all others.

Fig. 20.

Number of relevant atlases selected by each method in the LONI dataset. Vertical axis shows the number of relevant atlases and horizontal axis shows the number of selected atlases. A black line denotes the number of relevant atlases in the case of a perfect selection (GTR).

To further evaluate the performance of the different atlas selection methods, in Table VIII we show the average surface distance errors incurred by the different methods on the 20 smallest structures in the LONI database.

TABLE VIII.

Mean and standard deviation of the average surface distances (in mm) incurred by the different methods in segmenting the 20 smallest structures in the LONI dataset by using K = 17 atlases.

Segmentation variant	Overall surface distance
MI+MV	1.0113 ± 0.7125
HOG+MV	1.0072 ± 0.7073
HSR+MV	0.9871 ± 0.6950
MI+LWV	0.9772 ± 0.7204
HOG+LWV	0.9659 ± 0.7060
HSR+LWV	0.9522 ± 0.6922
MI+NLWV	0.9367 ± 0.7553
HOG+NLWV	0.9334 ± 0.7414
HSR+NLWV	0.9120 ± 0.7270

As we can see, segmentation methods using our proposed atlas selection technique achieve the lowest average distances and standard deviations compared to the other methods. Simpler label fusion methods are outperformed by more complex ones in terms of average surface distance. However, in terms of standard deviations, more complex label fusion methods show slightly less stability than simpler ones. The overall best performance is achieved by combining our atlas selection method with NLWV-based label fusion.

IV. Conclusions

We have presented a novel learning-based method for selecting the relevant atlases for multiple atlas segmentation. Our relevance score is directly defined to be related to the expected Dice ratio after non-rigid registration of an atlas and a target image. This measure is thus more related to the segmentation performance than a simple image similarity measure. Then, we use a learning-based method to map the image features before non-rigid registration to our relevance score. In this way, we avoid using the costly non-rigid registration prior to the atlas selection. Compared to similar state-of-the-art learning-based methods, our method can effectively deal with training sets of small size, as is usually the case in the case of multiple-atlas segmentation. Our proposed atlas selection leads to significant improvements in labeling various structures in the ADNI, SATA, IXI and LONI-LPBA40 datasets, compared to other atlas selection methods. Specifically, as shown by the ADNI dataset, our atlas selection method compares favorably to similar state-of-the-art learning-based methods as well as to image similarity based atlas selection methods. Moreover, it requires fewer atlases than image similarity based methods to get better performance, thus, considerably reducing the computational cost for the multiple-atlas segmentation. As we have seen in the SATA dataset, our atlas selection method can boost the performance of NLWV label fusion from the 2^nd to the 4^th position in the global ranking. Our method gets significant improvements on labeling several structures in the IXI and LONI-LPBA40 datasets, with respect to selection of atlases based on mutual information. Our future works include (1) evaluate our method on other clinical datasets such as 3D lung CT and infant brain images and (2) integrate our method with other MAS methods such as a sparse patch-based label fusion method [44] and a joint label fusion method [45].