A custom correlation coefficient (CCC) approach for fast identification of multi-SNP association patterns in genome-wide SNPs data

Abstract

Complex diseases are often associated with sets of multiple interacting genetic factors and possibly with unique sets of the genetic factors in different groups of individuals (genetic heterogeneity). We introduce a novel concept of Custom Correlation Coefficient (CCC) between single nucleotide polymorphisms (SNPs) that address genetic heterogeneity by measuring subset correlations autonomously. It is used to develop a 3-step process to identify candidate multi-SNP patterns: (1) pairwise (SNP-SNP) correlations are computed using CCC; (2) clusters of so-correlated SNPs identified; and (3) frequencies of these clusters in disease cases and controls compared to identify disease-associated multi-SNP patterns. This method identified 42 candidate multi-SNP associations with hypertensive heart disease (HHD), among which one cluster of 22 SNPs (6 genes) included 13 in SLC8A1 (aka NCX1, an essential component of cardiac excitation-contraction coupling) and another of 32 SNPs had 29 from a different segment of SLC8A1. While allele frequencies show little difference between cases and controls, the cluster of 22 associated alleles were found in 20% of controls but no cases and the other in 3% of controls but 20% of cases. These suggest that both protective and risk effects on HHD could be exerted by combinations of variants in different regions of SLC8A1, modified by variants from other genes. The results demonstrate that this new correlation metric identifies disease-associated multi-SNP patterns overlooked by commonly used correlation measures. Furthermore, computation time using CCC is a small fraction of that required by other methods, thereby enabling the analyses of large GWAS datasets.

Introduction

Genome-wide association (GWAS) studies have successfully identified numerous single nucleotide polymorphisms (SNPs) associated with human diseases [Manolio, et al. 2008]. However, complex diseases such as hypertensive heart disease (HHD) are results of multiple genetic factors with complex interactions amongst themselves and with the environment. Identifying these disease-associated SNPs with high-order (interaction) effects presents a great challenge for in-depth analysis of GWAS data due to genetic heterogeneity and the prohibitive number of potential interactions.

Complex diseases are generally characterized by genetic heterogeneity in which unique makeup of causative genetic factors are responsible for different patient groups exhibiting the same clinical disease trait. As such, genetic heterogeneity may result in a cluster of SNPs collectively associated with the disease trait for only a subset of all cases, which may render existing correlation measures useless. This may be illustrated by an example where two SNPs are perfectly correlated in half of the cases, but not at all for the remaining patients. In that case, Pearson’s correlation coefficient (PCC) and the linkage disequilibrium (LD) measure r², two commonly used metrics for SNP-SNP correlation [Carlson, et al. 2003; Devlin and Risch 1995; Thomas 2004], unduly penalize the scores by those individuals where the SNPs were uncorrelated and return low score values of 0.3 and 0.0, respectively. (see SNPs 5&6 in Table 1, which contains more examples.) In general, existing correlation measures return a single scalar value that is equally influenced by the entire sample, and as such, are not suitable for evaluating data of disease traits bearing appreciable genetic heterogeneity.

Table 1. Examples of 3 pairs of SNPs in 10 individuals (P1, …, P10) that illustrate theability of the maximum relationship R_ij, and maximum CCC_ij, i e {A,a}, j e {B, b}, to capture more meaningful and robust SNP correlations compared to PCC and r².

	Genotype of 10 individuals										|PCC|	r2	max Rij	max CCCij
	P1	P2	P3	P4	P5	P6	P7	P8	P9	P10
SNP 1	Aa	AA	AA	AA	AA	AA	AA	AA	AA	AA	0.1	0.0	0.9	0.5
SNP 2	bb	Bb	bb	bb	bb	bb	bb	bb	bb	bb
SNP 3	Aa	Aa	AA	AA	AA	AA	AA	AA	AA	AA	0.7	0.5	0.9	0.6
SNP 4	bb	Bb	bb	bb	bb	bb	bb	bb	bb	bb
SNP 5	AA	AA	AA	AA	AA	aa	Aa	AA	aa	aa	0.3	0.0	0.5	0.7
SNP 6	bb	bb	bb	bb	bb	Bb	BB	Bb	BB	bb

Note: For the first two pairs of SNPs, P3-P10 are perfectly matched with ‘AA’|‘bb’genotypes. The only difference between the two examples is that for individual P2, SNP 1 is ‘AA’ and SNP 3 is ‘Aa’. While the PCC and r² values are highly sensitive to this small difference, CCC exhibits little sensitivity. In the third example, SNPs 5 and 6 are perfectly matched for P1-P5 in half of the individuals and uncorrelated in individuals P6-P10. PCC and r² were overwhelmed by the lack of correlation in P6-P10 and returned low values. In contrast, CCC looked over the heterogeneity and correctly captured a high correlation value CCC_Ab for the ‘Ab’ relationship in P1-P5. Note that the CCC value for ‘Ab’ is higher for this example than it is for the first two pairs of SNPs, despite the fact that had more ‘AA’|‘bb’ individuals. This is because CCC adjusts for chance pairing due to varying allelic frequencies. In the second pair, the allele frequency is 0.90 for ‘A’ of SNP 3 and 0.95 for ‘b’ of SNP 4, which gives an expected frequency of 0.73 (0.90*0.90*0.95*0.95) for ‘AA’|‘bb’ just by chance paring. Since the observed frequency of ‘AA’|‘bb’ of 0.8 is only slighter greater than expected by chance, the CCCAb value is lower. However, in the third pair, where the expected frequency for ‘AA’|‘bb’ is 0.21 and the observed frequency is 0.50, the CCC gives a high CCC_Ab value owing to the excess of ‘AA’|‘bb’ pairing than expected by chance.Thus, CCC is able to capture meaningful correlations more accurately than PCC or r².

On a separate front, for complex diseases resulted from concerted action of multiple SNPs and environmental factors, the effect size of any individual SNP is likely very small. It is then desirable to identify clusters of multiple SNPs that collectively influence the disease phenotypes. However, GWAS studies typically test hundreds of thousands or even millions of SNPs, and the computations required to directly examine multi-SNP patterns quickly becomes infeasible: one million SNPs would result in 5.0 × 10¹¹ SNP-SNP pairings, but a computationally prohibitive 1.7 × 10¹⁷ SNP-trios. Therefore, clustering of SNPs in the network of all pairwise SNP interactions can be used to approximate (or to find candidates of) true multi-SNP association patterns. Unfortunately, existing correlation measures are again not suitable: two pairwise interactions involving a common SNP does not necessarily mean that all three SNPs are acting together because the pairwise interactions may have occurred in two distinct subgroups of people.

Herein we present an approach employing a novel Custom Correlation Coefficient (CCC, “triple C”) that is sensitive to relationships in subgroups of study samples, with a three-step procedure designed specifically to test for multi-SNP association with complex traits in genome-wide studies comprising: (1) fast-computation of genome-wide pairwise (SNP-SNP) correlations using CCC; (2) clustering of subgroups of SNPs connected by the pairwise correlations; and (3) identifying important clusters of SNPs that vary significantly between cases and controls.

At the core of this new approach, CCC is different from existing correlation measures in several ways. First, CCC identifies correlations autonomously, honing in on informative subgroups of samples without being overwhelmed by uninformative ones. Second, rather than a single scalar value, CCC returns a vector of four values representing the four different types of relationships for pairs of SNPs. This way, not only the correlated SNPs are identified, so are the relevant alleles and the individuals contributing to the correlation (see Methods). Finally, CCC is more robust with rare variants since, unlike other methods, CCC is defined for private mutations so they do not need to be discarded during analysis. This is of practical value when, say, running bootstrapping trials where a random sampling of rare variants may be monomorphic.

CCC is a simple and intuitive measure with low computational complexity, and further improvement is achieved by pre-computing a table of CCC values. We present an efficient algorithm to compute CCC, a breadth-first search to identify clusters of SNPs linked by pairwise correlations, and a simple filter that identifies patterns of correlated SNPs associated with disease phenotype. This novel procedure is computationally very efficient: in our experiments PCC took more than 15 times and r² more than 10,000 times as much computation time compared to CCC. While fast, the CCC-based approach still captures informative SNP pairs that are overlooked by other methods in real studies. Using genotype data in cases and controls from a GWAS study of hypertensive heart disease (HHD), we demonstrate CCC’s utility for identifying multi-SNP patterns that vary substantially between HHD cases and controls. These clusters are missed by conventional methods including PCC, r², and log odds ratio-based test of pairwise interactions such as fast-epistasis in the popular GWAS analysis package PLINK [Blaustein and Lederer 1999; Purcell, et al. 2007; Schulze, et al. 2003].

Methods

Custom correlation coefficient

Given the genotypes of two SNPs for a set of individuals exhibiting a particular phenotype, the goal is to quantify the relationships between alleles of the two SNPs among these individuals. The relationships will be obscured when some of the genotypes are heterozygous. In this study, we only consider biallelic SNPs. Let ‘A’ and ‘a’ represent the alleles for SNP 1, and ‘B’ and ‘b’ for SNP 2. The question is whether there is evidence for a different than chance occurrence for any of the four possible relationships: ‘AB’, ‘Ab’, ‘aB’, or ‘ab’. A positive evidence would indicate a correlation, or lack of independence, between the SNPs among these individuals. Several issues need to be sorted out to quantify the evidence. For instance, how to properly measure that the ‘a’ allele for the first SNP and the ‘B’ allele for the second SNP appear simultaneously for a substantial number of individuals? How does heterozygosity in the sample affect our characterization of this relationship? Moreover, some alleles are rare in the overall population and their prevalence within a relationship is an additional departure from randomness. How can the correlation measure reflect this additional information?

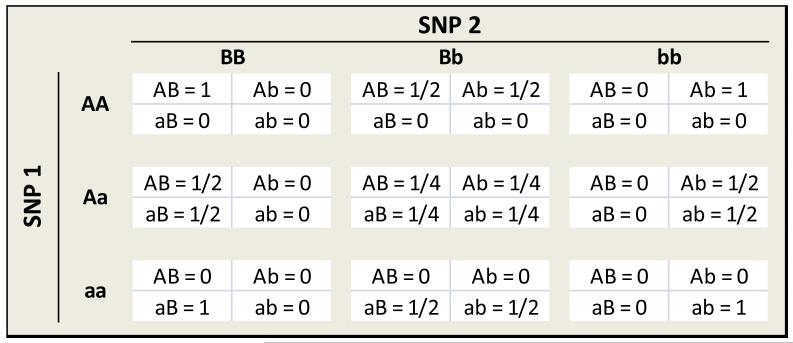
For quantifying co-occurrence of a pair of alleles, CCC uses a weighting score based on the expected frequency of the 2-locus haplotype conditional on observed genotypes. Figure 4 tabulates the weights assigned by CCC for the four relationships between a pair of biallelic SNPs. For a set of n individuals, the average value of these weights is computed for each of the four relationships. Let R_ij equal the average relationship value for alleles i and j. For example, R_ab equals the average weight for an ‘ab’ relationship for the group of individuals. Then R_ij values range from 0 to 1, and R_AB + R_Ab + R_aB + R_ab = 1.

Figure 4.

CCC weights for each of four relationship types for a pair of SNPs.

For adjusting the effect of rare alleles, we note that the correlation of rare alleles is a greater departure from randomness than is alleles with high frequency. CCC uses the following frequency factor:

$$F_i=1-\frac{f_i}{q}$$

where f_i is the frequency of allele i and q is a tuning parameter that is set to 1.5. The choice of this parameter is discussed in Section SI.2 of the Supporting Information. The R_ij values are each multiplied by the two frequency factors corresponding to the relevant alleles. This value is rescaled to have a broader range between 0 and 1 by multiplying it by 9/2. Thus, the definition of CCC_ij follows:

$$CC{C}_{ij}=9∕2R_{ij}{F}_i{F}_j$$

The special property of CCC is illustrated by examples in Table 1: robustness of CCC is shown by the first 2 pairs of SNPs: SNPs 1 and 2 are homozygous for all of the individuals, except individuals 1 and 2 are heterozygous for one SNP each. SNPs 3 and 4 are the same as SNPs 1 and 2 except individual 2 is heterozygous for two SNPs, instead of just one. This one small difference caused surprising increases in the PCC and r² values, while the maximum R_ij value (attended by an ‘Ab’ relationship) remained the same. Advantage of CCC under potential genetic heterogeneity is shown by the relationship between SNPs 5 and 6: they are perfectly correlated for half of the individuals and uncorrelated for the other half. While both PCC and r² overly penalized the uncorrelated individuals and detected low/no correlation (|PCC|=0.3, r²=0.0), CCC picked up the strong correlation which occurred in half of the samples and correctly detected a strong correlation of 0.7 for the ‘Ab’ relationship.

We note that this sensitivity of CCC partially came from its use of a vector of four values representing the four different types of coupling of pairs of alleles SNPs, rather than producing a single scalar to represent an “overall” relationship of the 2 SNPs. In general, using a global measure leads to loss of information encoded by specific pairwise relationships in subset of samples. For example, the program fast-epistasis implemented by PLINK [Purcell, et al. 2007] also computes the same four R_ij values (differ by a constant factor). However, it subsequently flattens these four values into a single scalar (log odds ratio) to test for SNP-SNP interaction by comparing the correlations in cases and controls. It is a popular method for identifying pairwise SNP interactions, and is used for comparisons presented here.

The computation of CCC for a pair of SNPs has the asymptotically fastest time possible, O(n), where n is the number of individuals. In other words, the computation time is equal to a constant multiplied by the amount of time required to just read in the genotype values. Furthermore, CCC is a divisible metric and as such allows subdividing large samples into manageable chunks. We have exploited this property and implemented a technique to further reduce computation time to less than a quarter of the original time by using an encoding and table look-up scheme, along with an option for conservative early terminations. This technique is described in Section SI.1 of the Supporting Information.

Network models

Using the concept of guilt-by-association [Quackenbush 2003; Stuart, et al. 2003] and any one of the correlation metrics, a network model can be constructed to identify clusters of multiple SNPs linked by pairwise correlations. One option is to create a network in which each node represents a SNP and each edge connects a pair of SNPs whose correlation is greater than a given threshold. The use of CCC allows for a second option -- to construct an allelic network. Because the relevant alleles are returned with the CCC values, the network is constructed with two nodes for each SNP. An allelic network maximizes information retention and improves the possibility of identifying relevant multi-SNP association patterns.

Breadth-first search

Genome-wide association studies typically assay hundreds of thousands, or even millions, of SNPs. Most of these SNPs are uncorrelated with each other. Therefore, both SNP and allele networks tend to be large and sparse. The large sparse networks that we have explored in this research typically contained thousands of disconnected components, or clusters. These clusters can be efficiently identified using breadth-first search (BFS) [Russell and Norvig 2010]. BFS explores each cluster one at a time, and identifies the memberships of the clusters that become multi-SNP patterns for downstream association analysis. A computer program optimized to perform BFS search for large, sparse networks was implemented. Pseudocode for BFS is included in Section SI.3 of the Supporting Information. Using this program, networks with one-half million nodes can be subdivided into thousands of disconnected clusters in less than 15 seconds.

Hypotheses checker (HC)

The HC is a simple and efficient program for testing a multi-SNP pattern for variation between cases and controls. It detects concerted action of the SNP cluster by checking the hypothesis for substantial association of the multi-SNP pattern with the disease status. For every cluster in the cases network, HC compares the number of cases and controls possessing the multi-SNP pattern. The relative difference between the two groups measures the strength of association and a threshold δ is used to determine those comprising SNPs/alleles whose concerted actions are associated with the disease. Similar checking is repeated for every cluster in the control network. Details of HC are described in Section SI.4 of the Supporting Information.

Pearson’s correlation coefficient (PCC), LD measure r²

PCC is a general correlation measure widely used in many domains including genetic data analysis. To measure correlation between 2 SNPs, one may simply count the copies of a designated allele at each marker (e.g., ‘A’ & ‘B’) in each subject, and calculate the correlation between the 2 vectors of allele counts:

$$PC{C}_{xy}=\frac{\mid x\mid \mid y\mid \cos \theta -n\overline{xy}}{(n-1){\sigma }_x{\sigma }_y}$$

where θ is the angle between vectors x and y, with dimension n that equals the number of individuals, and σ is the standard deviation. Or, the correlation may be directly calculated between the designated alleles of the 2 markers:

$$r=D∕\sqrt{p\left(A\right)\times p\left(a\right)\times p\left(B\right)\times p\left(b\right)}$$

where p(x) is the observed probability of x, and D is defined as

$$D=p\left(AB\right)-p\left(A\right)\times p\left(B\right)$$

The squared value r² is a commonly used measure of linkage disequilibrium (LD) in genetic analysis. For biallelic SNPs, the r² value is invariant of the choices of designated alleles.

PLINK’s fast-epistasis

Related to the concept of pairwise correlation of SNPs, epistasis or SNP-SNP interaction refers to the phenomenon where strength of the correlation changes according to disease status, or, the phenotypic expression of a disease allele at one locus depends on an allele at the other locus [Cordell 2002]. For case-control studies, SNP-SNP interaction may be tested by any 2-sample statistics for significant changes in correlation strength between cases and controls. In the popular GWAS analysis package PLINK, a log odds ratio-based test is implemented (called fast-epistasis) to perform such test for pairwise SNP-SNP interactions.

It begins by computing four values similar to R_ij utilized by CCC, in a in a 2×2 table, denoted as a, b, c, and d:

$$\begin{array}{cc}\hfill a=& R_{AB}\times 4n\hfill \\ \hfill b=& R_{Ab}\times 4n\hfill \\ \hfill c=& R_{aB}\times 4n\hfill \\ \hfill d=& R_{ab}\times 4n\hfill \end{array}$$

where n = the number of individuals in the group. These values are computed separately for cases and controls, and a Z-score test for epistasis is performed on the difference of log odds ratios:

$$Z=\frac{\log \left(R\right)-\log \left(S\right)}{\sqrt{SE\left(R\right)+SE\left(S\right)}}$$

where R and S are equal to ab/cd for cases and controls, respectively, and SE is the standard error.

Datasets

Both real and simulated random data were used in our experiments. Real genotype and phenotype data were obtained from a subset of genome-wide study of Hypertensive Heart Disease at Washington University; the subset consisted of 74 HHD cases and 70 controls.

Hypertension affects millions of people and HHD is associated with elevated cardiovascular morbidity and mortality[Fields, et al. 2004]. Genetic variants of hypertension and HHD were implicated by numerous studies including several recent GWAS, but the findings are mostly about single variants and little is known about the effect of multi-marker patterns[Arnett, et al. 2007]. The clinical phenotypes of HHD for this study were carefully evaluated using structure (LVM/Ht^2.7), systolic function (EF), diastolic function (E’), and carotid artery intima-media thickness (CIMT). Fasting BMP, glucose, insulin, lipids, plasma/serum, and DNA were collected and utilized with echocardiographs, carotid artery ultrasounds, 24-hour ABPM, arterial compliance, cardiovascular history, and physical exam (VS and body habitus) in these evaluations. Case or control status was determined by a risk score derived by independent component analysis of the panel of 46 clinical HHD traits and covariates [Gu, et al. 2008]; a total of 150 subjects were sampled from the high and low end of the distribution of the risk score and genotyped using the Affymetrix Mapping 500K Array Set. The SNPs data underwent quality control using commonly accepted criteria on array quality (missing rate ≤ 0.05, mean heterozygosity between 0.25 and 0.3) and on marker quality (call rate ≥ 0.99 for SNPs with MAF ≤ 0.05, call rate ≥ 0.95 for all other SNPs, and Hardy-Weinberg test p-value > 10⁻⁶). After QC, 74 cases and 70 controls were retained with data on 389,344 SNPs. We further removed all SNPs with missing values and the X and Y chromosomes, resulting with 219,407 complete and autosomal SNPs for analysis. While omitting SNPs with one or more missing values decreased the number of SNPs, we did not impute data for this study as the errors introduced by imputation are biased toward increased linkage disequilibrium and may skew the results.

The random genotypes were generated by first randomly selecting a minor allele frequency (MAF), followed by randomly selecting genotypes based on these MAF values. This dataset has 72 individuals and 219,407 SNPs, so as to mimic the size of the biological datasets.

Results

Definition of CCC and the details of the CCC-based 3-step approach for fast genome-wide scan of multi-SNP patterns are presented in Online Methods. Findings of our experiments applying the CCC method to a GWAS study of HHD are described in this section. Details of the datasets are also described in Online Methods.

Determination of a significant threshold of CCC

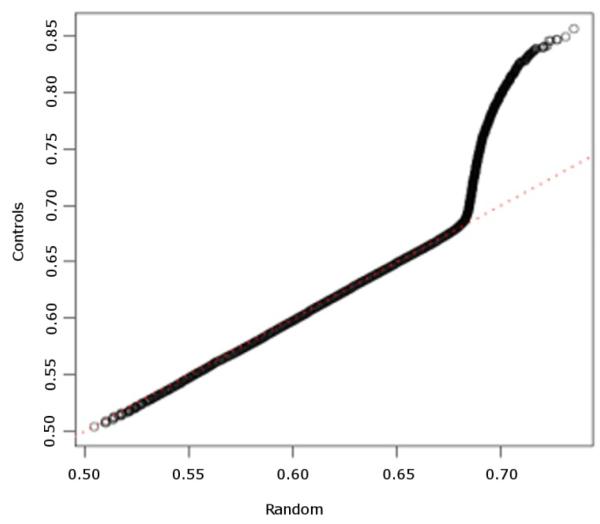
Because the distribution of CCC values is mathematically intractable, we used simulation to determine an appropriate threshold for significant CCC values. The threshold is determined by examining distributions of CCC in a sample of normal (control) subjects and that of a simulated dataset of random genotypes with no biologically meaningful SNP-SNP correlations. We ran CCC on the HHD controls dataset and a simulated dataset of random genotypes (see Methods) and created histograms from resulting CCC values. For each pair of SNPs, the maximum CCC_ij value was used in the tally of values for each of 10,000 bins. Figure 1 is a QQ-plot of CCC values in the controls and in the simulated data. The CCC values for the controls began diverging from the random values at about 0.68. Based on this observation, a threshold of 0.7 was used for CCC in all our experiments to declare significant SNP-SNP correlations.

Figure 1.

QQ-plot of CCC values for HHD controls and randomly-generated data.

Network models constructed by CCC, PCC, and r²

For each correlation method, we constructed networks in HHD cases and controls separately; each was composed of nodes (SNPs or alleles) with edges connecting pairs of nodes if the correlation between the two nodes was above a significance threshold.

First, CCC was computed for all pairs of SNPs in the HHD cases and controls data (analyzed separately). As discussed above, all CCC_ij values that were ≥ 0.7 were recorded as edges between the relevant alleles/SNPs in the networks. This produced 211,255 edges for the cases network and 204,538 edges for the controls network. These networks were highly sparse, and the percentages of pairwise correlations that had scores of at least 0.7 were 0.00088% and 0.00085% for cases and controls, respectively.

To construct the PCC network, a comparable threshold for PCC should be found ideally by extracting the highest 211,255 and 204,538 pairwise PCC absolute values for the cases and controls, respectively. However, PCC does not discriminate high correlation values as well as CCC or r², and all of the extracted edges had PCC absolute values of one. In fact, cases had 881,785 edges and controls had 923,331 edges with PCC absolute values of one. We set the threshold for PCC to one, resulting with networks that have more than four times as many edges as the CCC networks.

The LD measure r² is computationally demanding and it was not computationally feasible to compute r² for all possible SNP pairs in GWAS datasets. To estimate a comparable threshold for r², we used data from chromosome 2, genotyped with 18,508 SNPs. Extracting the same percentage of edges (0.00088% and 0.00085% for cases and controls, respectively) with the highest r² values, the corresponding thresholds were 0.999387 for cases and 0.999390 for controls.

Subsequently, four additional networks using PCC and r² were constructed separately in the case and control datasets. Numbers of edges in each of the six networks are displayed in Table 2.

Table 2. Structural characteristics of correlation networks identified by BFS and the three correlation measures: CCC, PCC and r², in the GWAS data of 74 HHD cases and 70 controls.

		CCC		PCC		r2(*)
		Controls	Cases	Controls	Cases	Controls	Cases
Number of Edges		211,255	204,538	881,785	923,331	1,678	1,619
Size of Clusters (†)	Median	3	3	2	2	2	2
	Average	5.157	4.575	2.863	2.867	2.499	2.547
Density of Clusters	Median	1	1	1	1	1	1
	Average	0.911	0.901	1.000	1.000	0.998	0.998
Number of Clusters with at Least 3 Nodes		10,101	11,697	8,522	8,268	211	191

^*The r² values are for Chromosome 2 only.

^†Singletons were not included in the calculations.

PCC, r², and CCC network comparisons

To further compare networks constructed by the three correlation methods, breadth-first search (BFS) was applied to identify connected components, or clusters, in each network. Sizes and densities of these clusters are listed in Table 2, together with the numbers of clusters with at least three nodes. The density is defined as the ratio of the number of edges in the cluster to the maximum number of edges possible. Singletons, which are nodes with no edges, were not included in the calculations.

For both cases and controls, CCC found substantially more clusters with at least three nodes than found by PCC. This result is quite surprising as the PCC network contained more than four times as many edges distributed over the same number of nodes. The r² results were derived from only chromosome 2, so this number is not comparable.

A doubleton, or a cluster comprised of two nodes and one edge, always has a density of one, as the edge connecting the nodes is the only edge possible. Noisy edges frequently appear as doubletons in networks; and a large number of doubletons likely reflect a high level of random noise in a network. As shown in Table 2, for both PCC and r² the median cluster size was 2 and average clusters sizes were also small (2.499 to 2.867). These combined with high average density values indicate a large number of doubletons for the two methods. In contrast, CCC had a greater proportion of clusters with at least three nodes, with median cluster sizes of 3 and much larger average clusters sizes (5.157 for cases and 4.575 for controls). In general, larger clusters tend to have lower densities due to the exponential growth of the number of possible edges. However, despite the larger cluster sizes, CCC clusters had surprisingly high average densities (> 0.9). For example, in a cluster consisting of five nodes, a density of 0.9 indicates that nine of the ten possible edges are present. Therefore, the CCC networks showed stronger community structure than those produced by PCC or r², because they contain a greater proportion of larger clusters (at least 3 nodes) and maintained high densities of edges.

CCC clusters exhibiting variations with HHD

In correlation networks of SNPs, tighter community structure could be the result of many SNPs genotyped from the same LD blocks, or of multiple SNPs from the sample biological functional units/pathways, or both. We expect that LD blocks of variants irrelevant to a disease phenotype will be largely the same in both cases and normal controls. Then, biologically important SNP clusters may be identified by comparing the communities of networks in cases and controls. We call these clusters SNP interaction (sub)networks or multi-SNP association patterns (see Methods).

Because CCC returns the specific alleles that are correlated, not just the pair of SNP loci, we were also able to construct allele networks, in which each SNP was represented by two nodes, one for each allele. Following the same procedure of applying breadth-first search we can derive the community structure of allele clusters. The advantage of using allele clusters is that it allows us to check if an individual possesses any or all alleles of the cluster. This was done as part of a procedure called Hypotheses Checker (HC) that examine clusters in allele networks and directly determines how many case and control subjects possess all of the alleles in each cluster and identify multi-SNP association patterns (clusters) that exhibit associations with the disease. (see Methods and Supporting Information (SI)).

For the HHD networks, this method identified 42 candidate clusters, 22 of which are more prominent for controls and 20 which are more prominent for HHD cases. The annotations for these 42 clusters are listed in Tables S2 and S3 of the Supporting Information.

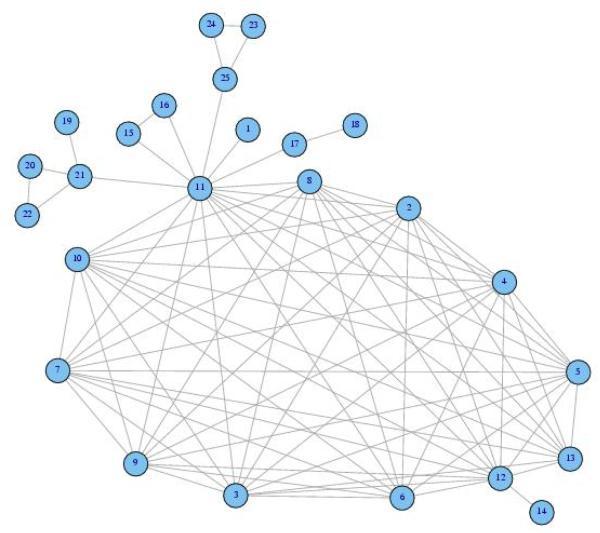
Details of two of the clusters are presented below as they include several SNPs from the SLC8A1 (aka NCX1) gene, which is essential for returning the heart to the resting state following excitation [Blaustein and Lederer 1999; Schulze, et al. 2003]. Cluster #22 contains 25 SNP alleles, including 13 from SLC8A1, spanning seven genes on six different chromosomes. This cluster is plotted in Figure 2; and Table 3 lists the 25 SNPs, the correlated alleles and their frequencies in cases and controls. Notably, while the entire cluster pattern is significantly more prominent for the controls, exerting a protective association, six of the correlated alleles have lower frequencies in the controls than the cases. This result highlights the fact that significant associations of clusters of SNPs can expose SNPs that would not exhibit associations when examined in isolation.

Figure 2.

Allele network of Cluster #22 including 25 SNPs. Edges are computed using CCC for genotype data from controls.

Table 3.

The associated alleles of the 25 SNPs comprising Cluster #22. Alleles that are less frequent in controls than cases are highlighted in yellow.

Node Number	Identified Allele	Frequency in Controls	Frequency in Cases	SNP	rs.ID	Chromo some	Position	Gene
1	G	0.436	0.473	SNP–A-1940790	rs42814	2	40679386	SLC8A1
2	T	0.386	0.358	SNP–A-2296948	rs10048831	2	40770673	SLC8A1
3	G	0.386	0.358	SNP–A-4208023	rs10490261	2	40771068	SLC8A1
4	C	0.507	0.432	SNP–A-2306108	rs7589309	2	40794558	SLC8A1
5	A	0.507	0.432	SNP–A-4296426	rs918013	2	40801916	SLC8A1
6	C	0.371	0.291	SNP–A-2128224	rs1107932	2	40802672	SLC8A1
7	T	0.436	0.345	SNP–A-2243130	rs4952645	2	40803110	SLC8A1
8	A	0.486	0.392	SNP–A-4208026	rs10490262	2	40805171	SLC8A1
9	G	0.379	0.291	SNP–A-4238930	rs12105490	2	40813313	SLC8A1
10	A	0.471	0.392	SNP–A-1962895	rs12712708	2	40817419	SLC8A1
11	A	0.329	0.324	SNP–A-4261874	rs1456587	2	40842768	SLC8A1
12	T	0.414	0.385	SNP–A-2097854	rs11124763	2	40891407	SLC8A1
13	A	0.514	0.446	SNP–A-1962896	rs7591057	2	40917895	SLC8A1
14	A	0.443	0.541	SNP–A-2110839	rs11726451	4	59534976	unknown
15	G	0.371	0.318	SNP–A-2251200	rs13253777	8	20116050	ATP6V1B2
16	C	0.379	0.324	SNP–A-4280883	rs11204102	8	20137423	LZTS1
17	T	0.307	0.176	SNP–A-2152050	rs7849064	9	72727974	TRPM3
18	G	0.279	0.149	SNP–A-1881292	rs7041925	9	72775609	TRPM3
19	T	0.343	0.405	SNP–A-2221667	rs11245048	10	128245557	C10orf90
20	T	0.471	0.527	SNP–A-2036244	rs12264765	10	128258265	C10orf90
21	T	0.400	0.453	SNP–A-1869292	rs10901638	10	128260689	C10orf90
22	T	0.471	0.547	SNP–A-2207236	rs10128487	10	128263169	C10orf90
23	G	0.300	0.264	SNP–A-2019879	rs8134934	21	41375695	unknown
24	C	0.293	0.257	SNP–A-2019884	rs2837941	21	41390710	unknown
25	T	0.350	0.324	SNP–A-2019889	rs2837956	21	41401386	unknown

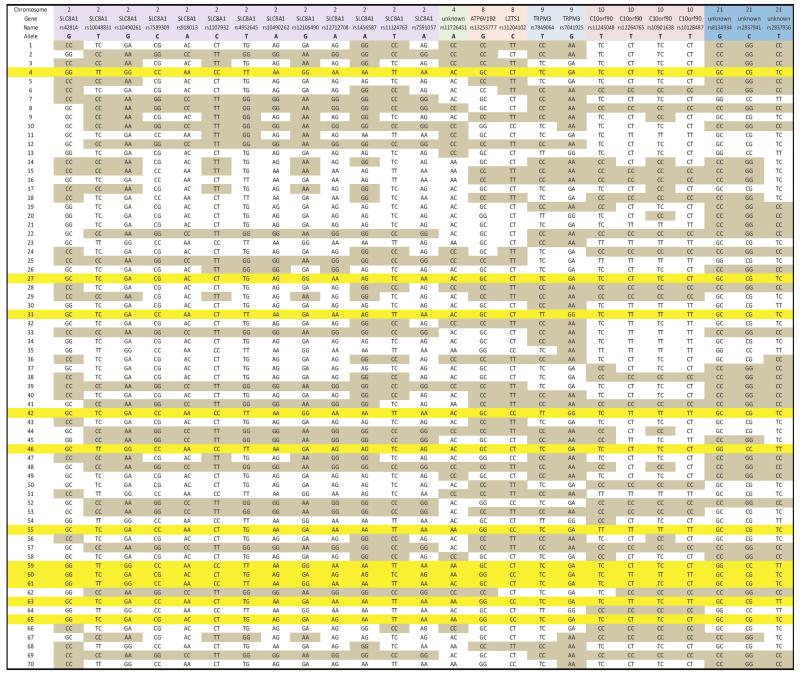
Tables 4 and 5 list the individual genotypes for the 25 SNPs in cases and controls, respectively. The rows for individuals with all 25 risk alleles identified by Cluster #22 in the controls are highlighted in yellow (16% of the controls, Table 5); no individual in the cases possessed all 25 associated alleles. Following visual inspection, it was observed that exclusion of three SNP alleles results in a cluster representing 20% of the controls and still none of the cases, as shown in Table S1. The odds ratios and p-values for the difference between cases and controls are undefined since none of the control individuals have all associated alleles.

Table 4.

Genotypes for the 25 SNPs from CCC Cluster #22 in 74 cases. Genotypes lacking the associated allele are shaded. None of the cases had all of the associated alleles.

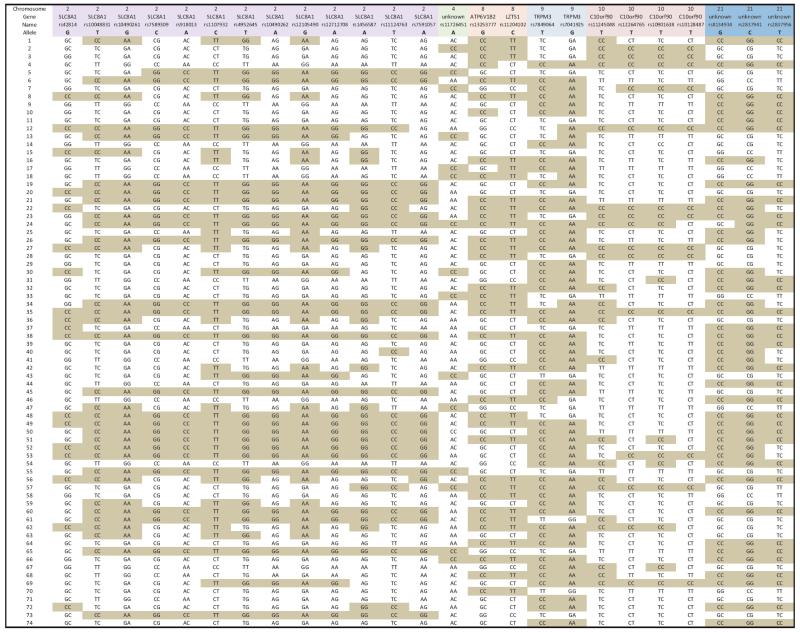
Table 5.

Genotypes for the 25 SNPs from CCC Cluster #22 in 70 controls. Genotypes lackingthe associated allele are shaded; the rows for individuals with all 25 of the identified alleles are highlighted in yellow (16% of the controls).

The second cluster of interest, Cluster #25, includes 32 SNP alleles with 29 from the SLC8A1 gene. Whereas the SNPs in Cluster #22 lie between positions 40679386 and 40917895, the SNPs from Cluster #25 lie between positions 41400411 and 41756046. Furthermore, unlike the pattern in Cluster #22, the allele pattern in Cluster #25 exhibits a risk association, as it is more common in cases than in controls.

The allele frequencies and additional information of all the clusters identified by HC in cases and in controls are listed in Table S2 and S3, respectively. As seen in Cluster #22, the frequencies of the alleles in Cluster #25 also are similar for cases and controls, with three of the alleles more frequent in the controls than cases. This 32-allele pattern was found in 3% of the controls and in 20% of the cases, yielding an odds ratio of 8.36 (p =9.2*10⁻⁴) and p =6.4*10⁻⁴ by G-test of independence [Sokal and Rohlf 1994]. Since the purpose of analyzing the HHD data is to demonstrate the application of CCC method, these values have not been adjusted for multiple testing. Validation of the findings using an independent dataset is an important next step for this research beyond the scope of this manuscript.

In summary, analysis using CCC identified 42 multi-SNP patterns that exhibit variations with HHD, two of which are of particular interest because they contain alleles in 2 regions of SLC8A1, a known candidate gene of cardiac function. When considered as a whole, each of these patterns exhibits strong association with HHD status, while the frequencies of individual alleles vary only slightly between cases and controls. This demonstrates the power of CCC for identifying subtle patterns that encode synergistic interactions of multiple causative (risk or protective) variants.

PCC and r² results for the two clusters

The numbers of edges identified by all three correlation metrics: CCC, PCC, and r², for the SNPs in clusters #22 & #25 are listed in Table 6. PCC and r² found only three to four disconnected doubleton correlations for the 25 SNPs in Cluster #22. Of the 25 SNPs, 17 to 19 were completely missed and didn’t have any comparable PCC or r² correlations. In contrast, CCC produced 80 and 71 edges for the cases and controls, respectively.

Table 6.

Number of edges found by each method for clusters #22 and #25.

	# of SNP Alleles	CCC		PCC		r2
		Controls	Cases	Controls	Cases	Controls	Cases
Cluster #22	25	80	71	3	4	3	3
Cluster #25	32	326	368	38	38	38	38

For Cluster #25, with 32 SNPs, there were 38 edges in networks derived using PCC or r². Interestingly, both methods returned identical networks for both cases and controls. These edges included four doubletons and two additional clusters connecting four and eight SNPs. Eleven of the 32 SNPs were singletons. In contrast, CCC produced 326 and 368 edges for this cluster of SNPs in the cases and controls, respectively.

Comparisons with Fast-epistasis

Next, the CCC-derived interaction networks (multi-SNP association patterns) were compared to those produced by log odds ratio-based test of epistasis implemented as fast-epistasis by PLINK [Purcell, et al. 2007]. Fast-epistasis compares correlations of each pair of SNPs by a log odds ratio test between cases and controls and returns a p-value that determines the significance of the variation (see Methods). It is used to construct an interaction network by placing edges between pairs of nodes representing SNPs with significant pairwise interactions. To obtain a comparable threshold for fast-epistasis, we computed fast-epistasis values for every pair of SNPs and simply extracted the 1,665 pairs with the highest values. This number of edges is equal to the number of edges in all 42 interaction networks identified by the 3-step procedure (CCC+BFS+HC). Subsequently, the same BFS procedure was used to identify all connected components (clusters).

The structural characteristics of the CCC+BFS+HC and fast-epistasis derived interaction networks are summarized in Table 7. Whereas fast-epistasis produced a substantially greater number of clusters with at least three nodes compared to CCC (343 versus 42, respectively), clusters produced by fast-epistasis were generally smaller (median and average sizes of 2 and 2.824 nodes, respectively). The CCC interaction network generated larger clusters with median and average sizes of 8 and 10.452 nodes, respectively. The 1,665 edges are spread over only 42 clusters with densities averaging 0.527. Finally, the fast-epistasis network completely missed the SNPs in Clusters #22 and #25 as there were no edges between any SNPs in these clusters.

Table 7.

Comparison of number of clusters with at least three nodes and sizes and densities of clusters for two interaction networks: Fast Epistasis and the CCC+BFS+HC combination.Singletons were not included in the calculations.

		Fast Epistasis	CCC+BFS+HC
Size of Clusters	Median	2	8
	Average	2.824	10.452
Density of Clusters	Median	1	0.5
	Average	0.825	0.527
	# of Clusters with at Least 3 Nodes	343	42

It is notable that fast-epistasis based approach process interactions of each pair of SNPs first, then construct the network. In contrast, the CCC+BFS+HC based construction first identifies potential networks, then compares entire clusters of SNPs/alleles between cases and controls, without filtering out SNP-SNP interaction pairs that do not independently vary between cohorts.

Computation Time

Each trial was divided into a number of subsets, which were run as single threads on a quad 2400 MHz processor with 8 GB of memory. Table 8 enumerates the computation times for CCC, PCC, r², fast-epistasis, and the 3-step CCC+BFS+HC combination. CCC could be further sped up by using a conservative early termination, as described in Section SI.1 of the Supporting Information. This feature is for extremely high-dimensional data and was not used by trials reported here.

Table 8.

Computation time required for each correlation and interaction method.

Method		# of Pairs Computed	% of Pairs Computed	Computation Time
Correlation	r2	3.42E+08	0.71%	40 days
	PCC	4.81E+10	100%	110 hours
	CCC	4.81E+10	100%	7 hours
Interaction	Fast Epistasis	4.81E+10	100%	48 hours
	CCC+BFS+HC	4.81E+10	100%	7 hours

Computation of the r² values for Chromosome 2 took 40 days, covering only 0.71% of all possible correlations for the GWAS data. PCC computed all of the correlations in 110 hours and CCC required only 7 hours. A pre-computed look-up table of values was used by CCC and this table was computed in about a half second. Therefore, PCC required more than 15 times, and r² required more than 10,000 times, of computation time than was used to compute CCC.

Once the correlated alleles were found by CCC, finding candidate multi-SNP association patterns (interaction networks) required a negligible amount of time. BFS computation times ranged between 2 and 15 seconds for the genome-wide networks and took less than 0.5 second to run BFS on the r² results for Chromosome 2. HC required 22 seconds to test 48,624 clusters. In contrast, fast-epistasis required 48 hours, which is almost 7 times as long as the 7 hours that were required by the CCC+BFS+HC combination. These results demonstrate that the new approach is significantly faster than existing methods and suitable for conducting genome-wide analysis of multi-SNP interactions.

Discussion

We have introduced a new correlation metric CCC that accommodates genetic heterogeneity and a network model that utilizes this metric to identify patterns of correlated SNP alleles. The application of this method to real data from a GWAS study of hypertensive heart disease (HHD) found 42 candidate multi-SNP association patterns. Two of these patterns (Cluster #22 & #25) appeared immediately interesting as they involve many variants in the vicinity of SLC8A1 (aka NCX1), which is essential for an Na⁺/Ca²⁺ exchanger involved in maintaining cellular calcium homeostasis for cardiac myocytes, a primary mechanism for the export of Ca²⁺ in the heart [Blaustein and Lederer 1999; Schulze, et al. 2003]. The effects of the two groups of SLC8A1 alleles are distinct; those in Cluster #22 appear to be protective as #22 was only present in controls, while those in Cluster #25 contribute to risk of HHD as the cluster was more prominent in cases. The two groups of SNPs reside in distinct LD blocks in the region, therefore possible cis-regulations of these variants on the expression of SLC8A1 deserve further investigation.

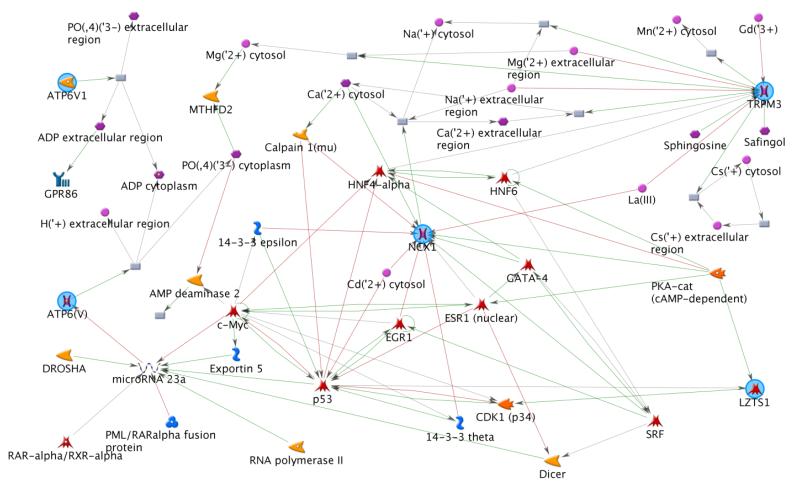
We were also intrigued by the interactions involving the SNP alleles in other genes. For Cluster #25, aside of the SNP alleles in/near SLC8A1, one allele in LRRK2 and two in an intergenic region on chromosome 16 were involved. Little is known about the region, but LRRK2 was associated with familial and sporadic Parkinson’s Disease, possibly involving cardiac sympathetic denervation [Gilks, et al. 2005]. For Cluster #22, more genes are involved besides SLC8A1, including SNP alleles from/near ATP6V1B2, LZTS1, TRPM3, and C10orf90, along with four in poorly annotated intergenic regions. It is unknown whether the genes representing these SNP alleles, or other genetic variants in close proximity, are responsible for the observed HHD phenotype. Short of a direct functional study of these genes, possible functional relationships among them were explored using GeneGO/MetaCore, an annotation database that includes more than 120,000 manually curated interaction pathways drawn from published research [Blow 2009]. (The open reading frame, C10orf90, was not included in the MetaCore analysis; however, we note that it is adjacent to ADAM12 on chromosome 10 which is associated with cardiac hypertrophy, a defining characteristic of HHD [Asakura, et al. 2002].) The network from the MetaCore analysis is shown in Figure 3 and revealed an abundant collection of known molecular interactions connecting the genes through mechanisms involving various RNAs, binding proteins, transfactors, inorganic ions, and enzymes, in multiple cellular regions.

Figure 3.

MetaCore network for five known genes associated with the 25-node candidate association cluster. SLC8A1/NCX1 is shown in the center. The open reading frame, C10orf90, was not included in the MetaCore network. C10orf90 is adjacent to ADAM12 on Chromosome 10.

Although the truth about the involvement of these potential pathways in HHD is unknown, they provide a way for designing further studies of specific mechanisms of HHD and a means for integrating findings from such studies using the components and topology described by the identified network. However, as shown above, none of the information would be detected when conventional correlation metrics such as PCC or r² were used. This demonstrates the unmet challenges of current methods for identifying subtle multi-SNP patterns in heterogeneous samples that show little variation in frequencies for single or pairwise SNPs. Because the conventional correlation metrics are insensitive to relationships in subsamples, they fragment large network components into small pieces and failed to integrate a substantial number of the (within-subsample) interacting SNPs into larger networks. Furthermore, because the existing methods filter out individual pairwise interactions first, variants that contribute only to larger multi-SNP patterns are prematurely excluded and will never become part of the network. In our HHD example, only two patterns including four and eight SNPs were identified by fast-epistasis, with the remaining networks consisting of only two SNPs each. Upon close examination, each of these doubleton networks was comprised of SNPs in close proximity, likely a reflection of LD.

The power for detecting interacting variants is apparent when a larger number of correlated SNPs are examined in unison. The CCC+BFS+HC procedure examines multi-SNP patterns within cases and controls without first filtering out pairwise interactions, and as so is able to retain large patterns of SNP alleles going beyond single-variant or pairwise effects. Indeed, in the HHD example, the two clusters of interest include SNP alleles with only small variations in allelic frequency between cohorts; and the fast-epistasis results confirm that none of the SNP-SNP pairs exhibit high variation between cases and controls.

A caveat of our “data-driven” approach should be noted. We determined the CCC threshold of 0.7 by comparisons of CCC values for the HHD controls and simulated random genotypes. Note that an optimal CCC threshold may be different for future studies dependent upon properties of the data of interest. More generally, the mathematical properties underlying the CCC metric, particularly the effects of sample sizes and genome-wide MAF distribution or genetic diversity, warrant further investigation.

In conclusion, this study has contributed to the existing body of research on genome-wide analysis of interactions by 1) presenting a novel analysis method that accommodates genetic heterogeneity; and 2) demonstrating the ability of this method to identify subtle multi-SNP association patterns hidden in GWAS data. Using this technique, 42 candidate association patterns for HHD were identified. These patterns are comprised of SNP alleles that show little, and sometimes misleading, variation of frequencies between cases and controls; yet synergistic combinations among these alleles associate with the HHD trait. Future studies are necessary to validate the candidate multi-SNP patterns associated with HHD in independent datasets and to explore causal mechanisms possibly tagged by the identified SNP alleles. While the CCC method is highly customized for SNP data, the concept of autonomous subset correlation can be extended to other domains (e.g., gene expression data analyses) where heterogeneity is problematic, to enable discovery of higher-order and subtle multi-variant patterns that will help explain the mechanisms of complex diseases.