Improved Subspace Estimation for Low-Rank Model-Based Accelerated Cardiac Imaging

Abstract

Sparse sampling methods have emerged as effective tools to accelerate cardiac magnetic resonance imaging (MRI). Low-rank model-based cardiac imaging uses a pre-determined temporal subspace for image reconstruction from highly under-sampled (k, t)-space data and has been demonstrated effective for high-speed cardiac MRI. The accuracy of the temporal subspace is a key factor in these methods, yet little work has been published on data acquisition strategies to improve subspace estimation. This paper investigates the use of non-Cartesian k-space trajectories to replace the Cartesian trajectories which are omnipresent but are highly sensitive to readout direction. We also propose “self-navigated” pulse sequences which collect both navigator data (for determining the temporal subspace) and imaging data after every RF pulse, allowing for even greater acceleration. We investigate subspace estimation strategies through analysis of phantom images and demonstrate in vivo cardiac imaging in rats and mice without the use of ECG or respiratory gating. The proposed methods achieved 3-D imaging of wall motion, first-pass myocardial perfusion, and late gadolinium enhancement in rats at 74 frames per second (fps), as well as 2-D imaging of wall motion in mice at 97 fps.

I. Introduction

THE practical utility of cardiac MRI is limited by its relatively low imaging speed. In recent years, significant effort has been made to accelerate cardiovascular MRI using sparse sampling data acquisition strategies. Early examples of sparse sampling for cardiac MRI include DIME [1], UNFOLD [2], and k-t BLAST [3]; more recent methods use sparsity models (often known as compressed sensing, e.g., [4]–[8]), low-rank models (e.g., [9]–[12]), or hybrids of both (e.g., [13]–[16]). It has been demonstrated that these methods are effective for accelerating cardiac MRI.

A key component in low-rank model-based imaging with explicit subspace constraints is the acquisition of navigators for subspace estimation. Existing methods collect navigators using separate RF pulses, often with Cartesian trajectories. Such methods have relatively low data acquisition efficiency and can miss temporal components (e.g., those associated with object translation in the direction perpendicular to the sampling trajectory). This paper focuses on investigating navigator strategies to improve temporal subspace estimation, increasing imaging speed and reducing sensitivity to orientation of the sampling trajectory. More specifically, we investigate the use of 2-D spiral and 3-D cone navigators, as these trajectories measure k-space locations more representative of the full set of k-space locations than do Cartesian navigators. We also introduce faster “self-navigated” pulse sequences that collect both navigator data and imaging data within each T_R (i.e., after every RF pulse). We accomplish self-navigation using a novel “music note” (♪) trajectory.

The rest of the paper is organized as follows: Section II provides background on subspace imaging with low-rank models; Section III describes the proposed method; Section IV shows simulated and experimental results, and Section V contains the conclusion.

II. Low-Rank Model-Based Imaging

A. Partial Separability and Subspace Modeling

The partial separability (PS) model expresses a cardiovascular image sequence ρ(r, t) as

$$\rho (\mathbf{r},t)=\sum _{\ell =1}^L{\psi }_{\ell }(\mathbf{r}){\phi }_{\ell }(t).$$ (1)

Correspondingly, the (k, t)-space signal d(k, t) = {ρ(r, t)} can be written as

$$d(\mathbf{k},t)=\int \rho (\mathbf{r},t)e^{-i2\pi \mathbf{k}·\mathbf{r}}d\mathbf{r}=\sum _{\ell =1}^L{\stackrel{\sim }{\psi }}_{\ell }(\mathbf{k}){\phi }_{\ell }(t),$$ (2)

where ψ̃_ℓ(k) = {ψ_ℓ(r)}. The Lth-order PS model in (2) implies that the following Casorati matrix formed from d(k_m, t_n) from any sampling points specified by ${\{{\mathbf{k}}_m\}}_{m=1}^M$ and ${\{t_n\}}_{n=1}^N$,

$$\mathbf{C}(d)=\left[\begin{array}{cccc}d({\mathbf{k}}_1,t_1)& d({\mathbf{k}}_1,t_2)& \cdots & d({\mathbf{k}}_1,t_N)\\ d({\mathbf{k}}_2,t_1)& d({\mathbf{k}}_2,t_2)& \cdots & d({\mathbf{k}}_2,t_N)\\ ⋮& ⋮& \ddots & ⋮\\ d({\mathbf{k}}_M,t_1)& d({\mathbf{k}}_M,t_2)& \cdots & d({\mathbf{k}}_M,t_N)\end{array}\right],$$

has a rank no larger than L [10], [11]; the same is true for C(ρ) (the Casorati matrix of the image ρ). Eqs. (1) and (2) permits matrix factorization: C(ρ) = ΨΦ and C(d) = Ψ̃Φ, where Ψ_ij = ψ_j(r_i), Ψ̃_ij = ψ̃_j(k_i), and Φ_ij = φ_i(t_j).

The partial separability of ρ(r, t) or d(k, t) implies the signal resides in a low-dimensional subspace. More specifically, in terms of its Casorati matrix representation, C(d) and C(ρ) belong, in general, to , but because of their low-rankness induced by partial separability, they actually reside in an L-dimensional subspace S_Φ, spanned by, for example, ${\{[{\phi }_{\ell }(t_1),{\phi }_{\ell }(t_2),\dots ,{\phi }_{\ell }(t_N)]\}}_{\ell =1}^L$. This subspace property enables accelerated imaging with sparse sampling.

B. Subspace-Based Accelerated Imaging

Subspace imaging can be implemented in two ways: Type-1) with a known temporal subspace S_Φ (determined from auxilary/navigator data [9], [10], [14]); and Type-2) with an unknown S_Φ (to be determined from the sparse imaging data [11], [15]). The paper is focused on type-1 subspace imaging.

Data acquisition for type-1 subspace imaging is characterized by the collection of two sets of (k, t)-space data: 1) a navigator data set 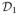which covers limited k-space locations at a high temporal rate (to enable high temporal resolution); and 2) an imaging data set 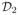with the desired contrast-weighting, which covers (k, t)-space sparsely (to enable high spatial resolution). The navigator data 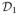are used to determine S_Φ and then Φ, which is often done using the L most significant right singular vectors of C( 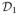). This approach is based on the assumption that 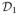and 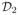share the same temporal subspace, which is valid. However, 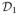often covers a very limited set of k-space locations (to obtain high temporal resolution), which may not capture all the temporal components in the extended k-space covered by 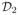. This paper is focused on addressing this issue.

Image reconstruction in type-1 subspace imaging is equivalent to recovery of Ψ from 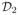given Φ. This is often accomplished through a regularized least-squares model fitting problem in the form

$$\widehat{\mathbf{\Psi }}=arg\underset{\mathbf{\Psi }}{min}{\Vert \mathbf{d}-\mathrm{\Omega }\{\stackrel{\sim }{\mathbf{\Psi }}\mathbf{\Phi }\}\Vert }^2+G(\mathbf{\Psi }),$$ (3)

where d is measured data, Ω{·} is the sparse sampling operator, and G(·) is the regularization function. For the purposes of this paper, we will consider the regularization function from [16]:

$$G(\mathbf{\Psi })={\lambda }_1{\Vert R\{\mathbf{\Psi }\}\Vert }_{1,2}+{\lambda }_2{\Vert \text{vec}(\mathbf{\Psi }\mathbf{\Phi }{\mathcal{F}}_t)\Vert }_1,$$ (4)

where ||R{Ψ}||_1,2 is a group sparsity penalty that imposes a spatially-varying model order constraint (allowing model order L₁ over the non-cardiac region and model order L₂ ≥ L₁ over the cardiac region), and ||vec(ΨΦ 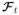)||₁ is the spatial-spectral sparsity contraint widely used in compressed sensing cardiac MRI (e.g., [4]–[6], [8], [13], [14]). The final reconstructed image is calculated as Ĉ(ρ) = Ψ̂Φ̂.

C. Subspace Error

Accurate estimation of the subspace S_Φ and thus Φ is essential for accurate image reconstruction in subspace imaging. Potential sources of error in the estimated subspace S_Φ̂ are measurement noise and limited k-space coverage of 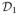. Both sources of error are closely tied to the choice of navigator trajectories (i.e., navigator k-space locations). Although measurement noise is unavoidable, navigator trajectories can be chosen to traverse regions of k-space which generally have high signal-to-noise ratio (SNR) (e.g., central k-space). The second source of error occurs when S_Φ nontrivially intersects a null space associated with the chosen navigator trajectory, preventing accurate subspace estimation even under noiseless conditions: C( 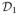) ∈ S_Φ̂ ⊂ S_Φ, with dim(S_Φ̂ ) < L.

A simple example of this null space problem arises for any navigator trajectory which is a line through the k-space origin: here, the navigator data are Fourier-transformed projections of ρ(r, t), so any translation of ρ(r, t) perpendicular to the navigator direction will have no effect on 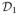and will therefore go undetected. Fig. 1 shows the results of projecting a numerical phantom onto subspaces estimated from horizontal (k_y = 0, pictured in Fig. 3-a) and vertical (k_x = 0) Cartesian navigators. This phantom depicts a large gray circle which translates vertically and a small white circle which translates horizontally; additionally, the two circles live in orthogonal temporal subspaces. The horizontal navigator fails to capture vertical translation, and the vertical navigator fails to capture horizontal translation.

Fig. 1.

Demonstration of the null space problem using central Cartesian navigators. (a) One frame of a numerical phantom and (b) a spatiotemporal slice through the dotted line. Spatiotemporal slices after projecting the phantom onto the subspace S_Φ̂ estimated from (c) horizontal and (d) vertical Cartesian navigators through the k-space origin. The vertical translation of the gray circle is not captured by the horizontal navigator, and the horizontal translational of the white circle is not captured by the vertical navigator.

Fig. 3.

Illustrations of the k-space trajectories used for simulations: (a) Cartesian, (b) spiral, (c) music note.

In this paper, we quantify the error between the estimated subspace S_Φ̂ and the true subspace S_Φ in terms of E_proj, the error which results from projecting C(ρ) onto S_Φ̂ (i.e., the distance between C(ρ) and S_Φ̂), as well as E_rec, the error which results from reconstructing C(ρ) ∈ S_Φ̂ from noisy sparse data. E_proj is defined as the normalized root-mean-square (NRMS) error of Ĉ_proj(ρ) = C(ρ) Φ̂^HΦ̂ = arg min_X∈SΦ̂||C(ρ) − X||_F :

$$E_{\text{proj}}(\widehat{\mathbf{\Phi }})=\frac{{\Vert \mathbf{C}(\rho )-{\widehat{\mathbf{C}}}_{\text{proj}}(\rho )\Vert }_F}{{\Vert \mathbf{C}(\rho )\Vert }_F}=\frac{{\Vert \mathbf{C}(\rho )(\mathbf{I}-{\widehat{\mathbf{\Phi }}}^H\widehat{\mathbf{\Phi }})\Vert }_F}{{\Vert \mathbf{C}(\rho )\Vert }_F}.$$

E_rec is the NRMS error of Ĉ_rec(ρ), the reconstruction from noisy sparse imaging data d = Ω{C(ρ)} + η (where η is the noise vector) according to (3) and (4):

$$E_{\text{rec}}(\widehat{\mathbf{\Phi }})=\frac{{\Vert \mathbf{C}(\rho )-{\widehat{\mathbf{C}}}_{\text{rec}}(\rho )\Vert }_F}{{\Vert \mathbf{C}(\rho )\Vert }_F}.$$

E_proj quantifies the optimal reconstruction (in the Frobenius norm sense) of C(ρ) given S_Φ̂ ; E_rec quantifies the error of a practically achievable reconstruction of C(ρ).

III. Improved Data Acquisition for Subspace Estimation

We propose to improve the data acquisition sequence for low-rank model-based cardiac MRI in the following ways (as illustrated in Fig. 2): 1) replace the conventional Cartesian trajectories with 2-D spiral trajectories (or 3-D cone trajectories, in the case of 3-D imaging); and 2) perform self-navigation using 2-D music note trajectories instead of using separate pulses for collecting the navigator signals. Unlike the Cartesian trajectories, each of these trajectories has no problem detecting translation perpendicular to the readout direction; this makes subspace estimation robust to navigator orientation. The self-navigated pulse sequence acquires navigator and imaging data within a single T_R, increasing the temporal resolution of the estimated subspace; this is especially useful for applications with very high temporal resolution requirements (e.g., mouse imaging).

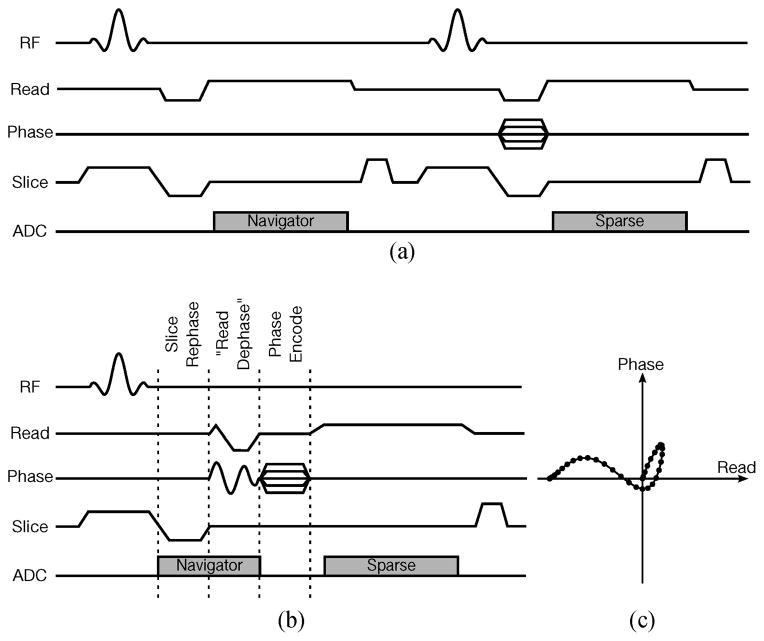
Fig. 2.

FLASH sequences with slice spoiler, illustrating (a) the conventional navigation strategy, (b) one possible variation of the proposed self-navigated strategy, and (c) the music note trajectory navigated during the “read dephase” portion of (b). The self-navigated sequence is shorter than the conventional sequence, leading to faster imaging at higher frame rates.

The proposed data acquisition strategy can be implemented by modifying existing low-rank model-based imaging sequences. Typically, an imaging readout is preceded by three gradient pulses: a slice rephasing pulse, a read dephasing pulse, and a phase encoding pulse, which can be applied either simultaneously or in sequence. Figure 2 shows an example of slice-spoiled FLASH pulse sequences implementing separated navigation and self-navigation, respectively. Note that for self-navigation, we applied the slice rephasing, read dephasing, and phase encoding pulses in sequence, collecting navigator data during slice rephasing and read dephasing (as seen in Fig. 2-b). Our “read dephasing” gradient actually traverses the 2-D music note trajectory illustrated in Fig. 2-c, ending in the same k-space location as the 1-D Cartesian read dephase trajectory which it replaces. The music note trajectory is a practical and efficient stand-in for a spiral trajectory, traversing a high-SNR region of k-space with low gradient slew rates. It should be also noted that other gradient combinations and k-space trajectories could be used for self-navigation, and that the pulse sequence described here simply represents one possible implementation of the proposed data acquisition strategy.

IV. Results and Discussion

A. Evaluation

1) Simulation Results

We used a numerical cardiac phantom to synthesize and compare different navigator trajectories and the accuracy of the resulting temporal subspaces. We measured six sets of noisy navigator data using the three trajectories in Fig. 3, as well as those same trajectories rotated clockwise by 90°. The SVD of the ith noisy navigator data set yielded each Φ̂_i, which were used to define the temporal subspaces.

The cardiac phantom was generated from 256 × 256 in vivo human MR cardiac images and features variable-rate cardiac and respiratory motion. The images were collected using retrospective ECG and respiratory gating, resulting in images of a single representative cardiac cycle. These images were looped and time-warped to simulate a variable-rate heartbeat, and then spatially deformed to simulate variable-rate respiration. White complex Gaussian noise with a blood-to-myocardium contrast-to-noise ratio of 10 was added to all simulated data to better represent realistic experimental conditions. For simulated sparse sampling, {·} retained only one random k-space line per time frame.

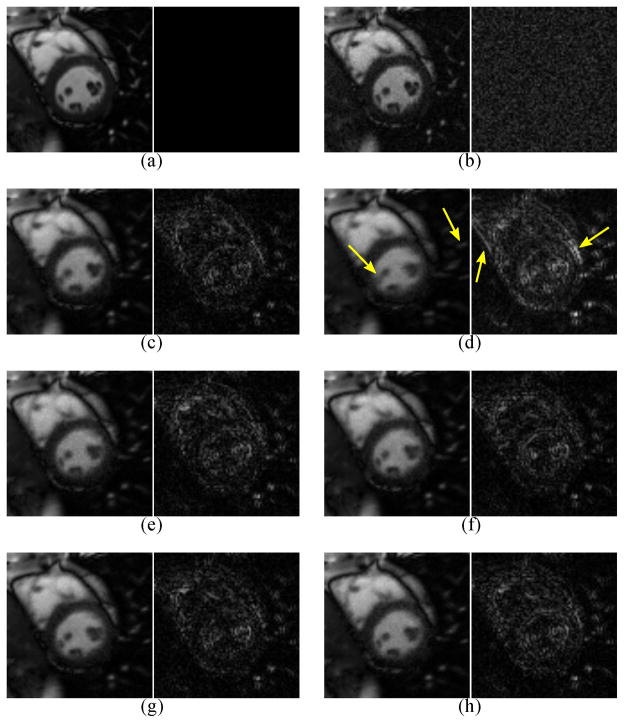
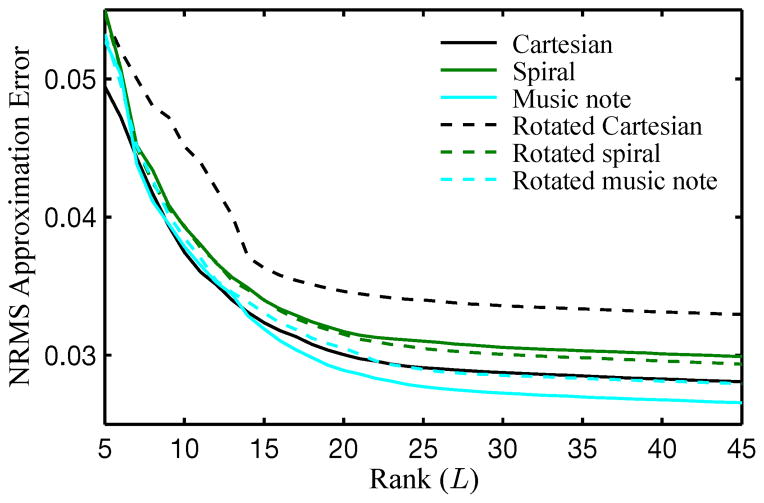
Figure 4 depicts an 81 × 81 closeup of the heart from the gold standard ρ(r, t), from the direct Fourier reconstruction of fully sampled noisy data, and from ${\{{\widehat{\mathbf{C}}}_{\text{rec},i}(\rho )\}}_{i=1}^6$, reconstructed from sparsely sampled noisy data using L₁ = 14 and L₂ = 32. Error images (scaled by a factor of 3) are also shown for all reconstructions. Table I shows the corresponding NRMS errors ${\{E_{\text{rec}}({\widehat{\mathbf{\Phi }}}_i)\}}_{i=1}^6$. Figure 5 shows the NRMS errors for ${\{E_{\text{proj}}({\widehat{\mathbf{\Phi }}}_i)\}}_{i=1}^6$ over a variety of ranks.

Fig. 4.

A closeup (left) and error image (right, scaled by a factor of 3) from one frame of (a) the gold standard image ρ(r, t), (b) the direct Fourier reconstruction from fully sampled noisy data, and (c–h) ${\{{\widehat{\mathbf{C}}}_{\text{rec},i}(\rho )\}}_{i=1}^6$ (L₁ = 14, L₂ = 32) reconstructed from sparsely sampled noisy data. The navigator data were collected using the (c) Cartesian, (d) rotated Cartesian, (e) spiral, (f) rotated spiral, (g) music note, and (h) rotated music note trajectories. Rotation of the Cartesian navigator causes spatiotemporal blurring, with examples indicated by the arrows. Regardless of rotation, the spiral and music note navigators yield similar visual quality to the unrotated Cartesian navigator.

TABLE I.

NRMS ERRORS ${\{E_{\text{rec}}({\widehat{\mathbf{\Phi }}}_i)\}}_{i=1}^6$

	Cartesian	Spiral	Music note
Standard	5.63%	5.70%	5.61%
Rotated	5.90%	5.67%	5.66%

Fig. 5.

NRMS errors ${\{E_{\text{proj}}({\widehat{\mathbf{\Phi }}}_i)\}}_{i=1}^6$ over a range of ranks. Rotation of the Cartesian navigator causes noticablely larger error. The spiral navigator is robust to rotation, yielding similar error amounts regardless of rotation. The music note navigators are the most accurate and are also robust to rotation.

2) Experimental Results

Throughout the rest of this paper, all pulse sequences are customized FLASH sequences. All animals received humane care in compliance with the Guide for the Care and Use of Laboratory Animals published by the National Academy of Science [17], and the animal protocol was approved by the Carnegie Mellon University Institutional Animal Care and Use Committee.

To compare subspace estimation schemes in vivo in rats, we implemented different navigator schemes using customized FLASH pulse sequences. We modified the two-pulse navigation strategy (Fig. 2-a) to use spiral navigators, and we performed self-navigation using a music note navigator. (Fig. 2-b). Both experiments used Cartesian trajectories to collect . For reference, we also acquired 2-D self-gated cine images using the Bruker IntraGate technique (Bruker BioSpin MRI, Ettlingen, Germany).

Experiments were conducted on a Bruker Avance AV1 4.7 T scanner equipped with a B-GA12 gradient set capable of 400 mT/m maximum gradient strength and a 4-channel array coil. Imaging data were collected with FA = 18°, FOV = 40 mm × 40 mm, matrix size = 256 × 256, spatial resolution = 0.16 mm × 0.16 mm, slice thickness = 2 mm, and imaging time = 5 min. Parallel acceleration was performed as in [16] with N_ACS = 32 and P = 2. The timing parameters for each imaging method were selected for maximum speed: the Cartesian- and spiral-navigated images were collected with T_E = 3.0 ms and T_R = 6.8 ms, for a frame rate of 74 frames per second (fps); the self-navigated images were collected with T_E = 4.9 ms and T_R = 10.5 ms, for a frame rate of 95 fps; and the IntraGate images were collected with T_E = 3.6 ms, T_R = 7.3 ms, and 10 frames per cardiac cycle (analogous to 67 fps for a 400 bpm heart rate). The animals used in the comparison study were Brown Norway (BN) rats. All data for subspace-based imaging were collected continually with neither ECG gating/triggering nor breath holding. Low-rank images were reconstructed with L₁ = 16, L₂ = 24 and shared regularization parameters.

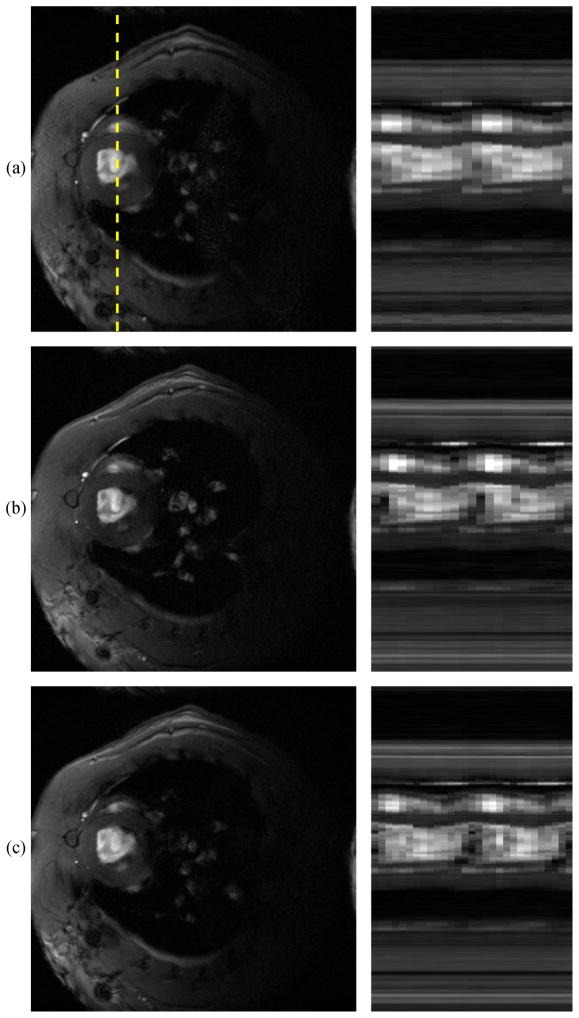
Figure 6 shows representative images and spatiotemporal slices from each method. The IntraGate method only reconstructs a single representative cardiac cycle; this cycle is repeated here to depict two cardiac cycles. The spiral-navigated images have a slightly higher frame rate than the gated images, and the self-navigated images are faster still, reaching 95 fps.

Fig. 6.

(a) Bruker IntraGate frame and a spatiotemporal slice through the dotted line, followed by frames and spatiotemporal slices of low-rank images using (b) two-pulse navigation with a spiral navigator trajectory, and (c) self-navigation with a music note trajectory. Gated scans reconstruct only a single representative cardiac cycle, so the same cycle is shown twice in (a). The spiral-navigated images have a slightly higher frame rate than the gated images, without the experimental burdens and sensitivities to arrhythmia and respiration associated with gated imaging. The self-navigated images share these benefits and are faster still, reaching 95 fps.

B. Applications

1) Self-Navigated Mouse Imaging

Mouse imaging is a particularly challenging application of cardiac MRI due to very high spatial and temporal resolution requirements. Mice have even smaller hearts and higher heart rates than do rats, making ungated, free-breathing cardiac imaging particularly difficult to perform. Here we employ self-navigation to image myocardial wall motion in mice at 0.12 mm × 0.12 mm spatial resolution at 97 fps.

Experiments were conducted on a Bruker Avance III 7 T scanner equipped with a B-GA12S32 gradient set capable of 480 mT/m maximum gradient strength and a quadrature surface coil. Imaging data were collected with FA = 18°, FOV = 30 mm × 30 mm, matrix size = 256 × 256, slice thickness = 1 mm, and imaging time = 11 min. No parallel acceleration was performed. Images were collected with T_E = 5.1 ms and T_R = 10.3 ms. Data were collected continually with neither ECG gating/triggering nor breath holding. Images were reconstructed with L₁ = 16 and L₂ = 24.

2) 3-D Myocardial Perfusion Imaging in Rats

Myocardial perfusion imaging has potential for tissue assessment and early detection of coronary artery disease (among other applications). It can be particularly useful in animal models, although it is difficult to perform in rodents even in 2-D. Major advantages of 3-D imaging over 2-D imaging include whole-heart coverage, no slice gaps, matched cardiac phases across slices, and no need for preparation pulses. However, imaging speed is a major concern for 3-D myocardial perfusion imaging, so 2-D methods are still more commonly performed. Here we demonstrate integrated whole-heart 3-D imaging of myocardial wall motion, first-pass perfusion, and late gadolinium enhancement (LGE) using two-pulse navigation with a cone navigator trajectory.

For this application, we employed a rodent ischemic reperfusion injury (IRI) animal model using male Brown Norway (BN) rats. For IRI experiments, rats had a 45 min transient left circumflex (LCx) coronary artery occlusion followed by re-perfusion. For control rats, no coronary artery occlusion was performed. Contrast enhancement was performed in all subjects by injecting a 0.2 mmol/kg bolus of gadolinium contrast agent (Gd-DTPA) 5 minutes after the start of data acquisition. For reference, the 2-D IntraGate method was used to image a mid-ventricular slice before and after each 3-D imaging experiment.

Experiments were conducted on the Bruker Avance AV1 4.7 T scanner described in Section IV-A-2. 3-D imaging data were collected with FA = 10°, FOV = 40 mm × 40 mm × 24 mm, matrix size = 128 × 128 × 24, spatial resolution = 0.31 mm × 0.31 mm × 1.0 mm, N_ACS = 24, P = 2, T_E = 2.5 ms, and T_R = 6.8 ms, for a frame rate of 74 fps. At 16 minutes, imaging time was short enough to remain practical and long enough to collect both first-pass and delayed myocardial perfusion images. All data for subspace-based imaging were collected continually with neither ECG gating/triggering nor breath holding. 3-D low-rank images were reconstructed with L₁ = L₂ = 24. IntraGate images were collected using the same parameters as the IntraGate images in Section IV-A-2.

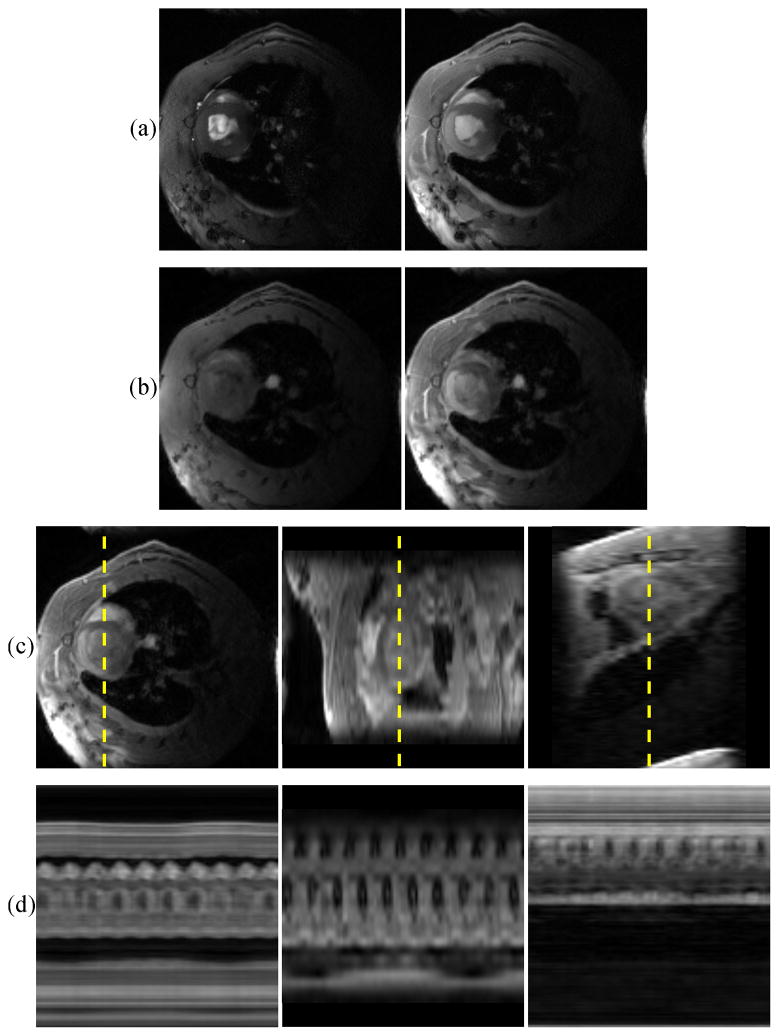
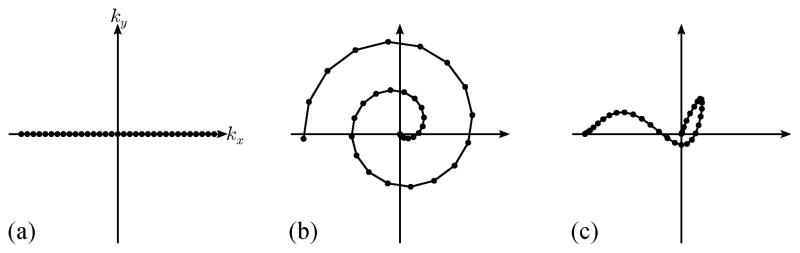
Figure 8 shows pre- and post-contrast images of an IRI subject on the day of surgery. The figure shows both 2-D IntraGate and 3-D cone-navigated low-rank images in order to compare the extent of the perfusion defect imaged by both methods. Figure 9 shows bullseye plots depicting time to peak concentration (TPC) of the first pass of Gd-DTPA through the myocardium of a) a control subject, and b) the same IRI subject as in Fig. 8. The bullseye plots conform to the American Heart Association 17-segment standard [18].

Fig. 8.

Representative IRI images on the day of surgery. (a) 2-D IntraGate images pre- and post-contrast, (b) corresponding slices from 3-D cone-navigated images pre- and post-contrast, (c) three perpendicular views of the 3-D cone-navigated images post-contrast, and (d) spatiotemporal slices through the dotted lines. The extent of the in-plane LGE perfusion defect match in (a) and (b). The images in (a) and (b) have different contrast due to the differences between slice and slab excitation. The spatial-coverage benefit of 3-D imaging can be seen in (c), which shows how far the perfusion defect extends towards the apex of the heart.

Fig. 9.

17-segment bullseye plots showing time to peak concentration (TPC) for: (a) a control rat; (b) a rat with IRI (the same rat shown in Fig. 8). The TPC measurements in (b) indicate extensive myocardial damage compared to (a), especially in the apical anterior, mid-ventricular anterior, mid-ventricular anterolateral, and apical lateral segments, consistent with the LGE images in Fig. 8

C. Discussion

Figures 4 and 5 demonstrate that the subspace accuracy when using Cartesian navigation is highly dependent on trajectory orientation: rotating the trajectory 90° caused a noticable degradation in image quality. The spiral and music note trajectories were more robust to orientation. For both projections and reconstructions, the rotated Cartesian navigator yielded the least accurate results, whereas the music note navigator provided the most accurate results.

Figure 6 depicts the same myocardial wall motion at different frame rates. The low-rank images are free of the experimental burdens and sensitivities to arrhythmia which are characteristic of ECG-gated images. Additionally, the low-rank images capture respiratory motion (the IntraGate images were created using retrospective respiratory gating) and depict the entire image sequence (as opposed to a single representative cardiac cycle). Each of the low-rank approaches reconstructed more cardiac phases per cycle than the IntraGate method, with the self-navigated images having the highest frame rate (95 fps).

The primary tradeoff of the speed boost from self-navigation is a later minimum echo time; however, the signal gain from a longer repetition time may offset the signal loss from the later echo time, depending on the T₁ and $T_2^{\ast }$ values of the tissue being imaged. Indeed, when compared to Fig. 6-b, the self-navigated images in Fig. 6-c have increased $T_2^{\ast }$-weighting due to the later echo time but higher overall SNR due to the longer repetition time. The importance of this tradeoff is application-dependent: for some $T_2^{\ast }$-weighted imaging applications, an even later echo time is desired, and the tradeoff disappears entirely.

Figure 7 demonstrates the effectiveness of the method for ungated, free-breathing imaging given particularly high spatial and temporal resolution requirements, successfully imaging mouse hearts at 97 fps with an in-plane spatial resolution of 0.12 mm.

Fig. 7.

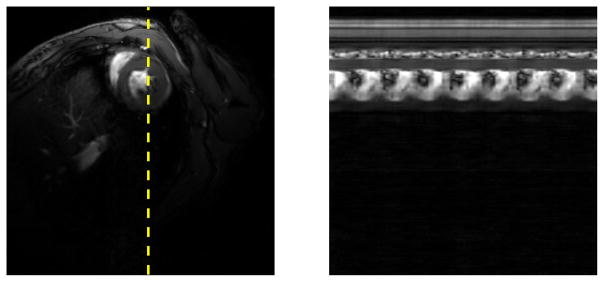
Single frame and spatiotemporal slice of a mouse heart using music note self-navigation. At 0.12 mm × 0.12 mm spatial resolution at 97 fps, these images show the capability of self-navigated imaging

In Fig. 8-a,b, the extent of the in-plane LGE perfusion defect matches in the 2-D IntraGate reference images and the corresponding slice from the 3-D images. The defect is specifically seen in the mid-ventricular anterior and anterolateral myocardial segments. The contrast weighting of the 2-D and 3-D images are different due to the differences between slice excitation and slab excitation; here, the 3-D images have a better contrast enhancement ratio. The additional benefit of 3-D imaging can be seen in Fig. 8-c, which shows how far the perfusion defect extends along the anterior and lateral walls of the myocardium towards the apex.

The first-pass perfusion measurements in Fig. 9-b indicate extensive myocardial damage when compared to the control rat in Fig. 9-a. This is clearest in the apical anterior, mid-ventricular anterior, mid-ventricular anterolateral, and apical lateral segments, which is consistent with the LGE images in Fig. 8.

V. Conclusion

This paper has presented an improved strategy to collect navigator data for subspace estimation in low-rank model-based cardiac MRI. We have shown that: 1) non-Cartesian navigation makes subspace estimation robust to navigator orientation; and 2) the data acquisition speed of subspace imaging can be further improved using self-navigated pulse sequences which collect both navigator and imaging data within the same T_R interval. These advantages of the proposed data acquisition schemes have been validated using both simulation and in vivo cardiac imaging data, and future work can include multiple in vivo studies to additionally substantiate improvement in subspace estimation accuracy. The advances presented in this paper may further improve the practical utility of low-rank model-based cardiac MRI.

Biographies

Anthony G. Christodoulou (S’10) received the B.S. and M.S. degrees in electrical engineering from the University of Southern California, Los Angeles, CA, USA, in 2008 and 2009, respectively. He is currently working toward the Ph.D. degree in electrical and computer engineering at the University of Illinois at Urbana-Champaign, Urbana, USA.

His research interests include pulse sequences and image reconstruction with application to real-time cardiac MRI. He is the recipient of an American Heart Association Predoctoral fellowship (2011–2012) and the IEEE-EMBC 2011 Best Paper award.

T. Kevin Hitchens received the B.S. degree in chemistry from West Virginia University, Morgantown, WV, USA, in 1991, the Ph.D. degree in chemistry from the University of Virginia, Charlottesville, VA, USA, in 1997, and an M.B.A. from the University of Pittsburgh, Pittsburgh, PA, USA, in 2007.

Following his Ph.D., he accepted a Postdoctoral appointment in the Department of Biological Sciences at Carnegie Mellon University. In 2001, he joined the Pittsburgh NMR Center for Biomedical Sciences at Carnegie Mellon and is currently the Assistant Director.

Yijen L. Wu received the B.S. degree in physical chemistry from the National Taiwan University, Taiwan and the Ph.D. degree from the Department of Biological Sciences and the Center for Neural Basis of Cognition at Carnegie Mellon University, Pittsburgh, PA, USA.

She received the I. I. Rabi Young Investigator Award from ISMRM in 1997. She is currently a research faculty at the Pittsburgh NMR Center for Biomedical Research, Pittsburgh, PA.

Chien Ho received the B.A. degree from Williams College, Williamstown, MA, USA, and the Ph.D. degree from, Yale University, New Haven, CT, USA.

He is an Alumni Professor of Biological Sciences at Carnegie Mellon University, Pittsburgh, PA, USA. He has coauthored more than 300 papers and has received several honors and awards, including the ISMRM Gold Medal for his contribution to the development of cell-tracking methodology by MRI.

Zhi-Pei Liang (M‘92–SM‘98–F‘06) received the Ph.D. degree in biomedical engineering from Case Western Reserve University, Cleveland, OH, USA, in 1989.

He is currently the Franklin W. Woeltge Professor of Electrical and Computer Engineering at the University of Illinois at Urbana-Champaign, Urbana, USA. His research interests include image formation theory, algorithms, and biomedical applications.

Dr. Liang served as President of the IEEE Engineering in Medicine and Biology Society from 2011 to 2012. He is a Fellow of ISMRM and AIMBE. He was elected to the International Academy of Medical and Biological Engineering in 2012.