Multiple imputation methods for nonparametric inference on cumulative incidence with missing cause of failure

Abstract

We propose a nonparametric approach for cumulative incidence estimation when causes of failure are unknown or missing for some subjects. Under the missing at random assumption, we estimate the cumulative incidence function using multiple imputation methods. We develop asymptotic theory for the cumulative incidence estimators obtained from multiple imputation methods. We also discuss how to construct confidence intervals for the cumulative incidence function and perform a test for comparing the cumulative incidence functions in two samples with missing cause of failure. Through simulation studies, we show that the proposed methods perform well. The methods are illustrated with data from a randomized clinical trial in early stage breast cancer.

1. Introduction

In studies of time to event data, competing risks, where individuals may fail from one of several mutually exclusive causes, are frequently present. For example, after cancer diagnosis and treatment, patients may die of cancer but also may die of other causes prior to death from cancer. In such a case, medical investigators may be interested in predicting the probability of dying of cancer by a particular time t in the presence of death from other causes. The probability is defined by the cumulative incidence function

$$F_k(t)=Pr(T\le t,\epsilon =k),$$ (1)

where T is the time to failure and ε ∈ {1, 2, … K} is the cause of failure. This quantity is useful in the analysis of competing risks in the sense that it reflects the risk of the cause of interest without ignoring the presence of other competing events. Another useful quantity in the analysis of competing risks is the cause-specific hazard function defined by

$${\lambda }_k(t)=\underset{\mathrm{\Delta }t\to 0}{lim}\frac{Pr(t\le T<t+\mathrm{\Delta }t,\epsilon =k\mid T\ge t)}{\mathrm{\Delta }t},$$

which is the instantaneous rate of cause k at time t in the presence of other competing risks. The cumulative incidence function given in (1) can be expressed as a function of all cause-specific hazards as

$$F_k(t)={\int }_0^{t}S(u)d{\mathrm{\Lambda }}_k(u),$$

where $S(t)=Pr(T>t)=exp\{-{\sum }_{k=1}^K{\mathrm{\Lambda }}_k(t)\}$ is the overall survival function and ${\mathrm{\Lambda }}_k(t)={\int }_0^t{\lambda }_k(u)du$ is the cumulative cause-specific hazard function for cause k.

In competing risk studies, it may be known that a failure has occurred but the failure type may be unknown. For example in the cancer example, the cause of death may be unknown or missing for some patients due to incomplete reporting or documentation, or other reasons. The simplest way to deal with missing causes of failure may be to exclude subjects with missing causes from the analysis. However, such an approach will result in information loss and may yield biased results. Goetghebeur and Ryan [1] and Lu and Tsiatis [2] proposed methods for estimating regression parameters under the cause-specific proportional hazards model for competing risk data with missing cause of failure. Gao and Tsiatis [3] and Lu and Liang [4] proposed inference procedures for estimation of regression parameters under a linear transformation model and an additive hazards model for competing risks with missing cause of failure, respectively. Bakoyannis et al. [5] used multiple imputation to estimate regression parameters for the proportional subdistribution hazards model. Moreno-Betancur and Latouche [6] proposed a general framework for regression modeling of the cumulative incidence function with missing causes of failure using pseudo-values.

However, methods for estimating the cumulative incidence function in the presence of missing cause of failure have not been widely studied. Recently, Lee et al. [7] proposed multiple imputation methods for estimating the cumulative incidence function with missing cause of failure under the cause-specific proportional hazards model. Nicolaie et al. [8] used vertical modeling to estimate the cumulative incidence function with missing cause of failure. In this paper, we propose nonparametric inferences for the cumulative incidence function with missing cause of failure using methods in Lin [9] and Lu and Tsiatis [2]. Assuming missingness is random conditional on the observed data, we impute missing cause of failure multiple times and estimate the cumulative incidence function by averaging nonparametric cumulative incidence estimators obtained from each of several imputed data sets. We prove the asymptotic normality of the cumulative incidence estimators obtained from multiple imputation methods and derive a consistent variance estimator for the cumulative incidence estimators. We describe how to construct confidence intervals for the cumulative incidence function and perform a test for comparing two cumulative incidence functions in the presence of missing cause of failure. The performance of the proposed methods are extensively evaluated by simulation studies. Finally, we apply the methods to study the influence of tamoxifen treatment on mortality from breast cancer, using data from a randomized clinical trial in early stage breast cancer.

2. Inference procedures

For simplicity, we consider two competing events, ε ∈ {1, 2}. Define X = min(T, C), where T and C are the failure time and censoring time, respectively. We assume that the censoring time C is independent of (T, ε). Let δ = I(T ≤ C)ε, where I(·) is an indicator function. When causes of failure are known for all subjects, the observed data consist of (X_i, δ_i) (i = 1, …, n).

A nonparametric estimator of the cumulative incidence function (called the Aalen-Johansen estimator [10]) is given by

$${\widehat{F}}_k(t)={\int }_0^t\widehat{S}(u-)d{\widehat{\mathrm{\Lambda }}}_k(u),k=1,2,$$ (2)

where Ŝ(t−) is the left-continuous Kaplan-Meier estimator [11] and Λ̂_k(t) is the Nelson-Aalen estimator [12] for Λ_k(t). Aalen [13] first established the uniform consistency and weak convergence of the Aalen-Johansen estimator using a non-homogeneous Markov process formulation. Recently, variance estimation of the Aalen-Johansen estimator in small samples has caused some discussion [14, 15, 16]. Aalen’s variance formula [13] is generally smaller than the so-called Greenwood estimator in small samples, resulting in narrow confidence intervals and inflated type I error rates (more power). Building off Aalen’s work [13], Lin [9] presented a martingale-based estimator for the asymptotic variance of the Aalen-Johansen estimator. Lee and Fine [17] note that Lin’s martingale-based variance estimator equals the Greenwood type estimator given in Equation (7) of Allignol et al. [18] in the absence of ties. As an alternative to Aalen’s work [13], we use Lin’s result for variance estimation of the Aalen-Johansen estimator.

Define the counting process notation N_ki(t) = I(X_i ≤ t, ε_i = k), Y_i(t) = I(X_i ≥ t), ${\overline{N}}_k(t)={\sum }_{i=1}^n{N}_{ki}(t)$, and $\overline{Y}(t)={\sum }_{i=1}^n{Y}_i(t)$. Let $M_{ki}(t)=N_{ki}(t)-{\int }_0^t{\lambda }_k(u)Y_i(u)du$. Lin (1997) showed that

$$\sqrt{n}\{{\widehat{F}}_1(t)-F_1(t)\}=\sqrt{n}\sum _{i=1}^n{\mathrm{\Psi }}_{1i}(t)+o_p(1),$$

where

$${\mathrm{\Psi }}_{1i}(t)={\int }_0^t\frac{\{1-F_2(u)-F_1(t)\}{dM}_{1i}(u)}{\overline{Y}(u)}+{\int }_0^t\frac{\{F_1(u)-F_1(t)\}{dM}_{2i}(u)}{\overline{Y}(u)},$$

by the martingale theory, $\sqrt{n}\{{\widehat{F}}_1(t)-F_1(t)\}$ converges weakly to a zero-mean Gaussian process, and the variance can be consistently estimated by

$$n\sum _{i=1}^n{\widehat{\mathrm{\Psi }}}_{1i}{(t)}^2=n\left[{\int }_0^t\frac{{\{1-{\widehat{F}}_2(u)-{\widehat{F}}_1(t)\}}^{2}d{\overline{N}}_1(u)}{\overline{Y}{(u)}^2}+{\int }_0^t\frac{{\{{\widehat{F}}_1(u)-{\widehat{F}}_1(t)\}}^{2}d{\overline{N}}_2(u)}{\overline{Y}{(u)}^2}\right].$$

When cause of failure is missing for some patients, the cumulative incidence estimator and its variance may be obtained from the above after excluding those with the missing cause information. However, such an approach may lead to biased inferences. We propose multiple imputation methods (referred to as improper multiple imputation) for nonparametric estimation of the cumulative incidence function with missing cause of failure.

2.1. Multiple imputation method

Lu and Tsiatis [2] proposed multiple imputation methods to estimate the proportional hazards regression parameters for competing risks data with missing cause of failure. In this section, we propose a nonparametric approach for estimating cumulative incidence with missing cause of failure using imputation methods described in Lu and Tsiatis [2].

Define the missingness indicator R_i, that is, R_i = 1 if the cause of failure is known and R_i = 0 if the cause of failure is missing or unknown. When the failure time is censored, we set R_i = 1 since this is known and it is not related to missing cause of failure. The observed data consist of (R_i, X_i, R_iδ_i) (i = 1, …, n). We assume that the cause of failure is missing at random [19], which implies that given δ_i(> 0) and X_i, the probability that the cause of failure is missing depends only on the observed information X_i, not on the unobserved δ_i. That is,

$$Pr(R_i=0\mid {\delta }_i,{\delta }_i>0,X_i)=Pr(R_i=0\mid {\delta }_i>0,X_i).$$

Let D_1i = I(δ_i = 1) and π(X_i) = Pr(δ_i = 1 | R_i = 0, δ_i > 0, X_i). When the cause of failure is missing, we impute missing D_1i values from the conditional distribution of D_1i given the observed data as in Lu and Tsiatis [2]. D_1i has a Bernoulli distribution with success probability π(X_i) which can be specified by a parametric model with an unknown parameter γ. It is natural to fit the logistic regression model for π(X_i), logitπ(X_i, γ) = γ₁ + γ₂X_i, where γ = (γ₁, γ₂). Let γ₀ = (γ₀₁, γ₀₂) be the true value of γ. The assumption that the cause of failure is missing at random implies

$$\pi (X_i,{\gamma }_0)=Pr({\delta }_i=1\mid R_i=0,{\delta }_i>0,X_i)=Pr({\delta }_i=1\mid R_i=1,{\delta }_i>0,X_i).$$

Thus we can infer π(X_i, γ₀) from the complete cases for whom (R_i = 1, δ_i > 0). Maximizing the likelihood function for the complete cases

$$\prod _{i=1}^n\pi {(X_i,\gamma )}^{D_{1i}I(R_i=1,{\delta }_i>0)}{\{1-\pi (X_i,\gamma )\}}^{(1-D_{1i})I(R_i=1,{\delta }_i>0)}$$

yields the maximum likelihood estimator γ̂ of γ. If the model π(X, γ) for π(X) is correctly specified, γ̂ is consistent and asymptotically normal under the regularity conditions. The asymptotic normality follows from the influence function expansion given in Appendix A. Using the maximum likelihood estimator γ̂, the missing value can be imputed as

$$D_{1ij}(R_i,\widehat{\gamma })=\{\begin{array}{cc}{D}_{1i}& \text{if}{R}_i=1,\\ \text{Bernoulli}(1,\pi (X_i,\widehat{\gamma }))& \text{if}{R}_i=0,\end{array}$$

where D_1ij(R_i, γ̂) is the imputed value of D_1i from the jth imputed data set, j = 1, …, m, and is randomly selected to be 1 or 0 from a Bernoulli distribution with success probability π(X_i, γ̂) when R_i = 0. Let F̂_kj(t) be a nonparametric estimator, estimated as in (2), of cumulative incidence for cause k from the jth imputed data set. The multiple imputation estimator for F_k(t) is given by averaging nonparametric estimators obtained from each of m imputed data sets as

$${\widehat{F}}_k(t)=\frac{1}{m}\sum _{j=1}^m{\widehat{F}}_{kj}(t),k=1,2.$$

As noted in Lu and Tsiatis [2], Rubin [20]’s variance calculation is not applicable here; since we generate imputations from the conditional distribution of missing data (D_1i) given the observed data evaluated at the fixed γ̂ across imputations, our imputation is not proper in the sense of Rubin [20]. Wang and Robins [21] indicates that under these conditions, Rubin’s variance will yield an inconsistent estimator for the sampling variance. We derive variance estimators for F̂_kj(t) and F̂_k(t) directly as in Lu and Tsiatis [2] (see Appendix A).

To establish the asymptotic properties for F̂_1j(t) and F̂₁(t), we assume that the parametric model for π(X) is correctly specified. Using the methods described in Lu and Tsiatis [2] or Tsiatis et al. [22], we show that U_1j(t) = n^1/2{F̂_1j(t) − F₁(t)} and U₁(t) = n^1/2{F̂₁(t) − F₁(t)} are asymptotically equivalent to (A.3) and (A.6) which converge weakly to mean zero Gaussian processes with respective variances V_1j(t) and V₁(t) given by equations (A.4) and (A.7) in Appendix A. The variances can be consistently estimated by V̂_1j(t) and V̂₁(t) in equations (A.5) and (A.8).

Note that we imputed missing causes of failure from the conditional distribution of missing data based on the maximum likelihood estimation of γ. The second term of V_1j(t) in (A.4) accounts the variability of γ̂ from single imputation. When there are no missing causes of failure, the second term vanishes since $\frac{\partial }{\partial \gamma }{\mu }_f({\gamma }_0,t)=0$ and our inference procedures reduce to those in Lin [9]. Equation (A.7) shows that V₁(t) ≤ V_1j(t) for all m and V₁(t) is decreased as the number of imputations m is increased, indicating an improvement in efficiency from multiple imputation over single imputation. Although more imputations provide more efficient estimators, the number of imputations should be determined based on the magnitude of V_1j(t) and the second term in equation (A.7). In practice, a few imputations (such as 5–10) would be sufficient to achieve good efficiency.

2.2. Confidence intervals

Pointwise (1 − α) confidence intervals for F₁(t) can be constructed based on a transformation of F₁(t) to let F₁ be bounded by 0 and 1 and improve the coverage probability. Denote K(t) = n^1/2ϕ(t) [g{F̂₁(t)} − g{F₁(t)}], where g is a known function with non-zero continuous derivative g′ and ϕ is a weight function which converges to a non-negative bounded function. By the functional delta method, the process K(t) is asymptotically equivalent to ϕ(t)g′{F̂₁(t)}U₁(t), where U₁(t) = n^1/2{F̂₁(t) − F₁(t)}. Pointwise (1 − α) confidence intervals for F₁(t) are given by

$$g^{-1}\left[g\{{\widehat{F}}_1(t)\}\pm n^{-1/2}{g}^{\prime }\{{\widehat{F}}_1(t)\}{\widehat{V}}_1{(t)}^{1/2}{z}_{\alpha /2}\right],$$

where z_α/2 is an upper α/2 percentile of the standard normal distribution. With g(x) = log{− log(x)} and ϕ(x) = F̂₁(t) log{F̂₁(t)}V̂₁(t)^−1/2, pointwise (1 − α) confidence intervals for F₁(t) are given by

$$exp\left[exp\left\{log\{-log({\widehat{F}}_1(t))\}\pm z_{\alpha /2}\frac{n^{-1/2}{\widehat{V}}_1{(t)}^{1/2}}{{\widehat{F}}_1(t)log\{{\widehat{F}}_1(t)\}}\right\}\right].$$ (3)

2.3. Two-sample tests

We consider a test which compares the cumulative incidence functions in two samples. Let $F_1^{(l)}$ be the cumulative incidence function for cause 1 in group l (l = 1, 2). With two competing risk samples, we are interested in testing the null hypothesis $H_0:F_1^{(1)}(t)=F_1^{(2)}(t)$ for all t ≤ τ, where τ is the observed largest time point. Gray [23] proposed a test comparing weighted averages of the subdistribution hazards in several groups. Pepe [24] proposed a test based on the integrated weighted difference between the cumulative incidence estimates in two samples. Lin [9] proposed a Kolmogorov-Smirnov type statistic which compares the maximum difference between the cumulative incidence estimates in two samples. Pepe’s test and Lin’s test directly compare the cumulative incidence functions in two samples while Gray’s test compares subdistribution hazards in several groups. Pepe’s test is sensitive to stochastic ordering alternatives $F_1^{(1)}(·)\ge F_1^{(2)}(·)$ with $F_1^{(1)}(t)\ne F_1^{(2)}(t)$ for some t and can be used as an alternative to Gray’s test when the cumulative incidence functions cross [24, 25]. Lin’s test uses the Kolmogorov-Smirnov type statistic which is rank-based thus it may share some shortcomings of the rank statistic. As noted in Pepe and Fleming [26], the Kolmogorov-Smirnov type statistic may be sensitive to a large difference over a short period of time but can be very insensitive to a moderate difference over a long period of time. The latter case is of more interest in practice. Among the three tests, we focus on Pepe’s test to directly compare the cumulative incidence functions in two samples.

Let ${\stackrel{\sim }{F}}_1^{(l)}$ be the Aalen-Johansen estimator of $F_1^{(l)}$ in group l (l = 1, 2). Pepe [24] developed a test statistic $Q/\sqrt{{\widehat{\sigma }}_Q^2}$ for comparing two cumulative incidence functions, where

$$Q=\sqrt{\frac{n_1{n}_2}{n_1+n_2}}{\int }_0^{\tau }W(u)\{{\stackrel{\sim }{F}}_1^{(1)}(u)-{\stackrel{\sim }{F}}_1^{(2)}(u)\}du,$$

${\widehat{\sigma }}_Q^2$ is a variance estimator of Q and n_l is the number of subjects in group l. Here, W(·) is a data-dependent weight function used to ensure stability of a test statistic under the null hypothesis $H_0:F_1^{(1)}(t)=F_1^{(2)}(t)$ for all t ≤ τ. In practice, the weight function should be chosen based on alternative hypotheses and the choice of the weight function is analogous to that for weighted Kaplan-Meier statistics [26, 27]. A decreasing (increasing) weight function gives less weight to differences between two cumulative incidence estimates over later (early) time periods. Under the null hypothesis $H_0:F_1^{(1)}(t)=F_1^{(2)}(t)$ for all t ≤ τ, the test statistic $Q/\sqrt{{\widehat{\sigma }}_Q^2}$ has an asymptotic standard normal distribution. Pepe [24] notes that method of moment type estimator ${\widehat{\sigma }}_Q^2$ tends to be too small and underestimates the variance, resulting in larger type I errors. As an alternative to method of moment type estimator ${\widehat{\sigma }}_Q^2$, Bajorunaite and Klein [28] proposed a martingale-based estimator for the variance of the statistic Q. Through simulation studies, they demonstrated that the method of moment type estimator underestimated the true variance and Pepe’s test with this variance estimator had larger type I errors, especially when the sample size was small, while the test with the martingale-based variance estimator performed well. Hence, we use Bajorunaite and Klein’s result for variance estimation of the statistic Q.

In the presence of missing cause of failure, we modify Pepe’s test statistic by using an imputation estimator for ${\stackrel{\sim }{F}}_1^{(l)}$. Let ${\widehat{F}}_{1j}^{(l)}$ be a nonparametric estimator of the cumulative incidence function for cause 1 from the jth imputed data set in group l and ${\widehat{F}}_1^{(l)}$ be the multiple imputation estimator obtained by averaging ${\widehat{F}}_{1j}^{(l)}$’s from m imputed data sets in group l. To simplify the presentation, we let W(t) = 1. Then the statistic Q can be defined by

$$Q_S=\sqrt{\frac{n_1{n}_2}{n_1+n_2}}{\int }_0^{\tau }\{{\widehat{F}}_{1j}^{(1)}(u)-{\widehat{F}}_{1j}^{(2)}(u)\}du$$

for single imputation and

$$Q_M=\sqrt{\frac{n_1{n}_2}{n_1+n_2}}{\int }_0^{\tau }\{{\widehat{F}}_1^{(1)}(u)-{\widehat{F}}_1^{(2)}(u)\}du$$

for multiple imputation. To establish the asymptotic properties for Q_S and Q_M, we assume that a parametric model for π(X) is correctly specified. We derive variance estimators for Q_S and Q_M in Appendix B. Under the null hypothesis $H_0:F_1^{(1)}(t)=F_1^{(2)}(t)$ for all t ≤ τ, we show that Q_S and Q_M have asymptotic normal distributions with respective variances

$${\sigma }_{Q_S}^2=\frac{n_2}{n_1+n_2}{\nu }_{1j}^{(1)}(\tau )+\frac{n_1}{n_1+n_2}{\nu }_{1j}^{(2)}(\tau )$$

and

$${\sigma }_{Q_M}^2=\frac{n_2}{n_1+n_2}{\nu }_1^{(1)}(\tau )+\frac{n_1}{n_1+n_2}{\nu }_1^{(2)}(\tau ),$$

where ${\nu }_{1j}^{(l)}(\tau )$ and ${\nu }_1^{(l)}(\tau )$ are given in (B.2) and (B.5) in Appendix B. The variances can be consistently estimated by replacing ${\nu }_{1j}^{(l)}(\tau )$ and ${\nu }_1^{(l)}(\tau )$ with their estimators ${\widehat{\nu }}_{1j}^{(l)}(\tau )$ and ${\widehat{\nu }}_1^{(l)}(\tau )$ given in (B.3) and (B.6). Note that when there are no missing causes of failure, our test statistic reduce to Pepe’s [24] test statistic with the martingale-based variance estimator proposed by Bajorunaite and Klein [28] since $\frac{\partial }{\partial {\gamma }_l}{\mu }_{\phi }^{(l)}({\gamma }_{0l},\tau )=0$ in (B.1).

3. Numerical studies

Simulation studies were conducted to evaluate the performance of the proposed estimators for the cumulative incidence function when the cause of failure is missing. Cumulative incidence estimators and corresponding variance estimators were examined under various missingness mechanisms, followed by evaluations of performance for the two-sample tests.

3.1. Performance under correct imputation model

The cumulative incidence functions for cause 1 and 2 are assumed to be F₁(t) = π₁{1 − exp(−v₁t^θ₁)} and F₂(t) = π₂{1 − exp(−v₂t^θ₂)} with (π₁, π₂, v₁, v₂, θ₁, θ₂) = (2/3, 1/3, 1, 0.8, 1, 1) as in configuration I described in Section 3.1 of Peng and Fine [25]. The type 1 and 2 failures were generated from a Bernoulli distribution with success probability Pr(ε = 1) = π₁. The failure times (T) were generated from the conditional distribution of T given ε = k, Pr(T ≤ t | ε = k) = F_k(t)/Pr(ε = k) for k = 1, 2. The censoring times (C) were generated from a uniform distribution U(0, 7.2). The observed times (X) were obtained by min(T, C) and the range of X was 4.568 on average. Under this setting, on average, we had 57% failures from cause 1, 28% failures from cause 2, and 15% censoring. We generated the missingness indicator R from logitPr(R = 0 | δ > 0, X) = η₁ + η₂X. With different choices of η’s, we generated 20, 30, and 40% missing causes of failure. Following Rubin’s taxonomy of missingness [19], given δ > 0 and X, if the probability that the cause of failure is missing does not depend on the unobserved cause of failure δ, the missingness mechanism is called missing at random (MAR), otherwise missing not at random (MNAR). If the missingness probability is constant, the missingness mechanism is called missing completely at random (MCAR). In Table 1, the first scenario indicates MCAR case and the second to fifth scenarios correspond to MAR case. Note that from the missing at random assumption, π(X) = Pr(δ = 1 | R = 0, δ > 0, X) = Pr(δ = 1 | δ > 0, X). Thus π(X) is related to the ratio of the cause-specific hazards for cause 1 and 2, that is, λ₁(x)/λ₂(x) = π(x)/{1 − π(x)}. By this relationship, the true model for π(X) is logitπ(X) = log(5/2) − 0.2X since ${\lambda }_k(x)=\frac{{dF}_k(x)}{dx}/\{1-F_1(x)-F_2(x)\}$ for k = 1, 2. We fitted a correctly specified logistic regression model logitπ(X, γ) = γ₁ + γ₂X. We conducted 1000 simulations with sample sizes of 100 and 300. Table 1 shows the true value of F₁(0.7), bias of F̂₁(0.7), empirical variance (Var(F̂₁)), averages of the variance estimate (E(V̂₁)), mean square error (MSE), and empirical coverage probabilities (CP) for 95% confidence intervals given in (3) from single imputation (m = 1), 10 imputations (m = 10), and the complete case analysis (CC) obtained by excluding subjects with missing cause of failure. Under the correct imputation model, the imputation estimate shows that the bias is small and the variance estimate agrees with the empirical variance. The empirical coverage probabilities are close to the nominal level. Multiple imputation estimates have slightly smaller variance estimates than single imputation estimates and have the smallest MSEs. However, the complete case estimates result in larger biases and MSEs, and lower coverage probabilities compared to the imputation estimates. Supplemental analyses (see Figures 1–3 in Supplementary Materials) show that the complete case analysis can either underestimate or overestimate cumulative incidence, depending on whether deaths with missing cause occur early or late in follow-up. In either case, the imputation method performs well.

Table 1.

Simulation results under the correct imputation model.

n	% missing	Method	F1(t = 0.7) = 0.3356
			Bias(F̂1)	Var(F̂1)	E(V̂1)	MSE	CP
100	20%	m=1	−0.00142	0.00264	0.00264	0.00264	0.949
	(η1, η2)	m=10	−0.00141	0.00248	0.00251	0.00248	0.951
	= (−1.38, 0)	CC	−0.01065	0.00274	0.00273	0.00286	0.944
		m*=10	−0.00162	0.00242	0.00256	0.00243	0.953
	30%	m=1	−0.00043	0.00313	0.00311	0.00313	0.947
	(η1, η2)	m=10	−0.00067	0.00279	0.00286	0.00279	0.953
	= (−1.38, 0.56)	CC	−0.06251	0.00290	0.00278	0.00681	0.770
		m*=10	−0.00167	0.00280	0.00296	0.00280	0.961
	40%	m=1	−0.00166	0.00340	0.00323	0.00340	0.949
	(η1, η2)	m=10	−0.00167	0.00294	0.00295	0.00294	0.950
	= (−1.38, 1.1)	CC	−0.05030	0.00333	0.00322	0.00586	0.837
		m*=10	−0.00268	0.00296	0.00307	0.00297	0.954
	30%	m=1	0.00100	0.00293	0.00273	0.00293	0.941
	(η1, η2)	m=10	0.00183	0.00264	0.00259	0.00264	0.945
	= (−0.1, −1)	CC	0.01730	0.00337	0.00319	0.00367	0.936
		m*=10	0.00122	0.00261	0.00262	0.00261	0.948
	40%	m=1	−0.00052	0.00308	0.00281	0.00308	0.942
	(η1, η2)	m=10	−0.00028	0.00283	0.00264	0.00283	0.946
	= (−0.1, −0.36)	CC	0.04804	0.00394	0.00377	0.00625	0.881
		m*=10	−0.00075	0.00285	0.00266	0.00285	0.949
300	20%	m=1	−0.00073	0.00091	0.00089	0.00091	0.958
	(η1, η2)	m=10	−0.00074	0.00082	0.00085	0.00082	0.960
	= (−1.38, 0)	CC	−0.00985	0.00093	0.00093	0.00102	0.933
		m*=10	−0.00078	0.00082	0.00086	0.00082	0.961
	30%	m=1	0.00090	0.00102	0.00105	0.00102	0.948
	(η1, η2)	m=10	0.00070	0.00090	0.00096	0.00090	0.952
	= (−1.38, 0.56)	CC	−0.06132	0.00094	0.00094	0.00470	0.482
		m*=10	0.00037	0.00091	0.00100	0.00091	0.953
	40%	m=1	−0.00079	0.00106	0.00110	0.00106	0.949
	(η1, η2)	m=10	−0.00068	0.00092	0.00100	0.00092	0.959
	= (−1.38, 1.1)	CC	−0.04953	0.00107	0.00110	0.00352	0.686
		m*=10	−0.00096	0.00093	0.00105	0.00093	0.965
	30%	m=1	−0.00003	0.00095	0.00092	0.00095	0.950
	(η1, η2)	m=10	0.00015	0.00089	0.00087	0.00089	0.956
	= (−0.1, −1)	CC	0.01678	0.00115	0.00108	0.00143	0.926
		m*=10	0.00009	0.00088	0.00089	0.00088	0.958
	40%	m=1	−0.00011	0.00099	0.00096	0.00099	0.939
	(η1, η2)	m=10	0.00018	0.00091	0.00090	0.00091	0.949
	= (−0.1, −0.36)	CC	0.05030	0.00140	0.00129	0.00393	0.717
		m*=10	0.00003	0.00091	0.00091	0.00091	0.948

m^*=10, 10 proper imputations based on methods of [5].

To deal with missing cause of failure, Bakoyannis et al. [5] considered Rubin’s multiple imputation procedure under the MAR assumption, which is referred to as proper imputation. Their imputation methods can be applied to nonparametric estimation of the cumulative incidence function with missing cause of failure by using proper multiple imputation to impute missing cause of failure. The cumulative incidence function F₁(t) can be estimated by averaging nonparametric estimators obtained from each of multiply imputed data sets. Its variance can be estimated by Rubin’s variance formula $\widehat{var}({\widehat{F}}_1)=W_{var}+(1+m^{-1})B_{var}$, where the within imputation variance W_var is the mean of the variance estimates across m imputations and the between imputation variance B_var is the sample variance of the m cumulative incidence estimates. Pointwise 95% confidence intervals for F₁(t) can be computed by using (3) with replacing z_0.025 by $t_{\psi }^{0.025}$, where $t_{\psi }^{0.025}$ is the upper 2.5th percentile of a t-distribution with ψ degrees of freedom, ψ = (m − 1)[1 + W_var/{(1 + m⁻¹)B_var}]². We compared our imputation procedure (referred to as improper imputation) with that of Bakoyannis et al. [5] in the case of nonparametric estimation of the cumulative incidence function with missing cause of failure. As an imputation model for methods of Bakoyannis et al. [5], we fitted a correctly specified logistic regression model logitπ(X, γ) = γ₁ + γ₂X. As shown in Table 1, under the correct imputation model, the multiple imputation estimates from 10 proper imputations (m^* = 10) show that the biases are small and the variance estimates agree with the empirical variance. The empirical coverage probabilities are close to the nominal level. However, the variance estimates from our imputation methods are smaller than those from Bakoyannis et al. [5]. This is because we derive variance estimators for imputation estimators directly. The MSEs of both methods are similar. This is because the proper multiple imputation estimators are consistent and unbiased, and its variances can be correctly estimated by Rubin’s variance formula when the imputation and analysis models agree (i.e., congenial as defined in [29]).

3.2. Performance under misspecified imputation model

Our imputation estimators are obtained based on the maximum likelihood estimation of γ from a parametric model specified for π(X). Therefore, the estimators may be biased if the parametric model is misspecified [30]. To justify the robustness of the imputation estimators, we fitted an incorrectly specified logistic regression model logitπ(X, γ) = γ₁ + γ₂ log(1 + exp(−X)), where we generated data from the same scenario as before. We conducted 1000 simulations with sample sizes of 100 and 300. In Table 2, the biases, variance estimates, and MSEs of the imputation estimates are small even if the parametric model is misspecified. The variance estimates agree with the empirical variances, and the empirical coverage probabilities of 95% confidence intervals are close to the nominal level. Supplemental analyses (see Supplemental Figures 4–6) confirm that the imputation method performs well under a misspecified parametric model.

Table 2.

Simulation results under the incorrect imputation model.

n	% missing	Method	F1(t = 0.7) = 0.3356
			Bias(F̂1)	Var(F̂1)	E(V̂1)	MSE	CP
100	20%	m=1	−0.00041	0.00276	0.00266	0.00276	0.945
	(η1, η2)	m=10	−0.00048	0.00258	0.00254	0.00258	0.945
	= (−1.38, 0)	CC	−0.00895	0.00290	0.00273	0.00298	0.935
		m*=10	−0.00096	0.00254	0.00256	0.00255	0.952
	30%	m=1	0.00071	0.00333	0.00322	0.00333	0.950
	(η1, η2)	m=10	0.00027	0.00305	0.00298	0.00305	0.953
	= (−1.38, 0.56)	CC	−0.06176	0.00300	0.00277	0.00682	0.759
		m*=10	−0.00125	0.00305	0.00301	0.00305	0.953
	40%	m=1	0.00193	0.00368	0.00336	0.00368	0.954
	(η1, η2)	m=10	0.00137	0.00322	0.00309	0.00322	0.955
	= (−1.38, 1.1)	CC	−0.04831	0.00350	0.00323	0.00583	0.846
		m*=10	−0.00002	0.00319	0.00310	0.00319	0.955
	30%	m=1	0.00098	0.00283	0.00274	0.00284	0.955
	(η1, η2)	m=10	0.00156	0.00263	0.00259	0.00263	0.956
	= (−0.1, −1)	CC	0.01797	0.00331	0.00318	0.00363	0.942
		m*=10	0.00089	0.00262	0.00260	0.00262	0.954
	40%	m=1	0.00160	0.00318	0.00281	0.00318	0.942
	(η1, η2)	m=10	0.00061	0.00288	0.00264	0.00288	0.946
	= (−0.1, −0.36)	CC	0.05067	0.00399	0.00378	0.00655	0.882
		m*=10	0.00008	0.00289	0.00267	0.00289	0.943
300	20%	m=1	−0.00025	0.00085	0.00091	0.00085	0.959
	(η1, η2)	m=10	0.000002	0.00081	0.00087	0.00081	0.959
	= (−1.38, 0)	CC	−0.00943	0.00087	0.00093	0.00096	0.942
		m*=10	0.00002	0.00081	0.00087	0.00081	0.960
	30%	m=1	−0.00054	0.00111	0.00110	0.00111	0.940
	(η1, η2)	m=10	−0.00107	0.00098	0.00101	0.00098	0.950
	= (−1.38, 0.56)	CC	−0.06315	0.00099	0.00094	0.00498	0.472
		m*=10	−0.00156	0.00098	0.00102	0.00098	0.945
	40%	m=1	0.00135	0.00123	0.00115	0.00123	0.935
	(η1, η2)	m=10	0.00131	0.00103	0.00105	0.00103	0.948
	= (−1.38, 1.1)	CC	−0.04836	0.00113	0.00110	0.00347	0.702
		m*=10	0.00040	0.00103	0.00106	0.00103	0.950
	30%	m=1	−0.00139	0.00099	0.00093	0.00099	0.944
	(η1, η2)	m=10	−0.00143	0.00091	0.00088	0.00091	0.944
	= (−0.1, −1)	CC	0.01495	0.00117	0.00108	0.00139	0.923
		m*=10	−0.00176	0.00089	0.00088	0.00089	0.944
	40%	m=1	0.00061	0.00098	0.00095	0.00098	0.955
	(η1, η2)	m=10	0.00075	0.00091	0.00090	0.00091	0.952
	= (−0.1, −0.36)	CC	0.05120	0.00140	0.00129	0.00402	0.710
		m*=10	0.00048	0.00091	0.00091	0.00091	0.952

m^*=10, 10 proper imputations based on methods of [5].

Table 2 shows results from proper multiple imputation of Bakoyannis et al. [5] under the misspecified imputation model logitπ(X, γ) = γ₁ + γ₂ log(1 + exp(−X)), where we did not use a non-parametric bootstrap method as suggested in [5] to avoid biases in the variance estimates $\widehat{var}({\widehat{F}}_1)$ obtained by Rubin’s variance formula under misspecification of an imputation model: because we found that the use of the bootstrap method for variance estimation was not necessary. The multiple imputation estimates show that the biases and variance estimates are small even if the imputation model is misspecified. The variance estimates agree with the empirical variances, and the empirical coverage probabilities for 95% confidence intervals are close to the nominal level. The variance estimates from our improper multiple imputation methods are slightly smaller than those from [5]. The MSEs of both approaches are similar.

3.3. Additional evaluations for two-sample tests

Additional numerical studies were conducted to evaluate the performance of the proposed test in two samples with missing cause of failure. As described in Section 3.1 of Peng and Fine [25], we considered configurations II, III, and IV along with configuration I; (π₁, π₂, v₁, v₂, θ₁, θ₂) = (2/3, 1/3, 1, 1.2, 1, 1) in configuration II, (2/3, 1/3, 1, 1.2, 0.5, 1) in configuration III, and (1/2, 1/2, 0.8, 1.2, 1, 1) in configuration IV. We generated the sample indicator Z from a Bernoulli distribution with success probability 0.5. When Z = 1 (denoted by group 1), we generated data from configuration I, while we generated data from configuration II, III, or IV when Z = 0 (denoted by group 2). The censoring times (C_l) were generated from a uniform distribution U(0, 7.2) for group 1 and from a uniform distribution U(c₁, c₂) for group 2, giving the censoring proportion of 15% for each group l (l = 1, 2). As noted in Peng and Fine [25], the cumulative incidence functions for cause 1 are identical under configurations I and II, there is a crossover of the cumulative incidence functions for cause 1 under configurations I and III, and the cumulative incidence function for cause 1 under configuration I is stochastically larger than that under configuration IV. For each group l (l = 1, 2), we generated the missingness indicator R_l from $\text{logitPr}(R_l=0\mid {\delta }_l>0,X_l)={\eta }_1^{(l)}+{\eta }_2^{(l)}{X}_l$, where X_l = min(T_l, C_l). With different choices of η^(l)’s, we generated 20, 30, and 40% missing causes of failure for group 1, and 10% missing causes of failure for group 2. The true model for π(X) is logitπ(X) = log(5/2) − 0.2X in configuration I, logitπ(X) = log(5/3) + 0.2X in configuration II, logitπ(X) = log(5/6) − 0.5 log(X) − X^1/2 + 1.2X in configuration III, and logitπ(X) = log(2/3) + 0.4X in configuration IV. We fitted a correctly specified logistic regression model logitπ(X, γ) = γ₁ + γ₂X in configurations I, II, and IV, and logitπ(X, γ) = γ₁ + γ₂ log(X) + γ₃X^1/2 + γ₄X in configuration III. We conducted 1000 simulations with sample sizes of 200 and 400. Table 3 shows that under the correct imputation model, the imputation tests have empirical sizes close to the nominal level 0.05 and high powers in detecting differences between the two cumulative incidence functions for cause 1, whereas the test obtained by the complete case analysis results in larger empirical size and less power compared to the imputation methods. Note that in configurations I vs. III and I vs. IV with ${\eta }_2^{(1)}>0$, the complete case test has higher power than the imputation tests. This is because the complete case analysis can overestimate cumulative incidence when deaths with missing cause of failure occur late in follow-up.

Table 3.

Empirical rejection rates and powers of two-sample tests under the correct imputation model; The null hypothesis scenario corresponds to the first column (I vs. II). The second and third columns (I vs. III and I vs. IV) indicate powers. Configuration I is the generation model for group 1 (Z = 1), which is fixed, and configurations II, III, and IV correspond to the generation models for group 2 (Z = 0).

n	% missing in configuration I	Method	10% missing in configurations II, III, and IV
			( ${\eta }_1^{(2)},{\eta }_2^{(2)}$)	( ${\eta }_1^{(2)},{\eta }_2^{(2)}$)	( ${\eta }_1^{(2)},{\eta }_2^{(2)}$)
			= (−2.65, 0.5)	= (−2.6, 0.5)	= (−2.68, 0.5)
			I vs. II	I vs. III	I vs. IV
200	20%	m=1	0.056	0.085	0.634
	( ${\eta }_1^{(1)},{\eta }_2^{(1)}$)	m=10	0.050	0.088	0.659
	= (−1.38, 0)	CC	0.062	0.075	0.601
	30%	m=1	0.060	0.070	0.548
	( ${\eta }_1^{(1)},{\eta }_2^{(1)}$)	m=10	0.054	0.075	0.578
	= (−0.1, −1)	CC	0.096	0.046	0.369
	40%	m=1	0.054	0.089	0.566
	( ${\eta }_1^{(1)},{\eta }_2^{(1)}$)	m=10	0.046	0.092	0.585
	= (−0.1, −0.36)	CC	0.105	0.058	0.398
	30%	m=1	0.057	0.095	0.649
	( ${\eta }_1^{(1)},{\eta }_2^{(1)}$)	m=10	0.054	0.079	0.663
	= (−1.38, 0.56)	CC	0.059	0.077	0.693
	40%	m=1	0.056	0.099	0.562
	( ${\eta }_1^{(1)},{\eta }_2^{(1)}$)	m=10	0.049	0.090	0.599
	= (−1.38, 1.1)	CC	0.072	0.117	0.712
400	20%	m=1	0.053	0.126	0.896
	( ${\eta }_1^{(1)},{\eta }_2^{(1)}$)	m=10	0.050	0.128	0.924
	= (−1.38, 0)	CC	0.061	0.115	0.897
	30%	m=1	0.061	0.118	0.861
	( ${\eta }_1^{(1)},{\eta }_2^{(1)}$)	m=10	0.050	0.121	0.886
	= (−0.1, −1)	CC	0.138	0.057	0.712
	40%	m=1	0.050	0.129	0.822
	( ${\eta }_1^{(1)},{\eta }_2^{(1)}$)	m=10	0.049	0.119	0.868
	= (−0.1, −0.36)	CC	0.113	0.064	0.687
	30%	m=1	0.057	0.117	0.867
	( ${\eta }_1^{(1)},{\eta }_2^{(1)}$)	m=10	0.054	0.118	0.878
	= (−1.38, 0.56)	CC	0.059	0.146	0.909
	40%	m=1	0.057	0.120	0.829
	( ${\eta }_1^{(1)},{\eta }_2^{(1)}$)	m=10	0.056	0.128	0.856
	= (−1.38, 1.1)	CC	0.070	0.204	0.928

To justify the robustness of the imputation test, we fitted an incorrectly specified logistic regression model logitπ(X, γ) = γ₁ + γ₂ log(1 + exp(−X)) in configurations I, II, III, and IV. We generated data from the same scenario as before. We conducted 1000 simulations with sample sizes of 200 and 400 (Table 4). Even with misspecified imputation model, the imputation tests result in empirical sizes close to the nominal level and high powers.

Table 4.

Empirical rejection rates and powers of two-sample tests under the incorrect imputation model; The null hypothesis scenario corresponds to the first column (I vs. II). The second and third columns (I vs. III and I vs. IV) indicate powers. Configuration I is the generation model for group 1 (Z = 1), which is fixed, and configurations II, III, and IV correspond to the generation models for group 2 (Z = 0).

n	% missing in configuration I	Method	10% missing in configurations II, III, and IV
			( ${\eta }_1^{(2)},{\eta }_2^{(2)}$)	( ${\eta }_1^{(2)},{\eta }_2^{(2)}$)	( ${\eta }_1^{(2)},{\eta }_2^{(2)}$)
			= (−2.65, 0.5)	= (−2.6, 0.5)	= (−2.68, 0.5)
			I vs. II	I vs. III	I vs. IV
200	20%	m=1	0.055	0.085	0.641
	( ${\eta }_1^{(1)},{\eta }_2^{(1)}$)	m=10	0.056	0.074	0.654
	= (−1.38, 0)	CC	0.064	0.064	0.593
	30%	m=1	0.064	0.084	0.590
	( ${\eta }_1^{(1)},{\eta }_2^{(1)}$)	m=10	0.052	0.090	0.629
	= (−0.1, −1)	CC	0.107	0.053	0.430
	40%	m=1	0.054	0.111	0.555
	( ${\eta }_1^{(1)},{\eta }_2^{(1)}$)	m=10	0.053	0.092	0.582
	= (−0.1, −0.36)	CC	0.105	0.065	0.392
	30%	m=1	0.060	0.084	0.604
	( ${\eta }_1^{(1)},{\eta }_2^{(1)}$)	m=10	0.057	0.094	0.634
	= (−1.38, 0.56)	CC	0.071	0.107	0.660
	40%	m=1	0.053	0.088	0.582
	( ${\eta }_1^{(1)},{\eta }_2^{(1)}$)	m=10	0.049	0.078	0.596
	= (−1.38, 1.1)	CC	0.085	0.105	0.700
400	20%	m=1	0.046	0.146	0.887
	( ${\eta }_1^{(1)},{\eta }_2^{(1)}$)	m=10	0.048	0.143	0.911
	= (−1.38, 0)	CC	0.060	0.120	0.881
	30%	m=1	0.054	0.122	0.840
	Equation	m=10	0.052	0.112	0.863
	= (−0.1, −1)	CC	0.148	0.064	0.675
	40%	m=1	0.045	0.144	0.822
	( ${\eta }_1^{(1)},{\eta }_2^{(1)}$)	m=10	0.045	0.138	0.856
	= (−0.1, −0.36)	CC	0.117	0.063	0.678
	30%	m=1	0.059	0.131	0.884
	( ${\eta }_1^{(1)},{\eta }_2^{(1)}$)	m=10	0.060	0.128	0.906
	= (−1.38, 0.56)	CC	0.061	0.161	0.924
	40%	m=1	0.055	0.134	0.857
	( ${\eta }_1^{(1)},{\eta }_2^{(1)}$)	m=10	0.045	0.131	0.887
	= (−1.38, 1.1)	CC	0.061	0.197	0.934

4. Application: Effect of tamoxifen on breast-cancer specific mortality in women with early stage breast cancer

4.1. Background

We illustrate the proposed methods using data from a randomized clinical trial in early stage breast cancer, obtained from the National Surgical Adjuvant Breast and Bowel Project (NSABP). The NSABP is a U.S. National Cancer Institute sponsored multi-center clinical trials group that conducts research into the treatment and prevention of breast and colorectal cancers. Tamoxifen is an estrogen-like compound used in the treatment of breast cancer [31].

Between 1982 and 1988, 2892 women with estrogen receptor-positive breast tumors and no axillary node involvement were enrolled in NSABP Protocol B-14, a double-blind randomized trial comparing five years of tamoxifen (20 mg/day) with placebo. The primary trial endpoints were overall survival (time surviving after surgery, with an event being death from any cause) and disease-free survival (time free of tumor recurrence, new breast cancer in the opposite breast, other cancers, or death from any cause preceding these events). Findings indicated a strong positive effect of tamoxifen on disease-free survival [32], and with longer follow-up duration, a significant reduction in overall mortality [33]. The latter endpoint (overall mortality) is used as a conservative approach in that it avoids complexities of accurate ascertainment of cause of death and also requires that the net effect of treatment be a longer lifetime. However, most of the influence on improvement in overall survival arises from avoidance of death from breast cancer. Thus cause-specific mortality (especially, breast cancer-specific mortality) is of interest. While information on cause of death was desired and requested, because the endpoint was overall survival, missing cause of death data were not rigorously resolved, and so there is a substantial portion of cases with missing cause. Table 5 shows vital status for 2817 trial eligible patients included in this analysis. Of patients who died, 20.9% of patients assigned to placebo and 26.3% of patients assigned to tamoxifen had missing cause of death.

Table 5.

Vital status among women from the NSABP B-14 randomized trial.

Status/Cause of Death	Treatment Arm		Total
	Placebo	Tamoxifen
Alive	919	1001	1920
Breast cancer	241	155	396
Other cause	150	142	292
Unknown	103	106	209
Total	1413	1404	2817

4.2. Results

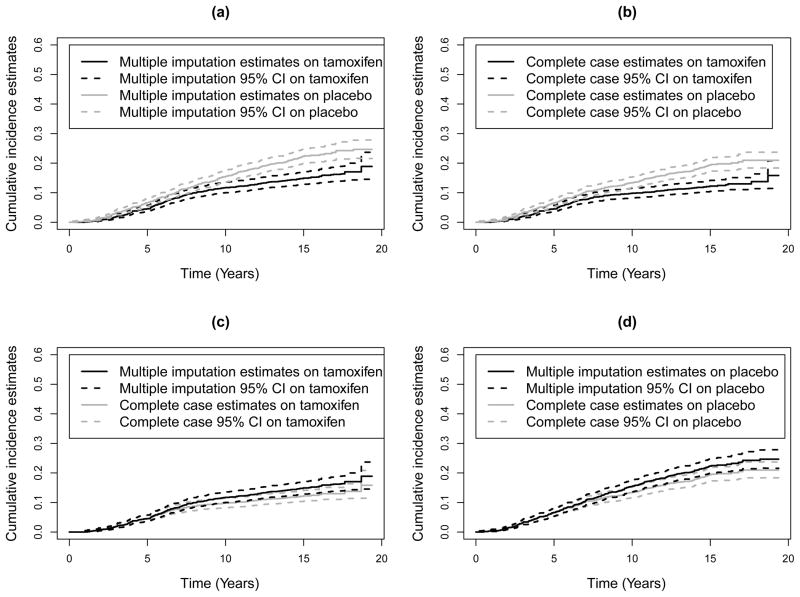
We applied our multiple imputation methods to estimate cumulative incidence of breast cancer-specific death on tamoxifen and placebo. In each group, the logistic imputation model for π(X) included time since diagnosis which was statistically significantly associated with breast cancer-specific mortality among those with complete cause of death information (R = 1, δ > 0). Figure 1 shows estimates of cumulative incidence of death due to breast cancer from 10 multiple imputations and the complete case estimates obtained by excluding patients with missing causes of death, along with their corresponding 95% pointwise confidence intervals (CI) given in (3). As shown in Figure 1(a) and (b), the estimates of cumulative incidence of breast cancer death in the tamoxifen group are lower than those in the placebo group in both multiple imputation and complete case analyses. In Figure 1(c) and (d), patients in the tamoxifen group from the multiple imputation methods have 10-year cumulative incidence of breast cancer death (with 95% confidence interval) of 11.7% (10.0–13.6%), while in the placebo group, 10-year cumulative incidence is 15.4% (13.5–17.4%). The complete case estimates are 9.8% (8.3–11.6%) for the tamoxifen group and 13.4% (11.6–15.3%) for the placebo group. The 10-year cumulative incidences of breast cancer death from the complete case analysis are 16% on tamoxifen and 13% on placebo lower than those from the multiple imputation methods. These differences continue to grow as follow-up lengthens.

Figure 1.

Estimates of cumulative incidence of breast cancer death with 95% pointwise confidence intervals (CI) by the multiple imputation method and complete case analysis. The upper panels show results by analysis and by group, whereas the lower panel shows results by group and by analysis.

In order to compare cumulative incidences of breast cancer death between tamoxifen and placebo groups, we computed the multiple imputation test based on 10 imputations and the complete case test. The test statistics (p-value) for breast cancer death are −3.746 (0.0002) for the multiple imputation test and −3.903 (0.00009) for the complete case test, both indicating that tamoxifen significantly reduces mortality from breast cancer. The result from the complete case test is very similar to that from the multiple imputation test. This may be because cumulative incidences of death due to breast cancer in both tamoxifen and placebo groups are underestimated to a similar extent by the complete case analysis (see Figure 1).

5. Discussion

We investigated multiple imputation methods for nonparametric inferences of the cumulative incidence function in the presence of missing causes of failure. Under the missing at random assumption, we develop asymptotic theory for multiple imputation methods to estimate the cumulative incidence function nonparametrically and perform a test for comparing the cumulative incidence functions in two samples. These procedures are straightforward to implement. When there are no missing causes of failure, our inference procedures reduce to those in Lin [9] and Pepe’s test with a martingale-based variance estimator [24, 28]. Simulation studies show that our multiple imputation methods perform well, even if the model for imputation is misspecified. The simulations also show that our improper imputation approach is slightly more efficient compared to the proper imputation [5]. In supplemental analyses, we show that the complete case analysis can either underestimate or overestimate cumulative incidence, depending on whether deaths with missing cause occur early or late in follow-up. In the breast cancer example, estimates of cumulative incidence of breast cancer death in both tamoxifen and placebo groups from the complete case analysis were lower than those from the multiple imputation methods. Since cumulative incidences of breast cancer death in both groups are underestimated to a similar extent by the complete case analysis, the complete case test provided a similar result to the multiple imputation test for comparing breast-cancer specific mortalities between the two groups. Thus, the complete case test is unlikely to be biased for comparing differences between the cumulative incidence functions in two samples where the missing cause of death mechanism is the same in each group.

We proposed nonparametric inferences of the cumulative incidence function with missing cause of failure under the assumption of missing at random when we observe (X_i, R_i, R_iδ_i) (i = 1, …, n). In a practical setting, covariate information may be available and one may include auxiliary covariates in the imputation model to make the missing at random assumption more plausible, as the methods of [2]. In the case, our multiple imputation methods for nonparametric inferences of the cumulative incidence function with missing causes of failure are applicable incorporating auxiliary covariates. A nonparametric estimator of the cumulative incidence function can be obtained by imputing missing cause of failure from a Bernoulli distribution with success probability π(W_i, γ̂) and averaging nonparametric estimators across several imputed data sets, where W_i = (X_i, Z_i), Z_i is auxiliary covariates, and the success probability π(W_i, γ̂) can be obtained by fitting a logistic regression model, $\text{logit}\pi (W_i,\gamma )=W_i^T\gamma$, under the missing at random assumption. The variance of the multiple imputation estimator can be estimated by V̂₁(t) in equation (A.8) with replacing π(X_i, γ̂) by π(W_i, γ̂) and π_γ(X_i, γ̂) by π_γ(W_i, γ̂) in equation (A.5). The variance estimator of the multiple imputation test in two samples can be obtained by replacing π_γl(X_il, γ̂_l) by π_γl(W_il, γ̂_l) in (B.3) and π(X_il, γ̂_l) by π(W_il, γ̂_l) in equation (B.6).

We assumed that the cause of failure is missing at random. Unfortunately, assumptions about the missing mechanism such as the missing at random are not testable from the observed data [5, 34]. Thus, one may conduct sensitivity analyses to assess the robustness of inferences to departures from the missing at random assumption [5, 6, 35].

We used the Aalen-Johansen estimator for nonparametric estimation of the cumulative incidence function. This is based on the assumption that the censoring time C is independent of (T, ε). When the censoring time is only independent of (T, ε) conditional on covariates, the Aalen-Johansen estimator is unbiased if the censoring distribution does not depend on covariates (i.e., Pr(C > t | Z = z) = Pr(C > t) for covariates Z) and hence censoring is independent of covariates. However, the estimator may be biased if censoring depends on covariates [36]. In that case, Binder et al. [36] proposed an alternative estimator to the Aalen-Johansen estimator by using a regression model for the censoring time. Thus, when the censoring time is only independent of (T, ε) given covariates, our imputation methods to estimate nonparametrically the cumulative incidence function with missing cause of failure are valid if censoring is independent of covariates. However, if censoring depends on covariates, alternative estimators proposed by Binder et al. [36] may be used. Similar derivations used in our paper may be applicable to multiple imputation inferences for the alternative estimators.

In this paper, we discussed multiple imputation inferences for nonparametric estimation of the cumulative incidence function with two types of failure in the presence of missing causes of failure. When there are more than two causes of death, the missing cause can be imputed from a multinomial distribution with probabilities estimated by using a parametric modeling under the missing at random assumption. A multinomial logistic regression can be considered as a parametric imputation model. In that case, the variance formula can be obtained following asymptotic theory given in Appendix A along with the influence function expansion of the maximum likelihood estimators of parameters in a multinomial logistic imputation model.

When the imputation and analysis models agree (i.e., congenial as defined in [29]), results from the proper multiple imputation approach may be similar to those from our improper multiple imputation methods, as shown in the simulation studies. When covariate information is available and censoring depends on some covariates, one may include covariates (including auxiliary covariates) in the imputation model to make the missing at random assumption more plausible and use a regression model for the censoring time. In that case, the imputation and analysis models may then be uncongenial, and Rubin’s variance formula may produce some bias in the variance estimates of the multiple imputation estimates, as noted in [29]. Note that we derive variance estimators for the multiple imputation estimators directly. This may suggest that our multiple imputation method is more efficient.

APPENDIX A

Define the counting process notation N_kij(t, R_i, γ) = I(X_i ≤ t, D_kij(R_i, γ) = 1), Y_i(t) = I(X_i ≥ t), and $\overline{Y}(t)={\sum }_{i=1}^n{Y}_i(t)$. Let

$$M_{\mathit{kij}}(t,R_i,\gamma )=N_{\mathit{kij}}(t,R_i,\gamma )-{\int }_0^t{\lambda }_k(u)Y_i(u)du.$$

Let Λ̂_kj(t) be the cumulative cause-specific hazard estimate for cause k from the jth imputed data set that can be expressed by the counting process notation as

$${\widehat{\mathrm{\Lambda }}}_{kj}(t)=\sum _{i=1}^n{\int }_0^t\frac{{dN}_{\mathit{kij}}(u,R_i,\widehat{\gamma })}{\overline{Y}(u)},k=1,2.$$

n^1/2{Λ̂_kj(t) − Λ_k(t)} is asymptotically equivalent to

$$n^{-1/2}\sum _{i=1}^n{\int }_0^t\frac{n}{\overline{Y}(u)}{dM}_{\mathit{kij}}(u,R_i,\widehat{\gamma })+o_p(1),k=1,2.$$ (A.1)

Using the consistency of Ŝ(·), Taylor expansion and integration by parts as described in Lin [9], U_1j(t) = n^1/2{F̂_1j(t) − F₁(t)} from the jth imputed data set can be expressed as

$$\begin{array}{l}{U}_{1j}(t)=n^{1/2}\left[{\int }_0^t\widehat{S}(u)d\{{\widehat{\mathrm{\Lambda }}}_{1j}(u)-{\mathrm{\Lambda }}_1(u)\}+{\int }_0^t\{\widehat{S}(u)-S(u)\}d{\mathrm{\Lambda }}_1(u)\right]\\ =n^{1/2}\left[{\int }_0^{t}S(u)d\{{\widehat{\mathrm{\Lambda }}}_{1j}(u)-{\mathrm{\Lambda }}_1(u)\}-\sum _{k=1}^2{\int }_0^{t}S(u)\{{\widehat{\mathrm{\Lambda }}}_{kj}(u)-{\mathrm{\Lambda }}_k(u)\}d{\mathrm{\Lambda }}_1(u)\right]+o_p(1)\\ =n^{1/2}\left[{\int }_0^{t}S(u)d\{{\widehat{\mathrm{\Lambda }}}_{1j}(u)-{\mathrm{\Lambda }}_1(u)\}-\sum _{k=1}^2{\int }_0^t\{F_1(t)-F_1(u)\}d\{{\widehat{\mathrm{\Lambda }}}_{kj}(u)-{\mathrm{\Lambda }}_k(u)\}\right]+o_p(1).\end{array}$$

Using (A.1) and S(t) = 1 − F₁(t) − F₂(t), U_1j(t) = n^1/2{F̂_1j(t) − F₁(t)} is given by

$$U_{1j}(t)=n^{-1/2}\sum _{i=1}^n{f}_{ij}(\widehat{\gamma },t)+o_p(1),$$ (A.2)

where

$$f_{ij}(\gamma ,t)={\int }_0^t\frac{n\{1-F_2(u)-F_1(t)\}{dM}_{1ij}(u,R_i,\gamma )}{\overline{Y}(u)}-{\int }_0^t\frac{n\{F_1(t)-F_1(u)\}{dM}_{2ij}(u,R_i,\gamma )}{\overline{Y}(u)}.$$

To establish the asymptotic theory for single imputation and multiple imputation estimates, we use the methods described in Lu and Tsiatis [2] or Tsiatis et al. [22]. Consider the centered sum $H_j(\gamma ,t)={\sum }_{i=1}^n\{f_{ij}(\gamma ,t)-{\mu }_f(\gamma ,t)\}$, where μ_f (γ, t) = E{f_ij(γ, t)}. Then n^−1/2{H_j(γ̂, t) − H_j(γ₀, t)} converges in probability to zero [37]. Using the convergence of the centered sum and Taylor series expansion,

$$\begin{array}{l}{U}_{1j}(t)=n^{-1/2}\sum _{i=1}^n{f}_{ij}({\gamma }_0,t)+n^{1/2}\{{\mu }_f(\widehat{\gamma },t)-{\mu }_f({\gamma }_0,t)\}+o_p(1)\\ =n^{-1/2}\sum _{i=1}^n{f}_{ij}({\gamma }_0,t)+{\left\{\frac{\partial }{\partial \gamma }{\mu }_f({\gamma }_0,t)\right\}}^T{n}^{1/2}(\widehat{\gamma }-{\gamma }_0)+o_p(1).\end{array}$$

Using arguments similar to those in Tsiatis et al. [22],

$$\frac{\partial }{\partial \gamma }{\mu }_f({\gamma }_0,t)=E\left[\frac{n\{1-F_1(X_i)-F_2(X_i)\}}{\overline{Y}(X_i)}I(X_i\le t)Pr(R_i=0\mid X_i){\pi }_{\gamma }(X_i,{\gamma }_0)\right],$$

which is estimated by

$$\frac{\partial }{\partial \gamma }{\widehat{\mu }}_f(\widehat{\gamma },t)=\sum _{i=1}^n\left[\frac{\left\{1-{\widehat{F}}_{1j}(X_i)-{\widehat{F}}_{2j}(X_i)\right\}}{\overline{Y}(X_i)}I(X_i\le t)I(R_i=0){\pi }_{\gamma }(X_i,\widehat{\gamma })\right],$$

where subscript j means that the corresponding estimate is obtained from the jth imputed data set and ${\pi }_{\gamma }(X_i,\gamma )=\frac{\partial }{\partial \gamma }\pi (X_i,\gamma )$.

The asymptotic normality of γ̂ follows from the influence function expansion

$$n^{1/2}(\widehat{\gamma }-{\gamma }_0)=n^{-1/2}\sum _{i=1}^n\varphi (O_i,{\gamma }_0)+o_p(1),$$

where O_i = (R_i = 1, δ_i > 0, X_i),

$$\varphi (O_i,{\gamma }_0)=J^{-1}({\gamma }_0){\pi }_{\gamma }(X_i,{\gamma }_0)I(R_i=1,{\delta }_i>0)\left[\frac{D_{1i}-\pi (X_i,{\gamma }_0)}{\pi (X_i,{\gamma }_0)\{1-\pi (X_i,{\gamma }_0)\}}\right],$$

and J(γ₀) is the information matrix

$$J({\gamma }_0)=E\left[{\pi }_{\gamma }{(X_i,{\gamma }_0)}^{\otimes 2}\frac{Pr(R_i=1,{\delta }_i>0\mid X_i)}{\pi (X_i,{\gamma }_0)\{1-\pi (X_i,{\gamma }_0)\}}\right].$$

Applying the approximation for n^1/2(γ̂ − γ₀), U_1j(t) is equal to

$$n^{-1/2}\sum _{i=1}^n\left[f_{ij}({\gamma }_0,t)+{\left\{\frac{\partial }{\partial \gamma }{\mu }_f({\gamma }_0,t)\right\}}^T\varphi (O_i,{\gamma }_0)\right]+o_p(1).$$ (A.3)

This is a sum of independent and identically distributed mean zero random variables, and the central limit theorem proves asymptotic normality. Its variance is given by

$$\begin{gathered} V_{1j}(t)=E\{f_{ij}{({\gamma }_0,t)}^{\otimes 2}\}+{\left\{\frac{\partial }{\partial \gamma }{\mu }_f({\gamma }_0,t)\right\}}^T{J}^{-1}({\gamma }_0)E[\frac{n\{1-F_1(X_i)-F_2(X_i)\}}{\overline{Y}(X_i)}I(X_i\le t) \\ \times \{Pr({\delta }_i>0\mid X_i)+Pr(R_i=1,{\delta }_i>0\mid X_i)\}{\pi }_{\gamma }(X_i,{\gamma }_0)], \end{gathered}$$ (A.4)

where E{f_ij(γ₀, t)^⊗2} is the asymptotic variance of n^1/2{F̂₁(t) − F₁(t)} when all causes of failure are observed and is estimated by

$${\widehat{\xi }}_{1j}(t)=n\sum _{i=1}^n\frac{{\{1-{\widehat{F}}_{2j}(X_i)-{\widehat{F}}_{1j}(t)\}}^2}{\overline{Y}{(X_i)}^2}I(X_i\le t,D_{1ij}(R_i,\widehat{\gamma })=1)+n\sum _{i=1}^n\frac{{\{{\widehat{F}}_{1j}(t)-{\widehat{F}}_{1j}(X_i)\}}^2}{\overline{Y}{(X_i)}^2}I(X_i\le t,D_{2ij}(R_i,\widehat{\gamma })=1),$$

and D_2ij(R_i, γ̂) is the imputed value of D_2i from the jth imputed data set as

$$D_{2ij}(R_i,\widehat{\gamma })=\{\begin{array}{cc}{D}_{2i}& \text{if}{R}_i=1,\\ 1-D_{1ij}(R_i,\widehat{\gamma })& \text{if}{R}_i=0.\end{array}$$

For any j (j = 1, …, m), the variance V_1j(t) is estimated by

$$\begin{gathered} {\widehat{V}}_{1j}(t)={\widehat{\xi }}_{1j}(t)+{\left\{\frac{\partial }{\partial \gamma }{\widehat{\mu }}_f(\widehat{\gamma },t)\right\}}^T{\widehat{J}}^{-1}(\widehat{\gamma })\sum _{i=1}^n[\frac{\{1-{\widehat{F}}_{2j}(X_i)-{\widehat{F}}_{1j}(X_i)\}}{\overline{Y}(X_i)}I(X_i\le t) \\ \times \{I({\delta }_i>0)+I(R_i=1,{\delta }_i>0)\}{\pi }_{\gamma }(X_i,\widehat{\gamma })]. \end{gathered}$$ (A.5)

For multiple imputation, U₁(t) = n^1/2{F̂₁(t) − F₁(t)} is asymptotically equivalent to

$$n^{-1/2}\sum _{i=1}^n\left[\frac{1}{m}\sum _{j=1}^m{f}_{ij}({\gamma }_0,t)+{\left\{\frac{\partial }{\partial \gamma }{\mu }_f({\gamma }_0,t)\right\}}^T\varphi (O_i,{\gamma }_0)\right]+o_p(1).$$ (A.6)

This is a sum of independent and identically distributed mean zero random variables, and the central limit theorem yields the asymptotic normality. Its variance is given by

$$V_1(t)=V_{1j}(t)-(1-1/m)E[[{\{1-F_2(X_i)-F_1(t)\}}^2+{\{F_1(t)-F_1(X_i)\}}^2]\frac{n^2}{\overline{Y}{(X_i)}^2}\times I(X_i\le t)\pi (X_i,{\gamma }_0)\{1-\pi (X_i,{\gamma }_0)\}Pr(R_i=0\mid X_i)].$$ (A.7)

The variance V₁(t) is estimated by

$${\widehat{V}}_1(t)=\frac{1}{m}\sum _{j=1}^m{\widehat{V}}_{1j}(t)-(1-1/m)\frac{1}{m}\sum _{j=1}^m[n\sum _{i=1}^n\left[{\{1-{\widehat{F}}_{2j}(X_i)-{\widehat{F}}_{1j}(t)\}}^2+{\{{\widehat{F}}_{1j}(t)-{\widehat{F}}_{1j}(X_i)\}}^2\right]\times \frac{1}{\overline{Y}{(X_i)}^2}I(X_i\le t)\pi (X_i,\widehat{\gamma })\{1-\pi (X_i,\widehat{\gamma })\}I(R_i=0)].$$ (A.8)

APPENDIX B

Suppose that there are two independent competing risk samples with missing cause of failure. In group l (l = 1, 2), the observed data consist of (R_il, X_il, R_ilδ_il) (i = 1, …, n_l), where R_il is the missingness indicator in group l, X_il = min(T_il, C_il), and δ_il = I(T_il ≤ C_il)ε_il. For the ith individual from the jth imputed data set in group l, define the counting process notation N_kijl(t, R_il, γ) = I(X_il ≤ t, D_kijl(R_il, γ) = 1), Y_il(t) = I(X_il ≥ t), and ${\overline{Y}}_l(t)={\sum }_{i=1}^{n_l}{Y}_{il}(t)$. Let

$$M_{\mathit{kijl}}(t,R_{il},\gamma )=N_{\mathit{kijl}}(t,R_{il},\gamma )-{\int }_0^t{\lambda }_k^{(l)}(u)Y_{il}(u)du.$$

The test statistic for single imputation can be written as

$$Q_S=\sqrt{\frac{n_1{n}_2}{n_1+n_2}}\left[{\int }_0^{\tau }\{{\widehat{F}}_{1j}^{(1)}(u)-F_1^{(1)}(u)\}du-{\int }_0^{\tau }\{{\widehat{F}}_{1j}^{(2)}(u)-F_1^{(2)}(u)\}du\right]+\sqrt{\frac{n_1{n}_2}{n_1+n_2}}\left[{\int }_0^{\tau }\{F_1^{(1)}(u)-F_1^{(2)}(u)\}du\right].$$

Under the null hypothesis $H_0:F_1^{(1)}(t)=F_1^{(2)}(t)$ for all t ≤ τ,

$$Q_S=\sqrt{\frac{n_1{n}_2}{n_1+n_2}}\left[{\int }_0^{\tau }\{{\widehat{F}}_{1j}^{(1)}(u)-F_1^{(1)}(u)\}du-{\int }_0^{\tau }\{{\widehat{F}}_{1j}^{(2)}(u)-F_1^{(2)}(u)\}du\right].$$

Using (A.2) and changing the order of integration, $n_l^{1/2}{\int }_0^{\tau }\{{\widehat{F}}_{1j}^{(l)}(u)-F_1^{(l)}(u)\}du$ is given by

$$\begin{array}{l}{n}_l^{1/2}{\int }_0^{\tau }\{{\widehat{F}}_{1j}^{(l)}(u)-F_1^{(l)}(u)\}du\\ =n_l^{-1/2}\sum _{i=1}^{n_l}[{\int }_0^{\tau }\left\{{\int }_0^u\frac{n_l\{1-F_2^{(l)}(s)-F_1^{(l)}(u)\}}{{\overline{Y}}_l(s)}{dM}_{1\mathit{ijl}}(s,R_{il},{\widehat{\gamma }}_l)\right\}du\\ -{\int }_0^{\tau }\left\{{\int }_0^u\frac{n_l\{F_1^{(l)}(u)-F_1^{(l)}(s)\}}{{\overline{Y}}_l(s)}{dM}_{2\mathit{ijl}}(s,R_{il},{\widehat{\gamma }}_l)\right\}du]+o_p(1)\\ =n_l^{-1/2}\sum _{i=1}^{n_l}[{\int }_0^{\tau }{n}_l\left\{(\tau -s)\frac{1-F_2^{(l)}(s)}{{\overline{Y}}_l(s)}-\frac{1}{{\overline{Y}}_l(s)}{\int }_s^{\tau }{F}_1^{(l)}(u)du\right\}{dM}_{1\mathit{ijl}}(s,R_{il},{\widehat{\gamma }}_l)\\ +{\int }_0^{\tau }{n}_l\{(\tau -s)\frac{F_1^{(l)}(s)}{{\overline{Y}}_l(s)}-\frac{1}{{\overline{Y}}_l(s)}{\int }_s^{\tau }{F}_1^{(l)}(u)du\}{dM}_{2\mathit{ijl}}(s,R_{il},{\widehat{\gamma }}_l)]+o_p(1)\\ =n_l^{-1/2}\sum _{i=1}^{n_l}{\phi }_{ij}^{(l)}({\widehat{\gamma }}_l,\tau )+o_p(1),\end{array}$$

where γ̂_l is the maximum likelihood estimator of γ in group l and

$$\begin{array}{l}{\phi }_{ij}^{(l)}(\gamma ,\tau )={\int }_0^{\tau }{n}_l\left\{(\tau -s)\frac{1-F_2^{(l)}(s)}{{\overline{Y}}_l(s)}-\frac{1}{{\overline{Y}}_l(s)}{\int }_s^{\tau }{F}_1^{(l)}(u)du\right\}{dM}_{1\mathit{ijl}}(s,R_{il},\gamma )\\ +{\int }_0^{\tau }{n}_l\left\{(\tau -s)\frac{F_1^{(l)}(s)}{{\overline{Y}}_l(s)}-\frac{1}{{\overline{Y}}_l(s)}{\int }_s^{\tau }{F}_1^{(l)}(u)du\right\}{dM}_{2\mathit{ijl}}(s,R_{il},\gamma ).\end{array}$$

To establish the asymptotic theory for single imputation and multiple imputation tests, we use the methods described in Lu and Tsiatis [2] or Tsiatis et al. [22]. We consider the centered sum for ${\phi }_{ij}^{(l)}(\gamma ,\tau )$ in group l, $H_j^{(l)}(\gamma ,\tau )={\sum }_{i=1}^{n_l}\{{\phi }_{ij}^{(l)}(\gamma ,\tau )-{\mu }_{\phi }^{(l)}(\gamma ,\tau )\}$, where ${\mu }_{\phi }^{(l)}(\gamma ,\tau )=E\{{\phi }_{ij}^{(l)}(\gamma ,\tau )\}$. Let γ_0l be the true value of γ_l. Then $n_l^{-1/2}\{H_j^{(l)}({\widehat{\gamma }}_l,\tau )-H_j^{(l)}({\gamma }_{0l},\tau )\}$ converges in probability to zero [37]. Using the convergence of the centered sum and Taylor series expansion, and applying the approximation for $n_l^{1/2}({\widehat{\gamma }}_l-{\gamma }_{0l})$ in group l, $n_l^{1/2}{\int }_0^{\tau }\{{\widehat{F}}_{1j}^{(l)}(u)-F_1^{(l)}(u)\}du$ is equal to

$$n_l^{-1/2}\sum _{i=1}^{n_l}\left[{\phi }_{ij}^{(l)}({\gamma }_{0l},\tau )+{\left\{\frac{\partial }{\partial {\gamma }_l}{\mu }_{\phi }^{(l)}({\gamma }_{0l},\tau )\right\}}^T{\varphi }^{(l)}(O_{li},{\gamma }_{0l})\right]+o_p(1),$$ (B.1)

where using arguments similar to those in Tsiatis et al. [22],

$$\frac{\partial }{\partial {\gamma }_l}{\mu }_{\phi }^{(l)}({\gamma }_{0l},\tau )=E\left[(\tau -X_{il})\frac{\left\{1-F_1^{(l)}(X_{il})-F_2^{(l)}(X_{il})\right\}}{{\overline{Y}}_l(X_{il})}I(X_{il}\le \tau )Pr(R_{il}=0\mid X_{il}){\pi }_{{\gamma }_l}(X_i,{\gamma }_{0l})\right].$$

This is a sum of independent and identically distributed mean zero random variables, and the central limit theorem yields the asymptotic normality. Its variance is given by

$$\begin{gathered} {\nu }_{1j}^{(l)}(\tau )=E\{{\phi }_{ij}^{(l)}{({\gamma }_{0l},\tau )}^{\otimes 2}\}+{\left\{\frac{\partial }{\partial {\gamma }_l}{\mu }_{\phi }^{(l)}({\gamma }_{0l},\tau )\right\}}^T{J}^{-1}({\gamma }_{0l})E[n_l\left\{(\tau -X_{il})\frac{1-F_2^{(l)}(X_{il})-F_1^{(l)}(X_{il})}{{\overline{Y}}_l(X_{il})}\right\} \\ \times I(X_{il}\le \tau )\{Pr({\delta }_{il}>0\mid X_{il})+Pr(R_{il}=1,{\delta }_{il}>0\mid X_{il})\}{\pi }_{{\gamma }_l}(X_{il},{\gamma }_{0l})], \end{gathered}$$ (B.2)

where $E\{{\phi }_{ij}^{(l)}{({\gamma }_{0l},\tau )}^{\otimes 2}\}$ is the asymptotic variance of $n_l^{1/2}{\int }_0^{\tau }\{{\widehat{F}}_{1j}^{(l)}(u)-F_1^{(l)}(u)\}du$ when all causes of failure are observed and is estimated by

$$\begin{array}{l}{\widehat{\zeta }}_{1j}^{(l)}(\tau )=n_l\sum _{i=1}^{n_l}{\left\{(\tau -X_{il})\frac{1-{\widehat{F}}_{2j}^{(l)}(X_{il})}{{\overline{Y}}_l(X_{il})}-\frac{1}{{\overline{Y}}_l(X_{il})}{\int }_{X_{il}}^{\tau }{\widehat{F}}_{1j}^{(l)}(u)du\right\}}^{2}I(X_{il}\le \tau ,D_{1\mathit{ijl}}(R_{il},{\widehat{\gamma }}_l)=1)\\ +n_l\sum _{i=1}^{n_l}{\left\{(\tau -X_{il})\frac{{\widehat{F}}_{1j}^{(l)}(X_{il})}{{\overline{Y}}_l(X_{il})}-\frac{1}{{\overline{Y}}_l(X_{il})}{\int }_{X_{il}}^{\tau }{\widehat{F}}_{1j}^{(l)}(u)du\right\}}^{2}I(X_{il}\le \tau ,D_{2\mathit{ijl}}(R_{il},{\widehat{\gamma }}_l)=1).\end{array}$$

For any j (j = 1, …, m), the variance ${\nu }_{1j}^{(l)}(\tau )$ is estimated by

$$\begin{gathered} {\widehat{\nu }}_{1j}^{(l)}(\tau )={\widehat{\zeta }}_{1j}^{(l)}(\tau )+{\left\{\frac{\partial }{\partial {\gamma }_l}{\widehat{\mu }}_{\phi }^{(l)}({\widehat{\gamma }}_l,\tau )\right\}}^T{\widehat{J}}^{-1}({\widehat{\gamma }}_l)\sum _{i=1}^{n_l}[\left\{(\tau -X_{il})\frac{1-{\widehat{F}}_{2j}^{(l)}(X_i)-{\widehat{F}}_{1j}^{(l)}(X_{il})}{{\overline{Y}}_l(X_{il})}\right\} \\ \times I(X_{il}\le \tau )\{I({\delta }_{il}>0)+I(R_{il}=1,{\delta }_{il}>0)\}{\pi }_{{\gamma }_l}(X_{il},{\widehat{\gamma }}_l)], \end{gathered}$$ (B.3)

where

$$\frac{\partial }{\partial {\gamma }_l}{\widehat{\mu }}_{\phi }^{(l)}({\widehat{\gamma }}_l,\tau )=\frac{1}{n_l}\sum _{i=1}^{n_l}\left[(\tau -X_{il})\frac{\left\{1-{\widehat{F}}_1^{(l)}(X_{il})-{\widehat{F}}_2^{(l)}(X_{il})\right\}}{{\overline{Y}}_l(X_{il})}I(X_{il}\le \tau )I(R_{il}=0){\pi }_{{\gamma }_l}(X_i,{\widehat{\gamma }}_l)\right].$$

Therefore, the variance estimate of the test statistic Q_S is given by

$${\widehat{\sigma }}_{Q_S}^2=\frac{n_2}{n_1+n_2}{\widehat{\nu }}_{1j}^{(1)}(\tau )+\frac{n_1}{n_1+n_2}{\widehat{\nu }}_{1j}^{(2)}(\tau ).$$

Under the null hypothesis H₀, the test statistic for multiple imputation is written as

$$Q_M=\sqrt{\frac{n_1{n}_2}{n_1+n_2}}\left[{\int }_0^{\tau }\{{\widehat{F}}_1^{(1)}(u)-F_1^{(1)}(u)\}du-{\int }_0^{\tau }\{{\widehat{F}}_1^{(2)}(u)-F_1^{(2)}(u)\}du\right].$$

Using (B.1), $n_l^{1/2}{\int }_0^{\tau }\{{\widehat{F}}_1^{(l)}(u)-F_1^{(l)}(u)\}du$ is asymptotically equivalent to

$$n_l^{-1/2}\sum _{i=1}^{n_l}\left[\frac{1}{m}\sum _{j=1}^m{\phi }_{ij}^{(l)}({\gamma }_{0l},\tau )+{\left\{\frac{\partial }{\partial {\gamma }_l}{\mu }_{\phi }^{(l)}({\gamma }_{0l},\tau )\right\}}^T{\varphi }^{(l)}(O_{il},{\gamma }_{0l})\right]+o_p(1).$$ (B.4)

This is a sum of independent and identically distributed mean zero random variables, and the central limit theorem yields the asymptotic normality. Its variance is given by

$$\begin{gathered} {\nu }_1^{(l)}(\tau )={\nu }_{1j}^{(l)}(\tau )-(1-1/m)\left[E\right[n_l^2{\left\{(\tau -X_{il})\frac{1-F_2^{(l)}(X_{il})}{{\overline{Y}}_l(X_{il})}-\frac{1}{{\overline{Y}}_l(X_{il})}{\int }_{X_{il}}^{\tau }{F}_1^{(l)}(u)du\right\}}^2 \\ \times I(X_{il}\le \tau )\pi (X_{il},{\gamma }_{0l})\{1-\pi (X_{il},{\gamma }_{0l})\}Pr(R_{il}=0\mid X_{il})] \\ +E[n_l^2{\left\{(\tau -X_{il})\frac{F_1^{(l)}(X_{il})}{{\overline{Y}}_l(X_{il})}-\frac{1}{{\overline{Y}}_l(X_{il})}{\int }_{X_{il}}^{\tau }{F}_1^{(l)}(u)du\right\}}^2 \\ \times I(X_{il}\le \tau )\pi (X_{il},{\gamma }_{0l})\{1-\pi (X_{il},{\gamma }_{0l})\}Pr(R_{il}=0\mid X_{il})\left]\right]. \end{gathered}$$ (B.5)

The variance ${\nu }_1^{(l)}(\tau )$ is estimated by

$$\begin{gathered} {\widehat{\nu }}_1^{(l)}(\tau )=\frac{1}{m}\sum _{j=1}^m{\widehat{\nu }}_{1j}^{(l)}(\tau )-(1-1/m)\frac{1}{m}\sum _{j=1}^m[n_l\sum _{i=1}^{n_l}[{\left\{(\tau -X_{il})\frac{1-{\widehat{F}}_{2j}^{(l)}(X_{il})}{{\overline{Y}}_l(X_{il})}-\frac{1}{{\overline{Y}}_l(X_{il})}{\int }_{X_{il}}^{\tau }{\widehat{F}}_{1j}^{(l)}(u)du\right\}}^2 \\ \times I(X_{il}\le \tau )\pi (X_{il},{\widehat{\gamma }}_l)\{1-\pi (X_{il},{\widehat{\gamma }}_l)\}I(R_{il}=0)] \\ +n_l\sum _{i=1}^{n_l}[{\left\{(\tau -X_{il})\frac{{\widehat{F}}_{1j}^{(l)}(X_{il})}{{\overline{Y}}_l(X_{il})}-\frac{1}{{\overline{Y}}_l(X_{il})}{\int }_{X_{il}}^{\tau }{\widehat{F}}_{1j}^{(l)}(u)du\right\}}^2 \\ \times I(X_{il}\le \tau )\pi (X_{il},{\widehat{\gamma }}_l)\{1-\pi (X_{il},{\widehat{\gamma }}_l)\}I(R_{il}=0)]]. \end{gathered}$$ (B.6)

We obtain the variance estimate of the test statistic Q_M as

$${\widehat{\sigma }}_{Q_M}^2=\frac{n_2}{n_1+n_2}{\widehat{\nu }}_1^{(1)}(\tau )+\frac{n_1}{n_1+n_2}{\widehat{\nu }}_1^{(2)}(\tau ).$$