Modest Influence of FRET Chromophores on the Properties of Unfolded Proteins

Abstract

Single-molecule Förster resonance energy transfer (FRET) experiments are often used to study the properties of unfolded and intrinsically disordered proteins. Because of their large extinction coefficients and quantum yields, synthetic heteroaromatic chromophores covalently linked to the protein are often used as donor and acceptor fluorophores. A key issue in the interpretation of such experiments is the extent to which the properties of the unfolded chain may be affected by the presence of these chromophores. In this article, we investigate this question using all-atom explicit solvent replica exchange molecular dynamics simulations of three different unfolded or intrinsically disordered proteins. We find that the secondary structure and long-range contacts are largely the same in the presence or absence of the fluorophores, and that the dimensions of the chain with and without chromophores are similar. This suggests that, at least in the cases studied, extrinsic fluorophores have little effect on the structural properties of unfolded or disordered proteins. We also find that the critical FRET orientational factor κ², has an average value and equilibrium distribution very close to that expected for isotropic orientations, which supports one of the assumptions frequently made when interpreting FRET efficiency in terms of distances.

Introduction

Förster resonance energy transfer (FRET) (1,2) is a biophysical technique that can yield information on distance distributions and dynamics in unfolded proteins (3–9), including inside cells (10). Single-molecule FRET can even be used to investigate separately the dynamics for subpopulations of a sample, for example the unfolded and folded states of a protein (11,12). The principle behind the method is that the efficiency of nonradiative energy transfer between two fluorophores is dependent primarily on their separation in space (although orientational factors may need to be considered in certain cases, as we discuss below) (1,2,13). FRET and small-angle x-ray scattering (SAXS) studies have produced divergent views of the dimensions of the unfolded states of proteins in low denaturant (5,6,14–18). There are many possible explanations for this inconsistency, which is still unresolved, but one concern is that the inclusion of large organic chromophores conjugated to the protein may somehow interfere with the properties of the protein—for example, by stabilizing a collapsed state of the chain. The controversy has largely centered around protein L (5,6,14,18), which has been studied by both methods; however, qualitatively similar results have been obtained for the unfolded states of other proteins by either FRET (collapse as denaturant is diluted) (19) or SAXS (no collapse) (20).

A commonly used pair of fluorophores, due to their stability and favorable spectroscopic properties, consists of AlexaFluor 488 as “donor” and AlexaFluor 594 as “acceptor”. These dyes have been shown to yield self-consistent information on distances in model systems (21,22). The effect of the dyes also appears to have at most a limited effect on protein stability, where this has been checked (23). However, the potential effects of these extrinsic fluorophores on the intrinsic properties of unfolded and intrinsically disordered proteins still needs to be addressed, something which has not been systematically done to date. Obtaining this information from experiment, while certainly possible, is challenging. Molecular simulations offer one avenue to compare the properties of the unfolded states of proteins with and without FRET chromophores. In this article, we use molecular simulations with a state-of-the-art protein force field and water model to address the effects of dyes on the formation of long-range contacts, distance distributions, and per-residue secondary structure propensities of the unfolded state of three different proteins. We find that the dyes have little effect on the structure formation and dimensions of the unfolded state, and that one of the key assumptions underlying quantitative distance calculations from FRET measurements is justified by our results.

Methods

We use the AMBER ff03w force field (24) for the protein model and TIP4P/2005 as the water model (25) to perform simulations using GROMACS 4.5.3 (26). Parameters for the dyes were derived using the AnteChamber feature of AmberTools (27), with the charges derived from the electrostatic potential from an HF/6-31+G^∗ calculation with the Gaussian program (28). Full parameters are available upon request from the authors. Temperature replica exchange was run with temperatures ranging from 285 to 493 K at a constant pressure of 1 bar, maintained using isotropic Parrinello-Rahman pressure coupling (29). The trajectory is propagated using Langevin dynamics with a 1 ps⁻¹ friction coefficient. Electrostatic interactions are calculated using the particle-mesh Ewald method (30) with a real space cutoff of 0.9 nm. For van der Waals interactions, a 1.2-nm cutoff is used. A key feature of these simulations is the optimized protein model AMBER ff03w, which results in an improved reproduction of the properties of unfolded proteins relative to earlier force fields in conjunction with TIP3P water, as has been demonstrated in previous studies (31–33). Sizes of the systems have been shown in Table S2 in the Supporting Material by the number of water molecules present in simulation boxes. Initial unfolded configurations were generated from initial high temperature unfolding simulations, and were solvated in their simulation boxes. For such large systems, temperature replica exchange, which provides much more enhanced sampling of phase space compared to molecular dynamics, is not a common method because of its computational cost. In this work, that large system of each peptide has been simulated for 200 ns per replica using 56 replicas.

Results and Discussion

To generalize how FRET dyes might affect the properties of unfolded polypeptides, we employ three different proteins with a variety of hydrophobic and electrostatic characteristics: namely the cold shock protein (CSP) from Thermotoga maritima, the DNA-binding domain of λ-repressor (LR), and the N-terminal domain of HIV integrase (IN) (7,8). CSP and LR are, respectively, 66-residue and 82-residue globular proteins, while IN is a 57 residue disordered protein, which folds in the presence of Zn²⁺ ions. The three proteins have quite different sequence and structural characteristics. CSP is an all-β fold, whereas LR and IN have all-α folds; the average hydrophobicities of the sequences, based on the Kyte-Doolittle score (34), are −0.55 for CSP, −0.25 for LR, and −0.49 for IN. The fraction of charged residues is 0.36, 0.26, and 0.32, respectively, for CSP, LR, and IN. In particular, both CSP and IN have been shown to collapse when denaturant is diluted (35) (although for IN there is a small reexpansion at the lowest concentrations of guanidinium chloride, due to the reduction in ionic screening).

In each case, we consider both the free protein and a variant with the FRET chromophores ligated to cysteine residues added at or near the termini, with the N- and C-terminal cysteines respectively labeled with the chromophores AlexaFluor 488 and AlexaFluor 594. The labeled forms of each protein are denoted “CSP dyes”, “LR dyes”, and “IN dyes”. The full sequences of each system are shown in Table S1. Unfolded proteins are notoriously difficult to treat with standard force fields and water models, as evident by analysis of unfolded states in the atomistic folding simulations by Lindorff-Larsen et al. (36), Best et al. (37), and Piana et al. (38), as well as earlier comparisons with FRET data on unfolded proteins (8). To address this issue, we have adopted the most accurate four-site water model for describing the properties of liquid water (25), essential for accurately capturing the hydrophobic effect (39), and we have tuned a protein force field, AMBER ff03 (40), for compatibility with this model (24). Although not perfect, this combination has resulted in improved properties in simulations of disordered and unfolded proteins (31–33).

To compare the properties of all three proteins (Protein Data Bank (PDB) IDs are 1G6P (41) for CSP, 1LMB (42) for LR and 1WJA (43) for IN) with and without dyes, we have performed replica-exchange molecular-dynamics simulations of each system in explicit solvent. We focus on the 300 K replica, for which we use 150 ns of data, after neglecting an initial equilibration period of 50 ns. As a measure of global structure formation, we have computed contact maps (Fig. 1), in which the entry for each pair of residues (i,j) represents the fraction of time that at least one heavy atom of backbone from i and one from j are within 0.8 nm of each other, averaged over 150 ns.

Figure 1.

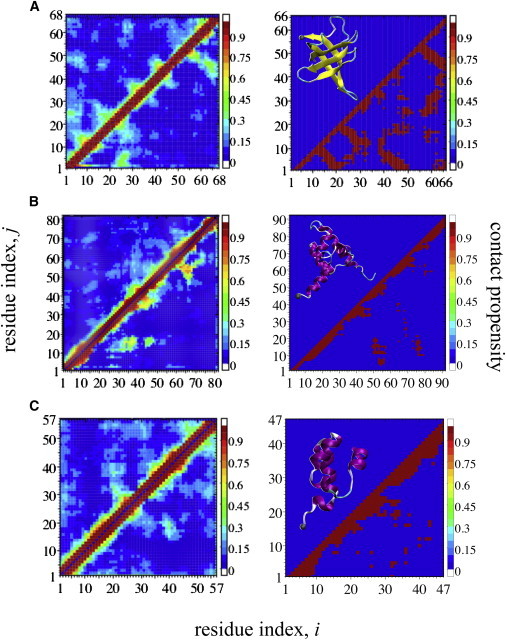
Contact maps of ensembles without (upper left triangle) and with (lower right triangle) extrinsic chromophores for three proteins (left column) along with their native contacts (right column). (A) CSP, (B) LR, and (C) IN. Folded structures of each protein are shown in the left corner of native contacts maps; (yellow and magenta) secondary structures; and (gray sphere) C-terminal α-carbon atom of each protein. For native contact maps and structures, the Protein Data Bank entries PDB:1G6P (41), PDB:1LMB (42), and PDB:1WJA (43) were used for CSP, LR, and IN, respectively. To see this figure in color, go online.

Residue-residue contact formation for the simulation ensembles with and without dyes are shown in Fig. 1 (left column), which indicates that the trajectories with and without dyes are sampling quite similar conformations. Additionally, all contact maps reveal a general absence of long-range contacts, reflecting a disordered chain. The structure formed in the unfolded state essentially reflects nativelike contacts with small sequence separation (Fig. 1, right column).

To assess local structure formation, we have computed the average residual secondary structure formation over the trajectory. In Fig. 2 we show α-helix and β-sheet secondary structure assignments obtained using DSSP definitions (45). The remaining DSSP-assigned structures (β-bridge, bend, turn, 3₁₀-helix, 5-helix) are given in Fig. S1, Fig. S2, and Fig. S3 in the Supporting Material. This shows that both CSP and CSP dyes are sampling mostly coil conformations (Fig. 2). The per-residue populations of secondary structure are similar for both chains. One apparent exception is in the region spanning residues 64–67, giving higher propensity to be in β-sheet for the chain with dyes, which may reflect a small effect of the dye at the C-terminus. For α-helix, the populations with and without dyes are very similar, considering the error range, except for the region spanning residues 24–30, where α-helix propensity is higher for naturally occurring CSP than for CSP dyes. For LR, a difference appears for α-helical propensities in residues 59–65, and residues 6–11 near the N-terminus. These regions might be affected by the presence of the dyes; however, they are still small regions when compared to the total length of sequence. For IN, the only clear difference appears in helical propensity for a limited region, but despite the difference in numbers, both IN and IN dyes keep same trend for that region as well. Overall, the dyes at both termini have very little effect on the secondary structures populated, when viewed at a residue level. Although our replica-exchange molecular-dynamics sampling provides a representative ensemble for each system, the sampling is nonetheless limited and so small differences between ensembles should not be overinterpreted.

Figure 2.

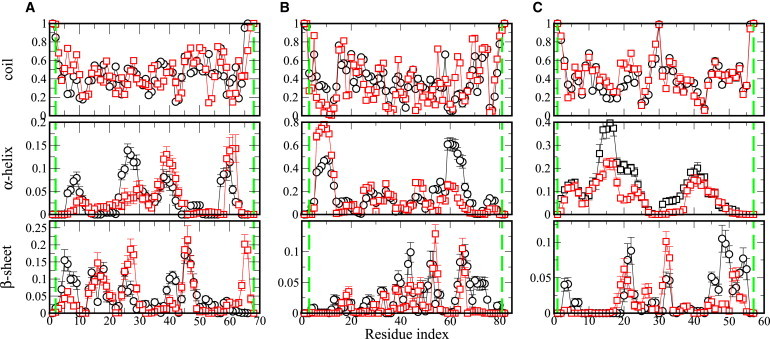
Per-residue secondary structure propensities calculated based on the DSSP definition. (A) CSP, (B) LR, (C) IN. (Black curves) Averages of ensembles without dyes; (red curves) averages of ensembles in presence of dyes. Standard errors are calculated using block averaging (44). (Vertical green lines) Residues to which the dyes are attached. To see this figure in color, go online.

Because FRET primarily reports on interresidue distances and dimensions of the chain, we have also computed distributions of the radius of gyration (R_g) (Fig. 3, top row) and end-to-end (E2E) distance (Fig. 3, second and third rows), and dye-to-dye (D2D) distances (Fig. 3, fourth row) from the simulations (19,46). E2E distance distributions are calculated from the distances between the backbone nitrogen at the N-terminus to the backbone oxygen at the C-terminus. D2D distances are calculated from the distances between the centers of masses of the dyes in the simulations of proteins with dyes. Average values of R_g and E2E distance both with and without dyes as well as average values of D2D distance obtained from our data are summarized in Table 1. To have a clearer comparison of the results with and without dyes, each E2E and D2D distance distribution is fitted to an ideal (Gaussian) chain model (red curve in Fig. 3) and self-avoiding random walk model (47) (green curve in Fig. 3). The E2E distance distribution P(x) for an ideal chain is given by the following equation,

$$P\left(x\right)=4\pi x^2{\left(\frac{3}{2\pi N{l}_k^2}\right)}^{\frac{3}{2}}\text{exp}\left(-\frac{3}{2}\frac{x^2}{N{l}_k^2}\right),$$ (1)

in which N is the number of residues and l_k is the segment or Kuhn length. The only free parameter in the ideal chain models is l_k, for which the fits yield very close numbers for E2E without and with dyes and D2D distributions for all proteins. All yielded fit parameters are summarized in Table 2. These segment lengths are slightly smaller than the α-carbon-to-α-carbon distance, which is always close to 0.38 nm; because the Cα-Cα-Cα angles are relatively inflexible, however, the shorter distances may reflect a projection of the Cα-Cα distance onto the local chain direction. The absolute values of l_k are comparable to, although slightly smaller than, those estimated from single molecule fluorescence experiments (35). Independent of the value of the parameters, their similarity indicates that the properties of the chain are relatively unaffected by the chromophores. Particularly, D2D distribution fittings reflect almost the same distribution as E2E distance without dyes. A more accurate representation of the chain should be given by a self-avoiding random walk (SAW). The E2E distance distribution for a SAW is given by

$$P\left(x\right)=\frac{a}{\langle x\rangle }{\left(\frac{x}{\langle x\rangle }\right)}^{2+\theta }\text{exp}\left[-b{\left(\frac{x}{\langle x\rangle }\right)}^{\delta }\right],$$ (2)

where θ, δ, a, and b are numerical parameters equal to 0.3, 2.5, 3.67853, and 1.23152, respectively (47). Thus, the average values of the end-to-end distances (〈x〉) are the only fit parameters that are summarized in Table 1. Similar to Gaussian chain fitting, self-avoiding random walk fits show a close similarity between different distributions of proteins with and without dyes. Additionally, 〈E2E〉 distance values from fits (Table 2) and our data (Table 1) are not particularly different from each other, except for E2E distance distribution of IN.

Figure 3.

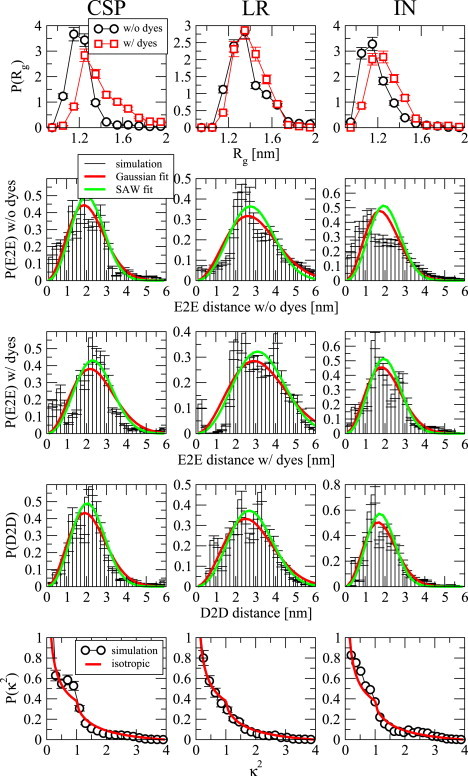
Distance distributions of proteins with and without dyes and orientational factor distribution of dyes. (From top to bottom) Radius of gyration (R_g) with and without dyes, End-to-end (E2E) distance without dyes, E2E distance with dyes, dye-to-dye (D2D) distance, and orientational factor κ² distributions of our data and the isotropic case. (Red curves) E2E and D2D distance distributions are Gaussian chain fits; (green curves) self-avoiding chain fits. To see this figure in color, go online.

Table 1.

Average values of radius of gyration (R_g), end-to-end (E2E), and dye-to-dye (D2D) distances and orientational factor (κ²) from simulations indicated in nanometers

Ensembles	〈Rg〉 without dyes	〈Rg〉 with dyes	〈E2E〉 without dyes	〈E2E〉 with dyes	〈D2D〉	κ2
CSP	1.23 ± 0.01	1.42 ± 0.02	2.06 ± 0.03	2.35 ± 0.09	2.34 ± 0.15	0.61 ± 0.05
LR	1.41 ± 0.04	1.40 ± 0.01	3.04 ± 0.08	3.24 ± 0.08	2.72 ± 0.09	0.58 ± 0.04
IN	1.19 ± 0.01	1.27 ± 0.01	1.19 ± 0.01	2.09 ± 0.09	1.93 ± 0.09	0.68 ± 0.03

Table 2.

Fit parameters l_k (nm) for Gaussian fitting and 〈E2E〉 (nm) for SAW fitting

Ensembles	Gaussian fitting lk (E2E without dyes)	Gaussian fitting lk (E2E with dyes)	Gaussian fitting lk (D2D)	SAW fitting 〈E2E〉 without dyes	SAW fitting 〈E2E〉 with dyes	SAW fitting 〈D2D〉
CSP	0.28(0.92)	0.33(0.82)	0.29(0.93)	2.26(0.91)	2.60(0.86)	2.28(0.95)
LR	0.36(0.91)	0.40(0.90)	0.34(0.92)	3.08(0.92)	3.48(0.91)	3.01(0.92)
IN	0.28(0.80)	0.30(0.92)	0.27(0.93)	2.18(0.80)	2.18(0.91)	1.96(0.92)

Values indicated in parentheses are correlation coefficients of fits.

Although the distributions of E2E distance are challenging to sample, because thorough exploration of essentially all internal degrees of freedom is required, sampling the R_g is easier because of a higher degree of self-averaging. The R_g distributions of all proteins with and without dyes are overall quite similar (Fig. 3, top row) with the average R_g value slightly higher in the presence of dyes for CSP and IN. The tendency of proteins with dyes to sample higher R_g values can be rationalized at the simplest level by the excluded volume effect of the dye molecules. For the case of CSP, the difference is a little more pronounced, most likely because of the difference in the total number of residues for CSP and CSP dyes. Note, however, that this would not help to explain the discrepancy between FRET and SAXS results, inasmuch as R_g estimates from FRET (with dyes) are generally smaller at low denaturant concentrations than those obtained by SAXS (without dyes). However, it may partially explain the fact that R_g computed from simulations is often smaller than that estimated from FRET.

To determine average distances from FRET efficiencies, one in principle has to consider the mutual orientation of the two chromophores, and not just their distance. The orientational contribution to the transfer efficiency is captured by the factor κ² in which κ is given by

$$\kappa ={\hat{\mu }}_D\cdot {\hat{\mu }}_A-3\left(\hat{r}\cdot {\hat{\mu }}_A\right)\left(\hat{r}\cdot {\hat{\mu }}_D\right),$$

(22) where $\hat{r}$ is the unit vector between donor and acceptor and ${\hat{\mu }}_A$ and ${\hat{\mu }}_D$ are the unit vectors along the donor and acceptor transition dipoles, which are shown in Fig. S4. In an ideal situation in which the dyes are reorienting quickly with respect to each other and adopting an approximately isotropic distribution of relative orientations, an average κ² value of 2/3 can be assumed. If this assumption was invalid, it would complicate the interpretation of FRET efficiencies in terms of distances, even for qualitative applications. In experiment, anisotropy measurements can be used to support κ² ∼ 2/3, but the distribution cannot be measured directly in real samples.

As we run replica exchange simulations, we do not have direct access to the timescales of reorientation, but we can nonetheless compute the equilibrium average, and distribution of κ² from the simulations for comparison with their ideal isotropic counterparts (48) in addition to distance distributions. We find that the average values of κ², which are tabulated in Table 1, are within 1.5 standard deviations of the isotropic value (2/3). Comparison with the isotropic distribution (Fig. 3, bottom row) shows a close similarity between the isotropic and simulation distributions. Thus, at least at an equilibrium level, it seems that the interdye κ² factor may safely be assumed to be 2/3; however, the dynamics of the dyes would also ultimately have to be considered (i.e., does κ² average to 2/3 within the fluorescence lifetime?).

In conclusion, we have compared the unfolded ensembles of naturally occurring CSP, LR, and IN and a CSP, LR, and IN with AlexaFluor 488 and AlexaFluor 594 fluorophores attached to it, similar to that used in FRET experiments. We find that both ensembles with and without dyes yielded negligible long-range contacts for all three sequences, indicating that they are disordered, and that the distributions of dye-to-dye distance of sequences with dyes and end-to-end distance of sequences without dyes are remarkably similar, and that the dyes did not affect the average secondary structure sampled by each residue. The major effect of the chromophores was a very slight expansion of the chain. Overall, our findings that extrinsic chromophores have little effect on the chain properties (at least for sequences studied here), and that the average κ² ∼ 2/3, lends confidence to the use of FRET chromophores to extract true dimensions for unfolded proteins. Even though we have studied a limited number of sequences, we believe results here can be generalized inasmuch as these three sequences accommodate a variety of different chain characteristics.