Uncovering the Mechanism of Trapping and Cell Orientation during Neisseria gonorrhoeae Twitching Motility

Abstract

Neisseria gonorrheae bacteria are the causative agent of the second most common sexually transmitted infection in the world. The bacteria move on a surface by means of twitching motility. Their movement is mediated by multiple long and flexible filaments, called type IV pili, that extend from the cell body, attach to the surface, and retract, thus generating a pulling force. Moving cells also use pili to aggregate and form microcolonies. However, the mechanism by which the pili surrounding the cell body work together to propel bacteria remains unclear. Understanding this process will help describe the motility of N. gonorrheae bacteria, and thus the dissemination of the disease which they cause. In this article we track individual twitching cells and observe that their trajectories consist of alternating moving and pausing intervals, while the cell body is preferably oriented with its wide side toward the direction of motion. Based on these data, we propose a model for the collective pili operation of N. gonorrheae bacteria that explains the experimentally observed behavior. Individual pili function independently but can lead to coordinated motion or pausing via the force balance. The geometry of the cell defines its orientation during motion. We show that by changing pili substrate interactions, the motility pattern can be altered in a predictable way. Although the model proposed is tangibly simple, it still has sufficient robustness to incorporate further advanced pili features and various cell geometries to describe other bacteria that employ pili to move on surfaces.

Introduction

Motility plays a critical role in the lifecycle of bacteria. For example, planktonic bacteria swim with the help of flagella (1); this is the predominant means of transport through a fluid. In addition, there are many means of locomotion along a surface (2), which is of particular importance in the formation of biofilms, complex microbial communities that can colonize almost any kind of interface (3,4). Twitching motility is one important example of locomotion that allows cells to move on the surface as they form microcolonies, a process that is crucial for the initial stage of biofilm formation (5). Although bacteria use flagella for swimming, twitching motility relies on appendages called type IV pili (TFP); because of the irregular and jerky character of the cell motion, this type of motility has been called “twitching” (6). Pili are thin, long, and flexible filaments that can grow up to several microns and have a diameter of 6–9 nm (7–9). The pili are assembled from pilin subunits that are processed from within the cell. As a pilus grows, it can extend to a distance noticeably larger than the cell size. When disassembly starts inside the cell, it shortens the pilus. If the pilus is attached to a surface, this shortening generates a pulling force that moves the cell. At the molecular level, TFP operation is driven by molecular motors that are similar in many Gram-negative bacteria, including Pseudomonas aeruginosa, Myxococcus xanthus, and Neisseria gonorrheae (7–9). The first direct measurements of the force generated by pili reported 100 pN, a record number for the microbial world (10). Shortly after, growth and retraction of pili were directly visualized in P. aeruginosa (11) and shown to be responsible for cell movement.

As of this writing, studies of twitching motility is a very active field of research. Recent work on N. gonorrheae (12,13) suggest that multiple pili and a tug-of-war mechanism are involved in cell motion. Twitching motility of rod-shaped P. aeruginosa bacteria was also studied in great detail (14–16). Studies of mechanomicrobiology of TFP show the possibility of pili bundling and conformation changes (17,18).

Interestingly, medically relevant N. gonorrheae uses twitching exclusively to move on surfaces and interact with its environment. These bacteria can move at speeds as large as one cell size per second. Moving cells use pili to aggregate and form microcolonies which are also motile. Unfortunately, the thickness of pili of the order of several nanometers and the intolerance of the cell to fluorescent molecules make it difficult to visualize the dynamics of pili over long periods of time. Therefore, it remains unclear how the pili surrounding the N. gonorrheae cell body organize and propel the bacteria. Resolving this issue will lead to a better understanding of the dynamics of N. gonorrheae microcolony formation, a process critical to the progression of gonorrhea infection of human epithelia.

In this article, we combine experimental measurements and modeling to explain the nature of the twitching motility of N. gonorrheae. We track bacteria twitching on a surface for an extended period of time, and observe that individual trajectories consist of alternating pausing and moving intervals. In addition, during twitching, cells show a clear preference for motion in the direction normal to the longer axis of the cell body. We propose a simple model that describes the collective operation of pili and explains these experimental findings. We also test the predictions of the model by varying the conditions on the surface where cells move.

Materials and Methods

Cells and imaging

The bacteria used in this work are MS11 wild-type strain bearing the same pilE sequence that was crystallized in Craig et al. (19). Bacteria were grown on GCB-medium base with agar (Becton Dickinson, Franklin Lakes, NJ) for 16–20 h at 37°C and 5% CO₂. Before recording, the bacteria were resuspended at a concentration of 5 × 10⁷ bacteria/mL in liquid GCB (Gonococcal broth) medium. For 1 L: protease peptone No. 3, 15 g; K₂HPO₄ 4 g, KH₂PO₄ 1 g, NaCl 5 g, and 10 mL of Kellogg’s Supplement 1: 100 g of Dextrose, 2.5 g of L-Glutamine, and 5 mg of thiamine pyrophosphate adjusted to 250 mL with water and 1 mL of Kellogg’s Supplement 2: 1.25 g of Fe(NO₃)3:9 H²O (ferric nitrate) adjusted to 250 mL with water. A quantity of 0.5 μL of the solution was added to 2 mL of DMEM medium (Gibco, Grand Island, NY) and then added to the bottom of the well of a 6-well tissue-culture plastic plate (Corning, Corning, NY). In the case of coating of the well, before the start of the experiment, either 2 mL of PBS (Growcells, Irvine, CA) with 30 μg/mL of Poly-L-Lysine (Sigma-Aldrich, Saint Louis, MO) or 2 mL of PBS with 1 mg/mL of bovine serum albumin (BSA, fraction V; Sigma-Aldrich) were added to the plate and left to interact for 1 h. Imaging was achieved by performing phase contrast microscopy with an inverted model No. IX81 microscope setup (Olympus, Center Valley, PA) with 40× air objective (Olympus) and a CoolSNAP digital camera (Photometrics, Tucson, AZ) providing grayscale images. A 1.5× magnifying lens was used for the 2-Hz recording.

Quantification of pili length and number

MS11 bacteria were grown as indicated above for 16–20 h in 37°C and 5% CO₂. Bacteria were resuspended at a concentration of 10⁹ bacteria/mL and 10 μL of the suspension was deposited on a plastic petri dish. A formvar/carbon-coated electron microscopy grid (Electron Microscopy Sciences, Hatfield, PA) was allowed to float on top of the 10 μL drop for 10 min. Excess liquid was bloated on a lint-free Kimwipes tissue (Kimberly-Clark, Irving, TX) and transferred onto a 10-μL drop of 3.7% formaldehyde in PBS for 5 min. The excess liquid was again removed and the grid placed onto a solution of 1% uranyl acetate. The excess liquid was removed and the grid imaged on a transmission electron microscope (JEOL, Peabody, MA). The number and length of pili were determined by analyzing micrographs of 20 bacteria in the software IMAGEJ (National Institutes of Health, Bethesda, MD). The number of pili obtained is N_p = 29 ± 15 (ranging 9–59) and length l_p = 1.2 ± 0.4 μm (mean ± SD) (compare Holz et al. (12) and Swanson et al. (20)).

Amino labeling of bacteria for total internal reflection fluorescence microscopy

One 1-μL loop of bacteria grown on GCB solid media (Acumedia, Lansing, MI) for 16–18 h was gently resuspended in 60 μL sterile PBS, to which 3 μL of Dylight 488 NHS Ester (Thermo Scientific, Waltham, MA) suspension was added (10 mg/mL, diluted in dimethylformamide). After 10-min incubation at 37°C, 5 μL of the labeled bacterial suspension was added to 35 mm poly-D-lysine-coated glass bottom dishes (MatTek, Ashland, MA), containing 3 mL GCB supplemented with 10% Kellogg’s supplement (D-glucose 222 mM, L-glutamine 0.342 mM, Fe(NO₃)3:9 H₂O 0.0124 mM, Cocarboxylase 0.434 mM) prewarmed to 37°C. The labeled bacteria were allowed to incubate for 20 min at 37°C in a 5% CO₂ atmosphere in the cell observer microscope (Carl Zeiss, Jena, Germany) before the start of the experiment. Live-cell time-lapse analysis was performed with total internal reflection fluorescence (TIRF) microscopy using a connected argon laser at 488 nm, and a 100× objective (NA 1.46; Carl Zeiss). Images were captured using an electron-multiplying charge-coupled device camera (Hamamatsu Photonics, Hamamatsu, Japan) at 12 images/s. Images captured during time-lapse experiments were further processed using Axiovision software (Carl Zeiss) and the software IMAGEJ (National Institutes of Health, Bethesda, MD).

Data analysis

In total, we use 133 and 105 tracks for noncoated and BSA-coated surfaces, respectively. In a single field of view of the microscope, there are usually 1–5 cells out of which we select motile cells that do not interact with each other (trajectories do not intersect). We performed several sets of measurements on different days. Trajectories contain from 150 to 1550 time points with 1-Hz sampling frequency. For each trajectory, we measure its average speed, and by building a histogram of these speeds, check the uniformity of the ensemble of cells. The experimental data contain a time series of cell coordinates r(t_i) = [x(t_i), y(t_i)]. Bacteria’s velocity is determined as

$$\mathbf{v}\left(t_i\right)=\frac{\mathbf{r}\left(t_i+\delta t\right)-\mathbf{r}\left(t_i\right)}{\delta t},$$ (1)

with δt = 1 s. We use velocity and position data to identify trapping events: if the cell has a velocity below a threshold velocity v_th = 0.4 μm/s and does not move further than 0.5 μm, it is in the trapped state. We check that the resulting distribution of trapping times is insensitive to the value of the threshold velocity in the range 0.3–0.5 μm/s and to the variation of the trap radius from 0.5 to 1 μm. The movement state occurs for motion of cells between consecutive traps. We calculate trapping and moving times for all trajectories to produce the corresponding distribution functions. For extracting the orientation of the cell during twitching, we use several tracks acquired with 2-Hz frequency. Similarly, a time series of each cell’s velocity is obtained from its position. In addition to determining the position of the center of the cell, we use the software IMAGEJ (NIH) to extract the orientation of the cell (angle of the long axis of an ellipsoid that was fitted to the shape of the cell at each time step). For all time points where the velocity of the cell is not zero, we determine the angle between velocity and orientation of the cell, and plot the normalized histogram of those angles.

Simulations

Based on the experimental observations, the cells in our simulations each consist of two spheres with radius r = 0.5 μm at a distance d = 0.6 μm between their centers. The number of pili is N_p = 10 and their mean length is l_p = 2.0 μm. The surface of the cell is divided in 10 equal sections. In every section one pilus is attached at a random position. The pili grow into a direction that is randomly chosen from a direction with an angle of up to π/10, with respect to the direction perpendicular to the surface. The velocity of the growing and retracting pili is v_e = v_r = 2 μm/s and the pulling force is f_p = 100 pN. We determine the total force F_tot on the cell by adding the pulling forces of all pili,

$${\mathbf{F}}_{\text{tot}}={\sum }_{j=1}^{N_{\text{p}}}{\mathbf{F}}_j.$$

The total torque is given by

$${\mathbf{M}}_{\text{tot}}={\sum }_{j=1}^{N_{\text{p}}}{\mathbf{r}}_j\times {\mathbf{F}}_j,$$

where r_j denotes vectors from the center of mass of the cell to the anchoring points of pili. The motion of the cell is determined by solving the overdamped equations of motion: dr_||/dt = μ_||F_|| for the direction parallel to the symmetry axis, dr_⊥/dt = μ_⊥F_⊥ for the perpendicular direction, and dϕ/dt = μ_rot|M| for the rotation. We chose the effective mobility of the cell in a way that the velocity distribution from simulations is comparable to the one obtained in experiments: for a motion along the symmetry axis (line connecting the centers of two cocci, see dashed line in Fig. 4), the mobility is μ_|| = 1.4 × 10⁴m/(Ns); for mobility in the perpendicular direction, we assume μ_⊥ = μ_||r/(r + d/2); and for the rotation, μ_rot = 3μ_⊥/4.

Figure 4.

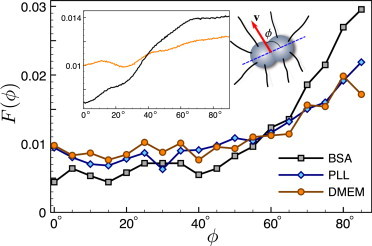
Orientation of the cell during twitching. Angular correlation function between the velocity of the cell and the axis connecting two spheres of the cell body. There is a noticeable preference toward the 90° angle. The effect of orientation is more pronounced for the BSA-coated surface, as explained in the text. Coating with poly-L-lysine has no visible effect on correlations that are similar to the case of the DMEM medium (see Materials and Methods). (Inset) Orientation of the cell obtained from numerical simulations of the two-dimensional model of twitching bacteria for two types of surfaces differing in the pili attachment probability A.

Note that this effective mobility is much smaller than the mobility of the cell body in water calculated according to the Stoke’s law. We neglect the cell surface friction, assuming that pulling forces are mainly along the substrate with a negligible normal component responsible for friction. There is also no indication of substrate-related traps, inasmuch as we can observe cells that freely pass regions on a surface where they were previously trapped. The ratio f_th/f_p = 1.43 and the pili attachment probabilities A = 0.5 or A = 0.9 are chosen such that the distributions of moving and trapping times are similar in experiment and simulations. The mean pili detachment time τ_s = 600 s is determined by comparing the decay of the tail of the trapping time distribution in simulations to that in experiments. We did not consider Brownian motion in the simulations. That leads to a sharper peak at zero velocity for the speed distribution in simulations as compared to the experimental data (see Fig. S1 in the Supporting Material), where Brownian motion of the cell, flexibility of pili, and fluctuations in pili pulling force and its dependence on load result in two broader peaks of the speed distribution. We choose the threshold velocity that determines the trapping event in the simulated data in a similar fashion, with respect to separating two velocity peaks, but having a different numerical value v_th^num = 0.2 μm/s. In the simulations, we followed the trajectory of the cell over a time of 4.2 × 10⁷ s.

Results

We track individual isolated cells of wild-type N. gonorrheae bacteria (MS11 strain) for an extended period of time, up to 25 min. This is a biologically relevant timescale when the motility and interaction of bacteria with each other and host cells leads to the formation of bacterial aggregates and trigger reactions from host cells (21). We image tracks with 1-Hz capturing frequency to identify moving and trapping events, and use higher magnification and 2-Hz frequency for the analysis of the cell orientation during twitching (see Materials and Methods for the details of the experimental setup, and see Movie S1 in the Supporting Material). A typical trajectory of the cell is shown in Fig. 1, where cell positions at 1-s intervals are marked by dots. A micrograph on the inset shows the transmission electron microscopy (TEM) image of the N. gonorrheae cell body surrounded by multiple pili filaments. We calculate cell velocities from the time series of the bacteria’s displacements. The speed distribution P(|v|) of the ensemble of cells has two distinct peaks, as shown in Fig. 2. There is a pronounced peak at zero speed, which implies that there must be pausing events when the cell does not move at all. The second peak at ∼0.9 μm reflects a typical speed of active motion of a cell. To probe the trapping events, we define the threshold speed v_th = 0.4 μm/s, and identify a sequence of points where the speed of the cell is below this threshold; this represents a possible trap. In addition, we require that the cells do not leave the circle of the trap radius r_t = 0.5 μm approximately one-half of the cell size (see zoomed part of the trajectory in Fig. 1); these two conditions allow us to identify trapping events and their duration. (On the sample trajectory of Fig. 1, small and larger points indicate the movement and trapped states of the cell, respectively.)

Figure 1.

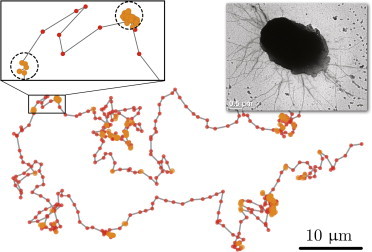
Typical trajectory of an N. gonorrheae cell. Points denote the location of the cell centroid on 1-s intervals. During trapping events (denoted by larger circles), the cell speed is low and its position does not change more than half of the cell size (denoted by a dashed circle of radius 0.5 μm on the zoomed piece of the trajectory). (Inset) TEM image of the diplococcus with multiple pili (scale bar is 0.5 μm).

Figure 2.

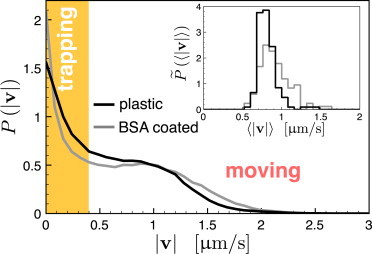
Probability distribution of bacterial speed during twitching for two different surface coatings. (Shaded region) Trapping events with speeds below the threshold v_th = 0.4 μm/s. Typical moving speed is 0.9 μm/s. BSA coating does not change the speed distribution qualitatively. (Inset) Probability distribution $\tilde{P}\left(\langle \left|\mathbf{v}\right|\rangle \right)$ of bacteria average moving speeds calculated for each trajectory. It indicates a rather uniform behavior among individual cells from different sets of experiments.

The distribution of trapping times has a shape resembling that of a double-exponential function, which on a semilogarithmic plot would look like two straight lines with different slopes. It is indicative of two regimes: short trapping events of duration 0–20 s, and much longer trapping events with a characteristic time of several minutes, as shown in Fig. 3. The average trapping time obtained from the data is 2.98 ± 0.05 s, but there is a distinct tail with trapping events lasting longer than 1 min. The distribution of moving times is closer to a single-exponential distribution but still has a tail of data indicating longer moving intervals; the average moving time is 4.27 ± 0.04 s. In addition to tracking experiments that give information about the macroscopic behavior of the cell during its motion, we are able to characterize the motion of the cell on a more detailed level. N. gonorrheae bacteria have a shape of a diplococcus—two spheres merged together, which allows us to define the orientation of the cell by the tilt of the axis that connects the two spheres. We use a higher magnification to determine the cell orientation and at each time step, when the speed of the cell is nonzero, find the angle between the direction of the cell velocity and its orientation, ϕ. The distribution of these angles, F(ϕ), has a maximum at ϕ = 90° showing that cells have a clear preference for moving in the direction orthogonal to the axis connecting two cocci—by its wider side forward (Fig. 4 and see Movie S1)—behavior that was noted previously (12,13).

Figure 3.

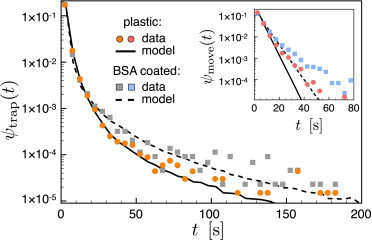
Probability density function of trapping and moving times. Trapping time has two distinct regimes of faster and slower decay attributed to two trapping mechanisms. Coating the surface with BSA leads to longer trapping events. However, moving time is also increased on a BSA-coated surface (inset). (Solid and dashed lines) Results of two-dimensional simulations of the model. For the trapping time, the model gives a very good match and accounts properly for different coatings of the surface. Although the simulations also reproduce the average value of moving times, the shape of the distribution deviates from the simulated curve for longer times.

We would like to show that orientation of the cell and its displacements are the results of collective pili operation. Although cell trajectories are sufficient to quantify the motility pattern, to build a model for the displacement of the bacteria we need to know some key physical characteristics of the cell, such as the number of pili per bacterium, their length, and the force characteristics of pili. The number of pili per bacterium, N_p, has been determined to be 7.7 ± 4.4 with an exponential distribution of pili lengths, having an average value of l_p = 0.9 ± 0.1 μm (12). Analysis of electron micrographs of MS11 bacteria enables us to measure the number and length of pili: N_p = 29 ± 15 and l_p = 1.2 ± 0.4 μm, respectively (see Materials and Methods). The trapping events that we observe have not previously been reported for N. gonorrheae. Previous measurements were restricted to shorter timescales and coverglass surface coated with BSA (12). In our measurements of cell trajectories, we study bacteria interacting with a plastic surface (but not glass), either by itself or coated with poly-l-lysine or BSA. It is always difficult to evaluate precisely the detachment force of a pilus from a surface. However, TFP retraction force measurements with the same MS11 strain showed that pili can have binding forces to the surface which can match their pulling force (17).

Theoretical model

We use the experimental results for the pausing and moving times and orientation of N. gonorrheae cells during their locomotion, along with the existing knowledge of pili properties, to put forward a model that both describes the collective operation of multiple pili and explains the motility mechanism of N. gonorrheae bacteria.

We assume that individual pili work independently of each other (11), and first will define what a single pilus can do. Each pilus can extend to a length whose value is random but can be well characterized by an exponential distribution (12) with an average length, l_p. The extension of pili occurs at speed v_e. After elongation, the pilus tries to attach to the surface; attachment is considered to be a stochastic process with A denoting the probability of binding to the surface, and 1 − A failing to do so. The pilus then starts to retract and, if a reliable contact with the surface is formed, generates a pulling force f_p (Fig. 5 a). The retraction speed of the pilus depends on the load it experiences (22). We relate the pilus retraction speed and pulling force by an effective friction coefficient of the cell body in the overdamped limit. If the pilus fails to attach, it retracts freely with a speed v_r without exerting any force on the cell. Previous results (11) and optical tweezer measurements indicate that retraction of the pilus occurs approximately at the same speed as its elongation (22). In the model, a pilus starts to regrow immediately after it is completely retracted. It is therefore important to follow the retracting pili to know when a new pilus can regrow in the system; this is consistent with the concept that the total number of pili N_p is fixed because there is a limited pool of pilin protein which is recycled to produce only a limited amount of filaments.

Figure 5.

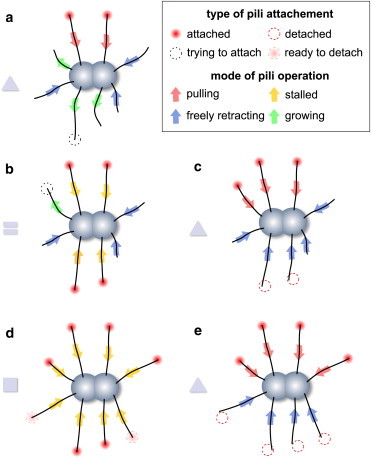
Model for the twitching motility. (a) Pili, which are attached to the surface and retract, propel the cell forward (shown by inward arrows and circles around their tips). (Outward arrows) Growing pili. A pilus that is trying to attach to the surfaces is shown (dashed circle around its tip). Those pili that failed to attach retract without generating any force acting on the cell (inward arrows; no circle at the tips). (b) Pili are pulling against each other and trap the cell. (c) A new coming pilus can attach and break the force balance, thus pulling the cell out of the trap. (d and e) When most of pili are trapped, some of them may randomly detach from the surface (dashed circles), giving an advantage to their opponents and releasing the cell from a longer trap.

The motion of the cell is governed by the collective dynamics of N_p pili surrounding the cell body. Multiple pili can pull at the same time in different directions with the same force, f_p. They can pull cooperatively or compete against each other. If a pilus experiences a net force from all other pulling pili larger than its own pulling force, it stalls (23). This pilus is able to withstand a load up to a threshold value, f_th > f_p. If the load force exceeds this threshold value, then the pilus detaches from the surface and retracts freely. If collective disposition of pulling pili is such that a force acting on each of the individual pili is above the pulling force but below the threshold value, the cell is trapped (Fig. 5, b and d).

Exit from the trap occurs in one of the following ways: an additional pilus or pili attaches to the surface and changes the force balance, leading to the total load force acting on one or several pili larger than a threshold force (Fig. 5 c). In this case, after the detachment of overloaded pili, the remaining subset of attached pili pulls the cell forward (Fig. 5 c). Alternatively, almost all pili of the cell can be trapped, and new attaching pili are not able to break the force balance (Fig. 5 d); this leads to an infinite trapping time. Therefore, we assume that pili can withstand a load only for a certain time. We assume this time to be random and exponentially distributed with some characteristic time t_s. Hence, some pili randomly start to detach and alternate the force balance, which releases the cell from the trap (Fig. 5 e). We argue that these two mechanisms correspond to the two characteristic regimes in the experimentally measured trapping times. The motion of the cell is due to the deployment of multiple pili (12). The period of the motion is terminated when the number of pulling pili decreases and some of the pili aiming in the opposite direction successfully attach to the surface, bringing the cell to a stop (Fig. 5 b). This cycle then repeats. We argue that the proposed set of microscopic rules for the collective operation of multiple pili is capable of explaining the experimentally observed behavior of N. gonorrheae cells. We use numerical simulations to quantitatively relate the model and experimental data.

Numerical simulations

To simulate the bacteria, we restrict our calculations to two spatial dimensions. We explicitly include the geometry of the cell, which we assume to be two spheres with radius r = 0.5 μm, with a separation d = 6.0 μm (circles in two-dimensional projection). Pili grow at random in the radial direction, at positions uniformly distributed along the cell circumference. Every attached pilus pulls with a force f_p, which we set to be equal to 100 pN (23). After calculating the total force and torque acting on the cell, we determine the velocity and the rotation of the cell by solving the overdamped equations of motion. If the total force and torque acting on the cell lead to motion where an attached pilus (or several pili) has to become longer, then the cell is stopped. If the total force acting on each pilus remains below the threshold, f_th, the cell is considered to be trapped. If the force acting on a pilus in a stopped cell is larger than f_th, then the pilus detaches from the surface and the new balance of forces is recalculated. In the simulations, we use overdamped equations of motion with the sources of randomness coming from the length of pili, their probability to attach, and exponentially distributed time for which a pilus can withstand its load. Further details of the simulation are given in Materials and Methods (see Movie S2). Depending on the parameters, we find two main regimes of motion of the cell.

For a small ratio of f_th/f_p, most pili that try to pull in a direction opposite to the direction of motion are detached. Therefore, the cell is in the moving state most of the time, and typical trapping times are small. In the other regime with large f_th/f_p, the cell is stalled most of the time and moving times are small. For intermediate values of f_th/f_p, typical moving and trapping times are comparable, similar to what we observe in the experiments. By proper choice of the parameters, close correspondence of simulations and experimental data can be achieved (Fig. 3). The calculated distribution of trapping times has two distinct regimes, whereas the moving times are better described by a single exponential function. We note that the proposed mechanism for multiple pili operation assumes that pili can hold to the surface stronger than they can pull. It provides explanation for the trapping with two characteristic regimes and nearly single-exponential moving time distribution. It also describes nearly 180° reversals visible in the individual cell trajectories—events when one side of the cell wins over the other and reverses the direction of velocity (see Movie S1). Previous experiments suggesting cooperative pili operation (12) were performed on much shorter timescales (∼1 min) and on a different type of substrate that apparently had much less pili interaction. We believe those are the key reasons why the trapping events were not previously reported.

Dependence on parameters

The theoretical model relies on six essential parameters giving a large space for optimization. Due to the assumption of independent work of individual pili, we can use the properties of random processes to predict the effects of different parameters on the motility of cells. In addition, available experimental data often provides a range in which some of the parameters can vary.

Pili extension and retraction speed

Pilus retraction speed, u_r, is directly related to the typical moving speed of the cell, as confirmed by previous work (10,11,22). We therefore vary the retraction speed in the range 1–3 μm/s to achieve average cell moving speeds consistent with the experiments. The final value of 2 μm/s we use is consistent with previous findings for gonorrheae bacteria (10,11,22). The pili growth speed was shown to be similar to the retraction (11), and therefore we fix them together in our simulations v_r = v_e.

Pili length

We vary the average pili length in the range 1–3 μm. Existing methods to measure pili length are invasive and cause pili to break up, leading to an underestimation of their length. As some individual TEM images in this article and in Holz et al. (12) demonstrate, pili often appear to be several microns long. In our model, the length of pili, divided by their growing speed (l_p/u_e), is the essential timescale defining the pili turnover time, and therefore moving time and short trapping times. By increasing the pilus length we extend the time required for a new pilus to attach and perturb the force balance, leading to a prolongation of short traps (initial slope of the trapping time distribution curve). This also extends the moving times because a longer pilus can pull for a longer time. By matching simulations and the model, we achieve the best results for l_p ∼ 2 μm.

Number of pili

The number of pili affects all aspects of motility. Average time for a new pilus to attach is of the order of pili turnover time divided by (N_p ⋅ A): t₁ ∝ N_p⁻¹l_pu_e⁻¹A⁻¹. Therefore, it defines a major timescale in the model. Larger N_p extends the regime of short traps that can be resolved by newly attaching pili. The rate of pili detachment in stalled cells is proportional to N_p/τ_s and affects the tail of long trapping times. Larger N_p also can extend moving times: if pili on one side of the cell are turning over sufficiently fast, they will also maintain a high average number of simultaneously pulling pili, making it difficult for pili to attach on the opposite side of the cell. We get the best match of the experimental data with N_p = 10. The N. gonorrheae cells have pili surrounding the whole cell body, therefore also growing out perpendicular to the surface upon which motility occurs. Only those pili situated close to the surface can contribute to the cell motility. In the model, it is therefore reasonable to have N_p values that are smaller than the total number of pili per cell we measured. In addition, N_p = 10 is also the value that falls between the value reported previously in Holz et al. (12) (N_p = 7.2) and our measurements.

Ratio of threshold and pulling force

A force that can be generated by a TFP motor is a well-characterized quantity that sets the force scale in our model. In the model, for the cell to be able to move, the ratio f_th/f_p should be larger than 1. For values close to 1, almost any excess over the pulling force detaches the pilus from the substrate and no trapping is possible. This regime could correspond to conditions of Holz et al. (12). In the opposite case of a high threshold force, the cells will be trapped most of the time. This ratio also contributes to the transition between short and long traps: if a cell uses up all available pili and is not able to break the force balance (for example, due to a high threshold force), it turns into a stalled situation of a longer trap. Also, a large value of the threshold force shortens the movement periods: it is easier for a single newly attaching pilus to compete with pili that are already pulling. In our experiments, moving times are comparable to the trapping times, implying an intermediate value of the ratio, which we determine to be f_th/f_p = 1.43. We show how the behavior of trapping and moving times changes in response to f_th/f_p in Fig. S2.

Pilus detachment time

In the model, we used a single time constant τ_s, which does not depend on the applied force, to describe the stochastic detachment of pili under load. It is directly responsible for the tail of pausing times pertinent to long traps. If a pilus can withstand its load only for a short time, the long time tail of trapping disappears. For very large τ_s, the tail of trapping times starts to saturate due to very long trapping events that are not resolved in time of simulations. The value of τ_s = 600 s leads to the best match of the tail of trapping times; in the case of 10 stalled pili, it corresponds to a detachment rate of one pilus/min. We show how the tail of the trapping times distribution responds to the variation of this parameter in Fig. S3.

Pilus attachment probability

Attachment probability has an obvious limitation 0 ≤ A ≤ 1 and contributes to the time required for a new pilus to attach, which is t₁ ∝ N_p⁻¹l_pu_e⁻¹A⁻¹. As it is seen from this relation, changing A can have similar effects on timescales as changing the number of pili. However, they are not completely interchangeable; for example, in the detachment of stalled pili, A has no effect, whereas N_p plays an essential role.

To conclude this subsection, we see that there is a number of parameters in the model (see Table 1), but also a corresponding number of experimental features to match, including full distribution of trapping times with two regimes, and moving times distribution. Most of the parameters, such as N_p, l_p, v_r, v_e, and f_p, have only a very limited variation range fixed by the experimental data. The remaining A, τ_s, and f_th/f_p can be considered as true fitting parameters.

Table 1.

List of the parameters used in the simulations

Np	lp [μm]	ve,vr [μm/s]	τs[s]	A	fp [pN]	fth/fp
10	2.0	2.0	600	0.5	100	1.43

The number and mean length of pili are denoted by N_p and l_p, respectively. Their extension and retraction speed is v_e and v_r. The average time for which a pilus can withstand its load is τ_s. The probability to attach, the pulling force, and the ratio of the threshold force to the pulling force are denoted by A, f_p, and f_th/f_p, respectively. For the BSA-coated surface, the value of A has to be set to 0.9.

Test of the model

The model predicts that the trapping and moving times behave in a certain way depending on the parameters of the problem. One of the easiest ways to check the validity of the model is to repeat the tracking experiments with a different coating of the surface. Within this model, this should change the distribution of moving and trapping events. Indeed, experiments show that BSA-coated plastic surfaces have longer average trapping and moving times: 3.77 ± 0.14 and 5.96 ± 0.09 s, respectively. It is consistent with previous observations on P. aeruginosa bacteria showing that BSA can stimulate their twitching, potentially by enhancing the binding of TFP to the substrate (24). The parameters of the model that can have this effect are the increased attachment probability A and the ratio of the threshold to the pulling force f_th/f_p. This is exactly what we obtain in the model: the attachment probability, A, must be increased to fit the second set of data on Fig. 3. In Table 1, we summarize the parameters that we use to fit the experimental data for the BSA-coated and uncoated surfaces.

The model also reproduces the average moving times for both surfaces. Long runs, as, for example, seen in some parts of a trajectory in Fig. 1, are also present in the model and constitute the tail of the nearly exponential run-time distribution. However, the model deviates from the data on a far tail for runs longer than 30 s. The deviation is small (note the semilogarithmic scale) but certainly detectable. An additional mechanism for even longer runs could be a reduced attachment probability in the direction opposite to that of the cell motion. When a pilus is trying to attach and start to pull against the motion of the cell, it immediately experiences a load of already pulling pili, thus reducing its chances to form a stable bond to the surface. By contrast, when trying to attach and pull cooperatively in the current moving direction, the attachment can only be hampered by elastic forces of the bending pilus, which is much smaller.

Remarkably, numerical simulations qualitatively describe the orientation of the cell during its motion, and how it changes depending on a type of a surface. We argue that, by a simple geometrical effect, a larger number of pili on the longer side of the cell leads to longer runs in the corresponding direction. Longer runs are explained by the larger number of pili available to attach and keep the cell moving, whereas with a smaller number of pili there is a higher probability to trap the cell. Similarly, cells on the coated surface have longer moving intervals, and a more pronounced preference of the cell to orient itself perpendicular to the direction of motion, moving by its wider side forward. Finally, we also directly visualize the dynamics of pili by using TIRF microscopy. This is possible to do only for a very short period of time (≲10 s) and in different experimental conditions (see Materials and Methods). Therefore, TIRF data cannot be directly compared with other results of this article. Nevertheless, it confirms that several pili engage to propel the cell (see Fig. 6 and see Movie S3), and they can also trap the cell (see Movie S4).

Figure 6.

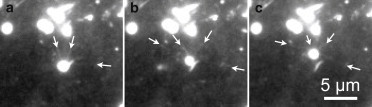
TIRF imaging of pili dynamics. Three snapshots of the moving cell with a time difference of 0.67 s. (Bright ellipsoidal spots) Cell bodies. (Arrows) Positions of presumed pili attachment points and the direction of the pilus fiber that were manually identified in frame-by-frame analysis of the recorded movies (see the Supporting Material). Note how several pili simultaneously engage in pulling the cell. See Movie S3 in the Supporting Material.

Discussion

Our model consists of the microscopic rules for the individual pilus cycle and the algorithm of collective pili operation based on the principle of the force balance. It has a minimal set of ingredients that allow the description of the experimentally observed trapping of the cell and the correlation of the orientation and the direction of motion. Remarkably, even this simple model is quantitatively successful, and consistently reproduces results for two different types of surface coatings. However, although the model might perform well in this study, it disregards a number of known pili-related effects that might be of importance in other situations. We list those properties briefly to provide a more complete picture of twitching motility.

Detailed properties of type IV pili

The retraction velocity of pili has a well-defined force dependence in that large loads result in lower retraction speeds (22,25). In what are now classic experiments, Skerker and Berg (11) also observed that pili did not always retract to the very end at once—they could pause. Moreover, pili do not necessarily start to grow right after retracting to the end. A pause may occur before the motor switches to the extension of the pilus. Similarly, pili disassembly is not necessarily correlated with attachment. Additionally, under a large load pili can experience a conformational change, leading to strong elongation without rupturing (18). Multiple pili can also form bundles, with a pulling force of the bundle being significantly higher than that of a single pilus (17). We have also suggested that the attachment probability in the direction opposite to current active motion may be reduced. Although these features of pili are not included in the model, some of them can be accounted for by a suitable renormalization of parameters. For example, the retraction or extension speed might take into account pausing during growth or retraction of pili; pausing of motors before growing a new pilus could be taken into account through the effective number of active pili. Most of these features can be implemented directly in our simulations. Therefore, we believe that the model describes the general mechanism of twitching of N. gonorrheae bacteria, while complying with a more complex phenomena involving the TFP.

Search strategy

It might seem inefficient for a cell to have pili surrounding its body and often competing with each other. However, M. xanthus bacteria can organize TFP relevant motors in a well-defined spatio-temporal pattern resulting in the alternating activity of pili on the opposite poles of the cell (26). When pili work on one pole of the cell, it moves forward with high persistence. By reversing the leading pole, it also abruptly changes the direction of motion, providing the major mechanism for effective exploration of the neighborhood. The frequency of reversals is connected to the chemotactic genetic pathway of the cell (27). We believe that pili of N. gonorrheae play a similar role in reorienting the cell after exiting from the trap, as often seen in trajectories, and therefore help it explore its neighborhood. Cells are surrounded by pili from all sides; due to the remarkable length and dynamical extension and retraction of pili, bacteria are able to probe an area significantly larger than the cell size. When finding a neighbor, cells can pull together, utilizing the strong retraction force of pili and building a microcolony (28).

Conclusions

We propose a model that describes the microscopic dynamics of individual pili and how multiple pili coordinate to propel N. gonorrheae bacteria. Although each pilus works independently, when several pili engage in pulling, the geometrical force balance determines whether the cell is going to move or stall. Numerical simulations take into account the actual geometry of the cell and therefore are easily applicable to rod-shaped bacteria as well, such as P. aeruginosa and M. xanthus (14–16,26,27). We show that by changing pili substrate interactions, the motion of bacteria can be altered in a predictable way. The knowledge of the N. gonorrheae cell motility is essential for the understanding of bacterial dispersal and formation of microcolonies. In the light of the rapid increase in the number of cases when gonorrhea infection is resistant to multiple common antibiotics, it is important to find new potential targets for the drugs of the next generation (29). Interfering with pili-driven bacterial motility may be one of the possible ways to inhibit the dispersal N. gonorrheae, and therefore can help control the progression of the gonorrhea infection.