Abstract
Hub proteins are proteins that maintain promiscuous molecular recognition. Because they are reported to play essential roles in cellular control, there has been a special interest in the study of their structural and functional properties, yet the mechanisms by which they evolve to maintain functional interactions are poorly understood. By combining biophysical simulations of coarse-grained proteins and analysis of proteins-complex crystallographic structures, we seek to elucidate those mechanisms. We focus on two types of hub proteins: Multi hubs, which interact with their partners through different interfaces, and Singlish hubs, which do so through a single interface. We show that loss of structural stability is required for the evolution of protein-protein-interaction (PPI) networks, and it is more profound in Singlish hub systems. In addition, different ratios of hydrophobic to electrostatic interfacial amino acids are shown to support distinct network topologies (i.e., Singlish and Multi systems), and therefore underlie a fundamental design principle of PPI in a crowded environment. We argue that the physical nature of hydrophobic and electrostatic interactions, in particular, their favoring of either same-type interactions (hydrophobic-hydrophobic), or opposite-type interactions (negatively-positively charged) plays a key role in maintaining the network topology while allowing the protein amino acid sequence to evolve.
Introduction
Proteins that maintain promiscuous molecular recognition, i.e., the ability to maintain functional interactions with multiple partners (1), represent hubs in protein-protein-interaction (PPI) networks. Those highly connected proteins in the cell PPI network are known to play essential roles in cellular control (2–4), and many of them are encoded by essential genes. Therefore, there has been a special interest in the study of the structural and functional properties of hubs that differentiate them from nonhubs (2,5). These differences are manifested in 1), structural properties of the interfaces, and 2), their thermodynamic stability, as further described below.
The identification of structural properties of hubs is based on gene expression patterns and localization of proteins within the cell, as defined by Han et al. (2,3). The authors identified two classes of hubs. The first class contains hubs that interact with all their partners at the same time and in the same space (referred to as Party hubs), and the second consists of hubs that interact with their partners at different times or locations (referred to as Date hubs). The differences between different types of hubs could be manifested in molecular properties (structure and sequence) of Party- and Date-hub proteins. Indeed, based on crystallographic data, Kim et al. (8,9) found two classes of hubs: Multi hubs, which interact with their partners through different interfaces, and Single or Singlish hubs, which interact with most of their partners through one interface. Therefore Singlish hubs cannot interact simultaneously with all their partners, and they generally tend to behave as Date hubs (10).
The next line of evidence highlighting the differences between hubs and nonhubs is based on structural disorder. A hypothetical folding-upon-binding mechanism to provide functional promiscuity in PPIs posits that hub proteins are disordered but get folded upon binding to a partner, potentially acquiring different tertiary structures with different interaction (11,12). Therefore, the study of hub proteins and their interaction partners is relevant for the understanding of the particular role that disorder might play in multifunctional molecular recognition. Bioinformatics analysis provided an initial support to the disorder hypothesis by showing that Singlish hubs and their partners have a higher level of predicted disorder than do Multi hubs, and higher than the proteome average (9). In addition, It has been shown that surfaces of some hubs are enriched in charged and polar amino acids and depleted of hydrophobic content (13–16), a signature of disordered proteins (17). However, despite significant efforts, a clear understanding, at the molecular level, of the physical mechanisms that use hydrophobicity and electrostatics to provide functional promiscuity of hubs in a PPI network remain elusive.
Recently, we developed a multiscale microscopic biophysics-based model to study evolution of functional and nonfunctional PPIs within a simple, yet nontrivial, functional PPI network (18,19). The analysis highlighted an intrinsic conflict in the evolution of hub proteins between the requirement to maintain multiple functional interactions and the need to avoid ever more abundant nonfunctional ones (20–23). The evolutionary compromise between these factors was achieved in the model (19) by modulating the intracellular abundance of hub proteins and simultaneously decreasing their surface hydrophobic content. Here, we employed the modified biophysics-based model, along with bioinformatics analysis and simple arguments, to study physical principles of evolutionary design of different types of functional PPI hubs. We provide reasoning as to why proteins belonging to Singlish hub systems are more prone to disorder than those belonging to Multi hub systems (9). We found that PPIs of hubs of different types are stabilized by different kinds of physical interactions (e.g., electrostatic, hydrophobic, etc.), both in the biophysics-based model and in the analysis of protein crystallographic databases (Structural Interaction Network (SIN) database (8,9,24)). Finally, we use combinatoric arguments to show that the physical nature of hydrophobic and electrostatic interactions, in particular, their favoring of either same-type (hydrophobic-hydrophobic) or opposite-type interactions (negatively-positively charged), plays a key role in maintaining the network topology while allowing the protein amino acid sequence to evolve. For clarity, we include a flowchart in Fig. 1, depicting our workflow and how results from the lattice-model proteins, SIN database, and combinatoric model are utilized.
Figure 1.
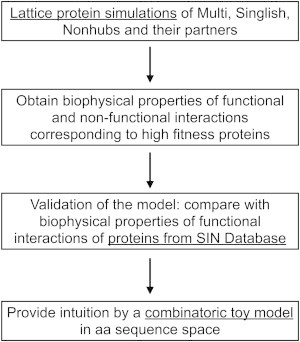
Flowchart depicting our workflow, and highlighting how results from each description level (lattice model proteins, SIN database, and combinatoric toy model) are utilized.
Methods
Lattice protein simulations
We build on a recent biophysics-based multiscale model of evolution wherein simple-lattice-model globular proteins are encoded in genomes of model cells. These genomes are subject to mutations, and the corresponding amino acid sequences determine the precise structure, stability, and interactions of the proteins involved (19,25). In previous work, these simulations have been successful in drawing a direct link between the genotype-phenotype relationship of an organism and several evolved biophysical properties of proteins in its cells, such as their stability, abundance, and PPI strength.
Each of our model proteins consists of 27 amino acid residues that fold into 3 × 3 × 3 cubic lattice conformations (Fig. 2 A). This 27-mer lattice model protein has 103,346 maximally compact conformations (26). Following Heo et al. (19), for computational efficiency, we use a subset of 10,000 randomly selected conformations as our ensemble. Only amino acids occupying neighboring sites on the lattice can interact, and the interaction energy depends on amino acid types according to the Miyazawa-Jernigan (MJ) potential (27), both for intra- and intermolecular interactions. We calculate the Boltzmann probability of folding to a native state, , for each protein:
| (1) |
where is the energy of the most stable, or native, conformation out of 10,000 conformations and T is the temperature in arbitrary units. The probability of folding, , is therefore a proxy for the degree of disorder of protein i. We impose the condition that the native conformation is the minimum energy conformation in the conformational ensemble. Mutations that lead to violation of this condition are considered lethal: every protein in the model proteome is deemed essential, so that its failure to fold deprives the cell of an essential function, causing the lethal phenotype. We model the PPIs with a rigid docking scheme. Six faces of a cubic lattice provide six possible interaction surfaces, and there are four possible directions (which correspond to rotational degrees of freedom) to dock two lattice proteins through two interaction surfaces. Hence, in total, there exist 6 × 6 × 4 = 144 docking modes for a binary protein complex. The Boltzmann probability of interaction in a functional binding mode between proteins i and j is
| (2) |
where is the interaction energy of a functional binding mode (defined below), and are the interaction energies for all 144 docking modes. We assume that each protein in the cell folds with a two-state folding kinetics,
| (3) |
where Ui denotes unfolded states and Fi the unique native state. and are the folding and unfolding rate constants, respectively. The steady-state solution is
| (4) |
We use the law of mass action (LMA) as described in Heo et al. (25) to calculate all possible functional and nonfunctional interactions between all proteins with folded conformations. We solve the LMA equations numerically (25) to obtain the concentrations of the complexes, with a permitted error of 10−15 for each protein concentration. Once the concentrations of protein complexes are obtained, we can define the concentration of functional complexes. The functional concentrations are
| (5) |
where are the concentrations of dimers formed by folded proteins i and j in any configuration. We consider both Multi and Singlish hubs (Fig. 2, B and C, respectively). For a Multi hub, each face of the hub is designated to functionally interact with a specific binding partner. For a Singlish hub, a single face is chosen as a functional interaction surface available to all partners, and interactions with different partners are physically mutually exclusive and thus cannot occur simultaneously. We limit the number of partner proteins, Np, to 6, i.e., the maximal proteome size (including the hub) is 7. Nonfunctional concentrations are defined as
| (6) |
where is the total concentration of protein i. The fitness of each cell in the population is given by the cell division rate,
| (7) |
where is a constant parameter chosen at the beginning of simulations to scale the rate, and thus the timescale, of evolution, and α scales the overexpression penalty. To limit protein overexpression, we set the parameters α = 500 and , as the initial protein concentration was chosen to be C = 0.1. We use the Gillespie algorithm (28) with fixed population size (N = 100). Upon cell division, a mother cell gives birth to a daughter cell. To keep the population size constant, a newborn cell replaces a randomly chosen cell in the population. Upon replication, both the mother and daughter cells are subjected to either a mutational event with constant rate (μ = 10−3/gene/replication) or to a change in the expression level of one protein in the cell. This protein is chosen randomly, and its expression level changes with a constant rate (r = 0.01/cell division) such that its concentration in the new cell is obtained from the old one as , where is a Gaussian random number with zero mean and variance 0.1. All simulations ran for 6 × 106 generations and were considered to be in a steady state when Ci, , and reached a plateau value. The random seed of each simulation is initialized with a unique value. The results described below are averaged over 50 different random simulations.
Figure 2.
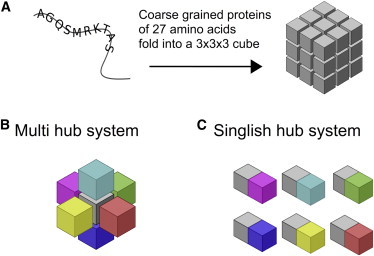
(A) Schematic representation of the lattice protein model. (B and C) Model proteins in the system, including the hub protein (gray) and up to six interaction partners (colors). For the Multi hub system (B), each face of the hub is designated to interact with a specific binding partner; For the Singlish hub system (C), only a single face is chosen as an interaction interface with all the partners. To see this figure in color, go online.
To calculate the evolutionary rates of proteins in the simulation, we count the number of fourfold, twofold, and nondegenerate sites (corresponding to four, two, and one amino acid representation in nucleotide space), and use the formula of Hartl and Clark ((29), page 340):
| (8) |
where is the number of synonymous sites at generation t, and is the number of nonsynonymous sites at generation t. Next, we calculate
| (9) |
where and are the numbers of synonymous and nonsynonymous sites, respectively, of the initial sequence. and are the numbers of synonymous and nonsynonymous amino acids, respectively, at generation t. The evolutionary rate is then defined to be dN/dS.
SIN database analysis
To compare the lattice proteins to natural proteins, we used the SIN database (8,9,24), which identified Multi and Singlish hubs and their available atomistic structures in complex with their partners at the Protein Data Bank (PDB). We used the information available for human proteins, in total 37 Multi, 36 Singlish, and 30 Nonhub interactions (see Table S1 in the Supporting Material for the list of PDB files considered). Nonhub interactions were defined as interactions between proteins that do not belong to a Singlish or Multi hub group. We identified and analyzed the interfaces, and studied the statistics of contacts (two residues are defined to be in contact when any pair of atoms from the two different amino acids are separated by <4 Å). To facilitate comparison with simulations we used the MJ potential to evaluate the contact energies.
Combinatoric toy model
The model consists of three proteins (a hub and two partners), where each protein has two interaction surfaces. The simulation space is one-dimensional (1D) and proteins can interact via a single interface. In total, there are six surfaces in the system, and surfaces can be hydrophobic, hydrophilic, or positively or negatively charged. This corresponds to the reduction of the amino acid pull from 20 to 4. We use an averaged MJ potential for the four types of amino acids, where hydrophobic amino acids were identified as M, F, I, L, V, W, P, and C, negatively charged as D and E, and positively charged as R and K (30) (as done for the lattice-model simulation and SIN database analysis). The model system has a countable sequence space. In particular, there are six surfaces, each of which can be one of four types; thus, there are a total of 46 = 4096 possible configurations.
For each configuration, we solve the LMA equations
| (10) |
where and are the concentrations of protein i and protein j, respectively. The initial concentrations were chosen to be and (the latter set for both partners). The association constants are defined as
| (11) |
where is the averaged MJ interaction energy mentioned above and k and m are the particular bound surfaces of proteins i and j, respectively. For interaction between two different proteins, there are four modes of interaction. For interaction between two identical proteins, there are three modes of interaction due to the 1D symmetry in the system. The functional concentrations are defined as
| (12) |
The functional pair varies between Multi, Singlish, and Nonhub systems. For Multi hubs, each surface of the hub is designated for a different partner. For Singlish hubs, the same surface of the hub interacts with both partners. For Nonhubs, we define a single functional interaction, whereas the second partner is required to remain in a monomeric form. For hub systems, the fitness of the configuration is
| (13) |
whereas for Nonhub systems, the fitness of the configuration is
| (14) |
Results
Lattice protein simulations
Even though the simulated-lattice-protein Multi, Singlish, and Nonhub systems considered here differ in their functional interaction networks and numbers of partners, some trends are similar in most systems. 1), Shortly after the beginning of the simulations, the concentration of the hub proteins increases such that (after ∼ generations; see Fig. 3 A). 2), Hub and partner proteins eventually evolve a stable structure ( increases), whereas some proteins experience a sharp drop in beforehand (see Fig. 3 B). 3), The nonfunctional concentration, , of the hub increases at first due to the increase in hub concentration, but when the hub concentration, C, stabilizes, the of the hub proteins decreases. The of partners decreases monotonically throughout the simulation (see Fig. 3 C). 4), The hub-partner pairs develop functional surfaces with increasing probability of functional interaction, (see Fig. 3 D).
Figure 3.
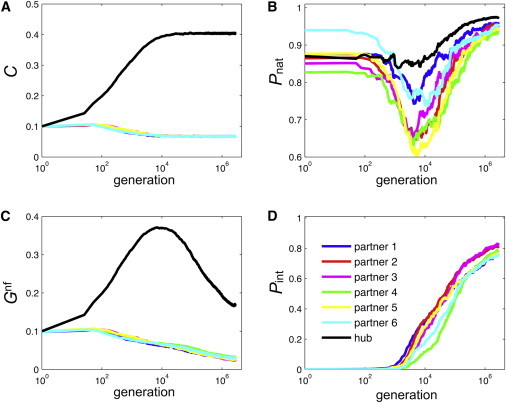
Evolution of molecular properties in Singlish hub systems with six interaction partners with regard to concentration, C, of hub (black) and partner proteins (colors; see legend in panel D) (A), thermodynamic stability, (B), nonfunctional concentration, (C), and functional interaction probabilities, (D). Data are plotted versus generation, averaged over 50 independent realizations (of different random-number seed), and shown in logarithmic scale for the x axis. The Multi hub system shows similar behavior for these quantities. To see this figure in color, go online.
Effect of number of partners
One particular goal was to understand the evolutionary processes that dominate changes in the thermodynamic stability of hub proteins and their level of disorder. In both Multi and Singlish hub systems, hub and partner proteins evolve a stable structure ( increases). Although the of hubs tends to increase monotonically, those of partner proteins experience a drop before maximal stability is reached. We studied the effect of number of partners on the evolution of protein stability, as reflected in . Fig. 4 shows the of hubs and partners for Multi (Fig. 4, A and C, respectively) and Singlish hub systems (Fig. 4, B and D, respectively) and compares systems with two, four, and six partners. The of partners of both Multi and Singlish hub systems drops with respect to its initial value. As the number of partners increases, both the amplitude of the drop and the time necessary for stabilization after reaching the minimal increase. The drop in is more profound for partners of Singlish hubs in comparison to those of Multi hubs. As partners lose stability, they open the sequence space needed to improve the interaction strength, (Fig. 5). However, functional interaction surfaces in Multi hub systems evolve more slowly and poorly, as can be seen in Fig. 5 for systems with a maximal partner number of six.
Figure 4.
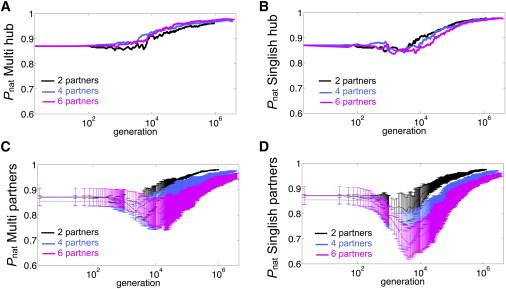
Effect of the number of partners on stability, , of proteins as a function of generation for Multi hubs (A), Singlish hubs (B), partners of Multi hubs (C), and partners of Singlish hubs (D). Systems with two, four, and six partners are shown in black, blue and magenta, respectively. For partner proteins, is averaged over all partners in the system, and error bars correspond to 1 Standard Deviation (SD). All plotted data (including averaged and SD) are averaged over 50 independent realizations and shown in logarithmic scale for the x axis. To see this figure in color, go online.
Figure 5.
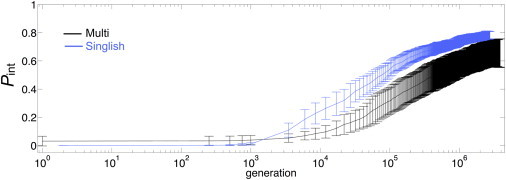
Comparing for Multi and Singlish hub systems with the maximal number of partners (six). is averaged over all partners in the system, and error bars correspond to 1 SD. and SD values are averaged over 50 independent realizations and shown in logarithmic scale for the x axis. To see this figure in color, go online.
Evolutionary rates
In previous studies, the evolutionary rate of proteins has been shown to correlate negatively with the number of functional interfaces (8), yet a clear understanding of the behavior of the evolutionary rates of hub proteins and partners throughout evolution remains elusive. Therefore, we calculated the evolutionary rates, , by counting the number of synonymous and nonsynonymous sites in the nucleotide sequence (see further details and Eq. 9 in Methods).
In Fig. 6, we plot the evolutionary rate for hub proteins (Fig. 6 A) and partner proteins (Fig. 6 B) as a function of generation. Our results are in agreement with those of Kim et al. (8) and show that the more functional interfaces a protein has, the lower is its evolutionary rate in steady state (once the evolutionary rate reaches a plateau); Singlish hubs, which have a single interaction surface, reach a higher evolutionary rate than do Multi hubs, which have six functional interfaces (Fig. 6 A). Partners of both Multi and Singlish hubs reach a similar plateau value (Fig. 6 B). Both Singlish hubs and their partners experience an increase in evolutionary rate, ∼ generations before Multi hubs and their partners.
Figure 6.
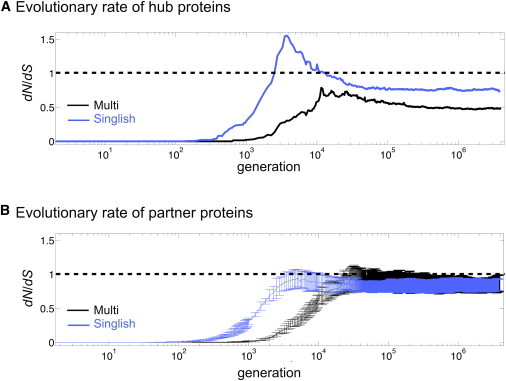
Evolutionary rates, , versus generation, for hub proteins (A) and partner proteins (B). In B, the data are averaged over all six partners, and error bars correspond to 1 SD. Plotted data are averaged over 50 independent realizations and shown in logarithmic scale for the x axis. To see this figure in color, go online.
Biophysics of specificity
Next we turn to the question of how hubs use the hydrophobic and charge interactions to design their surfaces to maximize functional interactions. To that end, we examined the functional energy contributions from hydrophobic and electrostatic contacts once simulations reached a steady state (after generations). Contacts between amino acid pairs were classified as hydrophobic contacts if both amino acids were hydrophobic (hydrophobic amino acids were identified as M, F, I, L, V, W, P, and C (30)), or as electrostatic contacts if the pair contained a positively and a negatively charged amino acid (negatively charged amino acids were identified as D and E, and positively charged amino acids as R and K (30)). Values of the hydrophobic and electrostatic energies were normalized by the total interaction energy of their corresponding functional interface. We extracted those energies for 50 different realizations, and we plot the hydrophobic and electrostatic functional energy histograms in Fig. 7 A and B, respectively. The latter show that Multi hubs use electrostatic contacts more than Singlishs do. In particular, the mean electrostatic contribution is and for Multi and Singlish hubs, respectively (± values represent the variance calculated over multiple realizations; Kolmogorov-Smirnov (KS) test, ). Nonhubs have a lower mean electrostatic contribution compared to hub systems. The same analysis for hydrophobic contacts shows an opposite trend: mean contributions of and for Multi and Singlish hubs, respectively (KS test, ). Nonhubs have a higher mean hydrophobic contribution in comparison to hubs.
Figure 7.
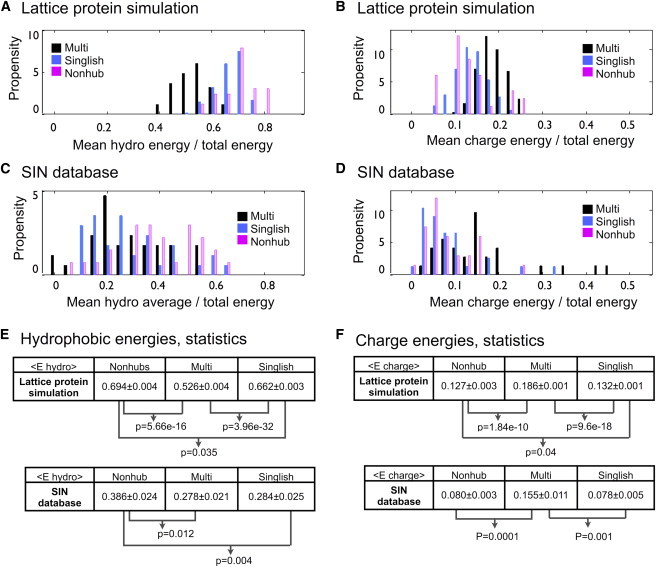
Mean interaction energy histograms showing fractions of hydrophobic and electrostatic contributions for lattice protein simulations (A and B, respectively) and SIN database (C and D, respectively). For the lattice protein, energies are calculated at the end of the simulations at generation . Multi and Singlish hub systems are shown in black and blue, respectively. Nonhub systems are shown in magenta. Data were binned to generate hydrophobic energy histograms (bin size ), and charge energy histograms (bin size ). (E) Statistics of hydrophobicity histograms expressed as mean ± variance. (F) Statistics of electrostatic histograms expressed as mean ± variance. The p values were extracted using the KS test. Only significant values are noted. To see this figure in color, go online.
As the simulations gave us clear insights and predictions regarding the steady-state biophysical properties of hub-protein systems, the next step was to test these predictions for natural proteins. To that end, we used the SIN database (8,9,24), which identified Multi and Singlish hubs and their available atomistic structures in complex with their partners at the PDB (see further details in Methods). As in the simulations analysis, we compared the percentages of hydrophobic-hydrophobic and opposite-charge contacts for both Multi and Singlish hubs (see Fig. 7, C and D). This analysis verified our prediction that electrostatic contacts are more predominant in Multi hubs and hydrophobic contacts are more predominant in Singlish hubs. The electrostatic contributions calculated using the SIN database are and for Multi and Singlish hubs, respectively (± values represent variance calculated over multiple PDB files; KS test, p = 0.001). Nonhubs have an electrostatic contribution comparable to that of Singlish hubs. The same analysis for hydrophobic contacts shows average contributions of and for Multi and Singlish hubs, respectively (KS test indicates a nonsignificant difference between the two). However, Nonhubs have a higher hydrophobic contribution in comparison to hubs (KS test, p = 0.012 and p = 0.004 for Multi and Singlish hubs, respectively).
Next, we analyzed the nonfunctional interaction energies. Due to the geometrical complexity of the crystallographic 3D structure of proteins, nonfunctional PPI interfaces are not clearly defined, and therefore, analysis of the nonfunctional energies is not feasible for proteins in the SIN database. However, nonfunctional interaction energies are accessible in the lattice-protein simulations, and their energetic contribution is calculated as for the functional ones. Again, we consider both hydrophobic and electrostatic contributions to the interaction energies. As we are interested in the negative design of nonfunctional interactions (i.e., minimizing nonfunctional interactions), we extract information about the following least favorable interactions: hydrophobic with nonhydrophobic (marked as the hydrophobic contribution), and electrostatic interactions between charges with the same sign (marked as the electrostatic contribution).
We plot the nonfunctional energy histograms in Fig. 8, showing the mean energetic contributions of both hydrophobic (Fig. 8 A) and electrostatic contacts (Fig. 8 B) divided by the total energy of the interaction. Similar to the case for functional interactions, Multi hubs use electrostatic contacts in their nonfunctional PPI network more than Singlish hubs and Nonhubs. In particular, the electrostatic contribution is for Multi hubs, and and for Singlish and Nonhubs, respectively (KS test, and for Multi-Singlish and Multi-Nonhub, respectively). The electrostatic contribution is not significantly different for Singlish hubs and Nonhubs. Therefore, in comparison to Singlish hubs and Nonhubs, Multi hubs use more electrostatic interactions to both maximize probabilities for functional interactions and minimize probabilities for nonfunctional interactions.
Figure 8.
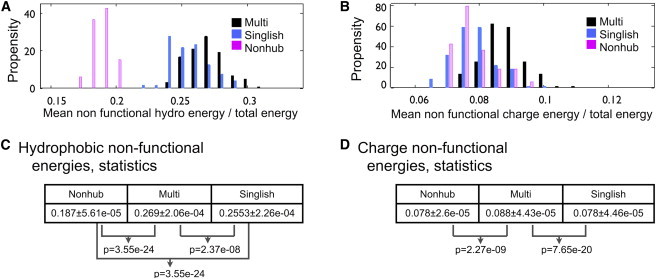
Negative design in the multiscale evolutionary model. Nonfunctional interaction energy histograms showing the contribution fraction of hydrophobic interactions (A) and electrostatic interactions (B) for lattice protein simulations. Multi and Singlish hub systems are shown in black and blue, respectively. Nonhub systems are shown in magenta. Bin sizes used to generate hydrophobic energy histograms and charge energy histograms were and , respectively. (C) Statistics of hydrophobicity histograms expressed as mean ± variance. (D) Statistics of electrostatic histograms expressed as mean ± variance. The p values were extracted using the KS test. Only significant values are noted. To see this figure in color, go online.
The same analysis for hydrophobic contacts shows that the distributions of Multi hubs, Singlish hubs, and Nonhubs are significantly different (see p values in Fig. 8 C). Nonhubs use the smallest number of hydrophobic contacts for the nonfunctional interactions, on average. The average hydrophobic contribution is for Singlish hubs and for Multi hubs. The trend showing the average hydrophobic contribution is highest for Multi hubs, intermediate for Singlish hubs, and lowest for Nonhubs is exactly the opposite of their relationship when accounting for functional interactions. Therefore, Multi hubs are highly efficient in negative design of their nonfunctional surfaces for minimizing unfavorable interactions, both hydrophobic and electrostatic.
Combinatoric toy model
Finally, we turn to a simpler model to provide insight into why Multi hubs rely on electrostatics to design their functional interaction surfaces, whereas Singlish hubs make predominant use of hydrophobic interactions. One possible explanation involves combinatorics, or counting of states, where a state is a certain amino acid sequence along the surfaces of the proteins. In particular, we wish to identify high-fitness sequences for Multi hubs, Singlish hubs, and Nonhubs and to classify them according to their hydrophobicity and charge content. To that end, we created a simplified 1D model of a hub and two partners, where each protein has two surfaces. Each surface is assigned to be one of four types: hydrophobic, positively or negatively charged, or neutral. The fitness (defined in Eqs. 13 and 14) is calculated according to the probability of functional interactions (see Methods for further details). The advantages of the simplified model are 1), the feasibility of sequence space enumeration, and 2), the isolation of surface energetics from thermodynamic stability. The combination of these advantages allowed us to address the fitness-maximization problem as a tiling puzzle, where electrostatic and hydrophobic surfaces are distributed among the proteins.
We start by considering the set of 80 top fitness configurations shown in Fig. 9, A–C, for Multi, Singlish, and Nonhub systems. The vertical axis indicates fitness. For each system, functional interactions are indicated in magenta for the top configuration. Hydrophobic surfaces are shown in green, hydrophilic in black, positively charged in red, and negatively charged in blue. We find that the maximal fitness configurations for both Multi and Singlish hub systems contain hydrophobic functional surfaces. For Multi hub systems, the first ∼40 configurations have two hydrophobic functional contacts, but the rest of the top configurations have one hydrophobic and one electrostatic functional contact. This is different from the Singlish- and Nonhub systems, where all top configurations have two hydrophobic functional contacts.
Figure 9.
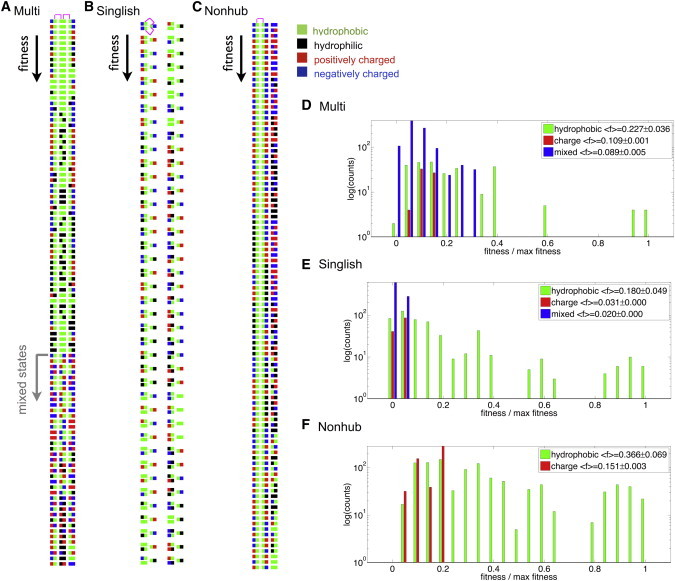
Results using a simplified 1D model. (A–C) The top 80 configurations for Multi (A), Singlish (B), and Nonhub systems (C). Configurations are arranged vertically according to their fitness (highest fitness at the top). For each system, functional interactions are indicated in magenta for the top configuration. Hydrophobic surfaces are shown in green, hydrophilic in black, positively charged in red, and negatively charged in blue. (D–F) Histograms of the number of configurations (in log scale) corresponding to a certain relative fitness (fitness divided by maximal fitness) are shown for Multi (D), Singlish (E), and Nonhub systems (F). The configuration count is divided for all hydrophobic functional contacts (green), all electrostatic functional contacts (red), and one hydrophobic and one electrostatic contact (blue; not available for the Nonhub system). Mean ± variance values of the distributions are indicated in the legend. To see this figure in color, go online.
Further understanding of the origin of the favoring of electrostatic functional interactions in Multi hub systems can be extracted from the fitness distributions plotted in Fig. 9, D–F, where we plot histograms of the number of configurations (in log scale) corresponding to a certain relative fitness (fitness divided by maximal fitness). The configuration count is divided for all hydrophobic functional contacts (green), all electrostatic functional contacts (red), and one hydrophobic and one electrostatic contact (blue, not available for the Nonhub systems, since they only have one functional contact). When fitness decreases, more configurations containing electrostatic functional surfaces become available, most profoundly for Multi hub systems. In situations where the maximal-fitness configuration is not easily approached (for example, due to limitations arising from thermodynamic stability considerations, i.e., stand-alone lattice proteins are known to be most stable when ∼30% of their amino acid sequence is hydrophobic (19)), the next available configurations are more likely to contain electrostatic functional interfaces in Multi hub systems in comparison to Singlish-hub systems. This may explain why Multi hubs use more electrostatic than hydrophobic functional interactions and why the reverse is true for Singlish hubs in the lattice protein simulations and in the SIN database (see Biophysics of specificity). This effect can be quantified by the average fitness of the configurations considered, and indeed, the average fitness of configurations involving electrostatic functional interactions for Multi hub systems is , which is approximately three times larger than that for Singlish-hub systems, .
Discussion
The findings presented here have implications for the conceptual understanding of the emergence of disorder in PPI networks, aswell as the design of functional interactions within them. We start by providing reasoning as to why proteins belonging to Singlish-hub systems are more prone to disorder than those belonging to Multi hub systems (9). Our simulations show that throughout evolution, partners of Singlish hubs experience a larger drop in stability, , (i.e., they explore more disordered configurations), and a longer time to recover their maximal , in comparison to Multi hub partners (Fig. 4, C and D). Hubs in the simulations experience a profoundly smaller drop in (Fig. 4, A and B), despite the bioinformatics analysis predicting a high level of disorder for Singlish hubs as well (9). This discrepancy could be attributed to the fact that in our simulations, proteins are assigned hub or partner exclusively, whereas in nature, hub proteins may become partners in other hub systems, particularly in Singlish-hub systems (9). Singlish-hub partners may utilize the drop in to open up a sequence space necessary for the evolution of functional interactions. Indeed, evolutionary rates of proteins in our simulations (Fig. 6) show a trend similar to that described by Kim et al. (8), who observed that evolutionary rates negatively correlate with the number of functional interfaces. Moreover, our simulations show that proteins in Singlish-hub systems spend more time in functional interaction complexes compared to proteins in Multi hub systems and therefore evolve a more robust and efficient PPI (Fig. 5).
In addition, our simulations and analysis of the SIN database reveal two different mechanisms of surface design: whereas Multi hubs rely on electrostatics to design their functional interaction surfaces, Singlish hubs make predominant use of hydrophobic interactions (Fig. 7, C and D). Despite the simplified nature of the protein structure in the simulations, estimation of the contact energies for both simulated coarse-grained and atomistic real protein structures follow the trend mentioned above (Fig. 7, A and B) and suggest that our coarse-grained simulations capture the fundamental physics of hub protein systems. It is remarkable that different ratios of hydrophobic to electrostatic interactions of interfacial amino acids maintain distinct network topologies (i.e., Multi and Singlish) and underlie a fundamental design principle of PPI. Furthermore, the PPI takes place in a crowded environment, where functional interactions must overcome nonfunctional ones. Indeed, we show that hubs are highly efficient in designing their nonfunctional surfaces as well, for minimizing energetically favorable yet nonfunctional interactions; hubs use more hydrophobic mismatches (noncompatible amino acid pairs at the hub-partner interface) than do Nonhubs (Fig. 8 A), and Multi hubs use more electrostatic mismatches than do Singlish hubs and Nonhubs do (Fig. 8 B).
To further understand the origin of the two design mechanisms, we turned to a simplified 1D system of a hub and two partners, where each protein has two surfaces. Each surface is modeled as one of four types: hydrophobic, positively or negatively charged, or neutral. The model provided evidence that the different design mechanisms of Multi and Singlish hub systems arise from a limited number of configurations (i.e., sequences of surface types) in the system. As for the lattice protein simulations, high fitness requires both maximizing probabilities of functional PPIs and minimizing probabilities of nonfunctional PPIs. After enumerating all possible configurations and ranking them according to their fitness, we revealed that there are more high-fitness configurations employing charge in Multi hub systems than in Singlish hub systems (Fig. 9). This combinatoric reasoning implies that the physical nature of hydrophobic and electrostatic interactions, in particular their favoring of either same-type interactions (hydrophobic-hydrophobic) or opposite-type interactions (negatively-positively charged), plays a key role in maintaining the network topology while allowing the protein amino acid sequence to evolve.
Conclusions
In conclusion, our results highlight the origin of thermodynamic instabilities and several biophysical steady-state properties of hub protein systems. Although our findings reveal the fundamental design principles of these systems, there are opportunities to extend the scope of this work, focusing, for example, on hierarchical systems composed of several hub networks and testing our predictions by experiments in vitro and possibly in vivo.
Acknowledgments
This work was financially supported by Swiss National Science Foundation (SNSF) grant no. PBEZP3_140130 4 (O.P.) and National Science Foundation grant MCB-1243837 (E.S.).
Supporting Material
References
- 1.Mosca R., Pache R.A., Aloy P. The role of structural disorder in the rewiring of protein interactions through evolution. Mol. Cell. Proteomics. 2012;11 doi: 10.1074/mcp.M111.014969. M111.014969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Han J.D.J., Bertin N., Vidal M. Evidence for dynamically organized modularity in the yeast protein-protein interaction network. Nature. 2004;430:88–93. doi: 10.1038/nature02555. [DOI] [PubMed] [Google Scholar]
- 3.Krogan N.J., Cagney G., Greenblatt J.F. Global landscape of protein complexes in the yeast Saccharomyces cerevisiae. Nature. 2006;440:637–643. doi: 10.1038/nature04670. [DOI] [PubMed] [Google Scholar]
- 4.Jeong H., Mason S.P., Oltvai Z.N. Lethality and centrality in protein networks. Nature. 2001;411:41–42. doi: 10.1038/35075138. [DOI] [PubMed] [Google Scholar]
- 5.Zotenko E., Mestre J., Przytycka T.M. Why do hubs in the yeast protein interaction network tend to be essential: reexamining the connection between the network topology and essentiality. PLOS Comput. Biol. 2008;4:e1000140. doi: 10.1371/journal.pcbi.1000140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Reference deleted in proof.
- 7.Reference deleted in proof.
- 8.Kim P.M., Lu L.J., Gerstein M.B. Relating three-dimensional structures to protein networks provides evolutionary insights. Science. 2006;314:1938–1941. doi: 10.1126/science.1136174. [DOI] [PubMed] [Google Scholar]
- 9.Kim P.M., Sboner A., Gerstein M. The role of disorder in interaction networks: a structural analysis. Mol. Syst. Biol. 2008;4:179. doi: 10.1038/msb.2008.16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Andorf C.M., Honavar V., Sen T.Z. Predicting the binding patterns of hub proteins: a study using yeast protein interaction networks. PLoS ONE. 2013;8:e56833. doi: 10.1371/journal.pone.0056833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Dunker A.K., Cortese M.S., Uversky V.N. Flexible nets. The roles of intrinsic disorder in protein interaction networks. FEBS J. 2005;272:5129–5148. doi: 10.1111/j.1742-4658.2005.04948.x. [DOI] [PubMed] [Google Scholar]
- 12.Dyson H.J., Wright P.E. Coupling of folding and binding for unstructured proteins. Curr. Opin. Struct. Biol. 2002;12:54–60. doi: 10.1016/s0959-440x(02)00289-0. [DOI] [PubMed] [Google Scholar]
- 13.Patil A., Nakamura H. Filtering high-throughput protein-protein interaction data using a combination of genomic features. BMC Bioinformatics. 2005;6:100. doi: 10.1186/1471-2105-6-100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Patil A., Nakamura H. Disordered domains and high surface charge confer hubs with the ability to interact with multiple proteins in interaction networks. FEBS Lett. 2006;580:2041–2045. doi: 10.1016/j.febslet.2006.03.003. [DOI] [PubMed] [Google Scholar]
- 15.Higurashi M., Ishida T., Kinoshita K. Identification of transient hub proteins and the possible structural basis for their multiple interactions. Protein Sci. 2008;17:72–78. doi: 10.1110/ps.073196308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Higurashi M., Ishida T., Kinoshita K. PiSite: a database of protein interaction sites using multiple binding states in the PDB. Nucleic Acids Res. 2009;37:D360–D364. doi: 10.1093/nar/gkn659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Uversky V.N., Gillespie J.R., Fink A.L. Why are “natively unfolded” proteins unstructured under physiologic conditions? Proteins. 2000;41:415–427. doi: 10.1002/1097-0134(20001115)41:3<415::aid-prot130>3.0.co;2-7. [DOI] [PubMed] [Google Scholar]
- 18.Cetinbaş M., Shakhnovich E.I. Catalysis of protein folding by chaperones accelerates evolutionary dynamics in adapting cell populations. PLOS Comput. Biol. 2013;9:e1003269. doi: 10.1371/journal.pcbi.1003269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Heo M., Maslov S., Shakhnovich E. Topology of protein interaction network shapes protein abundances and strengths of their functional and nonspecific interactions. Proc. Natl. Acad. Sci. USA. 2011;108:4258–4263. doi: 10.1073/pnas.1009392108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zhang J., Maslov S., Shakhnovich E.I. Constraints imposed by non-functional protein-protein interactions on gene expression and proteome size. Mol. Syst. Biol. 2008;4:210. doi: 10.1038/msb.2008.48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Deeds E.J., Ashenberg O., Shakhnovich E.I. Robust protein protein interactions in crowded cellular environments. Proc. Natl. Acad. Sci. USA. 2007;104:14952–14957. doi: 10.1073/pnas.0702766104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Johnson M.E., Hummer G. Nonspecific binding limits the number of proteins in a cell and shapes their interaction networks. Proc. Natl. Acad. Sci. USA. 2011;108:603–608. doi: 10.1073/pnas.1010954108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Levy E.D., De S., Teichmann S.A. Cellular crowding imposes global constraints on the chemistry and evolution of proteomes. Proc. Natl. Acad. Sci. USA. 2012;109:20461–20466. doi: 10.1073/pnas.1209312109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bhardwaj N., Abyzov A., Gerstein M.B. Integration of protein motions with molecular networks reveals different mechanisms for permanent and transient interactions. Protein Sci. 2011;20:1745–1754. doi: 10.1002/pro.710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Heo M., Kang L., Shakhnovich E.I. Emergence of species in evolutionary “simulated annealing”. Proc. Natl. Acad. Sci. USA. 2009;106:1869–1874. doi: 10.1073/pnas.0809852106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Shakhnovich E., Gutin A. Enumeration of all compact conformations of copolymers with random sequence of links. J. Chem. Phys. 1990;93:5967–5971. [Google Scholar]
- 27.Miyazawa S., Jernigan R.L. Residue-residue potentials with a favorable contact pair term and an unfavorable high packing density term, for simulation and threading. J. Mol. Biol. 1996;256:623–644. doi: 10.1006/jmbi.1996.0114. [DOI] [PubMed] [Google Scholar]
- 28.Gillespie D.T. Stochastic simulation of chemical kinetics. Annu. Rev. Phys. Chem. 2007;58:35–55. doi: 10.1146/annurev.physchem.58.032806.104637. [DOI] [PubMed] [Google Scholar]
- 29.Hartl D.L., Clark A.G. Sinauer Associates; Sunderland, MA: 2007. Principles of Population Genetics. [Google Scholar]
- 30.Berezovsky I.N., Zeldovich K.B., Shakhnovich E.I. Positive and negative design in stability and thermal adaptation of natural proteins. PLOS Comput. Biol. 2007;3:e52. doi: 10.1371/journal.pcbi.0030052. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


