Abstract
Many group-living animals construct transportation networks of trails, galleries and burrows by modifying the environment to facilitate faster, safer or more efficient movement. Animal transportation networks can have direct influences on the fitness of individuals, whereas the shape and structure of transportation networks can influence community dynamics by facilitating contacts between different individuals and species. In this review, we discuss three key areas in the study of animal transportation networks: the topological properties of networks, network morphogenesis and growth, and the behaviour of network users. We present a brief primer on elements of network theory, and then discuss the different ways in which animal groups deal with the fundamental trade-off between the competing network properties of travel efficiency, robustness and infrastructure cost. We consider how the behaviour of network users can impact network efficiency, and call for studies that integrate both network topology and user behaviour. We finish with a prospectus for future research.
Keywords: biological transportation networks, collective animal behaviour, pattern formation, animal trails, tunnels
1. Introduction
Human societies depend on transportation networks to ensure the efficient distribution of people, products and information. Animals also construct transportation networks by modifying the environment to facilitate faster, safer and more efficient movement via trails or burrows. Here, we use the term ‘animal transportation networks’ to indicate networks built by groups of animals, leaving aside the internal resource distribution networks that form distinct and separate systems within the body of organisms (for example, vascular and lymphatic networks). Examples of animal transportation networks include mixed-species wild mammal trails, vole runway systems, termite tunnels, gastropod slime trails and ant trail networks.
The use of a transportation network has numerous benefits to network users. Following established trails can yield substantial energetic benefits: for example, walking on snow increases the heart rate of dogs by 4–6% compared with walking on hard surfaces (i.e. compacted snow) [1]. In marine snails, crawling across a previously laid mucous trail can reduce energetically costly mucous production by 28% [2]. In addition to energetic savings, trail systems form an externalized ‘index’ of resource distribution, allowing individuals to easily and quickly locate key resources without the need to memorize their exact location [3]. It has been hypothesized that the walled trenches built by some ant species aid the colony by reducing the number of individuals that get lost [3]. Underground burrows such as those built by naked mole rats, termites and some ant species provide a safe, easily defensible transportation system between a central nest and food resources. Transportation networks may therefore serve an anti-predator function by allowing users to make a rapid (and sometimes concealed) escape. When attacked, voles (Microtus) use expert knowledge of their trail networks (called ‘runways’), and their many escape routes to out-manoeuvre attacking predators [4]. Transportation networks can also protect network users from harsh environments. Subterranean species living in arid environments are often sensitive to dry, desiccating air; underground tunnel systems provide an acceptable microclimate allowing individuals to forage even when the external environment is inhospitable (e.g. [5]).
Although transportation networks are found in a variety of animals, spanning from insects to mammals, only recently have they been analysed in terms of their network properties. The lack of a unifying framework for studying animal transportation networks results in missed opportunities. For example, although many studies have mapped ant trail networks (examples include but are not limited to [3,6–12]), only a handful have used the tools of graph theory to determine the network's topological properties and functionality (examples include but are not limited to [13–16]). Those few studies that have analysed the topology of animal networks have found that animals are able to achieve remarkably good solutions to some of the central problems of network design. In this review, we aim to bring together disparate studies on animal transportation networks by focusing on three key areas of research: network topology, network morphogenesis and the behaviour of network users. We argue that a unified approach to understanding animal transportation networks will yield fruitful results in several fields of biology.
2. Network topology
2.1. Elements of network theory
Networks are a useful way to approximate the structure and topology of animal trail, gallery and tunnel systems. In graph theory, a graph (or network) consists of a set of objects called ‘nodes’ connected to one another via edges. In order to analyse animal transportation systems using the toolbox of network analysis and graph theory, we must first choose a way to represent the system using standard graph theory notation. The simplest and most commonly used method of representing animal transportation networks consists of representing branching points, intersections and dead ends as nodes, and classifying segments of trail between two nodes as edges. This method is often described in the scientific literature as the ‘primal network mapping’ (table 1).
Table 1.
Network measures. In this table, we provide an overview of commonly used measures that have a specific relevance for describing animal transportation networks. There exist several more detailed publications on networks, such as [17], for network properties in general and [18] for spatial networks in particular.
| Network mapping |
| Primal network. The simplest way to associate a graph to a pattern of trails or galleries consists in mapping all branching points, intersections and dead-ends onto network nodes and the segments comprised between two intersections onto network edges. The network obtained in this way is often referred to as the ‘primal’ network. |
| Dual network. Studies of human transportation networks have often preferred to adopt an alternative approach often referred to in the literature as the ‘dual’ network mapping, in which an entire trail, or street, or subway line, is mapped onto a node and there is an edge whenever two trails intersect [19–21]. However, this dual mapping has found few applications to animal transportation networks so far, mainly because of the difficulty of assigning segments to the same or to a different trail across an intersection. |
| Classes of networks |
| Spatial networks. Spatial networks are networks in which the nodes are embedded in some metric space, and the probability of existence of an edge between two nodes depends on their distance in this metric space. As an example, in air transportation networks the nodes (the airports) associated with specific locations and edges (direct flights between the airports) are more frequent within certain ranges of distances. Animal transportation networks are spatial networks in which not only the nodes, but also the edges (trails, galleries) are embedded in the Euclidean space, which imposes even further constraints to network topology. |
|
Trees. A connected network that does not contain any cycles is called a tree. If a graph is a tree with N nodes and it is connected, then it has exactly N – 1 edges. As these edges can be arranged in different configurations, it is possible to connect the same set of nodes to form several different trees. All these trees are spanning trees of the set of nodes, and spanning trees that minimize or maximize particular properties are of particular interest. For instance, the minimum spanning tree is the tree in which the N – 1 edges are chosen to minimize the total length of the network. The Euclidean Steiner tree also interconnects N points with the minimal length of network, but it also allows adding intermediate extra nodes and edges. |
| Rooted networks. In a tree network, it is possible to define a special node, called the root, and assign an orientation to all network edges ‘towards’ the root, or ‘away’ from it. For instance, in a river network, the estuary can be marked as the root, so that the orientation of the edges matches the direction of the flow. It is sometimes possible to define a root also for networks that are not tree, if we can identify one node as the source or the sink of network flows. |
| Triangulations. Triangulated network are networks that connect all the nodes to form triangles (in the plane) or tetrahedra (in three dimensions). They are often used to model the network with the maximum number of edges compatible with physical constraints, for instance, the constraint of planarity for networks embedded in two dimensions. |
| Network measurements |
| Node degree. The degree of a node is the number of edges connected to it. In many social or interaction networks, the degree of a node is a proxy for the importance of the element represented by that node. One can also describe a network in term of the network-level measure of the node degree distribution, which describes the frequency distribution of all node degrees in the network. |
| Scale-free degree distribution. A network is said to have a ‘scale-free’ degree distribution (or to be ‘scale-free’) if the frequency P(k) of nodes with degree k is approximately given by P(k) ∼ k−γ. While many interaction networks have been found to be approximately scale-free, spatial networks are never scale-free and the degree of their nodes always falls within a narrow range. In planar networks, for instance, the average degree cannot be larger than six, as a consequence of Euler formula (described below). |
| Cycles are sequences of adjacent edges starting and ending at the same node, such that there are at least two non-overlapping paths between any two nodes of the same cycle. For planar networks, which is the case for all trail networks on the surface of the ground, it is often interesting to focus on faces, which are cycles that do not contain other cycles, or the smallest regions of the plane bounded by edges. The Euler formula for planar graphs states that the number of faces F (including the unbounded infinite face outside the graph) is related to the number of nodes N and edges E through the relation N – E + F = 2. |
| Robustness. Robustness can be defined as the capacity of a network to preserve connectivity as increasing fractions of edges are removed. Edge removal typically leads to the fragmentation of a network in multiple disconnected components, and robustness can be measured by the fraction of nodes remaining in the largest connected component of the network. |
The path length d(vi, vj) between the corresponding network nodes vi and vj, that is, the minimal length that an animal must traverse to navigate between vi and vj. The average path length over the entire network is defined as 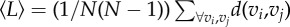 , where N is the total number of nodes. Distances can be measured either as metric distances (metric length of the shortest path) or topological distances (number of edges forming the path). , where N is the total number of nodes. Distances can be measured either as metric distances (metric length of the shortest path) or topological distances (number of edges forming the path). |
| The frequently used measure of branching order [9] is also essentially a measure of topologic path length, which counts the number of bifurcations on the path from a given network location to a root node (usually represented by a nest). Some networks can be disconnected, so that not all the destinations can be reached through the network (imagine trails on either side of a large river). When the network is disconnected, the path length between disconnected nodes is infinite and as soon as a single node is disconnected it is no longer possible to compute the average path length for the entire network. To overcome these problems, the measure of network efficiency was introduced, which is defined in a similar way to the average path length, but sums the inverse of distances 1/d(vi, vj) instead of the distances themselves. As the distance between two disconnected nodes is infinite, couples of nodes vi and vj that belong to disconnected components of the network contribute with zero to the total efficiency [22]. |
Centrality. Different network measures quantify how ‘central’ a node or an edge is with respect to the network. The node degree itself is a sort of local centrality measure. The betweenness centrality (or simply betweenness) of a node or edge v is defined as 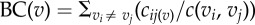 , where c(vi, vj) is the sum of all the shortest paths between the nodes vi and vj, and cij(v) is the sum of the shortest paths from vi to vj that pass through v. The random walk betweenness is identical to the previous measure, but where cij(v) and c(vi, vj) are random walk paths between vi and vj. , where c(vi, vj) is the sum of all the shortest paths between the nodes vi and vj, and cij(v) is the sum of the shortest paths from vi to vj that pass through v. The random walk betweenness is identical to the previous measure, but where cij(v) and c(vi, vj) are random walk paths between vi and vj. |
Animal transportation networks can be described as either ‘rooted’ or ‘non-rooted’. In rooted networks, the flow of resources is directed from multiple sources to a single sink. This is typically the case for foraging networks among central place foragers, where individuals repeatedly leave a home territory or nest (the sink) to exploit multiple resources (sources). By contrast, non-rooted networks have multiple sources and sinks. The food and nest networks of polydomous (multi-nest) ant species are examples of non-rooted networks, as there is no central sink and the network instead consists of many interconnected nests and food sources.
An important feature that characterizes animal transportation networks is the number and the presence of cycles (table 1). Cycles provide multiple alternative paths between destinations, and their presence is associated with the robustness of the network (table 1). A connected network that does not contain any cycles is said to be a tree. Given a set of N points or destinations (nodes), it is possible to build several different trees that connect all the destinations; all such trees are ‘spanning trees’ of the predefined set of destinations (nodes). Spanning trees that minimize or maximize particular network metrics are of special interest in the study of animal transportation networks. For instance, minimum spanning trees (figure 1d,h) minimize the total length of the network (the cumulative length of all the edges present in the network). The Euclidean Steiner tree (figure 1b,f) also interconnects N points with the minimal length of network, but it also allows for the addition of intermediate extra nodes and edges. An important quantity that characterizes transportation networks is the length of the path that an animal must traverse to navigate between two destinations. This is expressed by the network measure of ‘path length’. Intuitively, a network is more efficient if path lengths are short on average. See table 1 for precise definitions of path length and efficiency.
Figure 1.
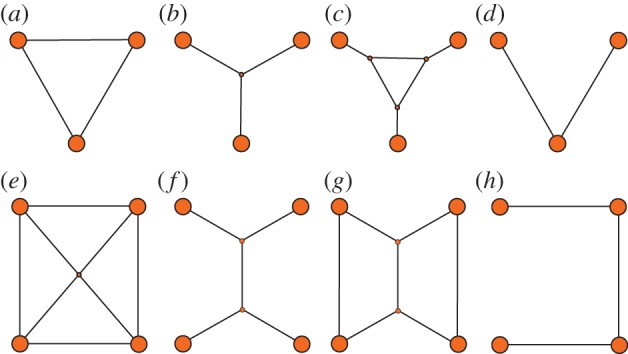
Examples of optimal networks. (a,e) Complete graphs: in these networks each pair of destinations is connected by a direct edge. These networks minimize the cost of transportation. (b,f) Euclidean Steiner tree graphs: the networks connecting the destinations with the minimum total length of infrastructure. (c,g) Intermediate networks with lower infrastructure cost than those in (a,d) and lower transportation cost than those in (b,e). (d,h) Minimum Spanning Trees. (Online version in colour.)
The individual nodes of a network are characterized by their degree, that is, the number of edges directly connected to them. The distribution of node degrees over the entire network can give clues about the overall properties of the network (table 1). For instance, many human and animal social networks, as well as other interaction networks, often have a ‘scale-free’ degree distribution, which means that they contain many nodes with low degree, but also some nodes with extremely high degree [23]. This is not the case for animal transportation networks, where the degrees of nodes are always small. This is largely a consequence of spatial constraints: it is unlikely that a large number of trails or galleries will intersect at exactly the same point. In addition, most transportation networks are built on the surface of the ground, and so are best described by planar graphs. In planar graphs, the average degree over all the nodes can never be larger than six (this is a consequence of the Euler formula for planar graphs, table 1). As node degrees lie in a relatively narrow range, the degree distribution of nodes in animal transportation networks is unlikely to be particularly informative. Nevertheless, some information can still be obtained from the comparison of the number of nodes of degree 3 and those of degree 4: nodes of degree 4 can be intersections of two trails of different animals that do not necessarily interact with each other, whereas nodes of degree 3 are bifurcations and always imply some form of interaction, in the sense that animals moving on different trails must share a common path at least on one branch of the bifurcation [24].
Any measure that quantifies how ‘central’ a node or an edge is with respect to movements across the network is called a centrality measure. The node degree itself is a local centrality measure. The betweenness centrality (table 1) of an edge measures the amount of traffic on that edge under the assumptions that (i) individuals move in similar proportions between all pairs of nodes and that (ii) they always follow the shortest path between their starting and ending destinations. This latter assumption can be relaxed, with the extremely opposite case corresponding to that of animals wandering completely at random until they find their target. This type of movement is captured by another betweenness measure, called random walk betweenness (table 1), which is identical to the previous measure, but where the movements between destinations are governed by random walks.
By carrying information on the amount of traffic on an edge, betweenness measures can, in principle, be ‘estimated’ by real animals, through the frequency of encounters with other individuals or the local density of pheromone. At the same time, high betweenness edges tend to be localized on the shorter paths through the network. This is by definition, in the case of shortest path betweenness centrality, and also occurs in the case of random walk betweenness centrality for the simple reason that it is unlikely (although not impossible) that a random walk between a source point and a destination point will become exceedingly long without reaching the destination [25]. Because of these properties, betweenness-like measures might provide local cues for the optimization of animal transportation networks, an aspect that we will discuss later in our review.
2.2. The transportation problem
Building efficient transportation networks, be that by animal groups, by cells during morphogenesis or by human engineers, always involves minimizing two different costs: the cost of transportation and the cost of infrastructure. This is the classic ‘transportation problem’, and its study can be traced back to French mathematician Gaspard Monge. Let us illustrate the problem here with an example. Suppose that you want to build a road system to exchange commodities between different cities. Independently of the number of cities, the solution that ensures fastest transportation consists of building a direct route between each pair of cities (figure 1a,e). This ‘complete’ network minimizes the path length between any two cities and ensures (all else being equal) the shortest travelling times and minimum fuel consumption. Complete networks therefore minimize the cost of transportation. However, the cost of such highly connected networks is staggeringly high since it requires the construction and maintenance of an extended road system, most of which will be underused.
The opposite solution would be to build the minimum length of roads necessary to connect all the different cities (figure 1b,f). Such networks, which correspond to the Euclidean Steiner trees defined above, minimize the cost of infrastructure. However, the distance and time necessary to move between any two cities is comparatively high, and may involve transiting through a number of non-target destinations. Thus, the ‘transportation cost’ is high. The cost of infrastructure and the cost of transportation cannot be optimized simultaneously and networks that optimize either of these criteria typically do so at the expense of the other criterion. Networks are often designed so that they provide a good balance between efficient transportation (short average path length) and low infrastructure cost (short total network length); see, for example, networks represented in figure 2c,g. These intermediate solutions are optimal if we can show that they minimize one of the two costs when fixing the other.
Figure 2.

Example of a transportation network built by animals together with two transportation networks formed in non-living systems. (a) Trail formed by a colony of Argentine ants after 60 min of exploration of an empty arena. (b) Mississippi river delta (source Nasa). (c) Electric discharge pattern in a luminglass disc. (Online version in colour.)
In rooted networks, theoretical considerations indicate that transportation and infrastructure costs are minimized when the network is a ‘tree’ (i.e. has no cycles) and has no dead ends [26]. If animal transportation networks are built to minimize either transportation and/or infrastructure costs, then we might expect the networks of central place foragers (which are rooted) to be predominantly tree-like. In agreement with these theoretical predictions, all 11 Formica aquilonia foraging networks studied by Buhl et al. [27] were trees. Studies of foraging galleries dug by termites have not specifically aimed at quantifying the prevalence of cycles, however, several studies depict patterns of foraging galleries that are tree-like (e.g. [28,29]).
For animals that forage completely underground, such as some species of termites, ants and mole rats, digging is synonymous with searching for food. From this perspective, forming a cycle is equivalent to ‘searching the same place twice’, so an efficient exploratory tunnel network should minimize the number of cycles by being tree-like. There are simple mechanisms that may allow animals to minimize the number of cycles in their transportation networks. One potential mechanism consists of initiating new galleries at angles as large as possible from each other [30]. Bardunias & Su [31] found that Coptotermes formosanus termites were able to maintain a digging direction oriented away from the point of initiation of the tunnel, a mechanism that also allows to minimize the appearance of cycles. A similar behaviour was observed when colonies encountered obstacles that forced them to change their heading.
Although some species seem to have developed theoretically optimal tree-like networks, it is important to note that cycles are frequently observed in the rooted foraging networks of both ant and termite species. Are there conditions under which cycles might increase network performance? In order to answer this question, we should recall that animal transportation networks develop in unpredictable environments, under the continuous risk of damage, and where the availability and location of resources is constantly changing. It is important that animal transportation networks remain efficient not only under ideal conditions, but also when individual connections are disrupted and traffic has to be rerouted along different paths. Theoretical arguments by Corson [32] and Katifori et al. [33] indicate that the presence of cycles in rooted transportation networks optimizes transport when the load is subjected to fluctuations (for instance, if foraging sites are repeatedly emptied and replenished), or under the risk of accidental disconnections (e.g. trails becoming impassable at times). Cycles can therefore play an important role in increasing the robustness of a transportation network (see table 1 for a definition of robustness).
2.3. Reference models of animal transportation networks
In order to determine whether a network is consistently maximizing or minimizing a particular parameter, we need to build theoretical ‘reference networks’ that fulfil the same spatial constraints as the real networks, but which are known to maximize particular network properties. Examples of reference networks include Euclidean Steiner trees (described in the previous section) and triangulations (table 1). Whereas Minimum Spanning Trees and Euclidean Steiner Trees minimize infrastructure cost at the expense of robustness, triangulations do the opposite, maximizing robustness and efficiency although with a higher cost.
Reference networks provide a basis for comparing networks; we can say, for example, that a given network achieves a solution that has 40% of the connections of a maximally connected network, or that its length is equivalent to 140% of the length of the corresponding Euclidean Steiner tree. For example, Buhl et al. [34] studied the networks of galleries excavated by ants in a two-dimensional layer of soil, and compared them with spanning and triangulated networks. They found that the gallery networks achieved a balance between the cost of infrastructure and the cost of transportation. Another way to examine the optimality of a network is to compare network performance to a random network. This allows the researcher to ascertain the extent to which a network's performance is ‘better than’ an equivalent random network. One option is to build random networks that match the number of edges of the real network (i.e. with the same cost), but have random connectivity (i.e. no optimization for efficiency). This can be done by first building a triangulated network, and then removing a fraction of edges, according to a probabilistic rule, until their number matches the one observed in the real animal-built transportation network [34,35].
Comparisons with simulated reference networks are a particularly useful tool when studying non-rooted networks. By comparing the properties of real inter-nest networks to reference networks, two laboratory studies found that Argentine ant networks were more similar to minimal spanning trees and Steiner trees than to triangulated networks, suggesting that ants minimize the cost of infrastructure at the expense of transportation [14,15]. By contrast, it seems that under field conditions, ants typically build inter-nest trail networks that balance transportation and infrastructure costs [16,27].
Reference networks can also be used to study the properties of rooted networks. For rooted networks, the cost of transportation is minimized if there is a direct, straight-line path connecting the root node to all the peripheral nodes (a ‘star network’). The cost of infrastructure is instead minimized if the network is a Steiner tree built on the root node and all the foraging sources. Buhl et al. [27,34,36] developed measures to quantify the performance of real foraging networks in comparison to reference networks with minimum cost of infrastructure (the Steiner tree) and minimum cost of transportation (the star network). Based on these two reference networks, Buhl et al. defined a ‘route (or transportation) efficiency’ and a ‘length efficiency’ metric by normalizing the efficiency and length of real networks within the extremes defined by the star network and Steiner tree. Networks with high route efficiency therefore had minimal infrastructure costs, whereas networks with high length efficiency had minimal transportation costs. Real ant networks achieved good performance in both route efficiency and length efficiency, obtaining similar values to those reported for human-built transportation networks in an earlier study by Gastner & Newman [37].
3. Network morphogenesis
In the simplest case, trails and tracks are formed as a by-product of individual animal movement, without any explicit communication or cooperation between network users. These self-organized networks arise because animals moving across space prefer to follow paths that are easier to traverse, such as areas of compacted ground or cleared vegetation. This is the case for the trail systems formed by ungulates across vegetation or snow [38]. The movement of animals contributes to soil compaction and helps to trample or remove vegetation and other obstacles, eventually making the newly formed tracks more attractive to other individuals, who are themselves seeking an easy walking surface. The increasingly compact trail becomes more and more attractive as new individuals preferentially move across it so that eventually a trail is formed. Network development is therefore an emergent process driven by the positive reinforcement generated by individuals trying to find the ‘least cost path’ through an environment [39]. The movement of human pedestrians across snow or grass can also produce trails through a similar mechanism [40,41]. We term this form of network construction ‘cue’ based construction, as individuals are attracted to a cue (a smooth path) that is produced as a by-product of another individual's movement. By contrast, some transportations networks are ‘signal-based’ where an individual (‘the sender’) produces a behaviour with the specific purpose of attracting others [42]. For example, in Argentine ants (Linepithema humile), pheromones are continually deposited as ants move through the environment, irrespective of whether or not they have discovered food [43]. Trails develop because individual ants prefer to move across areas that have pheromone rather than areas that are unmarked, and attraction to trail pheromone increases with the amount of pheromone laid [7,44].
3.1. Reinforced random walk models
Trail formation in ants and other animals has often been modelled as a reinforced random walk phenomenon. For instance, Deneubourg and co-workers proposed a model for the formation of army ant trail patterns [45] inspired by empirical observations of ant collective behaviour in a controlled experimental set-up [46]. In their model, ants moved randomly from node to node along a lattice network, but experienced a higher probability of transiting to nodes with more pheromone marking. In turn, the amount of pheromone on the nodes increased as a function of the number of ants that had previously passed through the same nodes.
Helbing et al. [40] studied a model of trail formation by ants and human pedestrians in a continuous two-dimensional space. In their model, agents move across space, and by doing so they increase the ‘ground potential’ (the attractiveness of the walking surface) at the position at which they are. The positive feedback loop is completed by the fact that individual walkers update their direction of movement based on the gradient of the ground potential produced by themselves and other individuals.
Because of the simple, self-organized nature of reinforced (random) walks, network formation by animal groups shares strong similarities with pattern-formation phenomena commonly produced in non-living systems (figure 2). From a mathematical point of view, Doyle & Snell [47] have shown that the random walk of particles or individuals along the edges of a network can be described with the same mathematical equations as those describing the flow of electric charges through an electric network, or the flow of fluids along hydraulic networks. The preference of animals for moving along the tracks already compacted by other animals has a parallel in the formation of dielectric breakdown patterns, whereby a non-conducting material increases its conductivity as a consequence of the passage of electric currents, or in the widening of a riverbed under the eroding influence of water current. Ma et al. [48] explored mathematically this analogy between trail formation phenomena and electric networks. In their model, the space is modelled as a network of wires with different conductivities, and animals move randomly along these wires with a probability that depends on the local conductivity of the edges. The positive feedback leading to the selection of a path is mediated by flow: the more electric charges/individual animals transit through an edge, the more conductivity increases along that edge.
3.2. The special case of digging
While the models described above differ from each other in many details, they all have in common the coupling between the movement of individuals and amplification mediated by trail attractiveness. In the case of underground galleries, the amplification mechanism reaches extreme proportions: as soon as a new gallery is formed, its attractiveness is immediately much higher than the attractiveness of the soil surrounding it. As a consequence, one expects that in the case of galleries, reinforcement is immediate and does not integrate information from multiple events, and the form and topology of the network is likely to reflect mainly the rules of movement of the individual random walk patterns. Consistent with this prediction, Buhl et al. could reproduce the growth and the general appearance of tunnel networks excavated by ants with a model that only implemented probabilistic rules for forming new branches with different orientations, but which lacked feedback loops [36].
3.3. Network growth
Both animal- and human-built transportation networks grow and change over time. Adding new connections to the network usually involves paying additional infrastructure costs. These are risky costs to pay, as it is usually not possible to predict what impact, if any, the added trail will have on the transportation efficiency of the original network. Human engineers and urban planners minimize these risks by collecting data and running simulations before construction begins. Similarly, animal network builders have behaviours that allow them to minimize the costs of network expansion by collecting information prior to constructing new network components. In underground burrow networks, the high cost of digging means that energy can be saved by selecting the direction of tunnel construction before actual constructing starts. Solitary mole rats (Spalax ehrenbergi) use ‘seismic echolocation’ to determine the shortest digging path around an obstacle [49,50]. Zambian mole rats use olfactory cues to orient their digging activity in the direction of potential food sources [51]. Furthermore, the cost of digging can also be reduced by concentrating digging activity at periods when the soil is easier to dig, such as when it is damp after a rain [39,52]. This situation, in which network construction and transportation take place in discontinuous bursts of activity, is common for animals living in arid environments. The cost of building a foraging network in arid environments is larger throughout most of the year than the expected returns in terms of food collected; the best strategy is to simply postpone network construction until digging conditions become favourable again (reviewed in [53]).
3.4. Pruning
In contrast to burrow systems, where digging a new tunnel involves a high energetic investment, animals moving on the surface of the ground may pay relatively low construction costs. Indeed, some species (e.g. Argentine ants Linepithema humile) are continuously laying trail pheromone [43], a process which, if left unchecked, would result in an overly complex transportation network containing many redundant trails with no coherent organization. In this case, network morphogenesis is dominated by reinforcement and pruning of already formed trails.
Pruning phenomena, in which branches of a transportation network are progressively abandoned, are common events in the formation of animal transportation networks. Pruning processes theoretically allow new trails to ‘prove their usefulness’ for transportation, and therefore allow groups to selectively remove poorly performing links. In Argentine ants, long meandering trails tend to be abandoned, while short, more direct trails are retained [46]. Pruning strategies have also been observed within some termite nests, where less central connections seem to be progressively abandoned, and eventually closed with pellets, resulting in the selection of networks characterized by a small number of highly efficient communication routes [35]. Often network formation involves both a growth phase, characterized by the appearance of multiple trails and a simplification phase in which a fraction of the formed trails are pruned away [7,14].
Interestingly, pruning phenomena are also observed in the morphogenesis of transportation networks at different levels of biological organization, including mammalian vascular networks [54], the mycelial networks of saprophytic fungi [55] and the pseudopod networks of slime moulds [56]. Pruning appears to be a widespread mechanism by which biological transportation networks are formed and optimized.
3.5. Network maintenance
Even the best transportation network will deteriorate over time if it is not maintained. Investing in road maintenance, although it involves short-term costs, can prevent the often large long-term cost of reconstructing a severely decayed network. Delayed infrastructure maintenance can also result in increased losses during transportation. In army ants (Eciton burchellii), gaps and spaces in the substrate are plugged by live ants who serve as ‘pot hole’ plugs [57]. Amazingly, individual pluggers carefully match their own size to the size of hole, and individuals cooperate to close larger holes [57]. Calculations suggest that plugging behaviour results in an increased resource-harvesting rate, by facilitating the rapid movement of food-laden foragers.
In ants, trail maintenance is often conducted by a specialized subset of the workforce. For example, leafcutter ants (Atta columbica) involved in trail-clearing have larger than average head widths, suggesting that they belong to a distinct morphological caste [58]. Although maintenance has largely been studied in ant species that make physical trails, the fact that pheromones generally evaporate over time means that pheromone trails are also in need of periodic maintenance. In pharaoh ants (Monomorium pharaonis), individual ants make frequent u-turns which serve to maintain trail quality by increasing the rate of pheromone deposition [59]. In leafcutter ants, the smallest caste (‘minims’) also perform frequent u-turns [60]. When a trail is interrupted, the number of minims on the trail increases, suggesting that these individuals play a specialized role in pheromone trail repair. In mole rats, larger workers tend to do a greater amount of burrow maintenance than do smaller workers, possibly because, as a consequence of their body size, they are better able to handle the metabolic costs of digging [61].
3.6. Cost of infrastructure and social behaviour
While efficient transportation infrastructures can ‘emerge’ simply because individuals follow each other's trails in the attempt to minimize their immediate transportation costs, when network morphogenesis is ‘signal-based’, animals directly invest time and energy in building their transportation networks. Most species of Microtus voles, for example, actively construct above ground ‘runway’ systems, which they clear by cutting vegetation [62]. Social caterpillars leave both pheromone and silk threads which are followed by other caterpillars [63], and which collectively create a foraging network used to connect the caterpillars' nest to food sources [64]. When founding new colonies, female spider mites leave silk trails which are attractive to other females [65], and which temporarily link founding colonies to new colonies.
The costs of network formation can be relatively high compared with the energy budget of the animal. Mikheyev & Tschinkel [66] estimated that subterranean colonies of the ant Formica pallidefulva invest up to 20% of their yearly energy budget on digging the galleries that form their transportation network. Vleck [67] estimated that for a small rodent such as Botta's pocket gopher (Thomomys bottae), the cost of digging underground burrows was 360–3400 times greater than the cost of moving the same distance on the surface (depending on soil conditions). The construction of above-ground networks can also entail significant costs. Several species of ant, including the meat ant (Iridomyrmex purpureus) and leaf-cutting ant (Atta and Acromyrmex spp.) actively clear their trails of fallen debris (reviewed in [68]). Howard [58] estimated that the total annual cost of trail maintenance in leafcutter ants was 11 000 ant hours or the energy equivalent of carrying 8000 leaf burdens. However, while the absolute cost of trail maintenance may seem high, the colonies investment was relatively low considering the number of available workers [58], and the potential benefit of clearing, which can reduce travel times by up to 10-fold (Johnson and Hubbell, unpublished, cited in [69]).
Even though the costs associated with building and maintaining signal-based transportation network are not always high, they are crucially different from the costs incurred by animals simply following the least cost path (cue-based networks) in that there is no immediate reward for the individuals involved in network construction. This raises the question: why should an individual spend energy building or maintaining a trail, instead of exploiting trails built by others? Perhaps unsurprisingly, signal-based networks are almost exclusively built by highly social species, where the benefits of collective resource exploitation presumably outweigh the cost of active network construction. Indeed, it has been suggested that the high level of sociality developed by some species of mole rats would have been enforced by the necessity of sharing the costs of digging large foraging networks of galleries (reviewed in [34]). There are, however, some reports of individuals ‘free loading’ by exploiting the established transportation networks of others. Several species of small mammal, for example, use the runway systems constructed by voles [4,70] though they do not contribute to network clearing or maintenance [62].
3.7. Decentralized optimization
Unlike many human-designed networks, animal transportation networks face the challenge of achieving efficient transportation in the absence of centralized control. The problem of network design is compounded by the fact that the individuals involved in network construction often have limited information about the properties of the network as a whole. The perceptual range of individual animals is relatively limited when compared against the size of their transportation networks. For instance, the networks of galleries inside an adult nest of the leafcutter ant Atta levigata consist of up to 7800 chambers [71]. In such large networks, it is unlikely that any single individual has a global view of the overall organization of the transportation network as a whole. For instance, no individual will likely know the size of the network, or how many individuals are in the colony. These are ‘extensive properties’ that scale with the size of the system: as the system becomes large compared with the size of an individual, no single individual can assess them directly. However, individuals can get information about the properties of the network by using the ratio between two extensive properties: these ratios are intensive properties that can be assessed on a local basis [72]. For example, the ratio between the number of individuals and the size of a nest is the average density. Many insect societies use density as a signal to regulate the size of their nest. Individuals that experience a high local density of neighbours are induced to perform actions, such as digging new chambers, with the result that the size of the nest matches the space requirements of the entire colony (e.g. [73,74]). Traffic is another intensive property that corresponds to the ratio between the number of individuals walking on a path, and the length of the path itself. Traffic can be signalled by pheromone concentration, direct encounters with other trail users or from the characteristics of the trail, and corresponds to the network measure of betweenness centrality introduced above.
As the traffic along an edge is proportional to its betweenness centrality, improving the conductivity of edges with high betweenness results in reduced travelling times along the many paths between various destinations that transit across high betweenness edges. Knowing the rate of traffic over a particular section of trail can help animals perform local adjustments to network topology which affect network performance at the global scale. The reinforcement mechanism used by Ma et al. [48] to model the formation of biological transportation networks is also essentially an amplification mechanism based on random walk betweenness.
4. User behaviour
4.1. Route selection and traffic control
In human networks, it has long been recognized that the behaviour of network users can have profound (and sometimes unexpected) effects on network efficiency. This fact is illustrated beautifully by ‘Braess's paradox’ [75,76]. Imagine a road network populated by drivers trying to reach their destination using the shortest path. Since roads have become congested, engineers decide to increase network capacity by adding an extra super-fast road. Intuitively, we might predict that such an action would decrease congestion along the network, however, the opposite occurs: adding an extra link can actually increase individual travel times. This counterintuitive finding results from the selfish behaviour of drivers; upon learning of a new, super-fast route, the majority of drivers choose the new route over the older route, resulting in increased congestion.
Similar to human drivers, animals travelling along a transportation network must make choices about which route to take. In a classic experiment, Dussutour et al. [77] forced ants (Laisius niger) to move across a diamond-shaped bridge linking their nest to a food source. When ant densities were low, the ants exploited a single branch, but as densities rose, the ants began exploiting the second branch. This switch from asymmetrical to symmetrical path use allowed ants to maintain an optimal flow rate despite greatly increased traffic. The mechanism allowing the optimal distribution of traffic appears to be driven by head-on collisions or ‘pushes’ from nestbound ants which redirect food-bound ants towards the second branch when densities are high [77]. This multidirectional flow contrasts sharply with the segregation into discrete one-dimensional lanes observed in army ants, where inbound foragers carrying food occupy the centre of the foraging column, while outgoing, un-laden ants move along the flanks [78]. A similar three-lane arrangement is observed in termites, and to a lesser degree in several species of leafcutter ants and wood ants (reviewed in [79]). By segregating traffic into lanes, ants can increase the capacity of trails by reducing the number of time-consuming head-on collisions.
The behaviour of trail users can have a significant impact on the efficiency of a trail network. In several ant species, the task of harvesting is divided such that larger ants cut vegetation fragments, while smaller ants carry the fragments back to the nest [80,81]. On larger trails, carrying is divided between two and five carrier ants, each of which carries the fragment a short distance and then deposits it for another ant to carry [80]. There are two main hypotheses explaining the adaptive value of these ‘bucket brigades’ or ‘transfer chains’. The ‘speedy leaf’ hypothesis suggests that bucket brigades increase transport speed because slow-moving ants are more likely to relinquish their load to faster moving ants [82]. The speed of ants before transfer tends to be lower than the post-transfer speed, suggesting that ants do indeed pass their loads on to faster moving ants. However, fragments transported by one ant directly from the nest took longer to arrive than did fragments transported by multiple ants. Thus, evidence in favour of the speedy leaf hypothesis is equivocal. The second hypothesis, known as the ‘information-transfer hypothesis’ proposes that bucket brigades act to increase information-transfer across trail networks, leading to a more rapid build-up of foragers at resources [80]. By dropping fragments along the trail, there is an increased chance that un-informed workers will become aware of the resource, either through contacts with load-carrying nest-mates, or by contact with the fragment itself. In addition, dropping their fragment allows foragers to run back to the resource and continue foraging, thereby increasing the rate at which the pheromone trail is reinforced, presumably leading to a stronger trail and increased recruitment. Support for the information-transfer hypothesis comes from a study by Röschard & Rosces [83], which found that ants were more likely to drop high-quality fragments.
4.2. Orientation
Transportation networks have a profound impact on the orientation mechanisms used by animals. On the one hand, trails and galleries constitute ‘a map of actual size’ that channels the movement of the animals directly to relevant destinations. Among the advantages of moving on a trail network is that the animal need not have a complete representation of space, but can instead memorize a list of salient points. The only points where navigational decisions need to be taken are at trail junctions and bifurcations, with the complexity of decision increasing with the number of branches at the junction [84].
Animals navigating through a network can further simplify these decisions by exploiting a number of cues. One study suggests that ants discriminate between nestbound and outbound trails based on the bifurcation geometry [85]. For most species, the simple tendency of ants to move in a straight direction, in the presence of asymmetric bifurcations, would be sufficient to maintain their orientation towards or away from the nest [86–89]. In ant foraging trails, the traffic originating from the nest splits across the two branches of a bifurcation. As a consequence, the traffic on the distal branches is always less intense than on the segment of trail closer to the nest. Individuals could potentially use this difference in traffic intensity to discriminate nestbound from outbound trails. Head-on encounters with other individuals moving on the trail can also provide direct information, for instance, by sensing if encountered individuals are carrying food (and are therefore nestbound) [90].
On the other hand, direction-based navigation (such as following a magnetic compass, for example) can be more difficult when moving on a trail network, for instance when none of the available trails matches the desired direction of movement. Some animals can opportunistically shift from moving freely across the substrate, when directional cues are available, to following the trail network when these same cues are absent, or are difficult to decipher. The slug Limax pseudoflavus follows air-borne chemical cues carried by the wind to find its resting sites, but when the wind direction changes and these cues become unavailable, it begins to orient by following slime trails [91,92]. The common vole (Microtus arvalis) marks its movement trails with olfactory cues (scent marks) [93]. However, when visual orientation cues are present, it ignores the olfactory trails and prefers to travel directly towards its goal, suggesting that direction-based navigation is prioritized over following chemical trails [93].
Animals might be adopting heuristic strategies as they move across their transportation network in search of targets: instead of abandoning the network when environmental cues become available, they can stay on the network, but prioritize at every junction the direction that better matches the direction indicated by their internal compass. Reid et al. [94] set up an experiment with ants moving in a complex artificial network of bridges whose topology was dynamically changed during the experiment. In response to these changes, real ants were capable of quickly adjusting their trails to the new maze configuration. Ramsch et al. [95] found in simulations that the ant's ability to rapidly adjust their trails could be explained by a model in which ants combined pheromone based navigation and directional information.
Different animals are sensitive to a variety of environmental cues and can use these cues to navigate through their network. Several species of subterranean rodent, for example, use the Earth's magnetic field to navigate through their burrow networks [96,97]. Ants and termites can sense gravity [98,99], gradients of gas concentrations [100] and temperature [101], and can use these cues to orient themselves. The Earth's magnetic field [102] and visual landmarks (for an example, see [103]) also provide cues for navigation. Often, the same cues used for network navigation also act as templates during network construction. Wind direction, for example, plays a role in determining the form of spatial structures built by ants, simply because ants are less likely to pick-up, and more likely to drop their loads downwind of the pile [28]. The nests of the termite species Amitermes meridionalis have a characteristic elongated shape oriented along a north–south direction with the Earth's magnetic field [104], which is likely reflected in the orientation of galleries internal to the nest.
The effects of environmental factors on network building behaviour potentially allow for mutual adaptations of network configuration and the prevailing navigation strategy of a species. For instance, if an animal can detect the north–south direction with its internal compass, it will find it easier to follow the desired path across a bifurcation if the branches of the bifurcation are oriented along the same north–south axis.
5. Prospectus
Self-organization phenomena play a large role in shaping the morphology and topology of animal transportation networks. The similarity between trail networks and physical systems such as streams (figure 2) begs an important question: to what extent are network properties the result of natural selection versus being the emergent result of simple physical rules? When confronted with Argentine ant networks that approximate Steiner trees [14], it is tempting to conclude that evolution has shaped ant behaviour in such a way as to minimize the costs of network construction. However, soap films can also produce Steiner trees [105], and oil droplets can follow chemical gradients to find the shortest path through a maze [106]. These examples remind us that seemingly ‘optimal behaviours’ can occur even in the absence of natural selection. Teasing apart the relative roles that adaptation, physical constraints and emergent behaviour play in determining the properties of networks is an on-going challenge. Future theoretical studies are needed to compare in greater detail models of network morphogenesis across the physical and biological domain, and to define the minimal conditions sufficient to reproduce realistic-looking networks. Experimental studies should aim at identifying the specific adaptations and modulations of individual-level behaviour underlying network construction in different animal species and under different environmental constraints. It will be particularly interesting to find examples of animal transportation networks for which the biological optimum cannot be achieved from simple ‘physical’ energy minimization, but requires specific regulations, which represent real biological adaptations. The study of animal transportation networks would also benefit from a comparison with other biological transportation networks, such as vascular and neural networks, for instance, because in this case the nature of the interactions that underlie network construction is different (e.g. cell to cell signalling and morphogenetic gradients versus animal interactions), but the biological function is similar (e.g. transporting nutrients or information).
The distinction between cue-based and signal-based network formation puts the focus on the symmetric relationship between investment in network infrastructure and ‘altruistic’ behaviour. If highly social animals invest in network infrastructure for the other members of the group, and non-social animals do not, it will be particularly interesting to see characterizations of the transportation networks produced by animals with intermediate levels of sociality. Gastropods are an interesting group in this respect, because they face a high cost of network infrastructure (the cost of mucus production; e.g. [107]) and their networks mediate a number of collective behaviours, such as individual aggregations and mate location [108]. Mammals, which can exhibit different degrees of social behaviour, are also interesting with respect to relating network costs and sociality. Their trails can be highly conspicuous and represent an excellent opportunity to study the topology and use of animal transportation networks, as do the runway systems of small mammals such as voles.
The topological characterizations of transportation networks, in particular of social insects, have often driven researchers to the conclusion that animal transportation networks are extremely efficient when compared with random models. This has clearly generated a lot of initial excitement, because of the apparent contrast with the unplanned, self-organized formation of these networks. However, the study of the topology and geometry of animal networks has the potentiality to provide us with much more information, not only on ‘how good’ a particular network is, but also on which features the network is optimizing at the expense of other features. For example, we might expect that species building networks in places where the costs of construction are high (say, due to the type of substrate) will minimize cost by reducing trail length. By contrast, species working in environments where trail damage occurs with a high probability should build networks that emphasize robustness. Such differences in network configuration could be genetically determined and species-specific, or groups could instead respond dynamically to factors such as changes in traffic, changes in resource locations/density/distribution, changes in colony size (in the case of social organisms) or the presence of predators or competitors (see [53,109,110]).
Another aspect that is missing from existing characterizations of network topology is the quantification of network efficiency and/or robustness in relation to direct measures of the actual network use. To give an example, if all the traffic through a network is concentrated between two or three major destinations, then the optimal network will be one that favours communication between these particular destinations, and not across all paths in general, as would be predicted in the absence of information about the ‘importance’ of each destination.
As tracking technologies are progressively improved, it becomes possible to collect increasing amounts of data on the movement of individual animals in their natural environment. For instance, PIT tags have been successfully used to monitor traffic in vole runway systems [111] and GPS tracking helps to collect movement data on progressively smaller animals (reviewed in [112]). This kind of data has traditionally been used to understand interactions of animals with the environment (e.g. home range studies (e.g. [113])). In parallel, literature on ‘collective motion’ has aimed at characterizing the inter-individual interactions that mediate group movement [114,115]. The current challenge is to understand the simultaneous effects of interactions with neighbours and interactions with the environment (e.g. [116]). Transportation networks are the physical materialization of simultaneous interactions between an individual, its environment and other animals, and as such deserve a key role in this new field of scientific research.
Animal trails can facilitate inter-species interactions by bringing individuals into contact with one another. Several predators are known to follow the trail systems of ants in order to locate nests [117], and predatory snails follow the trails of prey species [118]. By mediating interactions between individuals, transportation networks can have substantial impacts on ecological interactions such as predation, herbivory and competition. Leafcutter ants (Atta sp.), for example, are key herbivores in Neotropical ecosystems and their distribution (and resultant effect on vegetation) is determined by their extensive trail networks [109]. Having an efficient trail network can give some species a competitive upper hand: indeed, the ability to rapidly mobilize and distribute their foraging force has been cited as a common characteristic of invasive ant species [119]. Thus, transportation networks have the potential to influence the structure of ecological communities by mediating interactions between conspecifics, competitors and predators.
In addition to ecological interactions across species, transportation networks are also likely to influence the role of individuals within their group. In ants, for instance, it had been hypothesized that division of labour and task specialization might be a direct consequence of the spatial positions that individuals occupy inside the nest, and of the tasks that become available at their locations [120,121]. Recent studies have mapped the ‘social network’ of ant colonies (the networks of spatial encounters between individuals), to find that the ‘social’ associations of an individual closely matched its pattern of occupation of space [122,123]. The social structure of groups of vertebrates may be more complex than that of ants, but we should remember that in this case as well, the spatial association of individuals is the first pre-requisite before stronger social bonds are formed [120], and spatial associations are largely determined by the way in which animals use their transportation network and by the properties of the transportation network itself. For example, it has been suggested that the greater complexity of the burrows of communally nesting voles Microtus ochrogaster (relative to the systems built by mating pairs) might explain why these groups can tolerate multiple reproductive individuals within the communal group [124].
We are in an exciting stage for research on animal transportation networks, in which many scientific questions are ripe for the answering. Mathematical network analysis provides a sufficient level of abstraction to measure and to compare the transportation networks formed by different animal groups, and helps us to formulate increasingly more precise predictions about how these networks are formed and their biological significance. In parallel, the recent advances in tracking technologies allow for the collection of movement data of unprecedented accuracy, making it possible to test theoretical predictions. In the coming years, we will learn a lot more about how transportation networks are built and used by different animals.
Funding statement
This work was funded by Australian Research Council Discovery grants to T.L. (DP140103643 and DP110102998), and by a Society in Science–Branco Weiss fellowship to T.L. A.P. acknowledges the Japanese–Swedish Cooperative Program on Multidisciplinary BIO from the Swedish Foundation for Strategic Research and the ‘Research in Paris’ Program for funding.
References
- 1.Crête M, Larivière S. 2003. Estimating the costs of locomotion in snow for coyotes. Can. J. Zool. 81, 1808–1814. ( 10.1139/z03-182) [DOI] [Google Scholar]
- 2.Davies MS, Blackwell J. 2007. Energy saving through trail following in a marine snail. Proc. R. Soc. B 274, 1233–1236. ( 10.1098/rspb.2007.0046) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Shepherd JD. 1982. Trunk trails and the searching strategy of a leaf-cutter ant, Atta colombica. Behav. Ecol. Sociobiol. 11, 77–84. ( 10.1007/BF00300095) [DOI] [Google Scholar]
- 4.Pearson OP. 1959. A traffic survey of Microtus-Reithrodontomys runways. J. Mammal. 40, 169–180. ( 10.2307/1376431) [DOI] [Google Scholar]
- 5.Šumbera R, Chitaukali WN, Elichová M, Kubová J, Burda H. 2004. Microclimatic stability in burrows of an Afrotropical solitary bathyergid rodent, the silvery mole-rat (Heliophobius argenteocinereus). J. Zool. 263, 409–416. ( 10.1017/S095283690400545X) [DOI] [Google Scholar]
- 6.Skinner GJ. 1980. Territory, trail structure and activity patterns in the wood-ant, Formica rufa (Hymenoptera: Formicidae) in Limestone Woodland in North-West England. J. Anim. Ecol. 49, 381–394. ( 10.2307/4253) [DOI] [Google Scholar]
- 7.Deneubourg JL, Aron S, Goss S, Pasteels JM. 1990. The self-organizing exploratory pattern of the argentine ant. J. Insect Behav. 3, 159–168. ( 10.1007/BF01417909) [DOI] [Google Scholar]
- 8.Ganeshaiah KN, Veena T. 1991. Topology of the foraging trails of Leptogenys processionalis—why are they branched? Behav. Ecol. Sociobiol. 29, 263–270. ( 10.1007/BF00163983) [DOI] [Google Scholar]
- 9.Lopez F, Acosta FJ, Serrano JM. 1994. Guerilla vs. phalanx strategies of resource capture: growth and structural plasticity in the trunk trail system of the harvester ant Messor barbarus. J. Anim. Ecol. 63, 127–138. ( 10.2307/5589) [DOI] [Google Scholar]
- 10.McIver JD. 1991. Dispersed central place foraging in Australian meat ants. Insectes Sociaux 38, 129–137. ( 10.1007/BF01240963) [DOI] [Google Scholar]
- 11.van Wilgenburg E, Elgar M. 2007. Colony structure and spatial distribution of food resources in the polydomous meat ant Iridomyrmex purpureus. Insectes Sociaux 54, 5–10. ( 10.1007/s00040-007-0903-3) [DOI] [Google Scholar]
- 12.Heller N, Ingram K, Gordon D. 2008. Nest connectivity and colony structure in unicolonial Argentine ants. Insectes Sociaux 55, 397–403. ( 10.1007/s00040-008-1019-0) [DOI] [Google Scholar]
- 13.Buhl J, Sword GA, Clissold FJ, Simpson SJ. 2010. Group structure in locust migratory bands. Behav. Ecol. Sociobiol. 65, 265–273. ( 10.1007/s00265-010-1041-x) [DOI] [Google Scholar]
- 14.Latty T, Ramsch K, Ito K, Nakagaki T, Sumpter DJT, Middendorf M, Beekman M. 2011. Structure and formation of ant transportation networks. J. R. Soc. Interface 8, 1298–1306. ( 10.1098/rsif.2010.0612) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Aron S, Deneubourg JL, Goss S, Pasteels JM. 1990. Functional self-organization illustrated by inter-nest traffic in ants: the case of the argentine ant. In Biological motion, vol. 89, pp. 533–547. Lecture notes in biomathematics Berlin, Germany: Springer. [Google Scholar]
- 16.Cook Z, Franks D, Robinson EH. 2014. Efficiency and robustness of ant colony transportation networks. Behav. Ecol. Sociobiol. 68, 509–517. ( 10.1007/s00265-013-1665-8) [DOI] [Google Scholar]
- 17.Newman M. 2010. Networks: an introduction. Oxford, UK: Oxford University Press. [Google Scholar]
- 18.Barthélemy M. 2011. Spatial networks. Phys. Rep. 499, 1–101. ( 10.1016/j.physrep.2010.11.002) [DOI] [Google Scholar]
- 19.Jiang B, Claramunt C. 2004. Topological analysis of urban street networks. Environ. Plann. B 31, 151–162. ( 10.1068/b306) [DOI] [Google Scholar]
- 20.Porta S, Crucitti P, Latora V. 2006. The network analysis of urban streets: a dual approach. Physica A 369, 853–856. ( 10.1016/j.physa.2005.12.063) [DOI] [Google Scholar]
- 21.Perna A, Kuntz P, Douady S. 2011. Characterization of spatial networklike patterns from junction geometry. Phys. Rev. E 83, 066106 ( 10.1103/PhysRevE.83.066106) [DOI] [PubMed] [Google Scholar]
- 22.Latora V, Marchiori M. 2001. Efficient behavior of small-world networks. Phys. Rev. Lett. 87, 198 701 ( 10.1103/PhysRevLett.87.198701) [DOI] [PubMed] [Google Scholar]
- 23.Barabási A-L, Albert R. 1999. Emergence of scaling in random networks. Science 286, 509–512. ( 10.1126/science.286.5439.509) [DOI] [PubMed] [Google Scholar]
- 24.Jamon M. 1994. An analysis of trail-following behaviour in the wood mouse, Apodemus sylvaticus. Anim. Behav. 47, 1127–1134. ( 10.1006/anbe.1994.1151) [DOI] [Google Scholar]
- 25.Newman MEJ. 2005. A measure of betweenness centrality based on random walks. Soc. Netw. 27, 39–54. ( 10.1016/j.socnet.2004.11.009) [DOI] [Google Scholar]
- 26.Durand M. 2007. Structure of optimal transport networks subject to a global constraint. Phys. Rev. Lett. 98, 088701 ( 10.1103/PhysRevLett.98.088701) [DOI] [PubMed] [Google Scholar]
- 27.Buhl J, Hicks K, Miller E, Persey S, Alinvi O, Sumpter D. 2009. Shape and efficiency of wood ant foraging networks. Behav. Ecol. Sociobiol. 63, 451–460. ( 10.1007/s00265-008-0680-7) [DOI] [Google Scholar]
- 28.Jost C, Verret J, Casellas E, Gautrais J, Challet M, Lluc J, Blanco S, Clifton MJ, Theraulaz G. 2007. The interplay between a self-organized process and an environmental template: corpse clustering under the influence of air currents in ants. J. R. Soc. Interface 4, 107–116. ( 10.1098/rsif.2006.0156) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Nobre T, Nunes L, Bignell DE. 2007. Tunnel geometry of the subterranean termite Reticulitermes grassei (Isoptera: Rhinotermitidae) in response to sand bulk density and the presence of food. Insect Sci. 14, 511–518. ( 10.1111/j.1744-7917.2007.00180.x) [DOI] [Google Scholar]
- 30.Robson SK, Lesniak MG, Kothandapani RV, Traniello JFA, Thorne BL, Fourcassié V. 1995. Nonrandom search geometry in subterranean termites. Naturwissenschaften 82, 526–528. ( 10.1007/BF01134490) [DOI] [Google Scholar]
- 31.Bardunias P, Su N-Y. 2009. Dead reckoning in tunnel propagation of the formosan subterranean termite (Isoptera: Rhinotermitidae). Ann. Entomol. Soc. Am. 102, 158–165. ( 10.1603/008.102.0118) [DOI] [Google Scholar]
- 32.Corson F. 2010. Fluctuations and redundancy in optimal transport networks. Phys. Rev. Lett. 104, 048703 ( 10.1103/PhysRevLett.104.048703) [DOI] [PubMed] [Google Scholar]
- 33.Katifori E, Szöllősi GJ, Magnasco MO. 2010. Damage and fluctuations induce loops in optimal transport networks. Phys. Rev. Lett. 104, 048704 ( 10.1103/PhysRevLett.104.048704) [DOI] [PubMed] [Google Scholar]
- 34.Buhl J, Gautrais J, Solé RV, Kuntz P, Valverde S, Deneubourg JL, Theraulaz G. 2004. Efficiency and robustness in ant networks of galleries. Eur. Phys. J. B 42, 123–129. ( 10.1140/epjb/e2004-00364-9) [DOI] [Google Scholar]
- 35.Perna A, Valverde S, Gautrais J, Jost C, Solé R, Kuntz P, Theraulaz G. 2008. Topological efficiency in three-dimensional gallery networks of termite nests. Physica A 387, 6235–6244. ( 10.1016/j.physa.2008.07.019) [DOI] [Google Scholar]
- 36.Buhl J, Gautrais J, Deneubourg JL, Kuntz P, Theraulaz G. 2006. The growth and form of tunnelling networks in ants. J. Theoret. Biol. 243, 287–298. ( 10.1016/j.jtbi.2006.06.018) [DOI] [PubMed] [Google Scholar]
- 37.Gastner MT, Newman MEJ. 2006. The spatial structure of networks. Eur. Phys. J. B 49, 247–252. ( 10.1140/epjb/e2006-00046-8) [DOI] [Google Scholar]
- 38.Newmark WD, Rickart EA. 2012. High-use movement pathways and habitat selection by ungulates. Mamm. Biol. 77, 293–298. ( 10.1016/j.mambio.2012.03.007) [DOI] [Google Scholar]
- 39.Lovegrove BG. 1989. The cost of burrowing by the social mole rats (Bathyergidae) Cryptomys damarensis and Heterocephalus glaber: the role of soil moisture. Physiol. Zool. 62, 449–469. [Google Scholar]
- 40.Helbing D, Schweitzer F, Keltsch J, Molnár P. 1997. Active walker models for the formation of human and animal trail systems. Phys. Rev. E 56, 2527–2539. ( 10.1103/PhysRevE.56.2527) [DOI] [Google Scholar]
- 41.Helbing D, Keltsch J, Molnár P. 1997. Modelling the evolution of human trail systems. Nature 388, 47–50. ( 10.1038/40353) [DOI] [PubMed] [Google Scholar]
- 42.Camazine S, Deneubourg J, Franks N, Sneyd J, Theraulaz G, Bonabeau E. 2003. Self-organization in biological systems. Princeton, NJ: Princeton University Press. [Google Scholar]
- 43.Aron S, Pasteels JM, Deneubourg JL. 1989. Trail-laying behaviour during exploratory recruitment in the Argentine ant, Iridomyrmex humilis (Mayr). Biol. Behav. 14, 207–217. [Google Scholar]
- 44.Perna A, Granovskiy B, Garnier S, Nicolis SC, Labédan M, Theraulaz G, Fourcassié V, Sumpter DJT. 2012. Individual rules for trail pattern formation in Argentine ants (Linepithema humile). PLoS Comput. Biol. 8, e1002592 ( 10.1371/journal.pcbi.1002592) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Deneubourg J, Goss S, Franks N, Pasteels J. 1989. The blind leading the blind: modeling chemically mediated army ant raid patterns. J. Insect Behav. 2, 719–725. ( 10.1007/BF01065789) [DOI] [Google Scholar]
- 46.Goss S, Aron S, Deneubourg J, Pasteels J. 1989. Self-organized shortcuts in the Argentine ant. Naturwissenschaften 76, 579–581. ( 10.1007/BF00462870) [DOI] [Google Scholar]
- 47.Doyle P, Snell L. 1984. Random walks and electrical networks (Carus mathematical monographs). Washington, DC: The Math Assoc. America. [Google Scholar]
- 48.Ma Q, Johansson A, Tero A, Nakagaki T, Sumpter DJT. 2013. Current-reinforced random walks for constructing transport networks. J. R. Soc. Interface 10, 20120864 ( 10.1098/rsif.2012.0864) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Kimchi T, Terkel J. 2003. Mole rats (Spalax ehrenbergi) select bypass burrowing strategies in accordance with obstacle size. Naturwissenschaften 90, 36–39. [DOI] [PubMed] [Google Scholar]
- 50.Kimchi T, Reshef M, Terkel J. 2005. Evidence for the use of reflected self-generated seismic waves for spatial orientation in a blind subterranean mammal. J. Exp. Biol. 208, 647–659. ( 10.1242/jeb.01396) [DOI] [PubMed] [Google Scholar]
- 51.Lange S, Neumann B, Hagemeyer P, Burda H. 2005. The smell of carrots: kairomone-guided food location in subterranean Zambian mole-rats (Cryptomys spp., Bathyergidae). Folia Zool. 54, 263–268. [Google Scholar]
- 52.Sichilima AM, Bennett NC, Faulkes CG, Le Comber SC. 2008. Evolution of African mole-rat sociality: burrow architecture, rainfall and foraging in colonies of the cooperatively breeding Fukomys mechowii. J. Zool. 275, 276–282. ( 10.1111/j.1469-7998.2008.00439.x) [DOI] [Google Scholar]
- 53.Gordon DM. 2014. The ecology of collective behavior. PLoS Biol. 12, e1001805 ( 10.1371/journal.pbio.1001805) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Udan RS, Culver JC, Dickinson ME. 2012. Understanding vascular development. Wiley Interdisc. Rev. Dev. Biol. 2, 327–346. ( 10.1002/wdev.91) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Heaton L, Obara B, Grau V, Jones N, Nakagaki T, Boddy L, Fricker MD. 2012. Analysis of fungal networks. Fungal Biol. Rev. 26, 12–29. ( 10.1016/j.fbr.2012.02.001) [DOI] [Google Scholar]
- 56.Nakagaki T, Kobayashi R, Nishiura Y, Ueda T. 2004. Obtaining multiple separate food sources: behavioural intelligence in the Physarum plasmodium. Proc. R. Soc. Lond. B 271, 2305–2310. ( 10.1098/rspb.2004.2856) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Powell S, Franks NR. 2007. How a few help all: living pothole plugs speed prey delivery in the army ant, Eciton burchellii. Anim. Behav. 73, 1067–1076. ( 10.1016/j.anbehav.2006.11.005) [DOI] [Google Scholar]
- 58.Howard JJ. 2001. Costs of trail construction and maintenance in the leaf-cutting ant Atta columbica. Behav. Ecol. Sociobiol. 49, 348–356. ( 10.1007/s002650000314) [DOI] [Google Scholar]
- 59.Hart A, Jackson DE. 2006. U-turns on ant pheromone trails. Curr. Biol. 16, R42–R43. ( 10.1016/j.cub.2006.01.015) [DOI] [PubMed] [Google Scholar]
- 60.Evison SE, Hart AG, Jackson DE. 2008. Minor workers have a major role in the maintenance of leafcutter ant pheromone trails. Anim. Behav. 75, 963–969. ( 10.1016/j.anbehav.2007.07.013) [DOI] [Google Scholar]
- 61.Gaylard A, Harrison Y, Bennett NC. 1998. Temporal changes in the social structure of a captive colony of the Damaraland mole-rat, Cryptomys damarensis: the relationship of sex and age to dominance and burrow-maintenance activity. J. Zool. 244, 313–321. ( 10.1111/j.1469-7998.1998.tb00035.x) [DOI] [Google Scholar]
- 62.Cook WM, Anderson RM, Schweiger EW. 2004. Is the matrix really inhospitable? Vole runway distribution in an experimentally fragmented landscape. Oikos 104, 5–14. ( 10.1111/j.0030-1299.2004.12761.x) [DOI] [Google Scholar]
- 63.Colasurdo N, Despland E. 2005. Social cues and following behavior in the forest tent caterpillar. J. Insect Behav. 18, 77–87. ( 10.1007/s10905-005-9348-6) [DOI] [Google Scholar]
- 64.Fitzgerald TD, Costa JT. 1999. Collective behavior in social caterpillars. In Information processing in social insects (eds Detrain C, Deneubourg JL, Pasteels JM.), pp. 379–400. Berlin, Germany: Springer. [Google Scholar]
- 65.Yano S. 2008. Collective and solitary behaviors of twospotted spider mite (Acari: Tetranychidae) are induced by trail following. Ann. Entomol. Soc. Am. 101, 247–252. ( 10.1603/0013-8746(2008)101[247:CASBOT]2.0.CO;2) [DOI] [Google Scholar]
- 66.Mikheyev A, Tschinkel W. 2004. Nest architecture of the ant Formica pallidefulva: structure, costs and rules of excavation. Insectes Sociaux 51, 30–36. ( 10.1007/s00040-003-0703-3) [DOI] [Google Scholar]
- 67.Vleck D. 1979. The energy cost of burrowing by the pocket gopher Thomomys bottae. Physiol. Zool. 49, 391–396. [Google Scholar]
- 68.Anderson C, McShea DW. 2001. Intermediate-level parts in insect societies: adaptive structures that ants build away from the nest. Insectes Sociaux 48, 291–301. ( 10.1007/PL00001781) [DOI] [Google Scholar]
- 69.Rockwood L, Hubbell SP. 1987. Host-plant selection, diet diversity, and optimal foraging in a tropical leafcutting ant. Oecologia 74, 55–61. ( 10.1007/BF00377345) [DOI] [PubMed] [Google Scholar]
- 70.Gauthier R, Bider JR. 1987. The effects of weather on runway use by rodents. Can. J Zool. 65, 2035–2038. ( 10.1139/z87-309) [DOI] [Google Scholar]
- 71.Bollazzi M, Forti LC, Roces F. 2012. Ventilation of the giant nests of Atta leaf-cutting ants: does underground circulating air enter the fungus chambers? Insectes Sociaux 59, 487–498. ( 10.1007/s00040-012-0243-9) [DOI] [Google Scholar]
- 72.Perna A, Kuntz P, Theraulaz G, Jost C. 2012. From local growth to global optimization in insect built networks. In Biologically inspired networking and sensing: algorithms and architectures (eds Lió P, Verma D.), pp. 132–144. Hershey, PA: IGI Global. [Google Scholar]
- 73.Franks NR, Wilby A, Silverman BW, Tofts C. 1992. Self-organizing nest construction in ants: sophisticated building by blind bulldozing. Anim. Behav. 44, 357–375. ( 10.1016/0003-3472(92)90041-7) [DOI] [Google Scholar]
- 74.Buhl J, Deneubourg JL, Grimal A, Theraulaz G. 2005. Self-organized digging activity in ant colonies. Behav. Ecol. Sociobiol. 58, 9–17. ( 10.1007/s00265-004-0906-2) [DOI] [Google Scholar]
- 75.Steinberg R, Zangwill WI. 1983. The prevalence of Braess’ paradox. Transp. Sci. 17, 301–318. ( 10.1287/trsc.17.3.301) [DOI] [Google Scholar]
- 76.Braess P-DDD. 1968. Über ein Paradoxon aus der Verkehrsplanung. Unternehmensforschung 12, 258. [Google Scholar]
- 77.Dussutour A, Fourcassié V, Helbing D, Deneubourg J. 2004. Optimal traffic organization in ants under crowded conditions. Nature 428, 70–73. ( 10.1038/nature02345) [DOI] [PubMed] [Google Scholar]
- 78.Burtin JL, Franks NR. 1985. The foraging ecology of the army ant Eciton rapax: an ergonomic enigma? Ecol. Entomol. 10, 131–141. ( 10.1111/j.1365-2311.1985.tb00542.x) [DOI] [Google Scholar]
- 79.Fourcassié V, Dussutour A, Deneubourg J-L. 2010. Ant traffic rules. J. Exp. Biol. 213, 2357–2363. ( 10.1242/jeb.031237) [DOI] [PubMed] [Google Scholar]
- 80.Röschard J, Roces F. 2003. Cutters, carriers and transport chains: distance-dependent foraging strategies in the grass-cutting ant Atta vollenweideri. Insectes Sociaux 50, 237–244. ( 10.1007/s00040-003-0663-7) [DOI] [Google Scholar]
- 81.Reyes-López J, Fernández-Haeger J. 2001. Some factors determining size-matching in the harvester ant Messor barbarus: food type, transfer activity, recruitment rate and size-range. Insectes sociaux 48, 118–124. ( 10.1007/PL00001753) [DOI] [Google Scholar]
- 82.Anderson C, Jadin J. 2001. The adaptive benefit of leaf transfer in Atta colombica. Insectes Sociaux 48, 404–405. ( 10.1007/PL00001798) [DOI] [Google Scholar]
- 83.Röschard J, Roces F. 2011. Sequential load transport in grass-cutting ants (Atta vollenweideri): maximization of plant delivery rate or improved information transfer? Psyche: A J. Entomol. 2011, 643127 ( 10.1155/2011/643127) [DOI] [Google Scholar]
- 84.Rosvall M, Trusina A, Minnhagen P, Sneppen K. 2005. Networks and cities: an information perspective. Phys. Rev. Lett. 94, 028701 ( 10.1103/PhysRevLett.94.028701) [DOI] [PubMed] [Google Scholar]
- 85.Jackson DE, Holcombe M, Ratnieks FL. 2004. Trail geometry gives polarity to ant foraging networks. Nature 432, 907–909. ( 10.1038/nature03105) [DOI] [PubMed] [Google Scholar]
- 86.Gerbier G, Garnier S, Rieu C, Theraulaz G, Fourcassié V. 2008. Are ants sensitive to the geometry of tunnel bifurcation? Anim. Cogn. 11, 637–642. ( 10.1007/s10071-008-0153-4) [DOI] [PubMed] [Google Scholar]
- 87.Garnier S, Guérécheau A, Combe M, Fourcassié V, Theraulaz G. 2009. Path selection and foraging efficiency in Argentine ant transport networks. Behav. Ecol. Sociobiol. 63, 1167–1179. ( 10.1007/s00265-009-0741-6) [DOI] [Google Scholar]
- 88.Vela-Pérez M, Fontelos MA, Velázquez JJL. 2013. Ant foraging and geodesic paths in labyrinths: analytical and computational results. J. Theoret. Biol. 320, 100–112. ( 10.1016/j.jtbi.2012.11.025) [DOI] [PubMed] [Google Scholar]
- 89.Garnier S, Combe M, Jost C, Theraulaz G. 2013. Do ants need to estimate the geometrical properties of trail bifurcations to find an efficient route? A swarm robotics test bed. PLoS Comput. Biol. 9, e1002903 ( 10.1371/journal.pcbi.1002903) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Farji-Brener AG, Amador-Vargas S, Chinchilla F, Escobar S, Cabrera S, Herrera MI, Sandoval C. 2010. Information transfer in head-on encounters between leaf-cutting ant workers: food, trail condition or orientation cues? Anim. Behav. 79, 343–349. ( 10.1016/j.anbehav.2009.11.009) [DOI] [Google Scholar]
- 91.Cook A. 1992. The function of trail following in the pulmonate slug Limax pseudoflavus. Anim. Behav. 43, 813–821. ( 10.1016/S0003-3472(05)80204-0) [DOI] [Google Scholar]
- 92.Cook A. 1980. Field studies of homing in the pulmonate slug limax pseudoflavus (evans). J. Molluscan Stud. 46, 100–105. [Google Scholar]
- 93.Dobly A. 2001. Movement patterns of male common voles (Microtus arvalis) in a network of Y junctions: role of distant visual cues and scent marks. Can. J. Zool. 79, 2228–2238. ( 10.1139/cjz-79-12-2228) [DOI] [Google Scholar]
- 94.Reid CR, Sumpter DJT, Beekman M. 2011. Optimisation in a natural system: argentine ants solve the Towers of Hanoi. J. Exp. Biol. 214, 50–58. ( 10.1242/jeb.048173) [DOI] [PubMed] [Google Scholar]
- 95.Ramsch K, Reid CR, Beekman M, Middendorf M. 2012. A mathematical model of foraging in a dynamic environment by trail-laying Argentine ants. J. Theoret. Biol. 306, 32–45. ( 10.1016/j.jtbi.2012.04.003) [DOI] [PubMed] [Google Scholar]
- 96.Burda H, Marhold S, Westenberger T, Wiltschko R, Wiltschko W. 1990. Magnetic compass orientation in the subterranean rodent Cryptomys hottentotus (Bathyergidae). Experientia 46, 528–530. ( 10.1007/BF01954256) [DOI] [PubMed] [Google Scholar]
- 97.Kimchi T, Terkel J. 2001. Magnetic compass orientation in the blind mole rat Spalax ehrenbergi. J. Exp. Biol. 204, 751–758. [DOI] [PubMed] [Google Scholar]
- 98.Jander R, Daumer K. 1974. Guide-line and gravity orientation of blind termites foraging in the open (Termitidae: Macrotermes, Hospitalitermes). Insectes sociaux 21, 45–69. ( 10.1007/BF02222979) [DOI] [Google Scholar]
- 99.Khuong A, Lecheval V, Fournier R, Blanco S, Weitz S, Bezian J-J, Gautrais J, Pratt SC. 2013. How do ants make sense of gravity? A Boltzmann walker analysis of Lasius niger trajectories on various inclines. PLoS ONE 8, e76531 ( 10.1371/journal.pone.0076531) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Cox M, Blanchard G. 2000. Gaseous templates in ant nests. J. Theoret. Biol. 204, 223–238. ( 10.1006/jtbi.2000.2010) [DOI] [PubMed] [Google Scholar]
- 101.Porter SD, Tschinkel WR. 1993. Fire ant thermal preferences: behavioral control of growth and metabolism. Behav. Ecol. Sociobiol. 32, 321–329. ( 10.1007/BF00183787) [DOI] [Google Scholar]
- 102.Riveros AJ, Srygley RB. 2008. Do leafcutter ants, Atta colombica, orient their path-integrated home vector with a magnetic compass? Anim. Behav. 75, 1273–1281. ( 10.1016/j.anbehav.2007.09.030) [DOI] [Google Scholar]
- 103.Evison S, Petchey O, Beckerman A, Ratnieks F. 2008. Combined use of pheromone trails and visual landmarks by the common garden ant Lasius niger. Behav. Ecol. Sociobiol. 63, 261–267. ( 10.1007/s00265-008-0657-6) [DOI] [Google Scholar]
- 104.Grigg GC, Underwood AJ. 1977. An analysis of the orientation of ‘magnetic’ termite mounds. Aust. J. Zool. 25, 87–94. ( 10.1071/ZO9770087) [DOI] [Google Scholar]
- 105.Dutta P, Khastgir SP, Roy A. 2010. Steiner trees and spanning trees in six-pin soap films. Am. J. Phys. 78, 215 ( 10.1119/1.3247982) [DOI] [Google Scholar]
- 106.Lagzi In, Soh S, Wesson PJ, Browne KP, Grzybowski BA. 2010. Maze solving by chemotactic droplets. J. Am. Chem. Soc. 132, 1198–1199. ( 10.1021/ja9076793) [DOI] [PubMed] [Google Scholar]
- 107.Denny M. 1980. Locomotion: the cost of gastropod crawling. Science 208, 1288–1290. ( 10.1126/science.208.4449.1288) [DOI] [PubMed] [Google Scholar]
- 108.Ng T, Saltin SH, Davies MS, Johannesson K, Stafford R, Williams GA. 2013. Snails and their trails: the multiple functions of trail-following in gastropods. Biol. Rev. 88, 683–700. ( 10.1111/brv.12023) [DOI] [PubMed] [Google Scholar]
- 109.Silva PSD, Bieber AGD, Knoch TA, Tabarelli M, Leal IR, Wirth R. 2013. Foraging in highly dynamic environments: leaf-cutting ants adjust foraging trail networks to pioneer plant availability. Entomol. Exp. Appl. 147, 110–119. ( 10.1111/eea.12050) [DOI] [Google Scholar]
- 110.Solé R, Bonabeau E, Delgado J, Fernández P, Marín J. 2000. Pattern formation and optimization in army ant raids. Artif. Life 6, 219–226. ( 10.1162/106454600568843) [DOI] [PubMed] [Google Scholar]
- 111.Harper SJ, Batzli GO. 1996. Monitoring use of runways by voles with passive integrated transponders. J. Mammal. 77, 364–369. ( 10.2307/1382809) [DOI] [Google Scholar]
- 112.Ponchon A, Grémillet D, Doligez B, Chambert T, Tveraa T, González-Solís J, Boulinier T, Rands S. 2013. Tracking prospecting movements involved in breeding habitat selection: insights, pitfalls and perspectives. Methods Ecol. Evol. 4, 143–150. ( 10.1111/j.2041-210x.2012.00259.x) [DOI] [Google Scholar]
- 113.Moorcroft PR, Barnett A. 2008. Mechanistic home range models and resource selection analysis: a reconciliation and unification. Ecology 89, 1112–1119. ( 10.1890/06-1985.1) [DOI] [PubMed] [Google Scholar]
- 114.Vicsek T, Zafeiris A. 2012. Collective motion. Phys. Rep. 517, 71–140. ( 10.1016/j.physrep.2012.03.004) [DOI] [Google Scholar]
- 115.Sumpter DJT, Mann RP, Perna A. 2012. The modelling cycle for collective animal behaviour. Interface Focus 2, 764–773. ( 10.1098/rsfs.2012.0031) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Bode NWF, Delcourt J. 2013. Individual-to-resource landscape interaction strength can explain different collective feeding behaviours. PLoS ONE 8, e75879 ( 10.1371/journal.pone.0075879) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Webb JK, Shine R. 1992. To find an ant: trail-following in Australian blindsnakes (Typhlopidae). Anim. Behav. 43, 941–948. ( 10.1016/S0003-3472(06)80007-2) [DOI] [Google Scholar]
- 118.Shaheen N, Patel K, Patel P, Moore M, Harrington MA. 2005. A predatory snail distinguishes between conspecific and heterospecific snails and trails based on chemical cues in slime. Anim. Behav. 70, 1067–1077. ( 10.1016/j.anbehav.2005.02.017) [DOI] [Google Scholar]
- 119.Holway DA, Lach L, Suarez AV, Tsutsui ND, Case TJ. 2003. The causes and consequences of ant invasions. Annu. Rev. Ecol. Syst. 33, 181–233. ( 10.1146/annurev.ecolsys.33.010802.150444) [DOI] [Google Scholar]
- 120.Franks NR, Tofts C. 1994. Foraging for work—how tasks allocate workers. Anim. Behav. 48, 470–472. ( 10.1006/anbe.1994.1261) [DOI] [Google Scholar]
- 121.Traniello JFA, Rosengaus RB. 1997. Ecology, evolution and division of labour in social insects. Anim. Behav. 53, 209–213. ( 10.1006/anbe.1996.0289) [DOI] [Google Scholar]
- 122.Jeanson R. 2012. Long-term dynamics in proximity networks in ants. Anim. Behav. 83, 915–923. ( 10.1016/j.anbehav.2012.01.009) [DOI] [Google Scholar]
- 123.Mersch DP, Crespi A, Keller L. 2013. Tracking individuals shows spatial fidelity is a key regulator of ant social organization. Science 340, 1090–1093. ( 10.1126/science.1234316) [DOI] [PubMed] [Google Scholar]
- 124.Mankin PC, Getz LL. 1994. Burrow morphology as related to social organization of Microtus ochrogaster. J. Mammal. 75, 492–499. ( 10.2307/1382573) [DOI] [Google Scholar]


