Blood flow dynamics reflect degree of outflow tract banding in Hamburger–Hamilton stage 18 chicken embryos

Abstract

Altered blood flow during embryonic development has been shown to cause cardiac defects; however, the mechanisms by which the resulting haemodynamic forces trigger heart malformation are unclear. This study used heart outflow tract banding to alter normal haemodynamics in a chick embryo model at HH18 and characterized the immediate blood flow response versus the degree of band tightness. Optical coherence tomography was used to acquire two-dimensional longitudinal structure and Doppler velocity images from control (n = 16) and banded (n = 25, 6–64% measured band tightness) embryos, from which structural and velocity data were extracted to estimate haemodynamic measures. Peak blood flow velocity and wall shear rate (WSR) initially increased linearly with band tightness (p < 0.01), but then velocity plateaued between 40% and 50% band tightness and started to decrease with constriction greater than 50%, whereas WSR continued to increase up to 60% constriction before it began decreasing with increased band tightness. Time of flow decreased with constriction greater than 20% (p < 0.01), while stroke volume in banded embryos remained comparable to control levels over the entire range of constriction (p > 0.1). The haemodynamic dependence on the degree of banding reveals immediate adaptations of the early embryonic cardiovascular system and could help elucidate a range of cardiac adaptations to gradually increased load.

1. Introduction

Haemodynamics play an important role in regulating early cardiovascular development [1], and previous studies have shown that altered flow conditions can result in cardiac defects [2–8]. Interactions between blood flow and cardiac tissues generate biomechanical stresses and strains, which modulate cardiogenesis. Throughout the development, blood pressure causes cardiomyocytes to alter their maturation and proliferation [7,9], and shear stresses (frictional forces exerted by flowing blood on the heart lumen wall) trigger biological responses, including endothelial cell organization and signalling [5,10,11]. Although the resulting defects from abnormal blood flow are known, the mechanisms by which haemodynamic forces lead to congenital heart disease are not clear.

This study focuses on the haemodynamics in the outflow tract (OFT) portion of the embryonic chick heart, which connects the primitive ventricle to the arterial vessel system during early development at Hamburger and Hamilton (HH) stage 18 [12]. At this early stage, the heart has a tubular structure, with atrium, ventricle and OFT connected in series. The OFT is frequently studied because it is very sensitive to haemodynamic changes and it later gives rise to the aorta, pulmonary trunk, interventricular septum and semilunar valves, which are often involved in congenital heart defects [3–5]. Chick embryos are commonly used as a biological model of cardiac development, because of ease of accessibility in the egg and developmental similarities with human embryos. We used a surgical intervention, cardiac outflow tract banding (OTB), to alter haemodynamic conditions through the chick embryo heart. In OTB (also called ‘banding’ here for simplicity), a suture band is tied around the OFT to decrease the cross-sectional area and restrict the motion of the OFT wall, resulting in increased resistance to flow, peak ventricular pressure [8,13] and blood flow velocities [14]. The high-shear and high-pressure flow conditions introduced by OTB have been shown to result in a wide spectrum of heart defects in the chick embryo [2,4,7,8,15].

The positioning of the OFT in the egg during early developmental stages allows for the implementation of a variety of imaging modalities to study cardiac blood flow and follow the progression of cardiac development. Optical coherence tomography (OCT) is a powerful non-invasive and non-contact tomographic imaging technique, which provides the high-resolution, tissue penetration depth, and acquisition rates necessary to capture the beating motion of heart microstructures in early chick heart development. OCT provides a combination of structural and Doppler images with the same spatial and time resolution, which makes OCT a valuable imaging technique to study embryonic blood flow haemodynamics [14,16–19]. Furthermore, OTB band tightness can also be measured directly from structural OCT images [13]. OCT detects light reflected back from a low coherence light source to capture structure, and blood flow velocity is then calculated from the Doppler frequency shift when backscattered light from moving particles either adds or subtracts from the fixed Doppler frequency [20]. Haemodynamic and functional cardiac data can be easily measured from OCT structural and Doppler flow data to assess response to surgical interventions intended to alter blood flow conditions such as banding [14].

In this study, we used Doppler OCT to measure blood flow velocity in the OFT after OTB over a measured range of band constrictions and in control embryos. Wall shear rate (WSR), stroke volume (SV) and normalized time of flow (percentage of the cardiac cycle in which blood flows through the OFT) were also calculated from the Doppler velocity and structural data to evaluate the immediate haemodynamic response to OTB. This study is novel because we assessed the varied haemodynamic responses due to measured degrees of band constriction, revealing how the developing system reacts over a range of loads. Characterization of the haemodynamics induced by OTB will help elucidate whether the wide spectrum of heart defects observed after banding may partly represent the range of haemodynamic changes, and thus the potentially different mechanisms by which biomechanical forces affect cardiac development. While WSR (which depends on blood flow velocities) is a major trigger of cardiovascular endothelial cell response, SV and time of flow serve as measures of cardiac efficiency and function. We present here, for the first time, how blood flow conditions (peak blood flow velocity, WSR, SV and time of flow) are dependent on the degree of band tightness.

2. Material and methods

2.1. Chick embryo preparation and haemodynamic intervention

Fertilized White Leghorn chicken eggs were incubated blunt-end up at 37.5°C and 80% humidity until they reached stage HH18 (approx. 3 days) [12]. Tweezers were used to remove a small section of the blunt-end shell and then the inner shell membrane directly over the embryo heart. Any embryos that bled upon membrane removal, had obvious structural defects, or were not at the correct developmental stage were discarded.

Three groups of embryos were studied: (i) normal group (NL), in which no interventions were performed; (ii) control group (CON) in which a 10-0 nylon suture was passed under the OFT but not tightened; and (iii) OTB group, in which a 10-0 nylon suture was passed under the OFT and tied in a knot around the midsection of the OFT to constrict the lumen cross-sectional area (figure 1). A range of loose bands to very tight bands were studied in the OTB group. Following interventions, the CON and OTB group eggs were sealed with saran wrap and incubated for an additional 2 h before OCT data acquisition. The OTB group was imaged with OCT immediately prior to banding and after 2 h of banding to calculate band tightness:

2.1

where D_a is the maximum external diameter of the OFT at the band site after banding, and D_b is the maximum external diameter of the OFT at the approximate band site location before banding.

Figure 1.

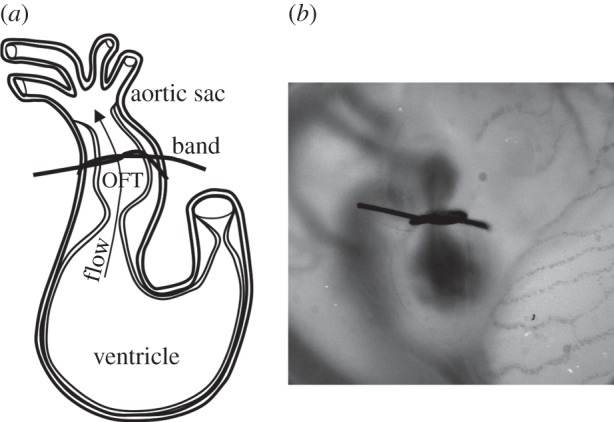
OFT banding of the chick embryo heart at HH18. (a) Sketch showing part of the embryonic tubular heart at HH18: the OFT is downstream of the primitive ventricle and upstream of the aortic sac. The band is placed around the midsection of the OFT. (b) Representative photograph of an embryo right-side up, immediately after banding.

2.2. Optical coherence tomography image acquisition

A custom-made OCT system was used in this study. The system has a spectral domain configuration consisting of a superluminescent diode centred at 1325 nm from Thorlabs Inc. (Newton, NJ, USA) and a 1024 pixel, 92 kHz maximal line-scan rate infrared InGaAs line-scan camera from Goodrich Inc. (Charlotte, NC, USA). This system allowed acquisition of 512 × 512 pixel (512 A-scans) two-dimensional images at approximately 140 frames per second with less than 10 µm resolution. In addition to structural images, this system can generate simultaneous Doppler flow phase images in post-processing by calculating the phase differences between two adjacent A-scans in a B-scan. Our group has previously used a similar system to image the embryonic chicken heart motion and blood flow dynamics [13,14,17,18]. Temperature during acquisition was maintained with a thermocouple-controlled heating pad surrounding the egg in a ceramic cup filled with water, which was enclosed in a plastic box. This apparatus kept the embryo near the normal physiological temperature of 37.5°C so that the heart rate remained close to the HH18 normal of 400 ms beat⁻¹, with variations of less than 40 ms beat⁻¹ (approx. 10% of cardiac cycle).

Each embryo was positioned within the OCT system so that a longitudinal section down the centre of the OFT was obtained. It was verified that the lumen completely filled the OFT at maximum expansion and made a silt-like shape in the centre of the OFT at maximum contraction [17,21]. Two hundred sequential B-scan longitudinal section frames were acquired for each embryo (approximately three to four cardiac cycles).

2.3. Structural and Doppler optical coherence tomography image analyses

Simultaneous structural and Doppler phase image datasets were extracted from the acquired OCT raw data, using a custom Matlab code (The MathWorks, Inc. Natick, MA, USA), to obtain an integrated view of blood flow and OFT wall movement (figure 2). The overall analysis process is shown in figure 3. Standards were imaged to calibrate conversion of pixel measurements to length measurements for all structural analyses. A flow rate-controlled syringe pump was used to push milk through a glass capillary tube, which confirmed Doppler velocities within 10.7% of theoretical values after flow angle adjustment (data included in the electronic supplementary material).

Figure 2.

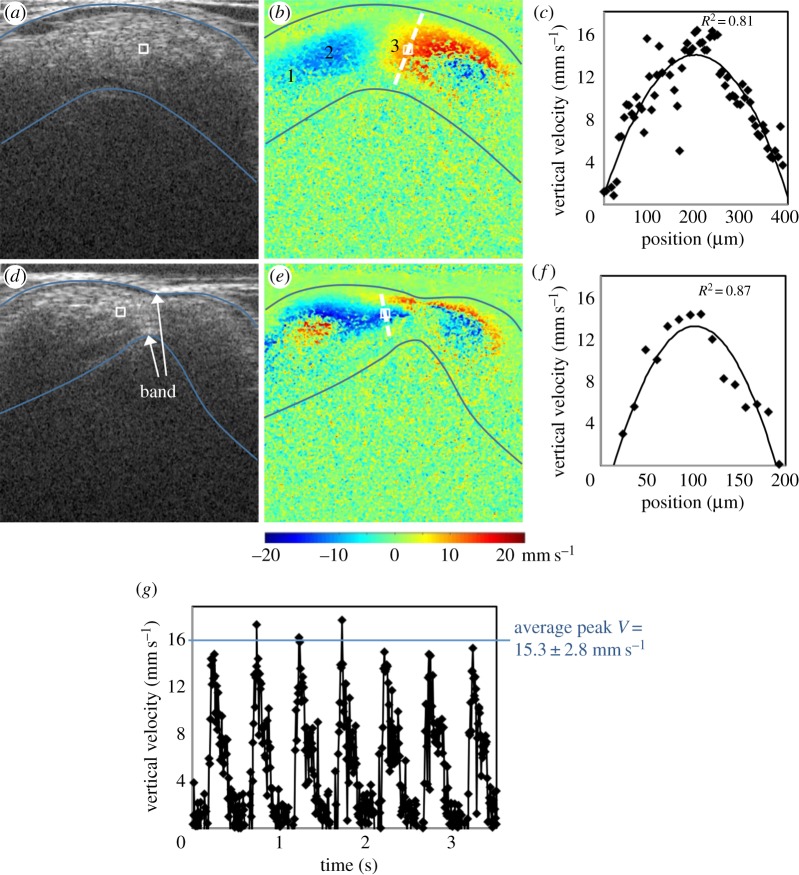
Representative OCT images of the HH18 chick heart OFT before and after banding at maximum expansion. (a) Structural image of a normal OFT. (b) Corresponding Doppler flow image of a normal OFT. Locations labelled 1, 2 and 3 along with the sampling area were chosen to compare maximum flow rate throughout the OFT, with comparable values (average maximum flow rate of 3.8 ± 0.1 mm³ s⁻¹) obtained. The myocardium is outlined on the structural image, and overlaid on the Doppler flow image, in blue. The approximate velocity sampling area is outlined by a white box in the Doppler flow images, and overlaid on the structural images. (c) Vertical velocity along dashed cross-sectional line in (b) showing a parabolic-like flow profile through the OFT under normal conditions. Experimental data are fit to a polynomial function with corresponding R²-value. (d) Structural image of the same embryo 2 h after banding. (e) Corresponding Doppler flow image 2 h after banding. (f) Vertical velocity along the dashed cross-sectional line in (e) showing a parabolic-like flow profile through the OFT under banded conditions. Less experimental data are given for the banded embryos as the diameter is reduced compared to before banding. (g) Vertical velocity versus time plot over several cardiac cycles.

Figure 3.

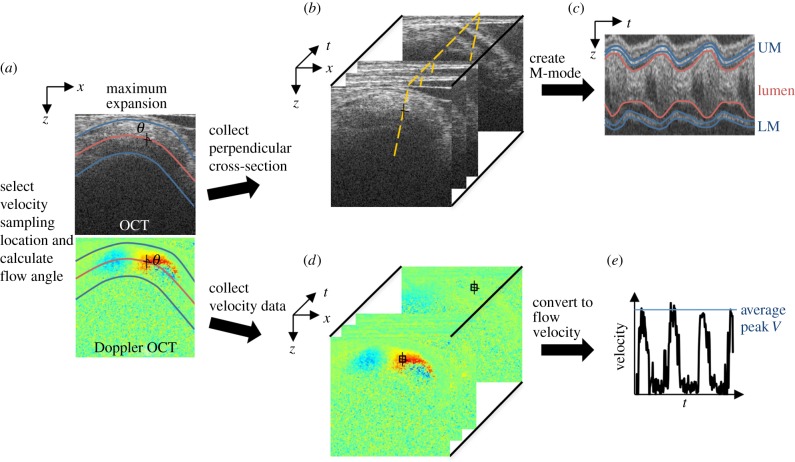
Flow chart of OCT image analysis. (a) Flow angle was measured by first outlining the myocardium walls in the two-dimensional structural image at maximum expansion, in blue, to calculate the OFT centreline, in red. The trace was then overlaid on the corresponding Doppler image and θ calculated. (b) The OFT cross-section perpendicular to flow at the velocity measurement location was identified, shown as the dashed line. (c) An M-mode image was extracted from the B scan dataset along the perpendicular dashed line for WSR and SV analysis. (d) Velocity data were extracted from the two-dimensional Doppler dataset from a 3 × 3 pixel area at the selected measurement location. (e) Vertical velocity from each two-dimensional frame was converted to the absolute flow velocity using θ to calculate peak V.

Phase wrapping was evident in the Doppler images of longitudinal scans (B-mode scans), when the phase shift exceeded ±π, which corresponded to vertical velocities higher than ±23.4 mm s⁻¹. Since the velocity flow profile in the OFT at HH18 is parabolic-like [14,18], the fastest flow frequently wraps in the centre of the OFT (negative phase enclosed by positive phase or vice versa depending on direction of flow), whereas the slowest/non-wrapped flow is present near the walls (figure 2). Areas with wrapped flow at peak blood velocities in the cardiac cycle were not chosen for the measurement location to avoid pixel-averaging errors associated with phase wrapping and corresponding unwrapping algorithms. Consistently located, non-wrapped flow regions were identified and used for flow comparisons.

A velocity sampling area was selected in the region of non-wrapped flow along the OFT centreline near the middle of the OFT in all embryo groups (figure 2). The ‘dog leg’ bend geometry of the OFT has a region of ‘upward’ flow followed by a region of ‘downward’ flow, which creates a perfect region for non-wrapped flow in control embryos near the position in which the band was placed in OTB embryos. The presence of the band in the OTB embryos slightly lifted the OFT so that flow approached the band at an angle, passed through it horizontally, and then flowed downstream, with high vertical velocity flow on either side of the band. This geometry again created a non-wrapped, parabolic flow region, just upstream of the band. This velocity measurement location was chosen in the OTB group to be the most representative of changes due to band constriction, as well as consistent with the location within the OFT across all embryo groups. We have further confirmed that the analysis technique measures similar flow rates throughout the length of the OFT. For example, the normal embryo shown in figure 2b has an average maximum flow rate of 3.8 ± 0.1 mm³ s⁻¹ measured from four different locations along the centreline. For comparisons among embryos, however, velocities from just one consistent location are compared.

To compute flow velocities from phase shift data (Δφ), the measured Δφ was converted to the vertical component of blood flow velocity (V_z) [17,18]

2.2

where λ₀ is the central wavelength, n is the refractive index of the tissue (approx. 1.35) and τ is the time difference between two adjacent A-scans. To reduce noise while minimally affecting flow velocity measurements, at each pixel Δφ was calculated as the average of a 9 pixel (3 × 3 box) sampling area. Then, the vertical velocity (obtained from equation (2.2)) at the sampling point over time was further averaged within the cycle and filtered in two iterations, excluding values more than 1.3 standard deviations away from the updated mean at each iteration. We then calculated the magnitude of the three-dimensional blood flow velocity (V)

2.3

where θ is the angle of the OFT centreline tangent with the vertical direction (the direction of V_z). The average peak V in the cardiac cycle was compared across all embryos.

A custom Matlab program was used to measure the angle θ. While θ is commonly set by operator estimation, our procedure calculates the angle by first computing the tangent to the curved OFT centreline at the selected velocity measurement location in a maximum expansion frame. Doppler flow and structural images show that blood flow follows the contour of the OFT in a parabolic-like profile, with the maximum velocity at the axial centre of the tube, consistent with low Reynolds (Re < 6) and Womersley (W < 0.5) numbers, and viscous forces dominating blood flow (figure 2). To obtain the OFT centreline, first the upper and lower myocardium walls were manually outlined on the structural image and then the centreline was computed as the middle position in the z-direction at each pixel along the OFT length in the x-direction (figure 3). The myocardium was outlined for the angle calculation as it is better defined in longitudinal frames, and since at maximum expansion the lumen fills the OFT and is roughly circular like the myocardium. The structural outlines were then overlaid on the corresponding Doppler flow image for the user to select the velocity measurement position along the centreline. Finally, the angle of the line tangent to the centreline with respect to the vertical direction at the measurement location was calculated to find θ and calculate V.

OFT characteristic diameters were measured from M-mode image analysis. M-modes are used to show cardiac wall motion over time, by displaying grey scales from a single line of every structural B-mode frame in a dataset. This organization results in cardiac structure along the selected line shown in the vertical direction versus time in the horizontal direction (figure 3). M-modes were generated from a line at the point along the OFT centreline that was chosen for velocity measurement or band tightness measurement and at an angle perpendicular to the centreline. The upper and lower myocardium or lumen interfaces in the M-mode were traced to calculate the OFT diameter of interest over the entire cardiac cycle.

WSR variation from OTB altered velocity was then evaluated. Shear rate at the wall was calculated using

2.4

where V is the velocity vector, r is a vector normal to the lumen wall surface, and dV/dr is the velocity gradient in the direction normal (perpendicular) to the lumen wall surface (e.g. [22–25]). Equation (2.5) can be derived from the Haagen–Poisseuille equation

2.5

where v_c is the OFT centreline velocity V, and D is the OFT lumen diameter at a single point in the cardiac cycle (e.g. [23,26]). A parabolic-like velocity profile in the OFT at HH18 [14,18] (figure 2) make this approximation valid. Although adult mammalian blood is non-Newtonian with biconcave red blood cells, embryonic chick blood has spherical red blood cells that are less deformable in flow [27] resulting in a fairly constant viscosity in the physiological shear rate range [28], and thus WSR should be proportional to wall shear stress. The WSR during peak V in the cardiac cycle was compared across all embryos.

SV was measured to assess cardiac function over a range of band tightness. SV was estimated using the centreline blood flow velocity over an entire cardiac cycle, and the diameter of the lumen walls in each frame at the selected measurement location. The volumetric flow rate corresponding to each frame was calculated using a form of the Poiseuille equation derived for a parabolic flow profile as the product of the mean centreline velocity and the cross-sectional area of the lumen [29,30]

2.6

where Q is the blood flow rate through the OFT, and D is the OFT lumen diameter. This approximation assumes that blood is homogeneous, and that blood flow is parabolic and laminar, with zero velocity at the OFT lumen wall. Since the OFT cross-sectional area (and thus D) and the centreline blood velocity change over the cardiac cycle, the flow rate was divided by the image acquisition rate to estimate the volume of blood passing in between each two-dimensional image acquired. SV was estimated by summing the blood volume calculated from each frame during blood flow in a full cardiac cycle

2.7

where Δt = 1/frame rate (140 fps for our system), Q is the blood flow rate calculated from each frame, and the sum takes into account one cardiac cycle (N approx. 25 frames, depending on actual cardiac cycle period and time of flow). The average SV value from two to three cardiac cycles was used to compare embryos.

To further characterize the relationship between blood flow and OFT wall dynamics, time of flow was measured in all embryo groups. Time of flow was defined as the average percentage of time in the cardiac cycle when blood was flowing through the measurement location in the OFT. The presence of flow was determined from the blood flow velocity versus time trace as clear peaks above the background noise level.

2.4. Statistical and uncertainty analyses

Embryo group data were analysed as the mean ± s.d. Statistical significance was determined with a two-sample Student's t-test, reporting two-tail p-values, and assuming significance with p-values of less than 0.05.

Two-dimensional OCT image analysis involves many assumptions that can introduce error into the final variable estimates. Maximum error was calculated with uncertainties for each variable involved in the approximation for peak blood flow velocity, WSR and SV. Assuming typical values and average variation, maximum possible error was estimated by

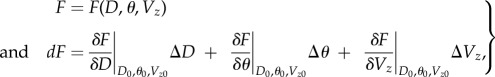2.8

where F is the variable in question (peak V, WSR, SV), and dF is the summation of individual partial derivative errors; D₀, θ₀ and V_z0 are typical reference values of 450 μm OFT diameter, 70° flow angle with respect to the vertical direction and 15 mm s⁻¹ vertical velocity, respectively; ΔD, Δθ are ΔV_z are average variations of 50 μm OFT diameter, 5° flow angle with respect to the vertical direction and 2.8 mm s⁻¹ vertical velocity (figure 2g), respectively. Typical reference and variation values were determined as averages from repeated measurements.

3. Results

Both the NL and CON control groups were comparable, with no significant differences across all measures (n = 8 for each group; p-values: 0.92 for peak velocity, 0.91 for WSR, 0.19 for SV, 0.83 for time of flow), indicating that any changes after OTB are from the constriction of the OFT and not due to the surgical manipulation. OTB constriction ranged between 0 and 64% band tightness. Individual embryo measurements are summarized in the electronic supplementary material.

3.1. Peak blood flow velocity response to outflow tract banding

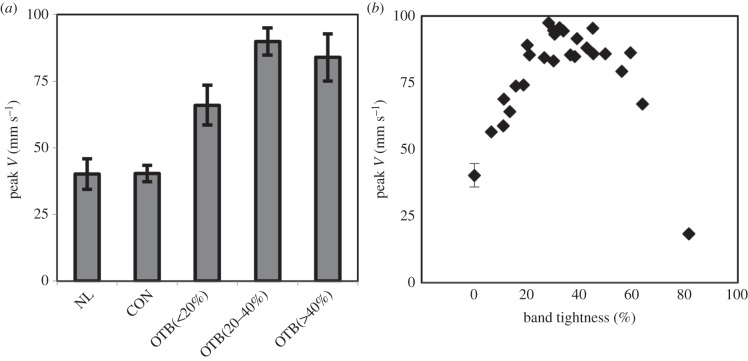
Maximum blood flow velocity through the OFT near the band site (figure 2) was analysed for all embryos (n = 41). Average peak blood flow velocity for NL and CON groups was 40.2 ± 5.7 mm s⁻¹ and 40.4 ± 3.1 mm s⁻¹, respectively, which corresponds to previously published values at HH18 [17,18,31,32]. Peak velocity was increased in OTB embryos, consistent with previous studies [14,33], but was also dependent on degree of band tightness with the largest increase of 2.5-fold near 40% band constriction. Peak velocity increased approximately linearly with band tightness between 0 and 40% constriction (R² = 0.91), and then plateaued near 40–50% band tightness. Above 50% constriction, peak velocity decreased with band tightness, while still remaining higher than CON and NL groups (figure 4 and table 1). Peak velocities from all ranges of OTB embryos tested were significantly higher than control groups (OTB n = 25; p-value = 2.2 × 10⁻⁴ for less than 20% constriction, n = 6; p-value = 2.7 × 10⁻¹⁸ for 20–40% constriction, n = 12 and p-value = 5.3 × 10⁻⁶ for greater than 40% constriction, n = 7). Figure 4b additionally includes one embryo that was severely compromised with 81% band tightness (OCT imaged immediately after OTB), to demonstrate that a tight band that allowed little blood flow through the lumen caused the peak velocity to decrease below that of control embryos.

Figure 4.

Blood flow peak velocity response to band tightness. (a) Comparison of average peak velocity of the normal (NL, n = 8), control (CON, n = 8) and the banded group (OTB) split between those embryos with bands less than 20% constriction (n = 6), 20–40% constriction (n = 12) and greater than 40% constriction (n = 7). Data presented as mean ± s.d. (b) Individual average peak velocity response over a range of 0–81% band tightness, with NL and CON groups shown with 0% band tightness.

Table 1.

Summary of average OFT flow parameters for NL, CON and OTB constriction groups separated by band tightness range. Data presented as means ± s.d.

embryo group	peak V (mm s−1)	WSR (s−1)	SV (mm3/beat)	time of flow (%)
NL	40.2 + 5.7	302.1 ± 73.2	0.51 ± 0.17	53.1 ± 6.4
CON	40.4 ± 3.1	305.5 ± 33.2	0.41 ± 0.10	52.5 ± 5.9
OTB (<20%)	66.0 ± 7.5a	572.3 ± 101.7a	0.51 ± 0.19	52.2 ± 7.0
OTB (20–40%)	89.9 ± 5.1a	797.5 ± 104.4a	0.45 ± 0.17	43.9 ± 5.0a
OTB (>40%)	83.9 ± 8.9a	783.0 ± 121.4a	0.39 ± 0.11	32.9 ± 2.7a

^aStatistically significant difference from control groups with p-value of less than 0.05.

Considering uncertainties in the measurements, the maximum possible error for the peak blood flow velocity calculation was 18.6 mm s⁻¹, with the largest error contribution from the θ estimation (table 2 and equation (2.8)). Since the θ estimation in this study was based on the outline of the myocardium walls from OCT structural images (instead of standard ultrasound angle measuring procedures where θ is manually set by the operator), angle estimations were probably very consistent.

Table 2.

Summary of maximum error calculations for total error (dF) and each error component (δF/δx).

error	F = V (mm s−1)	F = WSR (s−1)	F = SV (mm3/beat)
dF	18.6	208.8	2.2 × 10−2
δF/δD	n.a.	43.3	1.1 × 10−2
δF/dθ	10.5	93.5	6.0 × 10−3
δF/dVz	8.1	72.0	5.0 × 10−3

3.2. Wall shear rate response to outflow tract banding

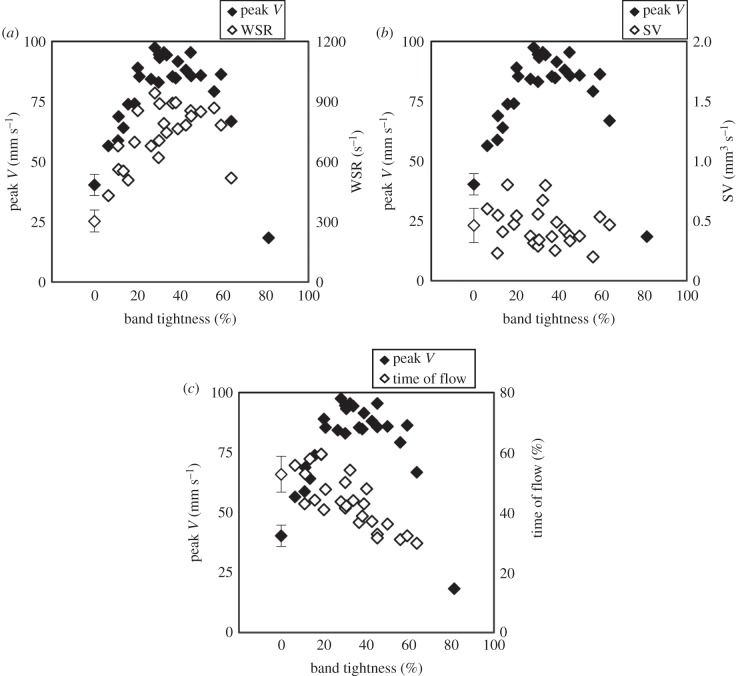
WSR at peak blood flow velocity near the band site (figure 2) was calculated across the range of band tightness (n = 40). Average maximum WSR across NL and CON embryos was 302.1 ± 73.2 s⁻¹ and 305.5 ± 33.2 s⁻¹, respectively, which is within previously published experimental and computational fluid dynamics model estimates in the chick embryo OFT [17,34]. Results are summarized in figure 5a and table 1. Error propagation analysis showed that the largest error contribution to WSR was from the θ estimation (table 2 and equation (2.8)). While the maximum hypothetical error could be large (208.8 s⁻¹) compared with the mean of control embryos, our computed standard deviations are relatively low (24% and 11% of the mean for NL and CON groups, respectively). Since velocity is one of the main variables in this estimation (see equation (2.5)), the WSR from the OTB group follows the general trend of the velocity versus band tightness curve (figure 5a) but does not begin to decrease until 60% band constriction. The WSR estimations in the OTB group were significantly higher than the control groups, across all OTB sub-divisions (OTB n = 24; p-value = 8.5 × 10⁻⁴ for less than 20% OTB constriction, n = 6; p-value = 8.9 × 10⁻¹⁰ for 20–40% OTB constriction, n = 11 and p-value = 2.1 × 10⁻⁵ for greater than 40% OTB constriction, n = 7). The range of band tightness studied therefore generated a range of WSR on cardiac tissues just upstream of the band at the chosen measurement location (figure 2).

Figure 5.

Haemodynamic measures as a function of band tightness compared to the average peak blood flow velocity response over a 0–64% constriction range. (a) WSR (s⁻¹) response, OTB n = 24. (b) SV (mm³/beat) response, OTB n = 24. (c) Time of flow (%) response, OTB n = 25. Normal (NL, n = 8) and control (CON, n = 8) embryo data shown at 0% band tightness averaged together with s.d. bars.

3.3. Stroke volume response to outflow tract banding

SV was measured over the range of band tightness (n = 40). Average SV values for NL and CON groups were 0.51 ± 0.17 mm³ beat⁻¹ and 0.41 ± 0.10 mm³ beat⁻¹, respectively, which is comparable to previously published data estimated with prolate spheroid ventricular volumes [35] and dorsal aortic flow [36,37]. SV in OTB embryos stayed approximately constant within the range of control groups, with no significant differences across all OTB sub-divisions (OTB n = 24; p-value = 0.59 for less than 20% OTB constriction, n = 6; p-value = 0.91 for 20–40% OTB constriction, n = 11 and p-value = 0.18 for greater than 40% OTB constriction, n = 7). Results are summarized in figure 5b and table 1. Considering uncertainties in the SV calculation, the maximum error for the SV calculation was 2.2 × 10⁻² mm³ beat⁻¹, with the largest error contribution from the OFT diameter estimation (see table 2 and equation (2.8)). While not measured over a range of band constriction, others have previously found that SV did not clearly differ between control and banded embryos [33,38].

3.4. Time of flow response to outflow tract banding

The time of flow was measured for all embryos that had clearly distinguishable periods of blood flow in the velocity versus time trace (n = 41). Time of flow, the percentage of time in the cardiac cycle when blood was flowing, for NL and CON groups was approximately half of the cardiac cycle, consistent with our previous observations [17]. Differences in time of flow were not significant between control groups and the OTB embryos with less than 20% band tightness (p-value = 0.86, n = 6). OTB embryos with greater than 20% band tightness had significantly lower time of flows (OTB n = 25; p-value = 3.3 × 10⁻⁴ for 20–40% OTB constriction, n = 11 and p-value = 5.6 × 10⁻⁶ for OTB greater than 40% constriction, n = 8). Figure 5c shows that time of flow decreased with increasing band tightness, and average values are summarized in table 1.

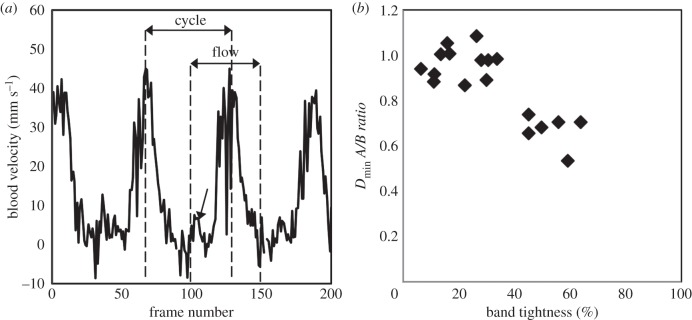
Control and loosely banded embryos (less than 30% OTB) consistently had an initial surge of blood flow through the OFT prior to the main flow of the cardiac cycle, shown in figure 6a with an arrow. The initial flow surge was not evident in OTB embryos with greater than 30% band tightness, consistent with the measured decrease in time of flow. Figure 6b shows the relationship between the minimum external OFT diameter in the cardiac cycle at the band site (D_min) and band tightness. While band tightness is measured from maximum OFT diameters (see equation (2.1)), the ratio of minimum OFT diameter after banding compared to before banding (A/B ratio) was decreased in bands tighter than 40% constriction, indicating the OFT is constricted beyond its normal contraction geometry with tight bands. The range of band tightness with decreased D_min was also consistent with the observed decrease in time of flow.

Figure 6.

Time of flow versus band tightness. (a) Blood flow velocity trace over approximately four cardiac cycles for an example NL embryo. The arrow designates the initial flow surge seen before the main flow of the cardiac cycle in loosely banded embryos. (b) OFT D_min ratios at banding site (after/before banding) versus band tightness. Diameters were measured only from M-mode images which clearly showed the upper and lower myocardium walls (n = 18).

4. Discussion

These results show the immediate haemodynamic response due to initial OTB mechanical stimuli. Since the embryonic cardiovascular system cannot fully remodel within 2 h, our haemodynamic assessment of banded embryonic hearts characterizes the initial flow alterations which have been shown to stimulate myocardial and endocardial layer response and tissue remodelling to cause cardiac defects [2,4,7,8,15]. Haemodynamic assessment is the first step in elucidating the mechanisms that cause altered blood flow to lead to cardiac malformations. We found that peak blood flow velocity increased with band tightness until near 40% constriction, where the velocity plateaued and then decreased with very tight bands, while the corresponding WSR followed a similar trend. SV remained constant with band tightness, while time of flow (the percentage of time with blood flow in the cardiac cycle) decreased with band tightness greater than 20% constriction. The combination of these results suggests that immediate adaptations to OTB promote the preservation of cardiac function.

Recent four-dimensional OCT analyses have been employed to accurately track the dynamics of myocardial tissue and blood flow over time using similar OCT systems that acquire multiple two-dimensional cross-sectional datasets before synchronization and four-dimensional reconstruction [17,18,39]. While four-dimensional analyses of the heart allow for accurate two-dimensional cross-sectional image generation and dynamic wall motion visualization, the simpler two-dimensional longitudinal images acquired in this study permit velocity comparisons across a large OTB sample group in a relatively easy and fast way. Two-dimensional acquisition is significantly faster than four-dimensional acquisition, and therefore can also be routinely used to scan embryos before performing other analyses (e.g. before tissue fixation). The high reproducibility exhibited in the control groups showed that our analyses, while not straightforward, were accurate enough to capture subtle changes in dynamic haemodynamic conditions that were not reported before.

4.1. Peak blood flow velocity response to outflow tract banding

This study complements recent work from Shi et al. [13], which assessed blood pressure changes due to a range of OTB constrictions. The study showed that as resistance to blood flow through the OFT increased with band tightness, so did blood pressure throughout the circulatory system. Not only did the ventricle, aortic sac and dorsal aorta pressures increase after OTB, but they were dependent on the relative band tightness. Both diastolic blood pressure (minimum pressure) and pulse pressure amplitude (and therefore systolic pressure) increased somewhat linearly with band tightness until near 40% band constriction, at which point pressure measures started to increase faster than linearly with band tightness. Forty per cent band tightness also corresponded to a sharper decrease in pulse transit time through the OFT and a plateau in the increase of the time lag for pressure to peak after cardiac depolarization (obtained from ECG measurements). In this study, 40% band tightness represents the point in the velocity versus band tightness curve, where the peak blood flow velocity stops increasing with band tightness. The faster pressure increase and pulse transit time decrease with band tightness may be related to the blood flow velocity plateau because of a combination of OTB effects, including decreased OFT active wall contraction at the band site, and afterload stretching of the ventricular cardiomyocytes.

Under normal conditions, blood is pushed through the OFT by a combination of pressure wave propagation after ventricular contraction and the active contraction of the OFT. The presence of active contraction through the OFT is supported by synchronized wall motion and pressure data, where the peak ventricular systolic pressure and peak aortic sac pressure occurs just prior to the maximum OFT inlet and outlet wall contractions, respectively [13,17,40]. Blood flow generated solely by ventricle contraction, followed by passive pressure wave propagation through the OFT, would instead cause the peak pressure to occur in phase with the maximum OFT expansion. Furthermore, we observed that the HH18 heart OFT alone contracts in warmed Hanks' balanced salt solution after being removed from the embryo and separated from the ventricle. OTB increases pressure wave propagation speed, while decreasing peristaltic-like patterns of OFT wall motion [13]. The suture in OTB physically anchors the OFT to surrounding membrane tissues, making the wall effectively stiffer and less compliant with increased band tightness. This lessens the contractile capacity of cardiomyocytes close to the band and thus decreases OFT active contraction. The diminishing effect OTB has on active wall contraction, together with increased constriction, may contribute to the velocity versus band tightness curve plateau near 40% constriction. The peak blood flow velocities in this range are still much higher than those measured in control embryos because of increased pressure and pressure wave propagation speeds, but may stop increasing with band tightness partially due to the loss of active wall contraction against an increased resistance to flow.

Previous studies suggest the OTB increase in cardiac afterload and resistance to ventricular ejection may extend the time for full myocardial force generation and increase the resultant ventricular contraction force [13,38]. The Starling Law establishes that the heart can change the force generated by contractile muscle fibres depending on the amount of overlap of the thin and thick myofilaments, with a reduced force generated with more or less fibre overlap than the optimal sarcomere length [41,42]. Increased afterload (resistance to flow) due to OTB may create greater contraction forces until a certain band tightness, where the optimal sarcomere length of ventricle muscle fibres is exceeded and additional ventricle load generates a diminished contraction force. Thus, a balance is established in which increased resistance to flow induced by the band is compensated by increased ventricular contraction force, resulting in increased velocities through a narrower lumen area. Increases in afterload and myocardium force generation with band tightness, however, are not proportional, and the peak blood flow velocity levels off and begins decreasing with constriction greater than 40% band tightness.

4.2. Wall shear rate response to outflow tract banding

Four-dimensional computational fluid dynamics models have been developed to account for the curved, moving geometry of the OFT during the pulsatile flow in the cardiac cycle [17], which is not accounted for by our WSR estimation using equation (2.5). The WSR estimation calculated from two-dimensional longitudinal images in this study only compares values at one OFT position at one time point in the cardiac cycle. Furthermore, equation (2.5) assumes a circular lumen, which is a good approximation when the OFT walls are fully expanded [17,21], and thus it is reasonable to compute WSR at peak blood flow velocity. Nevertheless, two-dimensional longitudinal images are easier to acquire and analyse than the four-dimensional motion of the OFT, resulting in an efficient (and relatively simple-to-implement) procedure to monitor the effect of increased OTB constriction on endocardial WSR.

The trend of maximum WSR loosely followed the velocity versus band tightness curve. This is somewhat expected as WSR is proportional to velocity and inversely proportional to lumen diameter (see equation (2.5)). WSR increased with band tightness and started to decrease only at very tight band constrictions near 60% band tightness. This decrease occurred after the diminished velocity response (figure 5a), when blood flow velocities were dramatically decreased. While the velocity versus band tightness curve plateaus near 40% constriction, the diameter at peak velocity continues to decrease with band tightness, which explains the continuous increase of WSR beyond 40% constriction and up to 60% band tightness.

4.3. Stroke volume response to outflow tract banding

SV values reported here are likely overestimates, since the calculation assumes the OFT is a circular cylinder throughout the cardiac cycle. In reality, cross-sectional OCT images of the OFT show the myocardium undergoes concentric narrowing and widening over the cardiac cycle while the lumen has an ellipse-like shape at maximum expansion and a slit-like shape during contraction [17,21]. While the dynamic and complex flow through the moving OFT is simplified in this estimation, the approach accounts for the velocity and OFT size changes over the cardiac cycle, and serves as a comparison across embryos over a range of band constriction.

SV remained constant under 0–64% band constriction conditions, even while the minimum OFT diameter and time of flow (portion of cardiac cycle with flow) decreased with band tightness. This conservation of SV indicates that the early embryonic cardiovascular system has a large range of functional adaptation in response to the increased afterload imposed by the band. The Starling Law of the heart may be partly responsible for the conserved SV over a large range of band constrictions presented in this study. The greater ventricular force generation that results from increased afterload and sarcomere lengthening could contribute to the heart's astonishing ability to preserve normal blood pumping even with tight OTB. The conservation of normal SV in embryos with band constriction greater than 50%, despite decreases in peak velocity and time of flow, is associated with an increased average flow rate (data included in the electronic supplementary material). Previous studies report a similar adaptive ability of the cardiovascular system to alter SV after end-diastolic volume infusions [38,43]. The fact that the heart at this stage has no valves, and the nervous system has not yet been formed, supports the idea that the cardiovascular adjustment to banding conditions is mainly mechanical in nature.

Although SV has been previously shown to be similar in control and banded embryos [33,38], it has not before been investigated over a range of measured band tightness. Keller et al. [38] used OTB to induce acute OFT occlusion using very tight bands alongside a volume infusion procedure, and calculated SV using ellipsoid ventricle volume estimations and pressure–volume loops. This SV measure demonstrated no striking difference between control and OFT occluded embryos with and without volume infusion at HH21. McQuinn et al. [33] compared the haemodynamic environments of control and OFT-banded embryos with ultrasound biomicroscopy, and found no difference in SV at HH24 and HH27 when calculated by tracking particle movement in the dorsal aorta. This study shows evidence of similar SV compensation, while over a wider documented range of haemodynamic alterations than previously reported.

4.4. Time of flow response to outflow tract banding

The time of flow (percentage time in which blood flows through the OFT in each cardiac cycle) significantly decreased with constriction greater than 20% band tightness. This result was not obvious a priori. The velocity versus time traces showed an initial flow surge in control and loosely banded embryos (less than 30% constriction) that was not evident in tight bands (figure 6a). The initial surge may be caused by the opening event of the OFT cushions which allows blood into the OFT before the main ventricle contraction. This could also been explained by a dynamic suction pumping model [44]. The dynamic beating movement of the OFT may also introduce an artefact in the velocity versus time trace, since only a stationary two-dimensional longitudinal plane is imaged. Tight bands anchor the OFT to surrounding membranes and tissues more than loose bands, which may cause the surge artefact to disappear in the tight OTB data. Further four-dimensional OCT analysis is needed to capture the longitudinal movement of the OFT, and determine whether the initial flow surge is present in the cardiac cycle or an artefact of the sample positioning. Nevertheless, the absence of the surge in tightly banded embryos contributed to the decreased time of flow.

Maximum OFT diameter decreased with band tightness, whereas the minimum OFT diameter remained relatively constant with constrictions up to approx. 40% band tightness. In embryos with greater than 40% band constriction, the myocardium was constricted beyond its minimum diameter prior to banding. This is likely explained by movement of the cardiac jelly layer away from the constricted region. When the band constricts the OFT myocardium beyond its normal contraction the lumen may remain closed for a larger portion of the cardiac cycle, and thus contribute to the decreased time of flow.

5. Conclusion

We have successfully measured blood flow triggers of tissue remodelling and cardiac function over an identified range of OTB constrictions using structural and Doppler OCT images. Peak blood flow velocity, WSR and time of flow were significantly affected by OTB with varied dependence on band tightness, while normal SV was preserved in banded embryos. Haemodynamic response assessment based on the degree of band tightness provides a novel view of functional adjustments and preservation in the early embryonic cardiovascular system, and advances understanding of the altered forces that affect cardiac development. The conservation of SV even under a dramatic range of band tightness highlights the adaptation capabilities present at this early stage of development. Furthermore, these outcomes suggest that cardiac malformations caused by OTB [3–5] result from a complex combination of altered ventricular function and blood flow resistance through the OFT. Moreover, the spectrum of cardiac malformations previously observed after OTB may be partly explained by different band tightness that generated diverse biomechanical conditions and thus distinct cardiac tissue growth and remodelling effects. Future studies will be needed to correlate the initial altered haemodynamics to early cardiac adaptations and the different types of cardiac defects that result later in development.

Funding statement

This work has been supported by grants NIH R01 HL094570 and NSF DBI-1052688.