Reliability and Validity in Hospital Case-Mix Measurement

Abstract

There is widespread interest in the development of a measure of hospital output. This paper describes the problem of measuring the expected cost of the mix of inpatient cases treated in a hospital (hospital case-mix) and a general approach to its solution. The solution is based on a set of homogenous groups of patients, defined by a patient classification system, and a set of estimated relative cost weights corresponding to the patient categories. This approach is applied to develop a summary measure of the expected relative costliness of the mix of Medicare patients treated in 5,576 participating hospitals.

The Medicare case-mix index is evaluated by estimating a hospital average cost function. This provides a direct test of the hypothesis that the relationship between Medicare case-mix and Medicare cost per case is proportional. The cost function analysis also provides a means of simulating the effects of classification error on our estimate of this relationship. Our results indicate that this general approach to measuring hospital case-mix provides a valid and robust measure of the expected cost of a hospital's case-mix.

Introduction

It is generally recognized that traditional public and private financing mechanisms have contributed to the continuing problem of inflation in hospital costs. Several approaches to this problem have been suggested in recent years, including major reforms in hospital reimbursement methods. Proposed alternatives to the current reimbursement system include negotiated rates, prospective budgeting, and the establishment of limits on either the rate of the increase or the level of hospital costs.

These alternative reimbursement methods are intended to create strong incentives, much like those found in a competitive market, for efficient use of hospital resources. Achievement of this objective is complicated, however, by the fact that hospitals treat patients for a wide variety of different diseases and conditions using many different combinations of diagnostic and therapeutic procedures. As a result, the average treatment cost per case for any hospital will vary with the clinical composition of its inpatient population (hospital case-mix).

Isolating differences in case-mix from other factors that affect hospital costs requires an independent measure of the expected costliness of a hospital's inpatient case-mix. This article describes research undertaken in the Office of Research of the Health Care Financing Administration (HCFA) to develop and test an independent measure of a hospital's Medicare inpatient case-mix. Although the research reported here has focused on measuring hospital case-mix for Medicare patients, these methods could be easily adapted to other classes of patients.

The discussion is organized in three parts. Part I presents a conceptual overview of the problem and an approach to its solution. It describes the application of this approach to the Medicare data and summarizes the empirical characteristics of the resultant hospital case-mix index. Part II describes the methods and results of our attempts to evaluate the reliability and validity of the index. Part III presents our conclusions.

Measurement Issues

Overview and General Approach

There are thousands of diseases and conditions that may cause a patient to be admitted to the hospital. Patients may have either mild or severe manifestations of their problems. In addition, they may have comorbid conditions or suffer complicating conditions during their stay. They may be treated medically or surgically, and the mode of treatment may vary in resource intensity, expected length of recovery time, and need for follow-up treatment. Finally, the problem may be only partly understood at the time of admission; it may require both diagnostic and treatment procedures or (as in admissions for elective surgery) only treatment procedures.

The number of possible combinations of diagnoses, procedures, complications and admitting status is obviously very large. For example, given 8,000 principal diagnoses,¹ five age classes, two treatment modes, and up to five potential co-morbidities or complications, 400,000 categories would be required to describe all possible combinations of these characteristics. The number of combinations that occur with significant frequency, however, is much smaller, and many of these combinations are similar in quantity of resources required in diagnosis and treatment. Thus, the essence of the problem is to find a method of summarizing this information so that we can predict, for any individual hospital, the relative costliness of the mix of patients that it treats in any given year.

The first step in resolving this problem is to classify hospital cases into a manageable number of categories so that cases within each category are reasonably homogeneous in cost. Such categories would then reduce the tremendous volume of patient information to a much smaller subset of distinct patient types.

The second step is to create weights that measure the national average cost of treating patients in different categories. If we normalize the average cost values by dividing each one by the average cost over all categories, then for any hospital (h) we can construct an overall summary measure of the relative costliness of its case-mix:

$${\text{CM}}_{\mathrm{h}}=\frac{\sum _i{\mathrm{P}}_{\text{ih}}\cdot {\mathrm{W}}_{\mathrm{i}}}{1/\mathrm{N}\sum _{\mathrm{h}}\sum _{\mathrm{i}}{\mathrm{P}}_{\text{ih}}\cdot {\mathrm{W}}_{\mathrm{i}.}}$$

That is, we multiply the hospital's proportion of patients in a given case category (P_ih) by the national normalized cost weight (W_i) associated with that category and sum these products across all categories. This sum, divided by the national average value over all hospitals, gives a measure of the hospital's expected costliness relative to all other hospitals, given its case-mix.² In other words, the index values would directly represent the relative costliness of each hospital's mix of cases compared to the national average mix of cases.

The accuracy and utility of this measure will depend on how the categories of cases and the weights are defined. The relevant criteria and the methods used to define each of these elements are described in the following section.

Case Type Categories

Criteria

The principal objective in developing a case-mix measure is to accurately reflect differences in average cost per case across hospitals that are solely attributable to differences in case-mix. The accuracy of this measure for individual hospitals will depend, in large part, on the degree to which cases in any category are homogeneous with respect to cost. If this is not true (for example, if the cases in each category represent a random collection of patients with varying treatment costs), then different categories would have similar expected cost values. As a result, case-mix index values for hospitals with different mixes of patients would not differ. Thus, from a measurement perspective, the most important criterion for case type categories is homogeneity of resources. The cost values for the cases in any particular category should be tightly distributed around the group average.

The potential use of a case-mix measure in a prospective payment system implies some additional criteria. The objective of prospective payment systems is to create incentives for economically efficient use of resources. The cost values attached to the case type categories implicitly define incentives for the hospital and standards of comparison against which hospital performance will be judged. The problem for the hospital administrator is to internalize these standards as a basis for control. The administrator's task will be facilitated if two additional criteria are met.

Number of Groups

The ability of a hospital administrator to reliably identify significant deviations from the standard depends on the number of groups in two conflicting ways. On the one hand, the administrator needs enough cases in a category to identify stable patterns of behavior. For example, one or two aberrant cases will not be significant in a hospital that treats 10,000 patients per year. This implies that a classification system with a large number of categories will not be useful at the hospital level. On the other hand, too few categories will tend to obscure significant patterns in the heterogeneity of the patients in each category. The ideal number of categories for a particular hospital will depend on the complexity and diversity of the cases it treats. An institution with a diverse and complex case load will need more groups than a hospital which treats a few simple case types. While there is no perfect number of categories for all hospitals, an order of magnitude of “hundreds instead of thousands” of categories (Fetter et al., 1980) should provide a reasonable trade-off between the level of homogeneity within the category and the hospital's need to have useful numbers of cases present in many categories.

Clinical Validity

Physicians strongly influence the use of hospital resources through their orders for tests and procedures. To control the use of resources within their institutions, hospital administrators must be able to communicate standards of behavior to the admitting physicians. This communication will be greatly facilitated if the categories are recognizable to physicians as representing clinically distinct types of patients.

Feasibility

Regardless of the intended application, a potential case-mix measure cannot be constructed unless the major characteristics required to classify patients can be readily measured. Thus, a fourth criterion is that the categories be defined by information that is neither difficult nor costly to obtain. This implies that applications of case-mix measurement methods in the present or near future will be restricted to using case type categories that can be distinguished on the basis of data that is already available or easily modified.

Additional criteria might also be included. It might be argued, for example, that a patient classification system should be defined only on the basis of patient characteristics (exogenous to the hospital), since the use of other variables may create undesirable incentives. For example, if procedures or specific services are used as surrogates for patient characteristics, then the hospital might attempt to influence the category to which any given case is assigned, that is, encourage the use of a specific procedure.

The potential seriousness of this problem, however, is counterbalanced in two ways. First, since performing a procedure entails costs for the institution, the difference in the payment rate would have to exceed the cost differential for such an incentive to exist at all. Second, even if the incentive were present, the hospital would have to influence its admitting physicians in the choice of treatment strategies. The physician's choice of treatment modality, however, is likely to be more strongly influenced by the relative risks to the patient and the economic incentives embedded in the physician fee structure than by any effects on hospital reimbursement. Accordingly, it seems reasonable to suppose that the administrator's influence on physicians regarding this choice would be minimal. Thus, although the use of exogenous patient characteristics in defining patient categories may seem desirable, we do not believe that it is critical.

Completed Patient Classification Systems

Three patient classification systems have been developed which define mutually exclusive and exhaustive case type categories that could be used as the basis of a hospital case-mix measure. Three additional systems are currently under development. These six systems are described and briefly evaluated below in terms of the extent to which their patient categories meet our criteria.

CPHA System (List A)

This sytem, developed in the late 1960s (Ament, 1976), groups patients into 3,510 categories based on a cross-classification of patient characteristics such as principal diagnosis, age, and whether the patient was treated surgically or medically. This system is simple to use and requires only readily available information from the patient's clinical abstract. However, many of the categories may contain dissimilar patients. For example, two patients with a broken hip who had operating room procedures would be grouped together, although one may have had a hip replacement and the other, surgical treatment for urinary blockage. In addition, the existence of co-morbid or complicating conditions is ignored. Thus, these groups are often not homogeneous, either clinically or in use of resources. Solving this problem (by distinguishing major and minor procedures and noting the presence or absence of complicating conditions) would raise the number of groups well above 7,000. However, a case-mix measure also requires a set of cost weights associated with the clinical categories. In this respect, a classification system with even 3,510 groups would pose serious difficulties in estimating reliable cost weights.

Diagnosis Related Groups (DRGs)

The original DRG patient classification system (Fetter et al., 1980, 1981) was developed at Yale University in the early 1970s. It groups patients into 383 categories (old DRGs) based on information from the discharge abstract such as principal diagnosis, secondary diagnoses, age, and surgical procedures. The old DRGs have been widely applied in utilization review and as a basis for case-mix measurement in hospital rate-setting systems (for example, in New Jersey, New York, Maryland, and Georgia).

This system has been superseded by an entirely new set of DRG definitions, (Fetter et al., 1982) designed for use with diagnosis and procedure information coded in the ICD-9-CM coding system (International Classification of Diseases, Ninth Revision-Clinical Modification). In the new DRG system, patients are grouped into 467 categories derived from a multistage process applied in conjunction with a nationally representative sample of 1.4 million patient discharge records. First, a panel of physicians allocated all ICD-9 diagnosis codes to 23 major diagnostic categories (MDCs), based on the body system affected and the specialty of the physician likely to treat the case. In successive stages, the panel subdivided the cases within each MDC according to the specific principal diagnosis, type of surgery, presence of specific complicating or co-morbid conditions, and patient age. The panel did not adopt potential distinctions based on these characteristics at any stage unless the national data base showed that they were important in explaining resource use and the panel determined that the distinction was clinically sensible. Thus, the new DRGs have the following advantages. The category definitions cover virtually the entire patient population. They have been extensively reviewed by physicians throughout their development. They conform to the actual delivery of inpatient care in the hospital. They group those inpatient cases together which are generally quite similar in use of resources. Finally, inpatient records may be easily classified by an efficient computer program using widely available discharge abstract data.

Systemetrics Disease Staging

In this approach, a panel of physicians has defined between four and seven disease stages for each of 406 diseases, resulting in approximately 2,000 categories (Gonnella et al., 1981). Each stage is intended to represent a medically homogeneous group of patients. However, since more than one diagnostic and therapeutic regimen may be associated with any stage of a disease, and since complicating or co-morbid conditions and type of procedures are not considered in staging, these categories are not homogeneous in treatment services or cost. In addition, accurate assignment of patients to severity stage categories requires that each patient's medical record be examined by specially trained personnel. The potential expense of individual chart review, the large number of categories, and the lack of resource homogeneity of the staging categories effectively eliminate this approach as a candidate for current use in measuring hospital case-mix.

Experimental Systems

Like disease staging, these systems use data from the patient's medical chart in addition to the standard abstract data. These projects were designed, in part, to assess the utility of additional clinical information in forming homogeneous patient groups.

George Washington University (GWU) Intensive Care Severity Study

This study was designed to measure the severity of illness among patients in hospital special care units (Knaus et al., 1981). Objective indicators (clinical test scores) of the necessity of intensive care were developed and tested in two hospitals. This project was not intended to develop a measure applicable over all patients, or for use in a reimbursement context. Expanding this project beyond the special care setting would require a major effort over a significant period of time. Even then, the severity scores would need to be integrated with other information to classify patients. Finally, beyond this developmental work, this system would require significant changes to the current discharge abstract.

Johns Hopkins' Severity Score

This approach is designed to measure severity of illness among hospital inpatients (Horn et al., 1981). The basic method involves assigning a severity score to each case based on an examination of the patient's medical record. In essence, a nurse or physician considers several aspects of severity and subjectively assigns a number indicating the relative severity of the case. Thus far, this approach has been applied to less than half of the 83 major diagnostic categories on which the old DRGs were based. To remove subjectivity from severity measurement, the scoring might ultimately be based on some combination of specific signs and symptoms and clinical test results, but this is a longer term project. Thus, like the GWU project, universal implementation of this approach is not an immediate alternative.

Blue Cross of Western Pennsylvania Patient Management Paths

This case type classification uses the patient's presenting condition/reason for admission (from the medical chart) as the initial classification variable (Young et al., 1982). The categories (patient management paths) are then based on the principal diagnosis, secondary diagnoses, and procedures. Paths for all disease entities are not yet defined.

The project is expected to be completed in late 1983. At that point, the paths will need to be reviewed by outside physicians and tested using data from other geographic areas. Additional time would then be required to revise the standard discharge abstract.

DRGs Revisited

After considering the advantages and disadvantages of the three complete patient classification systems that are currently available, we chose to use the new DRGs in this research. This is not to imply that the DRGs completely meet our criteria. The homogeneity of the cases within a category in terms of resource use (cost) varies substantially among the DRGs. As might be expected, this variation occurs for several reasons. First, the DRGs reflect the limitations of the current state of clinical knowledge. Some categories, such as treatment for cataracts, are well defined and homogeneous, while others, such as psychiatric diagnoses are poorly defined and therefore provide a weak basis for predictions of resource use. Second, even well defined categories will reflect variations in patterns of medical practice involving both service intensity and length of stay. In some hospitals, for example, cataract patients consistently have an average stay of three days, but in others, the average stay is five days. Third, individual patients respond differently to both the disease and its treatment. Finally, problems with the quality of the clinical data also contribute to apparent heterogeneity within any category.

These problems would exist in any system of case type classification. The question is not whether the DRGs are perfect, but rather what the consequences are of such heterogeneity. We discuss this issue in detail in Part II.

Our second criterion, the number of groups, concerns the extent of reduction in the dimensionality of the data. Since all possible combinations of principal diagnoses, age categories, procedures, and complicating or co-morbid conditions could result in 400,000 or more categories, 467 groups represent a very substantial reduction in dimensionality.

Our third criterion is clinical validity. As we noted earlier, clinical judgments are central to the entire process of defining DRGs, from the initial definition of the MDCs to the decision to accept, reject, or modify any DRG definition suggested by analysis of the sample clinical records within each MDC. Nevertheless, physicians have criticized both the old and the new DRGs on several grounds. First, given the process, some clinically heterogeneous DRGs are inevitable. However, these “other” categories, representing the cases remaining in an MDC after all clinically distinct DRGs have been defined, usually contain relatively small numbers of cases. Second, the clinical homogeneity of some major DRGs (acute myocardial infarction, for example) has also been questioned. However, DRGs based on the information conveyed by the physician's choice of principal diagnosis cannot be clinically homogeneous if that information is unclear. If heart disease is not well understood, or if the diagnostic terminology is not used distinctly (for example, etiological and manifestational diagnoses are frequently interchanged), then no classification system can isolate clinically distinct groups of heart patients. Third, the DRGs are sometimes criticized on the basis of small numbers of aberrant cases that appear in otherwise homogeneous groups. Unusual cases, such as patients who had major procedures apparently unrelated to any of their diagnoses, will appear in virtually any set of patient records. Some of these represent miscoded or incomplete medical records, while others are unusual but still legitimate. A substantial effort was made in the development of the new DRGs to Isolate such aberrant cases by placing them in the “other” categories, or by excluding them entirely when they were clearly incomplete or logically invalid. Thus, the number of aberrant cases remaining in any DRG is generally quite small.

These problems with the DRG classification system are real, and the individual criticisms are generally valid. Clinical validity, however, (like resource homogeneity) is a question of more or less, not yes or no. To conclude on the basis of these limitations that the entire system is invalid would be to risk committing the fallacy of composition, that is, extrapolating from specific examples to reach a general conclusion. Instead, judgments regarding the clinical validity of any patient classification system should refer to the performance of the system as a whole. Thus, despite these criticisms, it seems clear to us that the advantages of the DRG classification system greatly outweigh its disadvantages.

Category Weights

Approaches to Weight Definition

The second element of a measure of relative costliness is a set of cost weights that correspond to the case categories. Under ideal circumstances, the expected cost weights for the DRGs should reflect the efficient marginal costs of producing an additional unit (case) in each DRG. At equilibrium in a fully competitive market, this would be equivalent to the minimum average cost of production and the market price in each DRG (given available technology, factor input prices, and the distribution of income). Thus, if we could be assured that markets for hospital inpatient treatment were characterized by strong price competition and profit maximization, then total hospital charges (prices) for different case types would provide suitable weights for the case categories.

The applicability of this assumption to the hospital industry, however, is somewhat doubtful. Hospitals produce a wide variety of individual services such as laboratory tests, radiologic procedures, and nursing care, which are bundled (ordered) in various combinations by physicians in diagnosing and treating individual patients. Insurance against the cost of these services dominates the entire transaction between patient, physician, and hospital. That is, the benefit provisions and payment methods in most health insurance plans do not encourage the patient, the physician, or the hospital to minimize the total cost of the bundle of services used to treat any particular case. Thus, although the hospital may produce specific tests and therapies efficiently, there is no assurance that the total cost of the aggregate of services will be minimized. Further, current hospital reimbursement methods encourage hospitals to set prices to cross-subsidize between ancillary and routine services and among ancillary services. As a result, there is little reason to believe that the average total hospital charges for each case category reflect efficient costs.

There are at least three potential solutions to the problem of defining efficient cost weights for the DRG categories. First, we could ask panels of expert clinicians to define the types and quantities of specific inpatient services, including days of routine and special care, that they believe a typical patient in each DRG category should receive. Then we could estimate the efficient unit cost for each type of service. By applying these estimates to the physician-specified quantities, we could obtain a normative total cost per case value for the typical bundle of services in each DRG category. This would be similar to the approach currently under study at Blue Cross of Western Pennsylvania (Young et al., 1982).

Although these normative values could be easily converted to a set of relative weights for the DRGs, this approach presents both conceptual and practical problems. The conceptual problem may be illustrated by the results of some previous research on methods of defining standards of care in office-based practice. Hare and Barnoon (1973) found that although physicians agreed about the services that specific types of patients should receive and about the services that patients actually received, there was little correspondence between the two. If this discrepancy reflects differences in decision-making between ideal and constrained circumstances, then neither set of standards would necessarily represent economically efficient relative costs.

In addition, the logistical difficulties and expense of any attempt to achieve national consensus on such normative or empirical standards of care for all types of hospital cases would be enormous. Therefore, despite whatever intuitive appeal it may have, we did not pursue this approach.

A second alternative would be to select one or more hospitals that treat patients with a high degree of efficiency. Then we could use clinical and cost data from these model institutions to calculate efficient relative cost weights for the DRG categories. In the absence of a prior measure of relative costliness due to case-mix, it is difficult, if not impossible, to identify “efficient” hospitals. Therefore, although this approach may be an interesting subject for future research, we have not pursued it thus far.

The third approach, and the one we have chosen, is to define empirical weights using data from a large number of hospitals on the clinical characteristics and billed charges of their patients, as well as detailed cost information for each institution. The objective of this approach is to use the total charges reported by the hospitals for each case in any DRG category to develop a surrogate measure of the efficient relative cost of treatment for that category. The total charges for individual cases in any DRG, however, will vary for a number of reasons that are unrelated to economic efficiency.

Hospital pricing policies, for example, result in differential mark-up rates (cross-subsidies) between ancillary and routine services and among ancillary services. Thus, hospital charges will not be proportional to average costs. In addition, since hospital treatment takes place in local rather than national markets (that is, hospital services cannot be easily transported or stored), the level, and perhaps the structure, of average costs among the case categories may differ among local markets according to the demand and supply conditions in each local area. Thus, in the short run, costs for individual cases may be relatively higher in a market area in which skilled labor and other health service inputs are relatively scarce (that is, factor input prices are higher).

Costs for individual cases will also vary with the level of graduate medical education in the hospital. Other sources of variation include differences in practice patterns across areas and among individual physicians, variations in the quality of care, hospital size, and the availability of specialized facilities.

We are able to adjust for the gross effects of hospital pricing policies, variations in factor input prices, and variations in the level of teaching activity. We cannot adjust for differences due to any of the remaining factors. By implication, this means that relative weights based on this approach reflect the average pattern of practice and the average quality of care in each DRG. More important, the relative structure of the average cost weights is assumed to reflect the structure of efficient costs among the case categories.

Application to the Medicare Data

Data Sources

The relative weights for the DRGs are constructed using data from five sources. The Medicare Cost Report (MCR) is an audited source of cost data which provides the basis for setting the amount of final payment for the hospital. Clinical characteristics and billed charges data for an approximate 20 percent sample of Medicare inpatient hospital discharges in short-stay hospitals are from the MedPar(MP) file. For calendar year 1979, this file contains approximately 1.93 million observations in 5,947 hospitals. The Bureau of Labor Statistics (BLS) compiles total hospital worker compensation and employment data from quarterly tax reports submitted to State employment security agencies. These county-specific aggregate data are used to construct a hospital wage index. Our data on the number of full-time equivalent interns and residents are from the Provider of Services (POS) file, which is derived from an annual survey of hospitals which participate in the Medicare program. The discharge file (DF) is the source for the number of Medicare cases treated by a hospital during the year. This source appears more complete than similar data from the cost reports. Technical Note A describes the origin and contents of these data sources and associated problems of data quality.

Method

For ease of exposition, we have separated the process of defining DRG weights into steps.

1. Classify all cases into DRGs.

   Because of the limitations of the MedPar clinical data (that is, the absence of specific secondary diagnoses and procedures and limited information about discharge status), the DRGs used for classifying Medicare cases are a subset of the 467 DRGs developed by Yale University. Thus, DRGs distinguished on the basis of specific secondary diagnoses (for example, DRGs 387 and 388—premature newborns with and without major problems) or on the basis of specific secondary procedures (for example, DRGs 106 and 107—coronary bypass with and without catheterization) are combined to form more general categories. A total of 20 DRGs had to be collapsed into 10 more general categories for use with the MedPar data.

2. Compute the adjusted cost for each case.

   The second step in calculating the weights is to create an adjusted cost for each case by 1) multiplying the number of days the patient spent in a regular room (MP) by the hospital's routine cost per day (MCR); 2) multiplying the number of days the patient spent in a special care unit (MP) by the hospital's special care unit cost per day (MCR); 3) multiplying the ancillary charges (MP) by the relevant departmental cost to charge ratios (MCR). This minimizes the effects of cross-subsidization between hospital service departments to make the billed charges more comparable across hospitals. Table 1 illustrates the computation of the adjusted cost.

3. Adjust for indirect teaching costs.

   The next step is to standardize the adjusted cost values for the gross indirect effects of variation in the level of teaching activity across hospitals. This is accomplished by dividing the adjusted cost for any case i in hospital h (step 2) by a variable representing the proportionate effect of the level of teaching activity on average costs:

   $$\text{Teaching Adjusted Cost i},\mathrm{h}=\frac{\text{Adjusted Cost i},\mathrm{h}}{\text{Teaching Adjustment Factor h}}$$

   where the teaching adjustment factor h = 1.0 + (.569 × residents/beds h). (Technical Note A describes the calculation of the ratio of residents per bed. Part II describes the origin of the teaching effect (.569).) Given the definition of this variable, a hospital with no residents would have an adjustment factor of 1.0. A hospital with .10 residents per bed would have its adjusted cost values reduced by a factor of 1.0569, or about 6 percent.

   This adjustment is somewhat crude for two reasons. First, it implies that the entire teaching effect is attributable to output of graduate medical education rather than patient care. Second, the effect of this teaching adjustment on the patient care costs of any hospital will be constant across DRGs, even though the real effect of teaching activity is likely to vary with the specialty composition of the hospital's teaching programs. Given the limitations of our data, however, we are unable to address either of these issues.

4. Standardize variation in area wages.

   In this step we attempt to account for the effects of differences in area wage and wage related costs across hospitals. The labor share of the teaching adjusted cost for each case is deflated by the wage index. The estimated labor share, obtained from HCFA's Office of Financial and Actuarial Analysis, measures the average proportion of total hospital costs likely to be affected by local variations in the level of wages and salaries of hospital workers. It is defined as the sum of the weights for selected items in the HCFA Hospital Market Basket Index (Freeland et al., 1979). In 1979, the estimated labor share was .8108. (Technical Note A describes the origin of this estimate and the calculation of the hospital wage index.)

   Using these measures, we can standardize the cost value for case i, hospital h as follows:

   $$\begin{array}{l}\text{Standardized cost i},\mathrm{h}\\ =((.8108\times \text{Teaching Adjusted Cost i},\mathrm{h})/\text{Wage Index h})\\ +\left(.1892\times \text{Teaching Adjusted Cost i},\mathrm{h}\right).\end{array}$$

   Since we have no measure of variations in prices of nonlabor inputs, we are unable to adjust for any differences that may exist. The implicit assumption in this case is that such variations are small or nonexistent.

5. Eliminate outlier cases from each DRG.

   Given the characteristics of the MedPar data, we know that some of the cases in each DRG are misclassified or are extreme values for other reasons. To prevent unusual cases from affecting the weights, we define maximum and minimum cost values for each DRG.

   Descriptive statistics for the standardized costs within each DRG indicate that the distributions are highly peaked (suggesting a high degree of central tendency) and skewed right. This leads us to believe that the appropriate representation of this distribution is log-normal; that is, the natural logarithms of the observations are normally distributed. This is not unusual for economic data: although standardized costs can be very large, they cannot be less than zero.

   To remove obviously extreme values, we have chosen a conservative statistical criterion (the mean plus or minus three standard deviations) that will eliminate approximately one-half of one percent of the cases at each end of the distribution. However, in this case the geometric mean reflects the skewness of the distribution, while the more usual arithmetic mean does not. Cut-off points defined by applying our criterion to the geometric mean are therefore asymmetric. We eliminated standardized cost values outside these cut-off points. This criterion eliminated approximately 10,000 cases out of approximately 1.83 million.

6. Compute the weight.

   The standardized weight for any DRG is the arithmetic mean of the remaining standardized costs. The arithmetic measure was selected because it is easily understood and has convenient mathematical properties. Moreover, the correlation between geometric means and arithmetic means over all DRGs is extremely high. We therefore lose nothing by choosing the more convenient value.

7. Evaluate reliability of cost weights in low volume DRGs.

   In any sample of patient records, some DRGs will contain relatively few cases (for example, obstetrical cases in the Medicare population). For a DRG in which there is little variation in treatment cost, a precise and reliable average cost weight may be computed even though the number of cases is small. If treatment cost is highly variable, however, we cannot be very confident that an average cost weight computed from a small number of records will provide an accurate representation of the relative costliness of the case type category. If the cases in DRGs of the latter type are drawn at random from all hospitals (that is, they are not concentrated in a few specialized hospitals), they may be eliminated without loss of useful information.

   To identify such DRGs, we focused on the relationship between the number of cases in each DRG (sample size) and the expected precision of its estimated mean value. For each DRG we have an estimate of both the mean (X̄_i) and the standard deviation (S_i) of the standardized costs values. We also know the number of cases in each DRG (N_i). This information is sufficient to estimate the standard deviation of the distribution of the estimated mean values (in repeated samples) around the true mean. This statistic, called the standard error (SE_i), indicates how precise our estimate of the mean really is. That is, if we took repeated samples of N_i cases from all possible cases in DRG_i, this statistic measures how much the estimated mean for the DRG would vary among the samples. From the law of large numbers we also know that the standard error of the mean will decline as the sample size (N_i) is increased.

   We can establish a precision criterion, that is, we want our estimated mean to be within an interval of ± 10 percent around the true mean 90 percent of the time. Then using the relationship between sample size and precision and our estimate of the standard deviation (S_i), we can find the minimum number of cases (N_i) required to meet the criterion. If we have at least this number, we retain the DRG. Otherwise we eliminate it from further analysis. The formula, solved for N_i is:

   $${\mathrm{N}}_{\mathrm{i}}={\left(\left(16.5\right){\mathrm{S}}_{\mathrm{i}}/\overline{{\mathrm{X}}_{\mathrm{i}}}\right)}^2.$$

   Application of this criterion identified 118 DRGs (of 470) with too few cases. A total of 47 of these (including the 10 categories that were previously collapsed) had no cases in our sample data. Of the remaining 71 categories, two sets of three DRGs were collapsed into one DRG each to retain information about expensive burn care patients and about alcohol and drug detoxification cases.

   Although neither of these clinical groups is important for the Medicare population generally, both may be important for some individual hospitals. In addition, we eliminated DRGs 468-470 because these categories contain different varieties of uninterpretable cases (for example, invalid diagnosis or diagnosis not reported). These procedures eliminated 119 DRGs, leaving 351 usable categories.

8. Derive relative (normalized) weights.

   To convert the standardized mean values to relative values, we divided each category mean by the average of the mean values over all (351) DRGs. We normalized the weights in this fashion to express comparisons in relative (as opposed to dollar) terms. This permits comparisons over time as well as across hospitals.

Table 1. Computation of Adjusted Cost for Each Case¹.

Data Source		Result
MCR	MedPar
Routine per Diem Cost	× Routine LOS	= Routine Cost
Special Care per Diem Cost	× Special Care LOS	= Special Care Cost
Ancillary Department Cost/Charge Ratio2	× Ancillary Charge	= Ancillary Cost
	Sum	= Adjusted Cost

¹This procedure was applied to 1.83 million records from hospitals for which adequate cost report data were available.

²

Departments:

1. Operating Room
2. Laboratory
3. Radiology
4. Drugs
5. Medical Supplies
6. Anesthesia
7. Other

The Case-Mix Index and Its Characteristics

For any hospital (h) we can now calculate the proportion (P_ih) of its sample patients falling into each of the 351 DRGs. We multiply these proportions by the relative weights (W_i, from step 8) and sum across all DRGs. This sum divided by the national average over all hospitals gives a measure of the expected relative costliness of the hospital's case-mix. For hospital “h” this is:

$${\text{CM}}_{\mathrm{h}}=\frac{\sum _{\mathrm{i}}{\mathrm{P}}_{\text{ih}}\cdot {\mathrm{W}}_{\mathrm{i}}}{1/\mathrm{N}\sum _{\mathrm{h}}\sum _{\mathrm{i}}{\mathrm{P}}_{\text{ih}}\cdot {\mathrm{W}}_{\mathrm{i}}}$$

Table 2 illustrates this calculation for five hospitals. This series, for all hospitals, is the Medicare case-mix index.

Table 2. Illustrative Calculation of the Medicare Case-Mix Index.

Percent of Medicare Discharges by DRG1
Hospital	DRG 1	DRG 2	DRG 3	DRG 4	DRG 5	Expected Cost per Case2	Index3
A	2.5	27.3	10.5	41.5	18.2	$1660.40	.8900
B	21.0	0.0	30.1	2.0	46.0	2401.30	1.2872
C	40.6	5.0	2.3	47.2	4.9	1346.30	.7217
D	5.1	18.4	62.5	10.0	4.0	2990.70	1.6031
E	30.4	65.0	1.0	1.6	2.0	929.00	.4980
National Average Percent
	19.92	23.32	21.46	20.46	15.02
National DRG Cost Weight
	1000.00	$800.00	$4100.00	$1500.00	$2000.00	$1865.54

¹Adjusted to make these five DRGs hypothetically represent all 351 Medicare DRGs.

²For hospital A, calculated as follows: .025 (1000) + .273(800) + .105(4100) + .415(1500) + .182(2000) = $1660.40.

³For hospital A, calculated as $1660.40 divided by $1865.54 = .8900.

This index is intended to predict expected relative cost per case for each hospital, given its case-mix, independent of other factors that may influence costs. An index value of 1 indicates expected Medicare costs equal to the average value for all hospitals, while a value of 1.5 indicates expected costs of one and one half times the average.

Descriptive Statistics for the Medicare Case-Mix Index

The Medicare case-mix index (CMI) for the 5,071 hospitals with more than 50 sample discharges in our 1979 data set ranges from a low of .51 to a high of 1.83, with a mean and standard deviation of 1.0 and .08 respectively.³ Third and fourth moment statistics indicate that the distribution of CMI values is more highly peaked than a normal distribution but not skewed.

Table 3 shows the Pearson correlation values between the case-mix index and other selected variables. Technical Note A contains detailed definitions of these variables. The signs and magnitudes of the correlation coefficients are generally consistent with our expectations. Thus, higher case-mix index values are found in larger hospitals and in larger cities; teaching hospitals treat costlier cases than non-teaching hospitals, and average cost per Medicare case is positively associated with the case-mix index.

Table 3. Case-Mix Correlations.

	MCD	WI	INT	BEDS	SCV	MCV	LCV
CMI	.60	.43	.36	.54	.07	.16	.29

CMI—Medicare case-mix index

MCD—Medicare average inpatient operating cost per discharge

Wl—Wage index

INT—Number of interns and residents per bed

BEDS—Hospital bed size

SCV—Urban area (SMSA or NECMA), population less than 250,000

MCV—Urban area, population 250,000 to 1,000,000

LCV—Urban area, population over 1,000,000

Number of observations = 5,071

These simple correlation values suggest that the case-mix index may provide a useful measure of the relative costliness of a hospital's case-mix. In the next part, we evaluate the reliability and validity of this measure.

Evaluation of the Medicare Case-Mix Index

Since we have no standard (that is, no certified independent measure) of the expected costliness of a hospital's case-mix, we cannot assess the validity of the index directly. However, because of the way the index was constructed, we expect its relationship to Medicare average operating cost per discharge (MCD) to be proportional. Thus, we can assess indirectly the validity of the index by evaluating the relationship between Medicare case-mix (CMI) and Medicare cost per case using a hospital average cost function. However, we must first resolve two problems to ensure the validity of this test.

First, our index values are based on a 20 percent sample of Medicare patient bills. Thus, for some hospitals the number of sample cases may be too small to provide a reliable measure of expected relative cost. Second, the use of national average weights to compute the index rests on the assumption that the relative structure of costs across the DRGs is similar for all hospitals (Klastorin and Watts, 1980). If this assumption is not (approximately) correct, then the case-mix index may only be computed and evaluated within groups of hospitals with similar cost structures.

Either of these potential problems would result in random error in the case-mix index values for the affected hospitals. Since this would damage our ability to obtain an accurate estimate of the empirical relationship between the case-mix index and Medicare cost per case, we address these problems first.

Sampling Error

To assess the effect of sampling error on our case-mix estimate for individual hospitals, we focused on the relationship between the precision of the estimate and the number of sample cases (sample size) used to obtain it. There is one case-mix index value for each hospital. Using these values, we wish to make inferences about how the estimated values would vary among repeated samples (of the same size) for each hospital and how rapidly the amount of variation would decrease in response to increases in the sample size. Then, for any level of reliability we choose, we can identify the minimum number of sample cases that a hospital must have to meet the reliability criterion. This is analogous to the treatment of low volume DRGs in Part I.

To carry out this analysis, we took ten 10 percent random samples of the cases reported by each hospital. For each hospital, we calculated 10 case-mix index values using the cases in each subsample and the original national weights. Then we calculated the standard deviation of these estimates for each hospital and divided it by the average of the hospital's subsample case-mix index values to get the coefficient of variation (CV). Thus, for each hospital we had an estimate of the relative variation in the subsample case-mix values associated with the size (number of cases) of the subsamples.

The next step was to estimate the unit coefficient of variation (UCV) of the parent population from which these subsamples were drawn. This is a single number that expresses the inherent variability, in terms of relative costliness, of the cases treated by any hospital. This number is not observable, but it may be estimated from the CVs just calculated. For a particular hospital (h), the UCV estimate is the product of the hospital's CV and the square root of its average subsample size; that is,

$${\text{UCV}}_{\mathrm{h}}={\text{CV}}_{\mathrm{h}}\cdot {\left({\mathrm{N}}_{\mathrm{h}}\right)}^{1/2}.$$

Thus, we have an estimate of the parent population UCV from each hospital. Although the estimates are more variable where the subsample size is smaller, the values are similar across all hospitals. (This suggests that all hospital subsamples have been drawn from the same or highly similar parent populations.) For the purpose of this analysis, our estimate of the UCV for the parent population is the simple average of the hospital UCVs, 0.384. (Alternative estimates of the parent population UCV ranged as high as 0.449.)

Given these UCV estimates, we can calculate the minimum number of cases required to meet any precision criterion. Table 4 presents the results of these calculations for selected precision criteria.

Table 4. Minimum Number of Sample Cases Required for Various Precision Criteria and UCV Estimates.

Criterion	UCV Estimate
(Precision Level1; Confidence Level2)	.384	.449
± 10; .90	32	44
± 10; .95	46	63
± 5; .90	129	175
± 5; .95	182	249

¹Precision level is defined as the maximum percentage of sampling error in the hospital's case-mix index that is acceptable under the criterion.

²Confidence level is defined as the probability that any sample estimate will fall within the specified precision level.

For example, for UCV = 0.384, if the desired criterion were that at least 90 percent of the estimated hospital index values be within plus or minus 10 percent of their “true” index value, at least 32 cases would be needed from each hospital.⁴

It should be noted that these precision criteria specify the maximum level of acceptable sampling error. Table 5 shows the theoretical sampling error distribution. Given a UCV value, it shows the percentage of hospitals in which sample case-mix index estimates are expected to be within a given percentage (“X”) of their true values for various sample sizes.

Table 5. The Percentage of Hospital Sample Index Estimates Within “X” Percent of Their True Values at Various Sample Sizes and UCV Estimates.

	@ UCV = .384, “X” =				@ UCV = .449, “X” =
Number of Sample Cases	1%	2.5%	5%	10%	1%	2.5%	5%	10%
30	13%	31%	57%	89%	11%	27%	50%	83%
40	15	35	64	93	13	31	57	88
50	16	39	70	96	14	34	62	92
60	18	43	74	98	15	37	66	95
70	19	46	78	99	16	40	70	96
100	23	53	85	99 +	20	47	79	99
200	32	70	96	99 +	28	62	92	99 +
500	48	90	99 +	99 +	42	84	99 +	99 +

Thus, for UCV = .384, 13 percent of the hospitals with 30 cases are expected to have estimated case-mix index values within 1 percent of their true values; 89 percent of the index estimates based on 30 cases would be within 10 percent of their true values.

Although the choice of a particular precision criterion is somewhat arbitrary, the use of the case-mix index in hospital reimbursement suggests that the criterion should reflect a balance between the risk to hospitals with index values that are underestimated as a result of sampling error and the cost to the program of providing special treatment to hospitals with too few sample cases to satisfy the criterion. An increase in the minimum sample size will reduce the risk of error for hospitals, but it also will increase the cost to the program of treating a larger number of hospitals with too few cases on an exception basis.

Although there is no perfect answer, a minimum of 50 sample cases seems to provide a reasonable balance of the competing risks. Under either UCV estimate, less than 40 percent of the hospitals with 50 sample cases could be expected to have a sample case-mix index with a sampling error greater than 5 percent. Half of these (or less than 20 percent) would have a sample index that underestimated the true index value. A substantial fraction of hospitals with underestimates would not suffer any adverse effect in terms of actual reimbursement under a system of reimbursement limits because their actual costs are below average. Thus, only about 10 percent of the hospitals with 50 sample cases would actually face any significant risk of loss due to sampling error, and these hospitals would have the right to submit complete data (rather than sample data) on an appeal basis. Of course, most hospitals have more than 50 sample cases, so the average probability of loss for all hospitals that meet this criterion would be still lower.

There are approximately 500 hospitals with less than 50 sample discharges in our data base. These hospitals tend to be small hospitals; 89.3 percent of the hospitals with less than 50 sample discharges have less than 50 beds.

Inappropriate Aggregation of Index Weights

The use of a single set of weights for all hospitals assumes that the structure of the relative cost values across the DRG categories is similar for all hospitals. If this assumption is not at least approximately correct, then case-mix comparisons among hospitals should be limited to groups In which the category weights are similar. If this is not done (that is, the weights are aggregated across dissimilar hospital groups), then the case-mix index values across all hospitals will be subject to random distortion. That is, within such a group, hospitals that have different index values based on the true group weight structure may appear more or less similar when the index is based on average aggregate weights. If the difference in structure is substantial, the rank order of the index values could actually be reversed between the two measures.⁵

There are several ways to test for systematic differences in cost structure. The most powerful method would be to use a fully specified cost function such as the translog type developed by Christensen, Jorgensen, and Lau (1973). This form would allow disaggregation of the case-mix index, since it relates multiple output quantities and multiple input prices to total cost. Disaggregation would let us identify any interaction effects between various case types and between case types and factor prices. Our ability to estimate cost functions of this type is limited, however, because we have no information on the non-Medicare case load of each hospital.

In a preliminary attempt to determine the extent of this problem, we estimated Pearson correlation coefficients using cost weights calculated separately for the hospitals in each of the seven hospital groups, distinguished by bed size and location (SMSA, non-SMSA), which are used in the Medicare Section 223 cost limits system. (See Technical Note A for group definitions.) Table 6 shows the results. We also computed correlations comparing national weights and index values with weights and index values computed within each of the four census regions. Table 7 displays these results.

Table 6. Correlation Results: Group Versus National Weights and Group Versus National Case-Mix Measures.

Pearson Correlation Values
	National Weights	National Case-Mix	(N)
Urban Hospitals (SMSA)
Group 1 (0.99)	.87	.98	(608)
Group 2 (100-404)	.99	.99	(1649)
Group 3 (405-684)	.98	.99	(398)
Group 4 (684)	.97	.98	(105)
Rural Hospitals (Non SMSA)
Group 5 (0-99)	.91	.98	(1683)
Group 6 (100-169)	.95	.98	(402)
Group 7 (169)	.97	.99	(226)
(N)	(351)	—	(5071)

Note: The correlation values for 1979 weights between groups ranged from .81 (Groups 1 and 6) to .96 (Groups 3 and 4).

Table 7. Correlation Results: Regional Versus National Weights and Case-Mix Indexes.

	National Weights	National Case-Mix	(N)
Region
Northeast	.97	.98	(826)
North Central	.99	.99	(1523)
South	.99	.99	(1903)
West	.99	.99	(819)
(N)	(351)	—	(5071)

Note: The range of correlation values for 1979 weights between regions ranged from a low of .94 (Northeast and West) to a high of .98 (South and North Central).

The correlations are generally higher than we expected. Differences in the DRG cost structure seem to occur (if at all) in small, rural hospitals. However, since some of the cost weights for the 351 DRGs included in the analysis for the small hospitals are based on relatively few cases, even this conclusion must be tentative.

It is also Instructive to compare case-mix index values for individual hospitals based alternately on their group and national weights. Table 6 shows Pearson correlation values between these index values for the hospitals in each group. Table 7 shows similar values for each region. As we might expect (since the DRG case proportions are fixed for any hospital), these values are even higher. Although there are some perceptible differences between the group weights and the national weights, especially among the smaller hospitals, they do not appear to affect the case-mix index values substantially. Thus, this problem does not appear to pose any significant obstacle to our evaluation of the Medicare case-mix index.

The Relationship of Medicare Case-Mix to Medicare Cost per Case

Our hypothesis (that the Medicare case-mix index (CMI) is proportionately related to Medicare cost per case (MCD)) implies that a hospital with a 10 percent higher CMI value should have a 10 percent higher MCD value compared to otherwise similar hospitals. Our assessment of the validity of the case-mix index will depend on how closely its actual relationship to cost per case meets this expectation. We can test this hypothesis directly by estimating a hospital average cost function in which we focus on the estimated coefficient for the Medicare case-mix index.

Cost Function Estimates

A hospital average cost function relates average cost to factors (for example, input prices) that are believed to affect costs but are outside hospital control (exogenous variables). An estimated cost function is normally interpreted as a representation of the economically efficient relationship between average cost and the exogenous variables. This interpretation rests, however, on the presumption that the industry operates under conditions that strongly encourage cost minimization. If hospitals do not minimize costs, then the relationships that determine minimum costs cannot be accurately estimated. The estimated equation will instead represent average behavior.

The best approach to this problem is to develop a model of hospital utility maximization. This simultaneous equation model would be used to isolate the economically efficient relationships between output mix, Input prices, scale of output, and average costs from the effects of other factors. However, a generally accepted model of hospital behavior is not available, and, even if it were, it is doubtful that we would have measures of all of the relevant variables. Thus, we are unable to pursue this approach.

Under these circumstances, the best available alternative is to estimate a single equation cost function. The estimated equation, however, will reflect the average relationship between hospital costs and the exogenous factors rather than the economically efficient relationship. In addition, interpretation of our results may be further clouded by all the usual difficulties of empirical estimation, for example, biases in coefficient estimates due to missing variables and errors in the dependent and independent variables. We treat these problems in more detail following the description of our results.

The cost function we have estimated treats Medicare cost per case (MCD) as a function of Medicare case-mix (CMI), teaching intensity (INT), hospital wages in the local area (Wl), bed size (BEDS), and small, medium, or large city (SMSA) size (SCV, MCV, LCV). We used ordinary least squares regression to estimate the coefficients of the independent variables. This technique permits estimation of the relationship of Medicare case-mix to Medicare cost per case while simultaneously controlling for the effects of the other included independent variables. The cost function is linear in logarithms (that is, the values of each variable were transformed into logarithms before the cost function was estimated) except for the city size variables. Thus:

$$\text{LNMCD}=\text{fn}\left(\text{LNCMI},\text{LNWI},\text{LNINT LNBEDS},\text{SCV},\text{MCV},\text{LCV}\right).$$

This approach is based on the assumption that the relationship between cost per case and each independent variable is multiplicative rather than additive.

The coefficients of continuous variables in a cost function of this type are direct measures of the degree to which the relationships between the independent variables and the dependent variable are proportional. Coefficient values less than 1.0 Imply a relationship that is less than proportional. For example, the bed size coefficient value (Table 8) of .107 means that a 10 percent increase in bed size (above the average) is associated with a 1.07 percent increase in Medicare cost per case. A coefficient greater than 1.0 is interpreted in a similar fashion. Thus, a 10 percent increase in the Medicare case-mix index is associated with a 10.81 percent increase in cost per case.

Table 8. Regression Results.

Variable	Coefficient	Standard Error	F Statistic
LN CMI	1.081	.045	570
LN Wl	1.000	.031	1,028
LN INT	.569	.042	185
LN BEDS	.107	.005	486
SVC	.0021	.011	.04
MCV	.037	.011	11
LCV	.149	.012	132

Variables are defined in Technical Note A.

Dependent variable = LN MCD.

Adj. R² = .72; standard error of estimate = .22.

Number of observations = 5071.

¹ = Not significantly different from zero.

Table 8 presents the estimated coefficients, their standard errors, and associated F statistics for a cost function based on data from 5,071 hospitals. The regression “explains” 72 percent of the variation in Medicare cost per case for the included hospitals.

The coefficient values are generally of the expected sign and magnitude. After we control for other factors that influence hospital costs, case-mix has a positive and substantial independent effect on average cost per case. Similarly, differences in area wage rates are associated with proportional differences in average cost. The urban area dummy variables (SCV, MCV, LCV) indicate that hospitals in larger urban areas are more expensive than otherwise similar rural hospitals. This effect increases with the population size of the urban area. The bed size coefficient is significant and positive. Larger hospitals are more expensive on a per case basis.

Teaching intensity bears a significant positive relationship to cost per case, even when case-mix differences are controlled for. Because of the definition of this variable, its coefficient in the equation has a different interpretation than that of continuous variables such as case-mix. A simplified interpretation of the coefficient value of .569 is that the hospital's expected cost per case would be increased by approximately 5.69 percent for every additional .1 in its resident to bed ratio. Thus, a teaching hospital with a ratio of full time equivalent residents to beds of .2 would be expected to have costs per case about 11.38 percent higher than an otherwise similar hospital with no residents.

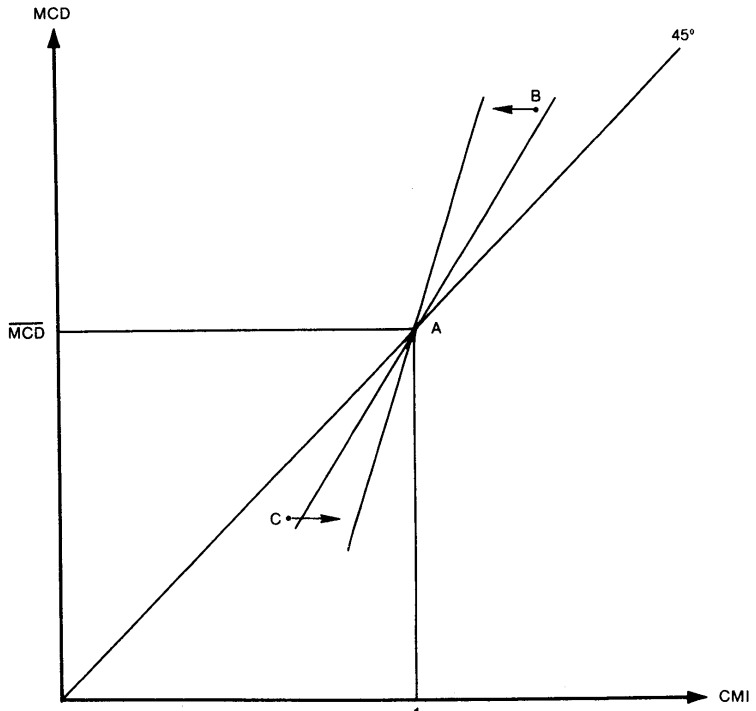
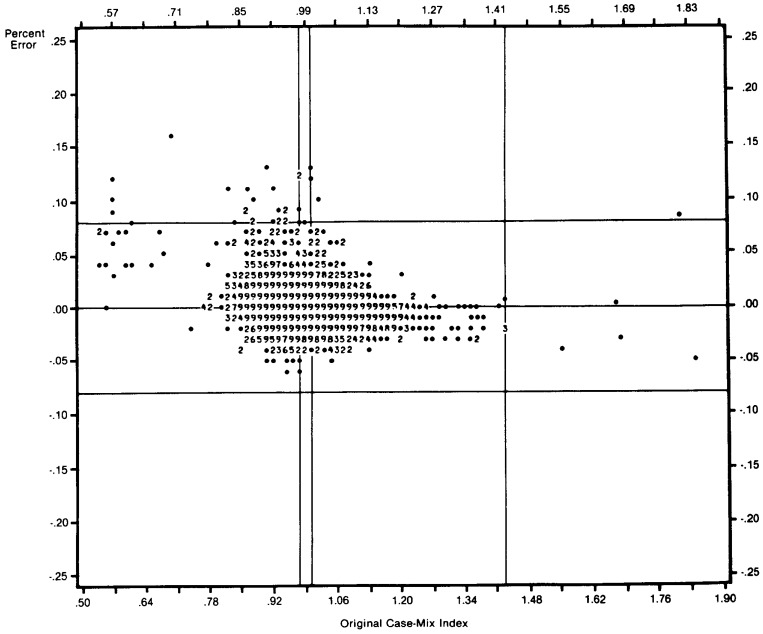
Our purpose in performing this analysis is to assess the validity of the Medicare case-mix index. Our most important finding in this regard is that the relationship between the case-mix index and Medicare operating cost per case is approximately proportional. Although the estimated coefficient value of 1.081 is higher than expected, when it is evaluated in a two-tailed test at the 5 percent level of significance, it is not significantly different from 1.0. This finding provides strong prima facie evidence of the validity of the Medicare case-mix index as a measure of the relative costliness of a hospital's Medicare cases.

Potential Distortions in the Measured Relationship

Under most circumstances, it would not be necessary to pursue this evaluation further. However, additional evaluation seems desirable in this case for several reasons. First, previous results (Pettengill and Vertrees, 1980), based on 1978 Medicare data and a case-mix index using the old ICDA-8 DRGs, indicated a case-mix index coefficient significantly greater than 1.0. Second, we know from econometric theory that coefficient estimates in a regression analysis may be biased by specification errors (for example, at least one significant omitted variable) and errors of measurement in the dependent or independent variables. We suspect that one or more important variables may be missing in this analysis. Further, we know that the data used to construct the case-mix index and to estimate the average cost function are subject to several known varieties of error. (See Technical Note A.) Since the estimated coefficient for the Medicare case-mix index reflects the net effect of any biases due to such errors, it is important to evaluate the direction of any biases due to particular types of error. Finally, the use of these methods to account for case-mix differences in hospital reimbursement suggests that the sensitivity of the case-mix index to errors in data may be an important issue for both policymakers and individual hospitals. Thus, an evaluation of the sources and effects of errors may provide valuable information about the relative importance of different kinds of error.

In the following sections we identify sources of error and evaluate their probable effects on the case-mix index and its relationship to cost per case.

Omitted Variables

An omitted variable is an important but unmeasured factor in a relationship. If this unmeasured factor is positively correlated with both the dependent and the independent variables in a regression, the coefficient estimates for the included independent variables may be biased upward.

An example of a variable omitted in this analysis is the hospital's non-Medicare case-mix. This variable is positively correlated with MCD and CMI. Therefore, the coefficient estimated for CMI may include the covariant effect of this omitted variable. This may be true for any omitted variable that is positively correlated with both Medicare case-mix and cost per case. Other potential candidates in this category include measures of the quality of care and nonlabor factor prices.

Errors In Variables

All of the variables used in this analysis are affected by errors of measurement.⁶ In the following sections we consider the sources and effects of error in the dependent variable and the case-mix index.

Errors in the Dependent Variable

The Medicare average inpatient operating cost per case (MOD) for any hospital is defined as total Medicare inpatient cost, less direct capital expenses and direct medical education expenses, divided by the number of Medicare discharges. These calculated values will reflect variations across hospitals in institutional practices and economic performance. Some hospitals, for example, contract for the delivery of some ancillary services such as laboratory, anesthesiology, or radiology to concessionaires who bill on a separate basis for the services they provide to inpatients. As a result, the costs for such services are not reported on the hospital's cost report or included in calculated operating cost per case. This practice is probably more common in smaller hospitals. Thus, we expect that this understatement of cost per case is negatively correlated with hospital case-mix. To the extent that this problem has any effect, it may cause a small upward bias in our coefficient estimate for Medicare case-mix. Similarly, some hospitals employ a large number of salaried physicians while others do not. Other things equal, the Medicare cost per case will be higher where physicians are employed than where they are not. It is reasonable to assume that this bias is positively correlated with both case-mix and teaching status. To the extent that this is true, our estimates of the effects of both variables will be biased upward. However, since physician salaries represent, at most, only a small proportion of total hospital costs, the resulting bias is also likely to be small.

A potentially more important source of bias in our coefficient estimate for Medicare case-mix arises from variations in hospital economic performance. Because the weights associated with the DRGs in the case-mix index represent average treatment costs (independent of wage differences, etc.), variations in treatment costs due to differences in practice patterns or relative efficiency among hospitals will not be reflected in the case-mix index. The effects of these differences will be observed, however, in the dependent variable, operating cost per case. To the extent that these variations are correlated with case-mix (for example, larger hospitals that treat a higher volume of relatively costly cases are relatively more efficient), the result will be a downward bias in the estimated coefficient for the case-mix index. Larger differences would produce a larger downward bias.

Variations in operating cost per case attributable to differences in practice patterns and relative efficiency may also account for a major share of the unexplained variance, that is, variance that remains after all of the independent variables have been accounted for in the estimated average cost function.

Errors in the Case-Mix Index

Because of the characteristics of the data and the method of construction, CMI values may be distorted by two general types of errors: errors in the cost data for individual cases and errors in classification. The sources of these errors and their effects on the key components of the index, the case type proportions and the category weights, are described in the following sections.

Errors in the Adjusted Cost Values for Individual Cases

Potential errors in the estimated cost values for individual cases may arise from three sources:

• The definition of routine and special care per diem costs—These cost items are used to obtain total routine and special care costs for each case. To conform to the definition of operating cost per case, these items should exclude direct expenses for capital and medical education. These expenses almost certainly vary from one hospital to another and among DRGs as well. The detailed data required to make such exclusions by DRG category, however, are not presently available in the cost report.

• Inaccurate cost to charge ratios—These average departmental ratios are used to adjust the billed ancillary charges. Each ancillary department may produce hundreds of different services with different individual mark-up rates. In addition, the specific combination of services rendered to patients will vary by DRG. Therefore, this adjustment is not precise at the individual case level.

• Adjustments for other factors that affect costs—The adjustments that are made to remove the effects of variations among hospitals in teaching activity and wage levels may be inaccurate for some hospitals. They are certainly inaccurate for some of the cases in a DRG.

The combination of these errors will affect the distribution of the standardized cost values In each DRG. Therefore, they have the potential to reduce the reliability of the estimated DRG weights. Although the extent of each type of error is unknown, it is reasonable to suppose that the magnitude of the net errors in the means of the DRG cost distributions (weights) is generally quite small. We would also expect that the direction of the error in the weights would vary by DRG category, with low cost categories biased upward and high cost categories biased downward. Thus, the expected net effect of these errors is to compress the weights somewhat. That is, the spread of the weights will be less than it would be with completely accurate data.

Classification Errors

Classification errors in the assignment of cases to case type categories (DRGs) arise from inaccurate clinical data and from grouping cases (based on the category definitions) that are dissimilar in their use of resources.

• Errors in the clinical data—The nature and extent of the problem of errors in the clinical data have been described in a study performed by the Institute of Medicine (1977). In that study, the authors noted that the error rate for principal diagnosis codes declined as cases were aggregated from the fourth digit level of the ICDA code to the level of the DRGs. (See Technical Note A.) Nevertheless, between 20 and 30 percent of the records in the MedPar file may be expected to have an erroneous principal diagnosis at the DRG level. In addition, a significant percentage of the records are incomplete. Although secondary diagnoses were present, they were not reported.

  These errors in the clinical data often, but not always, will cause assignment of the cases involved and their associated cost values to the wrong DRG. This will distort the proportion of cases in particular DRGs for any hospital that reported erroneous or incomplete clinical descriptions. It also will affect the distribution of the standardized cost values in each DRG and, therefore, the category weights. The cost values for each DRG (especially categories that include patients under age 70 without secondary diagnoses) will be less homogeneous, and the DRG weights will be less distinct than they would be in the absence of data errors.⁷

  Incomplete reporting of secondary diagnoses may result in allocation of the affected records to lower cost DRGs.⁸ This will lead to an upward bias in the weights for those lower cost DRGs, a net downward bias in the index values for hospitals that reported incomplete data, and a slight upward bias for hospitals that reported complete data.

• Errors in the DRG definitions—The second type of error in classification results from grouping dissimilar cases (in terms of resource use) due to inadequacies in the DRG definitions. The Institute of Medicine did not attempt to evaluate the effectiveness of the DRGs in discriminating among dissimilar cases. Thus, the extent of this kind of error has not been measured. However, the effect of classification error is similar to the effect of errors in the clinical data; as the amount of error increases, the proportion of cases in particular DRGs for each hospital becomes more random, the cost values within each DRG become less homogeneous, and the DRG weights become less distinct.

The combined effect of the two kinds of classification errors (and errors in the cost values as well) on the case-mix index is complex. The results depend upon the degree to which these errors are random. We know that error rates in the clinical data vary by DRG, and we suspect that errors due to the DRG definitions vary in the same way. What is important here, however, is whether the amount of the difference in costliness between the correct DRG and the assigned DRG is random. It also matters whether the errors in DRG proportions are random across hospitals. If both are random, the case-mix index values will tend to collapse toward 1.0, the mean value. To test this hypothesis, we simulated the effects of random error in classification on the case-mix index.

Simulated Effects of Random Error

Using 1.65 million cases from 5,010 hospitals, we selected various percentages of the cases at random and reassigned them to different DRGs.⁹ On the assumption that a classification error would be more likely to result in assignment of the case to a DRG within the same major diagnostic category (MDC), we reallocated 70 percent of the selected cases to DRGs within the original MDC. We reassigned the remaining 30 percent of the selected cases to DRGs in other MDCs. On the assumption that the presence of a reported surgical procedure is a reliable indication that surgery occurred, we constrained the reassignment of surgical cases to surgical DRGs and medical cases to medical DRGs. When we reassigned a case we also reassigned its cost value.

We then recalculated the DRG proportions for all hospitals and the DRG weights for all categories by the original method. With these data and the original data, we simulated the case-mix index values for all hospitals for three index definitions: simulated proportions with original weights, original proportions with simulated weights, and simulated proportions with simulated weights.

The Effect of Classification Error on the Case-Mix Index

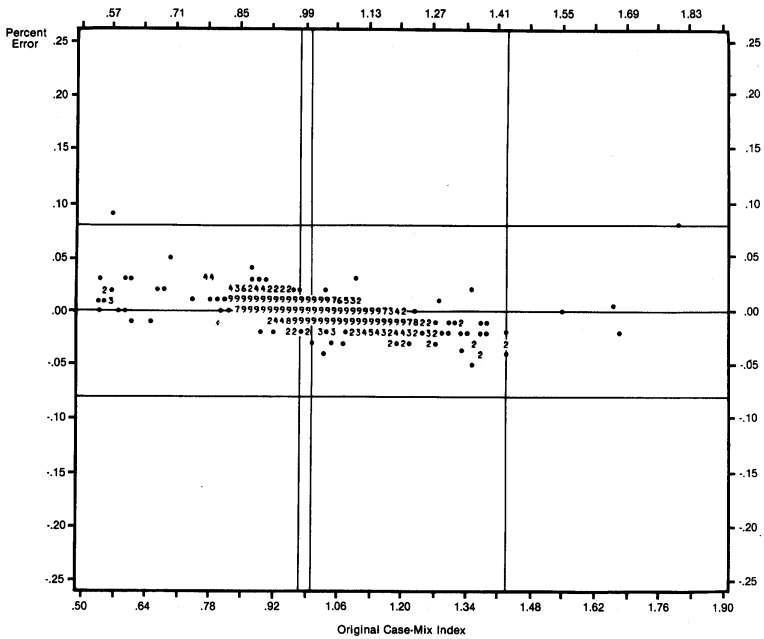
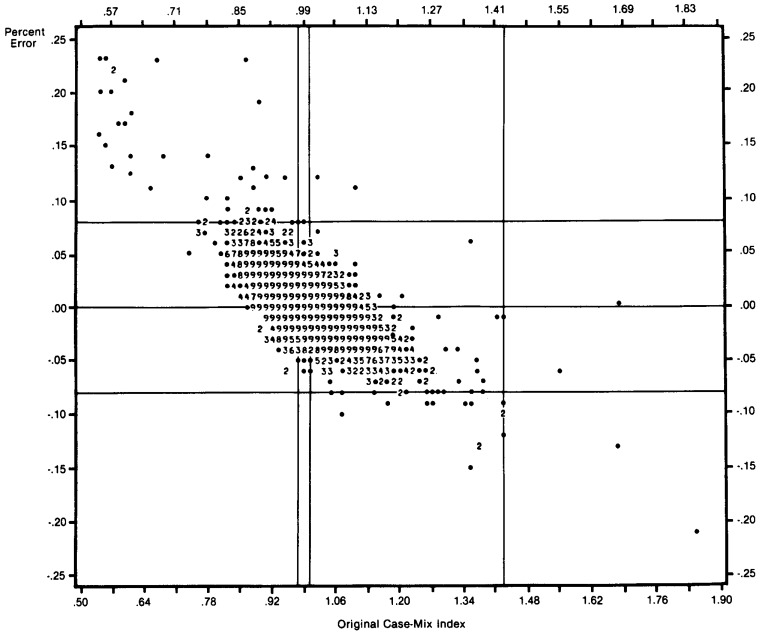
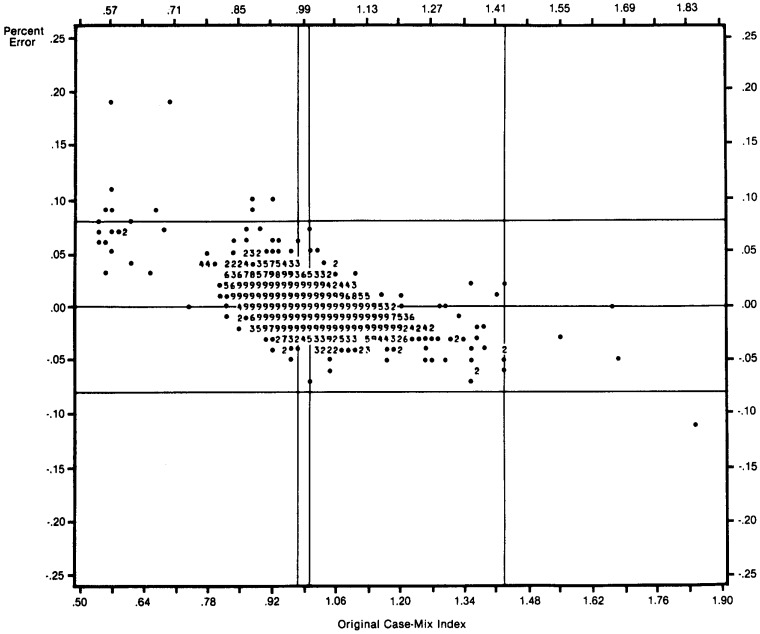
We repeated this procedure, reclassifying from 5 to 30 percent of the cases to reveal the trend of these effects. Table 9 shows the effect of 10, 20, and 30 percent additional error on the parameters of the distribution of case-mix index values compared to the parameters of the distribution of the original index. Error in either the proportions or the weights compresses the index values. Both the range of the index values and the standard deviation of the distribution clearly decrease in the presence of error in either of the index components. The only difference is that the effect of error in the proportions is somewhat more random than for the weights. The combined effect of errors in both components is similar. In all three cases, the degree of compression increases with the amount of additional error.

Table 9. Simulation Results: Effect of Simulated Random Error on the Case-Mix Index Values and Correlation of Simulated Index with Original Index (N = 5010).

% Error	Minimum	Maximum	Mean	Standard Deviation	Correlations
0	.54	1.83	1.000	.086	—
Errors in Weights
10	.55	1.70	1.00	.081	.99
20	.55	1.62	1.00	.078	.99
30	.56	1.60	1.00	.075	.99
Errors in Proportions
10	.56	1.74	1.00	.083	.98
20	.56	1.69	1.00	.081	.96
30	.60	1.67	1.00	.078	.94
Errors in Weights and Proportions
10	.58	1.63	1.00	.078	.99
20	.59	1.52	1.00	.073	.97
30	.63	1.46	1.00	.068	.96

The last column of Table 9 shows the correlations between simulated index values and original index values. These correlations measure the stability of the index in the presence of error. The results suggest that errors in the proportions cause more serious distortion than errors in the weights. This should be expected, since errors in the proportions affect the index values for individual hospitals directly. Because high and low errors tend to cancel each other, the weights are less sensitive to error.

The effects of error are graphically illustrated in Figures 1 through 4. In percentage terms, we plotted the difference between the simulated index value and the original index value against the original index value for all hospitals. Figures 1 through 3 show the effects of errors in the weights, the proportions, and both in combination, assuming that 10 percent of the cases were misclassified. Figure 4 shows the combined effect of errors in both components when 30 percent of the cases were misclassified.

Figure 1. Simulation Results Distribution of Percentage Error in the Case-Mix Index Values Due to Error in DRG Weights: 10 Percent Error.

Figure 4. Simulation Results Distribution of Percentage Error in the Case-Mix Index Values Due to Errors in Both Index Components: 30 Percent Error.

Figure 3. Simulation Results Distribution of Percentage Error in the Case-Mix Index Values Due to Errors in Both Index Components: 10 Percent Error.

The compression of the index is obvious. The relative costliness of the hospital's case-mix is overstated for hospitals with low values and understated for hospitals with high values. This effect is increased for hospitals with original case-mix values further away from the average case-mix. However, even with 30 percent error added to the data, the vast bulk of the simulated hospital index values are within ± 10 percent of the corresponding values in the original index.

The Effect of Errors in the Case-Mix Index on the Case-Mix Coefficient

In evaluating the reliability and validity of the case-mix index, it is important to know how errors of measurement affect the index values. It is also important to know how such errors affect the apparent relationship between the Medicare case-mix index and Medicare cost per case.

To study the effects of compression in the case-mix index, we re-estimated the cost function using the simulated case-mix index values described earlier. Table 10 shows the effect on the estimated case-mix coefficients of introducing various percentages of simulated error in both the proportions and weights. As the additional error rate moves from 5 percent to 30 percent, the coefficient of LNCMI increases. Thus, error in the case-mix variable causes its coefficient estimate to be biased upward.

Table 10. Effect of Additional Error on Coefficient Estimates.

Percent Additional Error	Estimated Coefficient
0	1.091
5	1.15
10	1.22
15	1.26
20	1.30
25	1.33
30	1.36

¹This coefficient is not equal to the coefficient in Table 8 because it is estimated using a data set which excluded 61 “all inclusive” providers.

Figure 5 illustrates this effect. It is important to remember that a regression line always goes through the mean values of both the dependent and the independent variable (point A). The 45 degree line is a reference line, indicating an exact proportional relationship (the expected result) and a coefficient of 1.0.

Figure 5. Coefficient Change Due to Compression Effect of Additional Classification Error on Medicare Case-Mix.

The Medicare cost per case values for individual hospitals do not change as error is added to CMI, but the CMI values compress toward one, the index mean value. For example, point B in Figure 5, representing a hospital with high MOD and high CMI, will shift to the left (toward CMI = 1.0) as error is added to CMI. Point C illustrates the same effect for a low MCD low CMI hospital. A regression line drawn through these points will appear to have rotated in a counterclockwise direction. Since the slope of this line is the coefficient of CMI, a steeper line means a higher coefficient value. Thus, as error increases, the slope of the line increases and the CMI coefficient value increases.

The simulation results and this illustration clearly indicate the direction of the bias in the case-mix coefficient caused by errors of classification. The simulation also provides the basis of a rough guess about the magnitude of the bias.

Extrapolating from the results presented in Table 10, we would guess that the case-mix coefficient would increase from .06 to .08 for every 5 percent error added to clinical data that was initially error free. Assuming a 20 percent error rate based on the IOM study of the MedPar data, this suggests a case-mix coefficient of 1.24 to 1.32, rather than the value of 1.08 that we obtained in our cost function estimates.

There are at least two possible explanations for this discrepancy. First, it is possible that other sources of bias in the data or in the specification of the cost function combine to offset the upward bias due to classification error. Alternatively, it is also possible that the simulation methods that we have used substantially overstate the true effects of classification error. For example, if errors tend to be systematic such that cases that should be assigned to relatively costly DRGs are usually misclassified to other costly DRGs and relatively inexpensive cases tend to be assigned to inexpensive DRGs, the effect of classification error would be much less pronounced than we have suggested.

The true explanation may be some combination of these reasons. We cannot evaluate these issues, however, with the data that are currently available.

Summary and Conclusions

We have described a general approach to solving the problem of measuring differences in hospital inpatient case-mix. This approach is based on a set of homogeneous groups of patients, defined by a patient classification system, and a set of estimated relative cost weights corresponding to the patient categories. These elements form an index measure of the overall expected relative costliness of the mix of illnesses and conditions treated in each hospital (the weighted sum of the proportions of patients in the case categories). Given the narrow objective of measuring differences in relative costliness attributable to patient case-mix across hospitals, this measure provides a logically valid solution to the problem.

We illustrated the application of this approach in measuring the overall relative costliness of the mix of Medicare patients treated in 5,071 participating hospitals. This application was based on the DRG patient classification system and a specific set of methods for estimating relative cost weights for the DRG categories. We described the criteria that the patient classification system should meet and the origins, process of definition, and limitations of the DRG categories. We also described the criteria and the limitations of the methods that we applied to the clinical information and billed charges for sample Medicare patients to develop relative cost weights for the DRG categories.

The Medicare case-mix index exhibits considerable surface validity. The distribution of index values across various types of hospitals closely follows our general expectations. For example, hospitals engaged in extensive graduate medical education treat a costlier mix of Medicare patients than otherwise similar hospitals with no teaching activity; small community hospitals tend to treat relatively lower cost cases. In addition, the case-mix index is positively and significantly related to hospital location (urban hospitals have higher values) and to the hospital's Medicare average cost per case.

Given the potential uses of such a measure, however, apparent face validity by itself can not serve as a sufficient basis for an overall evaluation. In particular, the limitations of both the DRGs and the Medicare data suggest the desirability of a thorough evaluation of the index. In evaluating the index in terms of these problems, however, we wanted to avoid the all too common error of the fallacy of composition.

Accordingly, we looked for a method of evaluation that would permit an overall empirical assessment of the validity of the index. If the Index value for any hospital is considered as a weighted average of the expected relative costliness values of its Medicare cases, the relationship across hospitals between the Medicare case-mix index and Medicare average cost per case should be approximately proportional. This hypothesis provided the basis for a powerful overall test of the empirical validity of the index.

To test this hypothesis, we estimated a hospital average cost function relating Medicare average cost per case to a set of independent variables including the Medicare case-mix index. This estimated cost function directly tested the proportionality hypothesis through the estimated coefficient value for the Medicare case-mix index. It also provided the means to directly assess the effects of classification errors and errors in the Medicare data on the relationship between the case-mix index and Medicare cost per case.

This evaluation suggested several important conclusions. First, we found that for some hospitals our 20 percent sample did not provide enough cases for a reliable estimate of the hospital's Medicare case-mix index value. This problem primarily affected small hospitals and low volume specialty providers (for example, hospitals with less than 50 beds or children's hospitals). Second, for the remaining hospitals the Medicare case-mix index is a powerful predictor, explaining about 30 percent of the variation in Medicare average cost per case. The coefficient of the case-mix index is positive and significant as we expected, and its value of 1.08 implies a relationship to Medicare cost per case that is approximately proportional.

We hypothesized that the case-mix index coefficient would be affected by measurement errors in the dependent variable, an important independent variable (for example, non-Medicare case-mix) not included in the cost function, and the effects of classification error and errors in the MedPar data. We deduced the likely direction of the coefficient bias due to errors in the dependent variable and missing variables. With regard to the last source of coefficient bias, we argued that either source of classification error (that is, due to limitations of the DRG definitions or from miscoded or misordered diagnoses in the clinical data) would have the same general effect. Such errors would compress the index values toward the mean (1.0), causing an upward bias in the cost function coefficient for the case-mix index. Our simulation of random error in the clinical data base substantiated this argument.

With respect to data quality, however, it is important to remember that the Med Par data originated in a passive reporting system. Since the data have previously been used mainly for research, hospitals have not had an incentive to ensure that their data are as accurate and complete as possible. We anticipate that many problems of data quality will be largely eliminated if the information is used in a context in which accuracy is of greater importance. In addition, we anticipate that the increasing sophistication and precision of future DRGs will result in improvements in our ability to make case-mix distinctions among hospitals.

Regardless of the errors which may exist, however, the most significant finding of our research is the relative insensitivity of the case-mix index to errors in the data. Even with 30 percent error, most simulated index values were within plus or minus 10 percent of the corresponding original values. We believe this indicates that the Medicare case-mix index provides a valid and generally accurate representation of the expected costliness of an individual hospital's patient mix.

Technical Note A

Data Sources and Variable Definitions

The following sections describe the origin and contents of the data sources used in this research and problems of data quality. A description of constructed variables is also included.

The MCR File

Description

Medicare hospital reimbursement is based on the actual allowable cost of providing inpatient care for Medicare beneficiaries. Each hospital submits a cost report to its Medicare fiscal intermediary shortly after the close of its fiscal year. This cost report provides the basis for settling the amount of final payment for the hospital for that fiscal year.

The standard HCFA cost reporting forms in 1979 were Form 2551 for hospitals of less than 100 beds and Form 2552 for larger hospitals. These reports differ only in that the latter requires greater detail.

We collected hospital cost reports from the Medicare fiscal intermediaries with end dates in 1979. Of the cost reports collected, some were from hospitals in U.S. territories or from hospitals reporting for less than a full year. We eliminated these reports from the file, leaving a base file of cost report data for 5,576 hospitals.

Data for routine per diem costs, special care per diem costs, and total Hospital Insurance (Medicare) inpatient operating costs were adjusted to reflect a common mid-point—June 30, 1979. To do this, we obtained estimates of the actual average inflation rates corresponding to the period between the mid-point of the reporting period and June 30, 1979 from HCFA actuarial staff.

Problems with MCR Data

Accuracy

The fiscal intermediaries audit the cost reports. However, all entries on the report are not audited; only those fields currently used as a basis for payment are consistently audited and accurately reported. Other fields are less reliable. For example, the number of Medicare discharges during the fiscal year is suspect, since current payment is not based on these data. The hospital may not always update other items (number of beds, for example) on an annual basis. Additional error may result from abstracting data from the cost reports. We eliminated as much of this error as possible through a series of edits.

Consistency

For comparative purposes, consistent data are preferable. Nonuniform reporting of cost data, however, is an on-going problem. The definition of cost centers varies with the organizational structure of the hospital. Cost allocation methods and statistics also vary. Moreover, certain components of costs that should be removed when comparing operating expenses (for example, physicians' salaries or malpractice insurance expenses) cannot be separately identified.

Bias

Hospitals frequently structure their service charges to maximize Medicare reimbursement. They also manipulate cost allocations to avoid the impact of routine cost limits. The net effect of this behavior is to bias Medicare cost per case upward and routine per diem cost downward. However, the extent of the bias is unknown.

The MedPar File

Description

The 1979 MedPar file is a data set consisting of approximately two million observations on patient diagnoses, procedures, and billed charges for a 20 percent sample of Medicare inpatient hospital claims for stays that occurred during calendar year 1979. The sample is based on the last number in the patient's Medicare ID number; cases with an ID number ending in 0 or 5 are selected.

The charge data submitted on the bill are available in some detail. Days and charges for general service, intensive care, coronary care, and other special types of care are listed separately, as are charges for pharmacy, radiology, laboratory, medical supplies, operating room, anesthesiology, and “other ancillary” services.

Along with the charge data, the hospital submits a narrative description of the principal diagnosis, the principal procedure, and the presence of secondary diagnoses and secondary procedures. The narrative description of principal diagnosis and principal procedure are centrally coded either manually or by machine. Approximately two million records for patients discharged after 1/1/79 were coded in ICD-9.

Problems with MedPar Data

There are three ways that error is introduced in the clinical data: hospitals may report incomplete or inaccurate clinical narratives, information may be lost in transmission, and information may be lost in coding.

Inaccurate Data

The narratives submitted by the hospital may not accurately reflect the diagnostic and surgical information available in the medical record. For example, instead of describing as “principal” the diagnosis that occasioned the admission, the hospital may describe a co-morbid condition or a complication that developed after admission. In addition, the description is sometimes incomplete. Secondary diagnoses might not be included in the description, even though they are present in the record. Similar problems occur in the description of procedures. The extent of this type of error varies from one hospital to another.

Transmission Losses

Additional errors result from the way intermediaries treat the information submitted by the hospital. Although a narrative clinical description is required on the bill, hospitals may be permitted to submit coded information at the intermediaries' discretion. In these cases, the codes are often translated by the intermediaries to standard narratives and submitted to HCFA, where they are again re-translated to codes.

Coding Losses

In extracting the data, Medicare notes only the presence or absence of a secondary diagnosis. This practice is also problematic, since secondary diagnoses are not uncommon in the elderly, and they often affect the use of resources in treatment.

The Extent of the Problem

A study done by the Institute of Medicine (IOM) in 1977 sheds some light on the magnitude of the problem of erroneous diagnosis information in the MedPar file. The IOM concluded that the average level of reliability of diagnosis data varied according to the level of aggregation of the code. The most detailed description of a diagnosis in the ICDA-8 coding system is at the fourth digit level. Tests for reliability were made on the four digit ICDA-8 code, on the first three digits only, and on the coded data collapsed into the old ICDA-8 DRGs. Reliability increased with the level of aggregation. No substantial discrepancy was found between the IOM principal diagnosis and the listed MedPar diagnosis 68.8 percent of the time at the fourth digit code level; the agreement rate was 74.1 percent at the three digit level of aggregation and 76.7 percent at the DRG level.

There was also wide variation in error rates among individual DRGs. This variation reflects the clinical understanding of the case types in the DRG. For cataracts, a clear-cut clinical category, there was no discrepancy in 97.5 percent of the records. For chronic ischemic heart disease, a poorly understood disease, there was no discrepancy in 40.8 percent of the cases. Among cases where discrepancies were found, the IOM concluded that many of the observed errors were preventable.

Bureau of Labor Statistics (BLS)

Description

This annual series contains total employment and total compensation data for hospital workers (Employment Series 202, Standard Industrial Code 806) covered by State unemployment laws and for Federal civilian hospital workers covered by the Unemployment Compensation Program for Federal employees. The data are compiled from quarterly tax reports submitted by hospitals to State employment security agencies and reported to the BLS as aggregate figures for each county.

Problems with ES 202

The ES 202 data have three basic limitations. First, the employment and compensation totals are affected by strikes, bonus payments, retroactive payments and seasonal variations in employment. Second, the employment figures are not full-time equivalents and, due to part-time job holders, they tend to overstate the number of individuals who were at work and receiving pay during the period. This is offset by the under-reporting of workers who had unpaid absences. Minor errors are also caused by the inclusion of estimates for late or missing unemployment insurance reports.

The third and most serious deficiency in this data source is the aggregation of employee skill levels. Wages for technicians, orderlies, LPNs, and secretaries are pooled. It is not reasonable to assume that the various types of labor employed by a hospital have wages determined in a common market. Indeed, a glance at the Help Wanted section of the “New York Times” will demonstrate that for highly skilled labor, the market is national (although skilled wage rates are not constant across the country), while unskilled labor participates in a general local market covering many industries.

Provider of Service File (POS)

Description

The POS file is a statistical file maintained in the HCFA central office. It contains a wide range of information about participating providers derived from annual surveys carried out by State agencies as part of the provider certification process. The only information that we use from this source is the number of full-time equivalent (FTE) interns and residents employed in the hospital during fiscal year 1979.

Problems with POS

Since resident training is not a condition of participation for hospital providers, the recording of resident employment is a low priority item in the survey. This results in inconsistent reporting. The number of residents listed on the survey does not necessarily represent full-time equivalents. In some cases it is apparent that all residents present at any time during the year have been included. In other cases the number of residents is understated or omitted entirely.

Discharge File (DF)

Description

At discharge, hospitals are required to file a final bill with the HCFA central office for each Medicare patient. These notices are accumulated by calendar quarter. Since this final bill is more complete than the HI admissions field on the cost report, we estimated the total number of Medicare cases (discharges) treated during a hospital's fiscal year from this source. A comparison of the two sources indicated that they are within ± 10 percent for about 90 percent of the cost reports.

Problems with the Discharge File

Hospital discharges vary seasonally, and hospital fiscal years do not always end with calendar quarters. Therefore, our estimate of discharges for some hospitals may not be accurate.

Definitions of Constructed Variables

In addition to the Medicare case-mix index, this analysis uses seven other variables. They are defined below.

The Combined Hospital Wage Index

The Combined Hospital Wage Index used to adjust the weights is intended to reflect variation in hospital unit labor costs across geographic areas. It is constructed from the data obtained from the Bureau of Labor Statistics. For each SMSA or non-SMSA (State) area, the county total wages and employment data are summed separately over all of the constituent counties in the area. Total area wages are divided by total area employment to obtain the area average wage. Thus, in each area the average wage is employee weighted. To convert area wage levels to an index, we compute the national average of the area wage values over all SMSA and non-SMSA areas and divide each area wage by the national average hospital wage rate. Thus, the index is area weighted.

The Labor Share

The “labor share” used to compute the fraction of total operating cost per case adjusted by the wage index is derived from the input shares (expense categories) of the National Hospital Input Price Index (Freeland et al., 1979). The labor share is the sum of:

payroll and fringe benefits	.6658
professional fees	.0059
other business and miscellaneous expenses	.1391
	.8108

The actual relative share values shown here are taken from a 1982 update of the price index, revised to reflect total hospital operating expenses.

Medicare HI Inpatient Operating Cost per Discharge (MCD)

MCD is based on reported Medicare HI inpatient operating cost per case normalized to June 30, 1978. This variable is calculated as total Medicare HI inpatient costs less direct capital expenses and direct medical education expenses divided by the number of Medicare discharges.

Direct capital expenses are calculated as the sum of reported rent, interest, and depreciation expenses (attributable to Medicare patients). Direct medical education expenses include salaries of interns and residents in approved programs and nursing education costs normally allocated to the nursing school cost center on the cost report.

Cost data are from the MCR file and discharges are from the Discharge Notice file. Thus, the MCD variable is subject to all of the problems identified earlier. In particular, MCD includes malpractice insurance costs and physician salaries.

Residents per Bed Ratio

The ratio of full-time equivalent interns and residents to beds (INT) is intended to measure relative teaching intensity at each hospital. Many hospitals do not have residents in approved programs and their INT value is zero. This is problematic in estimating the effect of teaching intensity on hospital Medicare costs per case, since the log (LN) of zero is not defined. Therefore, since LN(1) = 0, this variable is redefined when transforming to logs by adding 1.0 to all values, that is, LNINT = LN(1 + INT).

Beds

The number of beds per hospital is obtained from the MCR file. It is used in the regression analysis to measure (control for) effects of hospital size on average cost per Medicare case. Bed size is also part of the definition of the Medicare hospital peer groups.

City Size (LCV, MCV, SCV)

If an SMSA has a total population greater than one million, it is classed as a large city (LCV). If the population is greater than 250,000 but less than one million, it is a medium size city (MCV). SMSAs with a total population less than 250,000 are defined as small cities (SCV). SMSA population values are based on 1977 sample updates of 1970 census county population data from the Bureau of the Census.

Hospital Peer Groups

HCFA currently uses seven groups based on location (urban/rural) and bed size to ensure that a hospital is compared only with similar hospitals. Thus, Massachusetts General Hospital is compared only with other large urban hospitals, while Flowers Hospital in Alabama is compared only with similar small rural institutions. The current seven groups are:

Urban (SMSA)

less than 100 beds 100-404 beds 405-684 beds greater than 684 beds

Rural (Non-SMSA)

5)less than 100 beds 6)100-169 beds 7)greater than 169 beds

Figure 2. Simulation Results Distribution of Percentage Error in the Case-Mix Values Due to Errors in DRG Proportions: 10 Percent Error.