Dimensionality of object representations in monkey inferotemporal cortex

Abstract

We have calculated the intrinsic dimensionality of visual object representations in anterior inferotemporal (AIT) cortex, based on responses of a large sample of cells stimulated with photographs of diverse objects. As dimensionality was dependent on data set size, we determined asymptotic dimensionality as both the number of neurons and number of stimulus image approached infinity. Our final dimensionality estimate was 93 (SD: ± 11), indicating that there is basis set of approximately a hundred independent features that characterize the dimensions of neural object space. We believe this is the first estimate of the dimensionality of neural visual representations based on single-cell neurophysiological data. The dimensionality of AIT object representations was much lower than the dimensionality of the stimuli. We suggest that there may be a gradual reduction in the dimensionality of object representations in neural populations going from retina to inferotemporal cortex, as receptive fields become increasingly complex.

Introduction

The nature of object representations within the visual system remains a mystery (see review by Kourtzi & Connor, 2011). Underlying the difficulty of the problem is the large dimensionality of the representation space, whose size is unknown. While it has long been known that the full richness of color in the world can be encoded in primates by three dimensions (red, blue, green), the question remains how many dimensions are required to encode all aspects of visual objects in general, including shape, texture, and color. The goal of this study is to provide a specific numerical estimate for the intrinsic dimensionality of object representations in inferotemporal cortex. To our knowledge this is the first study to measure the dimensionality of neural representations using single-cell neurophysiological recordings, though there has been previous work based on human psychophysics (Meytlis & Sirovich, 2007; Sirovich & Meytlis, 2009) and fMRI (Haxby et al., 2011).

Intrinsic dimensionality is the number of independent parameters required to fully describe a data set (Fukunaga, 1990; Lee & Verleysen, 2007). In this case the data are neural population responses to object stimuli. We will not be interested in the number of parameters required to represent one object stimulus, but rather the number of parameters required to describe responses to all objects collectively in a large stimulus set. Dimensionality is equivalent to the minimum neural population size needed to encode a collection of objects, provided the response of each neuron is statistically independent from all others. In reality, of course, neural responses are not independent but show correlations and other, higher order, statistical dependencies. Therefore actual neural populations for encoding objects will undoubtedly be much larger than this minimum size.

The dimensionality of population responses and the sparseness of population responses are unrelated concepts. Population sparseness is the fraction of neurons stimulated by a single object. Sparseness for this data set was presented previously (Lehky, Kiani, Esteky, & Tanaka, 2011). Population dimensionality, on the other hand, is the minimum size of the population required to encode all objects.

Anterior inferotemporal cortex is an appropriate region to measure the intrinsic dimensionality of neural objects representations because it is a high level visual area believed to be important for object recognition (Logothetis & Sheinberg, 1996; Tanaka, 1996). It forms the highest predominantly visual area along the ventral visual pathway, after which projections run forward to multimodal areas such as perirhinal cortex and prefrontal cortex. Visual stimuli required to stimulate inferotemporal neurons are more complex than in any of the earlier visual areas.

Unraveling the neural basis of object recognition has had less success than some other visual modalities such as color or motion. This is largely due to the high dimensionality of object representations. Color has three dimensions, at least in the early visual stages, and 2D motion also has three dimensions (speed, and the x and y motion direction components). In those low dimensional systems it is fairly obvious which stimuli to apply to neurons to characterize the system. In a high dimensional system such as object representation it is not clear which stimuli to use. This problem has led to two general approaches in experimental design when dealing with object recognition. One is to stimulate neurons with as many random object images as possible and use that as a starting point to search for regularities in the responses (e.g., Roozbeh Kiani, Esteky, Mirpour, & Tanaka, 2007). Another is to select some image parameter for close study on the basis of intuition without principled knowledge of the neural object space (e.g., surface curvature, Yamane, Carlson, Bowman, Wang, & Connor, 2008). In this difficult situation, quantitatively characterizing the space of object representations would be of benefit. Measuring the dimensionality of the space provides an early step towards that goal.

Methods

A. Recording

Extracellular single cell recordings were collected from two macaque monkeys (M. mulatta). Recordings were conducted in three regions of anterior inferotemporal cortex as anatomically defined by Saleem and Tanaka (1996): superior temporal sulcus (STS), anterior dorsal TE (TEad), and anterior ventral TE (TEav). The STS region ran along the lower bank of the superior temporal sulcus. TEad extended across the lateral convexity of inferotemporal cortex from the lip of STS to the lateral lip of the anterior medial temporal sulcus (AMTS). TEav extended across the entire AMTS including its lateral bank, and continued along the lateral half of the inferior temporal gyrus. Penetration positions were evenly distributed over anterior 15-20 mm (monkey 1, right side) and anterior 13-20 mm (monkey 2, left side). All cells that remained reliably isolated throughout the stimulus presentation period were included in the data set, regardless of selectivity. Because we did not find major differences in the statistical properties of the three areas (Lehky et al., 2011), all these data were pooled for the dimensionality calculations below. Further details of the recording methods and other aspects of the procedures have been previously described (R. Kiani, Esteky, & Tanaka, 2005; Roozbeh Kiani et al., 2007; Lehky et al., 2011).

Recording procedures were in accord with NIH guidelines as well as those of the Iranian Physiological Society.

B. Stimuli and task

The stimulus set consisted of color photographs of natural and artificial objects (125×125 pixels), isolated on a gray background. Object sizes were approximately 7° across at their largest dimension. Stimulus images were drawn from a wide variety of categories, including human, monkey and non-primate faces, human and animal bodies, reptiles, fishes, fruits, vegetables, trees and various kinds of artifacts (Figure 1 shows examples). Image presentations were repeated a median of ten times to each neuron. We used color images because we were interested in the dimensionality of object representations in general, and not just object shape. We expect using colored images would only slightly increase dimensionality over grayscale images, as it doesn't appear many dimensions are required to represent color (perhaps just three).

Figure 1.

Examples of object images used as stimuli.

Each neuron was presented with 1271 images on average. However, not all those images were the same for every neuron. Therefore we only used data from the overlapping set of 806 images that were presented to all 674 neurons. This produced a response matrix with 806 rows and 674 columns, leading to 806×674=543,244 elements in the matrix.

The task of the monkey was to maintain fixation within 2° of a 0.5° fixation spot presented at the center of the screen. Eye position was monitored by an infrared eye-tracker.

At the start of each trial the monkey fixated the central spot for 300 ms. After that, a series of images was presented using rapid serial visual presentation (RSVP) (Földiák, Xiao, Keysers, Edwards, & Perrett, 2004; Keysers, Xiao, Földiák, & Perrett, 2001). Each image appeared for 105 ms followed immediately by the next image without gap, with images in pseudorandom order. A trial lasted for 60 images or until the monkey broke fixation. The monkey received a juice reward every 1.5-2.0 seconds while maintaining fixation.

C. Spike train analysis

We measured neural activity for each stimulus presentation during a 140-ms window, offset by the earliest significant response within the inferotemporal population (70 ms) (Tamura & Tanaka, 2001). Dimensionality calculations described below were based on the mean response to each image over that time period. Responses to the last two stimuli in each image series were not included because the data analysis window extended beyond the end of the trial.

Using the RSVP procedure depended on sparseness in the responses of inferotemporal cortex, in which it was unlikely that two successive stimuli would both evoke a strong response. To minimize crosstalk of neural activity measurements in cases where the previous stimulus did have a strong response, we excluded presentations with large activity (exceeding the spontaneous activity by 2 × SD) within the first 50 ms of the latency period, immediately following stimulus onset. This resulted in exclusion of 15% of presentations. Spontaneous activity was measured in a 200 ms window at the start of each trial, preceding the series of stimulus presentations.

D. Dimensionality calculations

For this analysis we started with the population response to each image. Because there were 674 neurons in the data set, each image was represented by a 674-element population response vector. The population response to each image could therefore be thought of as a point in a 674-dimensional space. As there were 804 images, we had 804 points in a 674-dimensional space.

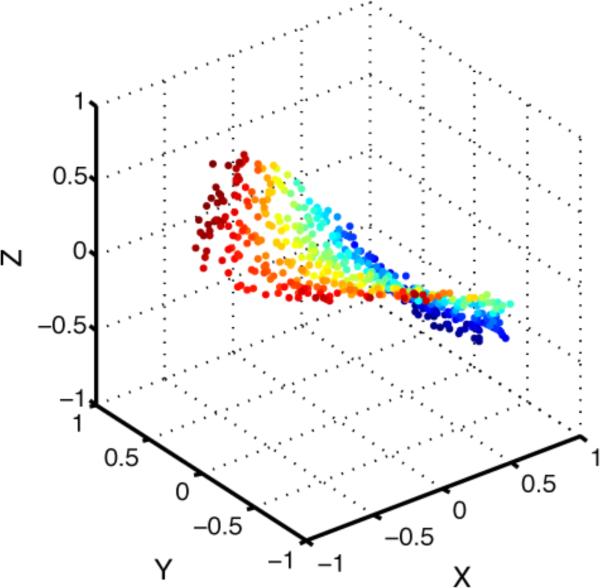
The presumption behind estimating the intrinsic dimensionality of this 674-dimensional space was that there was some degree of redundancy in the responses of the 674 neurons, so that in fact the number of independent dimensions was actually smaller than 674. In that case the 804 points would be confined to a lower dimensional subspace (or manifold) within the original 674-dimensional space. A simple example of this is shown in Figure 2, where the points are nominally in a three-dimensional space, but in reality are confined to a two-dimensional surface (2D manifold) within that 3D space.

Figure 2.

Two-dimensional saddle-shaped manifold embedded in a three-dimensional space. Although points are nominally in 3D space, they are confined to lying on a lower dimensional, 2D surface (aside from slight noise jitter) and therefore have an intrinsic dimensionality of 2. This illustrates the idea that although neural population responses to object stimuli may nominally be in a very high dimensional space (defined by the number of neurons in the encoding population), because of redundancies between neurons, population responses may be confined to a lower dimensional subspace.

Two unrelated methods were used to calculate intrinsic dimensionality of neural object representations. One was a local method and the other a global method. As described by Camastra (2003), a local method uses only information in the neighborhood of each data point, while a global method first pools the information from all data points before doing any calculations. The local method we used was the Grassberger–Procaccia algorithm (Grassberger & Procaccia, 1983), while the global method was based on eigenvalues from a principal components analysis (PCA) of the data. The two methods were first used to check the consistency of their dimensionality estimates, and then after that a more detailed analysis was performed using the PCA eigenvalue method.

i. Grassberger-Procaccia algorithm

The Grassberger-Procaccia algorithm finds what is called the correlation dimension of data. Although best known for calculating fractal dimensions, it can be used for estimates of intrinsic dimensionality in general (Camastra & Vinciarelli, 2002; Lee & Verleysen, 2007; Martinez, Martinez, & Solka, 2012).

Implementing the Grassberger-Procaccia algorithm, a hypersphere was placed around each data point. In our data, that would be a 674-dimensional sphere around each of the 804 data points. Then the fraction of other data points falling inside the hyperspheres was counted as a function of hypersphere radius. The assumption under the algorithm is that the fraction of data points inside the hyperspheres is proportional to r^d for small values of r, where r is the radius of the hyperspheres and d is the intrinsic dimensionality of the data.

In terms of equations (using the notation of Martinez et al. (2012)):

$$C\left(r\right)=\frac{2}{n(n-1)}\sum _{i=1}^n\sum _{j=1}^n{c}_{ij}\left(r\right)$$ (1)

where

$$c_{ij}=\{\begin{array}{cc}1,\hfill & \text{if}\Vert x_i-x_j\Vert \le r\hfill \\ 0,\hfill & \text{if}\Vert x_i-x_j\Vert >r\hfill \end{array}\phantom{\}}$$ (2)

In Eq. (1), the indices i and j refer to images in the data set, C(r) is the fraction of data points falling inside the hyperspheres as a function of hypersphere radius r. C(r) is therefore bounded in the range [0.0 1.0]. The term c(r) is a counter for the number of data points falling inside each hypersphere. The total number of data points in the data set is given by n (804 in this case), so that the total number of distances between all data points is n(n − 1)/2. In Eq. (2), x is an individual data point (corresponding to the neural population response vector to one image). The equation increments the count c_ij(r) if the Euclidean distance between two data points is less than r in the 674-dimensional space defined by the 674 neurons in the dataset.

As C(r) is proportional to r^d for small values of r, then:

$$d=\underset{r\to 0}{\lim }\frac{\log \left(C\left(r\right)\right)}{\log \left(r\right)}$$ (3)

The intrinsic dimensionality d of the data can therefore be estimated by plotting the log(C(r)) vs. log(r) curve and determining the slope of the curve when values of r are small.

In our implementation of the Grassberger-Procaccia algorithm we did a linear least squares regression over points in the leftmost portion of the log(C(r)) vs. log(r) curve (small values of r) and used the slope of that line as our estimate of intrinsic dimensionality. The region of the curve included in the linear regression calculations was selected as follows. Because the amount of data was finite, hyperspheres with extremely small radii had very few data points falling within them and small-sample noise therefore made it impossible to do a meaningful linear regression under that condition. We therefore excluded the portion of the curve where the total number of points included in the hyperspheres was less than 16. That formed the lower bound in the region used to calculate the linear regression. The upper bound was set at 2.2×10⁻³. That value was based on visual inspection of the curve, as a reasonable estimate of where the asymptotic region of the left portion of the curve ended.

ii. Principal components analysis algorithm

The basis for using PCA to estimate intrinsic dimensionality lies in observations such as those of Farmer (1971) that for noisy data, large eigenvalues from the PCA analysis correspond to “signal” and small eigenvalues to “noise”. The dimensionality of the data then becomes in principle just a matter of counting the number of large eigenvalues. The practical problem is finding a formal criterion to define the eigenvalue categories “large” and “small”.

The general starting point for this kind of analysis is to plot log eigenvalues as a function of their rank order, starting with the largest eigenvalue to the left. This forms a rapidly decreasing curve even when plotted logarithmically. Many algorithms then differentiate “large” from “small” eigenvalues by trying to find some discontinuity in that curve, either in slope or in the size of the difference between successive eigenvalues.

Here we introduce a different approach in which PCA eigenvalues for the data are compared with eigenvalues produced by a randomly shuffled version of the data. The assumption is that the shuffling destroys whatever signal was present in the data.

To implement this, two curves were plotted. One curve was for eigenvalues from the original data and the other from the shuffled data. Each set of eigenvalues was first normalized so that it summed to 1. Total number of eigenvalues in each case was 674. That was equal the number of elements in the population response vector for each image.

Original eigenvalues larger than the shuffled eigenvalues were then categorized as “large”, corresponding to “signal” in the data. The rest were “small”, corresponding to “noise”. Counting the number of “large” eigenvalues gave the intrinsic dimensionality of the data. Graphically, the point at which the original and shuffled eigenvalue curves crossed indicated intrinsic dimensionality. For a given set of eigenvalues only one shuffling was used, as there was little change in the intrinsic dimensionality estimate for repeated reshufflings (an occasional change in the value by one).

In this procedure, we shuffled the data in the 806×674 response matrix by assigning each neural response to a randomly selected stimulus image. In practice that was done by unfolding the 806×674 matrix into a 543,244×1 matrix, randomly permuting the elements of that 1D matrix, and then reshaping it back to an 806×674 matrix.

This method, comparing original and shuffled data, is a variant of the parallel analysis technique introduced by Horn (1965). A variety of procedures in this genre are reviewed by Peres-Neto et al. (2005).

iii. Effects of neural correlation

Population responses to images were synthesized from neurons recorded individually with single electrodes, rather than in parallel with multielectrodes. Because of that, we would expect actual neural correlations in our sample population to have been higher than what we measured. To investigate the effect this might have on our dimensionality estimates, we mathematically increased correlations in the data.

To do that, we defined a 674×674 correlation matrix C for the 674 neurons in our sample. The correlation values in the matrix were all set to a constant value c, except for self-correlations on the matrix diagonal that were set to 1.0. The correlation matrix then underwent a Cholesky decomposition to generate a matrix U according to the formula U^TU = C. Finally, for each population response vector r_i in our data, corresponding to the ith image in the stimulus set, a new response vector r′_i with higher correlations between neurons was generated by r′_i = r_iU.

This procedure is designed to generate random variables with correlation c starting from uncorrelated random variables. However, our raw data was not uncorrelated but already had non-zero correlations between neurons. Because of that, the value c set in the correlation matrix C we defined did not accurately reflect the final correlations in our transformed data. Therefore we adjusted the value of c empirically to produce the level of neural correlation we desired.

iv. Effects of data set size

Intrinsic dimensionality depends on data set size. Dimensionality increases as either the number of stimulus images or the number of neurons increases. As more images are added, new features are included that weren't present in any previous images. As new neurons are added, new feature selectivities are included that weren't present in any previous neurons. Assuming that the number of independent feature dimensions is not indefinitely large (see discussion), at some point dimensionality reaches an asymptotic limit as the number of stimulus images approach infinity and the number of neurons approach infinity. The asymptotic intrinsic dimensionality of neural object representations is the fundamental measure we are interested in, not dimensionality calculated on the basis of an arbitrary, limited sampling of images and neurons in the available data set.

To estimate asymptotic dimensionality, we first constructed curves that plotted dimensionality as a function of both the number of stimulus images and the number of neurons. Then an asymptotic function (see next section) was fit to these curves, allowing us to estimate dimensionality as data set size approached infinity. The curves themselves were constructed by taking various-sized subsamples of the data (various numbers of images, various numbers of neurons) from the full data set and calculating dimensionality for each subsample size.

We estimated asymptotic dimensionality using only the global method (PCA eigenvalues) and not the local method (Grassberger-Procaccia), as it was judged to be more robust when using small subsamples of the data as required by the procedure. The PCA method requiring determination of the point where two curves crossed. On the other hand the Grassberger-Procaccia calculated the asymptotic slope of a curve, which was more sensitive to uncertainty at small sample sizes and also required a decision about what points to include in the “asymptotic” region of the curve.

Bootstrap resampling was used to subsample data. For example, if we wanted to estimate dimensionality for 300 neurons presented with 200 images, we took a random sample of 300 neurons from the data and a random sample of 200 stimulus images and calculated dimensionality based on that. This subsampling was repeated 20,000 times, each time with a different random set of 300 neurons and 200 images, and the dimensionality estimates averaged.

Dimensionality was calculated over a two-dimensional grid using different neuron sample sizes and different image sample sizes. The dimensionality could thus be plotted as a three-dimensional surface, as a function of the number of neurons and number of images. Both the number of neurons and number of images were sampled at increments of 20, so image sample sizes were [20, 40, 60, ..., 800] and neuron sample sizes were [20, 40, 60, ..., 660]. Including points on the axes (zero images or zero neurons), the total number of points on the dimensionality surface was 1394. At 20,000 replications for each point on the grid, dimensionality calculations were performed over 20 million times.

Finding the asymptotic dimensionality as both neurons → ∞ and images → ∞ was a two-step process in which a one-dimensional asymptotic function was first fit along one parameter (either number of neurons or number of images), and then fit along the other parameter. The curve fitting could be done in either order, along the neuron parameter first and image parameter second [Neurons → Images], or the opposite way [Images → Neurons]. Reversing the order of curve fitting produced two independent estimates of asymptotic dimensionality for any given asymptotic function. These two estimates ideally should both be identical. We repeated all curve fitting with two completely different asymptotic functions to check reproducibility. Therefore, using two asymptotic functions each fitted to the two parameters in opposite orders, we produced four estimates of asymptotic dimensionality.

Below we will describe the procedure for the [Neurons → Images] curve fitting order. The [Images → Neurons] procedure was entirely analogous. For the [Neurons → Images] process, we first took a set of cross sections of the dimensionality surface along the number-of-neurons axis. This produced a family of curves showing dimensionality as a function of neurons, each curve corresponding to a different number of images. There was one dimensionality vs. neurons curve when number of images = 20, another curve when number of images = 40, and so forth, all the way up to number of images = 800, for a total of 40 curves. Each of these curves was then fit with an asymptotic function. When this curve fitting was done, we had 40 estimates of dimensionality, each for different numbers of images, all under the condition that the number of neurons approached infinity (plus a 41st^stpoint for the trivial condition of zero dimensionality for the representation of zero stimulus images).

Next we moved to fitting along the second parameter, number of images. The 41 estimates derived above were plotted to form a single curve (dimensionality vs. number of images). This curve was fit with the same asymptotic function as before. The value of the asymptote for this curve gave the final answer, the asymptotic intrinsic dimensionality of the data for the neural representation of objects, as both the number of images and the number of neurons both approached infinity.

For the [Images → Neurons] process, we took cross sections of the dimensionality surface along the number-of-images axis rather than number-of-neurons axis, producing a set of curves showing dimensionality as a function of number of images. Everything proceeded analogously from there. As all the curve fitting was performed on an entirely different set of curves, this provided a second, independent estimate of asymptotic dimensionality.

The asymptotic functions we used had 6 parameters. Because a different set of parameters was used to fit each cross section of the dimensionality surface, the total number of parameters was six times the number of cross sections along the first variable (neurons or images) plus six more parameters to fit along the second variable. Therefore, for the [Neurons → Images] order, there were a total of (41×6)+6=252 parameters to fit the surface, and in the [Images → Neurons] order there were (34×6)+6=210 parameters. These are both much lower than the 1394 data points defining the surface.

The reason we divided the fitting of the dimensionality surface into a series of 1D fittings instead of a single 2D fitting is because of the general unwieldiness of dealing with a large 2D equation with hundreds of parameters, including defining a form of the equation capable of generating good fits as well as searching for optimal parameter values within such a large parameter space. On the other hand, approximating the surface with a simple 2D equation having few parameters would have led to relatively large fitting errors rendering extrapolations unreliable.

v. Curve fitting procedure

Curve fitting was replicated with two independent asymptotic functions. The first was adapted from Nilson (2002):

$$y=a{\left[1-{\left(\frac{b}{\exp (x^c∕d)-1+b}\right)}^e\right]}^f$$ (4)

where y was the dimensionality and x was the number of neurons or images in the data set. Equation (4) reduces to the widely used asymptotic function y = 1− e^−x when all six parameters [a, b, c, d, e, f] are set to one. The second asymptotic equation was:

$$y=a{\left[\tanh (b{x}^c=d\log \left({[x+1]}^e\right))\right]}^f$$ (5)

This reduces to tanh(x + log(x +1)) when all parameters are set to one. In both cases the parameter we were primarily interested in estimating was a, which defined the asymptotic values of the curves generated by these equations. Nonlinear curve fitting was done with the ‘lsqcurvefit’ command in the Matlab Optimization Toolbox, using the ‘fmincon’ algorithm with the interior point option set. Both the ‘MaxFunEvals’ and ‘TolFun’ options were set to 10⁴, and both the ‘TolFun’ and ’TolX’ options were set to 10⁻⁸.

All nonlinear curve-fitting algorithms require an initial guess of the parameters. Starting from that initialization, the algorithm iteratively adjusts parameter values to reduce error between the fitted curve and the data, until a local error minimum is reached. There is no guarantee that this local error minimum is the global error minimum. Therefore, “best-fit” parameters produced by the curve-fitting algorithm, including estimated values of asymptotes, frequently depend on the initial parameter setting.

We started the fit of each curve by trial and error setting of initial parameters until a reasonable fit to the data was obtained as determined by visual inspection of the plots. This was then refined by manually adjusting initial conditions to produce the smallest calculated fit error. In the final stage of fitting, we followed an automated iterative procedure in which the output parameter estimates from the fitting algorithm were fed back as initialization parameters for the next run of the algorithm. This caused a drop in fitting error with each iteration (measured as RMS error), as the input and output values of the parameters gradually converged. The iterative running of the fitting algorithm was continued until the change in the asymptotic dimensionality estimate produced by 10,000 iterations was less than 0.01.

vi. Dimensionality of stimulus images

In addition to computing the asymptotic dimensionality of the neural data, we determined the asymptotic dimensionality of the physical stimulus images producing the data, following an identical procedure. In this case, we looked at the dimensionality of the physical image set as the number of images approached infinity. To reduce the computational load, these calculations were done on 60×60 pixel versions of the images. That would have the effect of slightly reduced dimensionality estimates relative to the 125x125 pixel versions actually used as stimuli in the experiments.

For these computations, the 60×60×3 matrix defining each color image was unfolded to a 1×10800 one-dimensional matrix. The 1302 images we had available were then pooled to form a 1302×10800 image matrix. PCA eigenvalues from the original and shuffled versions of this image matrix were compared to form the dimensionality estimate of the image set. Random subsampling of the image set was used to generate a dimensionality vs. number of images curve, with 1000 bootstrap resamplings for each point. Finally the two asymptotic functions (Eqs. (4) and (5)) were fit to this curve, producing two estimates of the asymptotic intrinsic dimensionality of the physical stimulus set.

Results

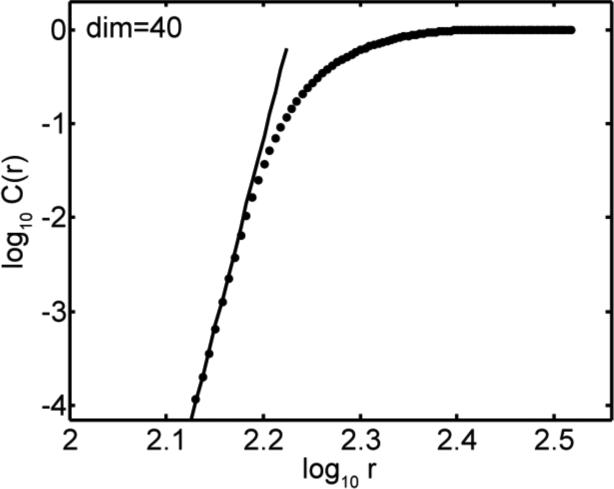
Using the full data set of 674 neurons, each presented with 804 images, the result of the local (Grassberger-Procaccia) method is shown in Figure 3. The estimate of intrinsic dimensionality of inferotemporal responses to object stimuli is given by the slope of the C(r) vs. r curve (for small r) in the figure. The value of the dimensionality produced by this analysis was 40.

Figure 3.

Estimating intrinsic dimensionality of the data using the Grassberger-Procaccia algorithm. The curve plots the relationship defined by Eq. (1). The asymptotic slope of the curve for small values of r gives the dimensionality.

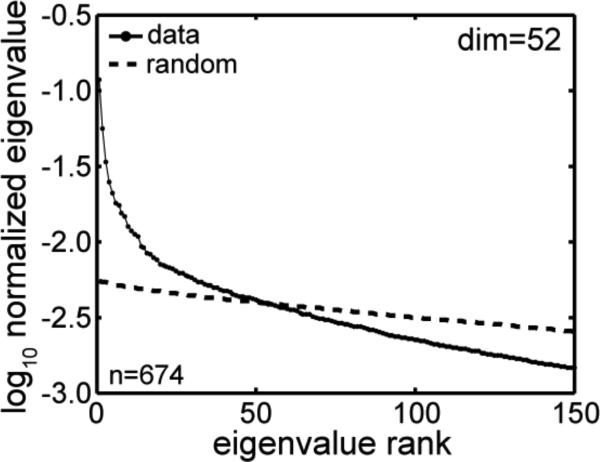
The result of the global method (PCA eigenvalues) analysis is shown in Figure 4. Plotted are two curves, the rank-ordered eigenvalues for the original data (based on the 674×806 neural response matrix), and the rank-ordered eigenvalues for randomly shuffled data. The point at which the two curves cross gives the dimensionality estimate for the data. The value of the dimensionality for this analysis was 52 (although occasionally a particular shuffling of the data produced a value of 53). Thus two unrelated techniques for estimated dimensionality, a local technique and a global technique, produced roughly similar values.

Figure 4.

Estimating intrinsic dimensionality of the data from eigenvalues associated with a principal components analysis. The solid lines plots eigenvalues from the data sorted in rank order, while the dashed line plots eigenvalues after the data has been randomly shuffled. In both cases eigenvalues are normalized to sum to 1.0. The point at which the two curves cross gives the dimensionality.

Dimensionality values were not affected in any way by subtracting spontaneous activity from each neuron prior to doing the calculations, or by any other subtractive (additive) constant. On the other hand, transforms of the data involving multiplicative constants did affect dimensionality. For example, normalizing all response vectors to have unit length increased the Grassberger-Procaccia dimensionality estimate from 40 to 53, and the PCA dimensionality estimate from 52 to 63. However, in the absence of compelling evidence for such normalization in vivo, we proceeded with data analysis using unnormalized response vectors.

Examination of these PCA eigenvalues can tell us how much of the response to object stimuli in inferotemporal cortex is signal and how much is noise. When eigenvalues are normalized to sum up to 1.0, the value of each eigenvalue indicates the fraction of variance in the data that the eigenvalue accounts for. Thus summing the 52 largest eigenvalues in data, corresponding to the dimensionality of the data, tells us the fraction of the neural response corresponding to signal. By this criterion, 59% of inferotemporal response was signal and 41% was noise. Of course, the category “noise” includes not only truly random effects but also all aspects of the signal not relevant to the present analysis. The first two principal components accounted for 17% of the variance, similar to 15% in the inferotemporal object data of Baldassi et al. (2013).

Effect of neural correlation

Neural populations were synthesized from neurons recorded individually with a single electrode, rather than in parallel using multielectrodes. Therefore we would expect that in reality correlations amongst neurons would have been higher than what we measured, due to noise correlation. We examined the effect that this would have on dimensionality estimates by mathematically transforming the data to increase correlations, as described in the Methods section.

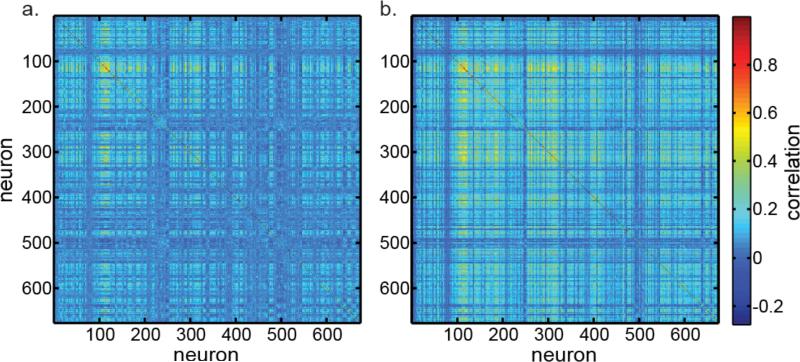
The correlation matrix for the 674 neurons in our data set is shown in Figure 5a, with correlation shown using a color code. Within a 674×674 matrix, it shows the correlation coefficient of the responses of each neuron with every other neuron. The mean of the absolute value of correlations was 0.063 (removing all self-correlations of 1.0 from the calculation). The Grassberger-Procaccia estimate of dimensionality for this data, as mentioned before, is 40 (Figure 3), and the PCA estimate is 52 (Figure 4). A second correlation matrix is shown in Figure 5b, in which the mean absolute correlation was doubled to 0.126. With this higher correlation data, the Grassberger-Procaccia dimensionality estimate changed from 40 to 41. The PCA estimate changed from 52 to 48.

Figure 5.

Correlation matrices of neural responses for 674 neurons in the data set. a. Correlation matrix for the original data. Mean absolute correlation is 0.063. The dimensionality for these data is 52, as shown in Figure 4. b. Correlation matrix for data that has been mathematically transformed to increase neural correlations, in order to examine effect on dimensionality. Mean absolute correlation doubled to 0.126. The increased correlation caused a slight decrease in dimensionality from 52 to 48.

Noise correlations between simultaneously recorded neurons have been reported to be 0.2 when the neurons were close, within several hundred micrometers of each other, declining as neural separation increased (Kaliukhovich & Vogels, 2012). Our neurons were widely separated, spread over more than a centimeter, so correlations would not have been high, almost certainly less than the correlation of 0.126 we examined. It therefore appears that the results of this study would not be substantially changed for modest increases in neural noise correlations provided by multielectrode recording techniques.

Effect of data set size

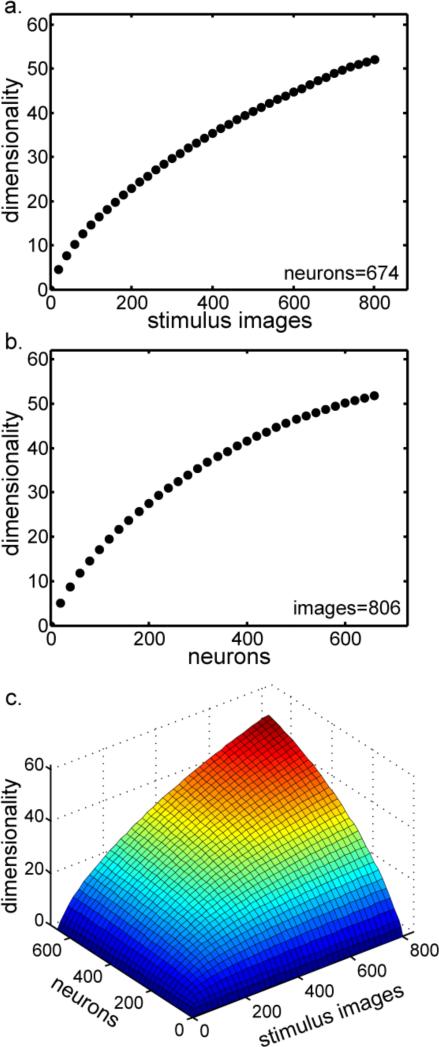
Dimensionality estimates depended on the size of the data set. Dimensionality increased as a function of the number of stimulus images (Figure 6a) and the number of neurons (Figure 6b), both figures produced by analyzing subsampled data using the PCA eigenvalue method. Varying both parameters simultaneously produced the dimensionality surface in Figure 6c.

Figure 6.

Dimensionality as a function of data set size. a. Dimensionality as a function of the number of stimulus images, holding the number of neurons constant at 674. b. Dimensionality as a function of the number neurons, holding the number of stimulus images constant at 806. c. Dimensionality as a function of data set size. Here the number of stimulus images and the number of neurons are both varied.

Therefore, the dimensionality values computed above are valid only for the limited sample of stimulus images and neurons in our data set. What is required is an estimate of asymptotic dimensionality of neural object representations as the size of the data set (both images and neurons) approached infinity.

In our two-step procedure for estimating asymptotic dimensionality, the two parameters ‘number-of-neurons’ and ‘number-of-images’ could be fit successively in either order, either [Neurons → Images] or [Images → Neurons]. Below, we show the estimation procedure in detail for [Neurons → Images], using Eq. (4) as the asymptotic function.

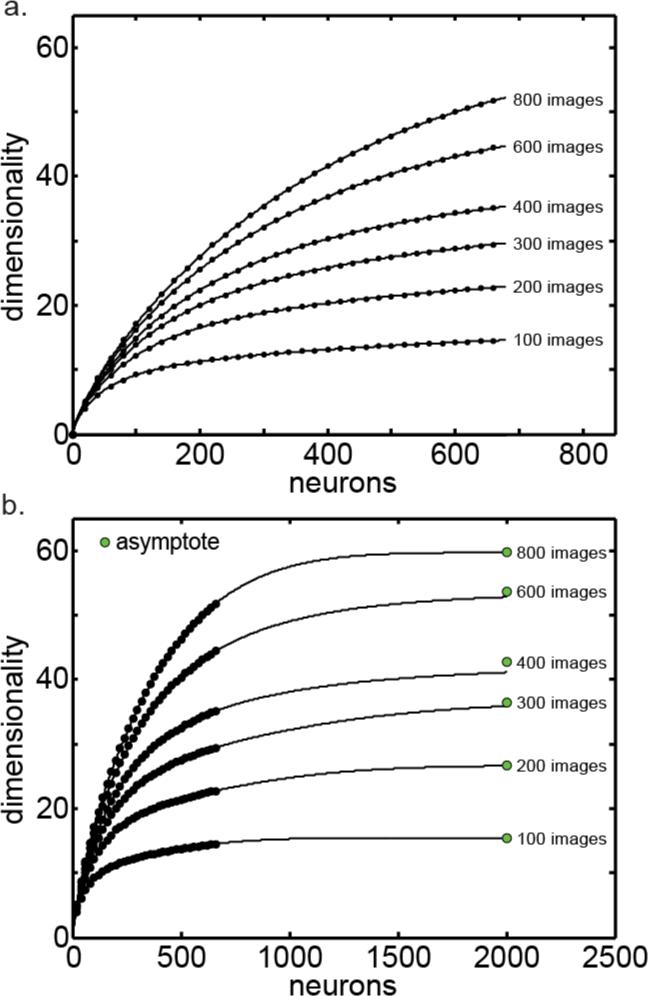
The first step in estimating the asymptotic dimensionality using the [Neurons → Images] order is illustrated in Figure 7. Shown is a series of curves plotting dimensionality as a function of the number of neurons, each curve for a different number of stimulus images. These curves are cross sections taken from the dimensionality surface in Figure 6c. Although Figure 7 shows curves at increments of 200 images, in reality we had curves at increments of 20 images, too many to show in an uncrowded manner.

Figure 7.

Asymptotic dimensionality as the number of neurons approaches infinity. a. Series of dimensionality curves plotted as a function of the number of neurons, each for a different number of stimulus images. Lines indicate fit of asymptotic function (Eq. (4)) to points. b. Same series of curves plotted further out to make the asymptotes more apparent. Green dots indicate actual asymptotic dimensionality as the number of neurons approach infinity.

Each curve in Figure 7 was individually fitted with an asymptotic function (Eq. (4)). Figure 7a gives a close-up perspective of the fits. Figure 7b gives a broader perspective showing the same curves as they approach their asymptotic values. The green dots in Figure 7b indicate the actual asymptote for each curve.

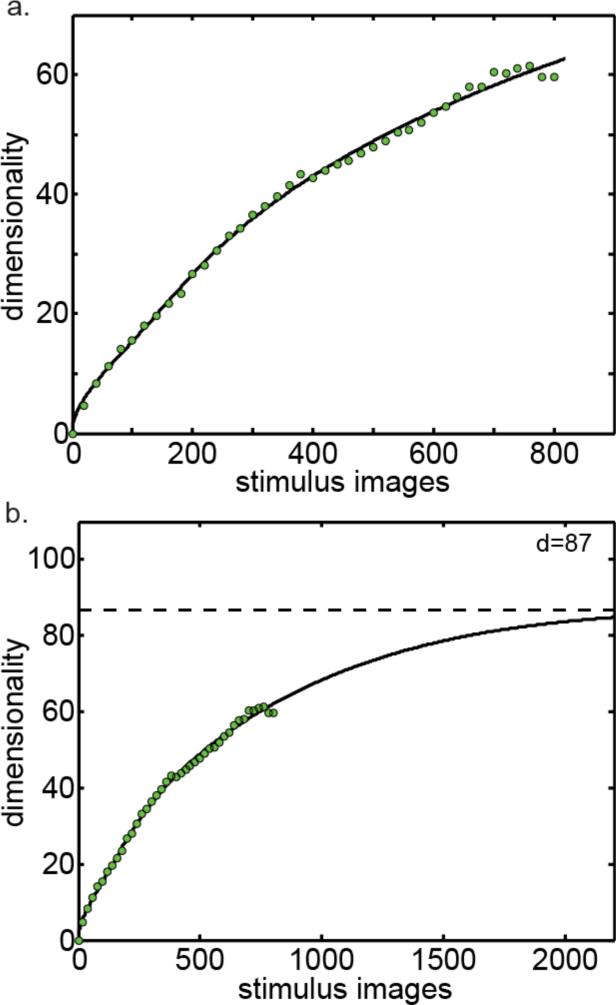
The next step was to take all the asymptotes in Figure 7b (the green dots) and plot them as a function of number of images (Figure 8). Thus we have dimensionality as a function of number of images, for the condition that the number of neurons approaches infinity.

Figure 8.

Asymptotic dimensionality as both the number of neurons and number of images approach infinity. a. Dimensionality plotted as a function of the number of stimulus images. Green points are from Figure 7b (plus additional points not shown in that figure), which already reflect the number of neurons going to infinity. Here we extend along the second dimension, number of stimulus images. Line indicates fit of asymptotic function (Eq. (4)). b. Same curve plotted further out to make the asymptote more apparent.

At this point the asymptotic function was fit to the set of points in Figure 8a, producing the line shown in the figure. The asymptote for that line is show in Figure 8b. That is the asymptotic dimensionality as both number of images and number of neurons approach infinity. The final value of the asymptotic intrinsic dimensionality provided by this analysis therefore was dim=87.

Another estimate of asymptotic dimensionality was found by reversing the order in which the two parameters were fit, this time following the [Images → Neurons] order. To do this, we started with a set of dimensionality curves plotted as a function of number of images rather than as a function of the number of neurons (cross sections of the dimensionality surface in Figure 6c taken parallel to the number-of-images axis). From there the procedure was completely analogous to that followed in Figure 7 and 8. Using Eq. (4) again as the asymptotic function, the estimated asymptotic in this case was dim=105.

Two more estimates of asymptotic dimensionality were found using Eq. (5) as the asymptotic function rather than Eq. (4), with both the [Neurons → Images] and [Images → Neurons] order of fit. These estimates were dim=80 and dim=97 respectively. The four estimates of asymptotic dimensionality are summarized in Table 1, providing a mean estimate of dim=93 (SD±11).

Table 1.

Four estimates of asymptotic dimensionality of object representations in inferotemporal cortex. These were derived using two different asymptotic equations, each with two orders of fit.

Asymptotic Function	Fit order	Dimensionality
Equation 4	Neurons→Images	87
Equation 4	Images→Neurons	105
Equation 5	Neurons→Images	80
Equation 5	Images→Neurons	97
		Mean: 93 ± 11

Attempts to apply this procedure to subsets of the data, such as to each monkey individually or to different classes of object stimuli, resulted in asymptote estimates that varied erratically within a single series of curves (such as those in Figure 7), indicating that the amount of data was too small.

Dimensionality of stimulus images

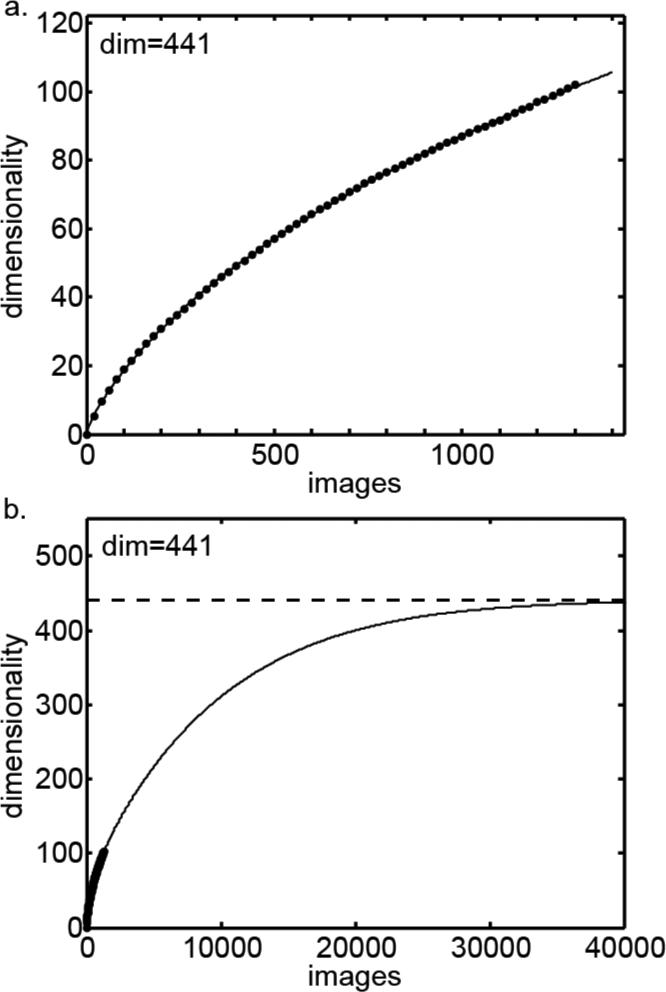
In addition to estimating the dimensionality of the neural responses, we followed an analogous procedure to estimate the dimensionality of the physical stimulus images. If each pixel in the images were statistically independent, then the dimensionality of the images would be equal to the number of pixels times three (for the three color channels), which for our calculations would be 60×60×3 = 10,800. However, images have a lot of structure such that nearby pixels tend to be correlated, producing a much lower dimensionality than if each point in the image were independent. Figure 9 shows dimensionality plotted as a function of the number of images, using Eq. (4) as the asymptotic function. This produced a dimensionality estimate of 441. Using Eq. (5) as the asymptotic function produced a second dimensionality estimate of 572, with the average of the two estimates being 507. This estimate will depend on the resolution of the images in pixels, with greater dimensionality with more pixels. As the actual stimuli were 125×125 pixel images rather than 60×60, the dimensionality of the stimuli would be somewhat greater than given here. In any case, the important point is that the dimensionality of the object stimuli was clearly much larger than the dimensionality of the neural representation of the stimuli.

Figure 9.

Asymptotic dimensionality of object images. This is dimensionality of the physical stimuli, and not dimensionality of neural responses to stimuli that was shown in previous figures. a. Dimensionality plotted as a function of number of images, with line indicate fit of asymptotic function (Eq. (4)). b. Same curve plotted further out to make the asymptote more apparent.

Discussion

This is the first estimate of the dimensionality of object representations in the primate visual system based on neurophysiological data. Two independent methods for estimating intrinsic dimensionality of neural object representations in inferotemporal cortex produced similar values. Estimates were 40 using a local method (Grassberger-Procaccia) and 52 using a global method (PCA eigenvalues). This consistency reinforces confidence that these methods are producing reasonable estimates of dimensionality. However, we found that dimensionality depended on the size of the data set, increasing as the amount of data increased. As more data was accumulated, either as the number of neurons or the number of images, a richer sampling of the world was created requiring a greater number of independent parameters, or dimensions, to describe. Once data set size was taken into account, the estimate of intrinsic dimensionality of object representations asymptoted at around one hundred.

For some, a hundred dimensions may intuitively not seem like a lot to provide a reasonable representation for every object or scene a creature is likely to encounter. However, once one recalls that merely three dimensions generate all the richness of colors in the world, then perhaps 100 dimensions doesn't seem so small to represent shape and texture as well.

Previous studies of the dimensionality of object representations have not considered the data-size factor. Estimates by Sirovitch and Meytlis (2009) of “less than 70” and by Haxby et al. (2011) of 35 are similar to our findings without taking sample size into account. However, when we extrapolated the data to larger sample sizes we found a larger measure of dimensionality.

The major limitation of this analysis is the requirement to extrapolate far beyond the available data. That is an issue that must ultimately be dealt with by collecting data on far larger numbers of neurons and stimulus images. An assumption of these analyses is that intrinsic dimensionalities asymptote to a finite value as sample size increases, both in terms of number of stimulus images and number of neurons. The samples we have are in fact too small and noisy to distinguish, purely on mathematical grounds, between a dimensionality function that asymptotes and one that increases without limit as the sample size goes to infinity. Given all this, the use of asymptotic functions to fit the data bears some examination.

Looking first at number of stimuli, an argument can be made why the dimensionality of inferotemporal responses might asymptote to a finite limit as the number of images goes to infinity. Photoreceptors in the retina are finite in number and noisy, leading to acuity limits (Westheimer, 1990). Having a finite number of spatial arrangements that can be reliably distinguished leads to a finite limit on the dimensionality of the retinal representation, as the number of stimulus images increases. The potential dimensionality in the retina is further constrained by the very high redundancy of retinal representations (Puchalla, Schneidman, Harris, & Berry, 2005). A finite dimensionality of population representations at the input stage would be inherited by subsequent stages, including inferotemporal cortex. We expect that as one moves up the visual hierarchy dimensionality will either remain the same or decrease, but never increase, so that finite-dimensionality at the input is retained at all levels. Neural processing rearranges the organization of response manifolds within a representation space (DiCarlo, Zoccolan, & Rust, 2012), but does not create new dimensions for that space.

If the stimulus inputs to AIT are finite-dimensional (where the immediate stimulus inputs would actually be signals from lower levels of the visual pathways), then responses of AIT would also be finite-dimensional, less than or equal to the dimensionality of its inputs. Given that situation, as the number of neurons in the AIT representation increases, the resulting dimensionality cannot exceed the limit imposed by the finite-dimensional input. In other words, dimensionality asymptotes as the number of neurons increases because the neurons run out of new stimulus dimensions to represent.

In looking at asymptotic dimensionalities, one might question the real-world significance of the concept of having an infinite amount of data. However, examining Figure 7 we see that the curve approaches its asymptote after just a couple of thousand neurons. For all practical purposes, “as the number of neurons approaches infinity” is well approximated by just a few thousand neurons, which is quite modest. Similarly, in Figure 8 we see that the curve approaches its asymptote after several tens of thousands of images, which is well within the experience of any individual. So, the dimensionality of object representations in the brain is likely to be close to the asymptotic limit we estimated, and not constrained to be far below that limit by the numbers of neurons and images that actually exist.

The intrinsic dimensionality computed here indicates that there is a basis set of approximately a hundred independent features that characterize the dimensions of neural object space. In other words, the theoretical minimum population size required to represent objects is about a hundred neurons. Clearly real population sizes are much larger than that, indicating a large degree of redundancy in the representation, possibly necessitated by noise, response correlation, and potential loss of neurons over the lifetime of the organism. Most likely the high degree of redundancy observed in retinal ganglion cells (Puchalla et al., 2005) is a general feature of visual representations, including in inferotemporal cortex.

The most obvious way to achieve redundancy is to make multiple copies of the same small basis set. However, we know from recordings that populations of inferotemporal neurons do not have a small set of feature selectivities that are encountered over and over again. Rather, inferotemporal neurons seem to have a bewilderingly large and varied set of feature selectivities. A previous statistical analysis of these same data (Lehky et al., 2011) indicated that there are an indefinitely large number of neurons each with different receptive field tunings for objects.

Having a limited number of independent, canonical features in the neural representation and at the same time having an indefinitely large number of different neural tunings for objects can be reconciled if neural feature selectivities in different neurons are not entirely independent. The object selectivity of each neuron must pool more than one feature from the canonical set, with a vastly large number of such combinations possible. For example, if each cell combined selectivity to five random feature dimensions out of 100 possibilities, that would produce approximately 9 billion different neural response characteristics to object stimuli. Individual face cells in macaque monkeys have been reported to combine selectivity to several feature dimensions (Freiwald, Tsao, & Livingstone, 2009), and we are suggesting such may be true in general for all neurons involved in object representations.

A technical limitation in the mathematical methods in the analyses was that they were fundamentally linear, and thus were unsuitable for extracting intrinsic dimensionality if the data points fell along a nonlinear manifold. Such nonlinear manifolds would have characteristics of being highly folded, twisted or curved. If a nonlinear manifold described the data better than a linear one, use of linear analysis methods would bias the results towards reporting a larger dimensionality than actually exists. For example, if the points fell on a 2D sheet that was highly folded so as to fill up 3D space (the prototypical example of this in the dimensionality reduction literature being the Swiss roll curve), our methods would not pick up the complex internal structure of that folded sheet, and would incorrectly report the intrinsic dimensionality as 3 rather than 2. It is possible, therefore, that when the PCA eigenvalue analysis estimated an intrinsic dimensionality of 93, it was really, for example, an 82-dimensional manifold folded up in a complex way so as to fill up a 93 dimensional space. Our methods would not discover that.

There are newer algorithms for dealing with such nonlinear manifolds, such as isometric feature mapping (ISOMAP) (Tenenbaum, de Silva, & Langford, 2000) and locally linear embedding (LLE) (Roweis & Saul, 2000), among others (see review by van der Maaten et al. (2009)). However, these algorithms have primarily been tested with artificial data sets having intrinsic dimensionalities in the range 2-4. As a practical matter it is doubtful how effective they would be when applied to an object space having a dimensionality on the order of a hundred. For these algorithms to operate, they would need to have the nonlinear manifold densely sampled with data points in order to resolve its fine internal structure. In a high dimensional space such dense sampling would require an impractically large amount of data. We therefore leave the issue of high-dimensional nonlinear manifolds with respect to the neural representations of objects as a future research problem. However, we believe that the potential overestimation of the dimensionality with our linear techniques would be minor and would not critically alter our conclusions.

The data here covered a wide variety of different object categories. Possibly, restricting the data to a single category, such as faces, would have produced a different estimate of intrinsic dimensionality. As different object categories cluster in different regions of object space (Roozbeh Kiani et al., 2007; Kriegeskorte et al., 2008), it is possible that those category clusters are occurring within lower-dimensional subspaces of the object space as a whole. In that case, individual object categories may have lower intrinsic dimensionalities than reported here. In this study we did not examine the dimensionalities of individual object categories because the number of examples we had in each category was too small for the methods we are using.

Different visual areas may have different intrinsic dimensionalities for stimulus representations. We saw that inferotemporal responses had a much lower dimensionality than the stimulus images. We suggest here that a reduction in dimensionality of population representations occurs gradually as one ascends the hierarchy of visually responsive regions in the ventral stream. Response patterns in the retina, most closely resembling the high-dimensional stimulus images, would have the highest dimensionality. Inferotemporal responses, with more abstract representations involving a small basis set of relatively complex features, would have the lowest dimensionality.

Visual shape selectivity occurs not only along the ventral pathway but also within parietal cortex along the dorsal pathway (Lehky & Sereno, 2007; Murata, Gallese, Luppino, Kaseda, & Sakata, 2000; A. B. Sereno & Maunsell, 1998; M. E. Sereno, Trinath, Augath, & Logothetis, 2002). Quantitative differences found in shape representation in AIT and LIP (Lehky & Sereno, 2007) raises the possibility that the dimensionality of visual representations in parietal cortex may be different than in inferotemporal cortex.

As we have noted, intrinsic dimensionality of inferotemporal responses to object images was much lower than the dimensionality of the physical stimuli. Most dimensions of physical object space appear not to be registered by inferotemporal cortex. Fewer dimensions in the neural object space than in the physical object space means that objects discriminability is reduced compared to what is in principle possible. That would be roughly analogous to the way that a colorblind person with two cone pigments (two-dimensional color representation) cannot make discriminations that a person with a normal three-dimensional color representation can. Thus, inferotemporal cortex would be forming an impoverished representation of objects compared to what physically exists. Perhaps this is an evolutionary consequence of resource limitations in the brain. So, with optimization for limited resources, primates get a particular object representation that is just good enough for all practical purposes in their daily lives but does not reach theoretical limits. The difference in dimensionality between neural object space and physical object space also relates to philosophical discussions about the relationship between our subjective experience of the world and the nature of the underlying physical reality.

It would be interesting to measure the dimensionality of visual representations in non-primates to see if there is a further decrease relative to physical object space in less visually oriented species. In addition, the same mathematical dimensionality methods could be applied to human fMRI data through voxel-based calculations.

Moving beyond counting dimensionality size, a key question for the future is obviously to identify what these dimensions specifically are, or in other words, what features in the world they correspond to. It is also an open question whether there exists an inborn inferotemporal object representation space with a particular dimensionality size, or if different individuals parse the world into different sets of dimensions based on experience. Even though there certainly is experience-dependent plasticity in feature responses of monkey inferotemporal cells or their human analog (Kobatake, Wang, & Tanaka, 1998; H. Op de Beeck, Baker, DiCarlo, & Kanwisher, 2006; Suzuki & Tanaka, 2011), it has been suggested that these changes may be confined to modulations of pre-existing properties (H. P. Op de Beeck & Baker, 2010).

To understand the biological basis of object recognition, we need to quantitatively describe the neural object representation space. Measuring the dimensionality of that space is a step towards that goal. The finding that object space has approximately one hundred dimensions highlights the complexity and challenge of the object recognition problem.