Soft spots and their structural signature in a metallic glass

Significance

This work demonstrates a structure–property correlation in metallic glasses for the community of amorphous solids. It associates geometrically unfavored motifs, i.e., those most disordered local polyhedral packing structures in a metallic glass, with the soft spots defined from the vibrational modes and correlates them with shear transformation zones composed of atoms with large nonaffine displacements. The statistical correlation established thus ties together the heterogeneity inherent in the amorphous structure with the spatial heterogeneity in the mechanical (elastic and plastic) properties of a metallic glass.

Abstract

In a 3D model mimicking realistic Cu₆₄Zr₃₆ metallic glass, we uncovered a direct link between the quasi-localized low-frequency vibrational modes and the local atomic packing structure. We also demonstrate that quasi-localized soft modes correlate strongly with fertile sites for shear transformations: geometrically unfavored motifs constitute the most flexible local environments that encourage soft modes and high propensity for shear transformations, whereas local configurations preferred in this alloy, i.e., the full icosahedra (around Cu) and Z16 Kasper polyhedra (around Zr), contribute the least.

Metallic glasses (MGs) have an inherently inhomogeneous internal structure, with a wide spectrum of atomic-packing heterogeneities (1–4). As a result, an a priori identification of structural defects that carry atomic rearrangements (strains) under imposed stimuli such as temperature and externally applied stresses has always been a major challenge (3–6). In several quasi-2D or 3D models of amorphous solids (such as jammed packings of soft spheres interacting via repulsive potentials or colloidal particles), low-frequency vibrational normal modes have been characterized, and it has recently been demonstrated that some of these modes are quasi-localized (7–14). A population of “soft spots” has been identified among them in terms of their low-energy barriers for local rearrangements (13, 14), correlating also with properties in supercooled liquids such as dynamic heterogeneity (15–17). However, it is not certain where the soft spots are in realistic MGs (18), in terms of an explicit correlation with local atomic packing and topological arrangements (18–20). In particular, there is a pressing need to determine whether it is possible to identify shear transformation zones, i.e., the local defects that carry inelastic deformation (21, 22). Accomplishing this would permit the characterization of MG microstructure in a way that directly ties atomic configuration with mechanical response beyond the elastic regime. We will show here that there is indeed a correlation between soft modes and atoms that undergo shear transformations, and both have their structural signature in specific atomic packing environments defined in terms of coordination polyhedra (3).

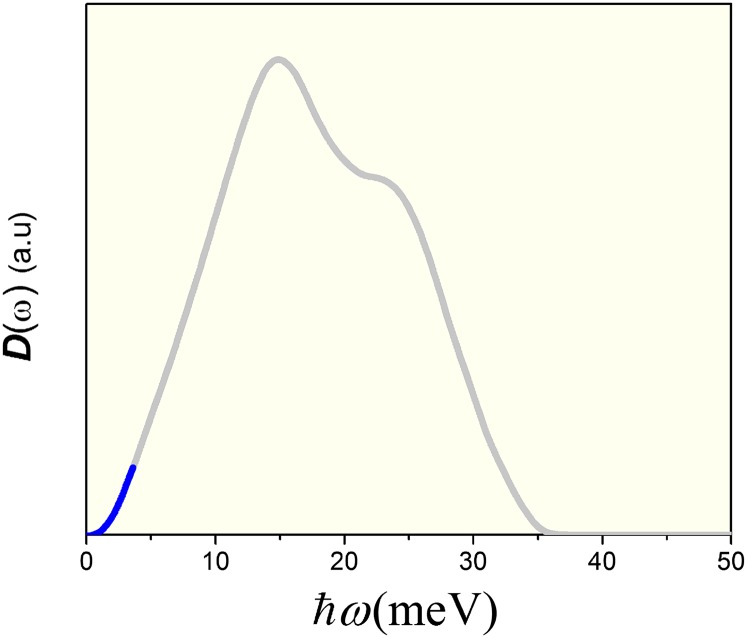
Fig. 1 displays the vibrational density of states (V-DOS), D(ω), calculated from the eigen-frequencies obtained by normal mode analysis of the Cu₆₄Zr₃₆MG prepared with a cooling rate of 10⁹ K/s (Methods). The main peak stays around 14 meV and becomes only slightly narrower (or wider) when the cooling rate used to prepare the MG is slower (or faster), as seen in Fig. S1; the glasses cooled at slower rates exhibit fewer low-frequency (or low-energy) vibrational modes. The blue portion in Fig. 1 indicates the 1% lowest-frequency normal modes, which will be summed over in our calculations of the participation fraction, P_i, in soft modes (Methods). Those low-frequency vibrational modes are confirmed to be quasi-localized, similar to previous work on 2D models (15), as they involve a compact group of atoms on the basis of the amplitude distribution of their corresponding eigenvectors (also see the contour maps in Fig. 4).

Fig. 1.

V-DOS of the inherent structure for Cu₆₄Zr₃₆ MG produced with the cooling rate of 10⁹ K/s. The blue portion indicates the 1% lowest frequency normal modes that were summed over to calculate the participation fraction (in soft modes) of atoms.

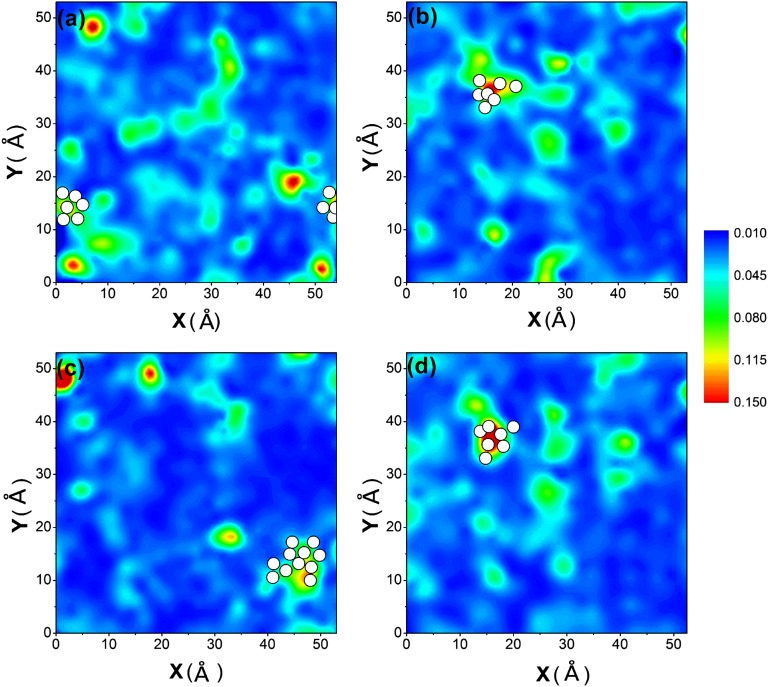
Fig. 4.

Contoured maps showing the spatial distribution of participation fraction P_i (see sidebar) for Cu and Zr atoms in the Cu₆₄Zr₃₆ metallic glass with the cooling rate of 10⁹ K/s. The four sampled representative thin slabs (A–D) each has a thickness of 2.5 Å. White spots superimposed in the maps mark the locations of atoms that have experienced clear shear transformations (Methods) under AQS to a strain of 5%.

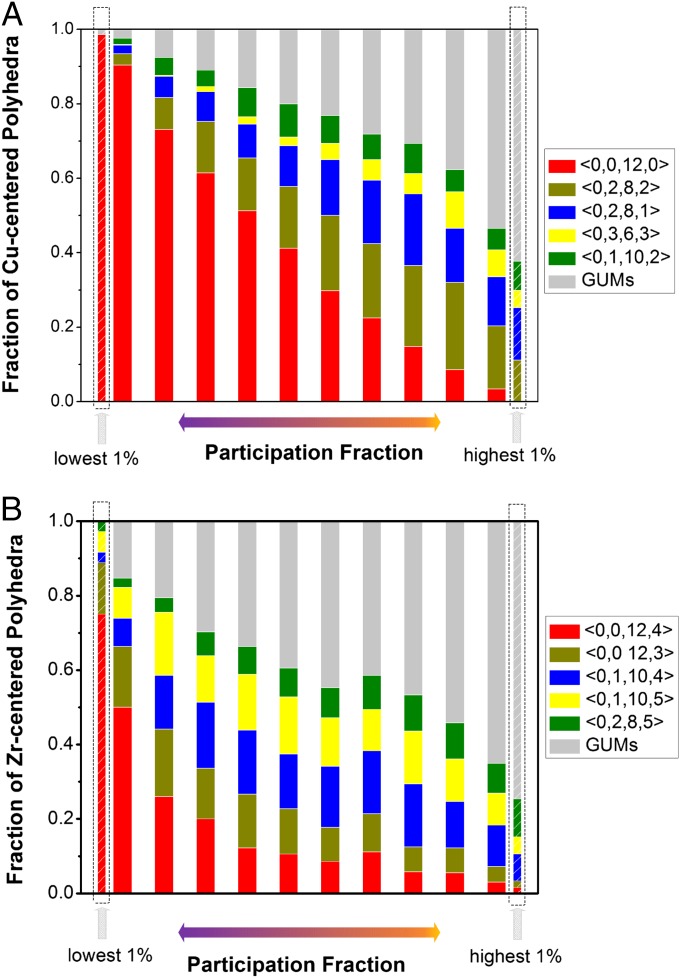
We first demonstrate that certain types of coordination polyhedra, specifically those geometrically unfavored motifs (GUMs), contribute preferentially to the quasi-localized soft modes identified above, whereas the geometrically preferable clusters at this alloy composition represent the short-range order that participate the least. To establish the connection between the low-frequency modes and atomic packing structure, we analyze the latter first from the perspective of Cu-centered coordination polyhedra (23), in terms of the P_i of Cu atoms that are in the center of different types of polyhedra. In Fig. 2A, from left to right, each solid bar represents a bin that contains 10% of all of the Cu atoms, in ascending order from the lowest to the highest P_i. In addition, the 1% Cu atoms with the lowest P_i and the top 1% with the highest P_i are displayed on either end, each with a separate bar. The Cu atoms in full icosahedra (with Voronoi index <0, 0, 12, 0>) dominate the lowest P_i, which is consistent with the notion that full icosahedra are the short-range order most energetically and geometrically comfortable and hence least likely to participate in soft spots at this MG composition (23). Specifically, ∼98% of the Cu atoms with the 1% lowest participation fraction are enclosed in <0, 0, 12, 0>, which is much greater than the average value that ∼40% of Cu atoms center full icosahedra in this MG sample (23). In stark contrast, the local configurations on the other end of the coordination polyhedra spectrum, i.e., the GUMs (see examples below) that deviate considerably from the coordination number (CN) = 12 full icosahedra and their close cousins (Fig. 2), are not found at all among the atoms with the lowest 1% participation fraction. For the 1% of Cu atoms with the highest participation fraction, GUMs account for as high as 63%, whereas the share of full icosahedra is as low as only 1.1%. This observation clearly indicates that atoms involved with soft spots in low-frequency normal modes (i.e., soft modes) are those with the most unfavorable local coordination polyhedra.

Fig. 2.

Atoms at the center of different types of (A) Cu-centered and (B) Zr-centered coordination polyhedra contribute differently to low-frequency normal modes. Each solid bar contains 10% of all of the Cu (or Zr) atoms; from left to right, the bins are ordered from the lowest to the highest participation fraction. Two additional bars describe the makeup of atoms contributing to the lowest 1% participation fraction and the highest 1% participation fraction, respectively. The latter is seen to be dominated by Cu (or Zr) atoms in GUMs.

We also examined the dependence on local environments for Zr atoms. A plot analogous to Fig. 2A, this time for Zr-centered coordination polyhedra, is shown in Fig. 2B. From left to right, each solid bar represents a bin that contains 10% of all of the Zr atoms, in ascending order from the lowest to the highest P_i. In addition, the 1% Zr atoms with the lowest P_i and the top 1% with the highest P_i are displayed on either end, each with a separate bar. The most favorable Zr-centered Kasper polyhedra in this MG are of the Z16 type (<0, 0, 12, 4>) (23). Interestingly, for the Zr atoms with the 1% lowest participation fraction, ∼75% of them are enclosed in <0, 0, 12, 4>, which is much greater than the sample average of ∼17% in this MG (23). In contrast, GUMs that deviate considerably from the CN = 16 Kasper polyhedra and their close cousins (Fig. 2) only constitute ∼5%. Conversely, for the 1% of Zr atoms with the highest participation fraction, GUMs account for as high as 76%, whereas the share of Z16 clusters is as low as 1.6%.

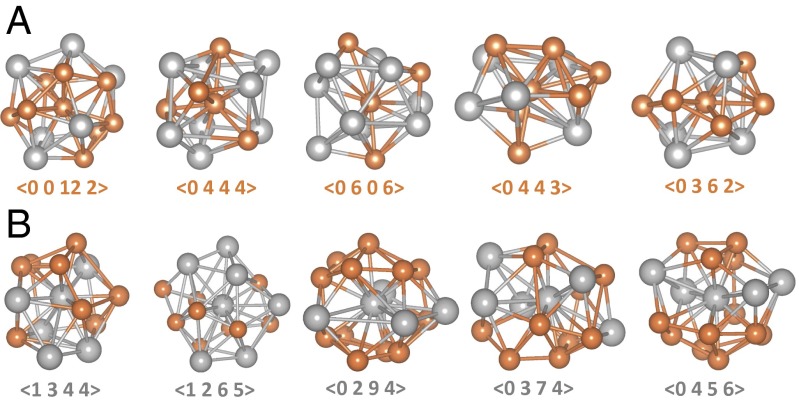
We now illustrate the GUMs, i.e., the typical types of coordination polyhedra that are strongly correlated with the soft modes. Fig. 3 A and B illustrates the local environments of the top five Cu atoms and Zr atoms, respectively, i.e., those with the highest participation fractions. For these five Cu-centered GUMs, the coordination polyhedra have Voronoi indices of <0, 0, 12, 2>, <0, 4, 4, 4>, <0, 6, 0, 6>, <0, 4, 4, 3>, and <0, 3, 6, 2>. For the five Zr GUMs, they are <1, 3, 4, 4>, <1, 2, 6, 5>, <0, 2, 9, 4>, <0, 3, 7, 4>, and <0, 4, 5, 6>. Clearly, they are among the polyhedra that deviate most significantly from the geometrically preferable Frank-Kasper polyhedra <0, 0, 12, 0> (for Cu) and <0, 0, 12, 4> (for Zr). Specifically, they are non-Kasper polyhedra and contain an increased density of extrinsic (e.g., fourfold) disclinations (3) at the favored CN, or clusters (including Kasper polyhedra) with unfavorable (too large or too small) CNs. In fact, those Zr-centered GUMs even contain sevenfold bonds, e.g., <1, 3, 4, 4> is actually <1, 3, 4, 4, 1> (except for these Zr-centered GUMs, the fifth digit is zero in the Voronoi indices for all the other coordination polyhedra in this work). From the perspective of either constituent element, Cu or Zr, these are the most geometrically unfavored clusters at the given alloy composition and atomic size ratio. According to ref. 24, transverse vibrational modes associated with defective (more disordered) soft structures could also be an origin of the boson peak [the excess rise in the D(ω) at low-frequency vibrational modes].

Fig. 3.

Configurations of five different (A) Cu-centered and (B) Zr-centered polyhedra, in which the center atoms are the top five atoms with the highest participation fractions for each constituent species. These are representatives of GUMs in this MG. Orange spheres are for Cu atoms and silver ones for Zr atoms.

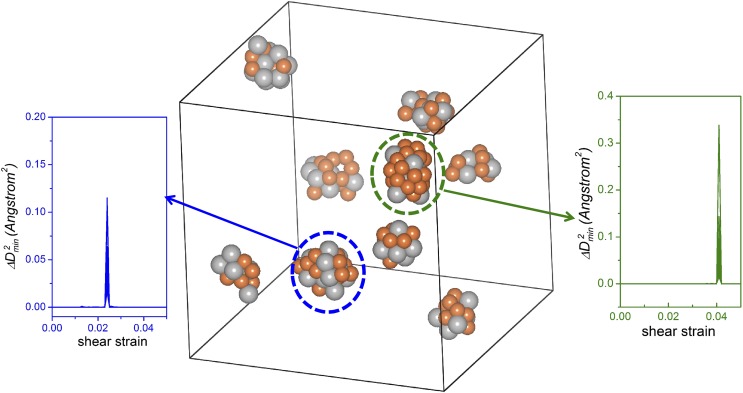
The next task at hand is to correlate the relaxation events with vibrational modes. In a 2D sheared model glass, Manning et al. (14) recently associated low-frequency vibrational modes with soft spots where particle rearrangements are initiated. Here we use a similar analysis on our 3D realistic Cu₆₄Zr₃₆ glass. The contoured maps of participation fraction P_i for all of the (Cu and Zr) atoms inside four representative slabs, each with a thickness of 2.5 Å (roughly the average atomic spacing), are plotted in Fig. 4 A–D. We notice that the P_i distributions are heterogeneous: atoms that participated the most in soft modes tend to aggregate together, with a typical correlation length of ∼1 nm. For a direct comparison, the local atomic rearrangements in sheared Cu₆₄Zr₃₆ MG [under athermal quasi-static shear (AQS) to a global shear strain γ = 5%, well before global yielding/flow of the entire sample at γ ∼ 12%] are superimposed in Fig. 4 A–D, where white spheres represent the (Cu or Zr) atoms that have experienced the most obvious shear transformations (indicated by their large and simultaneous jumps of ${\mathit{D}}_{\min }^2$ that are clearly above other atoms; Methods, Fig. S2, and SI Text). The distribution of these atoms is also inhomogeneous and, interestingly, almost always overlaps with the regions with high P_i. This observation is consistent with the correlation between quasi-localized low-frequency modes and low energy barriers (13). Fig. 5 displays the locations of all such Cu and Zr atoms in the simulation model, which are about 2% of the total number of atoms in the box. Two features are highly noteworthy. First, they cluster into patches (only 6 atoms are exceptions, being isolated in a group of <3 atoms), each comprising 10–40 atoms (Cu in orange and Zr in gray color). Second, the atoms in each cluster record a simultaneous jump in ${\mathit{D}}_{\min }^2$. Taken together, the spatial and temporal correlations clearly indicate that these are the clusters of atoms that each has been through a well-defined shear transformation. The several representative cases in Fig. 4 (and Fig. S3) give a visual illustration of the correlation that, under imposed deformation, the most obvious shear transformations have a strong tendency to arise from the collection of atoms involved in soft modes. Each group (cluster) of the activated atoms in Fig. 5 centers a shear transformation zone.

Fig. 5.

Cluster of atoms that have undergone obvious shear transformations (Methods) (24) in Cu₆₄Zr₃₆ MG sheared to γ = 5%. Atoms in each cluster are activated at the same time, as indicated by their simultaneous jump in $\mathrm{\Delta }{\mathit{D}}_{\min }^2$ at the same shear strain γ. Two such shear transformation zones are circled, with the Inset displaying the overlapping $\mathrm{\Delta }{\mathit{D}}_{\min }^2$ jumps of the atoms involved in each cluster.

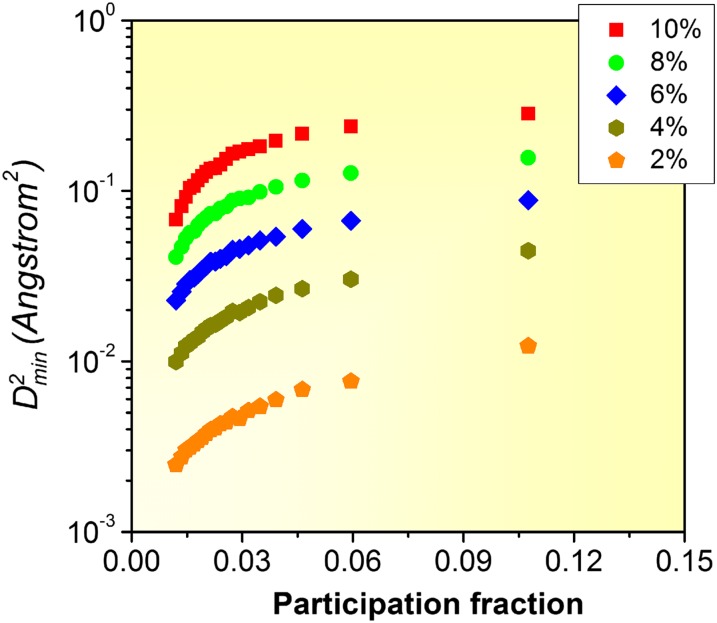
Note here that not all of the regions with the highest participation fraction P_i would undergo shear transformation for a particular loading condition, as seen in Fig. 4 and Fig. S3. One should keep in mind that such a local structure–property correlation in an amorphous system is expected to be statistical (better perceived in Fig. 6), rather than deterministic with a one-to-one correspondence (12, 14). The soft spots are only candidates for potential shear transformation zones. The ones actually activated are not necessarily the softest, and would be determined by the loading direction and local stress field interacting with the anisotropy of the soft spots. The statistical correlation is obvious for the entire range of imposed γ, from 2% to 10%. The contour maps similar to those in Fig. 4 for γ = 10% (before global yielding) are shown in Fig. S3. As another way to see this correlation, we present in Fig. 6 a plot correlating the average participation fraction with ${\mathit{D}}_{\min }^2$ (with respect to the undeformed configuration) for γ from 2% to 10%. Each data point is an average for 5% of all of the atoms inside a bin (each bin contains atoms grouped in ascending participation fraction). Obviously, the atoms with higher participation in soft mode contribute more to the nonaffine deformation and therefore shear transformations. This trend persists throughout the entire range of strains we studied and is therefore statistically valid for all the atoms in the metallic glass.

Fig. 6.

Correlation between the average ${\mathit{D}}_{\min }^2$ (with reference to undeformed configuration) with participation fraction P_i for all of the (Cu and Zr) atoms in the Cu₆₄Zr₃₆ MG deformed to different γ levels (2–10%). Each data point is the average for 5% of all of the atoms, sorted in the order of increasing P_i.

In conclusion, we identified soft spots in an MG. They are soft in the sense that the atoms (Cu and Zr in our case) in those local environments participate preferentially in soft vibrational modes and at the same time they have the highest propensity to undergo shear transformations. These two aspects are found to be strongly correlated: shear transformations in an MG preferentially occur at localized soft modes. In the language of the potential energy landscape, we established a correlation between the curvature at the bottom of the basin (stiffness) with the barrier for transitions between basins (energy barrier against reconfiguration). Importantly, we showed that both have a common signature in the local atomic packing environments: the GUMs are the local configurations most prone to instability. The GUMs, as the most disordered atomic arrangements, hence tend to constitute or center the “liquid-like regions” often hypothesized in the literature (4, 5, 25). They tend to be soft and fertile for shear transformations. Such a correlation, albeit statistical (not all soft modes or GUMs would be activated to undergo shear transformations for a given stress state/magnitude and loading duration), is very useful and important as a step forward in establishing a concrete structure–property relationship for MGs, i.e., a direct connection between short-range order and vibrational soft modes, as well as stress-induced atomic rearrangements. The spatial distribution of nanometer-scale patches observed in Fig. 4 and Fig. S3 (a 3D view from outside the MD box is in Fig. S4), in terms of property (soft spots) and corresponding structure (GUMs), may also help explain the origin of the heterogeneity in local elastic modulus and local viscoelasticity recently mapped out in experiments (26–28).

Methods

Our molecular dynamics (MD) simulations used the embedded atom method (EAM) potentials optimized for realistic amorphous Cu–Zr structures (29), using 10,000 atoms at the Cu₆₄Zr₃₆ composition. The MG was prepared by quenching the system at cooling rates between 10⁹ and 10¹³ K/s from a liquid state equilibrated at 2,500 K using a Nose–Hoover thermostat (27). The external pressure was held at zero during the quenching process using a Parinello Rahman barostat (30). Periodic boundary conditions (PBCs) were applied in all three dimensions. Structural analysis was implemented using Voronoi tessellation to characterize the nearest-neighbor CN and short-range order (3). The normal mode analysis of the glass was conducted by diagonalizing the dynamical matrix of the MG inherent structure obtained using the conjugate-gradient (CG) method. The participation fraction of particle i in eigenmode e_ω is defined by $p_i={\left|{\overrightarrow{e}}_{\omega }^i\right|}^2$, where ${\overrightarrow{e}}_{\omega }^i$ is the corresponding polarization vector of particle i (15). Similar to ref. 15, $p_i$ was summed over a small fraction [1%, which is between the previously used cutoffs of 0.6% (14) and 1.5% (15); only slight variation was found when the cutoff criterion was varied over this range] of the lowest-frequency normal modes and denoted as the participation fraction P_i for the ith atom, which measures the involvement in soft modes for that atom. AQS (31) was imposed on the MG to different shear strains (γ) to induce atomic rearrangements during deformation, which were monitored using the local minimum nonaffine displacement (${\mathit{D}}_{\min }^2$) (22, 32) (SI Text). To identify the atoms most likely involved in shear transformation zones, the atomic strain of each atom was tracked during deformation and dissociated into the best affine fit and the nonaffine residue (22). When a shear transformation event sets in, the group of atoms contributing to the shape change cooperatively rearrange relative to one another, such that there will be a jump in ${\mathit{D}}_{\min }^2$ to different magnitudes for each of the atoms involved. SI Text and Fig. S2 present the details of our procedure to monitor the ${\mathit{D}}_{\min }^2$ jumps. The Cu and Zr atoms that are located next to one another and undergo simultaneous ${\mathit{D}}_{\min }^2$ jumps are identified as those that have experienced an obvious shear transformation and contributed the most to inelastic relaxation.