Understanding the frustration arising from the competition between function, misfolding, and aggregation in a globular protein

Significance

The amino acid sequence of a protein encodes a wide range of different properties, including function, folding, and avoidance of aggregation. The resulting requirements on the sequence may be in conflict with each other, thus creating the possibility of misfolding and dysfunction. To investigate possible mechanisms whereby such unwanted outcomes can be prevented, we study the folding process of frataxin, a protein whose aberrant folding is associated with Friedreich’s ataxia. Our results indicate that the regions prone to misfolding are highly protected against aggregation along the folding pathway of this protein.

Abstract

Folding and function may impose different requirements on the amino acid sequences of proteins, thus potentially giving rise to conflict. Such a conflict, or frustration, can result in the formation of partially misfolded intermediates that can compromise folding and promote aggregation. We investigate this phenomenon by studying frataxin, a protein whose normal function is to facilitate the formation of iron–sulfur clusters but whose mutations are associated with Friedreich’s ataxia. To characterize the folding pathway of this protein we carry out a Φ-value analysis and use the resulting structural information to determine the structure of the folding transition state, which we then validate by a second round of rationally designed mutagenesis. The analysis of the transition-state structure reveals that the regions involved in the folding process are highly aggregation-prone. By contrast, the regions that are functionally important are partially misfolded in the transition state but highly resistant to aggregation. Taken together, these results indicate that in frataxin the competition between folding and function creates the possibility of misfolding, and that to prevent aggregation the amino acid sequence of this protein is optimized to be highly resistant to aggregation in the regions involved in misfolding.

Frustration is a general condition that arises in the presence of conflicting requirements. A system is frustrated when it is impossible to fully minimize its energy by optimizing simultaneously all of the possible interactions among its components (1). Although complex systems tend in general to exhibit frustration because of the large number and heterogeneity of their components, protein molecules are remarkable in that their folding process involves interactions that express a minimal level of frustration. According to the so-called principle of minimal frustration, the energy of proteins decreases as they explore conformations increasingly similar in structure to the native state (2). Consequently, the free energy landscape of proteins is characterized by the presence of a well-defined global minimum and very few other local minima, which are typically intermediate states along the folding pathway. This organization of conformational space normally ensures rapid and reliable folding (2–6).

Proteins, however, have evolved not only to fold, but also to function. Because the evolutionary constraints that select for a given function may be in conflict with the folding process, it is possible that local frustration patterns may localize in specific regions of proteins, in particular in their active sites. Indeed, a statistical survey of different proteins has shown that frustrated interactions tend to cluster at binding sites and that such frustration decreases upon complex formation (7). Because frustration is associated with the presence of local minima in the free energy landscape, it is important to understand how proteins have evolved to minimize the possible effects associated with these local minima, which are likely to contain misfolded elements and thus to potentially give rise to aggregation.

To address this question we studied frataxin, a mitochondrial protein that binds both Fe²⁺ and Fe³⁺ ions and forms a ternary complex with the two main components of the iron–sulfur cluster biogenesis machinery (8–11). This protein offers good opportunities for investigating the relationships between folding, misfolding, and disease. Indeed, its dysfunction is related to a neurodegenerative disease called Friedreich’s ataxia (12). Frataxin is also capable of binding different divalent and trivalent cations, whose recognition sites have been mapped (13). Furthermore, frataxin is involved in donating iron to ferrochelatease via direct interaction through an extended binding site involving some of the residues implicated in metal binding (14).

We have previously shown that frataxin folds via a complex mechanism, which we described through a broad free energy barrier (15). This feature, which has been associated with frustration (16), allows the experimental characterization of both the early and late events of folding (16–19). In this work we explored the mechanistic details of the folding reaction of frataxin at residue-level resolution. This result was achieved by characterizing the structures of both the early and late events of folding using Φ-value analysis (20) and restrained molecular dynamics simulations (21). By analyzing the structures of the different states along the folding process we found an unexpected number of nonnative interactions that slow down folding and superpose with the highly frustrated regions, as detected by the frustratometer server (22). The nonnative regions, which display peculiar Φ values, either negative or greater than unity, were predicted on the basis of the transition state structures determined from the Φ values, and subsequently confirmed by a second round of amino acid substitutions rationally designed to probe misfolded regions along the folding pathway.

The characterization of the folding pathway of frataxin and of its misfolded elements enables us to discuss the competition between folding and function and its consequences for misfolding and aggregation.

Results

Φ-Value Analysis.

We performed Φ-value analysis (20) and restrained molecular dynamics simulations (21) to characterize the folding pathway of yeast frataxin at residue-level resolution. Taking advantage of the characteristic folding of frataxin, which involves a broad free energy barrier, Φ values were experimentally measured for early, intermediate, and late events along the folding pathway, by following a methodology previously described (17) and briefly summarized below.

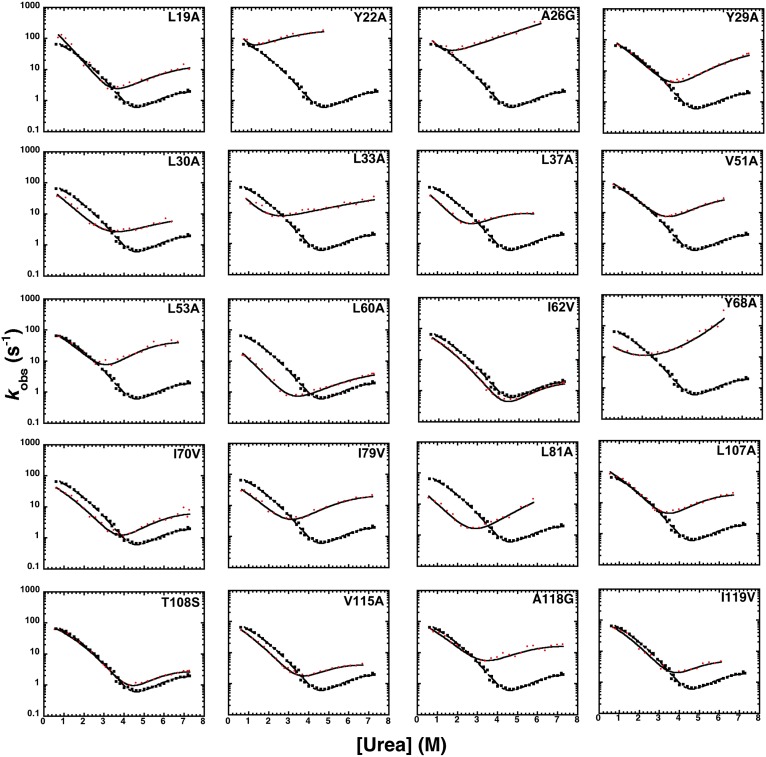
Twenty-one site-directed mutants of frataxin were designed, expressed, and purified (Fig. 1 and Table S1). One of these mutants expressed poorly and could not be analyzed; the remaining mutants were subjected to kinetic folding studies and 18 Φ values could be calculated. Kinetic folding experiments were performed by an 11-fold dilution of protein in buffer into a urea-containing buffer (unfolding), or protein in urea mixed into buffer solutions at different final urea concentrations (refolding). Experimental traces were fitted by single exponential functions at all final denaturant concentrations. Typical folding and unfolding time courses observed in stopped-flow experiments are shown in Fig. S1. Semilogarithmic plots of the observed unfolding and refolding rate constants versus denaturant concentration (chevron plot) for frataxin and its mutants are shown in Fig. 1. The quantitative analysis of the observed folding and unfolding amplitudes for frataxin (Fig. S2) confirms the absence of burst-phase intermediates lost in the dead time of the stopped flow, which is consistent with earlier suggestions of a broad-barrier model (15).

Fig. 1.

Chevron plots of wild-type (black filled squares) and mutants (red filled circles) of frataxin. Rate constants were measured as a function of urea at pH 7, with 0.4 M Na₂SO₄, and at 25 °C. All of the chevron plots were obtained by using a stopped-flow apparatus. Lines are the best fit to a model involving a broad free energy barrier, fitted globally to a quadratic equation with a global m_total value as previously described (17, 19).

In agreement with previous observations on wild-type frataxin (15), all mutants displayed a pronounced curvature in both the folding and unfolding arms of the chevron plot. Different mutations, however, had distinct effects on the folding and unfolding rate constants and on the curvature of the chevron plots. For example, the A26G, L33A, L81A, and Y68A mutants display nearly V-shaped chevron plots, with Y68A showing the onset of an upward curvature. By contrast, the L37A and V115A mutants display a degree of curvature more pronounced than that of wild-type frataxin. These positions are in direct contact in the native state, forming a major portion of its hydrophobic nucleus. Consequently, we analyzed the data by following a model involving a broad free energy barrier (17). According to this model, a complexity in the chevron plot arises from progressive changes in structure of the transition state as the native state is destabilized (23–25). If the transition state can be associated with a broad barrier, its structure may be malleable to changes in experimental conditions (i.e., change in denaturant concentrations) and may resemble a more native-like conformation as the native state stability drops, according to the Hammond effect (26). A useful parameter to study the structure of the transition state is Tanford’s β_T value (27), which reflects the accessible surface area of the transition state relative to that of the denatured (with a value of 0) and native (with a value of 1) states. In analogy to those described for U1A (17) and azurin (16), the curvature observed in the case of frataxin allows reliable Φ values to be calculated along different positions of the reaction coordinate (i.e., at different values of β_T). As previously described by Oliveberg and coworkers (17), the broad barrier model allows the transition state to be explored over a wide range of conditions and β_T values. Because of the complexity of the model, however, it is important to avoid extrapolations and to limit the experimental analysis to the conditions that can be directly measured. Accordingly, we considered the folding of frataxin at the most denatured-like and native-like conditions that were experimentally accessible without extrapolation (i.e., at β_T of 0.45 and 0.85). Additionally, the value of 0.65 was also analyzed to add an intermediate case between these two extreme conditions. The Φ values at early (β_T = 0.45), intermediate (β_T = 0.65), and late (β_T = 0.85) stages for folding, as well as the change in free energy of unfolding upon mutation, are reported in Table S1.

Structures of the Folding Transition States.

The structural information provided by the Φ values can be used to obtain structural ensembles representing the transition states for folding (21). In this approach, a trajectory is generated by integrating the equations of motion of a protein with a bias based on the incorporation of the Φ values in the force field (28–32). This approach is analogous to the use of interatomic distances obtained through NOEs to determine native state structures (28–32).

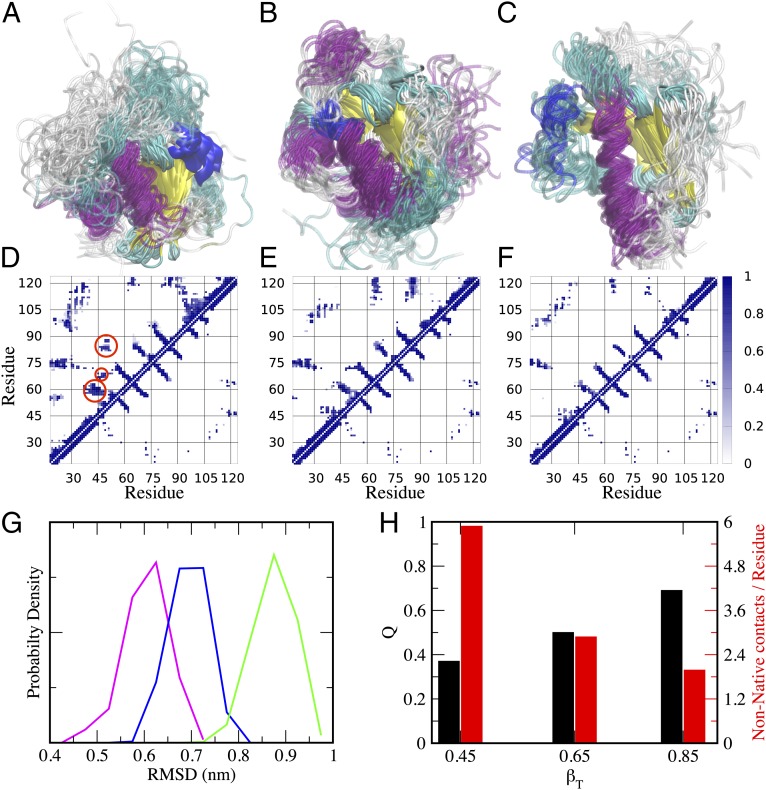
In this work, we have used this method to characterize the structure of the transition state at different stages of folding, as probed by the different β_T values (i.e., β_T = 0.45, β_T = 0.65, and β_T = 0.85) by using the values reported in Table S1 and the Protein Data Bank structure of frataxin (33). The structures of the transition states, as well as their contact maps compared with that of the native state, are shown in Fig. 2. Although it is evident that in all cases the overall transition state structure resembles the native state topology with the β-sheet in the process of being formed, we observed a significant fraction of nonnative interactions at the early stages of folding, which seems to decrease as the native state is approached. The nonnative interactions are highlighted with red circles in Fig. 2D at β_T = 0.45. In agreement with the predictions of the frustratometer server, it seems that nonnative interactions are located in the region of the α-helices and, more importantly, in their interactions with the β-sheet.

Fig. 2.

Folding transition state ensembles of frataxin. (A–C) Structures obtained by restrained molecular dynamics simulations at β_T = 0.45, β_T = 0.65, and β_T = 0.85, respectively. (D–F) Contact maps of the corresponding transition states compared with the native state. In each contact map, the bottom right triangle refers to the contacts in the native state, whereas the top left refers to the transition state. The misfolded regions, which are clearly evident in the early transition state at β_T = 0.45 (highlighted by red circles), were used to design the second round of mutagenesis. (G and H) Structural properties of the three transition states, including (G) the rmsd from the native state (β_T = 0.45, green; β_T = 0.65, blue; β_T = 0.85, purple) and (H) the fraction of native contacts Q and nonnative contacts.

Validation of the Transition State Structure by a Second Round of Mutagenesis.

To validate the structures obtained by restrained molecular dynamics simulations, with particular attention to the nonnative interactions, we designed and characterized a series of additional mutants. Our procedure was based on the investigation of the contact map reported in Fig. 2D, which enabled us to identify three clusters of interacting residues that seem in contact in the transition state but not in the native state. Therefore, we predicted that mutations in these regions should result in nonclassical Φ values (i.e., negative or higher than unity), which are considered a signature of misfolding (34, 35). Because the early transition state at β_T = 0.45 exhibits the highest degree of misfolding (Fig. 2), we focused the validation of the structure generated by molecular dynamics simulation on this state. By following this strategy, we designed two groups of mutants spanning the entire sequence of the protein, which were chosen consistently with the standard rules of Φ-value analysis. The first group was composed of seven mutants (V57A, M58A, A64G, F65A, A82G, S83A, and L85A) with a variety of different effects on the secondary (A65G and A82G) and tertiary contacts (V57A, M58A, F65A, S83A, and L85A), as well as misfolding behavior, in the transition state. The second group of mutants was composed of four mutants (H32A, I48V, I110V, and T112A) that do not display misfolding or relevant contacts in the transition state. The mapping on the structure of frataxin of the mutated positions is shown in Fig. S3 together with the positions used for the Φ-value analysis in the first round of mutagenesis.

Two of these mutants, V57A and L85A, did not express in sufficient quantities and thus could not be characterized. Remarkably, however, out of the remaining five mutants, three resulted in nonclassical negative Φ values (Fig. 3 and Table S2). These results are of particular significance given that unusual Φ values are rarely observed (36, 37). Furthermore, these three mutants affect the three different clusters of nonnative interactions that were predicted on the basis of the transition state ensembles resulting from the first round of mutagenesis. To further support these conclusions, none of the second group of mutants displayed a relevant effect on the folding rate constants, with the mutants H32A, I110V, and T112A being essentially identical to the wild-type protein and the mutant I48V exhibiting a Φ value close to zero (Fig. S4). Overall, the possibility of using the structural models of the transition states generated by restrained molecular dynamics simulations to make quantitative predictions of additional Φ-value measurements (38) provides a validation of this method, as well as more generally of the Φ-value analysis.

Fig. 3.

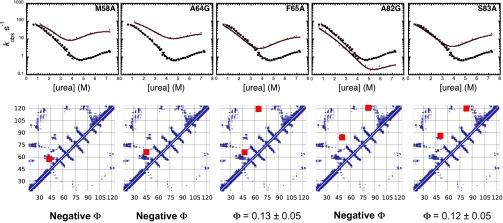
Validation of the transition state ensembles of frataxin via a second round of mutagenesis. Chevron plots of the wild type (black filled squares) and five single-residue mutants (red filled circles). Rate constants were measured as described in Fig. 1 (see also Materials and Methods). Lines are the best fit to a model involving a broad free energy barrier. The contact map for the early transition state (β_T = 0.45) is reported below each plot and the contacts that are affected by the mutation are indicated with red squares.

Discussion

Frustration in the Native Structure of Frataxin.

We performed an analysis using the frustratometer server (22) on the 3D structure of frataxin in the absence of ligands, which reveals a frustration pattern with peculiar and characteristic features (Fig. S5), with nonfrustrated interactions located in the β-sheet and highly frustrated interactions in the two α-helices and their contacts with the β-sheet. Thus, the overall structure of frataxin seems to be split into halves with respectively low and high frustration. As discussed below, it is likely that the frustrated regions in frataxin are correalated to the peculiar function of this protein, which involves multiple binding sites with both divalent and trivalent metals (13) as well as to ferrochelatase (14).

Frustration Arising from the Competition Between Folding and Function.

The free energy landscape of proteins tends to exhibit a strong bias toward the native states (2, 4, 5). In this view, the organization of the conformational space of these macromolecules is consistent with the principle of minimal frustration, which seems to characterize the majority of proteins and implies the presence of converging pathways leading to the native state, where nonnative alternative free energy minima tend to be limited in number. In some cases, however, possibly related to their function, proteins display signatures of local frustration (7, 39), which, as in the case of frataxin, may involve a relatively large portion of the whole structure. The description presented in this work of the folding pathway of frataxin at residue-level resolution, and the identification of transient misfolding events, allows some conclusions to be proposed about the links between frustration, function, folding, and misfolding. To highlight the conflicting demands between folding and function we compared the structural distribution of the residues that govern these different aspects of the behavior of frataxin (Fig. 4). We found a remarkable superposition between the residues involved in the function of frataxin and those that have a greater tendency to misfold during the early stages of folding. The residues involved in the binding of ferrochelatase have a structural distribution similar to those located in the largely misfolded regions seen at the early stages of folding as well as those energetically frustrated in the native state. Our data thus support the general view that the presence of frustrated patterns in proteins leads to a malleable structure of their folding transition state, which is the origin of broad barriers and curvatures in chevron plots and backtracks protein folding (16).

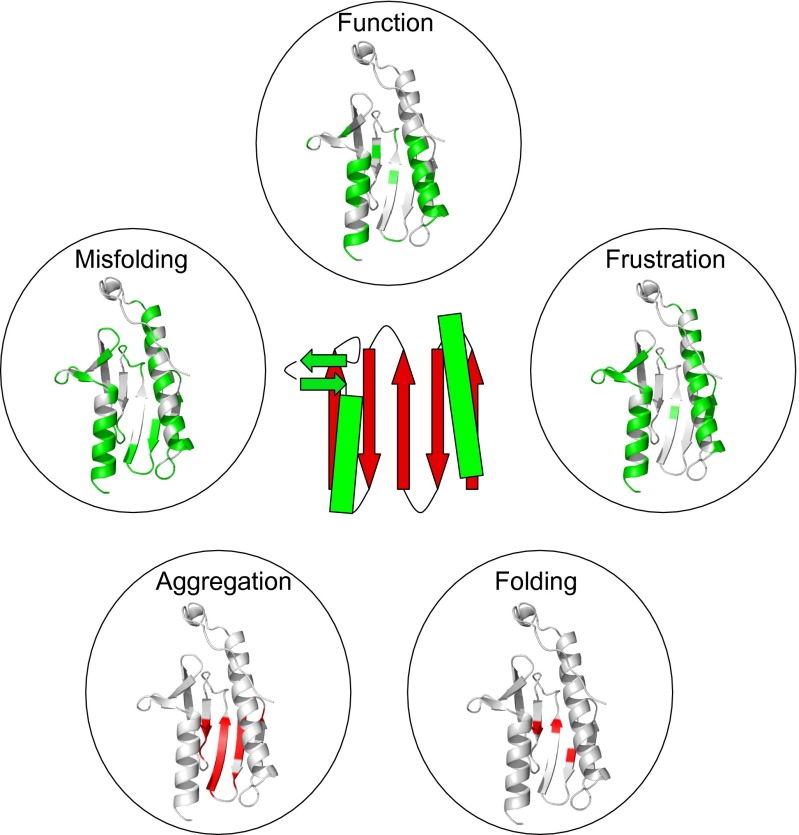
Fig. 4.

Relationship between function, misfolding, frustration, and aggregation propensity in frataxin. A schematic diagram of the structure of frataxin is reported at the center. Function: The key residues involved in the function of frataxin, as detected from the binding to ferrochelatase, are highlighted in green on the structure; residues correspond to those identified in Fig. 3 of ref. 14. For completeness, the negatively charged residues involved in metal binding in frataxin are reported in Fig. S7. Misfolding: To identify on the structure the regions that are mainly involved in the transient misfolding, we highlighted in green the residues with more than 50% nonnative interactions in the early transition state of β_T = 0.45; frustration was calculated from the web server www.frustratometer.tk (22) and residues forming highly frustrated interactions are reported in green (see also Fig. S1). Folding: The three residues (L60, I70, and L81) with the highest Φvalues are highlighter in red; these residues are identified as those most important for folding (21). Aggregation propensity: The aggregation propensity was calculated at a residue level using the Zyggregator algorithm (40, 41) and mapped on the structure; residues displaying a high propensity to aggregate are represented in red.

Protection of the Frustrated Regions from Aggregation.

Given the close relationships between frustration, folding, and function in frataxin, it is of interest to analyze its sequence composition in the light of its tendency to misfold. In particular, because of the close link between misfolding and aggregation events, we evaluated the propensity of frataxin to aggregate. To investigate the competition between folding and aggregation we used the the Zyggregator method (40, 41) to calculate the aggregation propensity of frataxin at the individual residue level (Fig. S6). We found that whereas the sequence of frataxin contains regions prone to aggregation, experimentally its tendency to aggregate under native-like conditions is very low, being soluble even at very high concentrations (14). This feature may be understood because the regions prone to aggregation are buried in the native structure and, therefore, protected from aggregation. Indeed, the Zyggregator method predicts a low “structurally corrected” aggregation propensity profile for frataxin (Fig. S4), implying that, when folded, the protein has a low propensity to aggregate. In analogy to the structural distribution of local frustration, also the aggregation propensities of frataxin seem to be split in two halves, with a low aggregation propensity region located in the α-helices and a region of higher aggregation propensity in the β-sheet. Thus, we observed that the localization of frustrated and aggregation-prone clusters in frataxin are topologically swapped (Fig. 4). A possible explanation for this behavior is that regions that are optimized for folding and stability (i.e., minimally frustrated) are intrinsically protected from aggregation and therefore are not necessarily selected to minimize their tendency to aggregate. However, in analogy with previous suggestions for superoxide dismutase 1 (42), when the functional requirements introduce a frustration in the protein, the structural elements are prone to local misfolding and must therefore minimize their aggregation propensity for the protein to be soluble and therefore functional.

Conclusions

By combining experiments and simulations we have characterized the folding pathway of frataxin at residue-level resolution and validated the resulting structures of the folding transition state by a second round of mutagenesis. A structural analysis of the transition state for folding has highlighted the specific structural patterns of frataxin that are prone to local misfolding. The presence of these patterns, which we predicted from the structure of the transition state and subsequently verified by site-directed mutagenesis, together with those involved in the recognition of ferrochelatase and with those in the frustrated regions of the protein, reveal the divergent demands imposed by folding and function on the amino acid sequence of frataxin. An analysis of the sequence composition of this protein suggests that frustrated regions, which may experience transient misfolding, are optimized to prevent aggregation. Our study on the folding pathway of frataxin thus reveals how competition between folding and function can in some cases lead to misfolding, which in turn requires a certain degree of sequence-based compensations to prevent aggregation.

Materials and Methods

Site-Directed Mutagenesis and Frataxin Expression and Purification.

Site-directed mutants were obtained using the QuikChange mutagenesis kit (Stratagene) according to the manufacturer’s instructions and the mutations were confirmed by DNA sequencing. We used yeast frataxin, which is highly homologous to human frataxin. The protein and its mutants were expressed in Escherichia coli BL-21 (DE3) and purified by using three steps of ion-exchange chromatography. The first was a Q-Sepharose column (GE Healtcare) equilibrated with 25 mM Tris⋅HCl and 10 mM EDTA, pH 8.0, the protein being eluted with 700 mM NaCl. After a buffer exchange step, the sample was loaded in sequence on Q and S-Sepharose columns (GE Healtcare) equilibrated with 50 mM AcOH, pH 5.0. The protein eluted from the S-column was bound to the Q-column and then eluted with 1 M NaCl. The purity of frataxin was confirmed by SDS/PAGE.

Stopped-Flow Measurements.

Kinetic folding experiments were carried out on a single-mixing SX-18 stopped-flow instrument (Applied Photophysics), the reaction being followed by Trp fluorescence emission. The excitation wavelength was 280 nm and emission was collected using a 320-nm cutoff glass filter. Protein concentration was typically 1 μM. The experiments were performed at 25 °C in 20 mM Hepes, pH 7.0, buffer with 0.4 M sodium sulfate and 8 M urea. The observed kinetic traces were largely independent of protein concentration (when experiments were performed for final protein concentrations ranging from 0.5 to 10 μM), as expected for a unimolecular reaction without effects due to transient aggregation (43).

Transition State Ensemble Calculations.

Molecular dynamics simulations were carried out starting from the native structure 2FQL using the Amber03W force field in explicit TIP4P05 water (44). Given a set of experimental Φ values, a pseudo energy term has been added to the force field as the squared difference between experimental and simulated Φ values:

$$E=0.5K{{\displaystyle \sum _{i=1}^N({\phi }_i^{\exp }-{\phi }_i^{sim}})}^2,$$

where K is the strength of the restraint and has been chosen to maximize the agreement with the experimental value while keeping the simulation stable. The Φ value for a residue i is calculated from the fraction of native contacts that it makes in a conformation (21, 28–32). Given two residues that are not nearest neighbors, the native contacts between them are defined as the number of heavy side-chain atoms within 0.65 nm in the native structure. To make the function differentiable, the contacts are defined through a step function:

$${\phi }_i^{sim}=\frac{1}{N_i^{Nat}}{\displaystyle \sum _j^{N_i^{Nat}}\frac{1}{1+\exp \left(150\right(r_j-0.65\left)\right)}},$$

where the sum is over the list j of the native contacts for residue i (21, 28–32). With this approach only Φ values between 0 and 1 can be incorporated as structural restraints.

The different transition state ensembles have been generated using simulated annealing. Each ensemble is the results of 300 annealing cycles, 150 ps long, in which the temperature is varied between 300 and 500 K. Only the structures sampled at 300 K are retained for further analysis, resulting in TSE of ∼300 structures each. In addition a standard 300 K molecular dynamics simulation has been performed as a reference for the native state ensemble. All of the simulations were performed using GROMACS and the restraint has been implemented using PLUMED (45).