A mixture of transition models for heterogeneous longitudinal ordinal data: with applications to longitudinal bacterial vaginosis data

Abstract

Markov models used to analyze transition patterns in discrete longitudinal data are based on the limiting assumption that individuals follow the common underlying transition process. However, when one is interested in diseases with different disease or severity subtypes, explicitly modeling subpopulation-specific transition patterns may be appropriate. We propose a model which captures heterogeneity in the transition process through a finite mixture model formulation and provides a framework for identifying subpopulations at different risks. We apply the procedure to longitudinal bacterial vaginosis (BV) study data and demonstrate that the model fits the data well. Further, we show that under the mixture model formulation, we can make the important distinction between how covariates affect transition patterns unique to each of the subpopulations and how they affect which subgroup a participant will belong to. Practically, covariate effects on subpopulation-specific transition behavior and those on subpopulation membership can be interpreted as effects on short-term and long-term transition behavior. We further investigate models with higher-order subpopulation-specific transition dependence.

1. Introduction

Bacterial vaginosis (BV) is characterized by disturbances in vaginal flora and is associated with adverse pregnancy outcomes and increased risk of HIV infection and sexually transmitted diseases [1]. The diagnosis is based on Gram-stained smears assessed using the Nugent score criterion, which derives an overall score from 0 to 10 corresponding to increasing severity of bacterial flora imbalance [2]. Most studies classify vaginal flora as a dichotomous state (i.e., BV versus no BV or abnormal versus normal vaginal flora) and analyze data with Markov models [3, 4]. However, to better understand dynamic changes in vaginal flora states by utilizing transient status information, we considered three severity levels of vaginal microbiome disturbance: normal (0 to 3 points), intermediate (4 to 6 points), and BV vaginal flora state (7 to 10 points). The intermediate state is thought to provide additional information when considering the natural history of vaginal ecosystem [5, 6].

BV recurrence is common [7], but the etiology of onset and remission is not yet clear. Interestingly, studies of short-term vaginal flora condition suggest different patterns of change may exist; a proportion of women rarely experience BV and vaginal statuses of others remain disturbed at medium to high level, whereas the majority fluctuate across all severity states [8, 9, 10, 11]. It is thought that those with distinct vaginal flora profile may be different with respect to their covariate patterns [9, 12]. Therefore, critical to our understanding of the etiology and avoiding possible adverse sequelae of this condition is elucidating factors contributing to differences between women with persistence or resistance for BV over time and those who frequently transition across all states.

To address this, we develop a framework which models the probability of being in each of the three groups as well as examines covariates for each of the three processes. More specifically, we utilize a mixture model of three transition processes that captures heterogeneity in the transition process across individuals and incorporates the ordinal nature of the level of bacterial flora imbalance. This model is a latent class model with three mixture components corresponding to groups of subjects who (a) alternate between normal and intermediate states (i.e., non-BV), (b) fluctuate between intermediate and BV states (i.e., abnormal vaginal flora), and (c) shift across all three states.

This mixture of transition processes extends the mover-stayer model introduced by Blumen et al. [13], which assumes that subjects either never leave their initial state or transition across states. The mover-stayer approach was previously used to study the natural history of BV by Sanders et al. [3], but that study was limited by having a small number of follow-up measurements and treated BV status as dichotomous. In our model, a “stayer” is newly defined as shifting between two states (either process (a) or (b)), and we apply it to vaginal flora data obtained from a large number of visits over a two-year period.

There exist statistical procedures for longitudinal categorical data including those by Miller et al. [14] and Azzalini [15]. Albert [16] proposed a Markov model for ordinal data for a relapsing-remitting disease by expanding to a state space with both the ordinal state and a trajectory in the ordinal state process. For bivariate ordered responses, Dale [17] and Williamson et al. [18] proposed Global cross-ratio models and global odds ratio models, respectively. These models were further extended for multivariate ordinal data by Molenberghs and Lesaffre [19]. Marginalized transition model for longitudinal data was presented for binary data by Heagerty [20] and ordinal categorical data by Lee and Daniels [21]. Cook [22] introduced a Markov model with random effects to incorporate heterogeneity in the transition patterns across individuals. When transition between unobserved states is of interest, a hidden Markov model (HMM) can be used by assuming a Markov process between latent states [23]. Our problem shares the idea of latent classes with HMM but involves biological phenomenon where transition occurs between observed states (severity levels), not between latent groups (i.e., groups A, B, and C); on the other hand, a finite mixture of transition processes is suitable for modeling heterogeneity in BV data, using both the probability of inclusion in a hidden subgroup as well as transition patterns within a group. We also compare our model with traditional Markov model and further investigate higher-order dependence structures. Initially, we assume the first-order transition process within each group, but we relax this assumption by the incorporation of second-order lag terms or the history of prior responses. We demonstrates our method with bacterial vaginosis (BV) study data conducted by the Rakai Health Science Program (RHSP) in southwestern Uganda [24, 25, 26].

Section 2 describes the BV longitudinal data from the RHSP study and presents models and computational methods. In Section 3, we demonstrate our procedure with RHSP BV data. We test the goodness of fit of our model to BV data and compare it with traditional Markov model in Section 3.1. We present inference under the simple Markov model and the proposed mixture model and discuss the extension of the mixture model with higher-order lag terms in Section 3.2. Section 3.3 shows simulation results, which indicates that the proposed method performs well. Section 4 summarizes our findings and provides a discussion.

2. Data, model formulation, and estimation

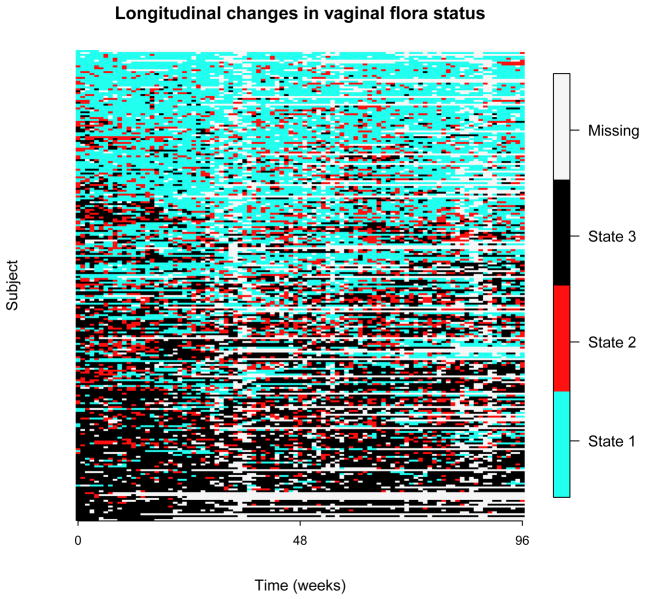
Two hundred fifty five postmenarcheal women were followed weekly for 96 weeks for vaginal microbiome assessment, and 246 subjects with non-missing measurements for HIV status and partners’ circumcision status at baseline were used for our analyses. Categories of vaginal flora described in the Introduction as normal, intermediate, and BV are referred to as states 1, 2, and 3, respectively. Eleven subjects never had BV, and 15 subjects never had normal vaginal flora. The numbers of women who stayed only in states 1, 2, and 3 are one, zero, and six, respectively. Sample proportions in states 1, 2, and 3 across all individuals and follow-up times are 0.44, 0.17, and 0.39, respectively. Figure 1 demonstrates heterogeneity in the transition process and provides visual evidence for the proposed three-group mixture model. We now introduce the traditional Markov model and compare it with the mixture model.

Figure 1.

Longitudinal changes in vaginal flora states. Follow-up time is marked on the x axis. Each row represents the status of vaginal flora of an individual over 96 weeks. Blue, red, and black colors correspond to BV states 1, 2, and 3, respectively, and white spots represent missing measurements (summarized in the right bar).

2.1. Traditional Markov model

A traditional first-order Markov model, referred to as Model 1, is given as

$$\mathit{logitP}(Y_{it}\le j\mid Y_{i(t-1)},{\mathbf{X}}_{it})={\eta }_j-{\mathbf{X}}_{it}\tau -{\tau }_5{I}_{(Y_{i(t-1)}=2)}-{\tau }_6{I}_{(Y_{i(t-1)}=3)},j=1,2$$ (1)

where there are three states, X_it and Y_it are the covariates and the ordinal outcome for the ith person at the tth time point, respectively. And I_{(Yi(t−1) = 2)} and I_{(Yi(t−1) = 3)} denote indicators of the outcome at the previous week being at state 2 or 3, respectively, i = 1, …, N, and t = 1, …, T where T=96.

The parameter τ is the effects of covariates and τ₅, and τ₆ are those for lag terms at state 2 or 3, respectively. Large values of τ, τ₅, and τ₆ are associated with an increase of vaginal flora severity levels. This model adopts a cumulative logit link function that utilizes the proportional odds assumption [27] to model the intrinsic ordering between response categories. It assumes that the odds ratios between the lowest and all higher levels of the response variable are the same as those between the next collapsed lowest level and all higher levels for each covariate.

2.2. Mixture transition model

The mixture transition model provides a richer framework designed to reflect the heterogeneous nature of the population, and we refer to it as Model 2. This model specifies that the population consists of three groups of women. Subjects who fluctuate between normal and intermediate states (states 1 and 2) are classified as group A. Those who persist with intermediate vaginal flora state and BV (states 2 and 3) are group B. Participants who stay at state 1 or state 2 for the entire study period are included in group A whereas those who are at state 3 at all weeks in group B. The remainder of the cohort, referred to as group C, represents women who transition across all three states. Note that factors for distinguishing groups A and B from group C are associated with long-term effects for resistance and persistence over two years (i.e., over the whole period of the study), whereas predictors for switching between BV statuses relate to short-range effects on weekly transitions. In an attempt to describe covariates consistent with long-term and short-term transition patterns, we model explanatory variables associated with group membership and factors for increasing Nugent score severity level within group membership. Let G_i be the true group membership variable for the ith person, where G_i = A, B, and C for groups A, B, and C, respectively. The parameter w_iA denotes P(G_i = A), the probability of the ith person belonging to group A. The parameters w_iB and w_iC are defined similarly for groups B and C, respectively. We incorporate the relationship of group membership with covariates with a polychotomous logistic model

$$\mathit{log}(w_{im}/w_{iC})={\lambda }_0^m+{\mathbf{Z}}_i^{\prime }{\lambda }^m,$$ (2)

where Z_i is a vector of covariates for the ith person, and m = A and B for groups A and B, respectively. The parameters λ^A and λ^B characterize covariate dependence for the probability of being in groups A and B over two years, respectively. Large positive estimates of ${\lambda }_0^m$ and λ^m suggest a high probability of being in group m rather than group C.

We now propose parameterization for the transition models that describe each of the three groups. For individuals whose true group membership is A, their responses are described as

$$\mathit{logitP}(Y_{it}=2\mid Y_{i(t-1)},G_i=A,{\mathbf{X}}_{it})={\alpha }_0+{\mathbf{X}}_{it}^{\prime }\alpha +{\alpha }_5{I}_{(Y_{i(t-1)}=2)},$$ (3)

while those for group B are modeled by

$$\mathit{logitP}(Y_{it}=3\mid Y_{i(t-1)},G_i=B,{\mathbf{X}}_{it})={\beta }_0+{\mathbf{X}}_{it}^{\prime }\beta +{\beta }_5{I}_{(Y_{i(t-1)}=3)},$$ (4)

where X_it denotes a vector of covariates and α₅ and β₅ describe the first-order transition dependence in groups A and B, respectively. The model for subjects whose vaginal flora states could potentially move across all three states (group C) is specified with a proportional odds parameterization to exploit the ordinal nature of the outcome as

$$\mathit{logitP}(Y_{it}\le j\mid Y_{i(t-1)},G_i=C,{\mathbf{X}}_{it})={\delta }_j-{\mathbf{X}}_{it}^{\prime }\gamma -{\gamma }_5{I}_{(Y_{i(t-1)}=2)}-{\gamma }_6{I}_{(Y_{i(t-1)}=3)},j=1,2$$ (5)

where j represents the two states. Positive estimates for α, β, and γ translate to short-term covariate effects on the increased odds for exacerbation in imbalanced vaginal flora. The dependence of vaginal microbiome states on prior measurements is modeled with α₅, β₅, and (γ₅, γ₆) in groups A, B, and C, respectively. This model reduces to Model 1 if proportions of both group A and group B are zero.

For the second-order models which will be discussed in Section 3.2, lag terms two weeks prior to the measurements are added and equations (3), (4), and (5) are modified as

$$\begin{array}{l}\mathit{logitP}(Y_{it}=2\mid Y_{i(t-1)},Y_{i(t-2)},G_i=A,{\mathbf{X}}_{it})={\alpha }_0+{\mathbf{X}}_{it}^{\prime }\alpha +{\alpha }_5{I}_{(Y_{i(t-1)}=2)}+{\alpha }_6{I}_{(Y_{i(t-2)}=2)},\\ \mathit{logitP}(Y_{it}=3\mid Y_{i(t-1)},Y_{i(t-2)},G_i=B,{\mathbf{X}}_{it})={\beta }_0+{\mathbf{X}}_{it}^{\prime }\beta +{\beta }_5{I}_{(Y_{i(t-1)}=3)}+{\beta }_6{I}_{(Y_{i(t-2)}=3)},\\ \mathit{logitP}(Y_{it}\le j\mid Y_{i(t-1)},Y_{i(t-2)},G_i=C,{\mathbf{X}}_{it})={\delta }_j-{\mathbf{X}}_{it}^{\prime }\gamma -{\gamma }_5{I}_{(Y_{i(t-1)}=2)}-{\gamma }_6{I}_{(Y_{i(t-1)}=3)}-{\gamma }_7{I}_{(Y_{i(t-2)}=2)}-{\gamma }_8{I}_{(Y_{i(t-2)}=3)},j=1,2.\end{array}$$

For building a likelihood, we introduce a variable O_i to classify participants based on their observed BV state sequences. The random variable O_i = 1 if the observed BV state of the ith person is always either 1 or 2 while their true membership G_i could be A or C. In a similar way, O_i = 2 for those who were never observed to be in state 1 and their true membership could be B or C. O_i = 3 if subjects visited all three states and their true membership G_i is always C. Then, the likelihood for the ith subject has the form

$$\begin{array}{l}{L}_i(\theta )={\left\{w_{iA}\prod _{t=1}^{T}P(Y_{it}\mid Y_{i(t-1)},G_i=A,{\mathbf{X}}_{it})+w_{iC}\prod _{t=1}^{T}P(Y_{it}\mid Y_{i(t-1)},G_i=C,{\mathbf{X}}_{it})\right\}}^{I(O_i=1)}\\ \times {\left\{w_{iB}\prod _{t=1}^{T}P(Y_{it}\mid Y_{i(t-1)},G_i=B,{\mathbf{X}}_{it})+w_{iC}\prod _{t=1}^{T}P(Y_{it}\mid Y_{i(t-1)},G_i=C,{\mathbf{X}}_{it})\right\}}^{I(O_i=2)}\\ \times {\left\{w_{iC}\prod _{t=1}^{T}P(Y_{it}\mid Y_{i(t-1)},G_i=C,{\mathbf{X}}_{it})\right\}}^{I(O_i=3)},\end{array}$$ (6)

where θ is a vector of all parameters for groups A, B, and C. We obtained maximum likelihood estimates of parameters with the Nelder-Mead algorithm. And the estimation was performed using only the observed data, which implicitly assumes missing at random (MAR). Model 1 can be estimated using any package for proportional odds regression such as R or SAS. We implemented log likelihood function in R and optimized it with the “optim” function for both Model 1 and Model 2. The log likelihood function for Model 2 is given in the appendix. The Hessian matrix was numerically evaluated in the algorithm and used to calculate asymptotic standard errors for hypothesis testing.

3. Analysis of the RHSP BV data

The proposed models are fit with the RHSP longitudinal study data on vaginal flora changes. Having provided graphical support for the presence of heterogeneity in Figure 1, we present more formal evidence for the mixture model in Section 3.1 and Section 3.3. Parameter estimates and their interpretation as well as the examination of dependence on prior BV history follow in Section 3.2.

3.1. Test of fit for mixture model

We assessed the fit for Model 2 to BV data in two ways due to missing observations in covariates as well as responses. First, we performed the test of fit using the base model including intercepts since the expected value for the test can be calculated in the absence of covariates. Based on the likelihood function equation (6), the expected transition count under the mixture model can be extended from that under the traditional Markov model (Model 1). More specifically, under Model 1, E_t,kl the expected transition number from state k at time (t − 1) to the state l at time t can be calculated as P(Y_t = l|Y_(t−1) = k)N_t,k where N_t,k represents the number of individuals in state k at time (t − 1). However, expected transition differs across groups under the mixture model as the transition probability depends on group membership. Since the true membership is unknown, we first partitioned the data according to variable O_i and computed observed and expected transitions within each partition. For example, for those with O_i = 1, their true group membership (G_i) could be A or C, therefore, their expected count of transitions within each membership group are calculated and averaged considering their group probabilities (w_iA and w_iC). In other words, for those with O_i = 1, E_t,kl is $w_A{E}_{t,kl}^A+w_C{E}_{t,kl}^C$ where $E_{t,kl}^m$ is expected transition counts for group m. Similarly, E_t,kl is estimated as $w_B{E}_{t,kl}^B+w_C{E}_{t,kl}^C$ if O_i = 2. For the rest of subjects whose O_i = 3, E_t,kl is equal to $w_C{E}_{t,kl}^C$. Then, the test statistic is

$$T=\sum _{h=1,2,3}\sum _{t=1}^T\sum _{k=1}^3\sum _{l=1}^3\frac{{(N_{t,kl}^h-E_{t,kl}^h)}^2}{E_{t,kl}^h},$$

where $N_{t,kl}^h$ and $E_{t,kl}^h$ represent the observed and expected numbers of transition from state k at time (t − 1) to the state l at time t for subjects whose O_i = h. The distribution of the test statistic T under Model 2 was estimated with 1000 parametric bootstrap samples [28]. For this purpose, data were created without any covariates (but including only lag terms) to facilitate the calculation of n-step transition probability. The missing data structure was preserved in bootstrap data generation in order for proper comparison with the test statistic computed on the actual data. P value was computed as Σ_q I(T_q > T_obs)/Q, where T_obs and T_q denote the values of the test statistic for data and the qth bootstrap sample and Q is the number of bootstrap replications. We obtained a T_obs of 10331.92 and p value of 0.95. The insignificant goodness of fit test result suggests that the proposed mixture of transition probabilities in base model adequately fits the BV longitudinal data. Second, the adequacy of Model 2 was compared with that of Model 1 using the AIC (Akaike information criterion) in the presence of covariates. AIC values under Model 1 and Model 2 were 25761.52 and 25440.07, respectively. The smaller AIC of Model 2 indicates a better fit of Model 2 than that of Model 1. Taken together, these results suggest that our model fits well.

3.2. Estimation results

We were interested in elucidating the effects of five covariates on the history of vaginal flora shifts. Baseline HIV status and self-reported partners’ circumcision status were used in the analysis as predictors of group membership. Measurements recorded weekly from participants included current menstruation, recency of sex (within 24 hours), and lag terms based on the vaginal flora status in the previous week. The estimates, Hessian-based asymptotic standard errors, and p values of parameters estimated under Model 1 and Model 2 are shown in Table 1 and Table 2, respectively.

Table 1.

Estimates, standard errors (SE), and p values for parameters for Model 1. HIV and circumcision are the indicators of HIV infection and the circumcision of subjects’ partners. Lag (state 2) and lag (state 3) are indicator variables for vaginal flora states at the previous week, corresponding to state 2 and state 3, respectively. Intercepts 1 and 2 refer to η₁ and log(η₂−η₁) in equation (1).

Parameter	Estimate	SE	P value
τ1 Circumcision	−0.12	0.04	<0.01
τ2 HIV	0.14	0.06	0.02
τ3 Menstruation	0.70	0.06	<0.01
τ4 Recency of sex	0.33	0.05	<0.01
τ5 Lag (state 2)	1.74	0.05	<0.01
τ6 Lag (state 3)	3.30	0.04	<0.01
Intercept 1	1.27	0.03	<0.01
Intercept 2	0.09	0.02	<0.01

Table 2.

Estimates, standard errors (SE), and p values for parameters obtained under Model 2. Intercepts 1 and 2 denote δ₁ and log(δ₂−δ₁) in equation (5).

Parameter	Estimate	SE	P value
${\lambda }_0^A$ Intercept	−3.38	0.45	<0.01
${\lambda }_1^A$ Circumcision	0.78	0.65	0.23
${\lambda }_2^A$ HIV	−0.01	1.05	0.99
${\lambda }_0^B$ Intercept	−3.38	0.45	<0.01
${\lambda }_1^B$ Circumcision	0.20	0.67	0.76
${\lambda }_2^B$ HIV	1.50	0.71	0.03
α0 Intercept	−3.04	0.26	<0.01
α1 Circumcision	0.34	0.29	0.24
α2 HIV	−1.38	0.96	0.15
α3 Menstruation	1.96	0.41	<0.01
α4 Recency of sex	1.08	0.33	<0.01
α5 Lag (state 2)	1.51	0.37	<0.01
β0 Intercept	2.51	1.11	0.02
β1 Circumcision	−0.14	0.60	0.82
β2 HIV	−0.39	0.65	0.55
β3 Menstruation	−0.50	0.98	0.61
β4 Recency of sex	−0.19	0.74	0.80
β5 Lag (state 3)	1.41	1.05	0.18
γ1 Circumcision	−0.11	0.04	<0.01
γ2 HIV	0.10	0.06	0.10
γ3 Menstruation	0.67	0.06	<0.01
γ4 Recency of sex	0.30	0.05	<0.01
γ5 Lag (state 2)	1.68	0.05	<0.01
γ6 Lag (state 3)	3.12	0.04	<0.01
Intercept 1	1.18	0.03	<0.01
Intercept 2	0.10	0.02	<0.01

All explanatory variables were found to be significant under Model 1. On the other hand, covariate effects varied across subgroups under Model 2. The estimate of ${\lambda }_2^B$ in Table 2 was positive and significant, which indicates that HIV-positive women were more likely to be in group B than group C. That is, HIV-infected subjects were more likely to persist with high Nugent scores rather than shift across all states. Large p values of ${\lambda }_1^A$ and ${\lambda }_2^A$ imply that neither HIV infection nor circumcision was a significant factor for distinguishing group A from C, suggesting that these factors are not related to differentiating normal and fluctuating long-term conditions. Covariates measured weekly (i.e., current menstruation, recency of sex, and first-order lag terms) were significantly related to transitioning between states in groups A and C, but not B. HIV was not associated with temporal fluctuation of vaginal flora states (see α₂, β₂, and γ₂ in Table 2). Parameter estimates and p values under Model 1 are similar to those for group C in Model 2, which confirms the notion that Model 1 captures common transition processes of the population (or the majority of women), not identifying subgroup specific mechanism. For instance, Model 2 estimates suggest that beneficial effect of circumcision is limited to group C. The estimated proportions of groups A and B, P(G_i = A) and P(G_i = B), are 0.032 and 0.032 for HIV-negative subjects and 0.028 and 0.128 for HIV-positive subjects, respectively, under Model 2. The estimates of P(O_i = 1) and P(O_i = 2) using observed proportion of the corresponding subjects are 0.046 and 0.050 for HIV-negative participants and 0.037 and 0.148 for HIV-positive participants. Equation (6) indicates that the differences between expected and observed proportions, 0.014 and 0.018 for HIV-negative subjects and 0.009 and 0.020 for HIV-positive subjects, represent people whose true group memberships were C but were not observed to visit all possible vaginal flora states. This suggests that a sizable fraction of women whose observed Nugent scores fluctuated at normal to intermediate states had the capacity to transition to a BV state. In other words, transient BV episodes were missed despite very frequent and long-term follow-up visits of this study. This may be important for future BV trials or other studies assessing frequently recurring conditions.

We also fitted a mixture transition model of order two. The second-order lag terms were positively related to increasing severity of vaginal flora states in groups A and C under Model 2 (data not shown). Parameter estimates and standard errors were similar to those of Model 2, resulting in similar inferences. To further investigate higher-order dependence while avoiding computational complexity, we incorporated into the model, in addition to the first-order lag terms, the proportion of time over the course of the study that each subject spent in the intermediate or BV state. These summary measures of prior history for BV were significant for group C under Model 2. This is consistent with the fact that the recurrence rate of BV is high and indicates that BV levels depend on two or more preceding values. The inferences for all long-term and short-term covariate effects were similar to those made with Model 2 containing only the first-order lags, except the long-term effect of HIV in group B ( ${\lambda }_2^B$) was not significant.

3.3. Simulation for mixture model

To validate the performance of our method, we conducted simulation under the formulation of Model 2. Using covariate observation patterns from BV data and parameter estimates obtained from Model 2 (listed in Table 2), 1000 data sets were generated and fit using Model 2. Coverage rates of 95% confidence intervals are near the nomial value (Table 2). Biases, calculated as differences of the mean parameter estimates from corresponding simulation values, were generally very small except one parameter ( ${\lambda }_2^A$ HIV). The large bias for this parameter seems related to the small sample size of the relevant group and low rate for HIV in BV data and simulated data; for example, this parameter was estimated from 11 women whose O_i = 1, only one of whom was HIV positive in the original BV data. The results from this simulation show the good performance of the proposed estimation procedure when applied to data simulation for the BV dataset.

4. Discussion

Transient shifts in vaginal flora states are common in women and may represent a normal physiologic process; however, long-term persistence with high Nugent scores may represent a pathologic process that differs from normal fluctuation. Our model has provided a new perspective on the etiology of BV by distinguishing factors for a transient severity shift from those for long-term persistence. The ordinary Markov model does not provide insight into this issue. Moreover, the validity of our results is substantiated by the findings in literature. For example, menstruation is associated with short-term fluctuation across vaginal flora states under Model 2 and it has been reported that BV occurrence is transient around the time of menses [11, 10].

The results of this study demonstrate the advantage of using our rich model. First, it detects differential effects of covariates in each group, revealing different mechanisms for vaginal flora changes across subpopulations. Second, this method is useful for identifying groups of subjects who may be at increased risk of adverse outcomes. Note that our model could be also utilized as a general framework to identify potential target subpopulation for treatments and intervention methods of other diseases. Third, our model has a better fit than the traditional Markov model according to the AIC and a good performance was demonstrated with simulation and bootstrap-based test. Moreover, the mixture transition model is less restrictive than the ordinary Markov model, as the dependence assumption is required only within each group, rather than for the whole population. We adapt the basic mixture transition model to incorporate higher-order dependence by increasing the order of lag terms or including the prior proportions of visits to each of the vaginal flora states as a summary of the prior BV history. Other higher-order transition models could be used for the group-specific models [29].

Our mixture transition model may be favored over other approaches when research focuses on characterizing both long-term and short-term changes in the longitudinal transition patterns. Our model is flexible in principle and may further be modified to accommodate other research questions by adding processes that stay at only one state. Corresponding to the BV example where disease severity is often treated as trichotomous, we formulated the model with a state space of three ordinal stages. For other applications, this modeling frame could be extended to incorporate more than three ordinal states. Our model does not allow changing membership over time since investigating factors for long lasting resistance or persistence is critical. But the method may be modified to allow moving from one class to another, when it is appropriate for research problems. Additionally, random effects can be incorporated to this mixture transition model. However, incorporating random effects in each subgroup model (i.e. groups A, B, and C) will result in very complex estimation and make the interpretation of parameter estimates difficult. The extension of our model to a mixture hidden Markov model may provide additional insight on the underlying biological processes. It may account for measurement error in the outcome, which could be beneficial in our setting considering that it involves histological exam of biological sample.

Table 3.

Parameter value used for simulation, bias, and coverage rate for each parameter. Intercepts 1 and 2 denote δ₁ and log(δ₂−δ₁) in equation (5).

Parameter	Simulation Value	Bias	Coverage
${\lambda }_0^A$ Intercept	−3.384	−0.021	0.959
${\lambda }_1^A$ Circumcision	0.775	−0.047	0.985
${\lambda }_2^A$ HIV	−0.013	0.548	0.923
${\lambda }_0^B$ Intercept	−3.382	−0.020	0.959
${\lambda }_1^B$ Circumcision	0.200	0.010	0.977
${\lambda }_2^B$ HIV	1.500	0.071	0.964
α0 Intercept	−3.044	0.017	0.951
α1 Circumcision	0.344	0.007	0.951
α2 HIV	−1.379	0.135	0.933
α3 Menstruation	1.962	−0.008	0.964
α4 Recency of sex	1.078	−0.011	0.946
α5 Lag 1 week (state 2)	1.508	−0.022	0.953
β0 Intercept	2.509	−0.041	0.937
β1 Circumcision	−0.136	0.072	0.952
β2 HIV	−0.387	0.031	0.952
β3 Menstruation	−0.503	0.080	0.964
β4 Recency of sex	−0.190	0.113	0.971
β5 Lag 1 week (state 3)	1.411	−0.057	0.949
γ1 Circumcision	−0.115	0.000	0.951
γ2 HIV	0.098	−0.008	0.963
γ3 Menstruation	0.673	−0.013	0.955
γ4 Recency of sex	0.301	0.004	0.947
γ5 Lag 1 week (state 2)	1.684	−0.007	0.953
γ6 Lag 1 week (state 3)	3.120	0.007	0.943
Intercept 1	1.182	−0.009	0.940
Intercept 2	0.095	0.002	0.952

APPENDIX

Log likelihood for the ith person under Model 2 is given by

$$\begin{array}{l}I(O_i=1)log[w_{iA}\prod _{t=1}^T{\left\{1-\frac{1}{1+exp\left(-({\alpha }_0+{\mathbf{X}}_{it}^{\prime }\alpha +{\alpha }_5{I}_{(Y_{i(t-1)}=2)})\right)}\right\}}^{I(Y_{it}=1)}{\left\{\frac{1}{1+exp\left(-({\alpha }_0+{\mathbf{X}}_{it}^{\prime }\alpha +{\alpha }_5{I}_{(Y_{i(t-1)}=2)})\right)}\right\}}^{I(Y_{it}=2)}\\ +w_{iC}\prod _{t=1}^T{\left\{\frac{1}{1+exp\left(-({\delta }_1-{\mathbf{X}}_{it}^{\prime }\gamma -{\gamma }_5{I}_{(Y_{i(t-1)}=2)}-{\gamma }_6{I}_{(Y_{i(t-1)}=3)})\right)}\right\}}^{I(Y_{it}=1)}\\ \times {\left\{\frac{1}{1+exp\left(-({\delta }_2-{\mathbf{X}}_{it}^{\prime }\gamma -{\gamma }_5{I}_{(Y_{i(t-1)}=2)}-{\gamma }_6{I}_{(Y_{i(t-1)}=3)})\right)}-\frac{1}{1+exp\left(-({\delta }_1-{\mathbf{X}}_{it}^{\prime }\gamma -{\gamma }_5{I}_{(Y_{i(t-1)}=2)}-{\gamma }_6{I}_{(Y_{i(t-1)}=3)})\right)}\right\}}^{I(Y_{it}=2)}]\\ +I(O_i=2)log[w_{iB}\prod _{t=1}^T{\left\{1-\frac{1}{1+exp\left(-({\beta }_0+{\mathbf{X}}_{it}^{\prime }\beta +{\beta }_5{I}_{(Y_{i(t-1)}=3)})\right)}\right\}}^{I(Y_{it}=2)}\\ \times {\left\{\frac{1}{1+exp\left(-({\beta }_0+{\mathbf{X}}_{it}^{\prime }\beta +{\beta }_5{I}_{(Y_{i(t-1)}=3)})\right)}\right\}}^{I(Y_{it}=3)}+\\ w_{iC}\prod _{t=1}^T{\left\{\frac{1}{1+exp\left(-({\delta }_2-{\mathbf{X}}_{it}^{\prime }\gamma -{\gamma }_5{I}_{(Y_{i(t-1)}=2)}-{\gamma }_6{I}_{(Y_{i(t-1)}=3)})\right)}-\frac{1}{1+exp\left(-({\delta }_1-{\mathbf{X}}_{it}^{\prime }\gamma -{\gamma }_5{I}_{(Y_{i(t-1)}=2)}-{\gamma }_6{I}_{(Y_{i(t-1)}=3)})\right)}\right\}}^{I(Y_{it}=2)}\\ \times {\left\{1-\frac{1}{1+exp\left(-({\delta }_2-{\mathbf{X}}_{it}^{\prime }\gamma -{\gamma }_5{I}_{(Y_{i(t-1)}=2)}-{\gamma }_6{I}_{(Y_{i(t-1)}=3)})\right)}\right\}}^{I(Y_{it}=3)}]\\ +I(O_i=3)[log(w_{iC})+\sum _{t=1}^{T}log{\left\{\frac{1}{1+exp\left(-({\delta }_1-{\mathbf{X}}_{it}^{\prime }\gamma -{\gamma }_5{I}_{(Y_{i(t-1)}=2)}-{\gamma }_6{I}_{(Y_{i(t-1)}=3)}\right)}\right\}}^{I(Y_{it}=1)}\\ +\sum _{t=1}^{T}log{\left\{\frac{1}{1+exp\left(-({\delta }_2-{\mathbf{X}}_{it}^{\prime }\gamma -{\gamma }_5{I}_{(Y_{i(t-1)}=2)}-{\gamma }_6{I}_{(Y_{i(t-1)}=3)}\right))}-\frac{1}{1+exp\left(-({\delta }_1-{\mathbf{X}}_{it}^{\prime }\gamma -{\gamma }_5{I}_{(Y_{i(t-1)}=2)}-{\gamma }_6{I}_{(Y_{i(t-1)}=3)}\right))}\right\}}^{I(Y_{it}=2)}\\ +\sum _{t=1}^{T}log{\left\{1-\frac{1}{1+exp\left(-({\delta }_2-{\mathbf{X}}_{it}^{\prime }\gamma -{\gamma }_5{I}_{(Y_{i(t-1)}=2)}-{\gamma }_6{I}_{(Y_{i(t-1)}=3)}\right))}\right\}}^{I(Y_{it}=3)}]\end{array}$$

where

$w_{iA}=\frac{\mathit{exp}({\lambda }_0^A+{\mathbf{Z}}_i^{\prime }{\lambda }^A)}{1+{\sum }_h\mathit{exp}({\lambda }_0^h+{\mathbf{Z}}_i^{\prime }{\lambda }^h)},w_{iB}=\frac{\mathit{exp}({\lambda }_0^B+{\mathbf{Z}}_i^{\prime }{\lambda }^B)}{1+{\sum }_h\mathit{exp}({\lambda }_0^h+{\mathbf{Z}}_i^{\prime }{\lambda }^h)}$, and $w_{iC}=\frac{1}{1+{\sum }_h\mathit{exp}({\lambda }_0^h+{\mathbf{Z}}_i^{\prime }{\lambda }^h)}$, h = A, B, and C.