Perceiving crowd attention: Ensemble perception of a crowd’s gaze

Abstract

Each time we encounter a person, we gather a wealth of socio-visual cues to guide our behavior. Intriguingly, social information is most effective in directing behavior when it is perceived in crowds. For example, the shared gaze of a crowd is more likely to direct attention than an individual’s gaze. Are we equipped with mechanisms to perceive a crowd’s gaze as an ensemble? Here, we provide the first evidence that the visual system extracts a summary representation of a crowd’s attention; people rapidly pooled information from multiple individuals to perceive the direction of a crowd’s collective gaze. This pooling occurred in high-level stages of visual processing, with gaze perceived as a global-level combination of information from head and pupil rotation. These findings reveal an important and efficient mechanism for assessing crowd gaze, which could underlie our ability to perceive group intentions, orchestrate joint attention, and guide behavior.

Introduction

Nearly every time we see another person, the visual system gathers a wealth of social information that we use to understand their behaviors and intentions (Allison, Puce, & McCarthy, 2000). This social perception, in turn, rapidly and automatically guides our own behavior (e.g., Dimberg, Thunberg, & Elmehed, 2000; Friesen & Kingstone, 1998). Intriguingly, when social information is available in crowds, our reactions are strong, even amplified. For example, a crowd’s direction of looking is more effective than an individual’s gaze for directing one’s attention (e.g., Gallup et al., 2012; Milner, Bickman, & Berkowitz, 1969). How do we gain access to social information at the group level, like a crowd’s attention? Can we engage the socio-crowd information at the core of group attention (e.g., Itier & Batty, 2009) at once, at the level of the collective? Perceiving crowds in this way would enable us to engage with groups of people rapidly and efficiently. Or is a crowd’s behavior only understood after an inferential process or complex cognitive deliberation?

Here, we tested these competing hypotheses by determining whether or not humans use a visual process of summary representation—ensemble encoding—to perceive where a crowd is looking. In ensemble coding, information about multiple objects is compressed into a statistic—a singular visual representation of the collective properties of the group (for reviews, see Alvarez, 2011; Whitney, Haberman, & Sweeny, 2013). This compression offers many benefits, including increased processing efficiency and reduction of noise, which can enable humans to perceive the gist of a group’s appearance with greater speed and precision than would be possible by inspecting each member, one-after-another (Alvarez, 2011; Sweeny, Haroz, & Whitney, 2012a). In fact, with ensemble coding, precise information about individuals is actually lost in favor of the group percept (Ariely, 2001; Haberman & Whitney, 2007). Moreover, ensemble codes need not be drawn from every member in a crowd—averaging across a subset of members provides surprisingly high sensitivity (Dakin, Bex, Cass, & Watt, 2009).

If efficient and rapid perception of crowd attention is important for behavior, then collective gaze information should be represented and experienced through ensemble coding. Here, we asked: when people see many faces briefly and at once, do they determine the collective gaze of the crowd by rapidly pooling information from many faces (i.e., ensemble coding), or do they make coarse judgments about the crowd based on a single face, as would be expected if understanding crowd gaze is a relatively slow cognitive process (e.g., Myczek & Simons, 2008)? We studied gaze because, unlike other ensemble-coded information, it uniquely amplifies behavior when seen in groups of more than two (Gallup, et al., 2012; Milner, et al., 1969), and perceiving gaze is vital for joint attention and social interaction (Baron-Cohen, 1995; Driver et al., 1999; Friesen & Kingstone, 1998; Itier & Batty, 2009). Finding that a crowd’s gaze is represented as a summary statistic would thus provide an important insight into perceptual mechanisms that may contribute to several important social behaviors.

Experiment 1: Crowd gaze perception with upright faces

Observers viewed crowds of computer-generated faces and estimated where each group was looking, on average. Each crowd had an average direction of looking (ranging from leftward to rightward) and, most importantly, each crowd member had a unique gaze direction. The crowds were shown for only one second and observers were not permitted to look directly at the faces. On some trials, observers viewed the full crowd of four faces and estimated their average gaze. On other trials, full crowds were generated, but observers viewed only a subset of the faces from the full crowd and they estimated the average gaze of this subset. Whether or not observers viewed all four faces or a subset of these faces, we recorded the full set of four’s average gaze for subsequent comparisons. We hypothesized that if observers use an ensemble code to perceive crowd gaze, then gaze estimates of subsets should approach the actual gaze of the full crowd when those subsets contain several faces, offering more information about the group. That is, when more gaze information is available to observers, even in short period of time, they will use it. Alternatively, if ensemble representation is not available for perceiving gaze, then observers should base estimates of a crowd on a single person’s gaze rather than an ensemble code, and their gaze estimates should not change even when more faces from the full crowd are visible in the subset.

Method

Observers

Eight psychophysical observers gave informed consent to participate. We used this number as our sample size and our stopping rule because, in a previous investigation with a nearly identical design and number of trials, we had sufficient power to detect and replicate a similar effect with a different dependent variable (Sweny, Haroz, & Whitney, 2012a). All had normal or corrected-to-normal visual acuity and were tested individually in a dimly lit room.

Stimuli

We manipulated gaze using a striking visual interaction (Wollaston, 1824), in which the direction toward which a person appears to be looking is determined by integrating local pupil information with the rotation of the head (Anstis, Mayhew, & Morley, 1969; Gibson & Pick, 1963). For example, Figure 1 illustrates how identical pairs of pupils will appear to have leftward or rightward gazes when superimposed onto heads with subtle leftward or rightward rotations, respectively (Cline, 1967; Langton, Honeyman, & Tessler, 2004). Here, we created a set of 16 computer-generated faces by independently manipulating head rotation and pupil rotation (Face Gen Modeller, Version 3.5.5, Singular Inversions, 2009). First, we created heads with −8°, −4°, +4° and +8° horizontal rotations (turned toward the observer’s left or right, respectively). Next, we used a head with a straightforward rotation (0°) to generate pupils with −15°, −5°, +5°, and +15° rotations around a vertical axis. We then used Photoshop (Adobe Photoshop CS5 Version 12.0) to merge each pair of these rotated pupils (and the surrounding eye contours) with each rotated head. Combining four head rotations with four pupil rotations produced 16 faces with unique gazes. This procedure of merging identical eyes with unique head rotations was crucial because it allowed us to manipulate perceived gaze without changing local pupil information. Put another way, each face’s perceived gaze was unique, and was the result of a global-level interaction between head rotation and pupil rotation.

Figure 1.

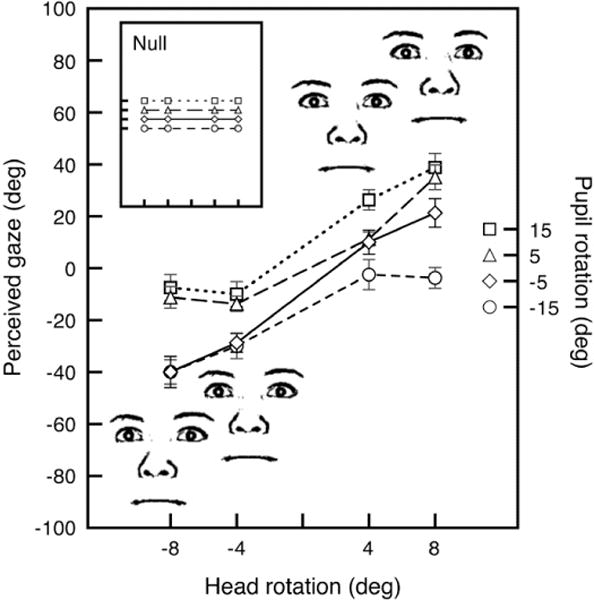
Results of a norming experiment measuring the perceived gazes that resulted from 16 unique combinations of head and pupil rotations. Head rotations attracted perceived gaze. For example, although the faces pictured here have identical pupil rotations (−5°, slightly leftward), leftward and rightward head rotations make their gazes appear heterogeneous. Inset box depicts null results that would have occurred if head rotations had no effect on perceived gaze. We utilized this visual interaction to ensure that the variability in each crowd’s gaze was the result of global-level integration of head and pupil rotations and not just an analysis of head or pupil position alone. Note that the faces in this figure constitute just one of the crowds that observers viewed. Other crowds had the same head rotations combined with different pupil rotations.

We schematized the faces using a four-step process in Photoshop. First, we eliminated the contour of the head and chin. Next, we applied a high-pass filter with a four-pixel radius. Then, we applied a threshold to the image (at a level of 120 in the thresholding tool) rendering pixels either black or white. Last, we applied a Gaussian blur with a 0.4 pixel radius. This procedure eliminated shading information, it equated all faces in terms of low-level visual information, and it ensured that only geometric information conveyed rotation. Each face subtended 2.56° × 2.31° of visual angle.

Preliminary Norming Experiment

The images in Figure 1 illustrate how combining head and pupil information can change the apparent direction of a person’s gaze. But in order to proceed with Experiment 1, it was first necessary to precisely measure the perceived gazes that resulted from each of the 16 combinations of head and pupil rotations. We thus conducted a norming experiment with a separate group of eight observers. Each observer viewed each of the 16 head-pupil combinations on a test face presented on the top half of the screen. Observers were told to imagine that the test face was looking out toward a point in space and to adjust the pupil position on a response face with straightforward features (the head had 0° of horizontal rotation) so that its direction of gaze appeared to match that of the test face. The response face was presented simultaneously and on the bottom half of the screen. Only the pupil positions of the response face could be rotated in 10° increments between −95° and +95°. The starting pupil position on the response face was randomly selected on each trial from a uniform distribution between −95° and +95°. The response face remained on the screen until the observer pressed the spacebar. Observers were allowed to look at both of the faces, although they were instructed to fixate only the bridge of the nose, and they had an unlimited amount of time to respond. We recorded the average pupil position on the response face (e.g., −5°, looking slightly toward the observer’s left) as the perceived gaze direction for each of the 16 head-pupil combinations.

As expected, head rotations were effective in modulating perceived gaze direction (Figure 1). This was confirmed by a main effect of head rotation in a repeated-measures ANOVA (four head rotations × four pupil rotations) (F[3,21] = 30.628, p < .001, h_p²= .813). Averaged across all head-pupil combinations, 1° of head rotation pulled perceived gaze by 2.97°. That is, even if the pupils stayed in a fixed position, rotating the head strongly pulled the apparent gaze direction. We used the average norming values for each head-pupil combination to obtain the average gaze directions (calculated as the linear means) of the subsets and full crowds of faces in the main experiment.

Crowds

By independently varying head rotation and pupil rotation, we ensured that the gaze of each crowd member, and also the collective gaze of each crowd, appeared to be unique (Figure 2). No two heads in any crowd faced exactly the same direction; every crowd contained a head with one of four distinct rotations (−8°, −4°, +4°, and +8°) on each trial. Every pair of pupils in a crowd gazed in exactly the same direction on a given trial (e.g., −5°, like in Figure 1, or +15°, like in Figure 2C), but across trials, the crowd’s pupils could have four different rotations (−15°, −5°, +5°, and +15°). These combinations ensured that variability in the crowd’s gaze did not occur in terms of low-level pupil information. The mandatory nature of the interaction we harnessed ensured that, instead, the perceived variability across the crowd members’ gazes occurred at a stage of visual processing where head and pupil information are globally integrated. Based on the values obtained from our norming procedure, these combinations produced a gaze range of 47.5° in our crowds, on average. The center of each possible face location in the crowd (upper-left, upper-right, bottom-left, bottom-right) was 3.21° diagonally from the fixation point.

Figure 2.

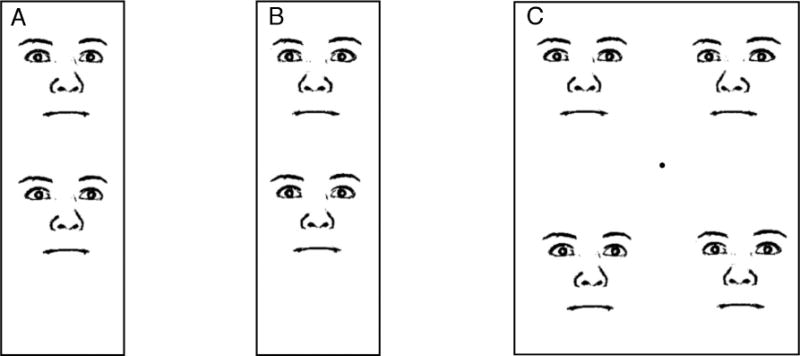
The perceived gazes in our experiment did not rely head or pupil rotations alone, but instead, relied on global integration of information across multiple features. (A) Two faces with identical head rotations and different pupil rotations appear to have different gaze directions. (B) Two faces with identical pupil rotations and different head rotations also appear to have unique gaze directions. (C) One of the crowds from our experiments, drawn to scale. The black rectangle was not present in the experiment.

Procedure

Observers initiated each trial by pressing the space bar, followed immediately by a white screen with a central fixation point shown for a randomly selected duration of 500, 700, or 900 ms. Next, a randomly selected subset of faces (one, two, or three) or the full set of four appeared for 1,000 ms followed by a white screen for 1000 ms. The fixation remained visible during both of these intervals. Observers were instructed never to look directly at any of the faces in the crowd. Next, a blank white screen was shown for 300 ms, followed by a single response face at the center of the screen. Observers indicated the subset’s (of full set’s) average direction of gaze by adjusting the pupils on the response face using the left and right arrows on a keypad. The response face always had straightforward features (the head had 0° of horizontal rotation); only the pupil positions could be rotated in 10° increments between −95° and +95°. The starting pupil position on the response face was randomly selected on each trial from a uniform distribution between −95° and +95°. The response face remained on the screen until the observer pressed the spacebar. A given set of faces (a subset of one, two, or three, or the full set of four faces) was paired with each of the four pupil rotations six times. This yielded a total of 96 trials run across two blocks. All stimuli were presented on a 20-inch CRT monitor while observers’ heads were secured in a chin rest at a viewing distance of 47 cm.

Results

We used our norming data to determine the perceived gaze direction (the linear average) of both the full crowd and the subset on each trial. Then, we calculated the difference between observers’ estimates and both of these values on each trial. Finally, for each observer, we calculated the variance across these difference scores as our dependent variable. We used a nearly identical approach in a previous investigation of crowd perception (Sweeny, et al., 2012a).

An ideal observer analysis illustrates the different patterns of results that would occur from integrating gaze information from different numbers of faces in each crowd, or from guessing (Figure 3). Note that the purpose of the ideal observer analysis is to illustrate these patterns and facilitate understanding of the empirical data. It is not intended to provide estimates of the exact numbers of gazes integrated or the amount of noise in any stage of the averaging process. Details of the ideal observer analysis can be found in the Supplemental Materials, but to summarize, this conservative simulation included the following steps: (1) we randomly generated a crowd with different head rotations and gazes, (2) we added early-stage noise to the gaze of each crowd member, (3) we obtained the linear mean of each noise-perturbed subset (one, two, or three randomly selected faces) or full crowd of gazes, (4) we then perturbed this mean with late-stage noise, and then (5) we recorded the difference between this simulated gaze estimate and the actual gazes of the full set and the subsets. Calculating the variance of these differences across thousands of trials allowed us to visualize the patterns of response error that would emerge with different amounts of integration. The parameter values in this simulation were chosen simply because they produced a baseline level of performance roughly consistent with our results. Changing these parameter estimates only produces quantitative, but not qualitative changes to these patterns.

Figure 3.

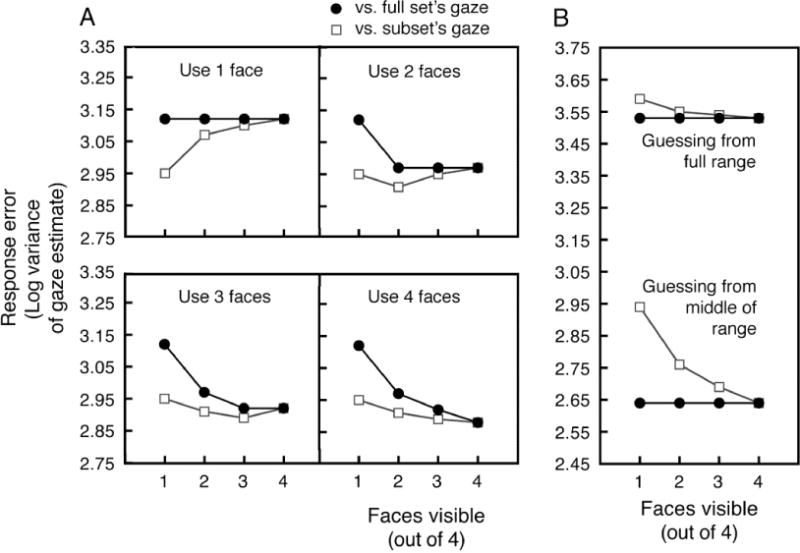
An ideal observer analysis conducted to show the general patterns of results that would occur from (A) integrating the gazes of one, two, three, or four faces in a crowd, or (B) simply guessing and making a random response from then entire range of response options or the middle third of the response range. For all panels, the simulated variance of errors in gaze estimates are compared against the full set’s gaze direction (black line) and the subset’s gaze direction (gray line).

If, in a brief glimpse, observers can only extract information from a single face’s gaze to estimate where a crowd is looking, errors against the full crowd’s gaze should remain the same even when more faces from the crowd are visible (black circles, top-left panel of Figure 3A). At the same time, errors against the subset’s gaze (open squares) should increase because, as the number of visible faces becomes larger, the single gaze observers use to make their estimate will become less representative of the subset’s direction of looking. A qualitatively different pattern will emerge if observers integrate multiple gazes (e.g., three) into an ensemble code. Errors against the full crowd’s gaze should decrease when more faces from the crowd are visible (bottom-left panel of Figure 3A). Errors against the subset’s gaze should also decrease, but only slightly—the result of redundancy gain from averaging noisy signals. This pattern will only occur if observers integrate multiple faces, and it cannot occur if observers always respond randomly (Figure 3B). Note that when the number of visible crowd members exceeds integration capacity (e.g., 2), error relative to the full set’s gaze plateaus and error relative to the subset’s gaze increases. These qualitative predictions from our ideal-observer analysis clearly illustrate the patterns of results that we might expect to obtain from our actual observers, which we now describe.

Gaze estimates from larger subsets were closer to the gaze of the full crowd (F[3,21] = 9.59, p < .01, h_p² = .578; black line in Figure 4A). This pattern indicates that observers integrated gaze information from multiple faces in a crowd. Measured against the subset’s gaze, response errors also tended to decrease with larger subsets sizes, although this trend was not significant (F[3,21] = 1.07, n.s.; gray line in Figure 4A). The interaction between crowd size and comparison gaze (full set vs. subset) was significant (F[3,21] = 3.95, p < .05, h_p²= .361). While a significant interaction is possible even when ensemble coding does not occur (e.g., top-left panel of Figure 3A or Figure 3B), it is meaningful in this case, when errors measured against the subset were lower than errors measured against the full set. Specifically, the interaction here shows that our primary effect is not simply the result of redundancy gain, in which multiple faces are easier to perceive than a single face (Won & Jiang, 2013). That is, the reduction in error measured against the full set’s gaze was greater than the reduction that would have occurred simply by viewing more faces (as measured by errors relative to the subset; the gray line) and increasing signal-to-noise ratio (Alvarez, 2011). Measuring the interaction is also important since, hypothetically, it may not have materialized if observers used a mix of strategies (e.g., using three faces on some trials and guessing from the middle of the response range on other trials).

Figure 4.

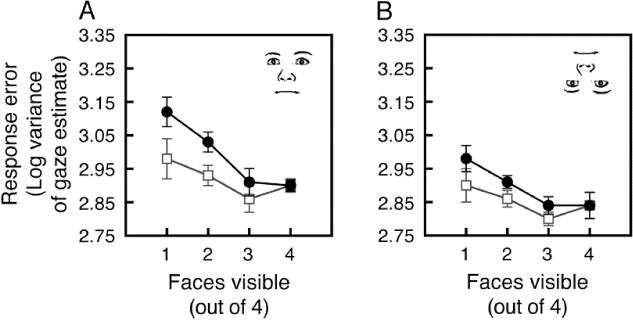
Ensemble perception of crowd’s collective gaze when faces were (A) upright in Experiment 1, and (B) inverted in Experiment 2. On a given trial, a subset of 1, 2, or 3 faces, or the full set of 4 faces was visible. For both panels, variance of errors in gaze estimates is compared against the full set’s gaze direction (black line) and the subset’s gaze direction (gray line). Error bars reflect ±1 SEM (adjusted for within-observer comparison).

While the previous analyses do not directly reveal the number of faces observers used to estimate the gaze of the crowd, the striking similarity of our results to the patterns from our ideal observer analysis (compare with the bottom-left panel of Figure 3A) suggests that observers integrated at least two, and probably three faces from the crowd. This conservative estimate is consistent with the suggestion that an effective sample size tends to be around $\sqrt{\mathrm{n}}$ (Dakin, et al., 2009). Pairwise comparisons of error relative to the full set’s mean are also consistent with this conclusion. Compared to viewing just a single face, viewing two faces tended to reduce error relative to the full set’s gaze (t[7] = 2.12, p = .07, d = 0.75). A similar improvement occurred when viewing three faces compared to viewing two (t[7] = 2.46, p < .05, d = 0.869), but the improvement gained from viewing four faces instead of three did not reach significance (t[7] = .131, n.s.).

It was important to verify that the ensemble percept of crowd gaze was constructed using global interactions across facial features and not just parts of the faces. To do this, we compared the perceived crowd gazes with the actual crowd gazes that emerged from combining pupil and head rotations, the heads alone, or the pupils alone. Specifically, we calculated the variance of the differences between gaze estimates and (1) the average gazes of the subsets of visible faces in terms of head and pupil combinations (the same values from the analysis above), (2) the average physical gaze of the visible faces in terms of head rotation, and (3) the average physical gaze of the visible faces in terms of pupil rotation.

The ensemble code was constructed using emergent crowd gaze; estimates followed the gazes determined from combining pupils and heads more closely than the gazes from heads alone (t[7] = 2.56, p < .05, d = 0.908) or pupils alone (t[7] = 2.62, p < .05, d = 0.927).

Experiment 2: Crowd gaze perception with inverted faces

The images and the norming data in Figures 1 and 2 clearly confirm that perception of a single person’s gaze relies on global-level interactions between facial features and is not based on head or pupil information alone. This is consistent with decades of research showing that face representation and perception occurs more at the level of grouped features and less at the level of individual features (e.g., Maurer, Le Grand, & Mondloch, 2002; Suzuki & Cavanagh, 1995). The final analysis from Experiment 1 shows that the ensemble perception of a crowd’s gaze is also rooted in a stage of visual analysis where gaze information is represented globally. In our second experiment, we sought to provide converging evidence to support this conclusion. Specifically, our goal was to determine whether or not weakening of the global feature interactions underlying the perception of a single face’s gaze would produce a concomitant weakening of our ensemble gaze effect with crowds. To accomplish this, we repeated Experiment 1 with inverted faces.

Inversion does not eliminate the Wollaston interaction—the global interactions underlying perception of emergent gaze—although previous work suggests that it does produce modest reductions in its strength (Langton, Honeyman, & Tessler, 2004; Maruyama & Endo, 1984). This is consistent with recent suggestions that face inversion effects reflect a quantitative change in encoding where interactions between facial features persist, albeit to a lesser extent (Farah, Wilson, Drain, & Tanaka, 1995; Loffler, Gordon, Wilkinson, Goren, & Wilson, 2005; Perrett, Oram, & Ashbridge, 1998; Riesenhuber, Jarudi, Gilad, & Sinha, 2004; Sekuler, Gaspar, Gold, & Bennett, 2004). If inverting a face reduces a rotated head’s pull on perceived gaze, and if the collective gazes in our crowds were the result of these global-level feature interactions, then inverting the faces in a crowd should produce a similar weakening of our pattern of ensemble integration. Note that we are not predicting that inversion will eliminate the pattern of gaze integration we found with upright faces. Rather, the same pattern should persist, but the benefit from pooling multiple gazes should be weaker. Such a finding would converge with our previous analysis (see Results from Experiment 1) to demonstrate that summary representation of a crowd’s gaze occurs in high-level visual processing.

Method

Observers

The same eight observers that participated in Experiment 1 gave informed consent to participate.

Stimuli

The stimuli were identical to those used in Experiment 1, except that they were inverted.

Preliminary Norming Experiment

The prediction of reduced integration in a crowd of inverted faces is based on the reasonable assumption that inverting a single face will reduce the attractive effect of head rotation on perceived gaze. If this were true, then the gazes in our crowds would appear more homogeneous, which would reduce the benefit of integrating multiple faces to estimate a crowd’s gaze. We verified this assumption before running Experiment 2 by repeating our norming experiment, but this time with inverted faces. The response face, which appeared below the test face, remained upright.

Inverted head rotations attracted perceived gaze direction. This was confirmed by a main effect of head rotation in a repeated-measures ANOVA (four head rotations × four pupil rotations) (F[3,21] = 18.57, p < .001, h_p² = .726). Compared with the attraction from upright head rotations in Experiment 1, equivalent rotations of inverted heads tended to be less effective at modulating perceived gaze, although this difference was not significant (F[3,21] = 1.95, p = .15, h_p² = .213). Averaged across all head-pupil combinations, 1° of inverted head rotation pulled perceived gaze by 2.24°. Based on this reduced but still substantial influence of inverted head rotation on perceived gaze, we predicted that ensemble integration would still occur in a crowd of inverted faces, but to a weaker extent than with upright faces. Consistency between the subtle effect of inversion in our norming experiment and a subtle reduction in ensemble integration with inverted faces would lend further support to our claim that the ensemble code is constructed from emergent gaze representations.

Results

We used the norming data from Experiment 1, with upright faces, to calculate the difference between observers’ estimates and the gazes of the subset and full set of inverted faces on each trial. Then, for each observer, we calculated the variance across these difference scores as our dependent variable. We calculated errors against upright norming values rather than against inverted norming values in order to make direct comparisons against the data with upright faces. If the perceived gazes used to estimate a crowd of upright faces’ gaze are present in a crowd of inverted faces, then results should be identical regardless of the choice of reference values.

Observers recovered gaze information from crowds of inverted faces, but the benefit gained from doing so was not as pronounced as with upright faces. Gaze estimates from larger subsets approached the gaze of the full crowd, (F[3,21] = 3.28, p < .05, h_p²p = .319; black line in Figure 4B). Measured against the subset’s gaze, response errors did not change as a function of subset size (F[3,21] = .974, n.s.; gray line in Figure 4B). Unlike with upright faces, the interaction between subset size and the comparison gaze (full set vs. subset) was not significant (F[3,21] = 1.48, n.s.).

It may seem paradoxical that overall response error was lower with inverted faces than with upright faces. This is, in fact, exactly what one would expect if the magnitude of the gaze shift from a rotated head were reduced. Our norming experiment showed that inverted faces would have been slightly more likely to be perceived as looking straight ahead, which would lead reports of crowd gaze to be clustered more around the middle of the response range. As is clear from Figure 3B, responses from the middle of the range do, in fact, reduce overall error. Note, however, that because inverting a face does not completely eliminate the influence of head rotation on perceived gaze (there is still a Wollaston interaction), we still found a pattern of gaze integration, albeit on top of a slight reduction in overall error.

To determine whether or not the benefit of ensemble integration was stronger with upright faces than with inverted faces, we compared the interactions across the two experiments. That is, for each number of faces visible (one through four), we calculated the difference between the variability of estimates measured against the full set’s gaze and against the subset’s gaze (i.e., the differences between the black and gray lines in Figures 4A and 4B). A main effect of face orientation in a within-subjects ANOVA revealed that observers tended to experience a greater improvement from integrating multiple faces when they were upright (F[1,7] = 5.47, p = .051, h_p² = .439). This is consistent with our prediction that the emergent single-face gazes measured in our norming experiments were the same gazes being integrated in our crowds.

Experiment 3: Crowd gaze perception with very brief presentation

Although our first two experiments clearly demonstrate that observers rapidly integrated multiple gazes to perceive a crowd’s direction of looking, it is nevertheless possible that with 1000 ms, observers could have serially attended to individual faces and cognitively computed their average gaze direction. Such a strategy would not necessarily qualify as ensemble coding, in which the average percept is achieved through rapid integration in parallel, bypassing the need for focused attention. Thus, in Experiment 3, we tested whether the integration we observed in Experiments 1 and 2 could occur even when observers viewed each crowd for only 200 ms. This extremely brief duration prevented observers from making saccades to multiple faces or initiating serial shifts of attention.

Method

Observers

Sixteen new observers gave informed consent to participate. We doubled the number of observers because we expected that the data might be noisier with the reduction in presentation time.

Stimuli and Procedure

The stimuli were identical to those used in Experiments 1 and 2. The procedure was also identical, except that faces were shown for only 200 ms, and each observer completed two blocks with upright faces and two blocks with inverted faces in alternating order. Half the observers started with an upright block and half started with an inverted block.

Results

The procedures for calculating the difference between each observer’s estimates and the gazes of the subset and full set were identical to those from Experiments 1 and 2. Even with only 200 ms, observers integrated gaze information from multiple upright faces in a crowd. Gaze estimates from larger subsets were closer to the gaze of the full crowd (F[3,45] = 12.06, p < .01, h_p² = .445; black line in Figure 5A). Measured against the subset’s gaze, there was a trend for response errors to decrease with larger subsets sizes (F[3,45] = 2.43, p = .077, h_p² = .139; gray line in Figure 5A). The interaction between crowd size and comparison gaze (full set vs. subset) was significant (F[3,45] = 28.96, p < .01, h_p² = .658). Compared to viewing just a single face, viewing two faces reduced error relative to the full set’s gaze (t[15] = 3.04, p < .01, d = 0.76). Although improvements when viewing three faces compared to viewing two (t[15] = 1.51, p = .15, d = 0.75) and for viewing four faces compared to viewing three (t[15] = 1.72, p = .10, d = 0.43) were not significant, viewing four faces was clearly better than viewing two faces (t[7] = 2.43, p < .05, d = 0.61).

Figure 5.

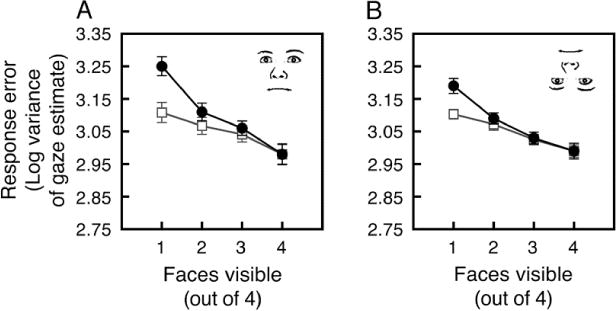
Ensemble perception of crowd’s collective gaze when upright (A) and inverted (B) faces were shown for only 200 ms. For both panels, variance of errors in gaze estimates is compared against the full set’s gaze direction (black line) and the subset’s gaze direction (gray line). Error bars reflect ±1 SEM (adjusted for within-observer comparison).

Observers also recovered ensemble gaze information from crowds of inverted faces seen for only 200 ms, but the benefit gained in doing so was not as pronounced as with upright faces. Gaze estimates from larger subsets approached the gaze of the full crowd, (F[3,45] = 13.41, p < .01, h_p² = .472). Measured against the subset’s gaze, response errors decreased as a function of subset size (F[3,45] = 6.06, p < .01, h_p² = .287). The interaction between subset size and the comparison gaze (full set vs. subset) was significant (F[3,45] = 7.881, p < .01, h_p² = .344).

Most importantly, we compared the interactions across the two face presentations to determine whether or not ensemble integration was stronger with upright faces than with inverted faces. A main effect of face orientation in a within-subjects ANOVA revealed that observers experienced a greater improvement from integrating multiple faces when they were upright (F[1,15] = 68.21, p < .01, h_p² = .819).

Discussion

We showed that the visual system pools the gazes of individual faces into an ensemble code, allowing humans to rapidly and efficiently perceive where a crowd is looking. The gazes in our faces were emergent—relying on the global integration of facial features and eyes—and inversion diminished the benefit of ensemble integration. These facts converge to suggest that ensemble perception of crowd gaze is achieved by integrating global-level facial representations (e.g., Maurer, et al., 2002; Suzuki & Cavanagh, 1995), and that this integration is rooted in high-level visual areas where head rotation and eye gaze are jointly represented (De Souza, Eifuki, Tamura, Nishijo, & Ono, 2005; Perrett et al., 1985). While it is possible that observers accessed the crowd’s gaze by separately extracting average pupil rotation and head rotation and then combining these average values, this possibility seems unlikely, at least when the faces were upright, since facial organization is known to block access to individual features (Suzuki and Cavanagh, 1995). Our results add to growing evidence (Haberman & Whitney, 2007; Sweeny, et al., 2012a; Sweeny, Haroz, & Whitney, 2012b) that ensemble coding operates at multiple levels of the visual hierarchy, not only enhancing the way we see groups of objects and textures (Ariely, 2001; Dakin, et al., 2009), but social information in crowds of people as well.

While several investigations have demonstrated the importance of perceiving a single person’s gaze (Baron-Cohen, 1995; Driver, et al., 1999; Friesen & Kingstone, 1998), sensitivity to individual gaze does not necessarily or inevitably lead to sensitivity to crowd gaze, nor do these studies begin to account for how gaze might be perceived in groups. Our results help to bridge this gap and may be useful for understanding other perceptual phenomena that occur in crowds. For example, ensemble representation of a crowd’s gaze may provide the underlying metric of similarity behind “pop-out” of gaze in visual search (Doi & Kazuhiro, 2007).

Most importantly, our results may break new ground in understanding behaviors and attributions that only occur in groups (Waytz & Young, 2012). Our results characterize the perceptual aspect of a sort of joint attention that is most potent at the level of the crowd—an emergent joint attention. When we see social information in a crowd, like gaze, our tendency to join in is strikingly amplified compared to when we view the same information in an individual (Gallup, et al., 2012; Milner, et al., 1969). This pull towards conformity is widespread in the animal kingdom (for a review, see Sumpter & Pratt, 2008) and is crucial for the maintenance of group cohesion and consensus decision making (i.e., the “wisdom of the crowd”). Our results show, for the first time, that visual mechanisms are capable of representing the collective crowd properties involved in this amplified joint attention. This type of summary encoding could also be especially useful for quickly evaluating and responding to other social cues uniquely conveyed by groups, like panic and rioting (Granovetter, 1978; Helbing, Farkas, & Vicsek, 2000). More generally, our results show that in order to understand visual processing, it is vital to consider the social pressures and group behaviors with which we evolved, and vice versa.