Chaperones Rescue Luciferase Folding by Separating Its Domains

Background: Bulk experiments show that Luciferase refolding requires the aid of chaperone proteins.

Results: Single-molecule experiments show that partially unfolded Luciferase can refold without chaperones but that chaperones are required for refolding from complete denaturation.

Conclusion: The N-terminal domain of Luciferase serves to chaperone refolding, and chaperones may serve to emulate this effect.

Significance: Understanding protein folding can be used to develop new therapeutics to target intermediates.

Abstract

Over the last 50 years, significant progress has been made toward understanding how small single-domain proteins fold. However, very little is known about folding mechanisms of medium and large multidomain proteins that predominate the proteomes of all forms of life. Large proteins frequently fold cotranslationally and/or require chaperones. Firefly (Photinus pyralis) luciferase (Luciferase, 550 residues) has been a model of a cotranslationally folding protein whose extremely slow refolding (approximately days) is catalyzed by chaperones. However, the mechanism by which Luciferase misfolds and how chaperones assist Luciferase refolding remains unknown. Here we combine single-molecule force spectroscopy (atomic force microscopy (AFM)/single-molecule force spectroscopy) with steered molecular dynamic computer simulations to unravel the mechanism of chaperone-assisted Luciferase refolding. Our AFM and steered molecular dynamic results show that partially unfolded Luciferase, with the N-terminal domain remaining folded, can refold robustly without chaperones. Complete unfolding causes Luciferase to get trapped in very stable non-native configurations involving interactions between N- and C-terminal residues. However, chaperones allow the completely unfolded Luciferase to refold quickly in AFM experiments, strongly suggesting that chaperones are able to sequester non-natively contacting residues. More generally, we suggest that many chaperones, rather than actively promoting the folding, mimic the ribosomal exit tunnel and physically separate protein domains, allowing them to fold in a cotranslational-like sequential process.

Introduction

The structure and function of proteins is fundamental to almost all biological processes, and the understanding of how proteins obtain their structure through folding is crucial for the prevention of many diseases (1, 2). There have been many experiments over 50 years of research on proteins (for example, see reviews in Refs. 3–7), but there are still crucial aspects of protein folding that need further study, one being the understanding of the protein intermediates and the energy landscapes of protein folding (e.g. the space of protein conformations and their associated free energies) (8). A complete understanding of protein folding pathways could allow drugs to be designed to intermediate states in the folding pathway, thus enabling a novel area of therapeutics. Numerous experiments have shown that proteins evolved by smoothing their folding energy landscapes to eliminate low-energy, non-native intermediate conformations (or kinetic traps) (9, 10). However, much of the work on protein folding has been on small single-domain proteins although they only make up less than 30% of the proteomes in all kingdoms of life (11). It has become clear that a simple smooth energy landscape does not apply to multidomain proteins because multidomain proteins can have non-Anfinsen mechanisms like kinetic partitioning (12), cotranslational folding (13, 14), co-existing intersecting folding pathways (15), or confinement by chaperonins (16, 17). Here we study the folding mechanism of firefly (Photinus pyralis) luciferase (Luciferase) as a model of a large multidomain protein and determine whether there are important differences between the folding of multidomain proteins and single-domain proteins.

Luciferase is a monomeric 61-kDa protein that uses MgATP to catalyze the oxidation of D-(-)-Luciferin (Luciferin) to produce a photon (18–20). The structural conformation of the firefly luciferase protein closely resembles other AMP-forming ligases like acyl-CoA ligases (21) and nonribosomal peptide synthetases (22) because it has a large N-terminal domain and a smaller C-terminal domain, and both are crucial for catalysis (23). Previous studies using traditional biochemical methods determined that once unfolded Luciferase does not refold in an appreciable amount of time (∼10–72 h) (24, 25). The folding time of Luciferase decreases by orders of magnitude (to approximately minutes) by folding cotranslationally on the ribosome or when given chaperones (24, 26–28). Although these experiments are elucidating, important questions remain: what prevents Luciferase from refolding quickly? How does cotranslational folding prevent misfolding? How exactly do chaperones allow relatively fast refolding? Here we address these questions using single-molecule force spectroscopy (SMFS).² SMFS has two unique advantages over traditional methods for studying large multidomain proteins. Their unfolding and refolding can be examined for individual proteins in isolation, therefore minimizing the opportunity for their aggregation in the unfolded state, and SMFS allows the precise manipulation of proteins and their subunits and, therefore, offers unprecedented control for denaturing single domains/subunits within multidomain proteins (29, 30). This approach reduces the complexity of the folding reaction and facilitates relating the experimental data to the structural information (29, 31, 32).

EXPERIMENTAL PROCEDURES

Protein Purification

We developed a construct containing full-length firefly luciferase (Promega) or truncated Luciferase (Luc203, containing only residues 1–203) flanked by three I27 domains and four I27 domains at the DNA level (Fig. 1A) and containing an N-terminal His₆ tag and a C-terminal Cys₂ tag. We purified protein produced from C41(DE3)pLysS cells (Lucigen Corp.) using nickel-nitrilotriacetic acid columns (Qiagen). The resulting purified protein was dialyzed into a buffer containing either 1× or 2× PBS (pH 7.6) at a concentration of 1–10 mg/ml and was used for AFM measurements. The protein was still active when flanked by I27 domains (Fig. 1).

FIGURE 1.

Luciferase activity in the I27-flanked construct, I27₃-Luciferase-I27₄, was tested for native enzymatic activity. A, B, and D, as shown in C, the protein construct still maintains native activity when cofactors are present, indicating that the protein construct maintains the native structure of the enzyme.

Atomic Force Microscopy

AFM experiments were performed using custom-built instruments (33). Proteins were diluted to 150 μg/ml in a 1× PBS buffer or 2× PBS buffer (for Luc203) and loaded onto a freshly evaporated gold substrate for 1 h. Buffers with ATP also contained 15 mm MgCl₂ (to ensure 99% bound), 4 mm EGTA, and 180 μm to 1 mm Luciferin (when noted). For measurements with chaperones, we used PBS with 15 mm MgCl₂, 2 mm ATP, and rabbit reticulocyte lysate (untreated) (Promega, catalog no. L4151). The substrate was then washed once and used for pulling experiments. We used either OBL cantilevers (spring constant, ∼6 pN/nm) or MLCT cantilevers (spring constant, ∼16 pN/nm) (Bruker). During experiments, the AFM cantilever was pressed against the sample at a contact force of 100–500 pN to nonspecifically bind to the protein. The presence of at least five I27 domains (ΔL_c, ∼28 nm; unfolding force, ∼200 pN) allowed for the unequivocal determination of the unfolding pattern of the Luciferase protein. The data were analyzed using Matlab 7.10 (Mathworks).

Force extension curves were fit using the worm-like chain (WLC) model. The persistence length for the WLC model was determined in an unbiased way using a global fitting procedure. All curves (>1000) were fit simultaneously with a WLC of various persistence lengths. The root mean square error was calculated for each fit. The root mean square error distribution closely follows the γ distribution, so the mode (peak of distribution) was calculated for each persistence length from fitting to a γ distribution. The root mean square error mode was plotted against a range of persistence lengths (0.1–1.0 nm), which created a smooth curve with a single minimum. The minimum indicates the best overall fit to all of the data (lowest root mean square error), and the value of the persistence length at this point was used for all subsequent WLC fits: 0.29 nm for I27 and 0.67 nm for peaks of Luciferase.

Determination of Domain Boundaries for Multidomain Proteins from Force Spectroscopy Measurements

Determining the number of amino acids unfolding from a force rip depends on the crystal structure of the corresponding protein. For a simple protein like I27, the number of amino acids is simply equal to the sum of the initial N-C extension from the crystal structure (the “hidden” residues) and the contour length increment measured by the AFM divided by the length per residue. And, vice versa, the length per residue can be calculated if the number of residues is known. Using I27, we calculated the length per residue. The median contour length increment for I27 (28.8 nm) and measured N-C extension (4.2 nm) and number of residues (89) estimated the length per extended residue to be 0.37 nm, which is consistent with the value provided by Dietz and Rief (34).

For a protein composed of intricately interacting domains, however, the simple initial N-C extension is not sufficient to capture the correct number of hidden residues. During the unfolding of each domain and its separation from the rest of the folded structure of the multidomain protein there is an associated reorientation of the remaining structure to align the rest of the protein to the new pulling direction. The realignment can contribute to the experimentally measured contour length increment. Therefore, the contour length increment measured is actually the total length for the residues in the domain minus the difference between the initial length of the new reoriented structure and the previous structure. This effect is illustrated in Fig. 2 and, if neglected, it could significantly increase the uncertainty of the number of hidden residues determined from the contour length increment.

FIGURE 2.

The contour length increments determined from the FE curve in AFM stretching measurements of a multidomain protein directly relate to the lengths of the polypeptide chains folded within the domains and also to their geometrical arrangement within the protein. A hypothetical protein containing two intricately interacting domains (red/blue rectangles) is being stretched between arbitrary protein handles (black ovals). The hypothetical force-extension curve is shown above each molecular schematic. The contour length increment upon each domain unfolding, L_x, is determined by the length of unfolded residues from each domain, U, as well as by the gain in length because of the reorientation of the domains that remained folded within the multidomain protein.

Fig. 2 shows a hypothetical protein containing two intricately interacting domains (red/blue rectangles) being stretched between arbitrary protein handles (black ovals). In this schematic, we assume that the protein handles are more mechanically stable than the protein containing the interacting red/blue domains. The stretching of this entire protein construct typically follows a worm-like chain model of polymer elasticity (35). The initial contour length of the whole folded protein construct, L₁, has contributions from the protein handles (black ovals, each providing a contour length of x) and from the N terminus to C terminus distance in the two-domain protein (providing a contour length of I₁).

When domain D1 unfolds and stretching of the entire polyprotein continues, the next contour length, L₂, will contain three contributions: the unchanged length of the protein handles (again, each providing a contour length of x), the length of the unfolded residues from D1 (which contribute a contour length, U₁, equal to the number of residues times the length per residue), and the N terminus to C terminus distance of domain D2 (which, after being reoriented, now contributes a contour length of I₂). Therefore, the difference between these two contour lengths, the contour length increment Lc1, contains contributions from the initial length, I₁, of the entire multidomain protein, the contour length U₁ from the unfolded polypeptides in domain D1, and the length I₂ from the reorientation of domain D2 during alignment to the pulling direction. Neglecting the reorientation of the domains in a multidomain protein can easily lead to overestimating or underestimating the number of amino acids that contribute to the contour length increment, as we demonstrate below, limiting the precision of domain boundaries estimation.

In general, the contour length increment provided by unfolding of domain i in a multidomain protein (Lci) is equal to the contour length from the unfolded residues in domain i, plus the N-C length of the remaining protein after unfolding domain i, minus the N-C length of the protein before unfolding of domain i. The final domain has a final contour length increment that contains contributions from only the unfolded polypeptide from the last domain (Fig. 2, domain D2) and contour length contributions from the initial length (Fig. 2, length I₂). That is, the final domain can be considered without any further contributions from reorientation because there are no further structural domains (e.g. I₃ = 0 in Fig. 2). Therefore, the calculation for contour length increments in single-domain proteins is equivalent to the calculation for the final domain of a multidomain protein.

The accuracy of this model is determined by residuals. The residuals are the errors in this model associated with either U-errors, which are caused by incorrect assumptions about the boundaries of interacting domains, or I-errors, which are true deviations from the real native structure after a partial domain unfolds (i.e. it is possible that the unfolding of a domain of a multidomain protein causes a total reconfiguration to which there is no crystal structure standard to compare). The residual of a domain is given by the absolute difference between the measured contour length increment and the expected contour length increment, which is determined by the unfolding length of the corresponding domain and the initial length of the protein before and after unfolding of the domain (Fig. 2). The total residual is the sum of the residuals from all domains.

The domains that correspond to mechanical unfolding can then be determined by finding the correct domain partitioning that minimizes the total residual. This can be done by iteratively solving for the total residuals of all possible sets of domain boundaries and selecting the domain boundaries that provide the minimum total residual. The number of domains is always determined by the number of unfolding events, so the only parameters being determined are the residues that are at the interface of each domain.

Applying this model to determine the domain boundaries is important because gross errors will occur if the reorientation is not taken into account. Luciferase unfolding is a test case that exemplifies this scenario. Our force spectroscopy data indicate that Luciferase unfolds in three domains (no ligands), four domains (+ATP), or five domains (+ATP and +Luciferin). Fortunately, there is a model of the apo form of Luciferase (PDB code 1BA3) and a model of the ligand bound form (PDB code 2D1S) that can be used for calculating residuals from all possible domain boundaries. After determining boundaries that minimize the total residuals, we find that accounting for the reorientation gives an average total residual of 0.49 nm (apo, 0.35 nm; +ATP, 0.66 nm; +ATP +Luciferin, 0.47 nm). This can be roughly interpreted to mean that the model is able to account for all but approximately two residues. Conversely, by not accounting for reorientation (i.e. considering each interacting domain as a single domain), the average total residual is 6.3 nm (apo, 1.78 nm; +ATP, 6.96 nm; +ATP +Luciferin, 10.1 nm), which means that the model cannot account for ∼17 residues, which is quite substantial considering that some domains are <100 residues. These errors increase when more domains are present because the reorientation would greatly affect each contour length increment. Therefore, we believe that, for multidomain proteins like Luciferase that have large interacting domains, it is absolutely crucial to account for reorientation when measuring mechanical domains by force spectroscopy to provide accurate estimates of the domain boundaries.

Simulations

Structure-based models were generated using the SMOG web server (36) using a Cα contact potential (37, 38). In this model, all residues are modeled as a single pseudoatom. The ATP ligand and Luciferin ligand were modeled as peptides that geometrically shared the same space as the ligands in the crystal structure to ensure that the same contacts were preserved when converted to a Cα model. The temperature was chosen as the folding temperature of the model Luciferase, T = 140 (Fig. 5). Simulations were conducted using GROMACS 4.5.5 (39) by pulling on the N terminus with reference to the C terminus at various speeds (0.1–1 nm/ns) and a spring constant of 6 pN/nm.

FIGURE 5.

Coarse-grain simulations are internally consistent but have a user-set parameter of temperature that essentially determines the relative strength of the contacts. The temperature was set so that the refolding simulations were able to fold in a reasonable amount of time (∼1 week) but did not fold instantly when quenched from a melting temperature of 300 K. A temperature that is too hot (red, T = 150) never enables refolding, whereas a temperature that is too cold (blue, T = 130) enables instant refolding, and the folding temperature (green, T = 140) maintains a balance between these (the folding temperature) and was used for all simulations.

RESULTS

For mechanical unfolding and refolding experiments, we developed a Luciferase construct at the DNA level containing three I27 domains at the N terminus and four I27 domains at the C terminus (Fig. 3A) using the I27 domains only as a single-molecule fingerprint and handles for pickup (see “Experimental Procedures”). The expressed I27₃-Luciferase-I27₄ protein construct still had native enzymatic activity (Fig. 1) and was used directly for AFM pulling measurements at constant velocity (see “Experimental Procedures”). The Luciferase protein unfolds in three distinct stages (Fig. 3B). The first peak (Peak 1, blue) has the smallest contour length increment (ΔL_c = 35.8 ± 1.0 nm, mean ± S.E., n = 548) and the lowest unfolding force (F_u = 20.5 ± 0.4 pN, mean ± S.E., n = 548) (Fig. 3C). The second peak (Fig. 3C, Peak 2, green) increases in force and contour length increment (ΔL_c = 71.9 ± 1.0 nm, F_u = 35.0 ± 0.5 pN, mean ± S.E., n = 548), and the third peak (Fig. 3C, Peak 3, red) has the highest force and the largest contour length increment (ΔL_c = 86.6 ± 1.1 nm, F_u = 50.5 ± 0.6 pN, mean ± S.E., n = 548). These forces were determined at a constant loading rate of ∼3900 pN/s. This was the only pathway detected for unfolding because the peak locations and relative unfolding forces followed the same pattern in all recordings, although, sometimes, the first peak in the force-extension trace was not detected or was possibly masked by breaking nonspecific interactions between the AFM tip and the substrate. To identify the origin of these peaks, we used a combination of computer models and experimental techniques.

FIGURE 3.

Unfolding of Luciferase flanked by I27 domains. A, schematic of the experiment. Luciferase is flanked by three I27 domains at the N terminus and four I27 domains at the C terminus. Cysteines on the C terminus of the construct help to specifically attach the protein to the gold substrate. A cantilever then picks up the protein by nonspecific adhesion and stretches the molecule. B, representative trace of the unfolding of a full protein. The seven peaks at the end correspond to the unfolding of the seven I27 domains. The three peaks before the unfolding of I27 correspond to the unfolding of Luciferase. Luciferase unfolds in a stepwise process, resulting in three peaks (peak 1 (blue), followed by peak 2 (green), followed by peak 3 (red)) corresponding to unfolding of specific domains. C, the regime of the force and contour length increments of all peaks (n = 548). The force and contour length increment of I27 (ΔL_c = 28.5 nm, Fu = 197.4 pN) is consistent with results published previously.

The Mechanical Unfolding Pathway of Luciferase Proceeds from the C Terminus to the N Terminus

We first looked at the large amplitude fluctuations and dynamics of Luciferase using an elastic network model to probe the normal modes of motion (40). The lowest non-zero global modes from the normal mode analysis were calculated using the AD-ENM tool (41) using a model of the apo Luciferase. Models of Luciferase showed that the dominant mode of motion was the rotation and hinge motion of the C-terminal domain. There are 102 residues involved in this harmonic motion, which corresponds very well to the number of residues predicted from the contour length of the first peak: (32.5 nm + 3.3 nm initial length) / 0.37 nm/residue = 97 residues. Therefore, this model predicts that the first peak corresponds to the C-terminal domain. All dominant modes of motion corresponded to the C-terminal domain, which indicates that the large N-terminal domain of the protein (residues 1–450) does not have an obvious mechanical separation and cannot directly determine the origins of peak 2 or peak 3.

We also conducted steered molecular dynamic simulations on Cα models (42) of the apo form of the crystal structure of Luciferase at the folding temperature (Fig. 5 and “Experimental Procedures”). We used an open conformation structure to model the apo conformation (43) of Luciferase and the closed conformation (44) to model the ligand-bound unfolding pathways. Missing residues in the x-ray crystal structure were modeled using the SWISS-MODEL repository (45) using models 1ba3A (open) and 2d1sA (closed) (46). The temperature was chosen so that both the unfolded state and the folded state were equally populated at long time scales (∼200 ns, 1 week of simulation time), as shown in Fig. 5. Steered molecular dynamic results showed excellent agreement with the AFM-FE curve of the apo form of Luciferase (Fig. 4, A and B, left panel) when simulated at the folding temperature (Fig. 5), suggesting that Luciferase stretching results in sequential unfolding of the C-terminal domain, the middle domain, and the N-terminal domain, corresponding to peaks 1, 2, and 3, respectively (Fig. 3B). Similar results were obtained for pulling on the C terminus with respect to the N terminus.

FIGURE 4.

Superposition of unfolding traces of Luciferase with no ligand (blue), +ATP (red), or +ATP +Luciferin (green). A, unfolding traces determined by experimental AFM measurements. Dashed lines are WLC fits with a persistence length of 0.67 nm. B, bottom panels, unfolding traces determined by simulated steered molecular dynamics from appropriate models of the structure (see details under “Experimental Procedures”). C, overlay of unfolding of Luciferase under all three conditions shows that peaks 1, 2, 2′, and 3 occur in the same place across conditions (see also Fig. 6). Horizontal scale bars, 50 nm extension; vertical scale bars, 50 pN.

Because the Luciferase ligands (ATP and Luciferin) bind to residues within 250 amino acids and 450 amino acids, AFM and steered molecular dynamic experiments with ligands should only affect the unfolding of the middle of Luciferase. We performed pulling experiments of the Luciferase construct in the presence of its ligands, MgATP or MgATP with Luciferin (Fig. 3). In the presence of MgATP, there was a mixed population of AFM force-extension recordings that either corresponded to the apo type (Fig. 4A, left panel) or a recording that had an additional peak, 2′, immediately after peak 2 (Fig. 4A, center panel). Interestingly, a third peak formed after peak 2′ appeared when Luciferin and MgATP were added, denoted peak 2″ (Fig. 4A, right panel). For either condition, the only difference between any force-extension recordings of the unfolding of Luciferase is the added presence/absence of peak 2′ and/or peak 2″ (Fig. 4C). The unfolding forces across different conditions for peak 1, peak 2, peak 2′, and peak 3 are comparable at similar loading rates because the null hypothesis that the force distributions have the same mean cannot be rejected after two-sample Student's t test (Fig. 6). Because ligands bind to the middle of Luciferase and only affect the unfolding of the domain that corresponds to peak 2 in the force-extension trace, we hypothesize that peak 2 corresponds to the unfolding of the middle of Luciferase.

FIGURE 6.

Left panel, the mean ± S.E. of each unfolding force is shown for each condition and each peak. The unfolding forces of different peaks do not differ across different conditions. The unfolding force increases steadily from peak 1 to peak 2″ and then decreases for peak 3. The presence of the ligands in the unfolding pathway only has the effect of splitting peak 2 and creating new peaks (peak 2′ or peak 2′ and peak 2″) because the unfolding forces for peaks 1, 2, and 3 are not statistically different. Right panel, The mean ± S.E. of each contour length increment from each peak is shown for each condition and each peak.

The observation that the unfolding force of peak 3 is much less than the unfolding force of the preceding peak 2″ strongly suggests that unfolding occurs from one end to the other, as also suggested by our computer simulations. If the unfolding did not occur from end to the other, then that part of the protein would be unfolded in the center, which would mechanically separate two domains. If two domains are mechanically separated (by the unfolded residues), then the first to unfold would be the domain that has less mechanical stability. Because this is not the case and because the unfolding of peak 2″ occurs at a much higher force than that of peak 3, then the unfolding must not separate the domains and must happen from one end to the other. We hypothesize that peak 2″ occurs at a higher unfolding force than peak 3 because the domain corresponding to peak 3 is stabilized by the domain corresponding to the unfolding event from peak 2″. When the domain corresponding to peak 2″ is unfolded, the domain corresponding to peak 3 loses some of its mechanical stability and unfolds at force lower than peak 2″.

We also did coarse-grained simulations of models of Luciferase with ligands that matched well the results of the experimental unfolding. The closed conformation of Luciferase (44) was used to model the ligand-bound unfolding pathways. The unfolding simulation of Luciferase with a modeled ATP ligand split peak 2 into a doublet of peaks 2 and 2′, and the simulations of models of Luciferase and a modeled ATP ligand and a modeled Luciferin ligand split peak 2 into a triplet of peaks 2, 2′, and 2″ (Fig. 3). The forces do not compare well to the experiment because the unrealistic forces of the simulations may be due to the simplistic contact model inherent in Cα model potentials. However, the relative effects compare very well with the experiment and again indicate that the unfolding occurs in subdomains from the C terminus to the N terminus, which is consistent with the simulations of the apo form and with the results of the AFM measurements.

To further examine the unfolding pathway, we performed experiments with denaturant guanidinium chloride (GdmCl). Previous groups have measured equilibrium unfolding in denaturants using tryptophan fluorescence and found that specific domains unfold at various concentrations of GdmCl on the basis of the quenching of the tryptophan fluorescence (24, 26, 47). Notably, Wang et al. (47) made single-tryptophan mutants of Luciferase with tryptophan residues placed at various locations of Luciferase, which allowed them to probe equilibrium unfolding of domains independently. These studies found that many of the mutated tryptophan residues located in the middle domain of Luciferase are quenched at lower denaturants than the tryptophan residues located in the N-terminal domain (Fig. 6B), indicating that only the middle domain unfolds at low denaturant concentrations (24, 26, 47). It is difficult to determine the stability of the C-terminal domain because there was only one study that determined the effect of GdmCl on a tryptophan in the C-terminal domain.

We hypothesized that, because the N-terminal domain remains folded at low concentrations of denaturant and the middle domain unfolds at low concentrations of denaturant, AFM measurements of Luciferase in low concentrations of denaturant would still show peak 3 but not peak 2. When denaturant was added, we found that a proportion of force-extension curves contained peaks 1, 2, and 3, and another proportion only had peak 3 (Fig. 7B). The recordings that only had peak 3 had a long initial length, which would indicate that the domains corresponding to peak 1 and peak 2 are unfolded under these conditions. This result further confirms our hypothesis that the unfolding of the N-terminal domain gives rise to peak 3.

FIGURE 7.

Unfolding experiments in the presence of denaturant. A, the unfolding forces for peak 2 and peak 3 are plotted without denaturant (blue) and with denaturant and showing all peaks (gold) and with denaturant but only showing Peak 3 (magenta). The forces do not differ statistically, implying that the denaturant acts simply to unfold the protein rather than destabilize and lower the mechanical unfolding force. B, aggregates of FE curves for luciferase in the presence of GdmCl with all three peaks appearing (gold) and with only the third peak present (magenta). C, the red, blue, and green lines are measurements from references (24, 26, 47) shown here for comparison with our own data (black). These colored lines show data from chemical denaturation and subsequent evaluation of tryptophan apparent fluorescence (normalized to 1 at 0 m GdmCl and normalized to 0 at 5 m GdmCl). Colors indicate the location of residues in the protein (red, N-terminal residues; green, middle of protein; blue, C-terminal domain of protein). SMFS measurements (black) counted the fraction of SMFS curves with peak 2.

The proportion of FE recordings that had all peaks was concentration-dependent and decreased to about 50% at 250 mm GdmCl. This trend follows very closely the equilibrium unfolding of the middle domain of Luciferase measured by tryptophan fluorescence (Fig. 7C). We also noted that the presence of GdmCl did not seem to mechanically weaken the folded domains. This conclusion was made on the basis of the observation that the unfolding forces of peaks that were recorded in the presence of denaturant were indistinguishable from unfolding forces without denaturant (Fig. 7A). This suggests that the denaturant acts to completely unfold and not simply mechanically weaken the domain. Interestingly, this might indicate that the signal from tryptophan fluorescence equilibrium unfolding may integrate two populations of Luciferase molecules: one that is in the native state and one that has the second domain denatured.

To further validate the origin of peak 3 being the N-terminal domain, we directly probed the N-terminal domain by creating a truncated version of Luciferase, Luc203, containing residues 1–203 (Fig. 8). The contour length increment of the corresponding unfolding event in the force-extension trace is 49.4 ± 3.9 nm (mean ± S.D.). The force of Luc203 is very similar to the unfolding force of peak 3, which indicates a similar level of stability. Because it is unlikely that a truncation would result in a higher force than the original protein and that peak 3 had the highest force of any peak, it is very likely that the similar stability of Luc203 reflects that the N-terminal domain corresponds to peak 3. The difference in contour length increment (84.3 nm in the full unfolding pathway for peak 3 of Luciferase and 49.4 nm for the truncated Luc203) can be explained by the long unstructured coils left over from the truncation (Fig. 8C). The first 22 residues and residues 172–203 in Luciferase form long coils that would normally interact with the middle domain of Luciferase (residues 230–400). Therefore, it is expected that these residues will be unstructured in the truncated form. Thus, assuming that these coils only contribute to the initial length, the contour length increment should be equal to the length contributed by the number of residues in the rest of the structure minus the N-C length of that structured fragment (149 residues × 0.37 nm/residue − 2.8 nm = 52.3 nm). Therefore, because the truncated Luciferase does not contain the full structure, it is expected to give only ∼52.3 nm of a contour length increment, which agrees well within the measured contour length increment of 49.4 ± 3.9 nm.

FIGURE 8.

Luciferase was truncated to residues 1–203 to determine whether the unfolding force was similar to peak 3 (which should correspond to the unfolding of the N-terminal domain). The unfolding FE curve is shown in A, and the unfolding force is not statistically different from peak 3 in the apo form (B). However, the contour length increment is much smaller because of the fact that large loops are left without their normal contacts, making them unstructured and not contributing to the unfolding event in the truncation, as shown in C.

Structural Origins of Domains Involved in the Mechanical Unfolding Pathway

We conclude that this combination of experimental and simulated forced unfolding shows unequivocally that Luciferase undergoes sequential unfolding, domain by domain, from the C terminus to the N terminus. The precise structural domains can then be accurately determined by using AFM-measured contour length increments and measures of initial length from the crystal structure. By correlating the AFM contour length increments to the number of residues gained during extension, although considering all possible domain boundaries (see “Experimental Procedures”), we determined that the C-terminal domain (which gives rise to peak 1) consists of residues 443–550 and that the N-terminal domain (which gives rise to peak 3) consists of residues 1–248, with a total residual of 0.4 nm for the apo form (Fig. 9, left panel). These results are similar to algorithm predictions (N-terminal domain, start-266; C-terminal domain, 434-end) that consider multidomain proteins as collections of self-contained cooperative units (48). These divisions are also very similar to the divisions determined during the simulated unfolding (Fig. 9).

FIGURE 9.

The unfolding domains corresponding to the peaks in the FE curves were calculated (see “Experimental Procedures”) and are shown as Experiment (top panel). The domain boundaries from Simulation come from the unfolding trajectories in the steered molecular dynamic simulations. Bottom panel, The experimental boundaries are colored on the relevant structures (open for Apo and closed for the ligand bound) below.

Similar methods can be used to determine the structural location of the domain unfolding events corresponding to peak 2′ and Peak 2″ in the FE profile by assuming four domains in the case of +ATP and five domains in the case of +ATP and +Luciferin (see “Experimental Procedures”). All possible interfaces were considered, and the residuals were minimized with respect to the interfacial residues. The residuals were 0.7 nm for the +ATP experiments and 0.5 nm for the +ATP, +Luciferin experiments, which indicates that there is good agreement between the theoretically determined domains and the experimentally determined contour length increments from those domains. Because all other peaks remained at the same position (Fig. 4C) and the same force (Fig. 9), these additional unfolding events must have originated from the structural rearrangement caused by ligand binding. Indeed, the boundary between peak 1 and peak 2 and the boundaries around peak 3 are similar in each condition (Fig. 8).

When ligands are added, peak 2 has a contour length increment of ∼8 nm (Fig. 5, right). Using domain boundaries determined by minimizing residuals, this contour length increment comes from the unfolding of residues 422–448. These residues have an initial length of ∼1.5 nm (after accounting for the reorientation of the multidomain protein), so its theoretical contour length increment would be 8.5 nm (27 residues × 0.37 nm/residue − 1.5 nm), which corresponds very well with the expected contour length increment of ∼8 nm. These residues correspond to a β-hairpin directly after the C-terminal hinge. The force required to rupture a single β-hairpin is ∼25–50 pN, which is consistent with the force of peak 2 (∼30 pN) (49). In the apo form, we expect that this is also the origin of peak 2 and that this unfolding event triggers a quick and subsequent unfolding of the rest of the middle of the protein (residues 248–422), which is otherwise stabilized by ligands in the ligand conditions. The structure that gives rise to peak 2′ in force-extension curves with ATP is likely the coil loop, which may make contacts with an unhydrolyzed ATP, and the stabilization of Luciferin in the middle of the protein likely gives rise to peak 2″. This study is being followed up by mutagenesis to confirm these structural origins.

Separated Domains of Luciferase Refold Robustly

First we examined only the N-terminal domain using the truncated Luciferase containing only residues 1–203 (Luc203). The mechanical stability of the truncated Luciferase in stretching measurements was similar to the stability of N-terminal domain in the full-length protein, as determined by peak 3. Therefore, we assumed that the mechanical behavior of the isolated N-terminal domain is similar to its behavior in the complete protein. After a single molecule of Luc203 was extended, it was retracted and allowed to refold for 10 s, and then subsequent pulses of extension and retraction were performed. On subsequent extension pulses, a similar peak appeared, indicating that the truncated N-terminal domain of Luciferase refolds (Fig. 10, 2–5). The refolding of the truncated Luciferase occurred in 56% of subsequent extension pulses (n = 102, 12 molecules) with a time delay of 10 s.

FIGURE 10.

Refolding experiments of the truncated Luciferase construct, I27₃-Luc203-I27₄ (where Luc203 contains only residues 1–203), showing extension (red) and retraction (blue) for sequential measurements (black is a template molecule of the unfolding of truncated Luciferase). The time between extension pulses is 10 s, which is enough for I27 domains to refold 100% of the time and also allows Luc203 to refold most of the time (correct Luc203 refolding events are marked by asterisks).

Next we selectively unraveled Luciferase domains of the full Luciferase protein by controlling the extension of stretching and tested their ability to refold from the mechanically relaxed state. Using the entire Luciferase protein, we performed similar refolding experiments, first by selectively unfolding the C-terminal domain (Fig. 11A), which corresponds to peak 1 in the full unfolding of Luciferase. Correct refolding produces a similar peak upon the next pulse of unfolding (Fig. 11A, 2–5). When unfolding and refolding only the C-terminal domain or the middle domain (peaks 1 and 2, extending to 40 nm or 60–80 nm, respectively), it was observed that the peaks corresponding to unfolding of one of those domains reappeared in subsequent pulling cycles, indicating refolding in about 78% of subsequent extension pulses (n = 23, six molecules). An estimate of the folding time can be obtained by decreasing the time delay between pulses. Refolding occurred when separating pulses by a time delay for 2 s, indicating a lower bound of the refolding rate of about ∼0.5 s⁻¹. We determined that, throughout these partial unfolding/refolding cyclic measurements, the N-terminal domain remained folded because the complete extension of the protein following these measurements captured its characteristic peak.

FIGURE 11.

Refolding experiments of the Luciferase construct showing extension (red) and retraction (blue) for sequential measurements (black is a template molecule). A, Luciferase is stretched only to the extension corresponding to the unfolding event of peak 1 or peak 2 and then relaxed and restretched with a time delay of 10–30 s, which showed the robust reappearance of peak 1 and peak 2. These peaks occur because of the unfolding of the C-terminal and middle domains, indicating that refolding occurs with a folded N-terminal domain. B, Luciferase is fully unfolded, and then cyclic unfolding/refolding measurements are performed after a delay of 30–180 s. In each cyclic measurement, the peaks do not reappear, and, instead, large nonspecific forces predominate, indicating stable misfolded states of Luciferase. C, Luciferase is fully unfolded in the presence of chaperones in the form of RRL, and subsequent pulses show peak reappearance, indicating successful partial refolding of Luciferase and no strong stable misfolds. Inset, the addition of RRL chaperones provides a statistically significant increase in the proportion of subsequent unfolding FE curves with refolded domains. Correct refolding events are marked by asterisks.

Complete Unfolding of Luciferase Prevents Refolding unless Provided with Chaperones

When Luciferase is fully stretched (thus completely unfolded) (extension 150–200 nm, showing peaks 1, 2, and 3) and then relaxed, the original unfolding peaks are never fully recovered in subsequent stretching cycles (Fig. 11B, 1–5), suggesting that refolding is inhibited in these experiments. Instead, each pulse after the initial unfolding pulse shows irregular high-force events (100–200 pN). This result is observed even with a long time delay of 120 s (n = 68, 30 molecules). This indicates an upper bound for the refolding rate of ∼0.006 s⁻¹, but, because refolding was never fully observed, it is likely that this is a liberal upper bound.

We also performed refolding simulations analogous to the AFM experiments. The full apo model of Luciferase was extended only to unfold a single domain at a time (indicated by peak 1, peak 2, or peak 3), at which point the molecule was retracted, and then the force was taken off to allow complete relaxation and refolding. When the N-terminal domain was left intact (extending past either peak 1 or peak 2), Luciferase refolded in < 3 ns. When refolding from completely denatured Luciferase, the refolding occurs domain by domain from the N-terminal domain to the C-terminal (12 of 13 simulations). From the unfolded state, the mean time for the N-terminal domain to fold is 79 ± 41 ns, after which the middle domain folded in 3 ± 2 ns and then the C-terminal domain refolded in 9 ± 6 ns (mean ± S.D.). Therefore, in simulations, the refolding rate when the N-terminal domain is folded is over 20 times faster than when refolding from completely denatured protein. Both simulations and experiments show that Luciferase refolds robustly and quickly when the N-terminal domain is folded and that the refolding time is much longer when Luciferase is completely unfolded (molecular dynamics results).

To determine whether the fully unfolded Luciferase can be rescued by chaperones, we performed the AFM refolding experiments in the presence of rabbit reticulocyte lysate (RRL), which has been shown to renature Luciferase (28), because of the presence of chaperone proteins at high concentration. With the addition of RRL, Luciferase was fully extended and then relaxed for 120 s before extending again to monitor refolding in the second pulse. The FE curve of the subsequent pulses frequently showed similar peaks as the original, indicating that refolding was successful (Figs. 11C and 12). This effect was statistically significant because the number of force-extension curves with at least two refolded domains increases from 13% without RRL (95% confidence interval, 6–24%, n = 68 on 30 molecules) to 46% with RRL (95% confidence interval, 33–61%, n = 54 on 16 molecules). This result suggests that the high-force peaks without RRL are due to misfolded states stabilized by non-native contacts and that chaperones inhibit these contacts helping the unfolded and relaxed protein to recover its native structure. We are actively investigating the specific chaperones that enable refolding.

FIGURE 12.

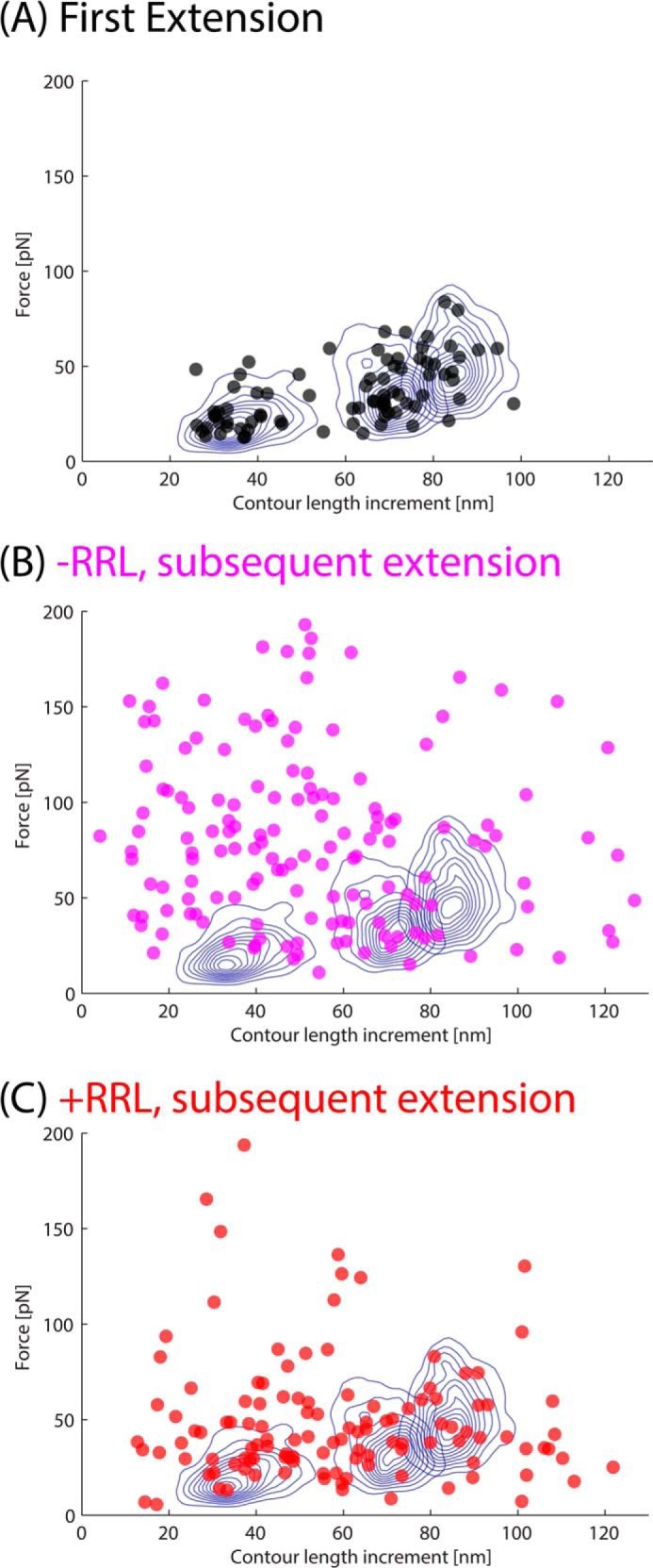
The force peaks from refolding experiments are plotted by their unfolding forces and their contour length increments. In each plot, blue contour lines indicate where 90% of the native Luciferase peaks lie. Events that refold to the native structure should have subsequent peaks that correspond to these contours. The peaks of the first extension (no refolding) fall directly into these contours (A). Without chaperones (B), the peaks fall mostly outside and above the contours because they are mostly nonspecific and high-force events. With the addition of chaperones (C), the refolding peaks fall mostly inside contours, which indicates native-like refolding. The proportion of recordings with at least two refolding events were calculated for the full extension with and without chaperones and are plotted in Fig. 11C, inset.

DISCUSSION

Firefly luciferase (Luciferase) is homologous to AMP-forming ligases and nonribosomal peptide synthetases and it is one of the first described large, multidomain proteins shown to undergo cotranslational folding and chaperone-assisted refolding. Important questions remain about how cotranslational folding prevents misfolding, how chaperones effectively refold the protein, and why Luciferase forms such a stable misfolded state. To address these questions, we used SMFS and computer simulations to selectively denature the C-terminal domain, the middle domain, or the full protein, including the N-terminal domain (corresponding to peak 1, peak 2, and peak 3 in the unfolding force-extension curve), and performed refolding studies on individual protein molecules.

The refolding studies on individual molecules with AFM has the drawback of possibly introducing unanticipated surface protein effects because the molecule of interest is attached to the surface nonspecifically. We believe our results circumvent this issue for three main reasons. All refolding measurements are done after retracting the tip away from the surface by at least 15 nm before performing any refolding; all constructs are flanked by I27 domains that should provide an additional buffer of 12–16 nm if tethered at the ends; and there are drastic differences between the refolding in different experiments (truncated Luciferase, fully denatured native Luciferase with/without chaperones, and partially denatured Luciferase), which would likely not be the case if nonspecific surface effects were prevalent. However, we are further investigating possible effects using a variety of surfaces.

Our first major observation is that Luciferase is able to prevent misfolding and refold robustly when the N-terminal domain is left folded. The C-terminal and middle domains of Luciferase can undergo many cycles of unfolding and refolding without forming observable non-native intermediates as long as the N terminus is folded. Their refolding rate (lower limit ∼0.5 s⁻¹) is also much faster than the typical cotranslational folding rate of Luciferase (∼0.005 s⁻¹). This suggests that the bottleneck of Luciferase folding is the folding of its N-terminal domain.

To probe the folding of the N-terminal domain by itself, we used a truncated domain consisting of only the first 203 residues (Luc203). This domain refolded robustly but not as efficiently as the C-terminal domains in the presence of the folded N-terminal domain. This experiment was performed on a truncated protein that may have had different properties than the native protein, and we are further investigating this by performing refolding with a pulling geometry that directly affects the N-terminal domain within the native protein.

The refolding of the full protein was prevented when Luciferase was fully denatured mechanically, which has been observed previously using chemical denaturants (24, 25). However, instead of attributing the lack of refolding to aggregation, we suggest that it is due to misfolding. Because we observed that refolding can occur in an isolated N-terminal domain (by protein truncation) and that refolding can occur in the C-terminal domains if the N-terminal is folded, we suggest that the misfolding is due to the interaction between the unfolded N-terminal and unfolded C-terminal residues of a single protein. Such misfolding is easily prevented in the cell, where the cotranslational folding of the N-terminal domain prevents interaction with the C-terminal residues, thereby preventing putative very stable, non-functional intermediates (50).

Finally, we observed that adding chaperones in the form of cell lysate can significantly increase the refolding of fully denatured Luciferase, as reported previously in the literature, using bulk methods (28). However, our results with partial denaturation and the truncated Luciferase also suggest a specific mechanism by which chaperones could act on Luciferase. Because partial unfolding does not require chaperones for efficient refolding, chaperones must act to specifically enable folding of the N-terminal domain, which should then catalyze the refolding of the rest of the protein. Whether this action is achieved by association of chaperones with the N-terminal domain and separating it from C-terminal residues or sequestering C-terminal residues from the N-terminal residues remains to be examined. The presence and action of these chaperones seem to emulate the conditions provided by the ribosomal exit tunnel, assisting the nascent chain in the vectorial nature of cotranslational folding. In this way, both the ribosome and the chaperone would allow the sequential folding to avoid the kinetic traps inherent in the energy landscape of Luciferase. It is likely that folding of other multidomain proteins may exploit a similar mechanism.