Non-contact fiber-optical trapping of motile bacteria: dynamics observation and energy estimation

Abstract

The dynamics and energy conversion of bacteria are strongly associated with bacterial activities, such as survival, spreading of bacterial diseases and their pathogenesis. Although different discoveries have been reported on trapped bacteria (i.e. immobilized bacteria), the investigation on the dynamics and energy conversion of motile bacteria in the process of trapping is highly desirable. Here, we report a non-contact optical trapping of motile bacteria using a modified tapered optical fiber. Using Escherichia coli as an example, both single and multiple motile bacteria have been trapped and manipulated in a non-contact manner. Bacterial dynamics has been observed and bacterial energy has been estimated in the trapping process. This non-contact optical trapping provides a new opportunity for better understanding the bacterial dynamics and energy conversion at the single cell level.

Like all biological organisms, bacteria must constantly interact with their living environment. During this interaction, the dynamics and energetics of the motile bacteria are crucial to diverse bacterial activities, such as survival¹,², response to the environment³,⁴,⁵, spreading of bacterial diseases and their pathogenesis⁶, etc. The bacterial dynamics and energetics are directly related to bacterial motility. For most of the peritrichously flagellated bacteria, their motility is caused by the “swimming” feature, composed of ‘runs' and ‘tumbles', which is generated by different states of the motors that rotate the bacterial flagella⁷. To get a direct study on a motile bacterium, a handy and noninvasive method is particularly desirable to catch the bacterium. Among all the methods for the catching of a motile bacterium, optical trapping is a versatile candidate benefiting from its noninvasive and precise nature⁸,⁹. Using optical trapping, different discoveries about bacteria, such as swimming behavior¹⁰,¹¹, chemotaxis¹², and cell mechanics¹³, have been obtained. This powerful optical trapping technique is generally based on a strongly focused laser beam, known as conventional optical tweezers⁸,⁹. Small objects can be trapped in the focus by a strong optical gradient force without any mechanical contact. To trap the motile bacteria, other effective and promising techniques, such as optical nanofiber¹⁴, silicon photonic crystal¹⁵, rotating magnetic micro-robot¹⁶, and tapered optical fiber¹⁷, have been designed and applied. Among these techniques, the tapered fiber-based trapping has the advantages of easy fabrication, easy integration with microfluidic devices, and high manipulation flexibility. Trapped objects can be delivered to any designated positions using a tapered fiber by moving the translation stage fixing the fiber. A tapered fiber has been widely used for the trapping of mesoscopic objects, such as dielectric particles, eukaryotic cells, and bacteria. Light output from a tapered fiber is focused near the fiber tip and an optical gradient force is generated to trap objects. This tapered fiber-based trapping is mechanical contact (i.e. the objects are directly in contact with the fiber) and will inevitably cause mechanical damage to the trapped objects. This damage is even more obvious and harmful for the living bacteria. To better understand the dynamics and energetics of a motile bacterium, a non-contact and damage-free trapping is necessary. To realize a non-contact trapping using optical fibers, single optical fiber with multiple cores¹⁸ and all-fiber probe with a fiber bundle¹⁹,²⁰ have been designed, but the ends of these fibers are relatively large (tens of microns¹⁸ or even hundreds of microns¹⁹,²⁰ in diameter). To realize non-contact trapping, and meanwhile, to remain the advantages of manipulation flexibility and miniaturization of a tapered fiber, in this work, a single mode tapered fiber with a modified end is reported for the non-contact optical trapping of motile bacteria. Using Escherichia coli (E. coli) as an example, it is demonstrated that the modified tapered fiber is capable of non-contact optical trapping of both single and multiple bacteria while the bacterial dynamics can be observed and the bacterial dynamics can be estimated in the process of trapping.

Results

Design and numerical calculation

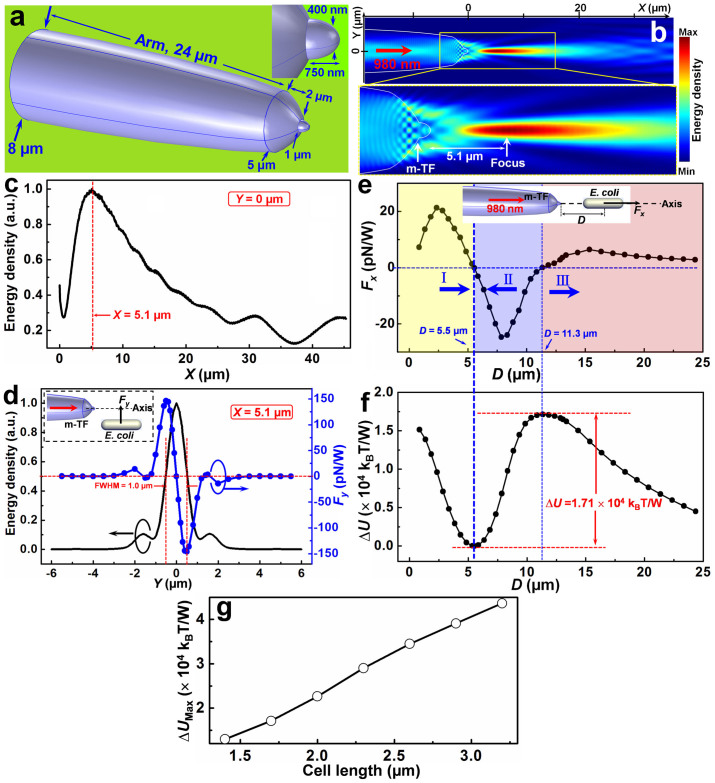
To realize the non-contact optical trapping, a modified tapered fiber is designed as shown in Fig. 1a. The diameter of the modified tapered fiber arm is gradually decreased from 8 to 5 µm over a length of 24 µm. And then an abruptly tapered region appears with the diameter decreased from 5 to 1 µm over a length of 2 µm, and the modified tapered fiber is finally ended with a modified protruding tip, with the diameter decreased from 1 µm to 400 nm over a length of 750 nm (see Inset of Fig. 1a). The reason to design such a modified tapered fiber with an abruptly tapered region and a protruding tip is that the focus of the light beam output from the fiber is away from the fiber tip, with a larger distance than that of a gradually tapered fiber (see Fig. S1 in the Supplementary Information for discussion). And thus, the bacterium can be trapped in the focus, non-contact to the fiber tip. To show the non-contact optical trapping ability of the modified tapered fiber, a finite-element method was used to simulate the light distribution output from the modified tapered fiber. Simulation details are shown in Fig. S2. To realize the trapping performance and meanwhile to induce little harm to the bacteria, a laser beam with a wavelength of 980 nm, which exhibits low absorption to most living matter²¹, was used. The simulated optical energy density distribution output from the modified tapered fiber tip is shown in Fig. 1b. Remarkably, different from the situation in the previously reported tapered fiber¹⁷, where light output from the fiber is focused at the fiber tip, the focus of the light output from the modified tapered fiber is 5.1 µm away from the fiber tip (inset of Fig. 1b and Fig. 1c). The optical energy density along the Y direction at the focus (X = 5.1 µm) is shown in Fig. 1d (black line). The full width at half maximum (FWHM) is 1.0 µm. Because light is highly focused at X = 5.1 µm, objects near the focus can be trapped by the exerted optical force, without contact to the fiber tip.

Figure 1. Model of the modified tapered fiber and numerical results.

m-TF: modified tapered fiber. (a) Model of the modified tapered fiber, inset shows the details of the protruding tip. (b) Simulated optical energy density distribution output from the modified tapered fiber, inset shows the enlargement of the focus, which is 5.1 µm away from the fiber tip. (c) Normalized energy density distribution along the fiber axis (Y = 0). (d) Normalized energy density and calculated F_y for the bacterium at the focal plane (X = 5.1 µm) with different Y locations, inset shows the calculation model. (e) Calculated F_x exerted on the bacterium along the modified tapered fiber axis as a function of distance D to the fiber tip, inset shows the calculation model. The yellow (I), blue (II), and red (III) regions indicate the regions with positive, negative, and positive F_x values in which the bacterium will be driven away, trapped, and driven away, respectively. (f) Calculated potential difference ΔU as a function of distance D. (g) Calculated maximum potential difference ΔU_Max as a function of cell length.

To numerically show the non-contact trapping ability, the optical force exerted on a single bacterium (length: 1.7 µm, diameter: 500 nm) was calculated. The optical force (F_O), which was obtained by integrating the time-independent Maxwell stress tensor 〈T_M〉 on the enclosing surface of the bacterium, can be expressed as¹⁴

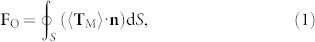where n is the surface normal vector. The calculated F_y, one component of F_O in the Y direction, exerted on the bacterium with different Y locations (X = 5.1 µm) is shown in Fig. 1d (the blue dotted line). It can be seen that F_y is directed to the fiber axis, thus the bacterium beside the axis can be trapped to the axis. Some typical examples of the simulated energy distribution and force calculation are shown in Fig. S3. The calculated F_x, one component of F_O in the X direction, exerted on the bacterium located along the fiber axis (Y = 0) is shown in Fig. 1e. Interestingly, F_x exhibits three different situations for different distances (D) to the fiber tip. For D < 5.5 µm, F_x is positive, indicating that the bacterium will be driven away from the fiber tip. For 5.5 µm < D < 11.3 µm, F_x is negative, indicating the bacterium will be trapped. Thus the elongated trap is suitable for trapping the needle like bacteria. For D > 11.3 µm, F_x is positive, indicating the bacterium will be driven away. Although F_x = 0 at D = 5.5 and 11.3 µm, only the location with D = 5.5 µm is the stable one. Because in this location, the slope of F_x is negative and the potential is minimum. Thus, non-contact trapping will be occurred at around D = 5.5 µm. By integrating F_x over distance starting from D = 5.5 µm, the trapping potential difference (ΔU) can be obtained according to

The calculated ΔU is shown in Fig. 1f. It can be seen that the minimum and maximum trapping potentials are occurred at D = 5.5 and 11.3 µm, respectively. Thus the location with D = 5.5 µm is the stable one. The maximum potential difference between D = 5.5 and 11.3 µm is ΔU = 1.71 × 10⁴ k_BT/W. To escape from the potential well, a minimum energy of 1.71 × 10⁴ k_BT/W should be exerted on the trapped object. Otherwise, the object will be confined in the potential well, and the dynamics of a motile bacterium can be observed in the potential well. To estimate the minimum energy to escape from the potential well for bacteria with different cell lengths, simulation and calculation were carried out on bacteria with different cell lengths from 1.4 to 3.2 μm using the same method. The calculated maximum potential difference (ΔU_Max), i.e., the minimum energy to escape from the trapping, is shown in Fig. 1g. It can be seen that ΔU_Max is increased with the increasing in cell length, thus for smaller bacteria, a smaller energy is required to escape from the trapping; while for larger bacteria, a larger energy is required to escape.

Experimental preparation

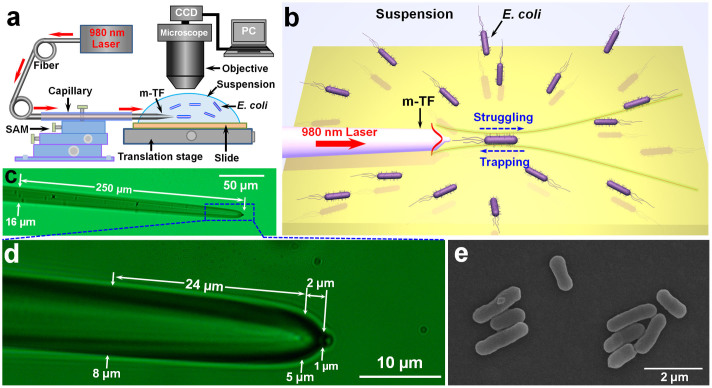
Based on the above analysis, an experimental setup was designed and built (see Fig. 2a). A laser beam at a wavelength of 980 nm was launched into a modified tapered fiber (see Methods and Fig. S4 for fabrication), the modified tapered fiber was sheathed with a glass capillary and fixed by a 3-dimensional (3D) six-axis manipulator (SAM). The tip of the modified tapered fiber was immersed in an E. coli bacteria suspension (see Methods for the suspension preparation) on a glass slide which was manipulated by a translation stage. The trapping process and bacterium dynamics were obtained by a microscope interfaced with a CCD camera through a personal computer (PC). Figure 2b presents a schematic illustration of the non-contact optical trapping and the dynamics of a single bacterium. E. coli bacteria are randomly swimming in the suspension. A single randomly swimming E. coli bacterium near the modified tapered fiber is trapped with a distance of several microns to the fiber tip. The bacterium is moving back and forth in the trapping potential well, resulting from the confrontation between the bacterial motility and optical trapping. On one hand, the bacterium is trapped toward the fiber tip and confined by optical trapping, but on the other hand, the bacterium can also move away from the fiber tip and escape from the trapping because of the bacterial motility. We call this moving process “struggling”. The retaining and escape of the trapping depend on the input optical power of the laser beam. The modified tapered fiber used in the experiment is shown in Fig. 2c. The diameter of the arm is about 16 µm and gradually decreased into a tapered end over a length of 250 µm. Details of the tapered end is shown in Fig. 2d. Similar to the modified tapered fiber designed in Fig. 1a, the diameter of the fabricated modified tapered fiber arm is gradually decreased from 8 to 5 µm over a length of 24 µm, and then an abruptly tapered region appears with the diameter decreased from 5 to 1 µm over a length of 2 µm, and finally the fiber is ended with a protruding tip. Figure 2e presents a typical scanning electron microscope (SEM) image of the E. coli bacteria used in the experiment, with an average length of 1.7 µm and a diameter of 500 nm.

Figure 2. Experimental schematic and characterization of the modified tapered fiber and E. coli.

(a) Schematic illustration of the experimental setup, the red arrows indicate the propagation of the laser beam. (b) Schematic illustration of the non-contact optical trapping and single bacterium dynamics. (c) Optical microscope image of the modified tapered fiber. (d) Details of the tapered region of the modified tapered fiber as shown in the dashed blue region of (c). (e) SEM image of the E. coli bacteria.

Non-contact optical trapping

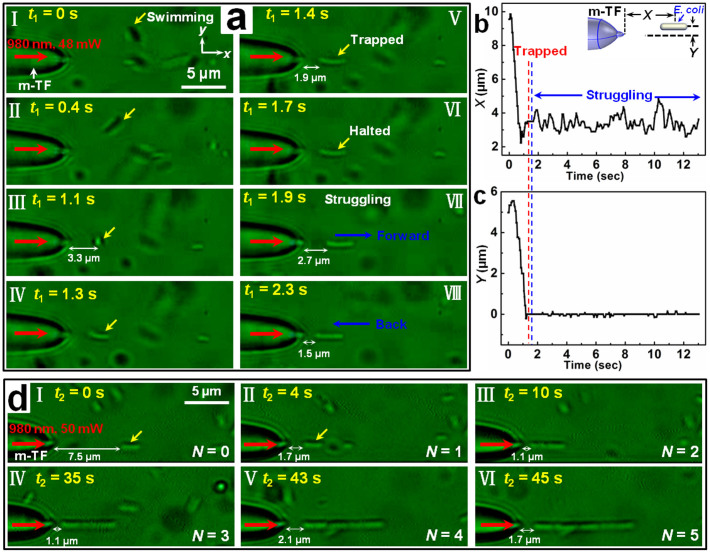
The experiments were begun by launching the 980-nm-wavelength laser beam into the modified tapered fiber. With the laser beam launched, a randomly swimming E. coli bacterium was trapped by the modified tapered fiber with a distance of several microns to the fiber tip. During the trapping, the highly active bacterium was struggling. Figure 3a shows the detailed process of the non-contact trapping and bacterium struggling with a laser beam of 48 mW launched into the modified tapered fiber. From t₁ = 0 to 1.1 s (Fig. 3aI-III), the bacterium was randomly swimming near the modified tapered fiber with an average swimming velocity of about 8.5 µm/s. At t₁ = 1.1 s, the bacterium entered into the trapping potential well, with a distance of 3.3 µm to the fiber tip, and the swimming state changed (Fig. 3aIII). The orientation of the bacterium gradually changed, and finally the bacterium was along the central axis of the fiber (Fig. 3aIII-V). This is because the restoring torque acting on the bacterium is zero when the bacterium is along the central axis of the fiber, and the motile bacterium was trapped with this stable orientation. At t₁ = 1.4 s, the motile bacterium was stably trapped with a gap of 1.9 µm to the fiber tip (Fig. 3aV). The trapped bacterium kept halted for about 0.3 s (t₁ = 1.7 s, Fig. 3aVI). Interestingly, after the halt, the trapped bacterium began to struggle in the potential well. At t₁ = 1.9 s, the bacterium struggled forward with a gap of 2.7 µm to the fiber tip (Fig. 3aVII). The bacterium was then trapped back toward the fiber. At t₁ = 2.3 s, the bacterium was trapped back with a gap of 1.5 µm to the fiber tip. The bacterium was then struggling in the potential well back and forth, resulting from the confrontation between the bacterial motility and optical trapping. Details of the trapping and struggling process is shown in Supplementary Movie S1. To further investigate the dynamics in detail, the trace of the bacterium was analyzed. The X and Y displacements of the bacterium are shown in Figs. 3b and c, respectively. From Fig. 3b, it can be seen that the X displacement is fluctuant after 1.7 s, which shows the struggling of the bacterium after the trapping in the x direction. While for the Y displacement (Fig. 3c), it is very stable, with a largest fluctuation of only 0.14 µm. This is because in the y direction, the bacterium was trapped by the transverse optical force as analyzed in Fig. 1d. Besides the non-contact trapping and dynamics observation of the bacterium, the trapped bacterium can also be manipulated and delivered to designated locations in 3D by manipulating the fiber flexibly. Figure S5, as an example, shows the detailed moving process of a non-contact trapped bacterium.

Figure 3. Non-contact optical trapping of single and multiple bacteria.

(a) Optical microscope images of the trapping and struggling process of a single bacterium. The red and yellow arrows indicate the input laser beam and the trapped bacterium, respectively. Panels I-III, III-V, and VI-VIII show the swimming, trapping, and struggling processes of the bacterium, respectively. (b) X displacement of the trapped bacterium as a function of time, inset shows the schematic of X and Y displacements. The red and blue dashed lines indicate the trapping and struggling, respectively. (c) Y displacement of the trapped bacterium as a function of time. (d) Optical microscope images of the non-contact trapping of 5 bacteria, the red arrows indicate the input laser beam.

Interestingly, this non-contact trapping is not only applicable for single bacterium, it can also be used for multiple bacteria trapping and bacteria chain formation. Figure 3d shows the process of the non-contact trapping of 5 E. coli bacteria with an optical power of 50 mW launched into the modified tapered fiber. At t₂ = 0 s, the first bacterium (yellow arrow indicated) is with a gap of 7.5 µm to the fiber tip (Fig. 3dI). At t₂ = 4 s, it was trapped with a gap of 1.7 µm (Fig. 3dII). After the first bacterium being trapped, the following bacteria swimming towards the first one can also be trapped orderly, and formed a bacteria chain. At t₂ = 10, 35, 43, and 45 s, 2, 3, 4, and 5 bacteria were trapped, with gaps of 1.1, 1.1, 2.1, and 1.7 µm, respectively to the fiber tip (Fig. 3dIII-VI). The reason for this non-contact optical trapping of multiple bacteria is that the input light can propagate along the former trapped bacteria. And light intensity gradient exists at the end of the bacterium with hemispherical caps. This intensity gradient can exert a gradient force to the coming bacterium. So the bacteria were trapped and connected to the former trapped bacteria one by one, realizing multiple bacteria trapping²². Also, the optical binding effect²³ resulting from the modification of optical field by the presence of trapped bacteria can also contribute to this multiple trapping.

Bacterium dynamics observation

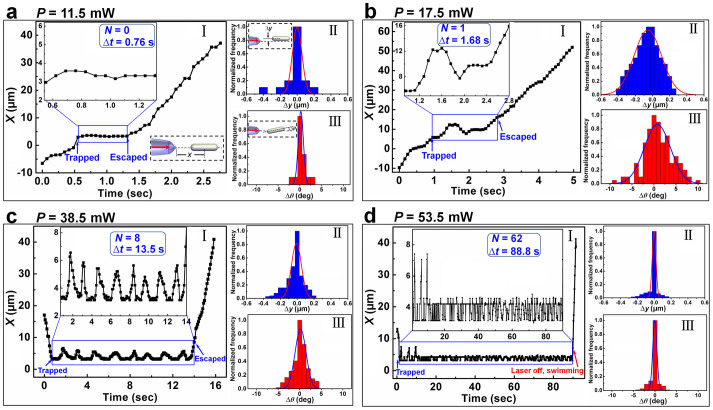
To observe the dynamics of a single bacterium, a series of experiments with different input optical powers (P) were performed. Results show that with different P, the trapped bacterium experienced different dynamic processes. For a small P, a single bacterium can be trapped, halted for about 0.1 ~ 1 s, and then escaped from the trapping. The reason for the escape is that the energy stored in the bacterium was released and converted into kinetic energy. So the bacterium was swimming away from the trapping. Figure 4a shows the dynamics of a bacterium in the trapping with P = 11.5 mW. At t = 0.55 s, the bacterium was trapped, and then halted for about Δt = 0.76 s in the potential well. At t = 1.31 s, the bacterium escaped from the trapping (Fig. 4aI). During the trapping, the variations of the Y displacement (Δy) and deflection angle (Δθ) is very small as shown in Fig. 4aII and III, respectively. Details of the dynamics are shown in Movie S2. As P was increased, a trapped bacterium first halted for about 0.1 ~ 1 s, then struggled for several rounds, and finally escaped from the trapping. Figures 4b and c shows the dynamics of a trapped bacterium with different struggling rounds numbers (N). With P = 17.5 mW (Fig. 4b), at t = 0.96 s, the bacterium was trapped and halted for about 0.16 s. At t = 1.12 s, the energy stored in the bacterium was released and converted into kinetic energy, and the bacterium was struggling in the potential well. After 1 struggling round, the bacterium escaped from the trapping (t = 2.64 s), with a total duration of Δt = 1.68 s in the trapping. Details of the dynamics are shown in Movie S3. With P = 38.5 mW (Fig. 4c), at t = 0.72 s, the bacterium was trapped and halted for about 0.56 s. At t = 1.28 s, the energy was released and converted, and the bacterium was struggling. Totally, the bacterium struggled with 8 rounds, and with duration of 13.5 s in the trapping. At t = 14.22 s, it escaped from the trapping. Details of the dynamics are shown in Movie S4. As P was further increased, after the energy released, the trapped bacterium cannot escape from the trapping. Figure 4d, as an example, shows the dynamics of a trapped bacterium with P = 53.5 mW. At t = 1.2 s, the bacterium was trapped and halted for about 0.5 s. At t = 1.7 s, the energy was released, and the bacterium began to struggle. 3 large struggling rounds with an average span of about 4.2 µm were firstly observed. Then the bacterium was continuously struggling in the trapping well, with an average span of about 1.1 µm. To verify that the trapping laser makes no harm to the motility of the bacterium, at t = 90 s, the laser was turned off and the bacterium swam away with an average velocity of 18.3 µm/s, indicating that the motility of the bacterium was not affected by the trapping laser. During the trapping, a total struggling rounds of N = 62 was experienced for the bacterium with a duration of 88.8 s. Details of the dynamics are shown in Movie S5. From the histograms in Fig. 4b–d, it can be seen that with the increase of optical power, the variations of Δy and Δθ are decreased, thus the trapping stability is increased. Note that the small variations of Δy and Δθ in Fig. 4a are resulting from the relatively short trapping duration (0.76 s).

Figure 4. Analysis of single bacterium dynamics in the non-contact trapping.

Panels I, II, and III in each figure show the X displacements as a function of time, histograms (and Gaussian fit) of Δy, and Δθ, respectively. (a) For optical power P = 11.5 mW, lower right and upper left insets in I show the schematic of X displacement and the enlargement of the X displacements in the trapping duration, respectively. The struggling rounds and trapping duration are N = 0 and Δt = 0.76 s, respectively. Insets in panels II and III show the schematic of Δy and Δθ, respectively. (b) For P = 17.5 mW, N = 1, and Δt = 1.68 s. (c) For P = 38.5 mW, N = 8, and Δt = 13.5 s. (d) For P = 53.5 mW, N = 62, and Δt = 88.8 s.

Overall, the dynamics of a bacterium in the non-contact trapping can be summarized as shown in Fig. 5. A swimming bacterium is firstly trapped by the modified tapered fiber, and then halted for about 0.1 ~ 1 s. After the halt, the energy stored in the bacterium is released and converted into kinetic energy. A critical optical power (P₁) exists for the dynamics. To any individual bacterium, for P < P₁, the bacterium will escape from the trapping after the energy release. For P ≥ P₁, the bacterium will struggle in the trapping potential well. We have performed experiments on a population of more than 100 bacteria with cell lengths changing from 1.4 to 3.2 µm. Fig. 6a shows the measured P₁ for bacteria with different cell lengths. For the bacteria with cell lengths changing from 1.4 to 3.2 µm, P₁ is in the range between 13.1 and 17.9 mW. After the struggling, a second critical optical power (P₂) exists for the dynamics. To any individual bacterium, for P₁ ≤ P < P₂, the bacterium will escape from the trapping after the struggling with several rounds. For P ≥ P₂, the trapping will be retained, and the bacterium will struggle in the trapping potential well continuously. The measured P₂ for bacteria with different cell lengths is in the range beween 47.3 and 52.2 mW (Fig. 6b).

Figure 5. Schematic of the bacterium dynamics in the non-contact trapping.

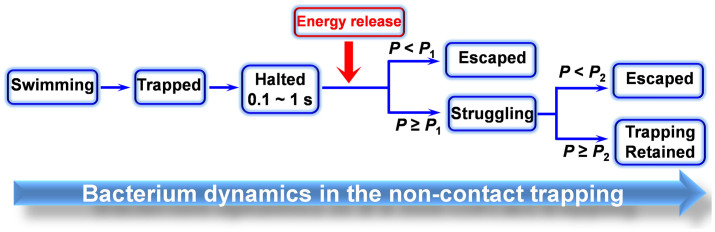
Different dynamic processes can be observed with different optical powers.

Figure 6. Statistical data on measurements performed on a population of more than 100 bacteria.

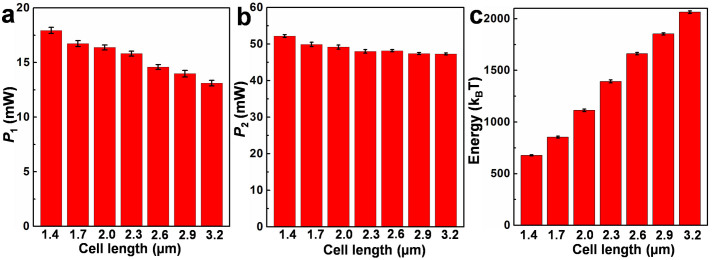
(a) Measured P₁, (b) measured P₂, and (c) estimated energy for bacteria with different cell lengths.

Energy estimation

Referring back to Fig. 1f and Fig. 1g, to escape from the trapping potential well, a minimum energy of ΔU_Max should be exerted on the trapped object. For the motile bacterium, to escape from the trapping, the energy to escape from the trapping is the kinetic energy. Thus the kinetic energy of an individual bacterium can be estimated from ΔU_Max and P₂. From the experimental results, P₂ is in the range between 47.3 and 52.2 mW for bacteria with cell lengths between 1.4 to 3.2 µm. By multiplying P₂ by ΔU_Max in Fig. 1g, the kinetic energy for bacteria with different cell lengths can be estimated and is shown in Fig. 6c. The estimated kinetic energy of the bacteria is in the range between 677.9 and 2063.6 k_BT (Fig. 6c).

Discussion

The above experimental results show that non-contact optical trapping of motile bacteria can be realized using a single modified tapered fiber. The elongated trap generated by the modified tapered fiber is suitable for trapping the needle like bacteria. It is easy to image the trapped particles from the side of the fiber axis, and gives the possibility to directly observe the movement and dynamics along the major axis of the fiber. While for the conventional optical tweezers, it is difficult to image the trapped particles from the side of the optical axis of the tweezers, and multiple tweezers may be needed for the direct observation of movement and dynamics of the motile bacteria. Although a lensed fiber can also realize the non-contact trapping of particles²⁴,²⁵,²⁶, there are three main advantages using our modified tapered fiber for non-contact optical trapping. First, the particles trapped by a lensed fiber are large in size (the reported results are for particles with diameter larger than 5 μm)²⁴,²⁵,²⁶, while for the modified tapered fiber tip used in our experiments, the particles (E. coli bacteria) are smaller in size (500 nm in diameter, and 1.4–3.2 μm in length). The smaller sized particles increase the difficulty for trapping and manipulation. Second, a lensed fiber is used for the trapping of immotile particles, while our modified tapered fiber can be used for the trapping of motile bacteria. The motility of the bacteria greatly increases the difficulty for trapping and manipulation. Third, the lensed fiber is difficult to trap multiple particles at the same time, while the modified tapered fiber can realize the trapping of multiple particles at the same time as shown in Fig. 3d. Although previously we have shown the optical trapping of bacteria using an optical nanofiber¹⁴ and a tapered optical fiber¹⁷, the trapped bacteria are in contact against the surface of the nanofiber and the tapered fiber tip. Compared to our previously results, there are two main advantages and novelties for the proposed method using a modified tapered fiber in this work. First, the trapped bacteria are without being in contact with the fiber surface, this greatly decreases the mechanical damage between the trapped bacteria and the fiber surface when directly contacted. Second, the dynamics of a motile bacterium can be directly observed in the trapping and the energy of the bacterium can be measured using the modified tapered fiber. These are previously impossible to realize using an optical nanofiber or a tapered optical fiber.

For the estimation of bacteria energy, recently Koch et al⁶. have demonstrated a time-sharing optical forces method using a line-scanning optical trap. Their obtained maximum energy for a helical bacterium, Spiroplasma melliferum, is about 200 k_BT. Comparing with their obtained results, the estimated energy of 677.9 to 2063.6 k_BT using our method is larger. There are two possible reasons for this difference. One is the different bacterial structures and sizes: Spiroplasma melliferum lacks a cell wall and flagella, with body thickness of about 200 nm, while the bacterium, E. coli, used in our method is a bacterium with cell wall and flagella, with body thickness of about 500 nm. The other is the scattering and absorption of light by the bacteria near the modified tapered fiber end. Due to this scattering and absorption, the optical power applied on the trapped bacterium in the experiments is smaller than that used in the simulation. And thus the actual value of bacterial energy is smaller than the estimated one. Note that although differences exist between the simulation model and experimental results, and the estimated energy may not exactly be the actual value, this estimation provides an approximate value of the E. coli bacterium energy. This is very beneficial for further investigation on the energetics of motile nanoscale organisms.

In summary, a strategy for non-contact optical trapping of motile bacteria using a modified tapered optical fiber was demonstrated. Both single and multiple motile bacteria can be trapped and manipulated using this non-contact optical trapping strategy. This provides a simple and handy method for the non-contact manipulation of motile nanoscale organisms. This strategy is further extended for the applications of single bacterium dynamics observation and energy estimation. The applications in bacterium dynamics observation and energy estimation may allow new insights into bacterial dynamics and energetics at the single cell level, and would be of great importance for the study of bacterial survival and the spread of bacterial diseases.

Methods

Fabrication of the modified tapered fiber

The modified tapered fiber was fabricated by applying a two-step method to a commercial single-mode optical fiber (connector type: FC/PC, core diameter: 9 mm, cladding diameter: 125 mm; Corning Inc.). The first step is called flame-heating technique. Before heating, the buffer and polymer jacket of the fiber were stripped off using a fiber stripper, and then the fiber was sheathed with a glass capillary (inner diameter: ~0.9 mm, wall thickness: ~0.1 mm, length: ~120 mm) to protect the fiber from breakage and warping. The fiber was first heated for approximately 1 min until its melting point was reached. Then, an initial drawing speed of 0.5 mm/s was applied to the heated fiber, and the diameter of the fiber was decreased from 125 µm to approximately 5 µm over a length of 2 mm to form a gradual taper. This was followed by a drawing speed of approximately 5 mm/s to form an abruptly tapered region. And the fiber was then broken to create a nano-tip at the end by applying a drawing speed of approximately 2 mm/s after the formation of the abruptly tapered region. The nano-tip at the end was formed by the surface tension of the melting fiber. The second step is to modify the tip. A drop of alcohol was firstly dropped on a piece of lens cleaning tissue (3 × 2 cm), and then the cleaning tissue was used to wrap the end of the tapered fiber with a nano-tip fabricated in the first step, and the nano-tip was then straightly pulled off. And finally, a modified tapered fiber was fabricated. Three typical images showing the modified tapered fiber fabrication process is shown in Fig. S4. Experimental results show that this two-step method for the modified tapered fiber fabrication is highly repeatable, different modified tapered fibers with similar shape and size can be fabricated using this method.

Suspension preparation

The E. coli (DH5α) bacteria were grown at 37°C in Lysogeny broth (LB), washed in phosphate buffered saline (PBS) buffer and resuspended in the PBS buffer (diluted with deionized water) to desired concentrations (bacteria density: ~1.5 × 10⁵ #/mL). To make sure the bacteria in a high-active condition, bacteria in the logarithmic phase were chosen and LB was added into the suspension. After preparation, the suspension was dripped by a pipette on the surface of a glass slide.

Author Contributions

B.L. supervised the project; H.X. and Q.L. performed the experiments; H.X. performed the simulation and calculation; H.X. and B.L. discussed the results and wrote the manuscript.

Supplementary Material

Supplementary Information

Supplementary Movie S1

Supplementary Information

Supplementary Movie S2

Supplementary Information

Supplementary Movie S3

Supplementary Information

Supplementary Movie S4

Supplementary Information

Supplementary Movie S5

Supplementary Information

Supplementary Information