Characterizing growth patterns in longitudinal MRI using image contrast

Abstract

Understanding the growth patterns of the early brain is crucial to the study of neuro-development. In the early stages of brain growth, a rapid sequence of biophysical and chemical processes take place. A crucial component of these processes, known as myelination, consists of the formation of a myelin sheath around a nerve fiber, enabling the effective transmission of neural impulses. As the brain undergoes myelination, there is a subsequent change in the contrast between gray matter and white matter as observed in MR scans. In this work, gray-white matter contrast is proposed as an effective measure of appearance which is relatively invariant to location, scanner type, and scanning conditions. To validate this, contrast is computed over various cortical regions for an adult human phantom. MR (Magnetic Resonance) images of the phantom were repeatedly generated using different scanners, and at different locations. Contrast displays less variability over changing conditions of scan compared to intensity-based measures, demonstrating that it is less dependent than intensity on external factors. Additionally, contrast is used to analyze longitudinal MR scans of the early brain, belonging to healthy controls and Down’s Syndrome (DS) patients. Kernel regression is used to model subject-specific trajectories of contrast changing with time. Trajectories of contrast changing with time, as well as time-based biomarkers extracted from contrast modeling, show large differences between groups. The preliminary applications of contrast based analysis indicate its future potential to reveal new information not covered by conventional volumetric or deformation-based analysis, particularly for distinguishing between normal and abnormal growth patterns.

1. INTRODUCTION

Understanding brain growth from birth to two years of age is crucial to the study of neuro-development and neurological disorders. During this time period, brain development consists of a sequence of rapid biophysical, structural, and chemical changes. Myelination, or the formation of a myelin sheath around nerve fibers, is an important component of the changes taking place in the early brain.¹ Myelination manifests in structural MR (Magnetic Resonance) images of the developing brain as changes in the intensity of white matter (WM) relative to gray matter (GM). These changes in MR appearance are captured in quantitative T1 and T2 values, and can be observed clearly in T1W (T1-weighted) and T2W (T2-weighted) scans.

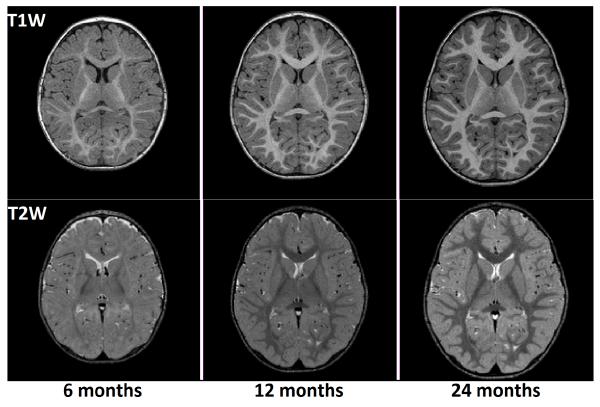
In MR (Magnetic Resonance) imaging, shortening of the T1 signal is hypothesized to occur due to the hydrophilic cholesterol and glycolipid components of the developing myelin sheath. T2 shortening is reported to occur at the time of tightening of myelin around the axon and may correlate best with the development of myelination determined based on histological methods.¹ As a result of WM myelination and the subsequent shortening of T1 and T2 relaxation times, it is observed that T1W (T1-weighted) MR images display increasing WM signal intensities with time, and T2W (T2-weighted) MR images display decreasing WM signal intensities as the brain develops during the first two years of age. At birth, the intensity of GM is higher than that of WM in T1W images, and the reverse is true for T2W images. With time, a reversal of the GM-WM intensity ratio takes place - i.e., the intensity of WM keeps increasing in T1W images, thereby exceeding the GM intensity, and in T2W images the intensity of WM keeps decreasing and becomes lower than that of GM. As a result of this, the white-gray contrast first decreases up to a time point between 3 and 6 months of age, and then increases up to 2 years. Therefore, it can be concluded that appearance changes of MR images are direct indicators of maturational processes taking place in the brain. The latter stage of contrast change, consisting of the increase in contrast from around 6 months to 2 years of age, can be seen in Figure 1, and will be the focus of this work.

Figure 1.

Axial slices of longitudinal, multimodal MR scans of a single subject from 6 months to 2 years of age.

Although several previous studies have dealt with changes in morphometry, shape, and microstructure of the early brain,^2-6 the use of appearance as an imaging measure has remained limited. The lack of extensive research based on image appearance could be primarily attributed to the fact that the intensities of MR scans are uncalibrated and hence result in images of variable intensity ranges. Appearance based research restricted to signal intensity changes in MR images of the pediatric brain demonstrated the rapid maturation process.^7,8 In one of these studies, the Gompertz function was used to model longitudinal changes in MR signal intensity over time.⁷ A second study modeled changes in the appearance of subcortical structures during early brain development in a cross-sectional manner,⁸ showing variable rates of maturation in central and peripheral cortical regions. A recent study used the relative intensity, or contrast, between gray matter and white matter to study patterns of regional brain growth.⁹ The contrast between gray matter and white matter was quantified by computing the Hellinger distance between their respective intensity histograms. When compared with using purely intensity to measure appearance, contrast was adopted as a metric in order to reduce dependence on external factors such as scanner type, scanning conditions, and intensity normalization.

The objective of this paper is to validate the application of this quantitative measure of contrast as a neuroimaging indicator of maturation. In this paper, we perform reliability analysis of contrast in comparison with conventional signal intensity measures. We show that for a single human phantom who has been scanned at different locations and time points, contrast remains relatively stable although the gray and white matter intensities are highly variable. This substantiates the statement that contrast as a metric is reliable even when external factors are changed at the time of scanning. Further, we compare the trajectories of contrast change for subjects with Down’s Syndrome (DS) and healthy controls. Finally, time-based biomarkers are extracted from the contrast change trajectories, demonstrating the clinical applicability of contrast in distinguishing patterns of normal and abnormal brain growth.

2. METHOD

The proposed method uses the Hellinger distance to measure the overlap between intensity distributions of gray and white matter.⁹ The Hellinger distance (HD) is a measure of the divergence between two distributions, derived from the Bhattacharyya coe cient (BC). It satisfies the properties of metrics such as identity, symmetry, non-negativity, and triangle inequality, therefore making it suitable for contrast computation compared with other measures. The intensity distributions for each tissue class are generated using Kernel Density Estimation (KDE). The measurement of overlap between these continuous intensity distributions is an improvement over the previous technique of measuring overlap between histograms.⁹ Intensity distributions generated by KDE are smooth and continuous, making them less susceptible to quantization errors than histograms.

Let I = (I₁, I₂,…I_M)^T denote a dataset of co-registered multimodal scans, such that I_i = (I_i,1, I_i,2, …I_i,M)^T is the intensity of the i-th voxel, observed across all M modalities. The images are first segmented such that each voxel is classified into one of the major tissue classes c = {white matter, gray matter, csf, non-brain}, and the probability of a voxel i belonging to a tissue class c_k is given by P_i,ck. This is done using the EM (Expectation-Maximization) algorithm, which performs segmentation with built-in intensity inhomogeneity correction.¹⁰ This segmentation algorithm also uses an atlas prior, which improves the classification scheme and makes it more robust, based on previous knowledge.¹¹ As a result of segmentation, the binary label map defining the presence or absence of a class c_k at a specific voxel location i is given by L_i,ck. When the voxel i is classified as belonging to class c_k, the corresponding label map value L_i,ck = 1, else L_i,ck = 0.

The intensity distributions for each tissue class c_k, are generated from the binary label map L_i,ck using KDE. Although segmentation is performed in a multimodal manner the intensity distributions are generated separately for each individual modality. In the experiment performed, we use a Gaussian kernel denoted by G for density estimation. The probability that a voxel belonging to the modality m and the tissue class c_k would exhibit an intensity I_j is given by:

$$P_m(I_j\mid c_k)=\frac{1}{h\sum _{i=1}^N{L}_{i,c_k}}\sum _{i=1}^N{L}_{i,c_k}\times G\left(\frac{I_j-I_{i,m}}{h}\right),$$ (1)

where there are a total of N voxels in the image, I_i,m refers to the intensity of voxel i in modality m, and h is the bandwidth of the kernel. Using KDE, a continuous probability distribution P_m(I|c_k) is generated for each class c_k, over all possible values of intensity I_j, for every modality m.

The Hellinger distance is then computed as the overlap between two probability distributions. The equation for the Hellinger distance as derived from the Bhattacharyya coe cient is defined in the following paragraph. The Bhattacharyya coe cient between two intensity distributions U and V defined over a range of y values is given by:

$$BC(U,V)={\int }_y\sqrt{U\left(y\right)V\left(y\right)}dy.$$ (2)

From the Bhattacharyya coe cient (BC) described above, the Hellinger distance (HD) can be defined as:

$$HD(U,V)=\sqrt{2(1-BC(U,V\left)\right)}.$$ (3)

Contrast, measured as the overlap between white and gray matter intensity distributions, is given as:

$$Contrast=HD\left(P\right(I\mid c=WM),P(I\mid c=GM\left)\right).$$ (4)

2.1 Validation of Contrast Measure using Traveling Phantom Dataset

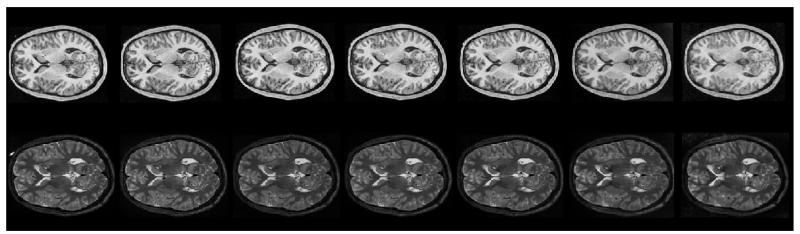
The traveling phantom study was designed to calibrate image data in a large multi-site pediatric neuroimaging study, and includes two subjects (Phantom 1 and Phantom 2), who have undergone repeated scans at various imaging sites. Two different scanners, a Siemens 3T Allegra head-only scanner, and a Siemens 3T Tim Trio were used in the study, to estimate the reliability of MR measures under changing conditions of scan.¹² The pulse sequences used were MPRage with 1 × 1 × 1 mm³ and high-resolution T2 (TSE) with 1 × 1 × 1 mm³. The two healthy male human phantoms of ages 26 and 27 were scanned at four different sites within a week. Two repeated scans of the same phantom were obtained at each site, using the same scanner, within 24 hours. The age of the phantom and health status, as well as the short time period between repeated scans, both indicate that subject-related changes were minimized. Since the entire image dataset for each phantom was acquired within a week, it is safe to assume that no major brain changes took place during this time period. The tuple of images belonging to each phantom p consists of a set of MR scans, attributed to different modalities, locations, time points, and scanners. Seven co-registered, multimodal scans of Phantom 1, obtained at 4 different scanning locations, using 2 different scanner types can be seen in Figure 2.

Figure 2.

Seven T1W (top row) and T2W (bottom row) scans of Phantom 1, across 2 scanner types and 4 locations. The scans are all co-registered, with the five leftmost scans belong to the Trio scanner, while the two rightmost scans belong to the Allegra scanner.

Initial pre-processing of the phantom images consisted of rigid registration to a template using the IRTK algorithm.¹³ This was followed by bias correction and tissue segmentation, which were both computed in an iterative manner as part of the EM algorithm.¹⁰ Prior to analysis of the traveling phantom images, we had to ensure that they were all co-registered in order to remove volumetric and morphometric differences. After co-registration by rigid transformation and bias correction, we created an unbiased atlas A_p from the set of T1W images from the Trio scans of Phantom p. Unbiased atlas building was done using an algorithm based on LDDMM (Large Deformation Diffeomorphic Metric Mapping).¹⁴ The T2W scans, and images belonging to the Allegra scanner were then deformed onto the atlas created using a fluid-based deformation method.¹² As a result of the steps described above, the images from all scanners, obtained at all time points and locations, belonging to a phantom denoted by p, were co-registered to the corresponding atlas A_p. After being co-registered, the entire tuple of images obtained for a single phantom p can be denoted by I_p, and the vector of intensities for a single voxel i is given by I_p,i. After atlas building, a parcellation map was registered to the generated atlas, and the major cortical regions were extracted. The final step in the processing pipeline consisted of intensity normalization of all images by linear scaling using the following normalization factors: (i) 90 percentile value of the fatty tissue region for T1W images, and (ii) 90 percentile value of the ventricular CSF region for the T2W images.

In order to measure the reliability of the contrast measure, we calculate the COV (Coe cient Of Variation) across all scans to obtain a normalized measure of variability. The COV of a quantity Q with mean value μ(Q), and standard deviation σ(Q) is given as:

$$COV\left(Q\right)=\frac{\sigma \left(Q\right)}{\mu \left(Q\right)}.$$ (5)

Since contrast is a regional measure, the COV of contrast is computed for each cortical region. Let the set of images belonging to phantom p obtained under different scanning conditions be denoted by I_p. The corresponding vector of contrast values for a region R of the brain is given by C_p,R. The COV of the contrast for a region R can be written as

$$COV\left({\mathrm{C}}_{p,R}\right)=\frac{\sigma \left({\mathrm{C}}_{p,R}\right)}{\mu \left({\mathrm{C}}_{p,R}\right)}.$$ (6)

In comparison with contrast, signal intensity measurements are computed in a voxel-wise manner, therefore leading to voxel-wise maps of COV. To obtain a regional estimate of the COV of signal intensity, we compute the mean COV of signal intensity averaged over all voxels in a distinct cortical region. As defined previously, for a set of images belonging to a phantom p, the voxel i has intensities denoted by I_p,i. The COV for the voxel i computed over the entire set of images is given by

$$COV\left({\mathbf{I}}_{p,i}\right)=\frac{\sigma \left({\mathbf{I}}_{p,i}\right)}{\mu \left({\mathbf{I}}_{p,i}\right)}.$$ (7)

From the above equation, the mean COV over all N_R voxels in a region R can be computed as

$$\overline{COV}\left({\mathbf{I}}_{p,R}\right)=\frac{{\Sigma }_{i\in R}COV\left({\mathbf{I}}_{p,i}\right)}{N_R}.$$ (8)

2.2 Application of Contrast Measure: Down’s Syndrome vs. Controls

In the following section, we outline the method for testing the contrast measure on an infant dataset. The pediatric dataset used comes from the ACE-IBIS study (Autism Centers for Excellence, Infant Brain Imaging study), of which 2 subjects diagnosed with Down’s Syndrome, and 22 healthy controls, are analyzed. The dataset consists of longitudinal scans of each subject, taken at 6 months, 1 year, and 2 years of age. All the scans in the dataset were generated using the same imaging protocols. The pre-processing procedure described above was also followed here, consisting of bias correction, co-registration of images, segmentation using the EM algorithm, and parcellation into cortical regions. An improved registration-segmentation pipeline for processing of longitudinal, infant brain images was implemented. Intra-subject registration was performed such that all images belonging to a subject are deformed to the 2 year old scans of that particular subject using IRTK.¹³ Since gray-white matter structures are not fully developed at 6 and 12 months of age, the result of the two-year-old segmentation is used as a probabilistic prior to obtain a better segmentation at earlier time points.¹¹

Contrast for the major cortical regions was computed at each time point of scan, and subject-specific trajectories of contrast change were obtained using kernel regression. The contrast value at time instant t for a subject s is given by:

$$C_s\left(t\right)=\frac{{\Sigma }_{t_{s,k}}K(t,t_{s,k})C_s\left(t_{s,k}\right)}{{\Sigma }_{t_{s,k}}K(t,t_{s,k})},$$ (9)

where s = subject, time of kth scan of sth subject = t_s,k, Contrast for subject s at t_s,k = C_s(t_s,k).

Once the individual trajectories of contrast change were generated, it was necessary to extract time-based biomarkers that can intuitively describe specific features that characterize populations. A time based biomarker τ was derived from the trajectories of contrast change, given by

$$\tau =\underset{t}{\min }{C}_s\left(t\right)\ge 0.5max\left(C_s\right).$$ (10)

This time marker indicates the minimum time at which the value of contrast reaches half that of the maximum value.

3. RESULTS

The following experiments will a) evaluate the variability of contrast as compared to MRI intensity values and b) demonstrate the use of contrast to compare early growth patterns in different populations.

3.1 Travelling Phantom Study

As described in the previous section, 2 phantoms were scanned repeatedly using 2 different scanners (Allegra and Trio), at 4 different locations. We apply the processing pipeline and the registration framework described above to the scans belonging to each phantom. The Coe cient Of Variation (COV) for contrast in each region R is computed. The mean COV for intensity in each region R is also computed, by averaging the voxel-wise COV over all voxels in the region R.

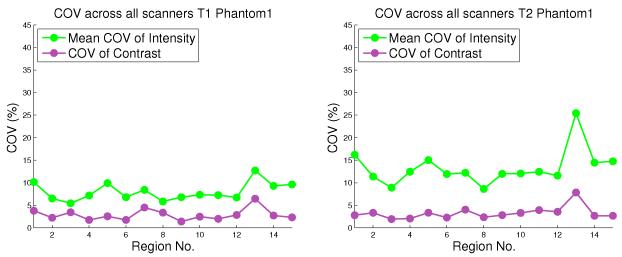
The results of the phantom experiment show that with changing external scanning conditions and scanner type, the COV of contrast is significantly lower than the mean COV of intensity values. This is illustrated in Figure 3, which shows the relative stability of contrast when external factors such as scanner type, locations, and conditions of scan are varied. Since the COV is analyzed in a region-wise manner, it is shown for each of the 15 lobar parcellation regions. In most regions of the brain the regional COV of contrast lies between 2 and 5 percent. Therefore, any changes in contrast across scans that lie in a much higher range can be predominantly attributed to actual changes in the appearance of images rather than to artifacts due to scanning conditions. In comparison, the mean COV of intensity for a region is much higher, ranging between 5 and 10 percent for T1W scans, and between 10 and 20 percent for T2W scans.

Figure 3.

The COV values of contrast, and Mean COV values of intensity, plotted for T1W (left) and T2W (right) scans belonging to Phantom 1, for 15 brain regions.

3.2 Early Brain Development: Down’s Syndrome vs. Controls

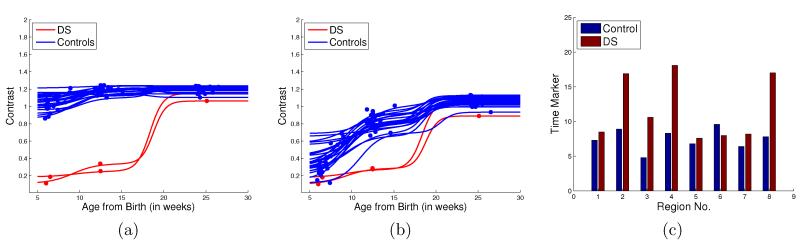
In early brain development, contrast is initially low and shows a period of rapid growth, followed by relatively slower growth. The results of computing contrast values across time using kernel regression are shown in Figure 5. The contrast values were computed across all lobes, although only the values in the occipital lobe are displayed. Previous studies have established that DS subjects show slower myelination when compared to healthy controls.¹⁶ The differences in contrast change trajectories between DS and controls are very apparent, and show that contrast has potential uses in the early diagnosis and study of brain abnormalities.

Figure 5.

Figures from left to right: a) and b) show contrast change for T1W and T2W scans in the Occipital Lobe in the left hemisphere, c) plots time-based biomarkers for T2W scans belonging to one subject each from the DS and Control groups. In c), the X-axis indicates 8 major cortical lobes give by: Frontal L (Left) = 1, Temporal L = 2, Parietal L = 3, Occipital L = 4, Frontal R (right) = 5, Temporal R = 6, Parietal R = 7, Occipital R = 8.

Several statistical markers can also be extracted from the modeling of contrast. Figure 5 displays the time-based marker τ defined earlier, which computes the time taken to reach half the maximum value, but several other markers could also be derived from the contrast curves.

4. CONCLUSIONS

The above research establishes that contrast may serve as a measure which provides new information on tissue properties that is complementary to conventional volumetric assessment. The contrast variations across different locations and scanning conditions were seen to be lower than that of intensity. In addition, contrast was modeled across time for each major cortical region using kernel regression. A major limitation of applying kernel regression to the longitudinal infant brain dataset used, is that the images belonging to each subject were obtained repeatedly at only a limited number of time points.¹⁵ However, kernel regression was still used due to its flexibility and applicability to both groups that were studied. Contrast showed distinct trajectories of variations with time for healthy controls and subjects diagnosed with Down’s Syndrome. Time based biomarkers that were extracted also showed interesting patterns of variation between the two groups. Future work will include extending the current applications of contrast studies to large databases, correlating contrast features with cognitive and behavioral scores, and performing in-depth statistical analysis of these features.

Figure 4.

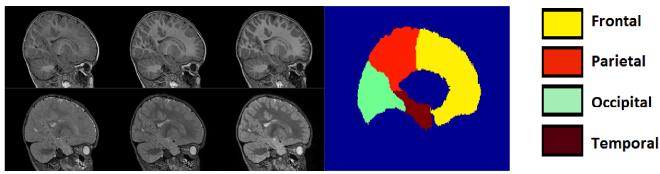
Longitudinal T1W (top) and T2W (bottom) MR images scanned at age 6, 12, and 24 months (from left to right). The brain parcellation with major lobar regions are shown as a color image on the right.