Calibration of Quality-Adjusted Life Years for Oncology Clinical Trials

Abstract

Context

Quality-adjusted life year (QALY) estimation is a well-known but little used technique to compare survival adjusted for complications. Lack of calibration and interpretation guidance hinders implementation of QALY analyses.

Objectives

We conducted simulation studies to assess the impact of differences in survival, toxicity rates, and utility values on QALY results.

Methods

Survival comparisons used both log-rank and Wilcoxon testing. We examined power considerations for a North Central Cancer Treatment Group Phase III lung cancer clinical trial (89-20-52).

Results

Sample sizes of 100 events per treatment have low power to generate a statistically significant difference in QALYs unless the toxicity rate is 44% higher in one arm. For sample sizes of 200 per arm and equal survival times, toxicity needs to be at least 38% more in one arm for the result to be statistically significant, using a utility of 0.3 for days with toxicity. Sample sizes of 300 (500)/arm provide 80% power if there is a 31% (25%) toxicity difference. If the overall survival hazard ratio between the two treatment arms is 1.25, then samples of at least 150 patients and 13% increased toxicity are necessary to have 80% power to detect QALY differences. In study 89-20-52, there was only 56% power to determine the statistical significance of the observed QALY differences, clarifying the enigmatic conclusion of no statistically significant difference in QALY despite an observed 14.5% increase in toxicity between treatments.

Conclusion

This calibration allows researchers to interpret the clinical significance of QALY analyses and facilitates QALY inclusion in clinical trials through improved study design.

Introduction

Quality-adjusted life years (QALYs) are a method of comparing treatment arms in clinical trials that combines survival time, time after cancer progression, and days with toxicity. The QALYs combine these three endpoints into one measure that can be tested using standard survival analysis methods. First proposed in 1989 by Gelber et al,¹ this method held intuitively appealing promise to combine quality and quantity of survival. The QALYs assume that days with high toxicity levels (such as days with any Grade 2 or higher adverse events) and days after cancer progression are not as valuable to the patient as days without toxicity or progression. These days are counted as less than one day of survival.

A comprehensive review of QALY literature can be found in Tsuchiya and Dolan.² Methodological considerations for incorporating quality of life (QOL) data into the QALY model are discussed in Revicki et al³ and Mounier et al.⁴ Previously, we have proposed methods for summarizing QALY data graphically.⁵

There are numerous examples of successful implementation of QALY estimates in clinical trials. For example, women who test positive for BRCA1/2 mutations in the U.S. may experience greater QALYs from prevention strategies.⁶ Among patients with non–small-cell lung cancer in Canada, it was demonstrated that adjuvant chemotherapy produced superior QALY estimates.⁷ In Europe, patients with sepsis who were treated with intensive care reported improved QALYs.⁸

The recent focus by health care policy and regulatory agencies on comparative effectiveness and cancer care delivery research would suggest that QALY estimates and analyses based on QALYs could contribute much to decision-making processes.⁹ The U.S. Public Health Service Panel on Cost-Effectiveness has recommended the use of QALYs as the best way to estimate outcomes in a cost-effectiveness analysis. The law enacting the Patient-centered Outcomes Research Institute (PCORI), however, explicitly forbids the PCORI from using cost per QALY as a decision-making tool, and cites the methodological, political, and interpretational challenges. The executive director of the PCORI (P. Selby) indicated that the QALY estimates themselves remain a valid and viable method for analysis. Lipscomb et al¹⁰ summarized the problems with QALY estimates as being related to methodology, assumptions, and interpretation while indicating that QALYs remain a natural benchmark for preferencebased approaches. Meta-analytic summaries of studies that have used QALYs, however, have empirically suggested that the method may be inadequate for capturing the vital QOL issues quantitatively.¹¹

The major barrier to the routine use of QALYs in clinical research is one of calibration.³ Specifically, it is difficult to define how much of a difference in QALYs is clinically meaningful. This clinical significance could be in relation to the patient, clinician, payer, or society. Among the key data needed to define clinical significance is the variability of the metric. To gain that understanding, one needs to be able to express statements of power regarding observed changes in QALYs so that the clinical meaning of a statistically significant value can be interpreted.

Although there is research dealing with the choice of the weights and defining clinical significance of QALYs, the power of QALY analyses has not been thoroughly explored. This manuscript explores the power of QALY analyses using simulations and calculates the power associated with a published clinical trial that used a QALY analysis.

QALY Definition

The QALY analyses involve partitioning the survival time for each patient into three parts, namely time without symptoms or toxicity (TWiST), time with high levels of toxicity (TOX), and time after disease progression or relapse (REL). The overall survival time (OS) for a patient can then be written as:

• OS = TOX + TWiST + REL

Days with toxicity and days after relapse are considered to be of less value than other days and are given less weight in the analyses. For example, days with high levels of toxicity may be counted as only half as good as a day without toxicity. The TOX and REL days are weighted by utilities to come up with the final QALYs for each patient:

• QALY = U_t·TOX + TWiST + U_r·REL

where U_t = utility for days with toxicity (between zero and one) and U_r = utility for days after relapse (between zero and one).

The differences in these QALYs can then be tested between treatment arms using standard survival analysis methods such as log-rank tests, Kaplan-Meier curves, and Cox proportional hazards models.

For a general overview of QALYs and a discussion of different methods of selecting utilities, see the monograph by Sloan et al.¹² A discussion of QALY application models in cancer is found in Cole et al.¹³ and a recent discussion of clinically important differences and QALYs is found in Revicki et al.³ Kilbridge¹⁴ provides a review of the current use of QALYs in oncology (health care), and their methodological limitations are discussed by Garau et al.¹¹

Methods

Simulations

Simulations were run using SAS 9.2 (SAS Institute, Inc., Cary, NC) assuming a Weibull distribution of survival times with constant failure rates over time. No censoring was used in the simulations, so all sample sizes in this article must be interpreted as the number of events in the study. Days with toxicity and days after progression were given the same weights and not simulated separately for the sake of simplicity without loss of generality. There is also no strong evidence that days with toxicity and days after relapse should be weighted with different utilities.¹³ Study design parameters were varied to explore their effects on the subsequent power. Parameters included utility scores (0 to 1 by 0.1), number of events (50, 100, 150, 200, 300, 500, and 1000 per group), hazard rates (HRs: 0.5, 0.75, 1.0, 1.25, and 1.5), and toxicity rate differences (assuming 10% of days in one arm have toxicity and simulating 10–100% toxicity in the other arm).

Between 1000 and 10,000 replications were done with each set of parameters depending on the sample size. The number of replications was constrained for larger sample sizes because of computer memory limitations. Table 1 shows the number of replications performed for each sample size and the resulting standard errors of the estimates. Power to detect a difference (effect size) between treatment arms for survival was based on the percentage of replications with a log-rank P-value less than 0.05, with separate analyses based on a Wilcoxon P-value less than 0.05. Power was calculated for the log-rank test of the hypothesis that the survival distributions in two populations are equal. The power is the probability of declaring a significant difference in QALYs between groups given that there truly is a difference. We assumed a Type I error rate of 5%.

Table 1.

Simulation Margins of Error for Each Sample Size

Sample Size Per Group	Number of Simulations	SE for a 5% Observed Power Result	SE for a 50% Observed Power Result	SE for an 80% Observed Power Result	SE for a 90% Observed Power Result
50	10,000	0.002	0.005	0.004	0.003
100	5000	0.003	0.007	0.006	0.004
150	5000	0.003	0.007	0.006	0.004
200	5000	0.003	0.007	0.006	0.004
300	3000	0.004	0.009	0.007	0.005
500	2000	0.005	0.011	0.009	0.007
1000	1000	0.007	0.016	0.013	0.009

SE = standard error.

Results

Power Relation to Utility for a Given Sample Size

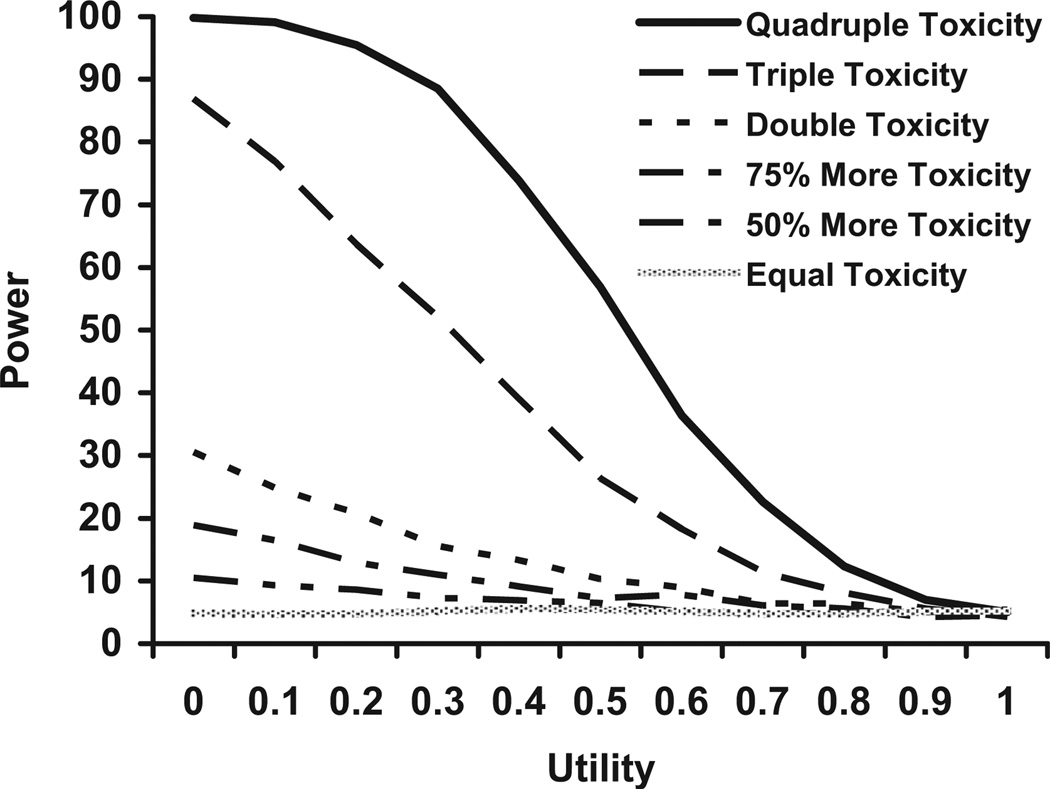
Fig. 1 shows power estimates for utilities varying from zero to one for a trial with 300 events in each group and an HR of 1.00 (no differences in survival). The simulation data for this figure assumed that 10% of a patient’s days had toxicity on one arm and the second arm had toxicity rates varying from being equal with the first arm to having quadruple the amount of toxicity (40%).

Fig. 1.

Power for n = 300 per group, HR = 1.0, 10% toxicity in the reference arm, and varying the toxicity rate in the other arm.

For small-to-moderate differences in toxicity (up to triple the rate in the first treatment arm) with a sample of 300 patients, 80% power is never achieved regardless of the value of the utility used. If the toxicity in one arm is triple the other (30% vs. 10%), the days with toxicity/postrecurrence would have to be reduced to U_t = 0.12 to achieve 80% power. Even with a quadrupling of toxicity, utilities need to be set to 0.4 or less to achieve 80% power. Hence, for a trial of this size (n = 300 events per group), for a QALY analysis to have 80% power to detect a difference between arms, the utilities would have to be very low even in the presence of substantial toxicity differences.

Table 2 shows the differences needed in toxicity rates to achieve a power of 80% as the sample size and utility vary. These results show that even for large sample sizes (n = 1000) and low utility values (U_t), the toxicity rate has to triple to have a good chance of finding a statistically significant result.

Table 2.

Smallest Difference in Percent of Days With Toxicity Needed For 80% Power With HR = 1.00 and 10% Toxicity in One Arm

N Per Group	Ut = 0.0	Ut = 0.1	Ut = 0.2	Ut = 0.3	Ut = 0.4	Ut = 0.5	Ut = 0.6	Ut = 0.7
50	—	—	—	—	—	—	—	—
100	Quadruple (40%)	—	—	—	—	—	—	—
150	Quadruple (40%)	Quadruple (40%)	—	—	—	—	—	—
200	Quadruple (40%)	Quadruple (40%)	Quadruple (40%)	—	—	—	—	—
300	Triple (30%)	Quadruple (40%)	Quadruple (40%)	—	—	—	—	—
500	Triple (30%)	Triple (30%)	Triple (30%)	Quadruple (40%)	—	—	—	—
1000	Triple (30%)	Triple (30%)	Triple (30%)	Triple (30%)	Triple (30%)	Quadruple (40%)	Quadruple (40%)	—

HR = hazard rate.

Missing cells mean that the toxicity rate has to be more than four times higher to reach 80% power.

Power Relation to Sample Size for Given Utilities

Tables 3–5 show the power of log-rank tests using QALYs with varying values of sample sizes, HRs, and differences in toxicity levels. These tables are based on a utility value of 0.5 and assume 10% of the days in one arm have toxicity or relapse. Fig. 2 shows power estimates by the HRs of the arm that had more toxicity. This figure is based on using a utility weight of 0.3 and twice as much toxicity in one arm.

Table 3.

Power for QALY Test of Equality for Utility = 0.5 and HR = 1.00 and a Basic Toxicity Rate of 10% in One Arm

	Difference in Percent of Days With Toxicity
N Per Group	Equal (10% of Days)	50% More (15% of Days)	75% More (17.5% of Days)	Double (20% of Days)	Triple (30% of Days)	Quadruple (40% of Days)
50	5	6	6	6	9	14
100	5	6	6	7	13	24
150	5	6	7	8	17	31
200	5	6	7	8	20	41
300	5	7	7	10	26	57
500	4	7	8	14	42	78
1000	4	8	12	22	72	98

QALY = quality-adjusted life year.

Values in bold indicate at least 80% power.

If the overall survival time is the same, you need a quadruple of toxicity rates (from 10% to 40%) and samples of 500 events to have 80% power to detect a difference in QALYs.

Table 5.

Power for QALY Test of Equality for Utility = 0.5 and HR = 1.50

	Difference in Percent of Days With Toxicity
N Per Group	Equal	50% More	75% More	Double	Triple	Quadruple
50	51	58	59	62	71	81
100	80	86	87	89	95	98
150	93	96	97	98	99	100
200	98	99	100	100	100	100
300	100	100	100	100	100	100
500	100	100	100	100	100	100
1000	100	100	100	100	100	100

QALY = quality-adjusted life year.

Values in bold indicate at least 80% power.

If the overall survival time hazard rate is 1.5, even a sample of 200 events per group will virtually guarantee a significant QALY test.

Fig. 2.

Power for double toxicity rate in one arm and utility of 0.3 for varying sample sizes and hazard rates.

If the OS is the same in both arms (HR = 1), a clinical trial would need a quadruple of the toxicity rate (from 10% to 40%) and observe 500 events per arm to have 80% power to detect a difference in QALYs. If the HR is 1.25, then a sample of 150 events per group will provide 80% power if the toxicity rates in the two arms are 10% and 30%. If the HR is 1.5, then even a sample size of 200 events per arm will virtually guarantee a significant QALY test for any difference in toxicity.

Power Relation to Percent of Toxicity in the Reference Arm for Given Sample Sizes, HRs, Utilities, and Differences in Toxicity Rates

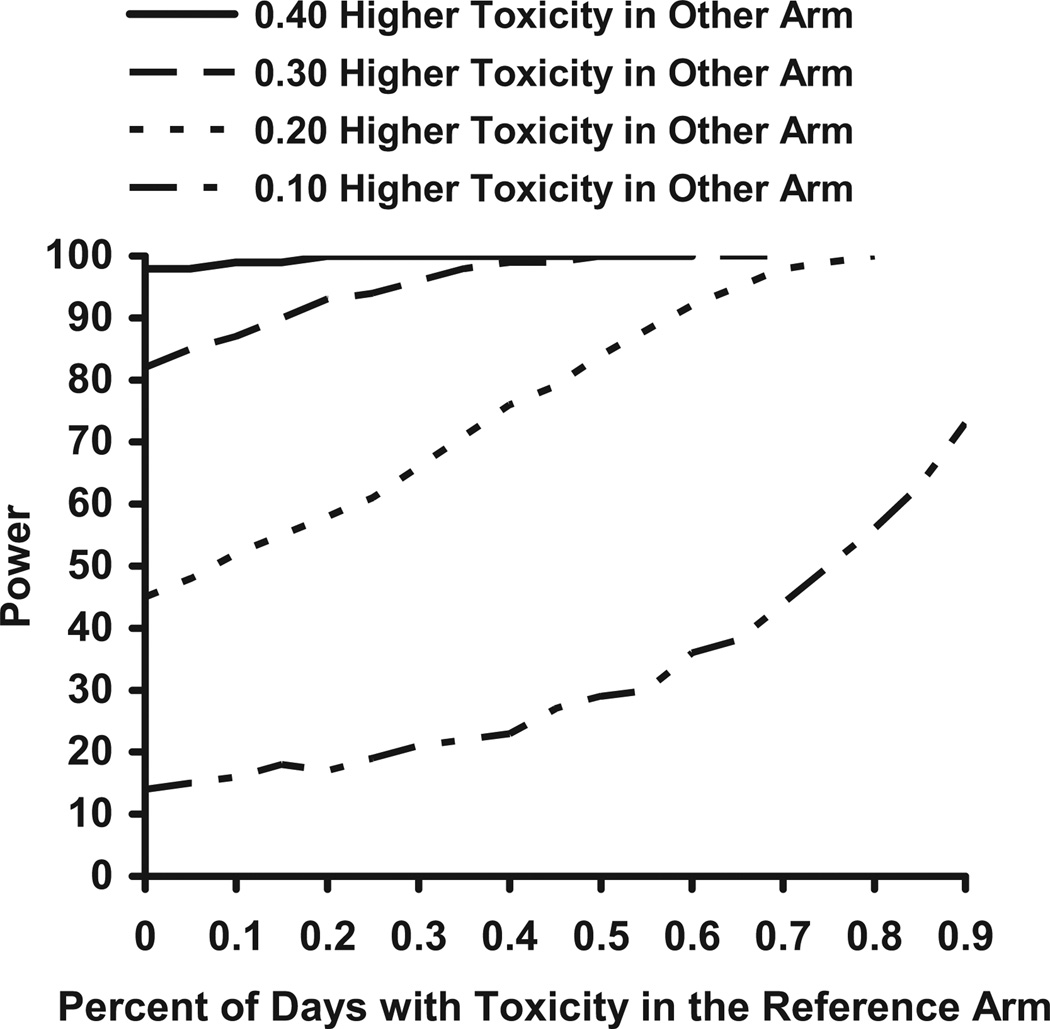
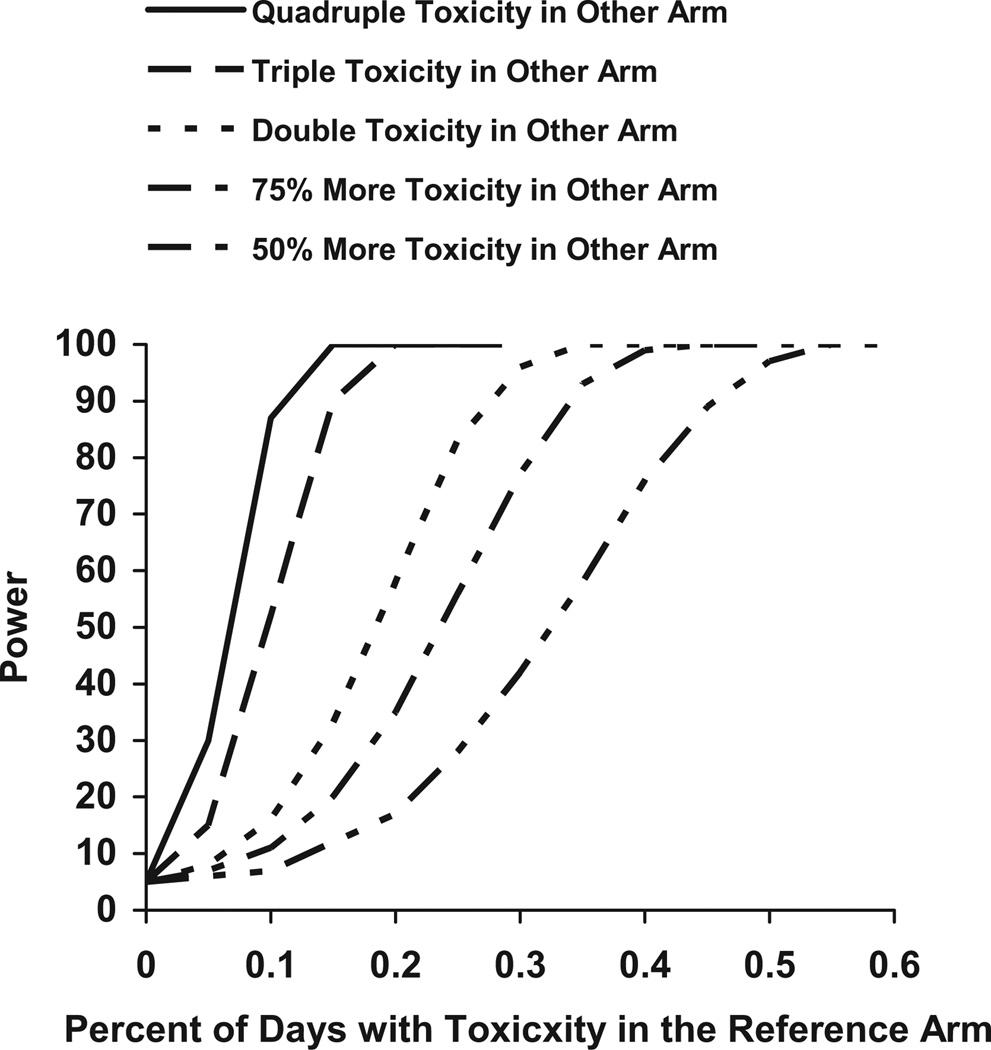
Figs. 3 and 4 show how power estimates change as the percent of days with toxicity in the reference arm increases. These figures assume that there are 300 events in each arm, a utility of 0.3, and an HR of 1.0. Fig. 3 shows power estimates as the toxicity rate in the second arm increases by 10%, 20%, 30%, and 40%. Fig. 4 shows the power estimates as the toxicity rate in the second arm increases by 50%, 75%, double, triple, or quadruple the toxicity rate in the first arm.

Fig. 3.

Power for n = 300 per group, HR = 1.0, and U_t = 0.3 for varying toxicity rates in the reference and other arm.

Fig. 4.

Power for n = 300 per group, HR = 1.0, and U_t = 0.3 for varying toxicity rates in the reference and other arm.

If the toxicity rate in the reference arm is between 0% and 40%, then QALY tests for a 10% difference in toxicity rates between two treatment arms will have almost the same power. The rate of toxicity in the reference arm has only a small impact on the resulting power. However, if the toxicity rate in the reference arm is more than 40% or the difference in toxicity rates is more than 10%, then the toxicity rate in the reference arm will affect the power. If the toxicity rate in the reference arm is low (about 10%), then it takes a large difference in toxicity rates (at least 30% or a tripling of toxicity) to have 80% power. If the toxicity rate in the reference arm is high (60%), then the difference in toxicity rates has to only be 20% points higher to reach 80% power.

Differences in Percent of Days With Toxicity Needed to Obtain Significant Results

Table 6 shows the differences in toxicity needed to achieve 80% or 90% power. These results assume that one arm has 10% of its days with toxicity and a utility of 0.3. If the HRs are the same in the two arms, there needs to be a very large difference in toxicities to obtain 80% power. With 100 events in each arm, 80% power is achieved if the difference in HRs is 44%. If the HR is 1.25, then sample sizes of 200–300 provide adequate power for a trial. With an HR of 1.5 or higher, any sample size of at least 100 and any difference in toxicities will likely result in a significant difference in QALYs.

Table 6.

Difference in Toxicity Rate Needed for 80% or 90% Power With U_t = 0.3 and 10% Toxicity in One Arm

	80% Power			90% Power
N Per Group	HR = 1.00	HR = 1.25	HR = 1.50	HR = 1.00	HR = 1.25	HR = 1.50
50	59	40	20	65	48	31
100	44	22	0	50	29	8
150	38	13	0	42	18	0
200	33	8	0	38	14	0
300	28	2	0	31	5	0
500	22	0	0	25	0	0
1000	16	0	0	19	0	0

HR = hazard rate.

For n = 100 per group, a hazard rate of 1, and 10% of days with toxicity in one arm, the other arm would need to have a 44% higher toxicity rate (or 54% of days with toxicity) to have 80% power of finding a significant differences between the two arms.

Differences in Percent of Days With Toxicity Needed to Dampen a Significant Survival Difference

Table 7 shows the differences in toxicity needed to achieve 10% or 20% power. With these low power levels, a study can have a non-significant QALY result even if there is a significant difference in survival between the two arms. These results assume that one arm has 10% of its days with toxicity and a utility of 0.3. With 150–300 events in each arm and an HR of 0.75, the QALY result will have low power if there is about 20% more toxicity in the arm with better survival times.

Table 7.

Difference in Toxicity Needed To Get Below 10% or 20% Power With U_t = 0.3 and 10% Toxicity in One Arm^a

N Per Group	10% Power		20% Power
	HR = 0.50	HR = 0.75	HR = 0.50	HR = 0.75
50	56	16	47	4
100	60	23	54	13
150	61	25	56	18
200	62	26	58	20
300	63	28	60	23
500	64	28	61	26
1000	65	31	64	29

HR = hazard rate.

For n = 100 per group, if one arm has 10% of days with toxicity and the other arm has a lower hazard rate of 0.50 but 60% more days with toxicity (a total of 70% of days with toxicity), then there is only a 10% chance that the results will be significantly different. Therefore, the study will likely report no difference in QALYs although the overall survival rate is lower in one arm.

^aLikely to report no significant difference between groups even with one arm having a lower hazard rate because it also has more toxicity.

Reanalysis of the North Central Cancer Treatment Group Study 89-20-52

Simulations can be used to determine the observed power for a completed clinical trial. The North Central Cancer Treatment Group study 89-20-52 was a blinded study of once vs. twice daily radiation in patients with small-cell lung cancer.¹⁵ The QALY analysis for this study showed no significant difference between arms although there was a large difference in toxicities. Details of this analysis are available in Creagan et al.¹⁵ or Sloan et al.¹²

In this study, the sample sizes in each arm were both about 130, both arms had about 10% of patients with censored survival times, and the HRs in the two arms were similar (HR not significantly different from one). However, patients receiving twice daily radiation had toxicity on 54% of their survival days, whereas patients in the other arm had toxicity on only 39% of their days. Based on simulations (Table 8), this study had only 56% power to detect a significant difference in QALYs. The simulations likely explain why the QALY difference was nonsignificant although the toxicity differences between arms were large.

Table 8.

Power for QALY in Study 89-20-52 for Varying Survival Hazard Rates (HRs) and Utilities

HR	Ut = 0.0	Ut = 0.3	Ut = 0.5	Ut = 0.7
0.50	90	99	100	100
0.75	6	20	32	45
1.00 (Observed HR)	56	22	11	7
1.25	97	82	68	57
1.50	100	99	97	94
1.75	100	100	100	100
2.00	100	100	100	100

QALY = quality-adjusted life year.

Values in bold indicate no survival difference.

No comparisons approached statistical significance because power for QALY differences was insufficient in this study.

Appendix (available at jpsmjournal.com) provides SAS code that can be used to explore the power of a QALY analysis for any study.

Discussion

The algorithm developed herein can be used to design QALY-based studies with appropriate (realistic) power and effect sizes, and is useful for reviewing the observed power of completed clinical trials. These simulations provide general guidelines that are helpful for designing future QALY studies.

The simulation results indicate that relatively large sample sizes are needed for designing QALY studies with a reasonable likelihood of detecting statistically significant differences. If double or triple the toxicity in one arm relative to another is expected, the study will need to accrue in excess of 1000 patients if there is no expected survival difference (e.g., if the goal is to demonstrate a QALY difference in a noninferiority trial). If the HR is 1.25 or greater, then sample sizes of 200 or 150 are needed to detect a significant difference if the toxicity rates are double or triple, respectively. To obtain significant results, utilities must be small, with values between 0.3 and 0.5 working reasonably well. If the HR is 1.5 or greater and the sample size exceeds 50 per arm, any utilities and any differences in toxicities will provide at least 80% power. In this case, there is no benefit in using QALYs. Large differences in toxicity rates are needed if the percentage of days with toxicity in the reference arm is small. The conclusions are similar if the Wilcoxon P-value is used instead of the log-rank P-value.

Results also indicated that the definition used for duration of toxicity has a huge impact on the design sensitivity and results of QALY studies. There are numerous alternative definitions that can be used to reflect either acute short-term toxicity or lingering long-term toxicity. Some authors have assumed that every incidence of toxicity lasted three months; others, including ourselves, assumed a more modest one cycle of impact as a result of any reported toxicity. This assumption by itself constrains the sensitivity of QALY models, but realistic assumptions need to be included in the model for its ultimate veracity.

These results have implications for QALYs in health care research. Based on our simulations, QALYs cannot be expected to be significantly different between two treatments unless there are large differences in either HRs or toxicities. Perhaps another metric can be created to generate results that better match intuition. For example, if having twice the toxicity rate is considered clinically meaningful, then QALYs should be set up to detect that. Future QALY research studies need to keep these power considerations in mind. There is also a need to refine the QALY parameters to bring the math in line with clinical perspective. If doctors are seeing a clinically meaningful difference in toxicities, the QALYs need to be adjusted to detect those differences. Until QALY models can more accurately reflect the clinical reality, they will remain a rarely used and poorly understood analytic method.

Table 4.

Power for QALY Test of Equality for Utility = 0.5 and HR = 1.25

	Difference in Percent of Days With Toxicity
N Per Group	Equal	50% More	75% More	Double	Triple	Quadruple
50	20	24	26	28	38	49
100	34	44	45	50	64	79
150	48	58	62	66	83	93
200	60	70	74	78	91	98
300	78	85	90	92	98	100
500	94	97	99	99	100	100
1000	100	100	100	100	100	100

QALY = quality-adjusted life year.

Values in bold indicate at least 80% power.

If the overall survival time hazard rate is 1.5, then a sample of 150 events per group will provide 80% power if the toxicity rates in the two groups are 10% and 30%.

Appendix

SAS Program to Calculate QALY Power for a Two-Arm Study

/****************************************************/
/* this program finds the power for a QALY analysis */
/* written by Paul Novotny 8/2010                   */
/* run with ‘sas memsize 128’ or more memory        */
/****************************************************/
options nonotes;

/*******************************************/
/* sets the parameters for the simulations */
/*******************************************/
%let reps=5000;      /* number of simulations */
%let size1=132;      /* events on arm 1 */
%let size2=130;      /* events on arm 2 */
%let ptox1=0.394;    /* percent of days with TOX/REL on arm 1 */
%let ptox2=0.539;    /* percent of days with TOX/REL on arm 2 */
%let pcensor1=0.10;  /* percent of patients with censored times on arm 1 */
%let pcensor2=0.10;  /*  percent of patients with censored times on arm 2 */

/************************************************/
/* calculates the observed power of a QALY test */
/************************************************/

data master (keep=hr2 ut nsample qtwist status group);
   call streaminit(0);                  /* initializes the randomization seed  */
   do hr2= 0.50,0.75,1,1.25,1.5,1.75,2; /* hazard rates in the second arm      */
   do ut = 0 to 1 by 0.1;               /* utility for each day of toxicity/REL */
   do nsample = 1 to &reps;             /* number of repeated samples    */

      %macro sim(group,hr);
         group=&group;
         do nsize = 1 to &&size&group;    /* sample size: number of observations in the group */
            b=l/&hr;              /* hazard rate for this arm */
            pcttox=&&ptox&group;  /* percent of time with tox on this arm */
            x=rand('WEIBULL',1,b); /* generates the random survival time */

            /*******************************************************/
            /* creates the censoring variable                      */
            /* assumes censoring is not related to survival time   */
            /* status=1 for deaths and status=2 for censored times */
             /*******************************************************/
            status=1;
            fu_time=x;
            u=rand('UNIFORM');
            if (u<&&pcensor&group) then do;
               u=rand('UNIFORM');
               fu_time=x*u;
               status=0;
            end;
            /***************************/
            /* creates the QTWIST time */
            /* and QALYs               */
            /***************************/
            tox=fu_time*pcttox;
            twist=fu_time-tox;
            qtwist=ut*tox+twist;

            label hr2=’HR in second arm’
                  ut=’Utility for TOX/REL days’
                  nsample=’Simulation Number’
                  qtwist=’Q-TWiST’
                  status=’Survival Status: l=Dead, 2=Censored’
                  group=’Arm’;
            output;
         end;
      %mend;

      %sim(1,1);    /* simulates the data for arm 1 with HR=1 */
      %sim(2,hr2);  /* simulates the data for arm 2 with HR=hr2 */
      end;
      end;
      end;
      run;

/********************************************************/
/* calculates the log-rank p-values for each simulation */
/********************************************************/
proc lifetest data=master outtest=pvalues noprint;
   time qtwist*status(0);
   test group;
   by hr2 ut nsample;

/* pulls off only the log-rank p-values from the output */
data pvalues (drop=group _NAME_);
   set pvalues;
   if (_NAME_='qtwist') & (_TYPE_='LOG RANK');
   pvalue=1-probchi(qtwist,1);

/* determines if the log-rank p-value is < 0.05 */
data p2 (keep=hr2 ut nsample plog siglog);
   set pvalues;
   by hr2 ut nsample;
   if (first.nsample) then plog=pvalue;
   if (.<plog<0.05) then siglog='Y';
                    else siglog='N';
   if (last.nsample) then output;
   retain plog siglog;

/* determines the percentage of samples that were significant */
proc freq data=p2 noprint;
   table siglog / missprint out=d;
   by hr2 ut;

data d;
   set d;
   if (siglog='Y');
   pctlog=count/&reps*100;

/*************************************/
/* outputs the power by each utility */
/*************************************/
data p2;
   set d;
   by hr2 ut;
   if (first.hr2) then do;
      ut00=0; ut01=0; ut02=0; ut03=0; ut04=0; ut05=0; ut06=0; ut07=0; ut08=0; ut09=0; utl0=0; end;

   if (ut<=0.050)      then ut00=pctlog;
   if (0.05<ut<0.15)   then ut01=pctlog;
   if (0.15<ut<0.25)   then ut02=pctlog;
   if (0.25<ut<0.35)   then ut03=pctlog;
   if (0.35<ut<0.45)   then ut04=pctlog;
   if (0.45<ut<0.55)   then ut05=pctlog;
   if (0.55<ut<0.65)   then ut06=pctlog;
   if (0.65<ut<0.75)   then ut07=pctlog;
   if (0.75<ut<0.85)   then ut08=pctlog;
   if (0.85<ut<0.95)   then ut09=pctlog;
   if (0.95<ut<1.05)   then ut10=pctlog;
   reps=&reps;
   size1=&size1;
   size2=&size2;
   ptox1=&ptox1;
   ptox2=&ptox2;
   pcensor1=&pcensor1;
   pcensor2=&pcensor2;

   if (last.hr2) then output;
   label ut00 ='Ut=0' ut01 ='Ut=0.1' ut02 ='Ut=0.2' ut03 ='Ut=0.3' ut04 ='Ut=0.4' ut05 ='Ut=0.5' ut06 ='Ut=0.6' ut07 ='Ut=0.7' ut08 ='Ut=0.8' ut09 ='Ut=0.9' ut10 ='Ut=1.0' hr2='Hazard Rate in Group 2';
   retain ut00  ut01  ut02  ut03  ut04  ut05  ut06  ut07  ut08  ut09  ut10;
   format ut00  ut01  ut02  ut03  ut04  ut05  ut06  ut07  ut08  ut09  ut10  5.1;

/****************************
/* prints the power summary */
/****************************/
proc print data=p2 label uniform;
   by hr2;
   id hr2;
   var ut00 ut01 ut02 ut03 ut04 ut05 ut06 ut07 ut08 ut09 ut10;
   title Power for Logrank Test: &reps Replications;
   title3 N1=&size1, &pcensor1.% Patients Censored, &ptox1.% Days With TOX/REL in Group 1;
   title4 N2=&size2, &pcensor2.% Patients Censored, &ptox2.% Days With TOX/REL in Group 2;
   run;