Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2014 Oct 10.
Published in final edited form as: Scand Stat Theory Appl. 2011 Sep;38(3):551–563. doi: 10.1111/j.1467-9469.2010.00722.x

Controlled direct and mediated effects: definition, identification and bounds

Tyler J VanderWeele 1
PMCID: PMC4193506  NIHMSID: NIHMS522342  PMID: 25309023

Abstract

Results are given which provide bounds for controlled direct effects when the no-unmeasured-confounding assumptions required for the identification of these effects do not hold. Previous results concerning bounds for controlled direct effects rely on monotonicity relationships between the treatment, mediator and the outcome themselves; the results presented in this paper instead assume that monotonicity relationships hold between the unmeasured confounding variable or variables and the treatment, mediator and outcome. Whereas prior results give bounds that contain the null hypothesis of no direct effect, the results presented here will in many instances yield bounds that do not contain the null hypothesis of no direct effect. For contexts in which a set of variables intercepts all paths between a treatment and an outcome, it is possible to provide a definition for a controlled mediated effect. We discuss the identification of these controlled mediated effects; the bounds for controlled direct effects are applicable also to controlled mediated effects. An example is given to illustrate how the results in the paper can be used to draw inferences about direct and mediated effects in the presence of unmeasured confounding variables.

Keywords: Bounds, causal inference, direct and indirect effects, mediation, unmeasured confounding

1. Introduction

A number of authors have considered different identification strategies for direct and indirect effects (Robins and Greenland, 1992; Pearl, 2001; Robins, 2003; Petersen et al., 2006; Didelez et al., 2006; Geneletti, 2007; Hafeman and VanderWeele, 2010; Imai, 2010). As pointed out by these authors, the identification conditions for direct and indirect effects are generally stronger than for total effects. In particular, in order to identify "controlled direct effects" (Pearl, 2001) data must generally be available not simply on the variables that confound the relationship between the treatment and the outcome but also on variables that confound the relationship between the mediator and the outcome. When so called "natural direct and indirect effects" (Pearl, 2001) are in view the identification conditions are even more stringent. In many studies the conditions required for the identification of direct and indirect effects will not be satisfied.

The aim of the present paper is to give several results concerning bounds which at least partially circumvent the more stringent identification conditions required for direct and indirect effects. Previous results concerning bounds for controlled direct effects (Kaufman et al., 2005, 2009; Cai et al., 2008) rely on monotonicity relationships between the treatment, mediator and outcome themselves; unfortunately, in many cases the existing results on bounds are such that the bounds obtained include the null hypothesis of no effect and thus are not of use in concluding whether a particular effect is in fact positive. The results presented in this paper instead assume that monotonicity relationships hold between the unmeasured confounding variable or variables and the treatment, mediator and outcome; in such cases it is often possible to obtain bounds that do not include the null hypothesis of no effect thereby further facilitating inference about direct and indirect effects in the presence of unmeasured confounding variables. Although considerable work exists for total effects for dealing with unmeasured confounding through bounds and sensitivity analysis, comparatively little work has been done on such inference for direct and indirect effects when these effects are not identified; this paper helps fill this gap in the literature.

The remainder of this paper is organized as follows. Section 2 reviews the counterfactual or potential outcomes framework and various definitions of direct and indirect effects that arise within this framework. Section 3 introduces the notion of a controlled mediated effect and discusses identification for this effect. Section 4 derives bounds for controlled direct and mediated effects in the presence of unmeasured confounding; cases in which there is an unmeasured confounder of either the treatment-outcome relationship or of the mediator-outcome relationship are considered. It is shown that in some cases, these results also apply to bounds for natural direct and indirect effects. The results concerning bounds are applied in Section 5 to an example examining the proportion of the effect of prenatal care on infant mortality that is mediated by medically-indicated preterm birth. Section 6 concludes with some additional discussion.

2. Counterfactual definitions of direct and indirect effects

We assume a counterfactual or potential outcomes framework (Neyman, 1923; Rubin, 1974, 1978). We will let Ω denote the sample space of individuals in the population and we will use ω for a particular sample point. Let A(ω) denote the treatment received by individual ω. Let Y(ω) denote some post-treatment outcome for individual ω. Let Z(ω) be a post-treatment variable that will denote the intermediate variable. Let Ya(ω) and Za(ω) denote respectively the counterfactual values (or potential outcomes) of Y and Z for individual ω if treatment A were set, possibly contrary to fact, to the value a. Let Yaz(ω) denote the counterfactual value for Y if A were set to a and Z were set to z; note that Z might be multivariate. These various counterfactuals can be conceived of as what would happen under interventions on one or both of the treatment and the mediator. If it is not at least possible to imagine hypothetical interventions to change the mediator Z then an alternative approach based on principal stratification may be utilized (Rubin, 2004; VanderWeele, 2008a; Gallop et al., 2009). Note also that we assume that the counterfactual values Za(ω), Ya(ω) and Yaz(ω) for individual ω do not depend on the treatments received by other individuals. Such assumptions are sometimes referred to as no-interference assumptions (Cox, 1958) or as the stable unit treatment value assumption (Rubin, 1990). We also require the "consistency" assumption i.e. that YA(ω)(ω) = Y(ω) so that the value of Y which would have been observed if A had been set to what it in fact was is equal to the value of Y which was in fact observed. Similarly, ZA(ω) (ω) = Z(ω) and YA(ω)Z(ω)(ω) = Y(ω). Finally, we make the "composition" assumption that Ya(ω) = YaZa(ω).

We will use the notation A ⫫ B|C to denote that A is independent of B given C. We say that treatment assignment A is ignorable (or weakly ignorable) given covariates X if Ya ⫫ A|X for all a. This condition is sometimes also referred to as the assumption of no unmeasured confounders. It is easily verified that if treatment assignment A is ignorable given covariates X then for all a, E(Ya)=∑xE(Y|a,x)P(x). The right hand side of the equation, unlike the left hand size, is given entirely in observable quantities. When X contains numerous covariates then the quantity E(Y|a, x) is often estimated by means of regression or propensity score analysis (e.g. Rosenbaum and Rubin, 1983).

Building on concepts proposed by Robins and Greenland (1992), Pearl (2001) introduced the terminology of "controlled direct effects" and "natural direct and indirect effects." The controlled direct effect of treatment A on outcome Y comparing A = a with A = a* and setting Z to z measures the effect of A on Y not mediated through Z i.e. the effect of A on Y after intervening to fix the mediator to some value z. The controlled direct effect for individual ω is denoted by CDE(a, a*; z)(ω) = Yaz(ω) − Ya*z(ω). The average controlled direct effect for the population is denoted by E{CDE(a, a*; z)} = E(Yaz − Ya*z). The controlled direct effect essentially corresponds to the direct A → Y arrow in Figure 1. The focus of this paper will be on controlled direct effects and on a counterpart to controlled direct effects to be introduced in the next section, controlled mediated effects. Although our focus will be on these controlled direct and mediated effects, the results on bounds will in some cases also be applicable to natural direct and indirect effects. Natural direct effects differ from controlled direct effects in that the intermediate Z is set to the level Za*, the level it would have naturally been under A = a*; natural direct effects thus take the form NDEa,a*(a*) = YaZa* − Ya*Za*. Similarly, natural indirect effects can be defined as NIEa,a*(a) = YaZa − YaZa* which compares the effect of the mediator at levels Za and Za* on the outcome when A is set to a. Natural direct and indirect effects have the property that a total effect Ya − Ya* decomposes into a natural direct and indirect effect Ya − Ya* = YaZa − Ya*Za* = (YaZa − YaZa*) + (YaZa* − Ya*Za*) = NIEa,a*(a) + NDEa,a*(a*); the decomposition holds even when there are non-linearities and interactions. In general controlled direct effects cannot be used for effect decomposition unless there is no interaction between the effects of the treatment and the mediator on the outcome; the difference between a total effect and a controlled direct effect cannot in general be interpretted as an indirect effect unless there is no interaction (Robins and Greenland, 1992; Kaufman et al., 2004). There is thus no generally applicable definition of a controlled indirect effect. In the next section we will give conditions under which a controlled mediated (or indirect) effect can be defined.

Figure 1.

Figure 1

Open in a new tab

Example illustrating direct effect of A on Y controlling for Z.

Controlled direct effects are often of greater interest in policy evaluation (Pearl, 2001; Robins, 2003); natural direct and indirect effects are often of greater interest in evaluating the action of various mechanisms (Robins, 2003; Joffe et al., 2007; Hafeman and Schwartz, 2009). Unfortunately, the identification assumptions required for natural direct and indirect effects are considerably stronger than for controlled direct effects (Pearl, 2001; Robins, 2003; Avin et al., 2005). As noted above, under certain conditions, the bounds that are derived below for controlled direct effects in the presence of unmeasured confounding will also be applicable to natural direct and indirect effects.

3. Controlled mediated effects - definitions and identification

In the previous section we reviewed the definition of a controlled direct effect. In this section we show that when the effect of a treatment on some outcome is completely mediated by some set of variables, it is also possible to introduce the notion of a controlled mediated effect. We thus begin our discussion with the formal definition of a completely mediated effect.

Definition 1 (Completely mediated effect). We say that the effect of A on Y is completely mediated by {Z1, …, Zn} if for all z1, …, zn we have that Yaz1 … zn does not vary with a.

If the effect of A on Y is completely mediated by {Z1, …, Zn}, then interventions on A will no longer have an effect on Y once interventions on {Z1, …, Zn} are also made; in such cases all of the effect of A on Y must be through one of {Z1, …, Zn}. Using this definition of a completely mediated effect, we can now define controlled mediated effects of A on Y in settings in which the effect of A on Y is completely mediated. In what follows we will assume that Z1 and Z2 constitute sets of variables.

Definition 2 (Controlled mediated effect). Suppose that the effect of A on Y is completely mediated by {Z1, Z2} where Z1 and Z2 are potentially multivariate then the controlled mediated effect of A on Y through Z1 controlling for Z2 is defined by CMEZ1(a, a*; z2) = Yaz2 − Ya*z2.

The controlled mediated effect of A on Y through Z1 controlling for Z2 essentially fixes the value of Z2 to some particular level, z2, and then considers the effect of A on Y with Z2 set to z2. Any effect of A on Y with Z2 set to z2 must be through Z1 since the effect of A on Y is completely mediated by {Z1, Z2}. Note that the definition of a controlled mediated effect does not require that the variables sets Z1 and Z2 not affect one another. However, some restriction on which of the intermediate variables affects the others may be important for identification.

From the definition of a controlled mediated effect, it can be seen that a controlled mediated effect is in fact a special case of a controlled direct effect. The controlled mediated effect of A on Y through Z1 controlling for Z2 as given in Definition 2 is CMEZ1(a, a*; z2) = Yaz2 − Ya*z2; this is the same quantity as intervening to set Z2 to z2 and comparing treatment level a and a* and is thus also a controlled direct effect of A on Y intervening to set Z2 to z2. Note, however, that the controlled mediated effect can be only defined when the effect of A on Y is completely mediated by some set of intermediate variables.

Pearl (2001) defined the natural indirect effect described above but noted that there was no general definition for a "controlled indirect effect"; Definition 2 provides such a definition but, importantly, only in the context when the effect of A on Y is completely mediated by some set of variables. When the controlled mediated effect can be defined, it can be used to assess mediation and at least the presence of an indirect effect; further remarks about this are given below.

We now turn to the identification of controlled direct and mediated effects. We will first review a prior identification result for controlled direct effects. Because a controlled mediated effect is simply a special case of a controlled direct effect, a result for the identification of controlled mediated effects will immediately follow. The following identification result follows immediately from the g-formula for causal effects (Robins, 1986, 1987; Pearl and Robins, 1995; Pearl, 2001).

Proposition 1. If for some observed covariates, X and W, we have

Yaz⫫A|X (1)
and Yaz⫫Z|A,X,W (2)

for all a, z then the average controlled direct effect is identified and given by: E(Yaz−Ya*z)=

∑x∑wE(Y|a,z,x,w)P(w|a,x)P(x)−∑x∑wE(Y|a*,z,x,w)P(w|a*,x)P(x) (3)

From Proposition 1 we see that the identification of controlled direct effects will in general require stronger assumptions than the identification of total effects. Whereas the identification of total effects requires only one ignorability condition, namely, Ya ⫫ A|X, the identification of controlled direct effects through Proposition 1 requires both Yaz ⫫ A|X and Yaz ⫫ Z|A, X, W. The identification of controlled direct effects by conditioning on confounding variables using assumptions (1) and (2) above requires that control be made not only for all confounders of the treatment-outcome relationship (assumption 1) but also of all confounders of the mediator-outcome relationship (assumption 2). When the confounders of the mediator-outcome relationship are not controlled for, this leads to biased estimates for the controlled direct effect (Judd and Kenny, 1981; Robins and Greenland, 1992; Pearl, 2001). Often control for all of these confounding variables will be difficult and so later in the paper we will develop bounds for controlled direct and mediated effects in the presence of unmeasured confounding variables.

Note that the choice of X and W in Proposition 1 will generally not be unique. If the set of variables X that suffices to control for confounding for the treatment-outcome relationship also suffices to control for confounding for the intermediate-outcome relationship (cf. Petersen et al., 2006; VanderWeele and Vansteelandt, 2009) then we could choose W = Ø and (3) reduces to

E(Yaz−Ya*z)=∑x{E(Y|x,a,z)−E(Y|x,a*,z)}P(x).

Also if (1) and (2) hold with W = Ø and if the relationship between Y and X, A and Z is linear and there is no interaction between the effects of A and Z on Y, then standard regression techniques for mediation can be used to estimate direct and indirect effects (Baron and Kenny, 1986; MacKinnon, 2008).

Because controlled mediated effects are a particular case of controlled direct effects it follows that Proposition 1 also gives identification conditions for controlled mediated effects. A restatement of Proposition 1 for controlled mediated effects is given below as Corollary 1.

Corollary 1. If the effect of A on Y is completely mediated by {Z1, Z2} and if for some observed covariates X and W,

Yaz2⫫A|X
and Yaz2⫫Z2|A,X,W

for all a, z2 then the controlled mediated effect of A on Y through Z1 controlled for Z2 is identified and given by: E{CMEZ1(a,a*;z2)}=E(Yaz2−Ya*z2)=

∑x∑wE(Y|a,z2,x,w)P(w|a,x)P(x)−∑x∑wE(Y|a*,z2,x,w)P(w|a*,x)P(x).

The proofs of all further results are given in the online supplement appendix. Corollary 1 states that if the effect of A on Y is unconfounded given X and if the effect of Z2 on Y is unconfounded given {A, X, W} then the controlled mediated effect of A on Y through Z1 controlling for Z2 is identified. This result follows immediately from previous identification results for controlled direct effects in the literature. In the online supplement we also note that when the effect of A on Y is completely mediated by some set Z, controlled direct and mediated effects can also be identified by a generalization of the front door path criterion (Pearl, 1995) for total effects; we give an illustration of such front door path identification using an example concern the effect of smoking on lung cancer as mediated through tar deposits on the left and the right lungs (Bennet et al., 2002).

Remark. Controlled direct effects cannot in general be used in a straightforward manner to assess mediation (Kaufman et al., 2004; VanderWeele, 2009a). This is because if there is interaction between the effects of treatment A and mediator Z on outcome Y, then controlled direct effects may differ from total effect even if A is not a cause of Z. If there is such interaction, then Yaz − Ya*z will differ for different values of z and thus for some z, one of the controlled direct effects Yaz − Ya*z will differ from Ya − Ya*. Obtaining a controlled direct effect that is different than the total effect is thus not evidence that mediation is present; see Robins and Greenland (1992) and Kaufman et al. (2004) for further critique of using controlled direct effects to assess mediation and indirect effects. Although controlled direct effects cannot in general be used as evidence in mediation, if it is the case that the effect of A on Y is completely mediated by Z = {Z1, Z2} then the presence of a non-zero controlled mediated effect of A on Y through Z1 controlling for Z2 does imply that Z1 is a mediator of the effect of A on Y. Equivalently, the presence of a non-zero controlled direct effect of A on Y controlling for Z2 implies that Z1 is a mediator. Moreover, note that if the conditions of Corollary 1 are satisfied with W = Ø, then whether Z1 is a mediator of the effect of A on Y could be assessed simply by examining whether A and Y are associated conditional on {X, Z2}.

4. Bounds for direct and mediated effects in the presence of unmeasured confounding variables

In many cases, there will likely be confounding variables of the mediator-outcome relationship. In these cases, controlled direct and mediated effects will not in general be identified. In this section we develop bounds for controlled direct and mediated effects when there are unmeasured confounding variables of either the treatment-outcome relationship or the mediator-outcome relationship. In certain instances, the bounds will also be applicable to natural direct and indirect effects. In our first result on bounds we will suppose that there is some unmeasured variable that confounds the treatment-outcome relationship but not the mediator-outcome relationship. In Theorem 1 below we will thus assume that, for the unmeasured variable U, we have the following independence relation for the specific value z of interest: P(z|a, x, u) = P(z|a, x). Under the conditions of Theorem 1 stated below, this would hold if U did not have an effect on Z except possibly through A and X.

Theorem 1. Suppose that the treatment A is binary and that for all a and z, (i) Yaz ⫫ A|X, U, (ii) Yaz ⫫ Z|A, X, U, (iii) E(Y|a, z, x, u) is non-decreasing in each component of u when the other components are fixed, for all x, (iv) E(A|x, u) is non-decreasing in each component of u when the other components are fixed, for all x, (v) Z ⫫ U|A, X and (vi) if U is multivariate then the components of U are conditionally independent given X, then ∑x E(Y|A = 1, z, x)P(x) ≥ E(Y1z) and ∑x E(Y|A = 0, z, x)P(x) ≤ E(Y0z).

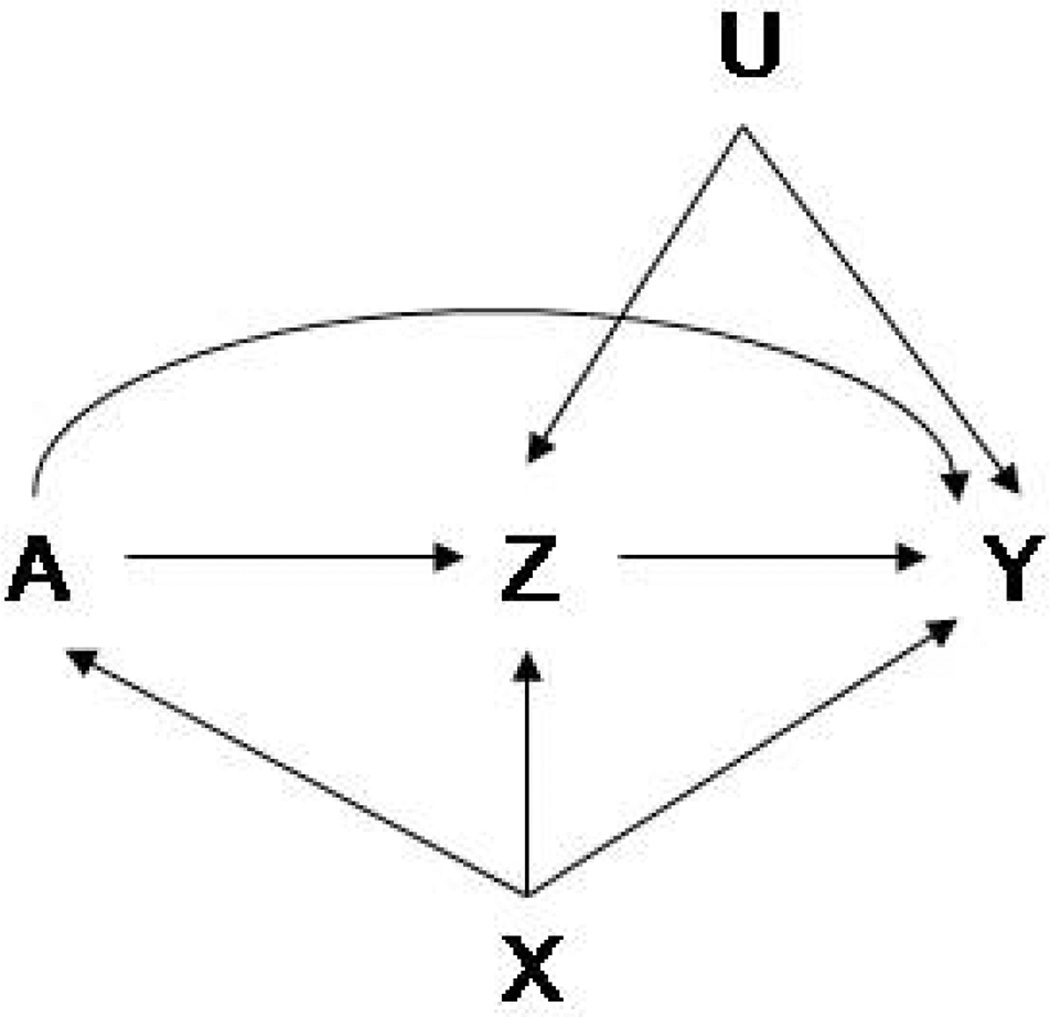
Theorem 1 allows for unmeasured confounding variables of the treatment-outcome relationship and would apply to causal directed acyclic graphs (Pearl, 1995, 2009) with structures like those of Figure 2. Note that assumption (vi) in Theorem 1 holds trivially if U is univariate.

Figure 2.

Figure 2

Open in a new tab

Causal directed acyclic graph to which Theorem 1 would apply.

If the conditions of Theorem 1 are satisfied then an empirical bound for the controlled direct effect can be obtained by

E(Y1z)−E(Y0z)≤∑xE(Y|A=1,z,x)P(x)−∑xE(Y|A=0,z,x)P(x).

The empirical expression on the right hand side of this inequality can be estimated from the data and is the quantity one would ordinarily estimate to obtain controlled direct effects if there were no unmeasured confounding variable U. If one of E(Y|a, z, x, u) or E(A|x, u) is non-increasing in each component of u rather than, non-decreasing in each component of u then the inequality signs will be reversed. Theorem 1 thus effectively allows a researcher to conclude whether the estimates of the controlled direct effect are biased upwards or downwards for the true effect due to unmeasured confounding. We can thus see that Theorem 1 can potentially allow one to obtain bounds that do not include the null hypothesis of no direct effect. This is in contrast with prior results on bounds which assumed that monotonicity relationships held between the treatment, mediator and outcome (Kaufman et al., 2005, 2009; Cai et al., 2008) and which yielded bounds that included the null hypothesis of no direct effect. Similar comments to those above pertain also to Theorem 2 and its corollary, stated below, concerning an unmeasured confounder of the mediator-outcome relationship.

Theorem 1 requires that the treatment A be binary; the result will also apply if A is not binary but the treatment effect comparing the maximum and minimum values of A is being considered. VanderWeele (2008b) discusses why results such as Theorem 1 may not hold if A is not binary and intermediate values of A are being compared.

A somewhat more general version of Theorem 1 is stated in the Appendix which allows for covariates W, which may be effects of treatment A, and which confound the mediator-outcome relationship but not the treatment-outcome relationship so that, in Theorem 1, the no-unmeasured confounding assumption (i) remains Yaz ⫫ A|X, U but assumption (ii) becomes Yaz ⫫ Z|A, X, U, W. See the Appendix for further details.

Note that Theorem 1 is applicable also to controlled mediated effects: if the effect of A on Y is completely mediated by {Z1, Z2} then bounds for the controlled mediated effect CMEZ1(a, a*; z2) can be obtained by applying Theorem 1 and choosing Z in Theorem 1 to be Z2.

In Theorem 2 we will suppose there is some unmeasured variable U that confounds the mediator-outcome relationship.

Theorem 2. Suppose that the mediator Z is binary and that for all a and z, (i) Yaz ⫫ A|X, (ii) Yaz ⫫ Z|A, X, U, (iii) E(Y|a, z, x, u) is non-decreasing in each component of u for all x, (iv) E(Z|a, x, u) is non-decreasing in each component of u for all x, and (v) if U is multivariate then the components of U are conditionally independent given {X, A}, then ∑x E(Y|a, Z = 1, x)P(x) ≥ E(Ya1) and ∑x E(Y|a, Z = 0, x)P(x) ≤ E(Ya0).

Theorem 2 allows for an unmeasured confounding variables of the mediator-outcome relationship and would apply to causal directed acyclic graphs with structures like those of Figure 3.

Figure 3.

Figure 3

Open in a new tab

Causal directed acyclic graph to which Theorem 2 would apply.

Similar to Theorem 1, if one of E(Y|a, z, x, u) or E(Z|a, x, u) is non-increasing in each component of u rather than non-decreasing in each component of u then the inequality signs in Theorem 2 will be reversed. Theorem 2 can also be applied if Z is not binary but the maximum and minimum values of Z are being considered. A somewhat more general version of Theorem 2 is stated in the Appendix which allows for covariates W, which may be effects of treatment A, and which confound the mediator-outcome relationship but not the treatment-outcome relationship so that, in Theorem 2, the no-unmeasured confounding assumption (i) remains Yaz ⫫ A|X but assumption (ii) becomes Yaz ⫫ Z|A, X, W, U. See the Appendix for further details.

Theorem 2 can be of use in providing bounds for controlled direct effects. Suppose, for example, that for the entire population Za=0 = 0 but Za=1 can take on the values 0 or 1 i.e. the mediator will not be present if the treatment is not present. In this case, in the causal directed acyclic graph in Figure 3, E(Ya=0, z=0) = E(Ya=0) is identified by E(Ya=0) = ∑x E(Y|A = 0, x)P(x) and a bound can be given for E(Ya=1, z=0), namely E(Ya=1, z=0) ≥ ∑x E(Y |A = 1, Z = 0, x)P(x). Thus E{CDE(1, 0; 0)} = E(Y10 − Y00) ≥ ∑x E(Y |A = 1, Z = 0, x)P(x) − ∑x E(Y|A = 0, x)P(x).

Note also that if for some value a*, Za*(ω) = z for all ω (e.g. Z0(ω) = 0 as above) then we can also use Theorem 2 to give bounds for natural direct and indirect effects. If Za*(ω) = z for all ω then YaZa* = Yaz and this establishes the following proposition which relates natural direct and indirect effects to controlled direct effects.

Proposition 2. If for some value a*, Za*(ω) = z for all ω, then for any a, YaZa* − Ya*Za* = Yaz − Ya*z and YaZa − YaZa* = Ya − Yaz.

Note that Proposition 2 implies that if Za*(ω) = z for all ω, then the natural direct effect E(YaZa* − Ya*Za*) is equal to the controlled direct effect E(Yaz − Ya*z) and the natural indirect effect E(YaZa − YaZa* ) is equal to the difference E(Ya) − E(Yaz). Thus if Za*(ω) = z for all ω, then whenever E(Ya) and E(Yaz) are identified, the natural direct and indirect effects, E(YaZa* − Ya*Za*) and E(YaZa − YaZa* ), will also be identified; consequently from the results of Robins (1986, 1987; cf. Pearl, 2001) we have the following identification result.

Proposition 3. If Za*(ω) = z for all ω and if for all a and z, Ya ⫫ A|X, Yaz ⫫ A|X and Yaz ⫫ Z|A, X, W then the natural direct effect is identified and given by: E(YaZa*−Ya*Za*)=

∑x∑wE(Y|a,z,x,w)P(w|a,x)P(x)−∑xE(Y|a*,x)P(x)

and the natural indirect effect is identified and given by: E(YaZa−YaZa*)=

∑xE(Y|a,x)P(x)−∑x∑wE(Y|a,z,x,w)P(w|a,x)P(x).

If Za*(ω) = z for all ω, Proposition 3 allows for the identification of natural direct and indirect effects provided essentially that the effect of A on Y is unconfounded given X and that the effect of Z on Y is unconfounded given {A, X, W}. Note that under these conditions, Proposition 3 allows for the identification of natural direct and indirect effects even if there is a variable W that is a consequence of treatment and that confounds the mediator-outcome relationship. Furthermore, if there is unmeasured confounder of the mediator-outcome relationship, we can use Proposition 2 and Theorem 2 to give bounds on natural direct and indirect effects as stated in the following Corollary.

Corollary 2. Suppose Za*(ω) = z for all ω, that the mediator Z is binary, and that (i) for all a and z Ya ⫫ A|X and Yaz ⫫ A|X, (ii) Yaz ⫫ Z|A, X, U for some univariate U, (iii) E(Y|a, z, x, u) is non-decreasing in u for all a and x and (iv) E(Z|a, x, u) is non-decreasing in u for all x then

E(YaZa*−Ya*Za*)≤∑xE(Y|a,z,x)P(x)−∑xE(Y|a*,x)P(x)E(YaZa−YaZa*)≥∑xE(Y|a,x)P(x)−∑xE(Y|a,z,x)P(x)

if z = 1 and

E(YaZa*−Ya*Za*)≥∑xE(Y|a,z,x)P(x)−∑xE(Y|a*,x)P(x)E(YaZa−YaZa*)≤∑xE(Y|a,x)P(x)−∑xE(Y|a,z,x)P(x).

if z = 0.

5. Application

We illustrate these results on bounds with an example concerning the proportion of the effect of prenatal care on infant mortality that is mediated by medically-indicated preterm birth. Over the last twenty years, utilization of prenatal care has increased in the United States; preterm birth rates, however, have also increased; c-section rates have increased; infant mortality has decreased. One possible explanation for these trends is that prenatal care allows for the early detection of pregnancy problems (e.g. preeclampsia) for which the appropriate response is preterm c-section or medically-induced labor. This would result in a greater number of preterm births but ultimately healthier infants. A potential question of interest is then the extent to which the effect of prenatal care on infant mortality is mediated by medically induced preterm birth. Let A denote the level of prenatal care (classified as no care, inadequate care, intermediate care, adequate care). Let Z denote medically-indicated preterm birth (i.e. whether, due to prenatal care, the physician determines that a pregnancy complication merits a preterm c-section or pre-term labor induction). Let Y denote an indicator variable of mortality at one year. For the treatment A, let A = 0 denote no care and let A = a denote adequate prenatal care. According to National Center for Health Statistics Linked Birth Certificate Infant Mortality files, over 39,000 women giving birth received no prenatal care in 2003. The total effect of prenatal care on infant mortality could be decomposed into the following indirect and direct effects, E(Ya − Y0) = E(YaZa − YaZ0) + E(YaZ0 − Y0Z0). In this decomposition, E(YaZ0 − Y0Z0) is the direct effect of prenatal care (comparing adequate care and no care) on infant mortality, had medically-indicated preterm birth been at the level it would have been had there been no prenatal care and E(YaZa − YaZ0) is the indirect effect of prenatal care on infant mortality mediated through medically-induced preterm birth. If the indirect effect E(YaZa − YaZ0) is non-zero then this would imply that some of the effect of prenatal care on infant mortality is mediated through medically-indicated preterm birth.

In many administrative datasets such as the National Center for Health Statistics Linked Birth Certificate Infant Mortality files, data is available on a number of variables X that may confound the relationship between treatment A and the outcome Y or confound the relationship between the intermediate Z and the outcome Y. Such variables include maternal age, race, place of birth, place of residence, education, marital status, plurality, gravidity, prior preterm birth and prior birth greater than 4000 grams, maternal smoking and maternal alcohol intake. However, such administrative data will often not include information about the presence of pregnancy complications, U, such as preeclampsia which may lead to a medically indicated preterm birth and is also related to infant mortality. Preeclampsia would thus be an unmeasured confounder of the mediator-outcome relationship as in Figure 3. Prenatal care would be unlikely to be able to prevent a condition such as preeclampsia (so preeclampsia would not be on the pathway from prenatal care and would not be a mediator) but prenatal care may allow for the detection of preeclampsia for which the appropriate response would be medically-indicated preterm birth. Such a pregnancy complication U will generally increase the likelihood of both medically-indicated preterm birth and of infant mortality. Because U is an unmeasured confounder of the mediator-outcome relationship, unbiased estimates of direct and indirect effects cannot therefore be obtained when data is not available on U.

Now if medically-indicated preterm birth is defined as preterm c-section or induced labor resulting from the detection of pregnancy complications through prenatal care then for those receiving no care we have that Z0 = 0. The natural indirect effect of interest, E(YaZa − YaZ0), is thus equal to E(Ya − Ya0). Suppose that the set of covariates X is sufficiently rich so that the effect of A on Y is unconfounded given X (i.e. Ya ⫫ A|X and Yaz ⫫ A|X) and that the effect of Z on Y is unconfounded given {A, X, U} (i.e. Yaz ⫫ Z|A, X, U). Because U increases the likelihood of both medically-indicated preterm birth and of infant mortality, we have that E(Y|a, z, x, u) and E(Z|a, x, u) are both non-decreasing in u. Thus, from the Corollary 2, we have that a lower bound for the natural indirect effect of interest, E(YaZa − YaZ0), is given by

E(YaZa−YaZ0)=E(Ya−Ya0)≤∑xE(Y|a,x)P(x)−∑xE(Y|a,Z=0,x)P(x).

Simple regression analysis using data from 2003 gives an estimate of ∑x E(Y|a, x)P(x) − ∑x E(Y|a, Z = 0, x)P(x) of −0.03% and under the assumptions of the Corollary above we would have E(YaZa − YaZ0) ≤ −0.03% which suggests that true effect of prenatal care on reducing infant mortality mediated by medically induced preterm birth is larger in magnitude (i.e. more negative) than −0.03%. Future research will consider more extensive modeling approaches in addressing this substantive research question.

6. Discussion

In many settings in which direct and indirect effects are of interest, there will be unmeasured confounding variables of either the treatment-outcome or mediator-outcome relationship. In this paper, we have shown that when monotonicity relationships hold between the unmeasured confounder and the treatment and outcome or the mediator and outcome, then it is possible to derive bounds for controlled direct effects. We also have given a new definition of a controlled mediated effect and the bounds we have derived will apply also to the controlled mediated effect. In some cases, the bounds also apply to natural direct and indirect effects. In many settings these bounds will allow a researcher to conclude that a particular confounded estimate is in fact conservative for the true effect. A complementary approach to direct and indirect effects using sensitivity analysis rather than bounds to assess unmeasured confounding is presented elsewhere (VanderWeele, 2010). There is a considerable causal inference literature on the estimation of controlled direct effects (Robins, 1999; Petersen et al., 2006; Ten Have et al., 2007; van der Laan and Petersen, 2008; Goetgeluk et al., 2008; Sobel, 2008; VanderWeele, 2009b; Vansteelandt, 2009; VanderWeele and Vansteelandt, 2009). The bounds developed here will be applicable to these various estimation techniques and will hopefully facilitate conclusions drawn about direct effects and mediation.

Acknowledgements

The author thanks the editor and two referees for helpful comments. The research was funded by National Institute of Health grant HD060696.

Appendix

Here we give more general statements of Theorems 1 and 2 that allow for variables W that are effects of treatment A and also confound the relationship between the mediator Z and the outcome Y. Proofs of these results make use of a lemma from Esary et al. (1967) and are given in the online supplement.

Generalization of Theorem 1. Suppose that A is binary and that for all a and z, (i) Yaz ⫫ A|X, U (ii) Yaz ⫫ Z|A, X, U, W, (iii) E(Y|a, z, x, u, w) is non-decreasing in each component of u for all x and w, (iv) E(A|x, u, w) is non-decreasing in each component of u for all x and w, (v) P(z|a, x, u, w) = P(z|a, x, w) for all u, x and w, (vi) U ⫫ W|X and U ⫫ W|A, X, and (vii) if U is multivariate then the components of U are conditionally independent given {X, W}, then ∑x E(Y|A = 1, z, x, w)P(w|A = 1, x)P(x) ≥ E(Y1z) and ∑x E(Y|A = 0, z, x, w)P(w|A = 0, x)P(x) ≤ E(Y0z).

Generalization of Theorem 2. Suppose that the intermediate Z is binary and that for all a and z, (i) Yaz ⫫ A|X, (ii) Yaz ⫫ Z|A, X, W, U, (iii) E(Y|a, z, x, w, u) is non-decreasing in each component of u for all x and w, (iv) E(Z|a, x, w, u) is non-decreasing in each component of u for all x and w and (v) if U is multivariate then the components of U are conditionally independent given {X, A, W}, then ∑x, w E(Y|a, Z = 1, x, w)P(w|a, x)P(x) ≥ E(Ya1) and ∑x, w E(Y|a, Z = 0, x)P(w|a, x)P(x) ≤ E(Ya0).

References

  1. Avin C, Shpitser I, Pearl J. Identifiability of path-specific effects; Proc, Int. Joint Conferences on Artificial Intelligence; 2005. pp. 357–363. [Google Scholar]
  2. Baron RM, Kenny DA. The moderator-mediator variable distinction in social psychological research: conceptual, strategic, and statistical considerations. Journal of Personality and Social Psychology. 1986;51:1173–1182. doi: 10.1037//0022-3514.51.6.1173. [DOI] [PubMed] [Google Scholar]
  3. Bennet WD, et al. Targeting delivery of aerosols to different lung regions. Journal of Aerosol Medicine. 2002;15:179–188. doi: 10.1089/089426802320282301. [DOI] [PubMed] [Google Scholar]
  4. Cai Z, Kuroki M, Pearl J, Tian J. Bounds on direct effects in the presence of confounded intermediate variables. Biometrics. 2008;64:695–701. doi: 10.1111/j.1541-0420.2007.00949.x. [DOI] [PubMed] [Google Scholar]
  5. Cox DR. The Planning of Experiments. New York: Wiley; 1958. [Google Scholar]
  6. Didelez V, Dawid AP, Geneletti S. Direct and indirect effects of sequential treatments. Proceedings of the Twenty-Second Conference on Uncertainty in Artificial Intelligence.2006. [Google Scholar]
  7. Esary JD, Proschan F, Walkup DW. Association of random variables, with applications. Annals of Mathematical Statistics. 1967;38:1466–1474. [Google Scholar]
  8. Gallop R, Small DS, Lin JY, Elliott MR, Joffe M, Ten Have TR. Mediation analysis with principal stratification. Statistics in Medicine. 2009;28:1108–1130. doi: 10.1002/sim.3533. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Geneletti S. Identifying direct and indirect effects in a non-counterfactual framework. Journal of the Royal Statistical Society, Series B. 2007;69:199–216. [Google Scholar]
  10. Goetgeluk S, Vansteelandt S, Goetghebeur E. Estimation of controlled direct effects. Journal of the Royal Statistical Society, Series B. 2008;70:1049–1066. [Google Scholar]
  11. Hafeman DM, Schwartz S. Opening the black box: A motivation for the assessment of mediation. International Journal of Epidemiology. 2009;38:838–845. doi: 10.1093/ije/dyn372. [DOI] [PubMed] [Google Scholar]
  12. Hafeman DM, VanderWeele TJ. Alternative assumptions for the identification of direct and indirect effects. Epidemiology. doi: 10.1097/EDE.0b013e3181c311b2. in press. [DOI] [PubMed] [Google Scholar]
  13. Imai K, Keele L, Yamamoto T. Identification, inference, and sensitivity analysis for causal mediation effects. Statistical Science. 2010 in press. [Google Scholar]
  14. Joffe M, Small D, Hsu C-Y. Defining and estimating intervention effects for groups that will develop an auxiliary outcome. Statistical Science. 2007;22:74–97. [Google Scholar]
  15. Judd CM, Kenny DA. Estimating mediation in treatment evaluations. Process Analysis. 1981;5:602–619. [Google Scholar]
  16. Kaufman JS, MacLehose RF, Kaufman S. A further critique of the analytic strategy of adjusting for covariates to identify biologic mediation. Epidemiologic Perspectives and Innovations. 2004;1:4. doi: 10.1186/1742-5573-1-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Kaufman S, Kaufman JS, MacLehose RF, Greenland S, Poole C. Improved estimation of controlled direct effects in the presence of unmeasured confounding of intermediate variables. Statistics in Medicine. 2005;24:1683–1702. doi: 10.1002/sim.2057. [DOI] [PubMed] [Google Scholar]
  18. Kaufman S, Kaufman JS, MacLehose RF. Analytic bounds on causal risk differences in directed acyclic graphs involving three observed binary variables. Journal of Statistical Planning and Inference. 2009;139:3473–3487. doi: 10.1016/j.jspi.2009.03.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Kuroki M, Miyakawa M. Identifiability criteria for causal effects of joint interventions. Journal of the Japan Statistical Society. 1999;29:105–117. [Google Scholar]
  20. MacKinnon DP. An Introduction to Statistical Mediation Analysis. New York: Lawrence Erlbaum Associates; 2008. [Google Scholar]
  21. Pearl J. Casual diagrams for empirical research (with discussion) Biometrika. 1995;82:669–710. [Google Scholar]
  22. Pearl J. Causality: Models, Reasoning, and Inference. 2nd Edition. Cambridge: Cambridge University Press; 2009. [Google Scholar]
  23. Pearl J. Direct and indirect effects. Proceedings of the Seventeenth Conference on Uncertainty and Artificial Intelligence; San Francisco: Morgan Kaufmann; 2001. pp. 411–420. [Google Scholar]
  24. Pearl J, Robins JM. Probabilistic evaluation of sequential plans from causal models with hidden variables. Proceedings of the Eleventh Conference on Uncertainty in Artificial Intelligence; 1995. pp. 444–453. [Google Scholar]
  25. Petersen ML, Sinisi SE, van der Laan MJ. Estimation of direct causal effects. Epidemiology. 2006;17:276–284. doi: 10.1097/01.ede.0000208475.99429.2d. [DOI] [PubMed] [Google Scholar]
  26. Robins JM. A new approach to causal inference in mortality studies with sustained exposure period - application to control of the healthy worker survivor effect. Mathematical Modelling. 1986;7:1393–1512. [Google Scholar]
  27. Robins JM. Addendum to a new approach to causal inference in mortality studies with sustained exposure period - application to control of the healthy worker survivor effect. Computers and Mathematics with Applications. 1987;14:923–945. [Google Scholar]
  28. Robins JM. Testing and estimation of direct effects by reparameterizing directed acyclic graphs with structural nested models. In: Glymour C, Cooper GF, editors. Computation, Causation, and Discovery. Menlo Park, CA, Cambridge, MA: AAAI Press/The MIT Press; 1999. pp. 349–405. [Google Scholar]
  29. Robins JM. Semantics of causal DAG models and the identification of direct and indirect effects. In: Green P, Hjort NL, Richardson S, editors. Highly Structured Stochastic Systems. New York: Oxford University Press; 2003. pp. 70–81. [Google Scholar]
  30. Robins JM, Greenland S. Identifiability and exchangeability for direct and indirect effects. Epidemiology. 1992;3:143–155. doi: 10.1097/00001648-199203000-00013. [DOI] [PubMed] [Google Scholar]
  31. Rubin D. Estimating causal effects of treatments in randomized and non-randomized studies. Journal of Educational Psychology. 1974;66:688–701. [Google Scholar]
  32. Rubin DB. Bayesian inference for causal effects: The role of randomization. Annals of Statistics. 1978;6:34–58. [Google Scholar]
  33. Rubin DB. Formal modes of statistical inference for causal effects. Journal of Statistical Planning and Inference. 1990;25:279–292. [Google Scholar]
  34. Rubin DB. Direct and indirect effects via potential outcomes. Scandinavian Journal of Statistics. 2004;31:161–170. [Google Scholar]
  35. Sobel ME. Identification of causal parameters in randomized studies with mediating variables. Journal of Educational and Behavioral Statistics. 2008;33:230–251. [Google Scholar]
  36. Ten Have TR, Joffe MM, Lynch KG, Brown GK, Maisto SA, Beck AT. Causal mediation analyses with rank preserving models. Biometrics. 2007;63:926–934. doi: 10.1111/j.1541-0420.2007.00766.x. [DOI] [PubMed] [Google Scholar]
  37. van der Laan MJ, Petersen ML. Direct effect models. International Journal of Biostatistics. 2008;4 doi: 10.2202/1557-4679.1064. Article 23. [DOI] [PubMed] [Google Scholar]
  38. VanderWeele TJ. Simple relations between principal stratification and direct and indirect effects. Statistics and Probability Letters. 2008a;78:2957–2962. [Google Scholar]
  39. VanderWeele TJ. The sign of the bias of unmeasured confounding. Biometrics. 2008b;64:702–706. doi: 10.1111/j.1541-0420.2007.00957.x. [DOI] [PubMed] [Google Scholar]
  40. VanderWeele TJ. Mediation and mechanism. European Journal of Epidemiology. 2009a;24:217–224. doi: 10.1007/s10654-009-9331-1. [DOI] [PubMed] [Google Scholar]
  41. VanderWeele TJ. Marginal structural models for the estimation of direct and indirect effects. Epidemiology. 2009b;20:18–26. doi: 10.1097/EDE.0b013e31818f69ce. [DOI] [PubMed] [Google Scholar]
  42. VanderWeele TJ. Bias formulas for sensitivity analysis for direct and indirect effects. Epidemiology. 2010;21:540–551. doi: 10.1097/EDE.0b013e3181df191c. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. VanderWeele TJ, Vansteelandt S. Conceptual issues concerning mediation, interventions and composition. Statistics and Its Interface - Special Issue on Mental Health and Social Behavioral Science. 2009;2:457–468. [Google Scholar]
  44. Vansteelandt S. Estimating direct effects in cohort and case-control studies. Epidemiology. 2009;20:851–860. doi: 10.1097/EDE.0b013e3181b6f4c9. [DOI] [PubMed] [Google Scholar]

RESOURCES